DOI:
https://doi.org/10.14483/22484728.3738Publicado:
2013-01-01Número:
Vol. 7 Núm. 1 (2013)Sección:
Visión de CasoDiseño e implementación de controladores análogos para un seguidor solar
Design and implementation of analog controllers for a solar tracker
Palabras clave:
Sistemas de control, seguidor solar, optimización, algoritmos genéticos, enjambre de partículas. (es).Palabras clave:
Control systems, solar tracker, optimization, genetic algorithms, particle swarm (en).Descargas
Referencias
F. Sierra, E. Caro, F. Mejía, ‘‘Tecnologías para el aprovechamiento de la energía solar’’, Universidad Nacional de Colombia’’, 2008.
S. Lakeou, E. Ososanya, O. Latigo, W. Mahmoud, G. Karanga, W. Oshumare, ‘‘Design of a low-cost digital controller for a solar tracking photo-voltaic (PV) module and wind turbine combination system’’, 21st European Photovoltaic Solar Energy Conference, 2006.
B. Lane, ‘‘Solar tracker’’, EEC 517, 2008.
B. Plesz, P. Sági, V. Timár-Horváth, ‘‘Enhancement of solar panels’ power generation by the usage of solar tracking’’, Proceedings of ECOpole Vol. 3, No. 1, 2009.
K. Ogata, ‘‘Ingeniería de Control Moderna’’, Pearson Prentice Hall, Cuarta edición, 2003.
M.A. Panait, T. Tudorache, ‘‘A simple neural network solar tracker for optimizing conversion efficiency in off-grid solar generators’’, International Conference on Renewable Energies and Power Quality, March, 2008.
Y.J. Huang, B.C. Wu, C.Y. Chen, C.H. Chang, T.C. Kuo, ‘‘Solar tracking fuzzy control system design using FPGA’’, IEEE, 2009.
K. Passino, ‘‘Biomimicry of bacterian foragin for distributed optimization and control’’, IEEE Control Systems Magazine, June 2002.
M. Birattari, P. Pellegrini, M. Dorigo, ‘‘On the invariance of ant colony optimization’’, IEEE Transactions on Evolutionary Computation, Vol. 11, No. 6, December 2007.
M. Dorigo, M. Birattari, T. Stützle, ‘‘Ant colony optimization. Artificial ants as a computational intelligence technique’’, IEEE Computational Intelligence Magazine, November 2006.
A.C. Zecchin, A.R. Simpson, H.R. Maier, J.B. Nixon, ‘‘Parametric study for an ant algorithm applied. water distribution system optimization’’, IEEE Transactions on Evolutionary Computation, Vol. 9, No. 2, April 2005.
S. Thakoor, J.M. Morookian, J. Chahl, B. Hine, S. Zornetzer, ‘‘BEES: Exploring Mars with bioinspired technologies’’, IEEE Computer Society 2004.
T. Weise, ‘‘Global optimization algorithms - theory and application’’, Self-Published Thomas Weise, 2009.
R. Eberhart, J. Kennedy, ‘‘Particle swarm optimization’’, IEEE Proceedings Neural Networks, 1995.
O. Arrieta, V. Alfaro, ‘‘Sintonización de controladores PI y PID utilizando los criterios Integrales IAE e ITAE’’, Ingeniería 13 (1,2): 31-39, 2003.
C.T. Chen, ‘‘Analog and digital control system design’’, Saunders College Publishing, 1993.
M. Gómez, C. Danglot, L. Vega, ‘‘Sinopsis de pruebas estadísticas no paramétricas. Cuándo usarlas’’, Revista Mexicana de Pediatría, Volumen 70 Número 2 Marzo-Abril 2003.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
VISIÓN DE CASO
Visión Electrónica, 2013-06-03 Volumen:7, Año:1 pág: 118–132
DISEÑO E IMPLEMENTACIÓN DE CONTROLADORES ANÁLOGOS PARA UN SEGUIDOR SOLAR
DESIGN AND IMPLEMENTATION OF ANALOG CONTROLLERS FOR A SOLAR TRACKER
Fecha de envío: julio de 2012
Fecha de recepción: agosto de 2012
Fecha de aceptación: marzo de 2013
Helbert E. Espitia
Ingeniero Electrónico y Mecatrónico, especialista en Telecomunicaciones Móviles, magíster en Ingeniería Industrial, magíster en Ingeniería Mecánica. Docente de la Univer sidad Distrital Francisco José de Caldas (Colombia). heespi tiac@udistrital.edu.co
Fabio E. Sierra
Ingeniero Mecánico, Esp. en Informá tica, Esp. en Ne gocios Internacionales, magíster en Automatización Industrial –Procesos Térmicos, PhD. En Ingeniería– Ener gías Renovables –Bio masa– Energía Solar. Docente Universidad Nacional de Colombia. fesierrav@unal.edu.co
RESUMEN
En la actualidad, el aprovechamiento racional de la energía es un aspecto fundamental para las comunidades humanas, motivo por el cual el desarrollo de equipos que permitan lograr este objetivo resulta de gran importancia. En el presente artículo, se muestra el diseño e implementación de diferentes controladores para un sistema de seguimiento solar, el cual es destinado para realizar mediciones de la energía solar captada. En este trabajo se describe la implementación de un controlador on-off, un controlador proporcional y un compensador del tipo polo cero y ganancia, el cual se optimiza empleado algoritmos genéticos y enjambres de partículas.
Palabras claveSistemas de control, seguidor solar, optimización, algoritmos genéticos, enjambre de partículas.
Abstract
At present, a reasonable use of energy represents a fundamental aspect. Therefore it is important to develop devices and equipment that facilitates the accomplishment of this goal. This paper shows the design and implementation of different drivers for a solar tracking system. This solar tracker is designed to take measurements of solar energy harvesting. In this paper we describe and explain various devices, namely an onoff controller, a proportional controller and a compensator, which has a pole-zero and gain that can be optimized using genetic algorithms and particle swarms.
Key WordsControl systems, solar tracker, optimization, genetic algorithms, particle swarm.
Introducción
Los requerimientos de la vida moderna están originando que la humanidad sea más dependiente de los recursos energéticos empleados en iluminación, refrigeración, calefacción y transporte. Lo anterior ha traído un alto consumo de combustibles fósiles ocasionando una aceleración del calentamiento global del planeta, una elevación del nivel de los océanos y un agotamiento de las reservas de combustibles fósiles [1].
Los problemas de contaminación, riesgo y deterioro del medio ambiente son el motivo por el cual es importante buscar fuentes alternativas de energía a la nuclear y la derivada de combustibles fósiles.
Los sistemas de energía solar aprovechan la radiación solar incidente sobre la tierra para generar energía eléctrica o calefacción. El aprovechamiento de la energía solar presenta ciertas dificultades sobre las cuales se está investigando para lograr de forma adecuada su aprovechamiento [1].
En Colombia existen muy pocos ejemplos de aplicaciones de energía solar, estos desarrollos se dieron durante la crisis energética de los años ochenta. Esta crisis energética resulta ser un llamado de alerta para la investigación en fuentes alternas de energía que puedan ser aprovechadas en el país. Particularmente Colombia posee buena localización geográfica para la explotación de energía solar [1].
En los sistemas de aprovechamiento de energía solar es de gran importancia tener la capacidad de realizar un seguimiento adecuado del sol, con la finalidad de poder adquirir la máxima cantidad de radicación en todo momento del día [2]-[4].
En los sistemas de aprovechamiento de energía solar es de gran importancia tener la capacidad de realizar un seguimiento adecuado del sol, con la finalidad de poder adquirir la máxima cantidad de radicación en todo momento del día [2]-[4].
En este artículo se muestra el diseño e implementación de diferentes controladores análogos para un seguidor solar. Los controladores análogos implementados son del tipo on-off proporcional y un compensador, el cual es optimizado mediante algoritmos bioinspirados.
1. Seguidor solar
La configuración física del seguidor solar puede apreciarse en la figura 1.
Figura 1. Seguidor solar

Fuente: elaboración propia.
Un modelo lineal para este sistema resulta al considerar un motor D.C. acoplado con una inercia Je en la presencia de fricción Be.
Para realizar el modelo del sistema se considera inicialmente la parte eléctrica y posteriormente la parte mecánica.
1.1 Parte eléctrica
El motor es una parte fundamental del modelo dinámico puesto que este proporciona el torque necesario para que el reflector parabólico gire. La figura 2 muestra el aspecto físico del motor como también el diagrama eléctrico.
Figura 2. Esquema físico y eléctrico del motor

Fuente: elaboración propia.
Para este modelo inicialmente se tiene que el torque del motor es proporcional a la corriente de armadura, tal como se presenta en la siguiente ecuación:
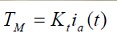 (1)
(1)
La fuerza contra-electromotriz es proporcional a la velocidad angular del motor según la ecuación (2).
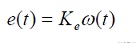 (2)
(2)
Por otro lado, al realizar el respectivo balance de energía del esquema eléctrico se tiene:
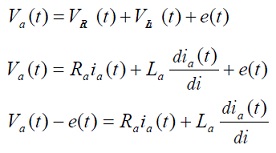 (3)
(3)
1.2 Parte mecánica
El modelo de esta parte se obtiene si se realiza la sumatoria de torques presentes en el rotor del motor. La figura 3 muestra el esquema propuesto para la parte mecánica del seguidor solar.
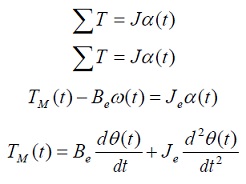 (4)
(4)
Donde:
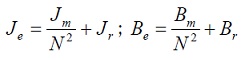 (5)
(5)
Figura 3. Torques presentes en el motor
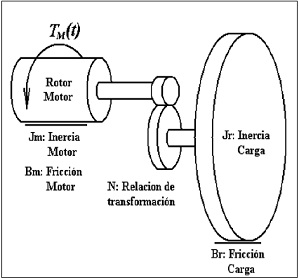
Fuente: elaboración propia.
Aplicando transformada de Laplace para las ecuaciones (1)-(4) se tiene la función de transferencia:
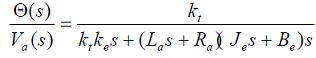 (6)
(6)
1.3 Modelo simplificado
Para el sistema en consideración, la parte mecánica presenta tiempos de respuesta más lentos que la componente eléctrica. Por lo anterior es posible considerar como dominante la parte mecánica de forma que se obtiene un modelo simplificado de primer orden con un integrador [5].
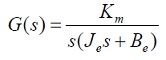 (7)
(7)
Por otra parte, la medición de los parámetros del modelo puede ser un proceso poco práctico por la dificultad técnica que esto involucra, por lo tanto, se lleva a cabo una identificación de parámetros del modelo simplificado mostrado en la figura 4.
Figura 4. Modelo simplificado del sistema

Fuente: elaboración propia.
1.4 Parámetros del modelo
Tal como se mencionó anteriormente el modelo considerado del sistema es:
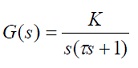 (8)
(8)
Para este tipo de sistema el parámetro K puede obtenerse como la relación de la entrada y la salida en estado estable, para el caso es:
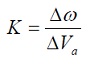 (9)
(9)
Donde ? es la velocidad angular. Con un voltaje de 12 V los tiempos gastados por el sistema para recorrer un ángulo de π/ 2 se relacionan en la siguiente tabla.
Tabla 1. Velocidad angular del sistema
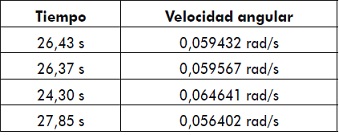
Fuente: elaboración propia.
La velocidad promedio del sistema fue de 0,06 rad/s, para una alimentación de 12 V, por lo tanto el valor del parámetro K es de 0,005 rad/(Vs).
Por otro lado, el parámetro τ puede determinarse como la cuarta parte del tiempo de establecimiento del sistema. Los tiempos de establecimiento del sistema para diferentes mediciones pueden apreciarse en la tabla 2.
Tabla 2. Tiempos de establecimiento del sistema

Fuente: elaboración propia.
En promedio el tiempo de establecimiento del sistema es de 1,53 s, por lo tanto el parámetro τ es de 0,38 s. Finalmente el modelo de la planta es:
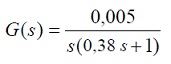 (10)
(10)
2. Controladores
En la presente sección se muestran los controladores implementados, los cuales consisten en un control on-off, un control proporcional y un compensador del tipo cero, polo y ganancia. Originalmente el seguidor presentaba el sistema de control on-off, por lo cual se elaboraron diseños adicionales para mejorar su funcionamiento.
2.1 Control on-off
Una primera estrategia de control implementada se basa en la diferencia de voltaje que se tiene sobre un arreglo de dos sensores, que en este caso son fotorresistencias. En la figura 5 puede apreciarse el diagrama para este arreglo de sensores como también su disposición física.
Figura 5. Arreglo de sensores empleado
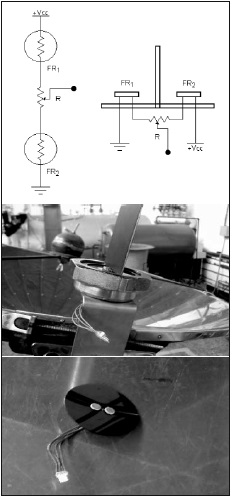
Fuente: elaboración propia.
Con este tipo de controlador se obtiene una acción de tipo todo o nada sobre el motor, es decir, que se conecta y desconecta dependiendo de la información suministrada por el sensor. El circuito consta de un amplificador operacional conectado como inversor donde se presenta una referencia dada por el divisor resistivo que se encuentra en su entrada no inversora. La etapa potencia es manejada por cuatro transistores, los cuales permiten el encendido y apagado del motor con la opción de inversión de giro. El circuito empleado para el control on-off puede apreciarse en la figura 6.
Figura 6. Circuito para el control on-off
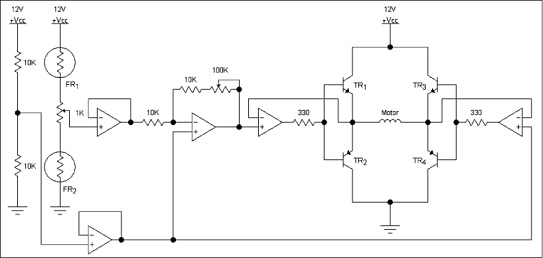
Fuente: elaboración propia.
En este caso, el circuito genera una ventana de umbral permitiendo que el sistema se estabilice en un rango correspondiente a la diferencia de iluminación presente en los sensores.
El circuito consta de un ajuste de referencia correspondiente al potenciómetro de 1 K (R) y un ajuste de ganancia, la cual está dada por el potenciómetro de 100 K (K). La localización física de los anteriores potenciómetros puede apreciarse en la figura 7.
Figura 7. Circuito de control on-off implementado

Fuente: elaboración propia.
2.2 Control proporcional
El diseño propuesto para implementar el control proporcional cuenta con un acople de impedancia, el cual toma la señal entregada por el sensor y la suministra a un amplificador inversor que la amplifica para luego ser entregada a la etapa de potencia. Adicionalmente, se cuenta con un circuito que genera un voltaje de referencia para los amplificadores operacionales con el fin de lograr una acción proporcional sobre el motor sin necesidad de emplear una fuente dual. El circuito implementado para el control proporcional puede apreciarse en la figura 8.
Figura 8. Circuito para el control proporcional
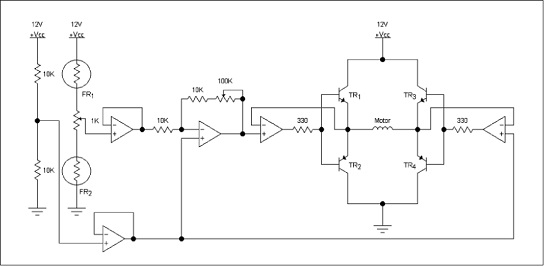
Fuente: elaboración propia.
La implementación de este controlador consta de un ajuste de referencia correspondiente al potenciómetro de 1 K (R) y un ajuste de ganancia de amplificación, el cual está dado por el potenciómetro de 100 K (K). La localización física de los anteriores potenciómetros puede apreciarse en la figura 9.
Figura 9. Circuito de control proporcional implementado

Fuente: elaboración propia.
El valor de K se escoge de tal forma que no se tenga una saturación del sistema superior al 10 % para una referencia de 0° a 30°, con un voltaje máximo de 6 V. Considerando lo anterior se toma K = 11.
2.3 Controlador cero polo y ganancia
El compensador de cero, polo y ganancia se implementa mediante el circuito mostrado en la figura 10. En este caso, al circuito del controlador proporcional se le adiciona un amplificador operacional en modo de inversor, el cual consta de dos impedancias compuestas por resistencias y condensadores. Estas impedancias permiten tener un polo y un cero en la función de transferencia del controlador.
Figura 10. Circuito para el compensador
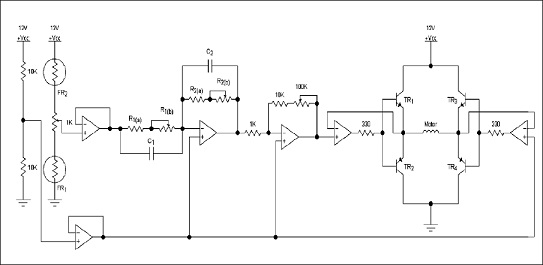
Fuente: elaboración propia.
La función de transferencia del compensador está dada por la ecuación (11).
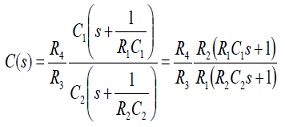 (11)
(11)
El circuito implementado del compensador puede apreciarse en la figura 11. En este caso se emplea parte del controlador proporcional para la implementación del compensador, lo cual permite ahorrar componentes y espacio.
Figura 11. Circuito del compensador implementado

Fuente: elaboración propia.
3. Optimización bioinspirada
La naturaleza es una fuente de inspiración para el planteamiento de soluciones en ingeniería, especialmente en optimización. Un ejemplo de optimización presente en la naturaleza se aprecia cuando animales o seres vivos con mejores técnicas para la búsqueda de alimento desarrollan una mayor posibilidad de sobrevivir [8].
Una de las técnicas de optimización bioinspirada se basa en el comportamiento de las hormigas [9]-[11]. También las colonias de abejas sirven de inspiración para solucionar problemas de búsqueda y exploración [12].
Otra de las técnicas de optimización inspirada en la biología consiste en el comportamiento presentado por seres unicelulares como las bacterias al momento de buscar el alimento. Lo anterior es fundamento para la optimización basada en quimiotaxis bacteriana, siendo la bacteria E. coli de las más estudiadas [8]. Por otro lado, los algoritmos genéticos y la evolución diferencial buscan emular el proceso que desarrolla la naturaleza al mejorar una especie a lo largo del tiempo [13]. Otros algoritmos de optimización se basan en el comportamiento de enjambres de animales como aves y peces, lo que da origen a la optimización centrada en enjambres de partículas.
3.1 Algoritmo de optimización basado enjambres
El concepto de optimización basada e n enjambres de partículas fue propuesto por James Kennedy y Russell Eberhart, quienes desarrollaron un algoritmo de búsqueda a partir del comportamiento social de bandadas de aves [14]. Bajo esta orientación el objetivo principal de estudiar el comportamiento colectivo de los animales es encontrar un eficiente y simple algoritmo de optimización. El algoritmo básico de optimización basada en enjambres de partículas (PSO, Particle Swarm Optimization) es el siguiente:
- Inicializar el enjambre en el espacio solución.
- Evaluar el desempeño de cada individuo (fitness).
- Encontrar el mejor desempeño individual y colectivo.
- Determinar la velocidad de cada individuo.
- Realizar el desplazamiento de cada individuo a la nueva posición.
- Repetir desde el segundo paso hasta tener convergencia o hasta cumplir algún criterio de finalización.
Un algoritmo básico PSO está regido por las ecuaciones de velocidad y posición. Para la velocidad de cada individuo se tiene:
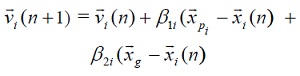 (12)
(12)
Para actualizar la posición de cada partícula se emplea la ecuación (13).
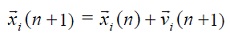 (13)
(13)
Donde 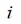 es el índice de cada individuo,
es el índice de cada individuo, 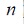 el
índice de tiempo discreto,
el
índice de tiempo discreto, 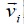 la velocidad del
la velocidad del 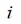 -ésimo individuo,
-ésimo individuo, 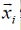 la posición del
la posición del 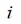 -ésimo
individuo,
-ésimo
individuo, 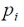 la mejor evaluación encontrada
por el
la mejor evaluación encontrada
por el 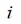 -ésimo individuo,
-ésimo individuo, 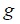 la mejor
evaluación encontrada por el enjambre,
la mejor
evaluación encontrada por el enjambre,
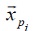 la mejor posición encontrada por el
la mejor posición encontrada por el 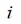 -ésimo
individuo,
-ésimo
individuo, 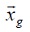 la mejor posición encontrada
por el enjambre y, finalmente,
la mejor posición encontrada
por el enjambre y, finalmente, 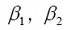 son
números aleatorios en el intervalo [0,1].
son
números aleatorios en el intervalo [0,1].
Un algoritmo PSO más elaborado incorpora un factor de inercia para el cálculo de la velocidad de la siguiente forma:
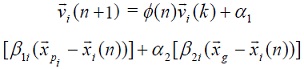 (14)
(14)
127
Siendo 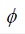 una función de inercia y
una función de inercia y 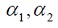 constantes de aceleración.
constantes de aceleración.
3.2 Algoritmos genéticos
Esta técnica de búsqueda se basa en la forma como las especies evolucionan para adaptarse a su medio ambiente [13]. Los algoritmos genéticos (AG) con frecuencia son empleados en problemas con espacios de búsqueda muy grandes y donde pueden presentarse múltiples extremos locales. La eficiencia de los AG reside en su modo de operación puesto que trabajan con criterios estocásticos derivados de la selección natural de las especies, los cuales son combinados con toma de decisiones deterministas proporcionando de esta forma la capacidad de evitar mínimos locales [13].
Un aspecto importante sobre la implementación de los algoritmos genéticos consiste en la respectiva codificación utilizada para representar los individuos. Por lo general, la codificación empleada consiste en secuencias binarias de la misma longitud.
El primer paso al desarrollar un AG radica en generar una población inicial, comúnmente de forma aleatoria. Luego se define un conjunto simple de operaciones que tomen esa población inicial y generen poblaciones sucesivas que se espera sean mejores a medida que avanza el tiempo. Los operadores básicos en un AG simple son: elitismo, cruce y mutación [13].
El elitismo es un proceso con el cual las cadenas individuales tienen la probabilidad de pasar a la siguiente generación teniendo como criterio su desempeño. En el proceso de cruce se toma la codificación de dos individuos y mediante criterios de selección estocásticos se combinan para generar nuevos individuos [13]. El proceso de mutación consiste en cambiar parte de la codificación de un individuo bajo algún criterio probabilístico.
Los pasos básicos involucrados en un algoritmo genético son:
- Generar la población inicial de forma aleatoria.
- Evaluar el desempeño de cada individuo (fitness).
- Seleccionar los mejores individuos de forma probabilística.
- Aplicar el operador de elitismo de forma probabilística.
- Aplicar el operador de cruce de forma probabilística.
- Aplicar el operador de mutación de forma probabilística.
- Bajo un criterio de parada detener el algoritmo o regresar al segundo paso.
3.3 Criterio de optimización
Cuando se realiza la optimización de sistemas de control pueden considerarse diferentes índices de control óptimo, los cuales pueden ser [15]:
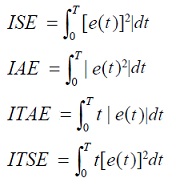 (15)
(15)
Considerando que la alimentación del sistema se efectúa mediante una batería de 12 V, entonces, un índice de desempeño adecuado debe incorporar la información de la energía suministrada al sistema. Según lo presentado en [5], [16], un índice de desempeño que incorpora la señal de error y la energía suministrada es:
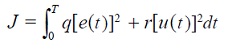 (16)
(16)
Donde 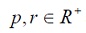 son dos constantes que
ponderan respectivamente el error y la acción
de control. En el ámbito computacional,
el anterior índice de desempeño se aproxima
como:
son dos constantes que
ponderan respectivamente el error y la acción
de control. En el ámbito computacional,
el anterior índice de desempeño se aproxima
como:
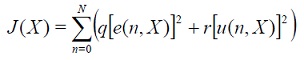 (17)
(17)
Donde 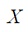 es el conjunto de parámetros
del controlador,
es el conjunto de parámetros
del controlador, 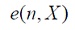 la señal de error,
la señal de error,
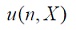 la energía suministrada,
la energía suministrada, 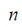 es el índice
de tiempo discreto y
es el índice
de tiempo discreto y 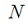 corresponde al
número total de datos tomados.
corresponde al
número total de datos tomados.
3.4 Implementación del proceso de optimización
Para llevar a cabo el proceso de optimización primero se crea una función en la cual se describe el sistema de control considerando el comportamiento dinámico de la planta y el controlador, incluyendo el lazo de realimentación; esta función tiene como entrada los parámetros del compensador y como salida la respuesta del sistema de control. Con los datos obtenidos del sistema de control se construye la función objetivo, la cual implementa el criterio de optimización seleccionado. Finalmente se realiza la optimización de la función objetivo empleando GA y PSO.
4. Resultados de optimización
Las poblaciones iniciales para GA y PSO se toman aleatorias con una distribución uniforme uniforme de 0 a 200. Se realizan 20 corridas tanto para GA como para PSO. La implementación de AG y PSO se realiza en Matlab mediante la herramienta especializada que este posee.
Los parámetros considerados para el AG son:
- Generaciones: 100
- Población: 20
- Factor de cruce: 0,8
- Elitismo: 5
- Factor de mutación: 0,05
Los parámetros del algoritmo PSO son:
- Número de partículas: 20
- Velocidad máxima: 10
- Aceleración constante: 20
- Inercia inicial y final: 0,9 y 0,6
- épocas de entrenamiento: 100
4.1 Resultados
Los resultados para 20 ejecuciones de los algoritmos pueden apreciarse en la tabla 3. Los datos consignados en esta tabla corresponden al valor de la función objetivo.
Tabla 3. Resultados de los algoritmos de optimización
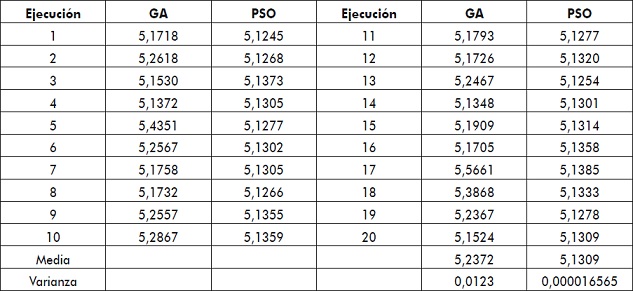
Fuente: elaboración propia.
4 .2 Análisis de resultados
Para determinar si existe una diferencia significativa en los resultados del proceso de optimización se establece una comparación estadística de dos grupos independientes. Para este fin se recurre a la opción de pruebas paramétricas y no paramétricas dependiendo si se cumplen los supuestos de normalidad y homocedasticidad (igualdad de varianza) [17].
Como alternativa paramétrica se tiene la prueba t de Student, para la cual deben comprobarse los supuestos de normalidad y de igualdad de varianza; en el caso de no cumplirse estos supuestos puede implementarse la prueba no paramétrica de U Mann-Whitney, la cual es equivalente a la prueba de suma de rangos de Wilcoxon [17].
Para determinar si el grupo de muestras presenta normalidad se realiza la prueba de Kolmogorov-Smirnov y mediante la prueba de Levene se determina si los datos cumplen con el supuesto de homocedasticidad [17].
Las hipótesis para este caso son:
- Hipótesis nula (Ho): las diferencias observadas entre los métodos de optimización se deben al azar.
- Hipótesis alterna (Ha): los resultados de optimización, según el método empleado, son diferentes.
Para aceptar o rechazar la hipótesis nula se considera el respectivo p-value que entrega la prueba. Considerando un nivel de significancia de 0,005 se tiene que para todo valor de probabilidad mayor que 0,05 se acepta Ho y se rechaza Ha.
Al realizar la prueba de normalidad de Kolmogorov-
Smirnov se obtiene un p-value de 0,0023
y un p-value de 0,000052434 para la prueba de
homocedasticidad de Levene. Considerando
lo anterior para comparar los resultados entregados
por los dos algoritmos se implementa
la prueba de suma de rangos de Wilcoxon,
la cual entrega un p-value de 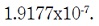 Este valor muestra que el resultado obtenido
con los dos algoritmos es diferente, por lo
cual se escoge la configuración de parámetros
que entregó un mejor índice de desempeño.
Según lo anterior, la función de transferencia
del controlador que se va a implementar es:
Este valor muestra que el resultado obtenido
con los dos algoritmos es diferente, por lo
cual se escoge la configuración de parámetros
que entregó un mejor índice de desempeño.
Según lo anterior, la función de transferencia
del controlador que se va a implementar es:
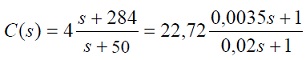 (18)
(18)
Para la implementación física del compensador
se emplean condensadores de 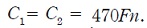 lo cual implica resistencias de
lo cual implica resistencias de 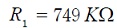 y
y 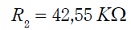 , las cuales se ajustan
con una resistencia fija de 6,8
, las cuales se ajustan
con una resistencia fija de 6,8  y un
potenciómetro 2
y un
potenciómetro 2  para
para 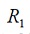 y para
y para 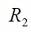 se
emplea una resistencia fija de 39
se
emplea una resistencia fija de 39 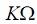 y un potenciómetro
de 5
y un potenciómetro
de 5 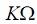 . Considerando que el
ajuste de la ganancia total se realiza mediante
un amplificador inversor con resistencias de
. Considerando que el
ajuste de la ganancia total se realiza mediante
un amplificador inversor con resistencias de
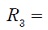 10
10 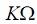 y
y 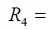 40
40 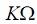 , entonces, para
, entonces, para
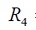 se emplea una resistencia fija de 39
se emplea una resistencia fija de 39 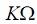 y
un potenciómetro de 5
y
un potenciómetro de 5 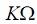 (se puede constatar
que
(se puede constatar
que 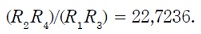
5. Resultados de los controladores implementados
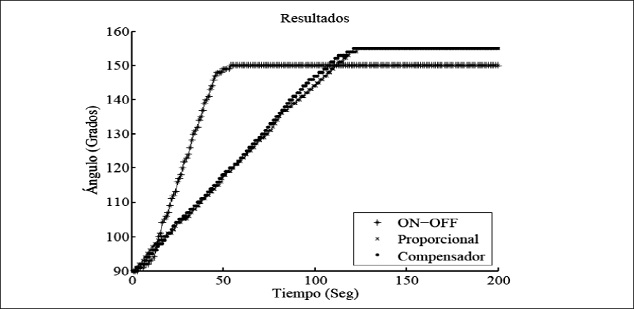
Luego de llevar a cabo la implementación física de los controladores diseñados se obtienen los resultados mostrados en la figura 12. En ellos puede apreciarse que el controlador on-off presenta el menor tiempo de establecimiento; sin embargo, para el circuito implementado se observa un error en estado estacionario de cinco grados. Adicionalmente, es de apreciar que tanto el controlador proporcional como el compensador en atraso no tienen error en estado estacionario, ahora bien, el compensador en atraso presenta un tiempo de establecimiento menor que el controlador proporcional.
Figura 12.
Fuente: elaboración propia.
6. Conclusiones
En la práctica los tres controladores implementados logran realizar el seguimiento deseado. El controlador on-off implementado presenta un tiempo de respuesta menor pero un mayor error en estado estacionario. El controlador proporcional y el compensador muestran comportamientos similares, sin embargo, el compensador evidencia un menor tiempo de respuesta que el controlador proporcional.
El análisis mostró que los resultados obtenidos con GA son estadísticamente diferentes a los obtenidos con PSO, esto debido a la diferencia de varianza de los resultados obtenidos para estos dos métodos.
Considerando que el modelo del seguidor solar presenta incertidumbres, en un trabajo futuro se puede realizar el diseño e implementación de un controlador robusto.
Referencias
- F. Sierra, E. Caro, F. Mejía, Tecnologías para el aprovechamiento de la energía solar. Bogotá: Universidad Nacional de Colombia, 2008.
- S. Lakeou, E. Ososanya, O. Latigo, W. Mahmoud, G. Karanga, W. Oshumare, “Design of a low-cost digital controller for a solar tracking photo-voltaic (PV) module and wind turbine combination system”, in 21st European Photovoltaic Solar Energy Conference. Dresden, Germany, 2006.
- Bill Lane. Solar Tracker. Department of Electrical and Computer Engineering Cleveland State University. Cleveland, Ohio. EEC 517. 2008. [En línea] disponible en http://www.8051projects.net/ e107_files/public/1242614085_16317_ FT0_using_pic_complete_tracker. pdfB. Lane, “Solar tracker”, EEC 517, 2008.
- B. Plesz, P. Sági, V. Timár-Horváth, “Enhancement of solar panels power generation by the usage of solar tracking”, Proceedings of ECOpole, vol. 3, n° 1, 2009.
- K. Ogata, Ingeniería de Control Moderna. 4a. ed. Madrid: Pearson Prentice Hall, Cuarta edición, 2003.
- M. A. Panait, T. Tudorache, “A simple neural network solar tracker for optimizing conversion efficiency in off-grid solar generators”, in International Conference on Renewable Energies and Power Quality, March. Bucharest, Romania, 2008.
- Y. J. Huang, B. C. Wu, C. Y. Chen, C. H. Chang, T. C. Kuo, “Solar tracking fuzzy control system design using FPGA”, Proceedings of the World Congress on Engineering. Vol. I. London, U.K., july, 2009. [En línea] disponible en http:// www.iaeng.org/publication/WCE2009/ WCE2009_pp340-344.pdfIEEE, 2009.
- K. Passino, “Biomimicry of bacterian foragin for distributed optimization and control”, IEEE Control Systems Magazine, june, 2002.
- M. Birattari, P. Pellegrini, M. Dorigo, “On the invariance of ant colony optimization”, IEEE Transactions on Evolutionary Computation, vol. 11, n°. 6, december, 2007.
- M. Dorigo, M. Birattari, T. St�tzle, “Ant colony optimization. Artificial ants as a computational intelligence technique”, IEEE Computational Intelligence Magazine, november, 2006.
- A. C. Zecchin, A. R. Simpson, H. R. Maier, J. B. Nixon, “Parametric study for an ant algorithm applied. Water distribution system optimization”, IEEE Transactions on Evolutionary Computation, vol. 9, n° 2, april 2005.
- S. Thakoor, J. M. Morookian, J. Chahl, B. Hine, S. Zornetzer, “BEES: exploring mars with bioinspired technologies”, IEEE Computer Society, vol. 37, n.° 9, pp. 38-47, Septiembre, 2004.
- T. Weise, Global optimization algorithms, theory and application”. Germ any: Self- Published, 2009.
- J. Kennedy, R. Eberhart, “Particle swarm optimization”, Proceedings, IEEE International Conference, vol., 4. Networks, 1995. R. Eberhart, J. Kennedy, “Particle swarm optimization”, IEEE Proceedings Neural Networks, 1995.
- O. Arrieta, V. Alfaro, “Sintonización de controladores PI y PID utilizando los criterios Integrales IAE e ITAE”, Ingeniería, vol. 13, n.° 1-2, pp. 31-39, 2003.
- C. T. Chen, Analog and digital control system design. Orlando, Florida: Saunders College Publishing, 1993.
- M. Gómez, C. Danglot, L. Vega, “Sinopsis de pruebas estadísticas no paramétricas. Cuándo usarlas”, Revista Mexicana de Pediatría, vol. 70, n.° 2, marzo-abril, 2003.
Creation date: Junio de 2013


.png)




.jpg)





