VISIÓN INVESTIGADORA

Visión Electrónica, 2013-06-03 Volumen:7, Año:1 pág: 40–52

ESTUDIO Y SIMULACIóN DE UN SISTEMA DE CONTROL DE TENSIóN CON POLYCORD

STUDY AND SIMULATION OF A TENSION CONTROL SYSTEM USING POLYCORD

Fecha de envío: enero de 2013
Fecha de recepción: enero de 2013
Fecha de aceptación: febrero de 2013

Luis H. Berrío

Ingeniero Electrónico de la Universidad de Antioquia. Especialista y estudiante de Maestría en Ingeniería de la Universidad Pontificia Bolivariana (UPB) (Colombia) y de la Maestría en Administración de la Universidad de Antioquia (Colombia). Funcionario Subdirección Investigación y Desarrollo de Negocios de Energía, Empresas Públicas de Medellín (EPM). berrio77@yahoo.com

Esteban Gómez

Ingeniero Electrónico de la Universidad Pontificia Bolivariana (UPB) (Colombia). Especialista en Ingeniería de la Universidad Pontificia Bolivariana (UPB) (Colombia). esgomie@gmail.com

RESUMEN

Este artículo realiza el estudio de un sistema de control de tensión de un proceso textil para su modelamiento, en el cual se describen las características de la arquitectura del proceso textil, se analizan las respuestas ante señales tipo escalón y el comportamiento en el tiempo del sistema frente a experimentos en lazo abierto y cerrado. Además, se proponen modelos de la planta de orden superior y se valida el modelo propuesto usando el criterio de error cuadrático medio como variable estadística y con el método del lugar de las raíces.

Controlador, Programmable Logic Controller (PLC), modelo estático, sistema de tercer orden, lugar de las raíces, polos, estabilidad.

Abstract

This article focuses on the analysis of a strain control system for a textile process through the use of a model. The characteristics of the textile process architecture are described together with the system’s responses to a step signal and the behavior, as a function of time, of the system for opened and closed-loop experiments. Also, higherorder models are proposed and a proposed model is validated using the mean squared error criterion, as statistical variable, and also using the root locus method.

Controller, PLC, static model, third-order system, root locus, poles, stability.

Introducción

El control de tensión en maquinaria textil es de gran importancia para evitar interrupciones o fallas en la producción. En muchos casos, dependiendo del tipo de textil o del proceso que se esté llevando a cabo, no es posible ubicar físicamente los sistemas de medición necesarios para efectuar el control de estados, incluso, es posible que la instalación de sensores no sea una opción económicamente viable.

Colombia es reconocida en el ámbito mundial como un país que presenta grandes fortalezas en el negocio de los textiles y las confecciones [1]. En 2011, la producción del sector textil en Colombia representó el 2,5 % del PIB manufacturero y el 0,3 % del PIB nacional [2]. Además, la industria textil ha construido una compleja y diversificada cadena productiva, lo que ha generado una importante contribución al crecimiento económico, a las exportaciones y al empleo del país durante más de ochenta años [3], por lo que se requiere de tecnologías blandas y duras que permitan al sector mejorar los estándares de calidad, los niveles de productividad y su competitividad.

Por otra parte, la identificación de un sistema consiste en la determinación de su función de transferencia o de sus parámetros fundamentales, a partir de mediciones experimentales [4]. Existe en la actualidad una gran cantidad de métodos de diseño de distinto origen, que permiten desarrollar sistemas de control dentro de una amplia gama de características y posibilidades [5]. Por consiguiente, lograr determinar, aunque sea en forma aproximada, los parámetros más importantes de una función de transferencia de un sistema se convierte en una necesidad insoslayable. Ese es el caso del método del lugar de las raíces (LDR), que es un conjunto de reglas mediante las cuales puede determinarse la posición de las soluciones de la ecuación característica en el plano complejo, cuando uno o varios parámetros de la función de transferencia del sistema en bucle abierto varían en su rango. El LDR da una idea sobre la estabilidad, la precisión y la naturaleza de la respuesta transitoria [6].

En la sección 1 se presenta la arquitectura de control del proceso textil y la obtención de la curva del modelo estático, en la sección 2 se muestra el comportamiento del sistema ante diferentes valores de los parámetros de diseño, en la sección 3 se exponen los resultados de los modelos candidatos de distinto orden y, finalmente, se refieren las conclusiones.

1. Arquitectura del control de tensión

El sistema de control completo está conformado por un PLC Unitronics (Vision 280), además de un computador con software de control implementado en Labview y con comunicación Modbus al PLC [7]. El sistema cuenta con dos interfaces para el monitoreo y control del sistema: interfaz por computador e interfaz en el tablero de control, esta última se muestra en la figura 1.

Figura 1. Panel de control de tensión para proceso textil

Fuente: elaboración propia.

Los parámetros geométricos empleados en el estudio del proceso textil se describen en la tabla 1. Por su parte, la figura 2 muestra los parámetros geométricos del proceso textil personalizados. Cuando se mueve el brazo del pivote del sistema mecánico se modifica la altura que alcanza el pivote para un mismo ángulo, mientras que la ubicación del carro determina la posición del eje de giro de todo el balancín.

Tabla 1. Parámetros geométricos personalizados

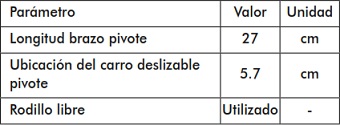
Fuente: elaboración propia.

Figura 2. Parámetros geométricos personalizados

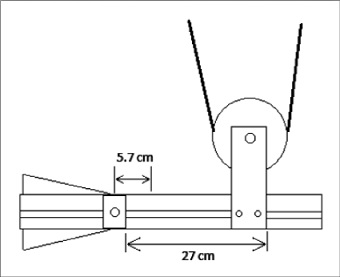
Fuente: elaboración propia.

1.1 Geometría del acumulador y relación entre el ángulo y el brazo pivotado

En la figura 3 se muestra el diagrama que representa la geometría del acumulador. Cuando el ángulo ? de la figura 3 aumenta, es decir que se mueve en sentido antihorario, la tela acumulada se hace menor. Por su parte, si el ángulo ? disminuye, es decir, la polea móvil se desplaza hacia abajo o ? varía en sentido horario, entonces la tela acumulada aumenta, por lo que hay una relación inversa entre el ángulo del brazo pivotado y la cantidad de tela acumulada.

Figura 3. Geometría del cabezote textil

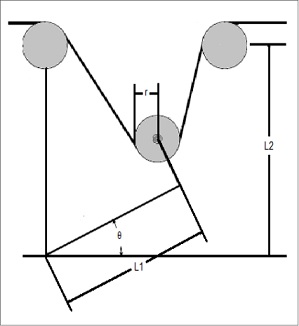
Fuente: elaboración propia.

1.2 Curva de modelo estático

La tabla 2 muestra los valores que se midieron experimentalmente sobre la arquitectura del proceso textil. La distancia fue medida cada octavo de vuelta de la polea del motor maestro.

Para llevar a cabo la toma de datos se requirió entrar al sistema en modo mantenimiento y seleccionar el motor esclavo y maestro de forma que se lograra ubicar el balancín desde la posición más extrema inferior, es decir con ángulo negativo, y llevarlo hasta una posición extrema superior, es decir, a un ángulo positivo. El motor esclavo permitía desplazar el balancín hacia ángulos positivos, donde el movimiento de ambos motores es en sentido horario.

Tabla 2. Datos experimentales para el modelo estático

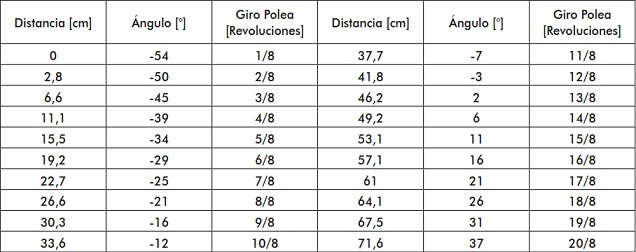
Fuente: elaboración propia.

En la figura 4 se muestra la gráfica que relaciona la distancia recorrida por un punto sobre el polycord cada octavo de vuelta de la polea del motor maestro contra el ángulo descrito por el balancín respecto al eje horizontal. La zona de operación escogida se encuentra entre [-16-16°], con el punto de operación a 0° del balancín respecto al eje horizontal. Se tiene que la ecuación que mejor relaciona linealmente al ángulo del balancín y la distancia recorrida por un punto del polycord es:

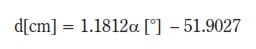        (1)

Figura 4. Curva estática del proceso experimental y teórico

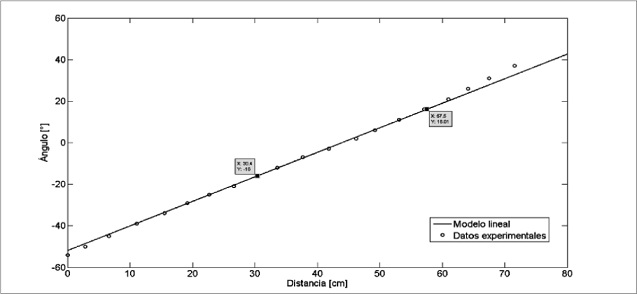
Fuente: elaboración propia.

Donde d[cm] es la distancia recorrida y ??°] es el ángulo del balancín. La distancia recorrida es el diferencial de tela acumulada en el sistema.

2. Resultados experimentales

Entre los resultados experimentales se encuentra la medición de la velocidad, donde la velocidad externa medida fue de 10.3 m/min sobre el polycord, mientras que la velocidad interna fue de 12.34 m/min sobre el diámetro interno de la polea. Luego de cerrar el lazo y con ayuda de una interfaz en Labview, que permitía tener control sobre el sistema de control de tensión, se llevaron a cabo diferentes experimentos con el fin de observar el comportamiento del sistema ante distintos valores en los parámetros de diseño.

Los experimentos se desarrollaron con base en valores de la amplitud de la planta (H), y de la ganancia del controlador (K), de forma que no existiera una saturación en el actuador. La tabla 3 describe los valores de K y H para ejecutar el control de tensión.

Tabla 3. Valores de K y H para el modelo de control de tensión

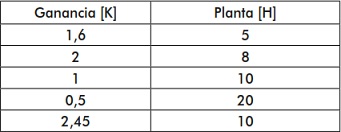
Fuente: elaboración propia.

Además, se suma un término adicional (Bias) con el fin de corregir la desviación en el punto de operación normal. El Bias se suma a nivel de simulación y tiene un valor de 16.3, el cual permite corregir el error en estado estable de cada experimento. Así mismo, en la figura 5 se muestra la respuesta experimental ante un escalón de subida, mientras que en la figura 6 se muestra la respuesta del sistema experimental frente a un escalón de bajada. En la figura 5 y 6 se evidencia que la respuesta del sistema depende tanto de la función de transferencia de la planta como de la ganancia del controlador.

Figura 5. Respuesta del sistema frente a un escalón de subida

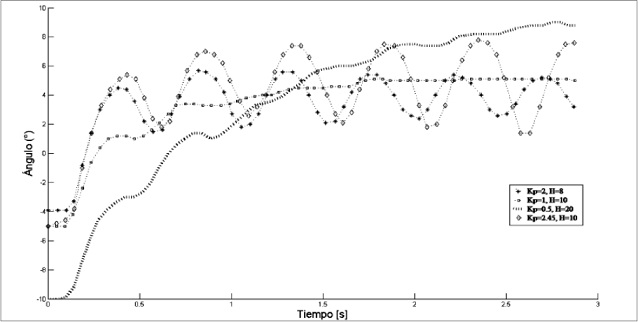
Fuente: elaboración propia.

Figura 6. Respuesta del sistema frente a un escalón de bajada

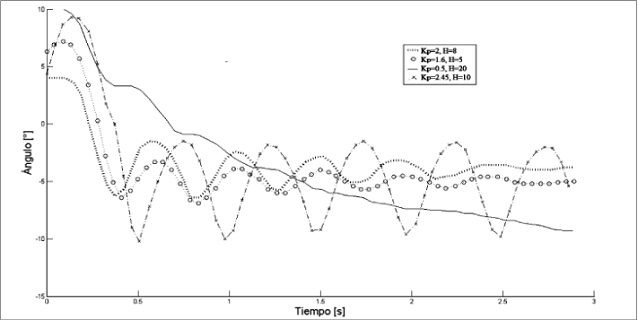
Fuente: elaboración propia.

Puede observarse que a medida que aumenta la ganancia proporcional, el sistema tiende a volverse cada vez más inestable, lo cual es evidente por las oscilaciones cada vez más notorias. Si se emplea un modelo candidato de orden 3 puede compararse la respuesta experimental del sistema con la obtenida en simulación. En la figura 7 se muestra la gráfica de la respuesta del sistema experimental y de la curva ajustada por medio de la simulación, para un escalón de subida, con ganancia de un controlador proporcional (Kp) igual 0.5 y H = 20, y la figura 8 para Kp = 1 y H = 10, que fueron obtenidas con el programa en Matlab de [8]. En la figura 9 se muestra la gráfica de la respuesta del sistema experimental y de la curva ajustada por medio de la simulación, para un escalón de bajada, Kp = 0.5 y H = 20, y la figura 10 para Kp = 1 y H = 10.

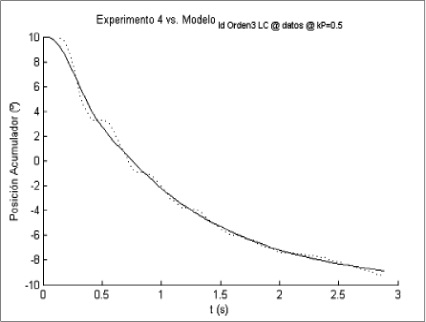
Figura 7. Respuesta experimental y respuesta ajustada en simulación, para un escalón de subida, Kp = 0.5 y H = 20

Fuente: elaboración propia.

Figura 8. Respuesta experimental y respuesta ajustada en simulación, para un escalón de subida, Kp=1 y H= 10

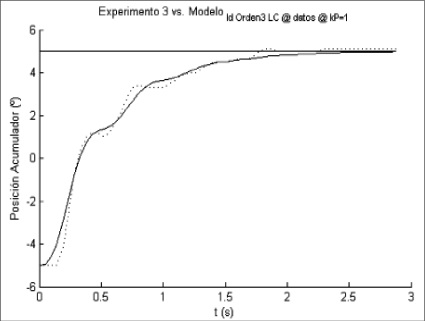
Fuente: elaboración propia.

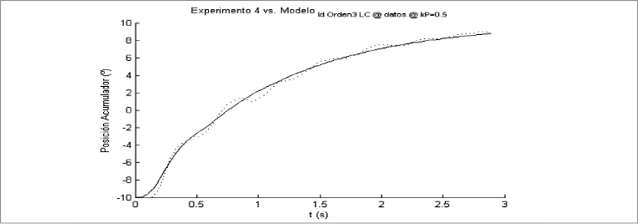
Figura 9. Respuesta experimental y respuesta ajustada en simulación, para un escalón de bajada, Kp=0.5 y H= 20

Fuente: elaboración propia.

El modelo ajustado se inclina a seguir la tendencia de los datos experimentales, por lo que es una buena aproximación del comportamiento real del sistema.

Figura 10. Respuesta experimental y respuesta ajustada en simulación, para un escalón de bajada, Kp=1 y H= 10

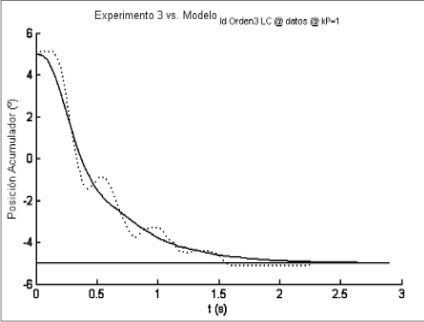
Fuente: elaboración propia.

3. Comparación entre modelos candidatos de distinto orden

Se compararon cada uno de los modelos de segundo, tercer y cuarto orden. No se comparó con un modelo de primer orden, puesto que de antemano se sabe que el sistema no se comporta de manera lineal. En la tabla 4 se muestran los datos arrojados por la simulación de cada uno de los modelos propuestos para un escalón de subida como señal de entrada, y en la tabla 5 los mismos parámetros, pero para un escalón de bajada. La decisión se basará en el modelo que promedie menor ECM, que es el valor promedio del error cuadrático medio total [9].

Tabla 4. Parámetros de los modelos empleados para el ajuste de un escalón de subida como señal de entrada

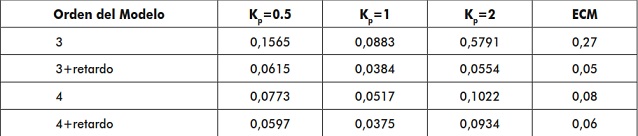
Fuente: elaboración propia.

Tabla 5. Parámetros de los modelos empleados para el ajuste de un escalón de bajada como señal de entrada

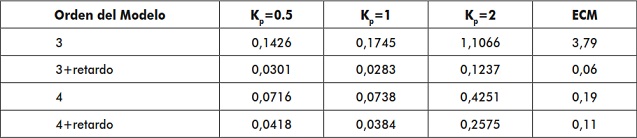
Fuente: elaboración propia.

Puede observarse que todos los modelos ensayados tienen un bajo ECM, lo que hace viable utilizar cualquiera de ellos, aunque el de mayor orden y con retardo modela mucho mejor el sistema. Además, se escogió el sistema de orden 3 sin retardo, ya que el retardo complica la realización del controlador. Por otra parte, un orden mayor requiere de más cálculo y parámetros, por lo que un orden menor puede suplir las necesidades y requerimientos buscados a un menor esfuerzo. En la figura 11 se muestra el diagrama de polos en lazo cerrado para los sistemas ensayados a diferentes ganancias, para el modelo de orden 3 sin retardo, la figura 12 para el de orden 3 con retardo, la figura 13 para el de orden 4 sin retardo y la figura 14 para el de orden 4 con retardo.

Figura 11. Diagrama de polos para el sistema de orden 3 sin retardo

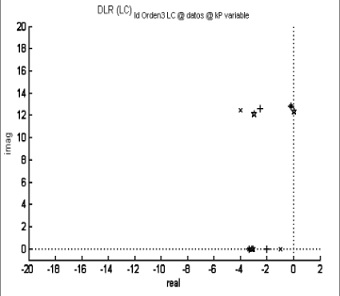
Fuente: elaboración propia.

Figura 12. Diagrama de polos para el sistema de orden 3 con retardo

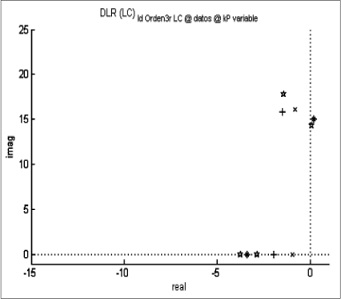
Fuente: elaboración propia.

Figura 13. Diagrama de polos para el sistema de orden 4 sin retardo

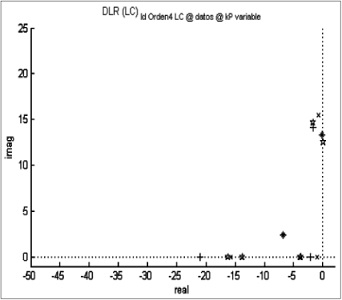
Fuente: elaboración propia.

Figura 14. Diagrama de polos para el sistema de orden 4 con retardo

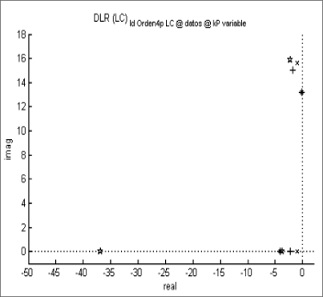
Fuente: elaboración propia.

De las figuras 11-14 se observa que los polos del modelo de orden 3 están alejados del eje imaginario y se ubican en el semiplano izquierdo. Esto permite decir que es un sistema estable, ya que no tiene polos a la derecha del eje imaginario, y tampoco es oscilante puro, puesto que sus polos no están sobre el eje imaginario [10].

3.1 Parámetros y modelo candidato por validar

El modelo de orden 3 fue el escogido para implementar el sistema. La tabla 6 muestra los valores de los parámetros para este modelo de orden 3 frente a una señal de entrada tipo escalón de subida y bajada, donde el parámetro k es la ganancia del bloque de la planta sola, ??es el coeficiente de amortiguamiento y wn es la frecuencia natural.

Tabla 6. Parámetros para el modelo de orden 3 para una señal escalón de subida y bajada

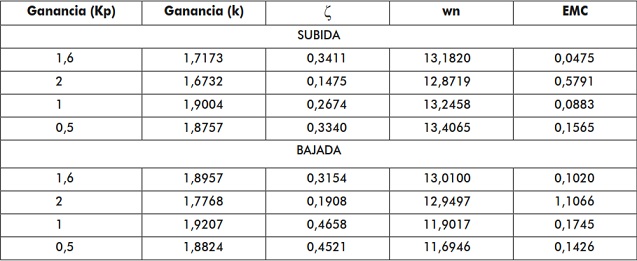
Fuente: elaboración propia.

Para calcular los valores finales de los parámetros del modelo de orden 3 se apeló a la estadística. Se realizó el promedio de todos los valores de las muestras de subida y bajada para encontrar el valor que llevaría consigo el modelo que se va a validar. La tabla 7 muestra los datos estadísticos hallados para encontrar un modelo de orden 3 que cumpla las expectativas de desviación estándar baja respecto a la media.

Tabla 7. Datos estadísticos para el cálculo de los parámetros del modelo de orden 3

Fuente: elaboración propia.

Puede observarse que los valores de la muestra de los parámetros tienen una desviación estándar baja con respecto a la media, lo que hace más confiable utilizar el promedio de los valores como magnitudes finales. Con estos valores ya es posible crear la función de transferencia del sistema y probar el diseño frente a señales de entrada clásicas para observar su comportamiento. Además, la función de transferencia del modelo de la planta típica para este tipo de sistemas textiles es:

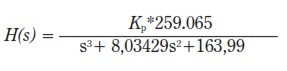        (2)

Donde Kp es la ganancia del sistema en lazo abierto. Con ayuda de Matlab® y dentro de la herramienta sisotool, se obtuvo la respuesta del sistema dado por (2), frente a una entrada tipo escalón para el sistema con retroalimentación (cerrado) [11]. La figura 15 muestra el resultado de aplicar dicha señal de entrada a (2).

Figura 15. Respuesta al escalón unitario para el modelo propuesto

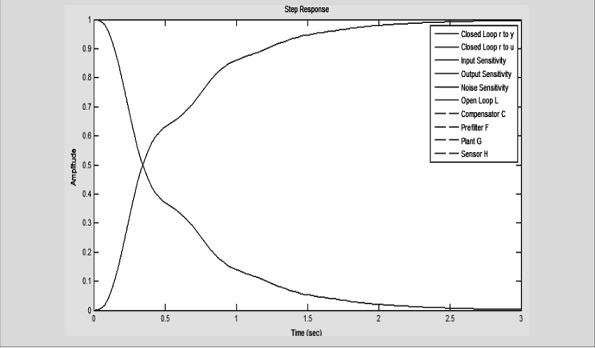
Fuente: elaboración propia.

Ahora, si se toma Kp = 0.5 se obtiene la respuesta al escalón de la figura 16.

Figura 16. Respuesta a un escalón de amplitud 20°

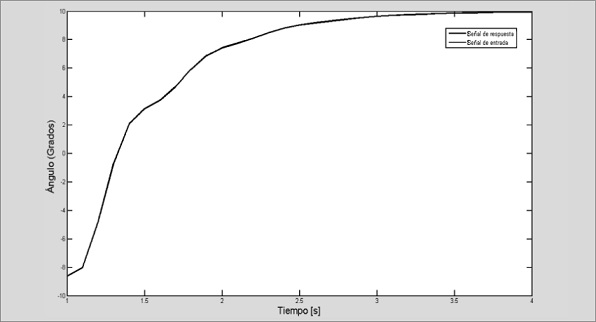
Fuente: elaboración propia.

Comparando la respuesta con la figura 7 puede observarse un resultado muy aproximado a los datos experimentales. Por otra parte, el lugar de las raíces y los diagramas de bode de magnitud y fase del sistema en lazo cerrado se observa en la figura 17.

Figura 17. Lugar de las raíces y diagramas de bode del sistema en lazo cerrado

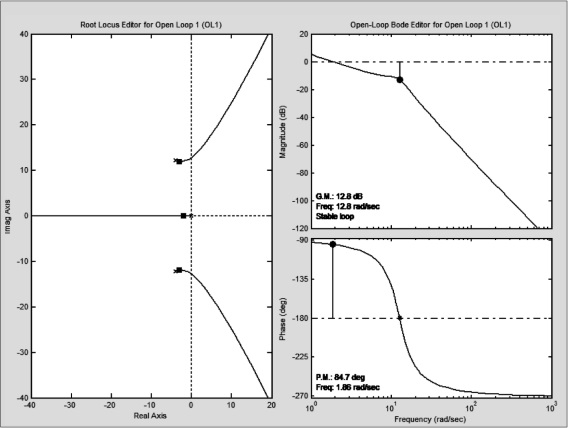
Fuente: elaboración propia.

Puede observarse que si se aumenta mucho la ganancia, el sistema se vuelve inestable, puesto que sus polos en lazo cerrado quedarán en el semiplano derecho [12].

4. Conclusiones

El modelo no lineal es más preciso y exacto que el modelo lineal. La desventaja del modelo no lineal es que no siempre es fácil de encontrar, pero para el proceso presentado fue sencillo desarrollarlo y de un orden superior a uno. Otra de las desventajas de emplear un modelo no lineal es que para hallarlo nececita más esfuerzos computacionales a medida que se agrega un orden al sistema.

Además, es importante identificar cada una de las señales y variables que intervienen en el proceso, ya que gracias a ello es posible un mejor entendimiento de este y, sobre todo, es posible identificar posteriormente un modelo que lo describa. Encontrar la relación entre ellas permite identificar un modelo apto para el proceso.

En algunas ocasiones no es posible llevar a cabo la toma de datos experimentales en lazo abierto ya que el sistema puede ser inestable, en estos casos es muy útil el método de lazo cerrado, puesto que al agregarle la realimentación negativa logra estabilizarse el sistema, si se usa una ganancia adecuada.

El modelo estático se obtuvo usando lazo abierto de forma manual, pero en algunos procesos no es posible utilizar este procedimiento, por esta razón es importante obtener una herramienta como la de lazo cerrado que permite adquirir tomas de datos en sistemas que pueden ser inestables sin realimentación.

References

1. MAPRE, “Informe sector textil y confecciones colombiano”, Análisis Sectorial. Medellín, Colombia, 2010.
2. PROEXPORT, “Sector textil y confección”, Promoción de Turismo, Inversión y Exportaciones. Colombia, 2012.
3. Unidad de Planeación Minero Energética (UPME). “Determinación del potencial técnico y económico de URE en el subsector industrial de textiles”. Bogotá, Colombia, 2002.
4. R. Rivero, Identificación de sistemas de segundo orden. Buenos Aires: Universidad Tecnológica Nacional, Facultad Regional Tucumán, 2011.
5. S. Kim, A. Kumar, J. L. Dorrity and G. Vachtsevanos, “Fuzzy modeling, control and optimization of textile processes”, in Fuzzy Information Processing Society Biannual Conference, Industrial Fuzzy Control and Intelligent Systems Conference, and the NASA Joint Technology Workshop on Neural Networks and Fuzzy Logic, pp. 32-38, 18-21., 1994.
6. Universidad Politécnica de Madrid (UPM), Lugar de las raíces. Departamento de Electrónica, Automática e Informática Industrial, España, 2010.
7. UNITRONICS, “VisiLogic - Software Manual”. (2004, diciembre). [En línea] disponible en http://www.unitronics. com/.
8. M. Betancur, “Moodle: laboratorios procesos continuos”, Universidad Pontificia Bolivariana. Medellín, Colombia, 2012.
9. A. Landro, “Estadística”, Maestría en Finanzas - Universidad del CEMA, 2011.
10. M. Hernández, et al., “Estabilización de sistemas de orden n con un polo inestable y tiempo de retardo, basado en un esquema predictor observador”, en Congreso Anual de la Asociación de México de Control Automático. Puerto Vallarta, Jalisco, México, 2010.
11. M. Modesti, et al., “Modelamiento e implementación de control a lazo cerrado por medio de redes de comunicación de datos”, Universidad Tecnológica Nacional - Grupo de Investigaciones en informática para la ingeniería. Córdoba, Argentina, 2011.
12. J. Ibánez, et al., “Breve estudio de la Estabilidad y Criterios de Estabilidad en Sistemas Continuos”, Universidad Politécnica de Madrid - ETSII, 2005.