DOI:
https://doi.org/10.14483/22484728.5509Publicado:
2013-12-09Número:
Vol. 7 Núm. 2 (2013)Sección:
Visión InvestigadoraColector solar de placa plana de paso doble con lecho poroso
Flat plate solar collector of porous bed double step
Palabras clave:
Solar collector, porous bed, model, thermofluid, hot air (en).Palabras clave:
Colector solar, lecho poroso, modelo, termofluido, aire caliente (es).Descargas
Referencias
. K. Sopian Supranto, W. R. W Daud, M. Y. Othman y B. Yatim, “Thermal performance of the double-pass solar collector wiht and wihtout porous media”, Renewable Energy, vol. 18, no. 4, pp. 557-64, 1999.
. J. Duffie y W. Beckman, Solar engineering of thermal processes, Wisconsin: Willey, 2006.
. B. Paul y J. S. Saini, “Optimization of bed parameters for packed bed solar energy collection system”, Renewable Energy, vol. 29, no. 11, pp. 1863-76, 2004.
. Agua Matter, Desalación por destilador y osmosis inversa [en línea], disponible: http://www.acquamatter.com/desalacion_del_agua.htm, consultado el 18 de febrero de 2011.
. Proyecto y Obra: Energía solar: aplicaciones en arquitectura [en línea], 2000, disponible: www.proyectoyobra.com, consultado el 18 de febrero de 2011.
. G. Cifuentes, C. Marín y D. Muños, “Behavior of the temperature of the flow of air in a solar absorber”, Biotecnología en el Sector Agropecuario y Agroindustrial, vol. 7, no. 2, pp.32-39, 2009.
. Y. Cengel, Transferencia de calor y masa, México: Mc Graw-Hill, 2007.
. D. Dewitt y F. Incropera, Fundamentos de tranferencia de calor y masa, Estados Unidos: Wiley, 2002.
. N. S. Thakur, J. S. Saini y S. C. Solanki, “Heat transfer and friction correlation for packed bed solar air heater for a low porosity sistem”, Solar Energy, vol. 74, no. 4, pp. 319-329, 2003.
. L. Varshney y J. S. Saini, “Heat transfer and friction factor correlations for rectangular solar air heater duct packed with wire mesh screen matrices”, Solar Energy, vol. 62, no. 4, pp. 255-65, 1998.
. M. K. Mittal y L. Varshney, “Optimal thermohydraulic performance of a wire mesh packed solar air heater”, Solar Energy, vol. 80, no. 9, pp. 1112-1120, 2006
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
COLECTOR SOLAR DE PLACA PLANA DE PASO DOBLE CON LECHO POROSO
FLAT PLATE SOLAR COLLECTOR OF POROUS BED DOUBLE STEP
Fecha de envío: mayo de 2013
Fecha de recepción: mayo de 2013
Fecha de aceptación: octubre de 2013
Arnaldo Verdeza V.
Ingeniero mecánico, Universidad Pontificia Bolivariana, Sede Montería, Colombia. MSc. en Ingeniería Mecánica, Universidad del Norte, Colombia. Docente de la Universidad del Norte, Colombia. Correo electrónico: averdeza@uninorte.edu.co
Jorge Mendoza F.
Ingeniero mecánico, Universidad Pontificia Bolivariana, Sede Medellín, Colombia. MSc. en Sistemas Energéticos, Universidad Pontificia Bolivariana, Sede Medellín, Colombia. Ph.D. en Ingeniería Mecánica, Universidad del Norte. Docente de la Universidad del Norte, Colombia. Correo electrónico jorgemmf@gmail.com, jorge.mendoza@upbmonteria.edu.co
Rafael Gómez V.
Ingeniero mecánico, Universidad Pontificia Bolivariana, Sede Montería, Colombia. MSc. en Ingeniería Mecánica, Fundación Universidad del Norte, Colombia. Docente de la Universidad del Norte, Colombia. Correo electrónico: rafael.gomez@upbmonteria.edu.co
Adrián Ávila G.
Ingeniero mecánico, Universidad del Norte, Colombia. MSc. en Ingeniería Mecánica, Universidad del Norte. Docente de la Universidad del Norte, Colombia. Correo electrónico: adrian.avila@upbmonteria.edu.co
Resumen
La utilización de aire caliente en diversos procesos hace necesario el desarrollo de investigaciones que hagan más eficientes y económicos los métodos de producirlo, donde la primera opción por evaluar son los colectores solares. Este trabajo desarrolla una modelación de un colector solar de placa plana y lecho poroso, empleando la solución de ecuaciones analíticas en diagramas de bloques, para estructurar un software que permite simular el comportamiento del colector en estado transitorio, bajo diversos parámetros. En la aplicación se evalúa teóricamente el comportamiento del lecho poroso, la eficiencia, la caída de presión, la distribución de temperaturas y los materiales empleados para su construcción. Esto permite un análisis del comportamiento térmico, con un error promedio comparado con resultados experimentales de 6 %. El modelo se valida experimentalmente, con datos de un colector real, donde se mantiene un flujo de aire de 0,119 kg/s y se varía la radiación entre 400 y 500 W/m2; se observa la distribución de temperaturas, la eficiencia térmica y las caídas de presión. En los resultados obtenidos se alcanzan temperaturas de 360 y 375 K en el aire de salida y caídas de presión de 10,27 y 14,27 Pa, con valores de eficiencia de 36,5 y 51,7%, respectivamente, para nivel de radiación. Esto demuestra la idoneidad de este tipo de colectores como una opción para captar energía solar.
Palabras Clave: Colector solar, lecho poroso, modelo, termofluido, aire caliente.
Abstract
The use of hot air in various processes, requires the development of research to make more efficient and economical methods of producing, where the first option to be evaluated are the solar collectors. As this work develops a modeling of a flat plate solar collector and porous bed using analytical equations solving in block diagrams to structure a software that can simulate the behavior in transient state manifold under various parameters (dimensional, known materials and environmental conditions). In the application to theoretically evaluate the behavior of the porous bed, efficiency, pressure drop, temperature distribution and material used for construction, allowing analysis of the thermal behavior, with an average error compared to experimental results 6%. The model is validated experimentally, with data from an actual collector, where they remain an airflow of 0.119 kg / s and radiation varies between 400-500 W/m2 and observe the temperature distribution, thermal efficiency and falls pressure. In the results reach temperatures of 360 and 375 K in the exhaust air and pressure drops of 10.27 and 14.27 Pa, recording efficiency values of 36.5 and 51.7% respectively for radiation level. This fact demonstrates the suitability of such collectors as an option to capture solar energy.
Keywords: Solar collector, porous bed, model, thermofluid, hot air
1. Introduccion
Los colectores solares para calentamiento de aire, aunque han sido objeto de estudios e investigación por numerosos autores a nivel mundial, no cuentan hasta la fecha con muchas aplicaciones industriales, aunque son bastante eficientes como medio de aprovechamiento del calor [1], asumiendo que la energía solar es “libre” de costos, de fácil obtención e inagotable, a pesar de los constantes cambios en el ambiente [2,3]. En este sentido, se cuenta con reducidas herramientas de simulación para la evaluación de su comportamiento. Un colector solar es un sistema de captación energética, en el que la energía solar incidente atraviesa una o varias capas de material transparente, antes de alcanzar una placa de absorción, donde la energía radiante es convertida en calor. Este es transferido por convección a un fluido de trabajo, el cual la transfiere a un medio de almacenamiento térmico. Este último es el que permite la posterior transformación del calor a un tipo de energía utilizable para cualquier proceso industrial o doméstico [4]. La energía solar se puede almacenar en diversos sistemas que se basan en los principios básicos de la naturaleza [5-7].
Una unidad de almacenamiento en lecho poroso o en lecho empacado, se basa en la capacidad calorífica de ciertos materiales ligeramente compactos, a través de los cuales se hace circular un fluido, generalmente aire, que remueve o adiciona el calor de la unidad de almacenamiento [5,8]. Un material poroso empacado es un sistema solido de calor sensible que consta de pequeñas unidades de material absolvente, amontonado en un contenedor. La forma de las unidades del material genera un vacío, lo que permite el paso de aire o de cualquier otro fluido a través del lecho, de un extremo a otro del contenedor.
El calor absorbido por material es transferido por contacto directo hacia el fluido de trabajo, con lo que se eliminan las pérdidas del intercambio de calor producidas por el equipo.
Así, se facilita la mejora en el rendimiento, al aumentar el área de transferencia de calor por unidad de volumen. Usualmente, esto va acompañado de un aumento en el coeficiente de transferencia de calor [2], además de aumentar el rendimiento térmico del colector. Asimismo, se genera un aumento en la caída de presión del sistema. En la actualidad, los materiales porosos empacados más empleados en colectores solares para el calentamiento de aire son: vidrio molido, lana de acero, mallas de aluminio, piedra caliza, gravilla, rocas o guijarros. El uso de cada material varía de acuerdo a parámetros de construcción del colecto.
En este tipo de colectores se presentan los tres tipos de fenómenos conocidos de transferencia de calor: la conducción, la convección y la radiación [9]. Fenómenos que se deben tener en cuenta para la construcción del software del colector solar de placa plana de doble paso, con material poroso empacado para el calentamiento de aire, donde los principales ítems son las dimensiones del colector, el material poroso empacado, la placa metálica absolvedora y el fluido de trabajo. Asimismo, hay que tener en cuenta parámetros que se relacionan indirectamente a la hora de la construcción de un colector [1]:
- Velocidad de circulación del fluido
- Caída de presión en el sistema
- Temperatura ambiente
- Pérdidas de calor debido a los materiales
- Factor de fricción generado entre el fluido y los materiales
- Rugosidad de los materiales
- Absortividad de los materiales y el fluido
- Transmitancia de los materiales y el fluido
- Emisividad de los materiales y el fluido
Se han desarrollado diversas configuraciones de colectores solares para el calentamiento de aire. Estos diseños no son capaces de reducir las pérdidas e incrementar la eficiencia térmica del colector. Por esta razón, se introdujo el concepto de material poroso, que ha sido usado para aplicaciones industriales y domésticos tales como sistemas de calefacción de hogares, secado de productos agrícolas y para la generación de energía eléctrica en países desarrollados, con el fin de mejorar aún más la eficiencia de estos colectores. El uso de colectores solares con doble paso se ha introducido para aumentar el área de transferencia y mejorar el rendimiento térmico [3, 9-11].
El objetivo principal de esta investigación fue simular y validar el funcionamiento térmicofluido de un colector solar de placa plana, de paso doble con lecho poroso para el calentamiento de aire en estado transitorio. Valga mencionar que el modelo se realizó a modo caja gris con las ecuaciones analíticas del proceso evaluado.
1.1. Materiales y métodos
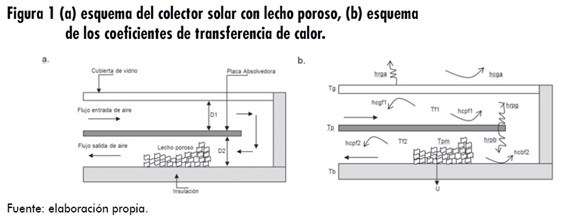
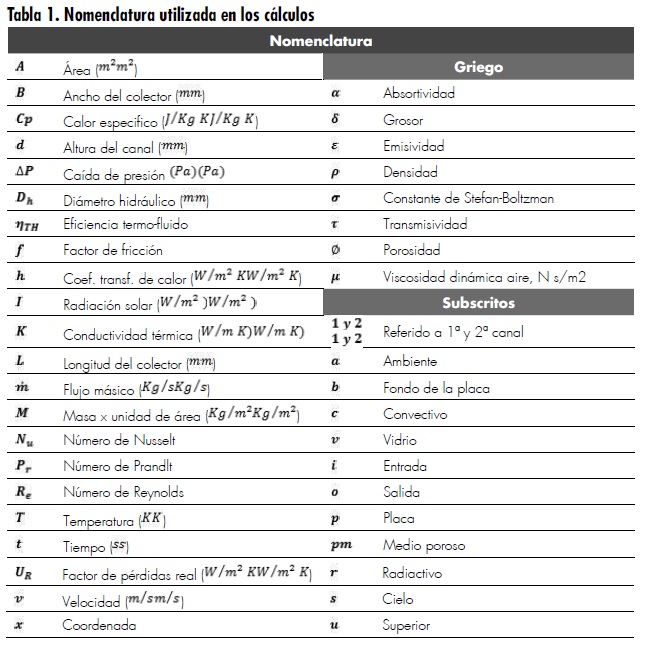
En la primera etapa se realizó un análisis termodinámico sobre el colector solar, donde se aplicaron ecuaciones de balance energético y de masa, de acuerdo a los fenómenos físicos presentes en cada componente del sistema. Teniendo en cuenta los conceptos termodinámicos y de transferencia de calor, se desarrolla un modelo matemático no estacionario (figura 1). Para simplificar el análisis, las ecuaciones de balance de energía se escriben de conformidad con los supuestos y la nomenclatura que se presentan en la tabla 1
- Las temperaturas de la cubierta y las placas varían solo en la dirección del flujo de aire (dirección x).
- Las pérdidas secundarias son insignificantes y las fugas de aire hacia o desde el colector también lo son.
- El aire se trabaja como gas ideal (calor específico constante).
- Se supone que el aire y el lecho sólido están en equilibrio térmico, es decir, la temperatura del lecho es igual a la temperatura del aire a nivel local. El valor de la conductividad térmica efectiva es una función de la porosidad.
Las siguientes son las ecuaciones que describen el comportamiento térmico de un colector solar de doble paso con lecho poroso:
- Balance energía a través de la cubierta de vidrio:
- Balance de energía en el flujo de aire entre la cubierta de vidrio y la placa absolvedora:
- Balance de energía a través de la placa absolvedora:
- Balance de energía en el flujo de aire entre la placa absolvedora y el fondo del colector:
- Balance de energía a través del fondo del colector:
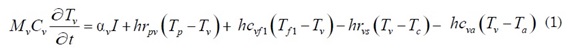
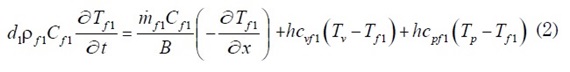
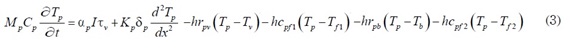
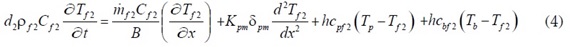
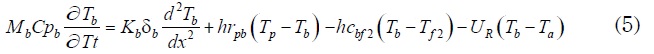
Las condiciones de frontera se obtienen con la condición de que no haya pérdida de calor desde los lados de la placa metálica. Una de las condiciones de estado es que la temperatura del aire en el punto de entrada, es igual a la temperatura ambiente, tales como:
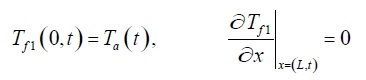
Las ecuaciones 1, 3 y 5 están sujetas a las siguientes condiciones de frontera:
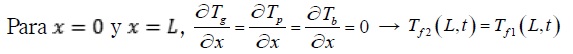
Los coeficientes de transferencia de calor radiactivo y convectivo deben ser conocidos, con el fin de resolver las ecuaciones anteriores. El coeficiente de transferencia de calor radiactivo es función de la temperatura de las superficies de ambos lados la cubierta de vidrio, la placa absolvedora y el fondo del colector.
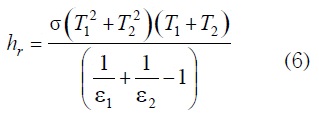
Mientras que el coeficiente de transferencia de calor por convección es función del parámetro adimensional conocido como número de Nusselt (Nu).
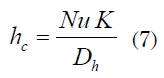
Donde Dh es el diámetro equivalente de los ductos (diámetro hidráulico). Para el caso de la sección donde no hay lecho poroso Dh se puede expresar como:
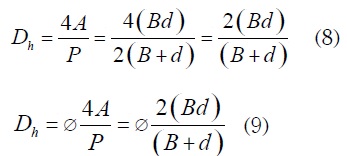
Nu, que es el número de Nusselt, está en función del número de Reynolds del flujo, el cual se expresa como:
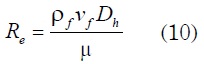
El flujo, dependiendo del número de Reynolds, se puede dividir en tres regímenes como:
- Régimen laminar (Re<2300)
- Régimen de flujo en transición (2300< Re<6000)
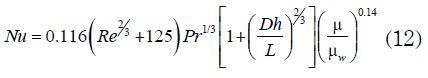
Donde μ está evaluada la temperatura de película y μw a la temperatura de las paredes del ducto.
- Régimen turbulento (Re < 6000)
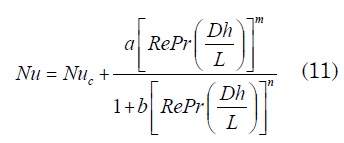
Donde las constantes son: a=0.0019; b=0.00563; m=1.71; n=1.17; Nu∞=5.4
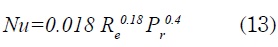
Donde Pr y K para cada una de las ecuaciones anteriores dependen de la temperatura del fluido.
La caída de presión total en el interior del colector se determina por la diferencia de presión antes y después del paso del fluido a través del lecho poroso ΔPpm la caída de presión producida por el paso de fluido en el primer ducto y a través de la UΔP1.
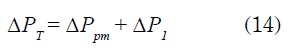
ΔPpm se calcula teniendo en cuenta la velocidad del fluido, la longitud de los ductos, la porosidad del material y el factor de fricción, y se expresa de la siguiente forma:
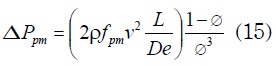
f es el factor de fricción y depende del tipo de material poroso utilizado. Si el material poroso es gravilla o piedra caliza, f se calcula:
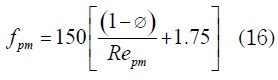
Si el material poroso es malla de alambre, f se calcula:
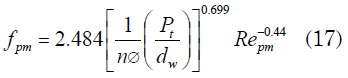
De es un valor característico longitudinal debido al material poroso y se obtiene de la siguiente ecuación:
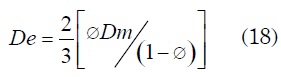
Dm es el diámetro equivalente del material poroso y se calcula:
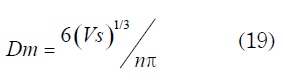
Donde Ds es el volumen total ocupado por el lecho y n es el número de partículas empleadas como lecho.
ΔP1 está definida como la diferencia entre la caída de presión en el primer ducto y la U, y depende directamente de la velocidad del fluido, la longitud del ducto y el factor de fricción que se presenta de acuerdo con el tipo de flujo generado (laminar o turbulento).
La eficiencia termo-fluido del colector se expresa como:
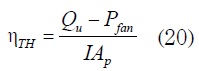
Donde Qu es la potencia térmica y se calcula:
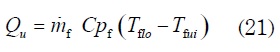
Y es la potencia del equipo de suministro del flujo de aire, para nuestro caso el ventilador, y se calcula:
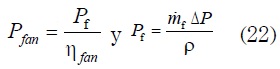
En la segunda parte se estudiaron las ecuaciones en estado transitorio y se seleccionan las correlaciones más adecuadas para describir los fenómenos físicos de transferencia de calor y mecánica de fluidos presentes, elaborando mapas conceptuales de cada balance en donde a cada término de esta se le anexó su respectiva correlación, restricciones y términos dependientes e independientes. Luego se procedió a la elaboración del modelo térmico en Matlab, mediante la aplicación Simulink, donde se ingresaron las ecuaciones junto con sus respectivas correlaciones, restricciones y términos dependientes e independientes.
Para validar el modelo teórico propuesto se realizarán comparaciones con resultados experimentales, obtenidos de un colector. El análisis de errores se llevará a cabo tomando los datos medidos y calculando, en términos de porcentaje, el error relativo y el error cuadrado. El porcentaje de error relativo (ER) y el error absoluto (EA) se define como:
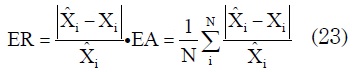
Donde &circleft; ; son los datos experimentales, Xi son los datos teóricos y N es el número de mediciones.
2. Resultados y discusión
Luego de la programación del modelo se procedió al ingreso de las propiedades y características del colector mostradas en la Tabla 2 para corroborarlas con los resultados experimentales.
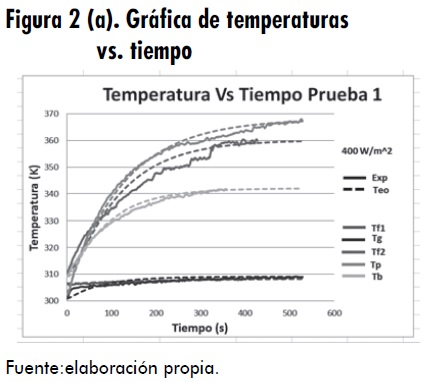
La Figura 2 (b). Gráfica de temperaturas vs. tiempo (a) muestra el rango de temperaturas obtenidas teóricamente, en líneas punteadas, las cuales se encuentran expresadas en Kelvin. De igual forma, se observa el comportamiento de las temperaturas teóricas Tf 1 y Tf 2 del aire en el colector, con valores máximos de 308,2 K (35,2°C) y 359,7 K (86,7°C) respectivamente, al igual que los valores de temperatura para Tp Tg y Tb, que alcanzaron valores de 367,2 K (94,2°C), 309 K (36°C) y 341,9 K (68,9°C). Esta prueba fue realizada con una radiación de 400 W/m2 y 0,119 kg/s.
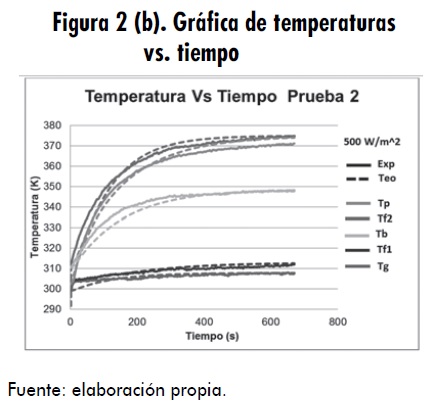
Por otra parte, la figura 2 (b) muestra las temperaturas teóricas Tf 1 y Tf 2 del aire en el colector, que alcanzaron un valor máximo de 312,5 K (39,5°C) y 375 K (102°C), respectivamente, al igual que los valores de temperatura para Tp Tg y Tb, que alcanzaron valores de 374 K (101°C), 307,7 K (34,7°C) y 348,3 K (75,3°C), realizada con una radiación de 500 W/m2 y el mismo flujo.
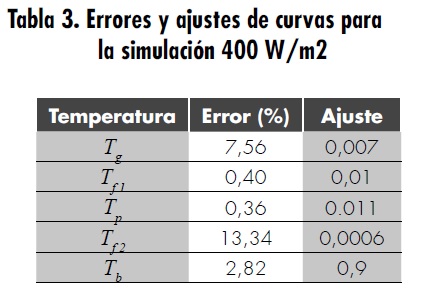
La tabla 3 muestra los valores obtenidos para el ajuste entre las curvas teórica y experimental, con una radiación de 400 W/m2. Además, el cálculo de los errores relativo y cuadrado promedio, obtenidos de cada ecuación, que se aproximan a los valores reales obtenidos experimentalmente para la primera prueba. El error absoluto del modelo para la primera prueba fue de 7,12 %.
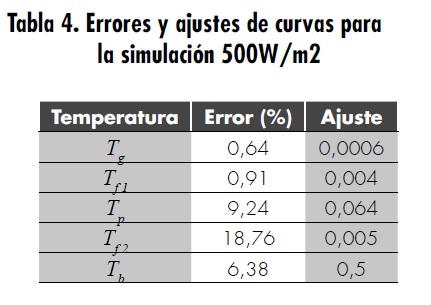
La tabla 4 ilustra los resultados para la segunda prueba; el error absoluto del modelo fue de 4,90 % (figura 3). Las diferencias en los resultados medidos y calculados para estas pruebas pueden provenir de errores en la parametrización del modelo, así como de las incertidumbres en las correlaciones utilizadas para el cálculo de los coeficientes de transferencia de calor. Las capacidades caloríficas de la cubierta de vidrio, la placa metálica y el fondo del colector también pueden influir en el análisis del modelo matemático y pueden introducir otra fuente de error. Además, no se incluyó la transferencia de calor por conducción en los componentes del colector y en el lecho, lo que también contribuye en gran manera a la incertidumbre de los errores.
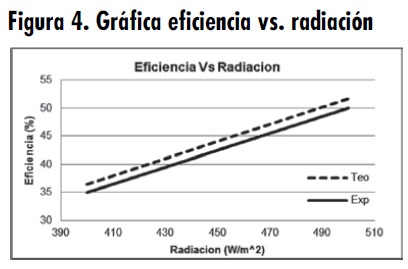
En cuanto a la eficiencia y caída de presión, la figura 4 muestra el comportamiento de la eficiencia termo-fluido obtenida en cada prueba, variando la radiación de 400 a 500 W/m2. En la figura 5 se puede observar que el comportamiento de la eficiencia térmica obtenida experimentalmente, con respecto a la eficiencia termo-fluido obtenida de manera teórica, tiende a ser lineal a medida que se aumenta la radiación. El valor máximo de eficiencia teórica obtenida para una radiación de 400 W/m2 fue 36,5% y para una radiación de 500 W/m2 fue 51,7%.
Los errores en la eficiencia fueron producto de las diferentes formas de cálculo. Las eficiencias experimentales se obtienen tomando en consideración la diferencia de temperatura entre la entrada y la salida de aire; en cambio, las eficiencias teóricas surgen teniendo en cuenta tanto la diferencia de temperatura entre la entrada y la salida de aire como la potencia del flujo de aire, lo que a la vez contribuye al aumento de la eficiencia. De igual forma, el grado de incertidumbre en las correlaciones utilizadas puede ser factor de error.
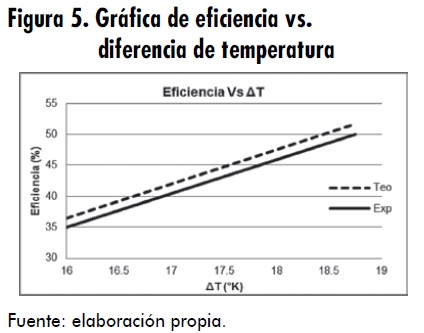
En la Figura 5. Gráfica de eficiencia vs. diferencia de temperaturaigura 5 se ilustra el comportamiento de la eficiencia termofluido obtenida en cada prueba, respecto a la diferencia de temperaturas entre la entrada y la salida de aire (Tf 1 y Tf 2) en el colector. Se puede observar que la eficiencia térmica obtenida experimentalmente tiende a ser lineal. A medida que aumenta la diferencia de temperatura entre la entrada y la salida de aire (Tf 1 y Tf 2) del colector, se incrementa la eficiencia. El valor máximo de eficiencia obtenida para una diferencia de temperatura de 16 K fue 36,5 % y para una diferencia de temperatura de 18,75 K fue 51,7 %. Los errores en la eficiencia teórica con respecto a la eficiencia experimental fueron del 4 %.
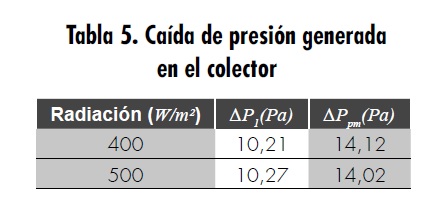
La tabla 5 muestra los resultados obtenidos de las caídas de presión que se generaron en el modelo a diferentes radiaciones. Se puede observar que el valor máximo de caída de presión entre el primer ducto y la U fue de 10,27 Pa, a 500 W/m2. De igual forma, la caída de presión generada en el lecho poroso alcanzó un valor máximo de 14,27 Pa, a una radiación de 400 W/m2.
3. Conclusiones
Al trabajar con este modelo se logró comparar el comportamiento del colector con los cálculos realizados por el modelo a dos niveles de radiación: 400 a 500 W/m2, y se obtuvo un aumento en la eficiencia de 29,4 % con un error promedio en sus cálculos de 6 %. De igual forma, se obtiene la eficiencia termo-fluido y la caída de presión a lo largo del recorrido del fluido en el interior de colector y la caída de presión generada por el lecho poroso. Son notables los efectos en la eficiencia del aumento de la radiación, sin dejar a un lado la diferencia de presión tanto en el lecho como en el colector. La distribución de temperatura obtenida demuestra que este tipo de colectores son una buena opción a la hora de almacenar energía.
Reconocimientos
A la Universidad Pontificia Bolivariana, Seccional Montería, por la financiación y asesoría en el desarrollo de esta investigación en integración energética.
Referencias
[1] K. Sopian Supranto, W. R. W Daud, M. Y. Othman y B. Yatim, “Thermal performance of the double-pass solar collector wiht and wihtout porous media”, Renewable Energy, vol. 18, no. 4, pp. 557-64, 1999.
[2] J. Duffie y W. Beckman, Solar engineering of thermal processes, Wisconsin: Willey, 2006.
[3] B. Paul y J. S. Saini, “Optimization of bed parameters for packed bed solar energy collection system”, Renewable Energy, vol. 29, no. 11, pp. 1863-76, 2004.
[4] Agua Matter, Desalación por destilador y osmosis inversa [en línea], disponible: http://www.acquamatter.com/desalacion_ del_agua.htm, consultado el 18 de febrero de 2011.
[5] Proyecto y Obra: Energía solar: aplicaciones en arquitectura [en línea], 2000, disponible: www.proyectoyobra.com, consultado el 18 de febrero de 2011.
[6] G. Cifuentes, C. Marín y D. Muños, “Behavior of the temperature of the flow of air in a solar absorber”, Biotecnología en el Sector Agropecuario y Agroindustrial, vol. 7, no. 2, pp. 32-39, 2009.
[7] Y. Cengel, Transferencia de calor y masa , México: Mc Graw- Hill, 2007.
[8] D. Dewitt y F. Incropera, Fundamentos de tranferencia de calor y masa, Estados Unidos: Wiley, 2002.
[9] N. S. Thakur, J. S. Saini y S. C. Solanki, “Heat transfer and friction correlation for packed bed solar air heater for a low porosity sistem”, Solar Energy, vol. 74, no. 4, pp. 319-329, 2003.
[10] L. Varshney y J. S. Saini, “Heat transfer and friction factor correlations for rectangular solar air heater duct packed with wire mesh screen matrices”, Solar Energy, vol. 62, no. 4, pp. 255-65, 1998.
[11] M. K. Mittal y L. Varshney, “Optimal thermohydraulic performance of a wire mesh packed solar air heater”, Solar Energy, vol. 80, no. 9, pp. 1112-1120, 2006.


.png)




.jpg)





