DOI:
https://doi.org/10.14483/22484728.5513Publicado:
2013-12-09Número:
Vol. 7 Núm. 2 (2013)Sección:
Visión InvestigadoraImplementacion de aritmetica de torres de campos finitos binarios de extension 2
Implementation of binary finite fields towers of extension 2
Palabras clave:
Field tower, finite field arithmetic, Galois field, computational arithmetic (en).Palabras clave:
Torres de campos, aritmética de campos finitos, campos de Galois, aritmética computacional (es).Descargas
Referencias
M. Merino, Una introducción a la criptografía. El Criptosistema R.S.A, I.E.S Cardenal López de Mendoza, 2004.
C. Ivorra C., Teoría de cuerpos de clases [en línea], Universidad de Valencia, 2008, disponible: www.uv.es/~ivorra/Libros/Cuerpos.pdf
L. Fuentes, Estudio y análisis de emparejamientos bilineales definidos sobre curvas ordinarias con alto nivel de seguridad, tesis de Maestría en Ciencias de la Computación, Centro de Investigaciones y Estudios Avanzados Cinvestav, Instituto Politécnico Nacional, Unidad Zacatengo, México D.F., 2011.
D. Hankerson, A. Menezes y S. Vanstone, Guide to elliptic curve cryptography, Springer-Verlag, 2004.
T. Itoh y S. Tsujii, “A fast algorithm for computing multiplicative inverses in GF(2m) using nomal bases”, Information and Computation, no. 78, pp. 171-17, 1988.
S. Baktir y B. Sunar, “Optimal tower fields”, IEEE trans, Comput. 53, no. 10, pp. 1231-43, 2004.
N. Cortez, Multiplicadores de arquitectura segmentada y su aplicación al cómputo de emparejamientos bilineales, tesis de Maestría en Ciencias de la Computación, Centro de Investigaciones y Estudios Avanzados Cinvestav, Instituto Politécnico Nacional, Unidad Zacatengo, México D. F., 2009.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
IMPLEMENTACIÓN DE ARITMÉTICA DE TORRES DE CAMPOS FINITOS BINARIOS DE EXTENSIÓN 2
IMPLEMENTATION OF BINARY FINITE FIELDS TOWERS OF EXTENSION 2
Fecha de envío: marzo 2013
Fecha de recepción: marzo 2013
Fecha de aceptación: mayo 2013
Fabián Velásquez
Ingeniero electrónico, Universidad de los Llanos, Colombia. MSc. (c) en Matemáticas Aplicadas, Universidad Eafit, Colombia. Profesor investigador, Grupo de Investigación Macrypt - Universidad de los Llanos, Colombia. Correo electrónico: fvelasquez@unillanos.edu.co
Javier F. Castaño
Ingeniero electrónico, Universidad de los Llanos, Colombia. Especialista en Diseño y Construcción de Soluciones Telemáticas, Universidad Autónoma de Colombia, Colombia. Profesor investigador, Grupo de Investigación Macrypt - Universidad de los Llanos, Colombia. Correo electrónico:jfcastano@unillanos.edu.co
Resumen:
En el presente trabajo se muestran los aspectos básicos de la aritmética de campos finitos binarios GF(2m) extendidos, usando el concepto de torres de campos GF(22m), en este caso con extensión 2 o cuadrática. El uso de torres de campos agiliza el cómputo de operaciones en los campos finitos, lo cual es aplicado en el cálculo de emparejamientos bilineales, parte fundamental de la criptografía basada en identidad. Se presentan los conceptos básicos de aritmética en GF(2m) y la construcción de las operaciones suma y multiplicación en campos binarios extendidos. De igual manera, se presentan los resultados de la implementación en un dispositivo FPGA XV5LX110T de Xilinx Inc., desarrollada usando lenguaje VHDL y la herramienta ISE Design Suite System Edition 13.4.
palabras Clave:
Torres de campos, aritmética de campos finitos, campos de Galois, aritmética computacional
Abstract:
The present work shows the basics of arithmetic of binary finite fields GF (2m), using the concept of extended towers of fields GF (22m), in this case with quadratic extension. Using field towers improve the computation of operations over finite fields, which is applied in the calculation of bilinear pairings, a main part of the identity- based cryptography; we present the basic concepts of arithmetic in GF (2m) and construction of operations addition, multiplication and multiplicative inverse in extended binary fields. Similarly presents the results of the implementation in a Xilinx FPGA device XV5LX110T, developed using VHDL language and tool ISE Design Suite System Edition 13.4.
Keywords:
Field tower, finite field arithmetic, Galois field, computational arithmetic
1. Introducción
En la actualidad la aplicación de matemática discreta, en especial de aritmética de campos finitos, es bastante amplia, principalmente en criptografía y codificación, técnicas de gran importancia en la tecnología moderna [1].
La criptografía es un área que se basa en algoritmos que, a su vez, se encuentran soportados en la aplicación, por ejemplo, de la teoría de Galois, la teoría de curvas modulares o el álgebra abstracta en general. La teoría de campos finitos proporciona operaciones en estructuras discretas, las cuales encajan perfectamente en los objetivos y necesidades de la criptografía. Para profundizar sobre el tema base remitimos al lector, por ejemplo, a [2].
De manera permanente, se presentan avances en esta área en dos frentes: la base matemática y la aplicación computacional. Uno de estos avances es la criptografía basada en identidad, que proporciona soluciones a diferentes problemáticas que posee el paradigma más usado hoy en día: la criptografía de clave pública.
La criptografía basada en identidad se encuentra totalmente definida en campos finitos, curvas modulares y, sobre todo, en la aplicación de torres de campos, estructura esta que permite precisamente construir de manera eficiente los emparejamientos bilineales, de cuyas propiedades surge la posibilidad de construir el concepto de identidad y su aplicación en criptografía.
En este trabajo se explican los conceptos básicos de aritmética en campos finitos y la construcción de torres de campos, se muestran los algoritmos requeridos y su enfoque computacional y, adicionalmente, se presentan los resultados de una implementación en FPGA de las operaciones suma, multiplicación e inverso multiplicativo en una torre de campo GF(22m). Estos resultados hacen parte de un proyecto global que busca la implementación funcional de criptografía basada en identidad en dispositivos FPGA, para su uso en diferentes entornos.
2. Estructuras algebraicas
Una estructura algebraica es un conjunto dotado de una o más operaciones binarias que cumple ciertas propiedades. Si el conjunto tiene finitos elementos se dice que la estructura algebraica tiene orden finito, de lo contrario tiene orden infinito. Entre las estructuras algebraicas más utilizadas en los algoritmos criptográficos están los grupos y los campos.
2.1. Grupos
Un conjunto G, dotado de una operación binaria*, ‹G,*›, que cumple las siguientes propiedades, tiene estructura algebraica de grupo.
- Clausurativa: a*b∈ G, ∀a,b ∈ G
- Asociativa: a*(b*c)=(a*b)*c,∀ a,b,c ∈ G
- Modulativa: ∃ e∈ G|a*e=e*a= a, ∀ a ∈G*
- Invertiva: ∃ a-1 ∈ G|a-1*a=e, ∀ a ∈ G
Si además de las propiedades anteriores se cumple la propiedad conmutativa, en la cual a*b=b*a, ∀ a,b ∈ G, entonces el grupo es abeliano.
En las aplicaciones criptográficas solo interesan los grupos de orden finito y en los cuales sus operaciones se realizan módulo un numero primo n, o módulo un polinomio irreducible f(x). Un subconjunto H de G que cumple las mismas propiedades de grupo se llama subgrupo y el orden de cualquier subgrupo de G divide al orden de G.
2.2. Anillos
Un anillo es un conjunto G dotado de dos operaciones binarias *, Δ De esta forma se genera una estructura algebraica ‹ G,*, Δ › que cumple las siguientes condiciones:
- La estructura algebraica ‹ G,* › es grupo abeliano.
- La estructura ‹ G, Δ › cumple las propiedades asociativa y clausurativa.
- El conjunto G dotado de las dos operaciones ‹ G,*, Δ › cumple la propiedad distributiva.
2.3. Cuerpos
Un conjunto G dotado de dos operaciones * y Δ que cumple las siguientes condiciones tiene estructura algebraica de campo:
- La estructura algebraica ‹ G,* › es grupo abeliano.
- El conjunto G con la operacion Δ es grupo abeliano
- La estructura ‹ G,*, Δ › cumple la propiedad distributiva a derecha e izquierda.
Los campos aplicados a la criptografía son aquellos que tienen orden finito, también llamados campos de Galois o campos finitos. La aritmética en estos campos permite, por ejemplo, las operaciones de suma y multiplicación de puntos racionales en la criptografía de curvas elípticas, ya que estos tienen estructura de grupo finito aditivo abeliano y las curvas elípticas se definen sobre campos de Galois [3]. La eficiencia, la velocidad y el espacio ocupado en un procesador por la aritmética de campos finitos constituyen un factor imprescindible en el momento de elegir un algoritmo para la implementación de cualquier operación en el campo. La investigación en esta área se encamina a lograr mayor eficiencia, tanto en la representación de los campos finitos como en la implementación de aritmética en estos campos, en software y en hardware.
3. Aritmética en campos finitos
3.1. Aritmética en campos finitos binarios GF(2m)
3.1.1. Conceptos de bases polinomiales
Si se considera una extensión finita F = Fqm del campo finito K=Fq como un espacio vectorial sobre K, entonces F tiene dimensiónm sobreK, y si (α1 ,α2... αm) es un conjunto de m elementos que forman una base de F sobre K, entonces cada elemento α ∈ Fse puede representar de forma única como: α = c1α1+ cm αm donde cj ∈ K 1 < j < m, de acuerdo con la noción tradicional de espacio vectorial y base de espacio vectorial. Se puede establecer la siguiente correspondencia lineal de F en K mediante la función traza TrF/K(α) sea K un campo finito y tómese una extensión finita de K. La base polinomial (1, α, α2...αm-1) es construida con las potencias de un elemento definitorio α de F sobre K, donde el elemento α es un elemento primitivo de F Con esta base se representan los elementos de un campo finito mediante polinomios con coeficientes ai ∈ Fq que pertenecen al campoK y las potencias de los elementos de la base. Cada polinomio es una clase residual módulo el polinomio irreducible, es decir:
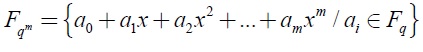
3.1.2. Multiplicación
Dos elementos A,B ∈ GF (2 m) con polinomio irreducible p(x) son representados en la forma de polinomios:
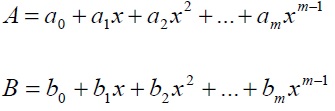
El producto C = A*B se representa como:
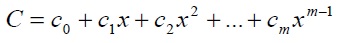
De esta expresión puede notarse que el producto C tiene el mismo grado que los operandos A y B, lo cual se debe a que son elementos de un campo finito.
Para realizar la multiplicación entre dos elementos de un campo finito con representación en base polinomial, se realiza la multiplicación normal de polinomios, lo que origina un polinomio de grado máximo 2m-2. Como puede observarse, este polinomio no pertenece al campo finito, por lo cual se implementa una reducción módulo el polinomio irreducible. Dado que la multiplicación de polinomios se puede realizar paso a paso, este tipo de multiplicadores se denominan seriales [4].
El otro enfoque es tomando el polinomio irreducible para generar una base, calcular las expresiones que generan cada uno de los coeficientes del resultado de la multiplicación, la cual por lo tanto se puede implementar en paralelo [4].
3.1.3. Adición en GF (2m)
Dados dos elementos:
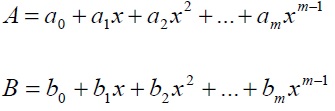
En el campo finito GF(2m), entonces A+B=C=c0+c1x+c2x2+...cmxm, donde ci=(ai+bi)mod2 lo que equivale a la operación XOR bit a bit.
3.1.4. Inverso multiplicativo GF(2m)
Para el caso del inverso multiplicativo se implementa el algoritmo de Itoh-Tsujii [5], el cual en forma recursiva realiza la exponenciación del valor al cual se le va a calcular el inverso multiplicativo. La expresión general para calcular el inverso multiplicativo, se deriva de la siguiente forma:
Dado un elemento A∈GF(2m), existe un elemento A-1 tal que se cumple AA-1=e, siendo e el elemento neutro de la operación producto, en este caso e = 1 = z0.La operación inversión es importante en sí misma y también para la implementación de la división, ya que:

Para esto es necesario calcular el inverso de B y luego realizar una multiplicación. La inversión es la operación más difícil de implementar en aritmética de campos finitos.
Existen dos tipos de algoritmos de inversión: basados el teorema extendido de Euclides y sus variantes y otros basados en multiplicaciones en el campo. Si se opta por un método basado el algoritmo extendido de Euclides, la complejidad computacional es bastante alta, lo que impacta directamente en el diseño. Si se opta por un método basado en multiplicaciones, se utiliza la función de multiplicación reduciendo la complejidad computacional.
La idea principal del inversor implementado radica en el “pequeño Teorema de Fermat”, el cual indica que para todo elemento no cero en un campo F2m
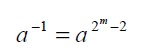
Esto se demuestra ya que por las propiedades de los campos F2m
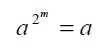
y haciendo una sustitución se llega a la expresion anterior. La expresión puede rescribirse como
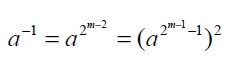
De esta manera, se puede reducir la complejidad de la inversión a un número menor de elevaciones al cuadrado.
Itoh y Tsujii [5] propusieron una ingeniosa manera de reducir aún más la complejidad de la operación, haciendo una nueva sustitución de tal forma que se obtienen las fórmulas:
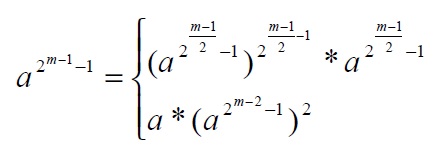
El primer caso es param impar y el otro para m par.
3.2. Aritmética en torres de campos
Las torres de campos surgen a partir del trabajo de Baktir y Sunar [6], quienes aportaron una forma eficiente de abordar la representación y las operaciones en campos finitos.
Una torre de campo es la extensión a su vez de un campo de extensión Fp / f (x) con característica p, es decir, un campo primo Fp que ha sido extendido módulo un polinomio irreducible f (x) de grado n. El campo de extensión F p / f (x) p se extiende módulo otro polinomio irreducible g(x) de grado n /m, generando un campo con un número mayor de elementos. La representación en torres de campos permite la ejecución de las operaciones suma y multiplicación en forma más eficiente, las cuales son ideales para la implementación de emparejamientos bilineales que presentan una alta complejidad computacional por causa del número elevado de operaciones en el campo de extensión donde se representan los polinomios en forma binaria.
La extensión cuadrática (de orden 2) del campo finito GF(2m) está representada como:
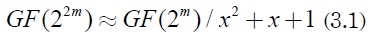
En este caso se realiza una extensión 2 del campo GF(2m), que da como resultado la torre de campo GF((2m)2) y, finalmente, GF(22m) De esta manera, un campo finito de característica 2, con m par, puede ser expresado en forma de torre de campo. Por ejemplo, el campo finito GF(28) puede ser expresado como la torre de campo GF((24)2) reduciendo la complejidad de la aritmética de GF(28) a GF(24)
3.2.1. Suma en GF(22m)
Dados dos elementos a y b que pertenecen a GF(22m) se calcula a + b aplicando el algoritmo siguiente, el cual requiere dos sumas en GF(2m)

3.2.2. Multiplicación en torres de campos
La multiplicación de dos elementos a,b que pertenecen a GF(22m), definida como (a0+a1u)(b0+b1u)=(a0b0+a1b1β)+(a0b1+a1b0 )u es implementada eficientemente, usando el método de Karatsuba-Ofman, en donde
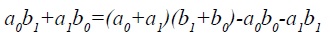
Esto se realiza mediante el algoritmo 3.2.

El algoritmo 3.2 requiere en total tres multiplicaciones y cinco sumas en GF(2m), así como un producto entre un elemento a0∈GF(2m) por la constante β de la ecuación (3.1).
3.2.3. Inverso multiplicativo en GF(22m)
El cálculo del inverso se realiza mediante el algoritmo 3.3, el cual requiere una inversión, tres multiplicaciones, dos sumas y una elevación al cuadrado en GF(2m) Sea un elemento
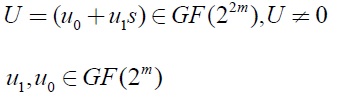
Su inverso multiplicativo se define como
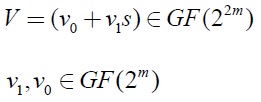
Dado que UV = 1, se tiene que
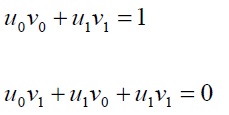
La solución de este sistema de ecuaciones, es
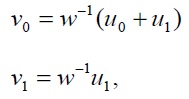
Donde
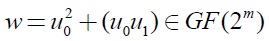

4. Resultados
La implementación se realizó sobre un dispositivo XV5LX110T de Xilinx, usando una tarjeta de desarrollo XUPV5 de Digilent. Para el desarrollo y simulación se usó el entorno ISE Design Suite 10.1 de Xilinx y descripción en VDHL.
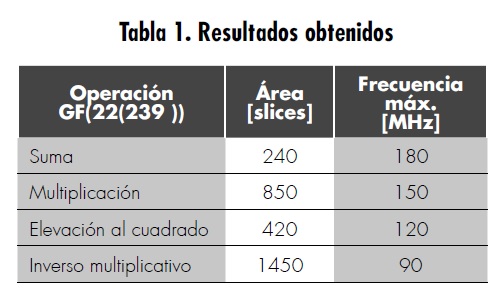
En la tabla 1 se presentan los resultados de la implementación, especificando la ocupación de área para cada módulo desarrollado para aritmética en GF((2m)2), con m = 239. Se especifican los resultados de la simulación post-place and route, realizada con el software ISE Design Suite 13.4 System Edition de la empresa Xilinx. Los resultados se expresan en términos de área ocupada en slices y frecuencia máxima de operación. Para cada caso la síntesis se realizó eligiendo la optimización respectiva, por área o por velocidad, como parámetro definido en el software de desarrollo. Por lo tanto, se presentan los mejores resultados posibles con dicha herramienta en ambos aspectos.
Para esta implementación se eligió un campo finito GF(2239), extendido en forma de torre de campo GF(22(239)). Las operaciones se realizan empleando los algoritmos 3.1, 3.2 y 3.3 en la torre de campo, usando operaciones suma, producto e inverso multiplicativo en el campo base GF(2239). La operación suma en el campo base se implementó eficientemente mediante la operación XOR bit a bit, mientras que la multiplicación en el campo se implementó mediante el algoritmo bit-serial, que requiere m ciclos de reloj para obtener el resultado final, [4]. El cálculo del inverso multiplicativo se implementó mediante el algoritmo de Itoh-Tsujii. Se tomaron como base los módulos de aritmética de campos finitos desarrollados por el grupo Macrypt de la Universidad de los Llanos.
5. Conclusiones
El concepto de torres de campos ha cobrado enorme importancia recientemente, debido a su gran utilidad, principalmente en el cálculo de emparejamientos bilineales, operación fundamental para la criptografía basada en identidad. Este nuevo paradigma, con fuerza avanza como la solución real a los múltiples problemas de la criptografía de clave pública.
Por esta razón es muy importante entender e implementar la aritmética en torres de campos en forma eficiente, en entornos como sistemas embebidos, microcontroladores y dispositivos fpga.
Se inició el trabajo en el entendimiento e implementación de este conjunto de técnicas, en este caso en dispositivos FPGA. Se logró evidenciar que, efectivamente, la aplicación de torres de campos reduce la complejidad de la aritmética en campos finitos, siempre y cuando se pueda escribir el campo finito requerido como una extensión cuadrática de un campo más pequeño.
6. Trabajo futuro
Como trabajo a corto plazo se tiene definida la implementación de otras operaciones en campos finitos, que se requieren para la implementación de emparejamientos bilineales, en este caso el cálculo de exponenciaciones, raíces cuadradas y cúbicas, así como la solución de ecuaciones cuadráticas. Esto enmarcado en el proyecto general que tiene como objetivo la implementación completa de criptografía basada en identidad en dispositivos FPGA para su aplicación en diferentes entornos como herramienta de seguridad informática. En el conocimiento de los autores de este trabajo, revisado el estado del arte en Colombia, puede afirmarse que este es el primer referente en el área de aritmética de torres de campos y de implementación de criptografía basada en identidad.
Reconocimientos
Los autores expresan sus reconocimientos a la Dirección General de Investigaciones de la Universidad de los Llanos, la cual financia el proyecto de investigación “Implementación en FPGA de criptografía basada en identidad”, en el marco del cual se obtienen los resultados presentados en este trabajo.
Referencias
[1] M. Merino, Una introducción a la criptografía. El Criptosistema R.S.A, I.E.S Cardenal López de Mendoza, 2004.
[2] C. Ivorra C., Teoría de cuerpos de clases [en línea], Universidad de Valencia, 2008, disponible: www.uv.es/~ivorra/ Libros/Cuerpos.pdf
[3] L. Fuentes, Estudio y análisis de emparejamientos bilineales definidos sobre curvas ordinarias con alto nivel de seguridad, tesis de Maestría en Ciencias de la Computación, Centro de Investigaciones y Estudios Avanzados Cinvestav, Instituto Politécnico Nacional, Unidad Zacatengo, México D.F., 2011.
[4] D. Hankerson, A. Menezes y S. Vanstone, Guide to elliptic curve cryptography, Springer-Verlag, 2004.
[5] T. Itoh y S. Tsujii, “A fast algorithm for computing multiplicative inverses in GF(2m) using nomal bases”, Information and Computation, no. 78, pp. 171-17, 1988.
[6] S. Baktir y B. Sunar, “Optimal tower fields”, IEEE trans, Comput. 53, no. 10, pp. 1231-43, 2004.
[7] N. Cortez, Multiplicadores de arquitectura segmentada y su aplicación al cómputo de emparejamientos bilineales, tesis de Maestría en Ciencias de la Computación, Centro de Investigaciones y Estudios Avanzados Cinvestav, Instituto Politécnico Nacional, Unidad Zacatengo, México D. F., 2009.


.png)




.jpg)





