Evaluación de la seguridad estructural de un sistema de seguimiento solar en colombia

EVALUACIÓN DE LA SEGURIDAD ESTRUCTURAL DE UN SISTEMA DE SEGUIMIENTO SOLAR EN COLOMBIA

EVALUATING STRUCTURAL SAFETY SOLAR TRACKING SYSTEM IN COLOMBIA

Fecha de envío: mayo de 2013
Fecha de recepción: mayo de 2013
Fecha de aceptación: octubre de 2013

Heylen Polo C.

Ingeniera mecánica, Universidad del Atlántico, Colombia. Miembro del grupo “Dimer”, Universidad del Atlántico, Colombia. Correo electrónico:hapolo@mail.uniatlantico.edu.co

Ambrosio Valencia R.

Ingeniero mecánico, Universidad del Atlántico, Colombia. Miembro del grupo “Dimer”, Universidad del Atlántico, Colombia. Correo electrónico: avalencia@mail.uniatlantico.edu.co

Javier Roldan M.

Ingeniero mecánico, Universidad del Atlántico, Colombia. Miembro del grupo “Dimer”, Universidad del Atlántico, Colombia. Correo electrónico:javierroldan@mail.uniatlantico.edu.co

James Díaz G.

Ingeniero mecánico, Universidad del Atlántico, Colombia. MSc. en Ingeniería mecánica, Universidad de Puerto Rico, Mayagüez, Puerto Rico. Ph.D. en Ingeniería Mecánica, Universidad de Florida, Estados Unidos. bmt Designers and Planners, Colombia. Correo electrónico: jjadigo@gmail.com

Resumen:

Para un mayor aprovechamiento de los sistemas de solares, es indispensable un adecuado dimensionamiento de cada uno de los componentes que los conforman. El presente trabajo describe una metodología para la seguridad de una estructura soporte para panel fotovoltaico con seguimiento solar y su integración a una interfaz gráfica de usuario-GUI desarrollada en Matlab®, la cual, de manera didáctica y a través de un entorno visual amigable e interactivo, reúne los parámetros mecánicos básicos que influyen en el factor de seguridad de la estructura, con la opción de adaptarse a las condiciones de operación del sistema. Usando SolidWorks®, se comparan los resultados de factor de seguridad obtenidos versus análisis de elementos finitos (FEA).

Palabras Clave:

Panel orientable, seguridad estructural, carga del viento, factor de seguridad, interfaz gráfica de usuario, análisis de elementos finitos.

Abstract:

An appropriate dimensioning of each component in a tracking solar system is needed to take maximum advantage of the solar panel. This work describes a methodology for the safety of a support structure of a photovoltaic panel with solar tracking, which is integrated into a graphical user interface-GUI written in Matlab®. In a very intuitive manner and through a friendly interactive visual tool, the GUI gathers the basic mechanical parameters that influence the safety factor of the structure, with the possibility to configure several operating conditions of the system. The results were compared to those found using finite element analysis-FEA with SolidWorks®.

Keywords

Swiveling panel, structural safety of the wind load, the safety factor, GUI, finite element analysis.

1. Introducción

Utilizar paneles solares con el fin de captar energía es imprescindible para disminuir la actual dependencia de los combustibles fósiles. De esta manera, se garantiza la sostenibilidad energética [1]. La excelente orientación de un panel permite la óptima captación de rayos solares, mejorándose con ello el porcentaje de conversión de energía solar a eléctrica y, así también, una adecuada valoración del desempeño de diseño bajo la acción del viento es fundamental para ajustar las dimensiones finales con base en los márgenes de seguridad estructural [2]. Partiendo de un análisis de esfuerzos en la base de la estructura, para diferentes ángulos de inclinación y carga de viento, es posible determinar la situación crítica en la cual opera el sistema. Luego es posible proceder a evaluar la resistencia de cada componente y determinar dimensiones adecuadas según condiciones de entorno.

La utilidad de una interfaz gráfica de usuario (GUI) sobre la plataforma de Matlab®, en el desarrollo de un proyecto, consiste en la capacidad de proporcionar comunicación visual interactiva con las operaciones y procesos de solución [3], siendo el mayor beneficio la posibilidad de post-procesar resultados de la simulación, proporcionando con ello una retroalimentación rápida.

Como objetivo principal de esta investigación se tiene el desarrollo de una herramienta computacional capaz de incluir todas las variables incidentes en el cálculo de los factores de seguridad de un modelo estructural para panel solar orientable. Luego de estimar la inercia del sistema y las cargas presentes, se utiliza la interfaz desarrollada para dimensionar la estructura en diferentes condiciones de trabajo y entornos locales y, asimismo, comprobar los resultados obtenidos en la fatiga, realizando cálculos con diferentes criterios de falla en un análisis de elementos finitos en Solid Works®. Este trabajo compone la etapa inicial en el futuro diseño de detalle, construcción y puesta en marcha de un sistema de seguimiento solar.

2. Materiales y métodos

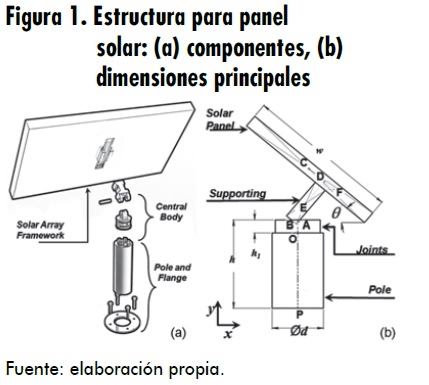
La forma genérica de las estructuras para panel solar orientable propone tres partes principales: 1) columna con base de apoyo, 2) cuerpo central y 3) marco para modulo solar [4] (figura 1).

La columna es diseñada con sección transversal circular hueca, con la finalidad de optimizar la cantidad de material [5]. En el cuerpo central se ubican las juntas revoluta activas de movimientos cenital y acimutal. El marco es el encargado de sostener los paneles solares. Las cargas para el diseño de la estructura serán las máximas esperadas de acuerdo con la condición de trabajo [6]. La rigidez de la estructura debe limitar deflexiones y cualquier deriva ante la carga del viento. Asimismo, cualquier otra deformación que propicie una falla funcional. Sobre el modelo estructural actúan tanto cargas determinísticas (peso del panel solar, peso de las juntas, etc.) como cargas estocásticas (fuerzas ambientales).

Se evalúa la carga debido al viento, a partir de la investigación desarrollada por el Solar Energy Research Institute (SERI) [7], donde se analiza el comportamiento de esta al variar ángulos de inclinación y azimut de los paneles. La magnitud F de la carga del viento se determinó como:

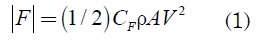
Donde C_F es el coeficiente adimensional de fuerza, ρ la densidad del viento, A el área sometida y V la velocidad del viento. Ante carga estática, el valor de la velocidad del viento corresponde al valor máximo registrado según el entorno, mientras que el valor utilizado para el análisis de cargas variables es el valor nominal según el tipo de terreno en operación normal [6], dado por:

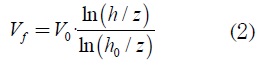
donde V₀es la velocidad de referencia medida a la altura h₀, h es la altura del centro del panel, y z es la rugosidad superficial del terreno en metros [6]. La velocidad de referencia es la velocidad máxima registrada, la cual corresponde a una altura de 10 m [6].

La ecuación (1) aplica para componentes perpendiculares y tangenciales al panel solar. Se consideró el peso del panel W_sp y el peso del elemento de apoyo W_BD. Para determinar los valores críticos a los que está sometida la columna bajo cargas estáticas, se utilizó el criterio de energía de distorsión de Von Mises. En la ecuación (3), S_y el límite elástico del material de la columna y FS el factor de seguridad. Las cuatro partes básicas que considerar son la columna, la placa base, los pernos de anclaje y la soldadura de la placa base con la columna.

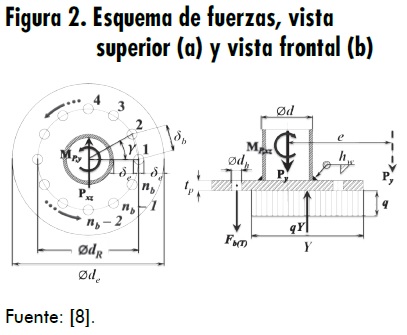
Las dimensiones de la placa base dependen directamente de la cantidad de pernos que el diseño solicite [8]. La Dirección de Seguridad y Salud Ocupacional de Estados Unidos (OSHA: Occupational Safety and Health Administration) impone el uso de mínimo cuatro pernos de anclaje en la placa base [8,9]. Esta debe ser circular, debido a la presencia de diferentes tipos de carga (figura 2) [8].

Ante la presencia de momentos flectores elevados, lo que es común en componentes bajo cargas sísmicas y cargas debido al viento, se cumple que:

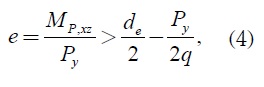
donde e es la excentricidad de la carga y q la presión de apoyo. Los esfuerzos mínimo y máximo resultantes para cargas combinadas se hallan igualmente a partir de la fórmula del criterio de energía de distorsión de Von Mises (ecuación 3).

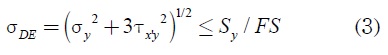
Los valores medio y alterno son, respectivamente [5]:

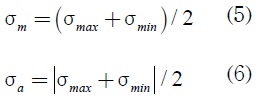
En trabajos anteriores [10], la curva ASMEelíptica (ecuación 7) fue el criterio seleccionado para obtener el factor de seguridad en fatiga n_f, para lo que se considera vida infinita (número de ciclos de esfuerzo N > 10⁶) [5].

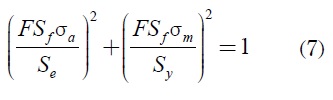
Con el fin de corroborar los resultados obtenidos por el criterio inicial seleccionado, se ha optado por evaluar la fatiga con los criterios de Goodman modificado, Soderberg y Gerber (ecuaciones 8, 9 y 10, respectivamente) [5]:

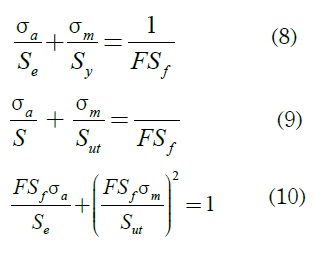
donde S_e es el límite de resistencia a la fatiga. De igual manera, se evaluó la resistencia a la fatiga de la soldadura y los pernos. Para la primera, S_e=S_sew, con S_sew resistencia al esfuerzo cortante en fatiga [5], teniendo presente los factores de Marín: k_a, k_c, k_d y k_e y S_sut=0,67S_ut

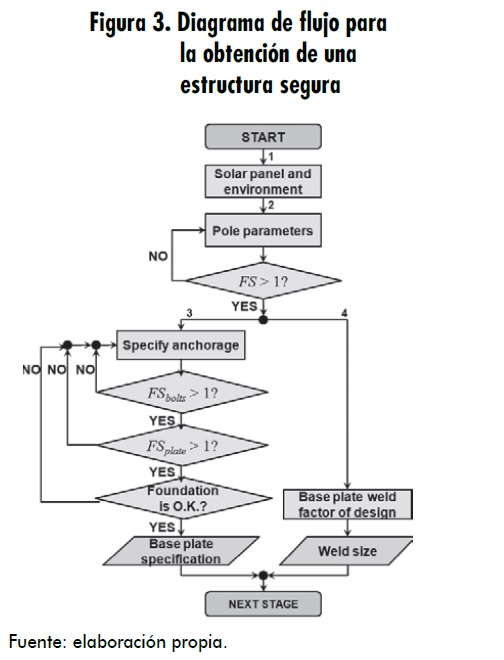
A partir del análisis mostrado en trabajos anteriores [10], se definieron cuatro pasos para la evaluación de la seguridad de la estructura:

1. Selección del panel solar (potencia pico absorbida, dimensiones), especificación del entorno (ciudad y tipo de terreno) y ángulo de inclinación máximo alcanzado, según horario de operación.
2. Selección de diámetro y material de tubería estructural de fábrica y especificación de la altura de la columna, donde el valor mínimo depende de la operación del panel.
3. Especificación de diámetro y cantidad de pernos, longitud del anclaje, espesor de placa base y materiales.
4. Especificación del factor de diseño de la soldadura y del material de aporte.

Asimismo, mediante el diagrama de flujo presentado en la figura 3, se indican los pasos que seguir para una correcta evaluación, con el fin de obtener seguras configuraciones. El pantallazo de la interfaz se muestra en la figura 4.

DESPLIEGUE DE FIGURA 4

3. Resultados

Con el fin de mostrar la utilidad y flexibilidad de la herramienta y comparar los resultados con los obtenidos por medio de análisis de elementos finitos, se evaluó la seguridad de la estructura propuesta considerando el lago Calima, a las afueras de la ciudad de Cali, Colombia, como un potencial sitio de instalación.

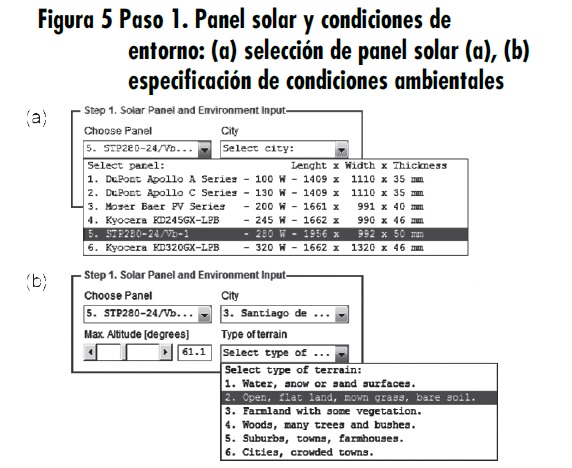
Paso 1: panel solar y condiciones de entorno. Para un horario de operación del panel de 9:00 a. m. a 4:00 p. m., mayor incidencia de la radiación solar, este alcanza un ángulo cenital máximo absoluto de inclinación θ (figura 1), aproximado, de 61.1 grados, respecto al marco de referencia. Este valor se obtiene a partir de datos, tomando como ejemplo el día 7 de enero de 2013, en las coordenadas 3° 27′ N, 76° 32′ W (Cali, Colombia), 5:00 horas al oeste de Greenwich (hora colombiana), usando la base de datos del Observatorio Naval de los Estados Unidos de América [11]

La referencia del panel solar seleccionado es “SuntechSTP280-24/Vb-1”, con potencia máxima absorbida de 280 W, dimensiones de área de 1956 × 992 mm y espesor de 50 mm (figura 5a). El tipo de terreno que más se ajusta a los alrededores del lago Calima es “Terrenos abiertos: pastos bajos, aeropuertos, cultivos bajos”, lo que determina el valor de rugosidad superficial [6] (figura 5b). La interfaz desarrollada también permite evaluar las ciudades de Barranquilla, Medellín, Bogotá y Bucaramanga.

Paso 2: diseño de la columna. A partir de catálogos de fabricantes y distribuidores locales de tubería estructural, se selecciona aquella de 2 1/2” fabricada por Steckerl Hierros y Aceros, con diámetro y espesor de 72,4 y 2,0 mm, respectivamente. Solo se ofrece el material ASTM A-500 grado C, con esfuerzo de tensión último de 430 MPa. La altura de la columna ingresada es de 0,45 m, teniendo en cuenta que, en función del tamaño de panel y la inclinación máxima de operación, existe un valor mínimo que permite que el panel no choque con el suelo en medio de la operación. El factor de seguridad obtenido ante carga estática es de 2,8136 y para el análisis de fatiga, según criterio ASME-elliptic: 2,34874, Goodman modificado: 2,03224, Soderberg: 1,92729 y Gerber: 234126 (figura 6).

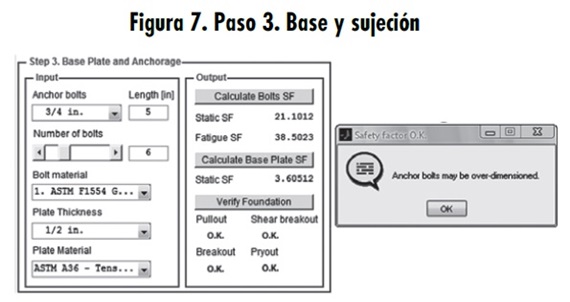
Paso 3: Base y sujeción. El diámetro seleccionado de perno de es de 3/4 in de diámetro y su largo (longitud de anclaje) de 5 in. Para la cantidad de pernos, la herramienta tiene en cuenta que el uso de al menos cuatro pernos según requerimientos de la OSHA, y de una cantidad máxima dependiente de la distancia entre pernos y bordes recomendada de 1,5 δε como mínimo (ver. Figura 2) [8,9]. Se especifica el uso de solo seis. El material elegido es el ASTM F1554 grado 55, esfuerzo de tensión último de 517 MPa. Para la placa base, se escoge un espesor de 1/2 in. El material utilizado es el acero ASTM A36 con esfuerzo de tensión último de 410 MPa. Los factores de seguridad ante carga estática y variable son 21,1012 y 38,5023, respectivamente. El programa muestra la notación de que “Los pernos de anclaje podrían estar sobredimensionados” (figura 7).

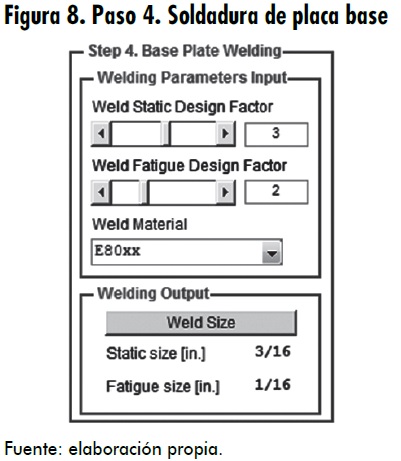
Paso 4: Soldadura de placa base. En el caso de factores de diseño para carga estática y para fatiga de 3,0 y 2,0, respectivamente, y material de aporte E80xx (80 ksi promedio de resistencia última a la tensión), el tamaño de garganta de soldadura para carga estática y carga variable es 3/16 y 1/16 in, respectivamente; 3/16 in es entonces el tamaño mínimo permisible (figura 8).

3.1. Confrontación de resultados con análisis de elementos finitos

En el caso de estudio de un panel solar ubicado en la ciudad de Cali (Colombia), se confrontaron los resultados del factor de seguridad obtenidos para fatiga mediante los diferentes criterios mostrados en la figura 6, contra los factores de carga arrojados por el FEA, según los criterios de falla por fatiga de Goodman modificado, Gerber y Soderberg con la ayuda de un software de gama media como Solid Works®. Los resultados se presentan en la figura 9.

Algunas de las características de la simulación fueron: malla basada en curvatura, de elementos cuadráticos de alto orden con cuatro puntos jacobianos, 15.846 nodos que generaron 8052 elementos. En la simulación (tres segundos de duración), los esfuerzos se alternan en un número de ciclos de 109 (vida infinita). Como dato de entrada se ingresó la curva S-N del material utilizado [12], acero ASTM A500 GC Solid Works®. Esta arroja la variación del factor de carga, el cual representa el coeficiente por el cual se debe multiplicar el esfuerzo alterno para producir una falla por fatiga, constituyéndose en el factor de seguridad de la estructura. Los valores mínimos obtenidos fueron 2,278 para el criterio de Goodman modificado (figura 9a); 2,204 para Soderberg (figura 9b); y 2,458 por el criterio de Gerber (figura 9c). Los resultados obtenidos mediante FEA, en general, están en concordancia con los valores arrojados por la GUI desarrollada, presentados previamente en la figura 6. Los valores obtenidos en la GUI son más conservadores.

3. Conclusiones

En este artículo se presentó el análisis de la seguridad estructural que requiere todo sistema solar orientable. Se establecieron las cargas del sistema y también los esfuerzos estáticos y variables de acuerdo a condiciones ambientales. La herramienta desarrollada integra la metodología de cálculos propuesta y se apoya en normas internacionales. Se fundamenta en ecuaciones y teorías de falla pertinentes para los esfuerzos a los que está sometido el sistema. Los resultados obtenidos mediante la herramienta se han comparado con los obtenidos por un análisis de elementos finitos, obteniendo resultados concordantes que garantizan la seguridad estructural por fatiga del sistema.

El desarrollo de esta interfaz gráfica de usuario constituye una plataforma inicial en el diseño de sistemas solares fotovoltaicos con orientación, logrando una dinámica y ágil toma de decisiones y fallos con respecto a la seguridad de la estructura. La interfaz puede ser usada previamente a las etapas de selección de actuadores, CAD, diseño del sistema de control y construcción. Como trabajo en curso derivado de este artículo, también se tiene el diseño de una interfaz similar programada en C++, de manera que trascienda el entorno académico de Matlab® y se facilite su uso en las industrias dedicadas a la construcción de estructuras.

Reconocimientos

A la Vicerrectoría de Investigaciones Extensión y Proyección Social de la Universidad del Atlántico.

Referencias

[1] “Paneles solares de alto rendimiento”, Revista Euronews [en línea], 14 de marzo de 2011, disponible: http://es.euronews. com/2011/03/14/paneles-solares-de-alto-rendimiento, última consulta: 7 de febrero de 2013.

[2] J. Cabanillas, “The wind and the panacea of the stow position in the solar trackers”, PV Resources [en línea], 2009, disponible: www.sunenergysite.eu/download/windload.pdf, última consulta: 9 de enero de 2013.

[3] S. Koç y Z. Aydoğmuş, “A Matlab®/gui based fault simulation tool for power system education”, Mathematical and Computational Applications, vol. 14, nº 3, pp. 207-17, 2009.

[4] A. Gil, A. Acín, F. Rueda e I. Mayor, “Structural and motion system dynamic analysis of a two-axes solar tracker under wind action”, Simulia Customer Conference, Inglaterra, Dassault Systèmes, 2009.

[5] R. Budynas y J. K. Nisbett, Shigley’s mechanical engineering design, eight ed., Estados Unidos: McGraw-Hill, 2006.

[6] Atlas de viento y energía eólica, Colombia: Ministerio de Minas y Energía, 2006.

[7] Solar Energy Research Institute (SERI), Mean and peak wind load reduction on heliostats, Estados Unidos: US Department of Energy, 1987

[8] W. C. Honeck y D. Westphal, Forell Elsesser Engineers, “Practical design and detailing of steel column base plates”, Steel Tips, California, Estados Unidos: Structural Steel Educational Council, 1999.

[9] J. Fisher y L. Kloiber, Steel design guide 1: base plate and anchor rod design, 2nd ed., Estados Unidos: Estados Unidos American Institute of Steel Construction, 2006.

[10] H. Polo, A. Valencia, J. Roldán y J. Díaz, “Una metodología para la evaluación de la seguridad estructural de un sistema de seguimiento solar en Colombia”, Revista Educación en Ingeniería [en línea], vol. 7, no. 14, pp. 92-103, 2012, disponible: http://www.educacioneningenieria.org/index.php/edi/article/ view/260/157

[11] Astronomical Applications Department of the us Naval Observatory, Sun or moon altitude/azimuth table [en línea], disponible: http://aa.usno.navy.mil/data/docs/AltAz.php, última consulta: 7 de febrero de 2013.

[12] asm International, Atlas of fatigue curves, sixth ed., Estados Unidos: Carnes Publication, 2006.