Exact solutions to cubic Duffing equation for a nonlinear electrical circuit

EXACT SOLUTIONS TO CUBIC DUFFING EQUATION FOR A NONLINEAR ELECTRICAL CIRCUIT

submitted date: November 2013
received date: December 2013
accepted date: April 2014

Álvaro H. Salas S.

B.Sc. In Mathematics, State University of Moldova (URSS). M.Sc. In Mathematics, Universidad Nacional de Colombia (Colombia). Research group FIZMAKO, Universidad de Caldas (Colombia). Current position: professor at Universidad de Caldas and Universidad Nacional de Colombia, Manizales-Nubia (Colombia). E-mail: asalash2002@yahoo.com

Jairo E. Castillo H.

B.Sc. In Physics and M.Sc. In Physics, Universidad rusa de la amistad de los pueblos (URSS). Research group FIZMAKO, Universidad Distrital Francisco José de Caldas, Bogotá (Colombia). Current position: professor at Universidad Distrital Francisco José de Caldas, Bogotá (Colombia). E-mail: jcastillo@udistrital.edu.co

Abstract

This work provides an exact solution to a cubic Duffing oscillator equation with initial conditions and bounded periodic solutions. This solution is expressed in terms of the Jacobi elliptic function (cn). This exact solution is used as a seed to give a good analytic approximate solution to a nonlinear equation that describes a nonlinear electrical circuit. This last equation is solved numerically and compared with the analytic solution obtained from solving the cubic Duffing equation. It is suggested that the methodology used herein may be useful in the study of other nonlinear problems described by differential equations of the form z′′ = F(z) , F(z) being an odd function in the sense thaFt (z) may be approximated by an appropriate solution to a cubic Duffing oscillator equation. In particular, the exact solution may be applied in the study of the cubic nonlinear Schrodinger equation, which is reduced to a cubic Duffing oscillator equation by means of a travelling wave transformation.

Key words

Duffing equation, cubic Duffing oscillator equation, third-order Duffing model, analytic solution, Jacobi elliptic functions.

Introduction

The cubic Duffing equation is a differential equation with third-power nonlinearity. There are many problems in physics and engineering that lead to the nonlinear differential cubic Duffing equation: from the oscillations of a simple pendulum, including nonlinear electrical circuits, to various applications in image processing [1,2,3]. The search for new methods that lead to the solution of the Duffing equation of different orders: third, fifth, seventh, and higher orders, is of vital importance since these solutions may be applied to a nonlinear cubic Schrodinger equation which has various applications in nonlinear optics, plasma physics, fluid mechanics and Bose-Einstein condensates [4,5]. By using the gauge transformation, the nonlinear cubic Schodinger equation may be reduced to a nonlinear ordinary differential cubic Duffing oscillator equation.

This work is aimed at finding, by means of the Jacobi elliptic functions, the exact periodic solution of the differential cubic Duffing equation with initial conditions that describe the behaviour of a nonlinear electrical circuit.

1. Nonlinear electrical circuit

Let us consider a capacitor of two terminals as a dipole in which a functional relationship between the electric charge , the voltage and the time has the following form:

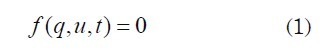
A nonlinear capacitor is said to be controlled by charge when it is possible to express the tension as a function of charge:

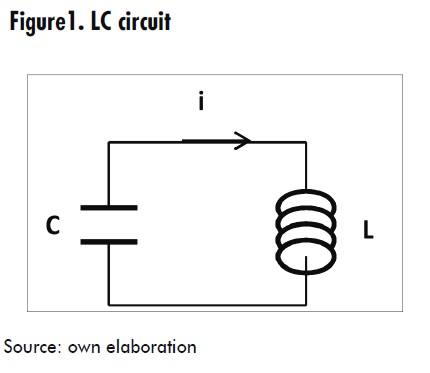
As an example of nonlinear electrical circuit, let us consider the circuit shown in Figure 1.

This circuit consists of a linear inductor in series with a nonlinear capacitor. The relationship between the charge of the nonlinear capacitor and the voltage drop across it may be approximated by the following cubic equations [6,7,8] :

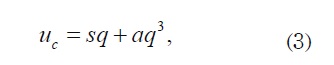
where U_c is the potential across the plates of the nonlinear capacitor, q is the charge , and s and a are constants. The equation of the circuit may be written as

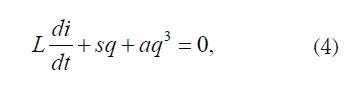
where L is the inductance of the coil. Dividing by L and considering that i = dq/dt we obtain the cubic Duffing equation in the form

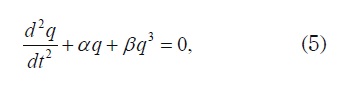
being α = s / L = 1 / LC and β = a / L = 1 / LCq²₀ constants.

2. A brief introduction to Jacobi elliptic functions cn, sn and dn

It is worth remembering that this work provides an exact solution to equation (5) in terms of the Jacobi elliptic function cn. This function is defined as follows:

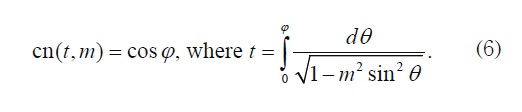
There are other two important elliptic Jacobi functions, namely sn and dn, which are defined by:

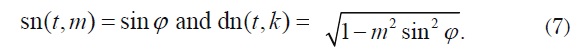
The number m ( 0 < m < 1) is called elliptic modulus and the number φ is called Jacobi amplitude, and it is denoted by am (t, m) . Thus,

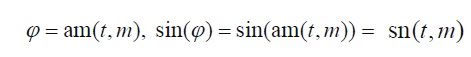
For these equations, the following identities hold:

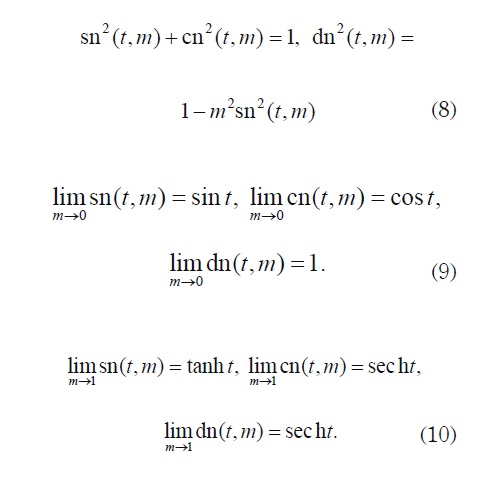
These functions are derivable and so:

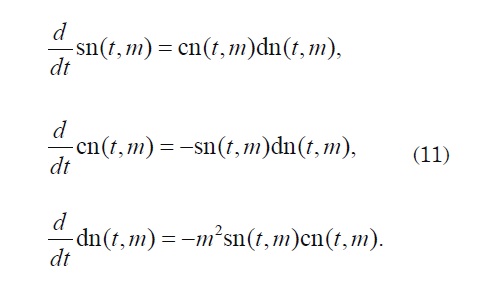
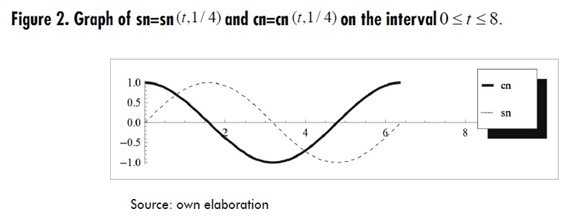
The graph of functions sn and cn are shown in Figure 2 for m = 1/4

From Figure 2, it can be observed that functions sn and cn are periodic. They have a common period equal to 4K(1/ 4) = 4K(m), where K = K(m) is called the elliptic K function for modulus m. In our case, K(1/ 4) ≈1.5962422 .

Equations (9) indicate that functions sn and cn generalize the sine and cosine functions, respectively.

Jacobi elliptic functions cn( t,m ), sn( t,m ) and dn( t,m ) may also be calculated for complex values of t = u + √−1v as follows :

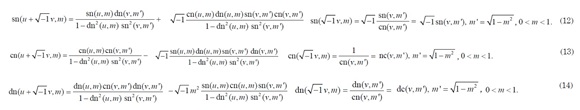
when m > 1 these functions are defined by the following equations

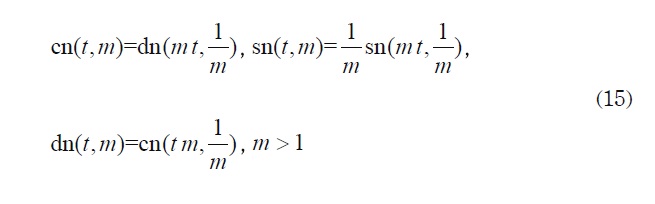
The following is also defined:

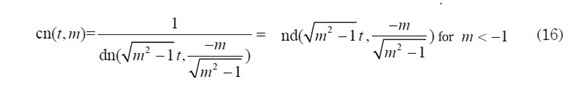
In some cases, it is necessary to deal with a function of the form cn (wt, k) , where w is any number (real or complex) and k is a pure imaginary number, say k= m√-1 where m is a real number. We may define the expression cn(wt, k) = cn(wt,m √-1) in a consistent way by using the formula:

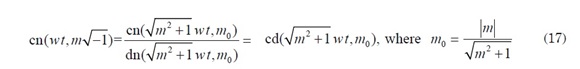
In the special case when both w and k are pure imaginary numbers, say w= ω√-1 and k= m√-1 (ω and m are real numbers), it is possible to define cn(wt, k) = cn(&omega√−1 t,m√−1) as follows:

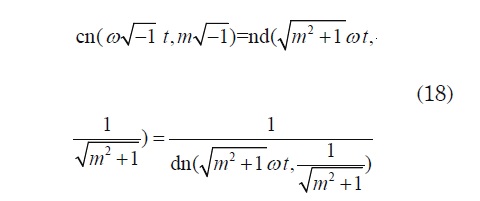
4. Exact solutions for the nonlinear model

In the linear case, the general solution to equation y" (t) + αy(t)=0 is y(t) = c₁ cos( √αt + c₂), where c₁ and c₂ are the constants of integration which are determined from the initial conditions y(0) = y₀ and y′(0) = y′₀ . When a cubic term is added we obtain the nonlinear equation y"(t) +α y(t) +β y³(t) = 0 and the solution cannot be expressed in terms of the cosine function. In this case, the Jacobi cn funtion solves this nonlinear equation. Indeed, direct calculations using equations (11) show that function y= c₁ cn (ωt + c₂,m) satisfies the following differential equation

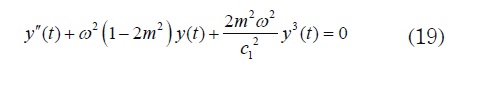
for any constants c₁ and c₂. Therefore the general solution to equation (5) is obtained by solving the system

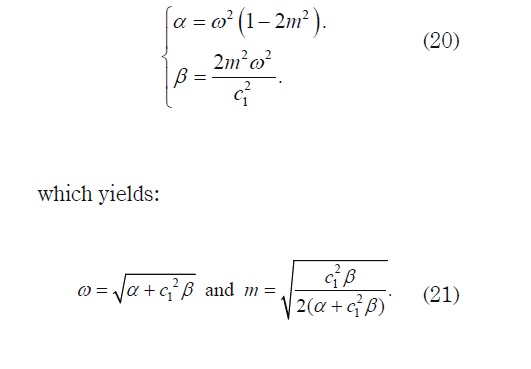
The values of c₁ and c₂ are determined from the initial conditions q(0) = q₀ and i = dq/dt |_t=0 If q'(0) = 0, then c₁ = q₀ and c₂ = 0 . Thus, the solution to problem:

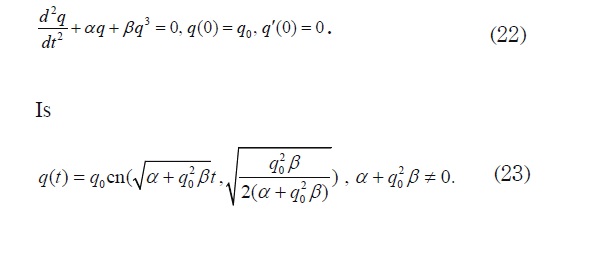
if

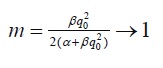
then

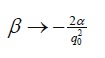
and since

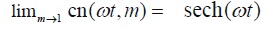
the solution to (23) results in:

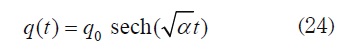
It is worth noting that solution (19) is bounded and non-periodic. This situation is typical for solitons. Some important non-linear differential equations admit soliton solutions that can be expressed in terms of sech.

On the other hand, if

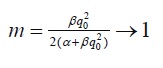
then β→0 and because lim _{m →0} cn (wt, m)=cos(wt) (23) reduces to:

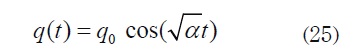
Which is the solution to linear equation y"(t) + α y(t) = 0. This result is consistent with the theory already known for the linear case.

The behaviour of solution (16) depends on parameters α and β as well as on the initial condition q₀ In this paper we will consider five cases:

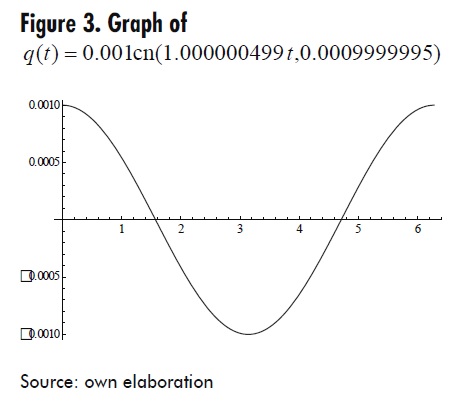
First Case: α + q₀²β>0 Let α=1, β=1 and q₀= 10^-3 Formula (23) yields q(t) = 0.001cn(1.000000499t,0.0009999995). This function is periodic with period T ≈ 6.2832 . The corresponding graph in the interval [0,T] is shown in Figure 3.

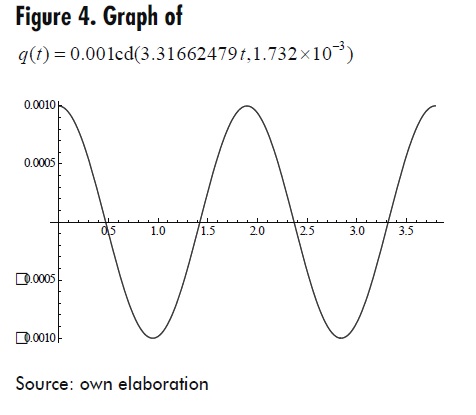
Second Case: α + q₀²β>0 abd β < 0, let β=-33 and α = 11 and q₀= 10^-3 By computing formulas (17) and (23)

q(t) = 0.001cd(3.31662479t,1.732×10⁻³ )

This function is periodic with period T ≈1.894 . The corresponding graph in the interval [0, 2T] is shown in Figure 4

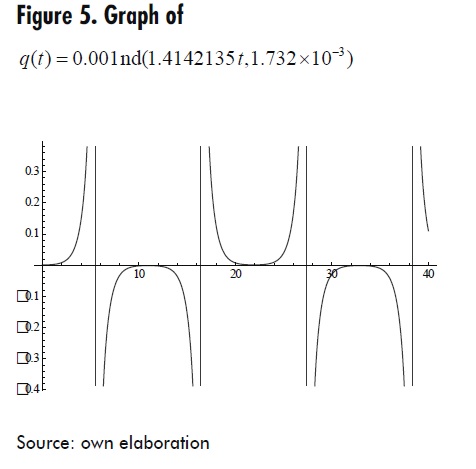
Third Case: α + q₀²β< 0 abd β < 0, let β=-6 and α = -2 and q₀= 10^-3 By computing formulas (18) and (23), q(t) = 0.001nd(1.4142135t,1.732×10−3 ) . This function is unbounded and periodic with period T ≈16.429 . The corresponding graph in the interval [0, 40] is shown in Figure 5.

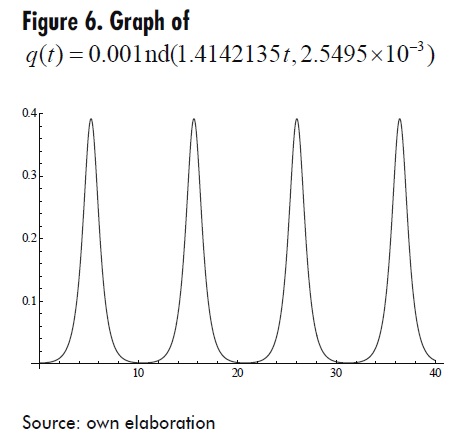
Fourth Case::α + q₀²β< 0 abd β > 0 let β=13 and α = -2 and q₀= 10^-3 This function is bounded and periodic with period T ≈10.406 . The corresponding graph in the interval [0, 40] is shown in Figure 6.

Fifth Case::α + q₀²β =0, In this case it is not possible to apply formula (23). Equation (22) then reduces to

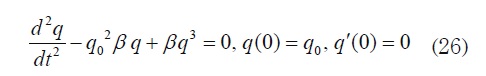
Direct calculations show that function

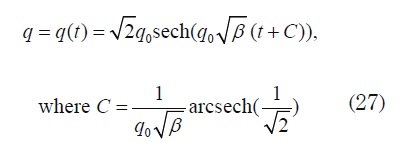
Finally, let us consider a nonlinear circuit consisting of a linear inductor in series with a nonlinear capacitor, as shown in Figure 1.

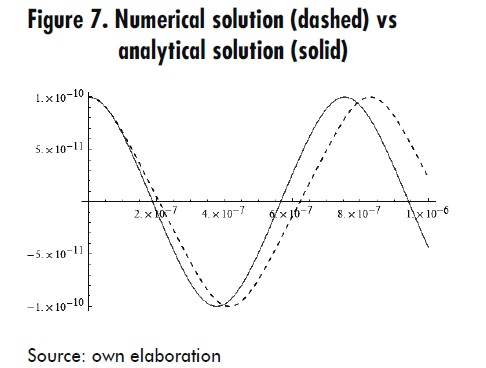
For L = 2,81mH, C = 9 pF, q₀ =10^-10 C, i₀ = 0, we have that α =1/ LC = 4×10¹³ and β =1/ LCq₀² = 4×10³³. The numerical solution for the Runge - Kutta method and the analytical solution we obtain from (23), i.e. q = q(t) = cn(8.94427×106 ,0.7071067811865475) are compared (graphically) in Figure 7.

5. Conclusions

A way to study non-linear circuits by means of the cubic Duffing differential equation has been shown, obtaining an exact solution in terms of a Jacobi elliptic function cn. It was possible to establish conditions under which the solution is periodic and harmonic. This is very important in the study of electric resonators and their applications in engineering. On the other hand, the results (already know) for the linear case were generalized for the nonlinear case in a consistent and natural way. It may be stated that the Jacobi elliptic functions are an essential way to solve many nonlinear problems.

Solutions (24) and (27) turned out to be very interesting because they represent a type of soliton solution (for a more thorough study of these solutions see [9]).

References

[1] A .N. Nayfeth, D.T. Mook, “Non-linear oscillations”. New York: John Wiley,1973.

[2] A .I. Maimistov,“Propagation of an ultimately short electromagnetic pulse in a nonlinear medium described by the fifthorder Duffing model”, Opt. Spectros, 94(2), 2003, pp.251-257

[3] S. Morfa, J.C. Comte, "A nonlinear oscilators netwok devoted to image processing", International Journal of Bifurcation and Chaos, vol. 14, No. 4 pp. 1385-1394, 2009

[4] Yi Fang Liu, Guo Rong Li, "Matter wave soliton solution of the cubicquintic nonlinear Schrodinger equation with an anharmonic potential", Applied Mathematics and Computation, Vol 219, pp. 4847-4852, 2013.

[5] Y Geng, J Li, L Zhang, "Exact explicit traveling wave solutions for two nonlinear Schrodinger type equatios" Applied Mathematics and Computation, pp. 1509-1521, 2010.

[6] R .E. Mickens. "Nonlinear oscillations", Cambridge University Press 1981, page 7.

[7] E . Gluskin, "A nonlinear resistor and nonlinear inductor using a nonlinear capacitor", Journal of the Franklin Institute, 1999, pp. 1035-1047.

[8] W. A. Edson, "Vacuum tube oscillators", New York: Wiley, pp 408-412, 1953.

[9] D.S. Wang, X. Zeng, Y.Q. Ma, "Exact vortex solitons in a quasi-two-dimensional Bose-Einstein condensate with spatially inhomogeneous cubic-quintic nonlinearity", Phys. Letters A, 376(2012),pp.3067-3070.