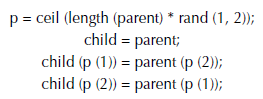DOI:
https://doi.org/10.14483/22487638.13653Publicado:
01-01-2019Número:
Vol. 23 Núm. 59 (2019): Enero - MarzoSección:
InvestigaciónLocalización del punto óptimo de partida en el problema de ruteo vehicular con capacidad restringida (CVRP)
Location of the optimal starting point in the vehicle routing problem with restricted capacity (CVRP)
Palabras clave:
algorithm, cluster, heuristics, tabú search, vehicle routing problem (en).Palabras clave:
algoritmo, conglomerados, heurística, metaheurísticas, tabú, ruteo de vehículos (es).Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 7 de julio de 2018; Aceptado: 12 de noviembre de 2018
Resumen
Contexto:
Esta investigación resuelve el problema de encontrar el punto óptimo de localización de una flota de vehículos recolectores de basura y las rutas óptimas para minimizar el costo de su recolección, en 144 barrios del municipio de Dosquebradas, Risaralda (Colombia), utilizando 8 vehículos con capacidad homogénea de 25 toneladas de la empresa Serviciudad.
Métodos:
Primero, se utilizó una heurística de barrido (Ospina Toro y Orrego, 2016) para encontrar un buen punto de partida para los vehículos de recolección y generar rutas iniciales de buena calidad. Posteriormente, estas rutas iniciales alimentan el algoritmo genético modificado de Chu-Beasley (Solarte, Castillo y Rodríguez, 2015) teniendo en cuenta la capacidad de carga del vehículo (Rondon et al., 2010). Finalmente, para garantizar un resultado óptimo, el mejor encontrado en la fase anterior es tratado nuevamente con una metaheurística tabú (Bodas, 2017).
Resultados:
Se diseñó una nueva metodología, denominada híbrida CSGTR (Clustering, sweep, genetic, tabu routing) que permitió aprovechar las ventajas de la clusterización (Rueda et al., 2017) antes del ruteo de vehículos (Hernández, 2017), incluyendo modelos heurísticos como la técnica de barrido (Ospina Toro y Orrego, 2016) y metaheurísticos como los algoritmos de Chu-Beasley y tabú (Grajales, Hincapié y Montoya, 2017). La aplicación de la metodología CSGTR permitió reducir el tiempo y los costos de los recorridos de los camiones recolectores de basura en el municipio de Dosquebradas, Risaralda (Colombia).
Conclusiones:
La metodología hibrida CSGTR para resolver el problema de ubicación de flotas de vehículos y generación de rutas de recolección se presenta como un enfoque alternativo, con mejores resultados que el enfoque previo.
Palabras clave:
algoritmo, conglomerados, heurística, metaheurísticas, tabú, ruteo de vehículos.Abstract
Context:
This research solves the problem of finding the optimal location point for a fleet of garbage collection vehicles, as well as their optimal routes in order to minimize the cost of garbage collection in 144 neighborhoods of the municipality of Dosquebradas, Risaralda, Colombia, using 8 vehicles with homogeneous capacity of 25 tons which belong to the company Serviciudad.
Methods:
Firstly, a scanning heuristic (Ospina Toro, Toro Ocampo, & Orrego Cardozo, 2016) was used to find a good point of departure for the group of all the vehicles in order to generate good-quality initial routes. Then, these initial routes feed the modified genetic algorithm of Chu-Beasley (Solarte Martinez, Castillo Gaspar, & Rodriguez, 2015), taking into account the load capacity of the vehicles. Finally, in search of an optimal result, the best result found in the previous step is treated again with a Tabu metaheuristic (Bodas López, 2017).
Results:
A new methodology was designed and called hybrid CSGTR (Clustering, sweep, genetic y tabú routing), which allows to take advantage of clustering before vehicle routing (Rueda Bayona, Elles Pérez, Sánchez Cotte, González Ariza, & Rivillas Ospina, 2017) and includs Heuristic models such as Scanning Technique and Metaheuristic models like the Chu-Beasley’s and Tabu Algorithm. The application of the CSGTR methodology allowed to reduce the time and costs of the routes of garbage trucks in the municipality of Dosquebradas, Risaralda, Colombia.
Conclusions:
The hybrid methodology CSGTR, to solve the problem of location of vehicle fleets and generation of collection routes, is presented as an alternative approach with better results than the previous approach.
Keywords:
algorithm, cluster, heuristics, metaheuristics, tabú search, vehicle routing problem.INTRODUCCIÓN
Los grandes volúmenes de basuras que se generan actualmente en las zonas urbanas crean un problema en la definición de las rutas y localización de la flota vehicular de recolección. En términos computacionales, toda esta información se convierte en grandes volúmenes de datos que se deben almacenar para la toma decisiones, teniendo en cuenta restricciones como: las distancias a recorrer, el número de vehículos, su capacidad, factores ambientales, tráfico, semaforización, horas pico, zonas urbanas y contaminación acústica. Todo esto conlleva a un aumento computacional significativo en costo y complejidad algorítmica (Balari, 2005).
Esta investigación resuelve el problema de encontrar el punto óptimo de localización de una flota de vehículos recolectores de basura y las rutas óptimas para minimizar el costo de su recolección en 144 barrios del municipio de Dosquebradas, Risaralda (Colombia), utilizando 8 vehículos con capacidad homogénea de 25 toneladas de la empresa Serviciudad. La situación resuelta forma parte del problema de ruteo vehicular con restricciones de capacidad (capacitated vehicle routing problema, CVRP) (Ospina, Toro y Orrego, 2016). Primero se utilizó una heurística de barrido para encontrar un buen punto de localización de los vehículos de recolección y generar rutas iniciales de buena calidad. Posteriormente, estas rutas iniciales alimentan el algoritmo genético modificado de Chu-Beasley, considerando en los vehículos su capacidad de transporte. El mejor resultado encontrado en la etapa anterior es tratado nuevamente con una metaheurística tabú (Ocampo, Escobar y Gallego, 2015)
En la sección 1 se muestra el estado de arte. En el marco teórico, se introducen los fundamentos de las técnicas usadas, técnica de barrido, algoritmo de Chu-Beasly y búsqueda tabú (Becerra y Alvarado, 2017). En la sección 3 se habla de la metodología. En la sección 4, se presenta el caso de estudio resuelto. En la sección 5 se presentan los resultados y se finaliza con conclusiones y bibliografía.
ESTADO DEL ARTE
Alina Martínez Oropeza y Marco Antonio Cruz, en 2011, realizaron una investigación para el problema de ruteo vehicular con restricciones de capacidad en vehículos (CA-CVRP) con el método de agrupamiento no supervisado. Esta propuesta evita recalcular distancias en cada iteración, tomando los centroides como clientes y no como puntos en el espacio; además, el algoritmo no requiere que se le especifique el número de agrupamientos a realizar, no necesita de otra heurística para evaluar las restricciones del problema debido a que los agrupamientos se llevan a cabo tomando en cuenta la característica de capacidad en vehículos, se puede deducir que el método es escalable y reduce el tiempo de cómputo al evitar recalcular distancias. De esta investigación se toma en el concepto de centroide.
Simón, Demaldé, Hernández y Carnero, en 2012, adelantaron una investigación en Argentina sobre optimización de recorridos para la recolección de residuos infecciosos con restricciones de capacidad, utilizando programación entera mixta. Se diseñó e implementó un método aproximado utilizando un algoritmo de búsqueda exacto y una heurística de búsqueda local para asegurar el aprovechamiento de los mejores espacios de búsqueda de las regiones, además de sus posibilidades de escalonamiento y el esfuerzo computacional asociado. Esta investigación compara el desempeño en tiempo y capacidad computacional de un algoritmo memético frente a la resolución exacta del CVRP con un algoritmo comercial, dando resultados favorables al utilizar la heurística ya que esta técnica es más robusta; además, el software comercial presenta marcadas dificultades en la disponibilidad de memoria, siendo necesario aumentar la capacidad con el consecuente deterioro de la calidad de la solución. Si se requiere trabajar problemas de mayor tamaño con el algoritmo memético, con tiempos de procesamiento razonables y buenas soluciones, es necesario diseñar un muestreo apropiado del espacio de búsqueda que permita diversificar la población e implementar la búsqueda local solo en unas pocas regiones promisorias. De esta investigación se toma en el concepto de búsqueda local.
Juan Jaramillo, en 2013 realizó una investigación en Colombia sobre algoritmos meméticos para resolver el problema de enrutamiento de vehículos con capacidad limitada. Esta propuesta utiliza un algoritmo memético llamado MEMVRP. Este enfoque maneja un módulo de programación inspirado en la mutación de los virus, para así generar nuevas generaciones de soluciones, además utiliza la metodología de tabú para mejorar cada una de las soluciones de la nueva generación, con resultados altamente favorables.
Orrego, Ospina y Toro, en 2013, proponen una solución dividiendo en dos etapas el problema SCVRP (symmetric capacitated vehicle routing problem), el cual utiliza una heurística de barrido (sweep) que sirve en la organización de los conglomerados, y recurre luego al algoritmo genético modificado (AGCB) para crear las rutas óptimas de cada camión, con el fin de minimizar las distancias totales recorridas por el conjunto de vehículos. Posteriormente Ocampo, Escobar y Gallego Rendon (2015) agregan técnicas heurísticas constructivas y aleatorias para generar la población inicial, buscando una disminución de la cantidad de ciclos locales que pertenecen a un clúster dado, a través de un AGCB (algoritmo genético especializado de Chu-Beasley), con lo que se obtuvieron mejores individuos desde el inicio del programa. De esta investigación se utiliza la metodología AGCB para encontrar un buen punto de inicio (centroide).
Fredy Alexander Guasmayan (2014) realizó una investigación para resolver el problema de ruteo de camiones, utilizando un algoritmo genético modificado, teniendo en cuenta tiempo y horario que tarda el camión para entregar la mercancía a cada uno de los clientes. Este problema del tipo TDVRP se enfoca en la utilización de técnicas heurísticas como instrumento de inicio que alimenta el algoritmo genético-Chu-Beasley (Chu y Beasley, 1997). La propuesta utiliza técnicas de selección por torneo y mutación para escoger el hijo más competitivo y generar una solución óptima, debido a la flexibilidad del algoritmo genético se logran mejoras en la solución final mediante intercambios en las rutas finales obtenidas de algunas aristas mediante rutinas simples como el vecino más cercano. De esta investigación se utiliza la técnica de selección por torneo, lo cual permite tomar el hijo más adecuado e introducirlo a la población inicial. La técnica permitió enfriar las soluciones de las poblaciones, ya que después de varias o muchas iteraciones tiende a una solución óptima local.
La presente orientación es tomada del enfoque de centroide de Martínez y Cruz (2011); el concepto de búsqueda local, de Simon et al. (2012); la búsqueda tabú, de Bodas (2017); la selección por torneo y el enfriamiento, de Guasmayan (2014), en los algoritmos genéticos.
Guillermo Roberto Solarte Martínez, Andrés Gaspar Castillo Sanz y Guillermo Rodríguez Gahona (2015), realizaron una investigación del problema de ruteo CVRP utilizando el algoritmo Chu-Beasley; se propuso un caso de estudio para aplicar esta metaheurística en Bogotá, ya que por ser la capital de Colombia tiene dificultad de movilidad y transporte, y se tomó como caso de estudio los Súper Almacenes Olímpica (SAO) de la cuidad, que deben comercializar sus productos y se ven obligados a optimizar sus recorridos de entrega para garantizar la satisfacción del cliente. Como resultado de esta investigación se creó una aplicación que género resultados aceptables, reduciendo notablemente los costos de recorrido.
Ospina, Toro y Orrego (2016) adelantaron una investigación del problema CVRP en el área de transporte, comunicaciones y logística mediante la heurística de barrido y el algoritmo genético modificado de Chu-Beasley. En el enfoque presentado crearon un modelo de dos fases: en la primera, una población inicial que luego, en una siguiente fase, es utilizada por el algoritmo genético generando resultados óptimos.
Rueda et al. (2017) demostraron, a partir de los componentes principales, que existe una representatividad mayor al 70 % para altas temperaturas y vientos, además se encontró en este estudio una correlación de 80 % que ayuda a reajustar los datos de velocidad y viento para toma de decisiones de la región del caribe.
Grajales, Hincapié y Montoya (2018) realizaron una investigación de selección óptima de conductores aplicando la técnica de tabú, además trabajaron con algoritmos constructivos para generar una buena solución inicial; se emplearon los métodos de búsqueda de árbol y teoría de grafos, para comprobar la aplicabilidad y eficiencia en los resultados.
En la siguiente sección se describen las técnicas heurísticas y metaheurísticas que fueron utilizadas para solucionar el problema de ruteo vehicular con restricción de capacidad CVRP.
MARCO TEÓRICO
Algoritmo genético de Chu-Beasley
Esta metaheurística permite un manejo particular tanto de la población objeto de estudio como de la población inicial, la cual debe ser totalmente surtida para evitar la aproximación prematura a soluciones óptimas locales. Este enfoque utiliza una serie de funciones que ayudan a mejorar el rendimiento computacional y a la vez lo hace competitivo con respecto a otras metaheurísticas como tabú o colonia de hormigas (Donati et al., 2008), haciendo uso de la función fitness. Se seleccionan los progenitores por torneo. Cada instancia se analiza en dos aspectos: i) el valor alcanzado por la función objetivo y ii) grado de verosimilitud, el cual se mide mediante una función cuyo valor es proporcional al grado de violación de las condiciones dadas por las restricciones. Esta última consiste en una función que retorna valores positivos proporcionales a la violación de las restricciones, y cero (0) cuando no hay violaciones haciendo la configuración factible.
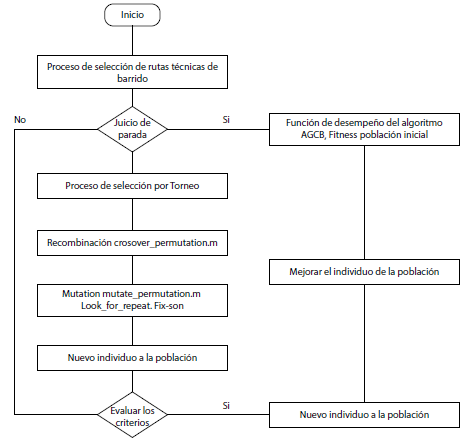
El algoritmo Chu-Beasley (1997) y el algoritmo genético (Guasmayan, 2014) tienen la opción de incluir nuevas fases de mejoramiento, mediante sus fases de selección, recombinación y mutación (Solarte, Castillo y Rodríguez, 2015) (ver diagrama de flujo en figura 1).
Figura 1: El algoritmo genético de Chu-Beasley modificado
Técnica de barrido
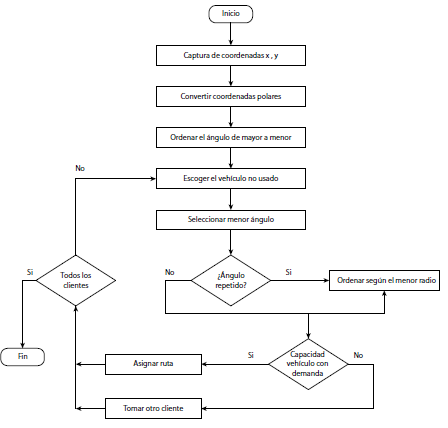
Esta metodología parte de una asignación preliminar que permite crear una ruta preliminar. Usa coordenadas angulares para determinar la posición de los clientes y simultáneamente ejecuta un barrido hasta encontrar el ángulo más cercano asociado con el vecino más cercano. Luego, traza una línea desde el origen-deposito hasta el cliente. Se guardan la información de la ruta si cumple con las restricciones de capacidad del vehículo, en el caso que existan dos clientes con los mismos ángulos de orientación se cataloga según el radio más cercano. En la figura 2 se muestra la heurística de barrido.
Figura 2: Diagrama de flujo: técnica de barrido
Metaheurística de búsqueda tabú
El objetivo de este proceso metaheurístico es evitar quedar apresado dentro de un óptimo local. El método tabú (Glover, 1987) adelanta búsquedas en el espacio de configuraciones, analizando de manera apropiada los óptimos locales. Se evita retornar al conjunto de óptimos locales ya evaluados, mediante la una marcación conocida como movimientos tabúes, para impedir que sean visitados de nuevo.
La búsqueda tabú (TS) (Bodas, 2017) hace uso de dos estrategias: intensificación y diversificación. La primera intensifica la búsqueda alrededor de las mejores soluciones. La segunda se enfoca en otros subespacios para nuevas búsquedas. Después de un conjunto de acciones se puede encontrar una mejor que sea candidata para remplazar la solución existente. Para lo anterior se implementa la llamada regla de aspiración, que permite eliminar la prohibición y facilita el movimiento. Tanto las estrategias de intensificación como de diversificación se completan con una estrategia de encadenamiento de trayectoria (o path relinking), que interconecta las buenas soluciones.
METODOLOGÍA
Caso de estudio
En el municipio de Dosquebradas, según los informes presentados al área de aseo de la empresa Serviciudad, se planean las rutas dentro de cada sector y para cada camión, con las siguientes condiciones:
-
A cada camión se le asigna una zona, el recorrido total alcanza 19 km, y el camión trabaja 6,5 horas.
-
A cada camión se le asignan 2 días por semana para recoger basura, el camión tiene una capacidad de 25 toneladas, tiene asignada la recolección de basura 2 días a la semana, la capacidad del vehículo es de 25 toneladas, y se dispone de un chofer y 2 colaboradores.
-
A las 6 de la mañana empieza la recolección de basura.
-
Se realizó un recorrido real a los 114 puntos de recolección de acuerdo con la tabla 1.
Fuente: elaboración propia
Tabla 1: Puntos de recolección por barrios
0
BARRIOS
DIRECCION
BARRIOS
DIRECCION
BARRIOS
DIRECCION
1
Centro Comercial Molinos
Calle 35 # 13-1
58
Seminario Mayor
Vía La Popa # 1 A 23
118
Altos de La Pradera
Calle 24 # 23-99
2
Éxito,
Calle 35 # 19-2
60
Colegio Diocesano
Vía La Popa # 2 A 24
3
Cam
Av. Simón Bolívar 36
61
Colegio Santa Sofía
Carrera 24A
119
La Pradera I
Calle 21 # 17-1
4
Centro Comercial Progreso
Simón Bolívar # 41-2
62
Maracay
Calle 20A # 10-42
120
Reservas Pradera.
Calle 21 # 23-12
5
San Fernando
Calle 46 # 14a-1
63
Bomberos 4
Simón Bolívar # 35B-
121
Coomnes,
Carrera 23 # 25
6
Santa Lucía
Carrera 21 # 35-2
64
Cambulo
Calle 43 # 16-100
122
Colmenares
Diagonal 25 # 19-1
7
La Pradera
Calle 21 # 17-1
65
Quin. San Rafael
I-29 # 2 A 100
123
Pradera II
Calle 21 # 21--99
8
El Progreso
Calle 44 # 23-2
66
Campestre B
Diagonal 25 # 10-2
124
Reservas del Milán
Carrera 8 # 41B-1
9
Quintas De Jardín Colonia
Transversal 26 #
67
Altos Santa Clara
Calle 12 # 20A-2
125
Colegio Salesiano
Colegio Salesiano
10
Jardín Colonial I,
Calle 42 # 22a-2
68
Quinta Buenavista
Calle 19 # 21-2
126
El Refugio
Calle 20A # 10-2 A
11
Jardín Colonial II
Calle 42 # 23-1 A 23-99
69
Campestre C
-29 # 1 A 99
127
Torres del Sol
Carrera 41B # 17-99
12
Molinos
Diagonal 46 # 21-
70
Asomeri,
Colombia 2.4 Km E
128
Torres del Sol II
Carrera 51B # 17-99
13
Cambulos
Carrera 21 # 36-100
71
Campeste B
Transversal 9 # 27-2
129
Portal del Sol
Diagonal 42 # 10d-2
14
Villa de Molinos
Calle 44 # 23-1 A 23-81
72
Campestre A,
Calle 19A # 2A-1
128
Los Cerezos
Calle 17 # 41B-1
15
Villa de Molinos II
Diagonal 42 # 10d-2
73
Villa Campestre
I-29 # 1 A 99
130
Quintas del Refugio
Calle 50 # 11-2
16
Villa del Pilar I
Carrera 10G # 45-2
74
Campestre D,
Calle 19A # 5A-100
131
La Macarena
Calle 16B # 2A
17
Villa del Pilar I
Carrera 11 # 60A-2
75
Urb. Macarena
Calle 16B # 2A-100
132
El Limonar
Carrera 2 # 32-53
18
Girasol
Carrera 10B # 34-2
76
Urb. Macaran
Calle 20A # 10-72
133
Quintas San Martin
Carrera 11 # 50
19
Colinas,
Carrera 10G # 45-2
77
Playa Rica
Carrera 10 # 38-2
134
San Nicolás,
Calle 33 # 12-1
20
Pablo VI
Pablo Sexto Calle 44,
78
Pilarica,
Calle 43 # 7-1
135
Guadalupe
Carrera 15A # 40A
21
La Esmeralda
Carrera 4 # 32-1
79
Andalucía
Calle 43 # 7-1 67
136
Buenos Aires.
Calle 41 # 15-2
22
Av. Simón Bolívar 43
Simón Bolívar # 1 A 99
80
Urb.Garma
Calle 42 # 10-1
137
Cámara del Comercio
Calle 41 # 15-1 A
23
Bario Guadalupe
Calle 36 # 15-1
81
Guayacanes
Calle 62 # 15-1
138
Colegio María A.
Calle 33 # 23-24
24
La Casa de la Cultura
Simón Bolívar # 49-2
82
Villa Del Campo
Calle 52 # 10-1
139
ICDB
Calle 45 # 14-2
25
La Romelia
Calle 66 # 15B-2 -100
83
Andalucía,
Carrera 7 # 31-2
140
Teatro Alcaraván
Carrera 14A # 49-1
26
Lara Bonilla
Calle 43 # 23-24
84
REYES
I-29 # 1
141
Hogar
Calle 43 # 23-24
27
Romelia Alta
Calle 43 # 23-22
85
Club Adulto
I-29 # 2 A 100
142
Juan Maria Gonzales
Carrera 10G # 45-2
28
Laureles,
Calle 44 # 23-2
86
Bomberos
Calle 36 # 16-1
143
Los Naranjos
Carrera 11 # 60A-2
29
Carlos Ariel Escobar
Calle 44 # 23-1
87
Quintas De Aragón
Carrera 9 # 45A-99
144
Panadería El Niño
Carrera 10B # 34-2
30
Bosques de la Acuarela,
Calle 33 # 23-24
88
Villa Elena
Calle 3 # 4-1
31
Los Guamos
Calle 53 # 23-22
89
Villa Elena I
Carrera 9 # 44-2 A
32
Barrio Júpiter
Calle 464 # 23-2
90
San Félix
Carrera 8 # 41B-1
33
Divino Niño
Calle 464 # 23-1 A
91
San Félix II
Carrera 8 # 41B--99
34
Manuel Elkin Patarroyo
Calle 763ABIS
92
Villa Mery
Carrera 8 # 42B-2
35
Variante Romelia El Pollo
Carrera 10G # 45-2
93
La Estación
-29 # 1 A 99
36
Calle de Las Aromas
Carrera 11 # 60A-2
94
Villa Perla
Carrera 54 Calle 132
37
Ensueño
Carrera 10B # 34-2
95
TCC
Diagonal 9 # 4-2
38
Cárcel de Mujeres
Carrera 8 # 41B-1
96
Nicole,
Vía La Popa # 2 A 84
39
Minuto de Dios
Carrera 8 # 41B--99
97
ABB
Vía La Popa # 1 A 29
40
Sakabuma
Carrera 8 # 42B-2
98
Zona Industrial
Diagonal 27A # 7-2
41
Minuto de Dios
Carrera 8 # 41B-1
99
Quintas del Bosque
I-29 # 2 A 100
42
Villa Alexandra
Carrera 4 # 11-100
100
Muebles Pabón
Vía La Popa # 1 A 83
43
Antigua Zona Industrial
Vía La Popa # 2 A 84
101
Villa Turín
Carrera 7 # 44-1
44
Plaza Comercial San Ángel
Calle 16B # 2A-100
102
Carrera 6 # 41A-2
Carrera 6 # 41A-2
45
La Graciela
Carrera 54 Calle 132
103
Makro
Simón Bolívar # 41
46
Carrera 4 # 9-38
Diagonal 9 # 4-99
104
Villa Diana
I29 # 1
47
Carrera 4 # 11-10
Carrera 54 Calle 132
105
Hacienda Bosque
I-29 # 45
48
Diagonal 8 # 4-1
Carrera 54 Calle 132
106
Santa María,
Carrera 6 # 41-99
49
Inquilinos
I-29 # 2 A 100
107
Milán
Calle 25 # 23-2 A 100
50
Ensueño
Calle 73ª BIS # 17A
108
Bosques Milán
Carrera 8 # 41B-1
51
Santa Teresita
Calle 64 15 45 Z
109
Quintas Milán
Carrera 8 # 41B--99
52
Parque Industrial La
Vía La Popa # 2 A 84
110
Casas Milán
Carrera 8 # 42B-2
53
Urbanización Macarena
Calle 16B # 2A-100
111
Terrazas De Milán
Diagonal 25 # 18-2
54
Servientrega
Simón Bolívar # 26
112
Guaduales Milán.
Diagonal 25 # 200
55
Zona Industrial Macarena,
Calle 16B # 2A-100
113
Santa Bárbara,
Diagonal 25 # 17-99
56
Inquilinos
Carrera 54 Calle 132
114
Carmelita,
Calle 16 # 41A-1
57
Parque Industrial La Badea
Carrera 64 Calle 62
115
Quintas Baleares
Carrera 21 # 41
58
Cárcel de Mujeres
Vía La Popa # 2 A 24
116
La Pradera,
Bolivar-2 A 78
58
Seminario Mayor
Vía La Popa # 1 A 23
117
Santa Mónica,
Carrera 19 # 17-2
En este caso se obtuvo una distancia promedio de 16,15 km con un tiempo real promedio de 6,12 h (tabla 2), para un tiempo de 1 hora con 37 minutos de lo que se puede obtener un valor de velocidad media para rutas sin congestión vehicular de 2,64 m/h. Ahora se escogerá una ruta con los puntos de recolección (tabla 1).
En la tabla 2 se muestra el resumen de las rutas y costos de la empresa de servicio de aseo Serviciudad.
Fuente: elaboración propia.
Tabla 2: Información de rutas de camiones
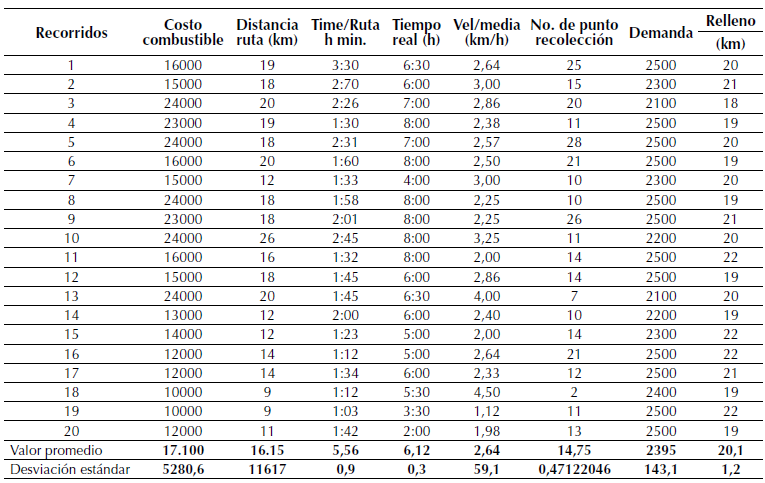
De acuerdo con la tabla 2 se identifica la velocidad a la cual se mueven los vehículos, se muestra la velocidad promedio, que es de 2,7 km/h, con un costo total promedio de aproximadamente 17.100 COP/km * 20 km = 342.000, por ruta hasta el relleno sanitario.
Modelo matemático base de la solución del problema
Tomando como referencia el modelo matemático propuesto por Olivera (2004), y sintetizado en las ecuaciones (1) a (11).
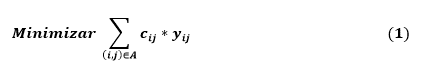
Sujeto A:

Cada camión tiene una capacidad de carga denominada q, un nodo (cliente) tiene una demanda. Tomando los datos valores enteros y no negativos, el modelo es determinístico, donde las restricciones buscan que se encuentren las rutas de costos mínimos. Además, se definen restricciones para cada vehículo de tal manera que:
-
Se satisfaga la demanda de cada cliente.
-
Se pase por un nodo o cliente una sola vez.
-
Todas las rutas tengan el mismo inicio y terminen en el mismo punto de inicio.
-
No se viole la capacidad de cada camión.
La ecuación (1), función objetivo, minimiza la suma de los costos de ir desde el punto de inicio hasta todos nodos. La ecuación (2) obliga a asignar un camión a la ruta (i,j), si esta va a ser transitada, y a no asignar si la ruta no va ser transitada. La restricción dada por la ecuación (2) usa la variable de decisión x, la cual para x=1, indica usar el vehículo k en el arco i, j, en caso contrario toma el valor de cero. En las ecuaciones (3) y (4) se describe la activación del arco (i, j) haciendo uso de la variable y. Al mismo tiempo se define un trayecto entre los nodos i, j, y se garantiza que un nodo sea visitado una vez por camión. Las ecuaciones (5) y (6) muestran para el parámetro k, la cantidad de vehículos utilizados en la solución que parten de un solo punto de inicio y deben regresar al mismo punto de inicio. En la ecuación (7) se define la capacidad del vehículo y se garantiza que no se sobrepase esta capacidad. La ecuación (8) se centra en evitar los ciclos para ello utiliza el conjunto de nodos. La ecuación (9) limita la cantidad de camiones que pueden ser utilizados, es decir la cantidad máxima y por último las ecuaciones (10) y (11) muestran que las variables x, y son binarias.
ENFOQUE DE SOLUCIÓN
Clustering, sweep, genetic y tabu routing (CSGTR)
La figura 3 muestra las tres fases de desarrollo del enfoque propuesto, CSGTR.
Figura 3: Modelo híbrido CSGTR
La metodología propuesta permite aprovechar las ventajas de la agregación (clúster) antes de iniciar el ruteo de los camiones, para lo cual emplea un enfoque heurístico, como la técnica de barrido, seguido de otros metaheurísticos (algoritmo genético Chu-Beasley y búsqueda tabú). Con este enfoque se pretende generar resultados más inteligentes, en aras de reducir los tiempos, distancias de recorridos y costos de los camiones recolectores de basuras, en el caso del municipio de Dosquebradas, Risaralda.
Primera fase (clustering y técnica de barrido)
Esta fase determina el lugar de partida de los camiones de recolección buscando disminuir la distancia de los recorridos, y los tiempos y costos asociados. Para lograrlo hace uso del algoritmo de conglomerados basados en medías, utilizando como herramienta de software SPSS.
Análisis clúster de las k-medias
El análisis de conglomerados (cluster analysis) (Rueda Bayona et al., 2017) permite, a partir de los valores de variables específicas, asignar casos similares a un número de grupos (clúster o conglomerados) cuyas características del conglomerado no se conocen previamente.
El análisis de conglomerados del tipo k-medias comienza con la especificación de k núcleos, como centro de los conglomerados. Posteriormente asigna los otros casos a estos núcleos según la distancia de ellos a los centros inicialmente creados. Luego actualiza las posiciones de los núcleos, basándose en el valor medio de todos los casos que ya hacen parte de un conglomerado. Este proceso se repite hasta que una reasignación de caso haga que los conglomerados aumenten su variabilidad. Se asigna como punto de partida, el del clúster que tenga el mayor número de casos agrupados. Luego de haber identificado la localización del punto de partida se procede a implementar la heurística de barrido.
La técnica heurística de barrido
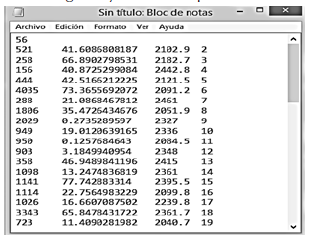
Como se mencionó anteriormente, la técnica de barrido parte de un punto inicial para generar una ruta preliminar. Mediante la implementación de la heurística de barrido se pretende clasificar los 144 puntos de recolección no solo por distancia, sino también por la capacidad de restricción del vehículo recolector, en este caso se obtiene una solución inicial del problema que luego será utilizado en la segunda fase. En la figura 4, se muestran los datos de algunos de los puntos de recolección de basura en ángulos y distancias polares.
Figura 4: Datos de entrada sweep_input
En el siguiente código 1 se presenta un extracto del código en C++ de la heurística de barrido:
Código 1: Heurística de barrido
El código de barrido genera un conjunto de rutas (vectores) de menor distancia que corresponden a los diferentes recorridos que deben realizar los camiones (7) para visitar todos los puntos (144) de recolección (ver “Resultados”).
Para visualizar estas rutas en un mapa se implementó el siguiente Código API de Google Maps, que las genera automáticamente utilizando el API de GoogleMaps®:
Código 2: Código de API de Google Maps modificado
Las rutas encontradas son pasadas como población inicial al algoritmo genético de Chu-Beasley.
Segunda fase (algoritmo de Chu-Beasley)
Como se puedo observar, el algoritmo de Chu-Beasley permite un manejo particular tanto de la población objeto de estudio como de la población inicial. Este enfoque utiliza una serie de funciones que ayudan a mejorar el rendimiento computacional y a la vez lo hace competitivo con respecto a otras metaheurísticas como la colonia de hormigas. A partir de la ruta preliminar encontrada en la fase anterior por la técnica de barrido, se utiliza en la segunda fase el algoritmo de Chu-Beasly modificado para encontrar mejores rutas (Toro, Ruiz y Salazar 2011). Esta metaheurística cuenta con una serie de funciones que se permiten modificar o adicionar nuevas restricciones, por eso en esta investigación se utiliza la función fitness para manejar la factibilidad y la función de recombinación para generar dos hijos, de los cuales solo se elige uno mediante la técnica de selección por torneo, en este caso se utiliza crossover_permutation.m: recibe como parámetros los mejores individuos que pasaron por la selección por torneo. Este script toma dos individuos y genera un punto de cruzamiento aleatorio. Además, cuenta con la función Fix_Sons que modifica un individuo creado en caso de que tenga alelos repetidos. Fix_sons fue creado acorde a las recomendaciones del algoritmo mutation_children.m: usa los padres para crear hijos mutados. Se seleccionan dos números aleatorios, los cuales hacen referencia a los alelos a modificar. A continuación, se describen el hardware y software a utilizar como también la funciones creadas y utilizadas en el desarrollo de la aplicación del algoritmo genético:
Este algoritmo fue ejecutado en un ordenador Hewlett-Packard HP, Procesador Intel® Core™ i7, cuatro núcleos, 12 GB de RAM, disco duro de 1 Tera de memoria ROM y sistema operativo Windows 8. El algoritmo fue implementado en Matlab R2013a y se hizo uso su Toolbox de algoritmos genéticos. Este último se basa en los siguientes scripts:
Script implementado por los autores
-
printing_routes.m: y usado para imprimir las rutas de la solución.
-
final.plot_routes.m: script implementado por los autores, usado para graficar las rutas en una ventana y generar los archivos internos de texto para cada ruta propuesta en el algoritmo.
-
GA_Routines.m: script principal que invoca los scripts mencionados anteriormente.
-
Ga_Routines.m: script principal que recibe como insumos un file de texto denominado “Puntos_Barrios.txt”. En este último se tienen las coordenadas geográficas de los puntos de recolección y otro archivo denominado “Matriz_Distancia.txt” que contiene la matriz de distancia encontrada en la fase de la heurística de barrido. La salida de este script es una variable denominada xs que contiene el orden en el que se deben visitar los diferentes puntos de recolección.
-
crossover_permutation.m: recibe como parámetros los mejores individuos que pasaron la selección por torneo. Este script toma dos individuos y genera un punto de cruzamiento aleatorio: este se realizó siguiendo Guasmayan (2014); el script cuenta con la función Fix_Sons que modifica un individuo creado en caso de que tenga alelos repetidos. Fix_Sons fue creado acorde a las recomendaciones del documento citado previamente.
-
mutation_children.m: usa los padres para crear hijos mutados. Se seleccionan dos números aleatorios, los cuales hacen referencia a los alelos a modificar. Lo anterior se logró con las siguientes instrucciones:
Código 3: mutation_children.m
-
traveling_salesman_fitness.m: script de Matlab usado para calcular la función de desempeño del algoritmo genético.
-
mutate_permutation.m: script usado para personalizar la forma en la que se mutan los individuos de una población.
-
Look_For_Repeated_Indexes.m: script auxiliar de mutate_permutations.m que le permite identificar si un individuo posee alelos repetidos.
-
Fix_Sons.m: script implementado por los autores, auxiliar de mutate_permutations.m que le permite reparar individuos en caso de que tengan alelos repetidos.
-
crossover_permutations.m: script de Matlab que permite cruzar los individuos de una población de manera personalizada.
-
create_permutations: script de Matlab que permite crear la población inicial del algoritmo.
-
create_permutations.m: crea un vector de permutaciones, el cual contiene los números que identifican los puntos de recolección. El rango de los elementos de este arreglo va desde 1 hasta el número de puntos de recolección. Se excluye el punto de donde salen los camiones y el relleno sanitario, ya que su posición en el vector solución es fija.
En cuanto al reemplazo de la población y las operaciones asociadas al algoritmo genético, son llevadas a cabo de manera automática por el toolbox a través de la instrucción contenida en el script GA_Routines: [x, fval, reason,output]=ga(FitnessFcn,numberOfVariables,options).
El siguiente script plot_routes.m: implementado por los autores, realiza las gráficas de las rutas e imprime las coordenadas geográficas de los puntos de recolección involucrados. Las distancias se calculan con el servicio de Distancia de Google, el cual facilita el cálculo de las distancias del origen a los otros 25 puntos. Para hacer uso del servicio, se debe crear una página web (HTML y JavaScript). Se generan dos archivos con las matrices de tiempo y distancias y distancias (costos). Con las matrices de tiempo y distancia de 144 × 144 y la demanda de cada uno de los puntos de recolección de basura se procede a ejecutar el algoritmo genético Chu-Beasley.
Una vez se adapte código algoritmo de Chu-Beasly mejorado, al problema de esta investigación, se procede a pasar los datos preliminares de la etapa anterior como datos iniciales, para encontrar una mejor solución al problema. Este enfoque se basa en el hecho de que si el algoritmo genético tiene una buena población inicial le permitirá de manera más eficiente encontrar mejores soluciones.
Los resultados, las rutas generadas, son las entradas iniciales de la tercera fase.
Tercera fase (búsqueda tabú)
En esta fase final se reciben los datos generados por la metaheurística del algoritmo genético Chu-Beasley mejorado y se pasan como datos iniciales a la metaheurística búsqueda de tabú (TS) (Becerra y Alvarado, 2017); con esta técnica se pretende optimizar las rutas tanto en tiempo computacional, distancia y costo del recorrido, para ello se utilizan las estrategias de intensificación y diversificación (seudocódigo búsqueda de tabú) (Bodas, 2017). Posteriormente, estas nuevas rutas se toman como datos de entrada para la metaheurística de tabú en el código Ts_init_solu_input. Posteriormente se procede a ejecutar el código de tabú implementado en Dev c++ por los autores (ver código 4 de tabú).
Código 4: Código de tabú
El resultado de esta tercera etapa genera la solución final que se muestra en la sección 4.3 Resultado final de la tercera fase (búsqueda tabú).
RESULTADOS
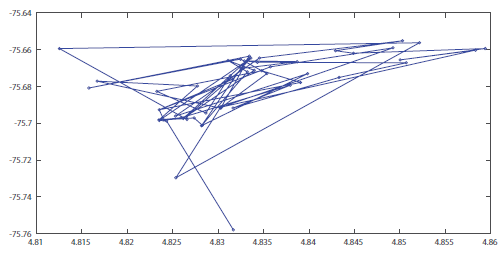
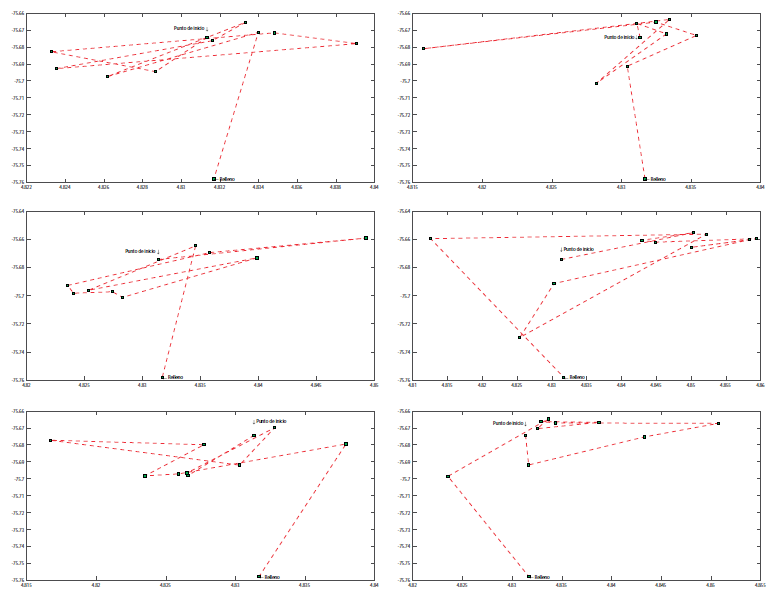
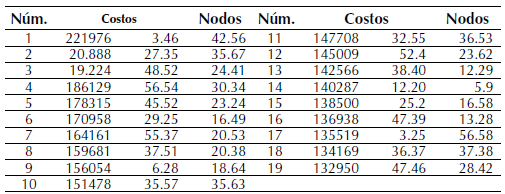
La figura 5 muestra la ubicación en latitud y longitud de los puntos de recolección de basura. La tabla 3 muestra los tiempos y costos reales de recorrido de estos vehículos de los 144 puntos.
Figura 5: Ubicación de los 144 puntos
Fuente: elaboración propia.
Tabla 3: Costos de los 144 puntos
Resultado de la primera fase (clustering y técnica de barrido)
El punto de partida encontrado por el análisis de conglomerado de medias y que proporciona la ubicación de punto de partida tuvo las siguientes coordenadas: latitud 4.833.974 y longitud -75.681499. Este punto corresponde a la ubicación de Centro Administrativo Municipal, Dosquebradas, Risaralda. A partir de este punto de partida de los camiones mediante la heurística de barrido se generaron una serie de potenciales rutas. Utilizando el código 1. Heurística de barrido, la técnica heurística de barrido generó un conjunto de rutas (vectores) de menor distancia que corresponden a los diferentes recorridos que deben realizar los camiones siete (7) para visitar todos los 144 puntos de recolección de basura (tabla 4).
Fuente: elaboración propia.
Tabla 4: Puntos de recolección de basura
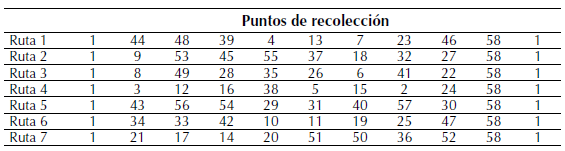
En la tabla anterior 4 se muestra el resultado de las rutas generadas según el código presentado en la tabla 2, donde se solo se pueden mostrar hasta 55 puntos, restricción de la API de Google Maps.
Figura 6: Técnica de barrido. Clasificación de las rutas
Resultado de la segunda fase algoritmo genético de Chu-Beasley
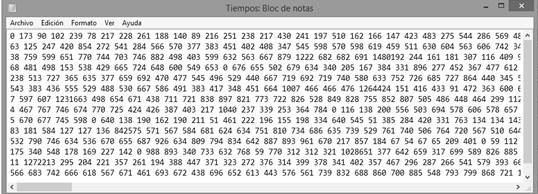
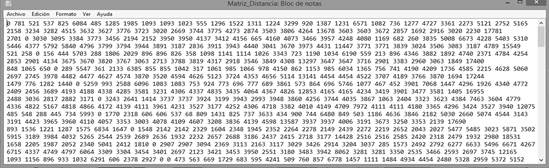
Las siete (7) rutas encontradas en la fase anterior fueron pasadas como población inicial al algoritmo genético de Chu-Beasley, además de las matrices de distancia y tiempos (de 144 × 144) generadas por Google Maps. En las figuras 8 y 9 se presenta un pantallazo de estas matrices.
Figura 7: Matriz de tiempos
Figura 8: Matriz de distancia
Los valores de recolección de demanda aleatoria uniforme entre 1500 a 2500 toneladas generadas fueron:
Demanda
A continuación, se muestran las demandas de los puntos de recolección. Así, el primer valor 2435.1, se refiere a la cantidad de basura en kg generados en un barrio dado por un punto específico de recolección.
Los resultados de correr el algoritmo Chu-Beasley con todos los datos anteriores se muestran en la figura 10. El primer valor 1 hasta el siguiente valor 1, después del valor 56, representa el recorrido de un vehículo recolector, a través de los puntos 7, 12, 19, 13, 2, 8, 52, 53, 56, considerando los valores de basura a recolectar en cada barrio. Un nuevo valor 1 significa el inicio de una nueva ruta.
Fuente: elaboración propia.
Tabla 5: Rutas para técnica del Barrido y algoritmo genético Chu-Beasly
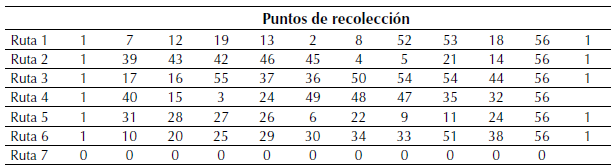
Resultado final de la tercera fase (búsqueda tabú)
Las siete (7) rutas de la etapa anterior, como datos de entrada para la metaheurística de tabú, generaron las siguientes seis (6) rutas (figura 11), donde se muestra el tiempo y la carga recolectada por cada carro, que corresponde a una dada ruta.
Como se puede evidenciar, al comparar los resultados presentados en “Metodología-Caso de estudio”, se obtuvo una reducción de 7 a 6 rutas, y una reducción de costo de $342.000 a solo $138.755, es decir una reducción del 40 % en costos, como resultado de la combinación de las tres técnicas (del barrido, algoritmo genético de Chu-Beasley y búsqueda tabú) para la solución del problema de recolección de basuras del municipio de Dosquebradas.
En el código 2 se observa la carga de cada recorrido de un vehículo, según una de las 6 rutas generadas por la metaheurística tabú, ademas del tiempo del recorrido del vehículo.
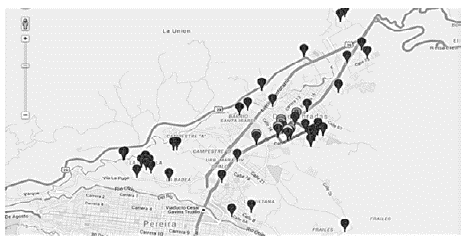
La tabla 6 permite visualizar las 6 rutas generadas haciendo uso del código 2 implementado utilizando el API de Gogle Maps.
Fuente: elaboración propia.
Tabla 6: Rutas resultado de la metaheurística tabú
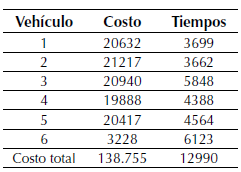
Figura 9: Por rutas generadas por la combinación de la técnica del barrido, genético de Chu-Beasley y tabú
Fuente: elaboración propia.
Tabla 7: Resultados modelo híbrido CSGTR

CONCLUSIONES
-
Se diseñó una nueva metodología llamada híbrida CSGTR, que permitió explorar las ventajas de la clusterización antes del ruteo de vehículos incluyendo así modelos heurísticos como la técnica de barrido y metaheurísticos como los algoritmos de Chu-Beasley y tabú. La aplicación de la metodología CSGTR permitió reducir el tiempo y los costos de los recorridos de los camiones recolectores de basura en el municipio de Dosquebradas, Risaralda (Colombia).
-
Como resultado del enfoque híbrido CSGTR que combina tres técnicas (del barrido, algoritmo genético de Chu-Beasley y búsqueda tabú) para resolver el problema de recolección de basuras del municipio de Dosquebradas se evidenció una reducción de 7 a 6 rutas, y una reducción del 40 % en los costos (de $342.000 a $138.755).
REFERENCIAS
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.