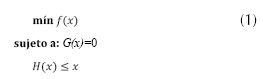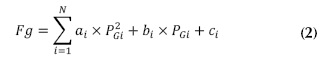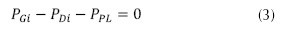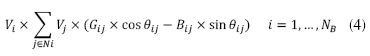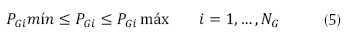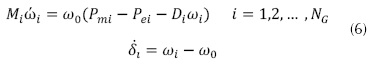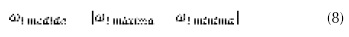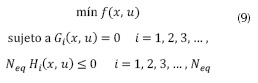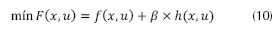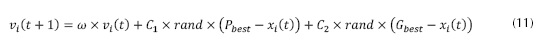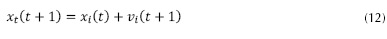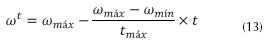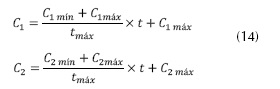Despacho económico en sistemas de potencia considerando estabilidad transitoria

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2017.1.a02

Despacho económico en sistemas de potencia considerando estabilidad transitoria

Economic dispatch in power systems considering transient stability

Diego Alejandro Díaz Tamayo¹, Alejandro Garcés Ruiz², Diego González Ocampo³

¹ Ingeniero Electricista, estudiante de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: dialdiaz@utp.edu.co

² Ingeniero Electricista, magíster en Ingeniería Eléctrica, doctor en Ingeniería Electrónica. Profesor de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: alejandro.garces@utp.edu.co

³ Ingeniero Electricista, magíster en Ingeniería Eléctrica. Profesor de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: diegogo@utp.edu.co

Fecha de recepción: 8 de marzo de 2016 Fecha de aceptación: 23 de noviembre de 2016

Cómo citar: Díaz T., D.A.; Garcés R., A. y González O., D. (2017). Despacho económico en sistemas de potencia considerando estabilidad transitoria. Revista Tecnura, 21(51), 27-41.

Resumen

Contexto: El despacho económico es una metodología clásica en los sistemas de potencia que generalmente se estudia en estado estacionario; no obstante, se trata de un sistema dinámico.

Método: En este artículo se abordó una metodología que presenta el problema incorporando restricciones de estabilidad transitoria. El modelo matemático incluye ecuaciones diferenciales que describen la evolución temporal de todos los generadores síncronos del sistema frente a un conjunto predefinido de contingencias. Dada la complejidad del problema se usó el algoritmo de Particle Swarm Optimization (PSO) para integrar todos los elementos considerados en el modelo.

Resultados: Se demostró una rápida convergencia y soluciones de buena calidad. La metodología propuesta fue evaluada en el sistema IEEE de 39 nodos de Nueva Inglaterra.

Conclusiones: Los resultados indican una reducción en el costo de operación, además de garantizar la estabilidad transitoria. El tiempo de cómputo es adecuado para ser implementado en sistemas reales.

Palabras clave: despacho económico, estabilidad, estabilidad transitoria, optimización, optimización por enjambre de partículas.

Abstract

Context: Economic dispatch is classic methodology in power systems which is studied in stationary state despite being a dynamical problem.

Method: This paper presents a methodology that considers this problem by including transient stability constraints. The mathematical model includes a set of ordinary differential equations which describes the dynamics of the systems after a failure. Due to the high complexity of the problem, we used an algorithm of Particle Swarm Optimization (PSO) to consider all the elements of the proposed model.

Results: The algorithm has proved to be fast and generated good quality solutions. The proposed methodology was evaluated in the IEEE 39 node system of New England.

Conclusions: The results demonstrated a reduction in the operative costs with a guaranteed stability index. Additionally, the computational time is low enough for the method to be implemented in real power systems.

Keywords: economic dispatch, optimization, particle swarm optimization, stability, transient stability.

INTRODUCCIÓN

Motivación

El despacho económico (DE) ha sido un área de investigación activa desde que se empezaron a operar los sistemas de potencia. El problema de DE tiene como objetivo lograr operar estos sistemas, de forma que se garantice mínimo costo, al igual que altos estándares de seguridad y confiabilidad. Por otra parte, el estudio de la estabilidad transitoria es una de las principales preocupaciones a la hora de operar los sistemas de potencia, ya que es necesario saber cómo se comporta ante perturbaciones severas y si es capaz de recuperar una estabilidad de operación.

En consecuencia, existe una necesidad de desarrollar modelos de DE que incorporen restricciones de seguridad y de estabilidad transitoria, con el fin de garantizar la continuidad en el servicio de energía eléctrica a los usuarios finales. Un método de despacho económico con restricciones de estabilidad transitoria (DE-RET) supone un modelo de optimización no lineal que además tenga en cuenta las restricciones en forma de ecuaciones diferenciales no lineales. Estas últimas se pueden modelar como simulaciones en el dominio del tiempo las cuales son exigentes computacionalmente. Otra dificultad inherente al problema es el desarrollo de una métrica que permita cuantificar la estabilidad del sistema, ya que un sistema es estable o inestable. Estas características particulares hacen necesario el uso técnicas metaheurísticas, a pesar de que el problema, en principio, es continuo.

Antecedentes

Actualmente la expansión e implementación de nuevas tecnologías en los sistemas de potencia crea un gran reto de operar el sistema de tal forma que el uso del DE sujeto a múltiples tipos de restricciones se hace cada vez más necesario debido al gran crecimiento de los sistemas eléctricos; por tanto, existe la necesidad de desarrollar modelos de DE que incorporen diversas restricciones de seguridad para garantizar un nivel de confiabilidad adecuado.

Por otro lado, para estudiar la estabilidad transitoria en función de una perturbación severa en el sistema se requiere de simulaciones en el dominio del tiempo que generalmente son complicadas. Incorporar las restricciones de estabilidad transitoria dentro de un modelo de DE plantea un desafío de la simulación en el tiempo y un modelo de optimización no lineal (R. Zarate-Minano, Van Cutsem, Milano y Conejo, 2010).

Dos aspectos principales se han planteado en los modelos del DE-RET: el primero es cómo incluir las restricciones de estabilidad transitoria en el problema del DE y el flujo de potencia óptimo; el segundo es cómo abordar la evaluación de la estabilidad transitoria (Zarate-Minano et al., 2010).

La estabilidad transitoria puede ser evaluada mediante la simulación en el dominio del tiempo teniendo en cuenta el modelo dinámico del sistema. Así se puede comprobar que las desviaciones angulares del rotor de la máquina se encuentren en un rango específico de valores (Zarate-Minano, et al., 2010). Ahora bien, la inclusión de restricciones de estabilidad transitoria en un DE resulta ser un problema de optimización no lineal difícil de solucionar. En Fang et al. (2007) la evaluación de la estabilidad transitoria se resuelve y los resultados se utilizan para determinar el límite en la generación de potencia de un grupo de máquinas críticas en el problema despacho económico. En la actualidad, una de las herramientas disponibles más comunes para solucionar este tipo de problemas de optimización es MINOS (Murtagh et al., 2002).

Alternativamente existen pocos procedimientos heurísticos para resolver problemas similares. Una de las técnicas más utilizadas en problemas continuos es la metodología de PSO, como se plantea en Mo, Zou, Chan y Pong (2007) y Xia, Chan, Bai y Guo (2015). Sin embargo, se encontraron muy pocos trabajos referentes al despacho económico considerando restricciones de estabilidad transitoria utilizando PSO.

Características del modelo

La formulación matemática del DE-RET puede entenderse como un modelo de optimización donde se tiene una función objetivo sujeta a restricciones de igualdad, desigualdad y ecuaciones diferenciales.

Un enfoque común para la solución del problema de optimización con restricciones es el uso de una función de penalización (Mo et al., 2007). El problema general se transforma a uno sin restricciones, penalizando la violación de algún límite establecido obteniendo como resultado una única función objetivo, que se minimiza mediante un algoritmo de optimización sin restricciones.

En este caso se propone un modelo en cual la estabilidad es evaluada mediante una simulación transitoria desarrollada en un conjunto de contingencias determinadas previamente. El modelo propuesto fue optimizado mediante el algoritmo de optimización heurístico PSO que se desarrolló en Matlab. La función objetivo planteada para el DE-RET tiene como variables de salida el costo total de la generación y las potencias de salida de cada generador, de forma que garantizan la estabilidad transitoria ante una serie de contingencias. Como datos de entrada en la función objetivo se tiene toda la información del sistema de potencia (líneas de trasmisión, cargas, datos de los generadores que son necesarios para el estudio de estabilidad transitoria), además se le debe proporcionar la información del fallo que se simulará, el instante en el que ocurre y el tiempo en el que se aclara.

METODOLOGÍA

Formulación DE clásico

El problema de DE se puede formular como se muestra en la ecuación (1).

Donde: x es el vector que contiene las variables de estado y las variables de control, f(·) es la función objetivo, G(·) son las restricciones de igualdad, H(·) son las restricciones de desigualdad. En este caso, la función objetivo representa el costo total de la generación. Las restricciones de igualdad son, por lo general, las de flujo de potencia para una condición de funcionamiento específico. Las restricciones de desigualdad representan los límites de las variables de control y los límites de funcionamiento del sistema.

Función objetivo

La función objetivo es una función cuadrática, como muestra la ecuación (2), propuesta para despacho de plantas térmicas (Kothari, 2006), puesto que el sistema de prueba es puramente térmico.

Donde: P_Gi potencia activa del i-ésimo generador, N es el número total de generadores y a_i b_i c_ison coeficientes de costo del i-ésimo generador.

Restricciones del DE-RET

El DE-RET puede ser considerado matemáticamente como un despacho económico convencional con restricciones de desigualdad adicionales impuestas ya sea por límites del ángulo del rotor o por la velocidad angular del mismo. La solución del flujo de potencia que no solo debe cumplir con las restricciones de estado estable impuestas por el problema de DE convencional, sino también las restricciones dinámicas impuestas por la velocidad angular del rotor durante el periodo transitorio en estudio para un conjunto dado de contingencias. Es importante resaltar que para este trabajo la métrica utilizada que define el criterio de estabilidad transitoria es la velocidad angular en comparación con lo propuesto en Zarate-Minano et al. (2010) y Mo et al. (2007) que es el ángulo del rotor.

Restricciones de igualdad

La ecuación (3) pertenece al balance del flujo de potencia y forma parte de las restricciones de igualdad.

Donde: P_Gi es la potencia generada en el i-ésimo nodo PV, P_Di es la potencia demanda en el i-ésimo nodo de carga PQ, y P_PL es la potencia de pérdidas en las líneas de trasmisión. El término P_PL de la ecuación (3) se define como se muestra en la ecuación (4) (Kothari, 2006; Garcés-Ruiz, Correa y Bolaños, 2015).

Donde N_B es el número total de nodos.

Restricciones de desigualdad

Las restricciones de desigualdad están dadas por los límites máximos y mínimos de generación de potencia activa, como se muestra en la ecuación (5).

Donde N_G es el número total de generadores.

Restricciones de estabilidad transitoria

Las máquinas síncronas son las responsables de generar gran parte de la energía eléctrica absorbida en la red. Así que su respuesta dinámica es determinante para la estabilidad del sistema después de una perturbación, el problema de estabilidad transitoria está descrito por un conjunto de ecuaciones algebraico-diferenciales. La ecuación (6) muestra el modelo de segundo orden de la máquina síncrona, para el i-ésimo generador del sistema (Kundur, Balu y Lauby, 1994; Grainger, Stevenson y Sousa, 1996).

Donde:

• δ_i es el ángulo del rotor del i-ésimo generador.
• ω_i es la velocidad angular del i-ésimo generador.
• D_i coeficiente de amortiguamiento del i-ésimo generador.
• P_mi potencia mecánica del i-ésimo generador.
• P_ei potencia eléctrica del i-ésimo generador.
• ω_o velocidad síncrono.

En este trabajo para simplificar el criterio de estabilidad transitoria en términos de la velocidad angular del rotor ω y, por tanto, la restricción de desigualdad se formula como se muestra en la ecuación (7).

Donde: ω_referencia fue un valor heurístico tomado como 1,5708 (rad/s) y ω_medida es la diferencia (ecuación (8)) entre la velocidad angular máxima (ωi_máxima) y la velocidad angular mínima (ωi_mínima) durante el posfallo del conjunto de generadores síncronos que conforman el sistema de potencia.

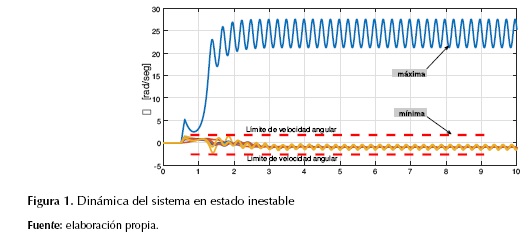
Para mejor comprensión del criterio de restricciones de estabilidad transitoria propuesta en este modelo, en la figura 1 se muestra el comportamiento del modelo dinámico del sistema en un estado inestable según la métrica planteada. Es evidente que la diferencia de velocidades angulares, ωi_máxima y ωi_mínima, durante el posfallo es mayor 1,5708 (rad/s), violando el límite establecido, de ahí que el sistema se considera en un estado inestable.

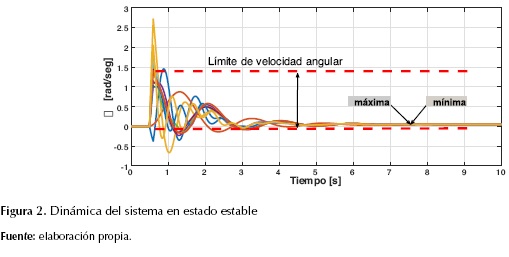
Ahora bien, en la figura 2 se muestra el comportamiento del modelo dinámico del sistema en un estado estable para la métrica planteada. Se puede observar que la diferencia de velocidades angulares, ωi_máxima y ωi_mínima durante el posfallo es igual a cero (0), manteniéndose dentro del rango establecido (1,5708 (rad/s)), de modo que se cumpla el criterio de estabilidad transitoria. El algoritmo propuesto siempre asegurará que el sistema cumpla con la métrica de estabilidad propuesta.

Planteamiento del problema del DE-RET

Teniendo la función objetivo de la ecuación (2) y agregando las restricciones de las ecuaciones (3) y (7), el problema del DE con restricciones de estabilidad transitoria puede ser formulado matemáticamente como la ecuación (9).

Función de evaluación

Como se mencionó anteriormente, la solución del problema de optimización con restricciones es el uso de una función de penalización, el problema general se transforma a uno sin restricciones, penalizando la violación de algún límite establecido, obteniendo como resultado una única función objetivo. La función objetivo resultante para el DE-RET se muestra en la ecuación (10).

Dado que la restricción de igualdad (ecuación (3)) se impone explícitamente por el cálculo del flujo de potencia, se elimina de la función objetivo. Por otro lado, la restricción de desigualdad de estabilidad transitoria (ecuación (7)) se le suma a la función objetivo acompañado de un factor de penalización β que fue escogido heurísticamente, buscando un valor representativo que significara un aumento considerable para la función objetivo si violaba el límite establecido por la restricción y presentara inestabilidad transitoria.

Implementación de la metodología

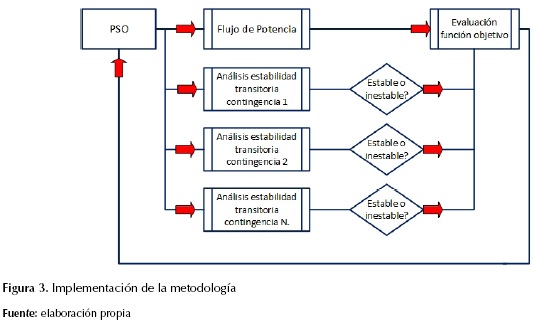
La metodología propuesta supone tres componentes: primero, un algoritmo de optimización PSO que propone las potencias inyectadas por los generadores y, al final de las iteraciones, entrega la solución más óptima; segundo, un flujo de potencia (Newton Raphson) que se ejecuta con las potencias propuestas por el PSO cumpliendo con el balance de potencias; tercero, un algoritmo que evalúa la estabilidad transitoria con los mismos datos del flujo de potencia, dicha estabilidad se evalúa utilizando el modelo de segundo orden de la máquina síncrona, ante diferentes contingencias en el sistema de prueba; finalmente, con los datos obtenidos en los pasos anteriores, se procede a la evaluación de la función objetivo obteniendo el mínimo costo en el despacho y asegurando la estabilidad transitoria. Un panorama general de la implementación de la metodología puede ser observado en la figura 3.

USO DEL PSO

Algoritmo PSO

La optimización por enjambre de partículas o PSO es un modelo de optimización para resolver problemas no lineales, inspirado en modelos de conductas sociales, como el movimiento descrito por las bandadas de aves o bancos de peces, desarrollado por los investigadores Kennedy y Eberhart, en 1995 (Zhu, 2009; Yang, 2010; Burke y Kendall, 2005). PSO es denominado como un modelo de optimización metaheurístico, puesto que asume pocas o ninguna hipótesis alrededor del problema a optimizar y puede aplicarse en amplios espacios de soluciones candidatas. La optimización por enjambre de partículas consiste en una población de individuos o partículas, estos identifican diferentes posiciones al interior del espacio de búsqueda y tienen, además, una velocidad por medio de la cual actualizan sus posiciones. Referente a la optimización, dentro del espacio de búsqueda cada posición tiene asociado un valor numérico que es cuantificado mediante la función objetivo, de tal forma que el óptimo de la función se encuentra en la posición en la que tome el valor mínimo o máximo, según lo que se desee.

En el algoritmo convencional de PSO, cada partícula se mueve con una velocidad dentro del espacio de solución y retiene en su memoria la mejor posición que encontró. En PSO un número de partículas forman un enjambre que vuela en todo el hiperespacio del problema para buscar una solución óptima. Las coordenadas de cada partícula representan una posible solución con dos vectores asociados a ella, la posición X y la velocidad V. Durante su búsqueda, las partículas interactúan entre sí de una manera determinada para optimizar su experiencia de búsqueda. En cada iteración, cada partícula guarda la mejor posición Pbest obtenida en su recorrido y a su vez guarda la mejor posición obtenida por el líder del cúmulo Gbest (Zhu, 2009). Conceptualmente, Pbest representa la memoria autobiográfica, a través de la cual cada partícula recuerda sus antiguas experiencias (Gallego, Escobar, Toro y Romero, 2010). La velocidad y la posición de cada partícula se pueden calcular utilizando las ecuaciones (11) y (12)

Dónde: v_i y x_i es la velocidad y posición actual de la iteración i-ésima; ω es el factor de inercia y se propone como se la ecuación (13).

Dónde: t_max es el máximo número de iteraciones, t es el número actual de la iteración, ω_max y ω_min son los límites superiores e inferiores del factor de inercia. Los valores típicos de ω están entre 0 y 1 (Burke y Kendall, 2005); para este trabajo, los valores de las w fueron de 0,4 y 0,9, respectivamente. Este factor permite controlar el balance entre la diversificación y la intensificación de la búsqueda en el espacio de soluciones y divide el cúmulo de partículas en individuos exploradores y colonizadores. Un valor grande de w produce partículas exploradoras, es decir, durante el proceso iterativo explora en gran parte el espacio de soluciones. Un valor pequeño de ω produce individuos colonizadores, es decir, enfocan su búsqueda en una región específica.

C₁ y C₂ son las constantes de aceleración que direccionan las partículas hacia una mejor posición local o global. La constante C₁ regula la influencia que tiene la mejor posición alcanzada por la partícula para la determinación de su nueva dirección. C₂ regula la influencia del líder del cúmulo en la dirección de búsqueda de cada partícula. Se propone que estas constantes de aceleración se modifiquen de manera adaptativa. De acuerdo con esto, estas constantes se determinan en concordancia con la ecuación (14).

rand() son dos números aleatorios generados por separado, uniformemente distribuidos en el intervalo 0 y 1 que añaden la naturaleza estocástica al modelo.

RESULTADOS

El algoritmo fue implementado en el sistema de prueba IEEE39 nodos de Nueva Inglaterra, el cual cuenta con 10 generadores, 46 líneas de trasmisión, una carga de 61,2450 p.u de potencia activa y 15,9336 en p.u de potencia reactiva (S_base=100MVA). En dicho algoritmo se buscaba obtener el mínimo costo del despacho económico garantizando la estabilidad transitoria mediante el análisis de las soluciones obtenidas y representadas en las gráficas de convergencia, verificar el comportamiento de las variables de estado del generador en el dominio del tiempo y el ajuste de los parámetros del modelo de optimización PSO. El tiempo de simulación para el análisis de estabilidad transitoria para cada iteración fue de 0 a 10 segundos, rango que es adecuado para revelar si se produce dicha inestabilidad.

A continuación, se muestran los resultados obtenidos de la optimización del despacho económico, considerando restricciones de estabilidad transitoria propuesto, desarrollado en el software Matlab y ejecutado en un computador portátil Intel(R) Core(TM)2 Duo 2.10GHz, 4,00 GB de memoria RAM. Los datos del sistema de prueba IEEE 39 nodos de Nueva Inglaterra se encuentran en Padiyar, 2008). Adicionalmente, los parámetros de ajuste del algoritmo de optimización PSO se muestra en la tabla 1.

Para cada caso de estudio se realizó una contingencia en una línea de trasmisión, en un periodo de 10 segundos para el análisis de estabilidad transitoria, donde el fallo ocurría a los 0,5 segundos y cuyo libramiento se lleva a cabo en el segundo 0,6. Cabe señalar que se utilizó en el modelo de la máquina síncrona un coeficiente de amortiguamiento (damping) de 0,5.

Para el caso 1 en particular, se mostrarán las gráficas de la velocidad angular (ω), ángulo (δ) y velocidad angular respecto al centro de inercia (Ω_COI), además, las gráficas de potencia mecánica y eléctrica cuando el sistema se encontraba en una condición estable e inestable. Para los demás casos, por simplicidad, se mostrará la solución óptima en una muestra de 10 despachos, enseñando las potencias inyectadas por cada generador, las pérdidas, el costo, el tiempo computacional y la gráfica de convergencia.

Caso base

Inicialmente se realizó una simulación del DE convencional dejando a un lado el análisis y las restricciones de estabilidad transitoria con el objetivo de probar el modelo de optimización PSO planteado y corroborar el correcto funcionamiento de este.

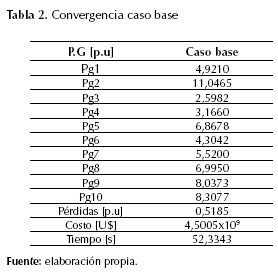
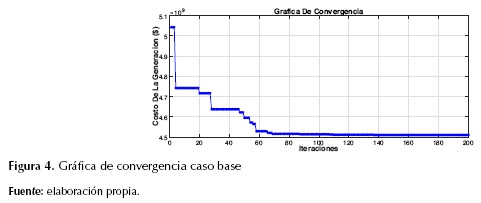
En la tabla 2 se muestra el mejor resultado obtenido de 10 ensayos, donde se tienen las potencias inyectadas por los diez generadores en p.u, las pérdidas en p.u, el costo total del despacho en dólares (US$) y el tiempo computacional en segundos (s). Para el caso base, el costo total de la generación fue de 4,5005×10⁹ US$. En la figura 4 se muestra la gráfica de convergencia de dicho despacho; en el eje vertical, el costo de la generación y en el eje horizontal las iteraciones.

Caso 1. Fallo en la línea que conecta los nodos 12 y 11

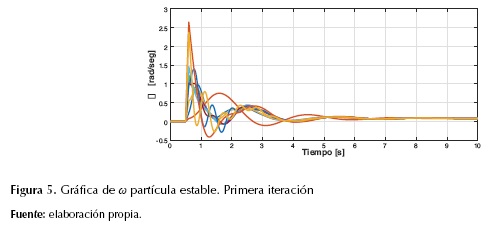
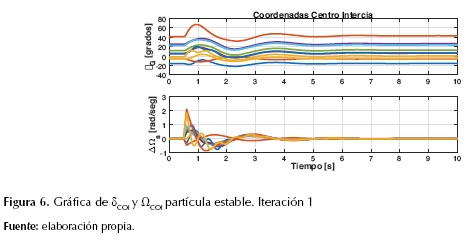
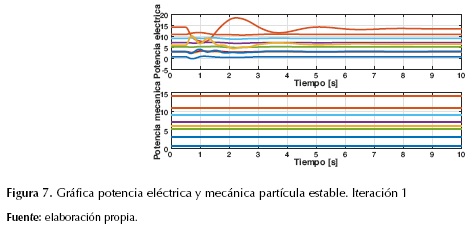
Para el algoritmo planteado, en cada iteración se obtenían 20 posibles soluciones debido a que en los parámetros de ajuste del modelo de optimización se tenía una población de 20 partículas. Entre esas posibles soluciones, se contaba con partículas que hacían el sistema estable e inestable. En las figuras 5, 6 y 7 se muestra la evolución de la velocidad angular ω, el ángulo δ_COI y la velocidad angular Ω_COI, las potencias mecánica y eléctrica de cada uno de los generadores en la primera iteración de una partícula estable.

Como se puede observar, las variables de estado después de ser sometidas a la contingencia regresaron a un punto de operación estable, garantizando mantener el sincronismo de los generadores del sistema.

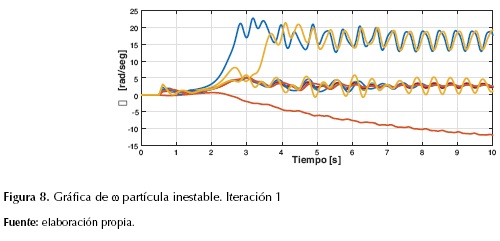
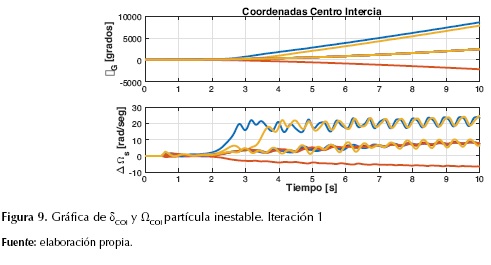
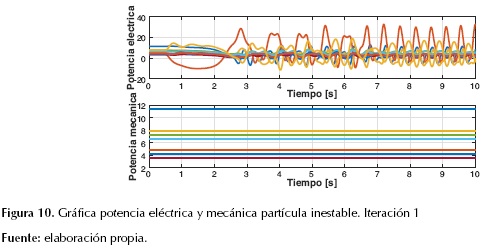
Por el contrario, en las figuras 8, 9 y 10 se muestra el comportamiento de las variables de estado de una partícula inestable en la primera iteración. Es evidente que los 10 generadores se aceleraron y se mantuvieron en estado transitorio, asimismo sus ángulos δ_COI y velocidades Ω_COI tienden a infinito, además, la potencia eléctrica es oscilante, lo que hace que los generadores pierdan el sincronismo. Por otro lado, la potencia mecánica se mantiene constante como característica del modelo propuesto.

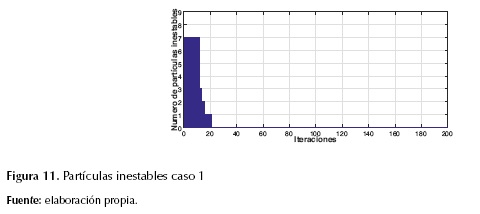
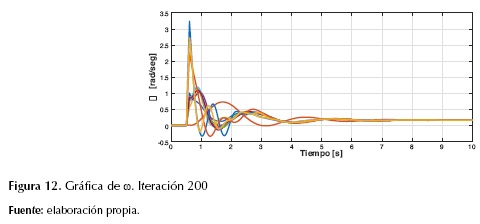
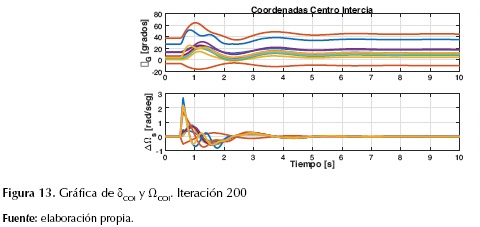
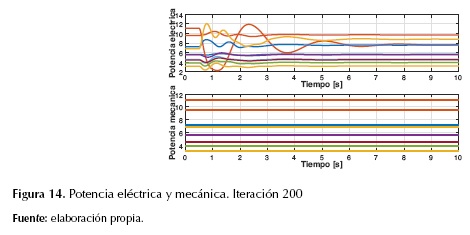
Cabe aclarar que el modelo de optimización, con el paso de las iteraciones, descartaba las partículas que fueran inestables, es decir, la solución final aseguraba la estabilidad transitoria de todas las partículas. En la figura 11 se muestra, para el caso de estudio, el número de partículas inestables durante el proceso iterativo. Como se puede observar, a partir de la iteración 28 el modelo de optimización garantizaba que todas las partículas fueran estables y se aseguraba un despacho económico garantizando la estabilidad transitoria, como se evidencia en las figuras 12, 13 y 14, las cuales corresponden a una partícula en la iteración final. Es importante resaltar que al final del proceso iterativo todas las partículas tuvieron el mismo comportamiento mostrado en dichas gráficas.

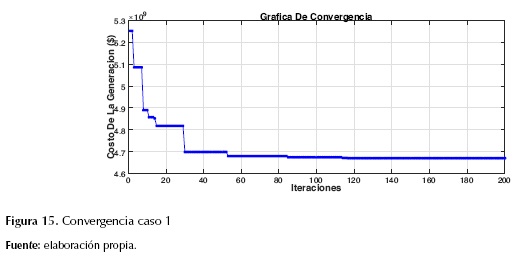
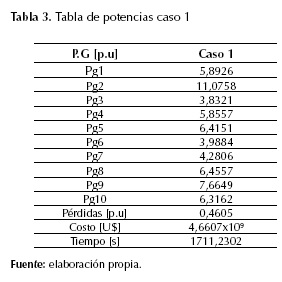
Entre tanto, en la figura 15 se muestra la gráfica de convergencia, de la cual se puede concluir que el método de optimización encontraba el óptimo global a partir de la iteración 115. Adicionalmente, en la tabla 3 se muestran las potencias inyectadas por los generadores, las pérdidas y el costo total del despacho en este caso.

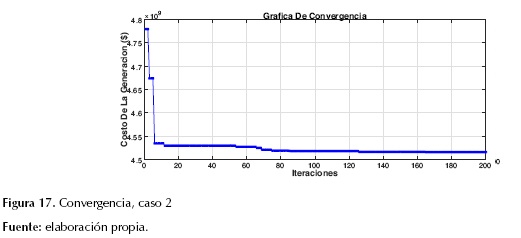
Caso 2. Fallo en la línea que conecta los nodos 14 y 34

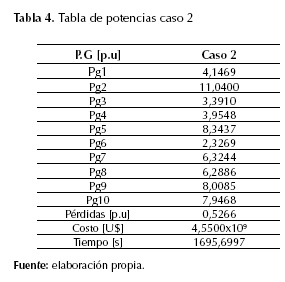
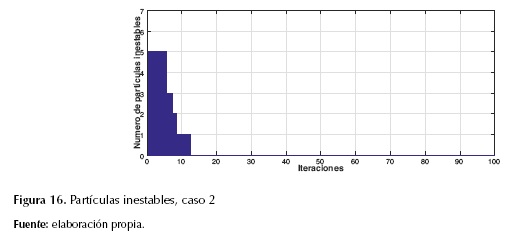
La tabla 4 muestra los resultados obtenidos del proceso de optimización del DE-RET para un fallo en la línea que conecta los nodos 14 y 34. Para este caso, el valor la desviación angular máxima δ_COI entre el grupo de los 10 generadores en la última iteración fue 51 grados, donde al final del proceso se aseguró la estabilidad transitoria. Para prueba de ello, se puede observar en la figura 16 que a partir de la iteración 74 el modelo de optimización descartaba las soluciones inestables.

El la figura 17 se muestra la evolución del valor final de la función objetivo en este caso.

CONCLUSIONES

Se presentó un modelo de optimización para determinar el punto de operación óptimo de un sistema de potencia cuando es sometido a una perturbación severa, considerando tanto las restricciones técnicas de operación del sistema como las restricciones de estabilidad transitoria del mismo. Además, el modelo de despacho económico considerando restricciones de estabilidad transitoria resultante, incluye la solución de ecuaciones en el dominio del tiempo que describen la evolución temporal de todas las máquinas del sistema. De ahí que el modelo propuesto es confiable y, generalmente, proporciona soluciones óptimas en los casos estudiados.

El conjunto de soluciones obtenidas muestra que con la variación de las potencias inyectadas por los generadores síncronos, puede cambiar el punto de operación del sistema desde el punto de vista de la estabilidad transitoria, es decir, se puede pasar de un estado inestable a uno estable mediante la variación de las mismas.

Los resultados demuestran la eficacia y potencialidad del modelo de optimización metaheurística Particle Swarm Optimization para la solución del DE-RET, asimismo, el PSO resulta ser un fuerte competidor de los modelos de optimización de búsqueda aleatoria como lo son los algoritmos genéticos, aplicados a la optimización de los sistemas de potencia.

REFERENCIAS BIBLIOGRÁFICAS

Bolaños, R. y Correa, C. (2014). Transmission planning considering security and demand uncertainty through non-linear programming and evolutionary techniques. Revista Tecnura, 18(39), 62-76.

Burke, E.K. y Kendall, G. (2005). Search methodologies. Springer, ISBN-10:0-387-23460-8, New York.

Espitia-Chuchango, E.; Sofrony-Esmeral, J. (2014). Vortex Particle Swarm Optimization with Individual and Group Search. Revista Tecnura, 18(42), 24-37.

Fang, D.; Xiaodong, Y.; Jingqiang, S.; Shiqiang, Y. y Yao, Z. (2007). An optimal generation rescheduling approach for transient stability enhancement. IEEE Transactions on Power Systems, 22(1), 386-394. [En línea]. Recuperado de: http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=4077106.

Gallego, R.; Escobar, A.; Toro, E. y Romero, R. Técnicas heurísticas y metaheurísticas de optimización. Editorial Universidad Tecnológica de Pereira, ISBN: 9789587222074, Pereira, 2015.

Garcés-Ruiz, A.; Sistemas de Generación de Energía, Editorial Universidad Tecnológica de, ISBN: 978-958-722-044- Pereira, Pereira, 2006.

Grainger, J.J.; Stevenson, W.D. y Sousa, C.L. (1996). Análisis de sistemas de potencia. McGraw-Hill, México.

Kothari, J. D. D.P. (2006). Power system optimization. Nueva Delhi: PHI Learning Pvt. Ltd.

Kundur, P.; Balu, N.J. y Lauby, M.G. (1994). Power system stability and control. Vol. 7. Nueva York: McGraw-Hill.

Mo, N.; Zou, Z.; Chan, K. y Pong, T. (2007). Transient stability constrained optimal power flow using particle swarm optimisation. IET Generation, Transmission & Distribution, 1(3), 476-483. Recuperado de: http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=4202028.

Murtagh, B.; Saunders, M.; Murray, W.; Gill, P.; Raman, R. y Kalvelagen, E. (2002). Gams/minos: A solver for large-scale nonlinear optimization problems. Recuperado de: https://pdfs.semanticscholar.org/5166/2c15571df1209b15293b2352a5ed70405b49.pdf

Padiyar, K. (2008). Power system dynamics. Hyderabad, India: BS Publications.

Xia, S.; Chan, K.W.; Bai, X. y Guo, Z. (2015). Enhanced particle swarm optimisation applied for transient angle and voltage constrained discrete optimal power flow with flexible AC transmission system. IET Generation, Transmission & Distribution, 9(1), 61-74. [En línea]. Recuperado de: http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=7024965.

Yang, X.S. (2010). Nature-inspired metaheuristic algorithms. Frome: Luniver Press.

Zarate-Minano, R.; Van Cutsem, T.; Milano, F. y Conejo, A. (2010). Securing transient stability using time-domain simulations within an optimal power flow. IEEE Transactions on Power Systemsvol, 25(1), 243-253. Recuperado de: http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=5288558.

Zhu, J. (2009). Optimization of power system operation. Nueva Jersey: John Wiley & Sons.