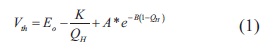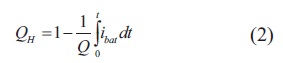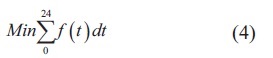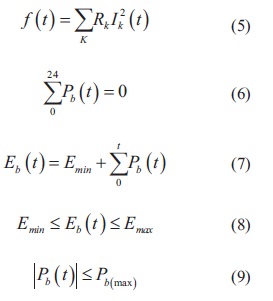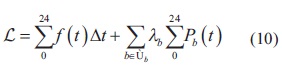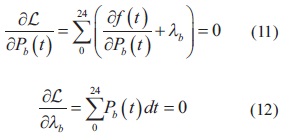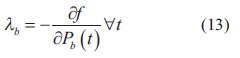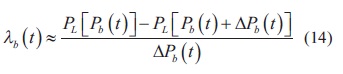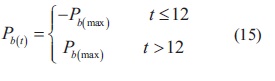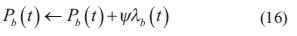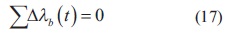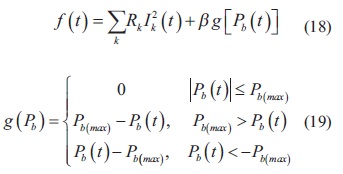DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2014.4.a04Published:
2014-10-01Issue:
Vol. 18 No. 42 (2014): October - DecemberSection:
ResearchOperación económica de dispositivos almacenadores de energía para disminución de pérdidas
Optimal Operation of Distributed Energy Storage Units for Minimizing Energy Losses
Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Operación económica de dispositivos almacenadores de energía para disminución de pérdidas
Optimal Operation of Distributed Energy Storage Units for Minimizing Energy Losses
Alejandro Garces Ruiz1, Carlos Adrián Correa Flórez2, Alejandro Sánchez Salcedo3
1Ingeniero electricista, magíster en Ingeniería, doctor en Ingeniería, profesor de la Universidad Tecnológica de Pereira, Pereira, Colombia. alejandro.garces@utp.edu.co
2Ingeniero electricista, magíster en Ingeniería Eléctrica, profesor de la Universidad de La Salle. Bogotá, Colombia. Contacto: carcorrea@unisalle.edu.co
3Ingeniero electricista, magíster en Ingeniería - Ingeniería Eléctrica, profesor de la Universidad de La Salle, Bogotá, Colombia. Contacto: alsanchez@unisalle.edu.co
Fecha de recepción: 18 de julio de 2013 Fecha de aceptación: 16 de mayo de 2014
Clasificación del artículo: investigación
Financiamiento: recursos propios
Resumen
Este artículo presenta un algoritmo para la operación óptima de unidades de almacenamiento de energía (UDAE), desde la perspectiva de las pérdidas de potencia activa. Se propone un modelo exacto basado en relajación lagrangeana. Los resultados de simulación sobre el alimentador de distribución IEEE de 37 nodos demuestran que un sistema de almacenamiento de energía puede ser utilizado para minimizar las pérdidas de un sistema de distribución, a través de la modificación de la curva de carga. La principal contribución de este enfoque consiste en el tratamiento de la función objetivo y el algoritmo de optimización. Los multiplicadores de Lagrange son usados para determinar la ubicación y el dimensionamiento óptimo de las unidades de almacenamiento. Se presenta además una discusión sobre el impacto de las UDAE en el planeamiento de la red de distribución.
Palabras clave: almacenamiento de energía, multiplicadores de Lagrange, optimización, pérdidas, sistemas de distribución.
Abstract
This paper presents an algorithm for the optimal operation of distributed energy storage units from perspective of active potential lost. An exact model based on Lagrange relaxation is proposed. Simulation results on the IEEE 37-bus test feeder demonstrate that energy storage system can be used for minimizing transmission losses in a distribution system by reshaping the load curve. The main contribution of this approach is the objective function and the optimization algorithm, Lagrange multipliers are used for determining optimal placement and sizing of the energy storage units. A discussion about the impact of energy storage units on the distribution planning is also presented.
Keywords: energy storage, Lagrange multipliers, losses, optimization, power distribution systems.
Introducción
Las unidades de almacenamiento de energía (UDAE) han demostrado ser una solución eficiente en aplicaciones a niveles de baja y media tensión en donde se presente una alta variabilidad de la generación o la demanda (Papic, 2006; Schoenung y Burns, 1996; Nguyen y Flueck, 2012). Estas contribuyen a suavizar la curva de carga en el sistema, incrementan la estabilidad y aumentan la eficiencia en sistemas con alta penetración de fuentes renovables, tales como la generación eólica (Brekken, Yokochi, VonJouanne, Yen, Hapke y Halamay, 2011; Yao, Choi, Tseng y Lie, 2012), la generación solar fotovoltaica (Ru, Kleissl y Martínez, 2012; Hill, Such, Chen, González y Grady, 2012) y la generación undimotriz (Muthukumar, Kakumanu, Sriram y Jayashankar, 2005), entre otras.
Se han propuesto diferentes técnicas para la operación óptima de UDAE. En la mayoría de los casos se han propuesto modelos discretos que son solucionados mediante diferentes técnicas de optimización, tales como programación dinámica (Maly y Kwan, 1995), enjambre de partículas (Lee, 2007) y algoritmos genéticos (Cau y Kaye, 2003). Igualmente, se han propuesto diferentes tipos de función objetivo entre las que se destacan la reducción de los costos de operación (Correa, Bolanos y Garces, 2012), suavizado de la curva de carga (Hess, Schegner y Hable, 2013) y aumento de la reserva rodante (Habib,i, 2001). En este artículo se presenta un modelamiento matemático con el fin de reducir las pérdidas de transmisión, utilizando la UDAE como un compensador de energía. Desde luego, debido a la necesidad de un convertidor AC para integrar el dispositivo almacenador de energía, el compensador de energía puede también ser utilizado como compensador de potencia usando la teoría ABC, también conocida como teoría vectorial, que es definida en el marco referencial trifásico.
Metodología
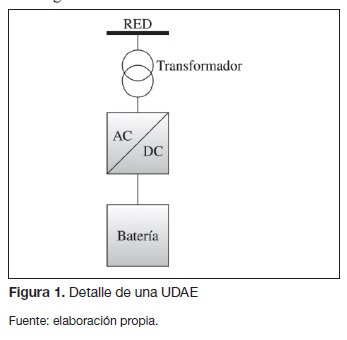
Una unidad almacenadora de energía consiste en un dispositivo de almacenamiento (batería, volante de inercia, súper capacitor, etc.) que es integrada al sistema de distribución mediante un inversor trifásico y un transformador. Un modelamiento detallado del sistema requiere una definición previa del tipo de tecnología de almacenamiento. En este caso se presenta un modelo simplificado de almacenamiento de energía, con el fin de mostrar un caso general que no dependa de la tecnología.
Tipos de sistemas con almacenamiento de energía
Debido a su capacidad de almacenamiento a largo plazo, los sistemas de almacenamiento de energía electroquímica son potencialmente los más adecuados para compensación de energía en sistemas de distribución. Las principales tecnologías de baterías son las de plomo-ácido, níquel-cadmio y litio-ion, entre otras. Las primeras son las más comunes en sistemas eléctricos debido a su bajo costo. Las baterías de níquel-cadmio, a pesar de ser una tecnología madura, han sido objeto de críticas debido a su alto impacto ambiental.
Como en todos los sistemas de almacenamiento estudiados anteriormente, se requiere un inversor con el fin de controlar la carga y descarga de la batería y para convertir de DC a AC (figura 1). Este puede ser utilizado también para compensar potencia reactiva y para reducir el contenido armónico de la corriente, a la vez que se requiere un transformador para aislamiento galvánico y para aumentar el nivel de tensión. En el mercado se encuentran sistemas almacenadores de energía basados en baterías de hasta 4 MW (ABB, 2011); las capacidades superiores son todavía materia de investigación.
El modelo clásico de una batería consiste en un equivalente de Thevenin, en donde el voltaje de Thevenin Vthestá dado por la ecuación (1).
En este modelo, Eorepresenta la tensión constante de la batería, K es el voltaje de polarización, A es la amplitud de la constante exponencial, B es proporcional a la constante de tiempo y QHes el estado de carga, que se calcula con la ecuación (2).
Finalmente, la tensión de la batería se calcula con la ecuación (3).
Estos parámetros corresponden a una única unidad. Sin embargo, para alcanzar el nivel de tensión adecuado, las baterías deben ser conectadas en arreglos serie/paralelo.
Modelo para pérdidas mínimas
Las pérdidas totales de potencia activa a lo largo de un alimentador f(t) son dependientes del tiempo, ya que la curva de demanda y la capacidad de generación distribuida cambian a lo largo del día. Así mismo, las UDAE que vayan a despacharse a lo largo del sistema pueden cambiar estas pérdidas inyectando o drenando un valor instantáneo de potencia Pb(t). En la ecuación (4) se presenta el modelo matemático para minimizar las pérdidas de energía en un día de operación.
Sujeto a las restricciones mostradas en las ecuaciones (5), (6), (7), (8) y (9).
En donde Rk es la resistencia en el k-esimo tramo del alimentador primario, Ik(t) es la corriente en el tramo de línea k en el tiempo t, y Eb(t) es la energía almacenada en cada UDAE b. Las variables de decisión Pb(t) corresponden a la potencia inyectada por cada UDAE b en el instante de tiempo t. Si este valor es negativo entonces la unidad está en proceso de carga mientras que en el caso contrario se encuentra en periodo de descarga. Q.b representa el conjunto de unidades de compensación con almacenamiento de energía instaladas a lo largo del alimentador primario, mientras que Ω.tes el conjunto de tramos de este.
De acuerdo con el modelo de la ecuación (4), la energía intercambiada por cada UDAE en un periodo de operación debe ser cero, como en la ecuación (6). Esto significa que se está asumiendo un perfil de demanda aproximadamente igual cada día a lo largo del año. Esta aproximación deja de ser válida en países en donde existen estaciones, pero se acerca más a la realidad de países como Colombia. Sin embargo, es importante aclarar que la curva de carga en Colombia difiere los días sábados, domingos y festivos con respecto a la curva entre lunes y viernes. Además, también pueden existir variaciones durante periodos de sequía o de lluvia abundante. Una variación en la curva de demanda puede ser fácilmente compensada si se tiene una adecuada predicción de esta. En un modelo más general, la energía total almacenada al finalizar un periodo de operación es dada como primera etapa de un modelo de optimización de largo plazo, tal y como ocurre en el problema de despacho hidrotérmico.
Por otro lado, el modelo interno del dispositivo almacenador de energía y el convertidor que lo integra a la red imponen algunas restricciones adicionales relacionadas con la capacidad de transmisión de potencia y el estado de carga. Estas restricciones son modeladas por las ecuaciones (8) y (9).
Al considerarse inicialmente un problema reducido, donde solo se analiza la ecuación (6), existe una restricción por cada unidad almacenadora y por tanto el lagrangeano requiere un multiplicador por cada unidad, como se muestra en la ecuación (10).
Las condiciones de optimalidad se obtienen derivando L como función de Pb(t) y ëb, como se muestra en las ecuaciones (11) y (12).
La ecuación (11) implica que la operación óptima se obtiene cuando la derivada de f respecto a Pbes invariante en el tiempo como se expresa en la ecuación (13).
Por tanto, un algoritmo que alcance iterativamente esta condición es suficiente para garantizar optimalidad si se mantiene la restricción representada por la ecuación (12).
Una dificultad de este algoritmo es el cálculo de la derivada de las pérdidas totales de transmisión, dada por la ecuación (13). Esta puede ser calculada por medio del jacobiano del sistema asumiendo que las pérdidas de potencia son proporcionales a la potencia suministrada por el nodo Slack, tal y como ocurre en las metodologías convencionales de flujo de carga óptimo. Sin embargo, el cálculo del jacobiano esta implícitamente relacionado con el uso de metodologías basadas en Newton-Raphson, las cuales no son adecuadas en sistemas de distribución debido a la baja relación X/R en este tipo de sistemas. Por tanto, un algoritmo de flujo de carga de barrido iterativo es mucho más recomendable, ya que no requiere el cálculo directo del jacobiano (Chen, Chen, Hwang, Ko-tas y Ea, 1991). El valor de ëb(t) en la ecuación (11) es por tanto calculado usando diferenciación numérica, como se expresa en la ecuación (14). Esta metodología requiere el cálculo de un flujo de carga adicional para una pequeña variación de potencia Pb(t)+ΔPb(t). Este flujo de carga puede ser inicializado con las tensiones encontradas por el flujo para Pb(t) y por tanto el esfuerzo computacional es reducido significativamente, pues la convergencia se obtiene en una o dos iteraciones adicionales.
El valor de Pb(t) en el algoritmo de optimización es inicializado de tal forma que se garantice el cumplimiento de la restricción representada por la ecuación (6). Se espera que la operación óptima se obtenga mediante la carga de la unidad almacenadora de energía durante los periodos de mínima demanda, con el fin de descargar los alimentadores durante las horas pico, cuya hora exacta dependerá de la época de la año. Modelos más completos pueden incluir los impactos de la potencia activa, ya que es posible que en muchos países (como en Colombia) los picos de potencia activa no coincidan con los de potencia reactiva, hecho que también puede incidir sobre las corrientes por los elementos, y por lo tanto sobre las pérdidas. De esta manera y para las condiciones del problema propuesto en este trabajo, la ecuación (15) da una posible condición inicial.
El valor de ëkes determinado para cada instante de tiempo por medio del flujo de carga de barrido iterativo, y el nuevo valor de Pb(t) es calculado mediante la ecuación (16), en donde Ψ representa un parámetro heurístico para asegurar la convergencia del algoritmo.
Cabe anotar que la restricción representada por la ecuación (6) se cumple durante todo el proceso de optimización, debido a la condición que se muestra en la ecuación (17).
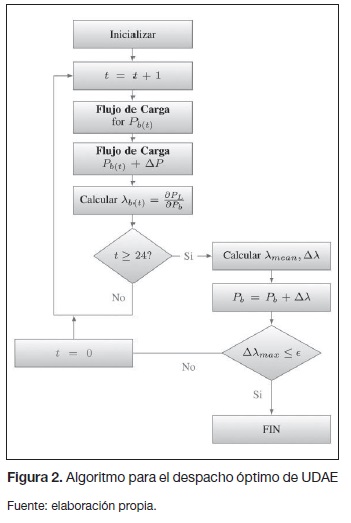
El algoritmo completo se muestra en la figura 2. Aunque simplificado, este problema puede dar valiosa información para la operación y el planeamiento del sistema de distribución. Por ejemplo, la capacidad de potencia de cada UDAE puede ser determinada con este modelo reducido, como se mostrará en la tercera sección.
Las restricciones de desigualdad en el modelo original pueden ser fácilmente incluidas en el algoritmo de optimización adicionando un factor de penalización en la función objetivo. Este factor de penalización es proporcional a la diferencia entre la potencia suministrada y el límite violado, como se expresa en las ecuaciones (18) y (19).
en donde â es un parámetro heurístico y g es la función de penalización.
Efecto de la capacidad de almacenamiento de energía en el planeamiento de la distribución
Las pérdidas de potencia activa en un alimentador primario están directamente relacionadas con la cargabilidad, teniendo en cuenta que dependiendo de su operación con respecto al SIL, estas pueden inyectar o absorber reactivos. A medida que las pérdidas de energía disminuyen, las corrientes máximas son proporcionalmente reducidas. Por lo tanto, la cargabilidad del sistema de distribución puede ser reducida ubicando compensadores con alta capacidad de almacenamiento de energía a lo largo del alimentador. Las unidades de compensación con almacenamiento de energía tienen un impacto en el planeamiento de la distribución como consecuencia de este comportamiento, ya que se puede evitar la construcción de nuevas líneas de distribución por medio de la homogenización de la curva de carga vista desde la subestación. El planeamiento energético y el planeamiento eléctrico, aunque relacionados, suelen ser solucionados de forma independiente. El planeamiento de la expansión de la transmisión o la distribución esta usualmente relacionado con los valores picos de potencia en su modelo tradicional, aunque en ocasiones dichos modelos pueden incluir múltiples escenarios de generación/demanda o inclusión de incertidumbre, para así relajar el modelo matemático y evitar sobredi-mensionamiento. Debido a esta homogenización de la curva de carga, el planeamiento energético y el planeamiento eléctrico pueden ser solucionados como un único problema.
El enfoque convencional es adecuado en sistemas de distribución en donde las nuevas líneas de transmisión suelen ser diseñadas para satisfacer únicamente la demanda pico. Sin embargo, esta demanda se presenta en menos del 10 % del tiempo de operación en el sistema. Usando un planeamiento energético, el resultado puede mejorar. El algoritmo de compensación presentado puede homogenizar la curva de carga de tal forma que la demanda pico sea disminuida. Desde luego, esto implica un aumento en las pérdidas de potencia durante los periodos de baja demanda ya que la unidad almacenadora de energía debe cargarse durante estos periodos. Sin embargo, el aumento en las pérdidas durante las horas valle se ve compensado por su disminución en la hora pico, por lo que el resultado global representa una disminución de pérdidas en el sistema.
Una función objetivo basada en la disminución de las pérdidas de energía difiere del convencional análisis económico usado en los dispositivos almacenadores de energía, en el modelo mismo así como en el análisis de los resultados. En un modelo que considere únicamente precios de bolsa o contratos, el costo es minimizado desde el punto de vista del usuario, pero no desde el punto de vista del sistema de distribución como tal. Este tipo de modelo es adecuado para mi-crorredes en donde una parte del sistema puede operar de forma aislada, aumentando con ello la confiabilidad del sistema. Sin embargo, un modelo basado en pérdidas puede mejorar en términos económicos los costos del usuario final, con la ventaja de que no se requiere información en tiempo real de variables del mercado como el precio de bolsa. En general, el precio de bolsa es proporcional a la demanda debido al esquema de despacho basado en orden de méritos. En sistemas hidrotérmicos como el colombiano, el precio de bolsa puede aumentar significativamente durante las horas pico debido a la inclusión de plantas de generación termoeléctricas. Sin embargo, puesto que el precio spot es unificado, el valor pico de la demanda total del sistema puede no coincidir exactamente con el pico de un alimentador en particular ya que la demanda no es coincidente en usuarios residenciales, industriales o comerciales. Consecuentemente, un modelo basado en el mercado puede no ser exactamente igual al modelo basado en pérdidas, pero sí están cercanos.
Resultados
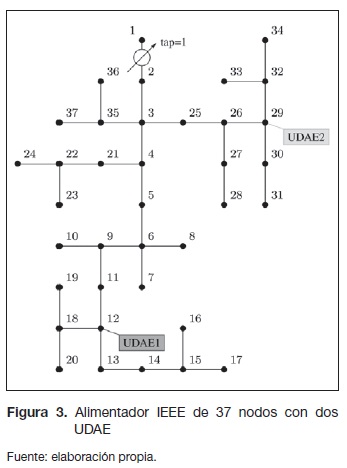
El algoritmo de optimización propuesto en este artículo es comprobado sobre el sistema IEEE de 37 nodos, modificado para simular un sistema balanceado agregando las cargas en cada nodo, e incluyendo dos UDAE en los nodos 29 y 12 como se muestra en la figura 3, con el fin de mostrar la metodología de manera detallada.
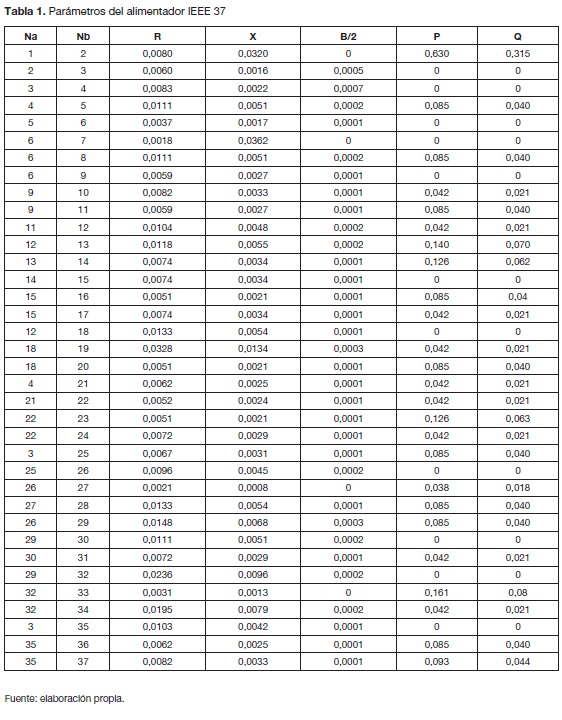
Los parámetros del alimentador para operación balanceada se presentan en la tabla 1 para una potencia base de SBASE = 1000 kW y un voltaje base trifásico de VBASE=4,8 kV. El voltaje del regulador ubicado en el nodo Slack del sistema original es mantenido en 1 pu, con el fin de determinar el efecto de la unidad de almacenamiento de energía en el perfil de tensión. El sistema presenta dos tipos de cargas: industrial y residencial.
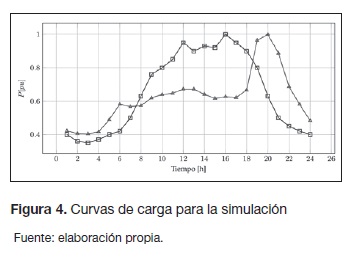
Las curvas de carga asociadas a cada tipo deusuario se muestran en la figura 4, donde los nodos 25 a 34 corresponden a cargas industriales y los demás son cargas residenciales.
La curva de carga para usuarios residenciales tiene una forma característica en la cual la hora pico es muy superior a las horas valle y se encuentra concentrada en un valor cercano a las 8 pm. Los usuarios industriales en cambio tienen una curva mucho más ancha, en donde el pico se presenta aproximadamente constante durante las horas de la jornada laboral. Es de esperarse un mayor efecto sobre las pérdidas en los usuarios residenciales debido a lo concentrado del valor pico.
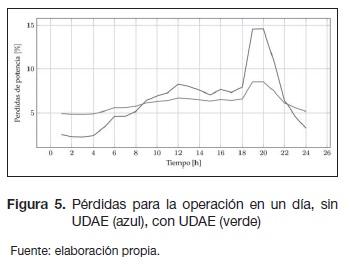
Las pérdidas de potencia activa para la operación del sistema con y sin unidades de compensación con almacenamiento de energía se presentan en la figura 5. Se evidencia una significativa reducción de las pérdidas de potencia activa durante las horas pico, mientras que se presenta un aumento de estas durante las horas valle debido al proceso de carga de las UDAE. El efecto total durante el periodo completo de operación es una disminución del 5,3 %. La reducción en términos de pérdidas de potencia en la hora pico es aún más significativa, pasando de 0,1458 a 0,085 pu, lo cual significa una reducción del 41,42%. Como se expuso anteriormente, esta disminución tiene influencia directa en el planeamiento de la expansión de la distribución, pudiendo incluso no ser necesaria la construcción de nuevas líneas, aun si el sistema se encontrara operando a un valor cercano al límite térmico.
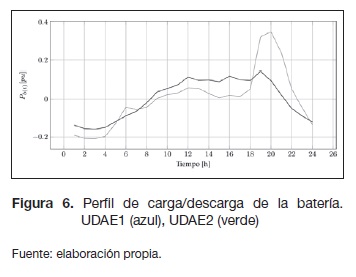
La potencia intercambiada entre cada unidad al-macenadora de energía y el alimentador primario se representa en la figura 6. Debido a que la primera unidad (UDAE1) está ubicada en una zona residencial, su perfil de potencia es similar a la curva de carga de los usuarios residenciales. La potencia máxima requerida para esta operación es menos de 400 kW, lo cual es un valor posible con la tecnología disponible comercialmente (ABB, 2011).
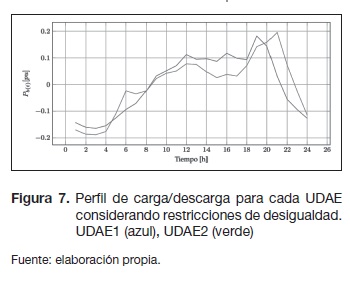
Las restricciones de desigualdad son igualmente consideradas en el algoritmo, en tanto que la capacidad máxima de potencia requerida por cada unidad es limitada a 0,2 pu. El perfil de carga y descarga para este caso es representado en la figura 7.
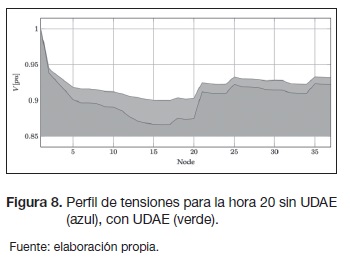
En razón de las características de los sistemas de distribución, el perfil de tensión en un alimentador primario está directamente relacionado con la potencia activa. Este comportamiento, claramente opuesto al de los sistemas de potencia, se debe a la alta relación entre el valor de r y x en cada línea de distribución. Por tanto, la operación óptima de UDAE tiene una influencia sobre el perfil de tensión, como se demuestra en la figura 8, en donde se aprecia la tensión en cada nodo del alimentador para la hora pico (t=20 h).
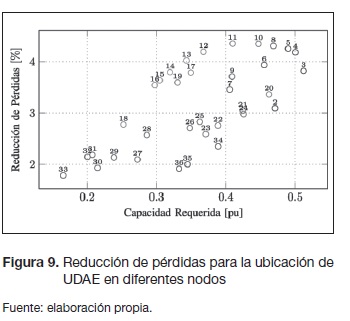
La disminución máxima en términos de pérdidas de potencia activa es determinada haciendo uso del modelo reducido presentado en la segunda sección. Así mismo, los multiplicadores de Lagrange asociados a la restricción de balance de energía pueden ser utilizados para definir la capacidad de potencia requerida por cada unidad. La figura 9 muestra la reducción de las pérdidas de energía en porcentaje sobre la capacidad de potencia requerida para la ubicación de una única UDAE en cada uno de los nodos del sistema de distribución. La reducción en términos de pérdidas de energía es diferente de acuerdo a la ubicación de la unidad. Por ejemplo, una unidad ubicada en el nodo 3 produce una reducción de energía de 3,8 % y requiere una capacidad de 0,51 pu, mientras que se puede obtener aproximadamente la misma reducción al ubicar una unidad almacenadora de energía en el nodo 14 con una capacidad de solo 0,31 pu. Los nodos cercanos al Slack, tales como los nodos 2 o 3, así como los nodos demasiado lejanos, son los menos aconsejables para minimizar las pérdidas totales con una baja capacidad requerida.
Cabe anotar que el problema de ubicación óptima y dimensionamiento de unidades de compensación con almacenamiento de energía puede ser planteado como un problema multiobjetivo con dos criterios en conflicto: pérdidas de energía mínima y mínima capacidad. Para el problema descrito anteriormente con una única unidad, el frente de Pareto está dado por la ubicación de unidades en los nodos N={33,32,31,18,16,15,14,13,12,11}.
Conclusiones
Se ha propuesto un novedoso algoritmo para la programación óptima de dispositivos de almacenamiento de energía, desde el punto de vista de las pérdidas. El algoritmo considera las principales restricciones de este tipo de unidades y permite operación en tiempo real si la curva de carga es adecuadamente anticipada. Los resultados de simulación sobre el sistema de prueba IEEE de 37 nodos demuestran las ventajas de la metodología propuesta.
Los multiplicadores de Lagrange son usados como factor de sensibilidad para determinar el tamaño y la ubicación óptima de las unidades distribuidas de almacenamiento.
El problema puede ser analizado desde la perspectiva multiobjetivo en donde dos objetivos se ven involucrados: pérdidas mínimas de transmisión y capacidad mínima instalada. El impacto de las unidades de almacenamiento en el planeamiento de la red también fue analizado.
El impacto sobre la red de distribución fue claramente mostrado, y es evidente que permite una operación más eficiente a través de la modificación de la curva de carga. De existir implementación masiva de dispositivos de almacenamiento, también se podrían impactar los precios de la electricidad, así como los costos de inversión de nuevos equipos para reforzar la infraestructura de los sistemas de distribución.
Al evidenciar los impactos positivos, se deberían promover ajustes en la regulación y políticas para estimular e implementar las unidades de almacenamiento, hecho que representa una de las mayores dificultades para hacer estos proyectos una realidad.
A través de la modificación de la curva de carga que se logra con las tecnologías de almacenamiento, se optimizan las fuentes convencionales de generación, logrando la mitigación de emisiones de CO2, que hoy constituye también un problema de gran importancia.
Referencias
ABB, Energy Storage Modules, Supporting Energy Demand and Optimizing Cost, 2011. Recuperado de ABB: http://www05.abb.com/global/scot/scot235.nsf/veritydisplay/2e1646ef5cef5713c1257a1400471d8b/$file/energy%20storage%20module%20 flyer%20hi-res.pdf.
Brekken, T., Yokochi, A., VonJouanne, A., Yen, Z., Hapke H. y Halamay D., "Optimal Energy Storage Sizing and Control for Wind Power Applications", IEEE Transactions on Sustainable Energy, Vol. 2, No. 1, 2011, pp. 69-77.
Cau, T. y Kaye, J., "Using Constructive Evolutionary Programming to Optimise Multi- Storage Electrical Power Supply Systems Operation", The 2003 Congress on Evolutionary Computation, CEC '03, Canberra, Australia, 2003, pp. 1310-14.
Chen, T. H., Chen, M. S., Hwang, K. J., Kotas, P. y Ea, C., "Distribution System Power Flow Analysis a Rigid Approach", IEEE Transactions on Power Delivery, Vol. 6, No. 3, 1991, pp. 1146-52.
Correa, C. A., Bolanos, R. A. y Garces, A., Optimal Operation of Microgrids in the Colombian Energy Market, 2012. Recuperado de IEEE Explore: http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&tp=&arnumber=6319106.
Habib, I M., "Model for Impact of Storage on Spinning Reserve Requirements and Distributed Generation", Proceedings of the 33rd Southeastern Symposium on System Theory, Athens, Ohio, 2001, pp. 161-165.
Hess, T., Schegner, P. y Hable, M., Improved Load Management Algorithm for Future Network Requirements, 2013. Recuperado de IEEE Explore: http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6683218&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D6683218.
Hill, C., Such, M., Chen, D., González, J. y Grady, W., "Battery Energy Storage for Enabling Integration of Distributed Solar Power Generation", IEEE Transactions on Smart Grid, Vol. 3, No. 2, 2012, pp. 850-57.
Lee, T. Y., "Operating Schedule of Battery Energy Storage System in a Time-of-Use Rate Industrial User with Wind Turbine Generators: A Multipass Iteration Particle Swarm Optimization Approach", IEEE Transactions on Energy Conversion, Vol. 22, No. 3, 2007, pp. 774-82.
Maly, D. y Kwan, K., "Optimal Battery Energy Storage System (Bess) Charge Scheduling with Dynamic Programming", Science, Measurement and Technology, IEE Proceedings, 1995,pp. 453-58.
Muthukumar, S., Kakumanu, S., Sriram, S. y Jayashankar, V., "Energy Storage Considerations for a Stand-Alone Wave Energy Plant", 2005 IEEE International Conference on Electric Machines and Drives, San Antonio, Texas, 2005, pp. 193-98.
Nguyen, C. y Flueck, A., "Agent Based Restoration with Distributed Energy Storage Support in Smart Grids", IEEE Transactions on Smart Grid, Vol. 3, No. 2, 2012, pp. 1029-38.
Papic, I., "Simulation Model for Discharging a Lead-Acid Battery Energy Storage System for Load Leveling", IEEE Transactions on Energy Conversion, Vol. 21, No. 2, 2006, pp. 608-15.
Ru, Y., Kleissl, J. y Martínez, S., "Storage Size Determination for Grid-Connected Photovoltaic Systems", IEEE Transactions on Sustainable Energy, 2012, Vol. 4, No. 1, pp. 1-14.
Schoenung, S. y Burns, C., "Utility Energy Storage Applications Studies", IEEE Transactions on Energy Conversion, Vol. 11, No. 3, 1996, pp. 658-65.
Yao, D., Choi, S., Tseng, K. y Lie, T., "Determination of Short-Term Power Dispatch Schedule for a Wind Farm Incorporated with Dual-Battery Energy Storage Scheme", IEEE Transactions on Sustainable Energy, Vol. 3, No. 1, 2012, pp. 74-84.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.