DOI:
https://doi.org/10.14483/22487638.16904Publicado:
01-10-2020Número:
Vol. 24 Núm. 66 (2020): Octubre - DiciembreSección:
InvestigaciónFusion of Hyperspectral and Multispectral Images Based on a Centralized Non-local Sparsity Model of Abundance Maps
Fusión de imágenes hiperespectrales y multiespectrales basado en un modelo de escacez centralizado no local de mapas de abundancias
Palabras clave:
Fusión de imágenes, aprendizaje de diccionarios, representación escasa no-local, desmezclado espectral, mapas de abundancias (es).Palabras clave:
Image fusion, dictionary learning, non-local sparse representation, spectral unmixing, abundance maps (en).Descargas
Referencias
Arias, K., Vargas, E., & Arguello, H. (2019, September). Hyperspectral and Multispectral Image Fusion based on a Non-locally Centralized Sparse Model and Adaptive Spatial-Spectral Dictionaries. In 2019 27th European Signal Processing Conference (EUSIPCO) (pp. 1-5). IEEE. https://doi.org/10.23919/EUSIPCO.2019.8903001
Beck, A., & Teboulle, M. (2009). A fast-iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM journal on imaging sciences, 2(1), 183-202. https://doi.org/10.1137/080716542
Bioucas-Dias, J. M., Plaza, A., Camps-Valls, G., Scheunders, P., Nasrabadi, N., & Chanussot, J. (2013). Hyperspectral remote sensing data analysis and future challenges. IEEE Geoscience and remote sensing magazine, 1(2), 6-36. https://doi.org/10.1109/MGRS.2013.2244672
Bruckstein, A. M., Donoho, D. L., & Elad, M. (2009). From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM review, 51(1), 34-81. https://doi.org/10.1137/060657704
Chakrabarti, A., & Zickler, T. (2011, June). Statistics of real-world hyperspectral images. In CVPR 2011 (pp. 193-200). IEEE.
https://doi.org/10.1109/CVPR.2011.5995660
Chan, T., Esedoglu, S., Park, F., & Yip, A. (2005). Recent developments in total variation image restoration. Mathematical Models of Computer Vision, 17(2).
Chen, S. S., Donoho, D. L., & Saunders, M. A. (2001). Atomic decomposition by basis pursuit. SIAM review, 43(1), 129-159. https://doi.org/10.1137/S003614450037906X
Daubechies, I., Defrise, M., & De Mol, C. (2004). An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics: A Journal Issued by the Courant Institute of Mathematical Sciences, 57(11), 1413-1457. https://doi.org/10.1002/cpa.20042
Dian, R., Fang, L., & Li, S. (2017). Hyperspectral image super-resolution via non-local sparse tensor factorization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 5344-5353). https://doi.org/10.1109/CVPR.2017.411
Dong, W., Zhang, L., Shi, G., & Wu, X. (2011). Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization. IEEE Trans. on image process., 20(7), 1838-1857. https://doi.org/10.1109/TIP.2011.2108306
Dong, W., Li, X., Zhang, L., & Shi, G. (2011, June). Sparsity-based image denoising via dictionary learning and structural clustering. In CVPR 2011 (pp. 457-464). IEEE. https://doi.org/10.1109/CVPR.2011.5995478
Dong, W., Zhang, L., & Shi, G. (2011, November). Centralized sparse representation for image restoration. In 2011 IEEE ICCV (pp. 1259-1266). https://doi.org/10.1109/ICCV.2011.6126377
Dong, W., Zhang, L., Shi, G., & Li, X. (2012). Nonlocally centralized sparse representation for image restoration. IEEE transactions on Image Processing, 22(4), 1620-1630. https://doi.org/10.1109/TIP.2012.2235847
Elad, M., & Aharon, M. (2006). Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image processing, 15(12), 3736-3745. https://doi.org/10.1109/TIP.2006.881969
Cardon, H. D. V., Álvarez, M. A., & Gutiérrez, Á. O. (2015). Representación óptima de señales MER aplicada a la identificación de estructuras cerebrales durante la estimulación cerebral profunda. Tecnura, 19(45), 15-27. https://doi.org/10.14483/udistrital.jour.tecnura.2015.3.a01
Medina Rojas, F., Arguello Fuentes, H., & Gómez Santamaría, C. (2017). A quantitative and qualitative performance analysis of compressive spectral imagers. Tecnura, 21(52), 53-67. https://doi.org/10.14483/udistrital.jour.tecnura.2017.2.a04
Velasco, A. C., García, C. A. V., & Fuentes, H. A. (2016). Un estudio comparativo de algoritmos de detección de objetivos en imágenes hiperespectrales aplicados a cultivos agrícolas en Colombia. Revista Tecnura, 20(49), 86-100.
Fu, Y., Lam, A., Sato, I., & Sato, Y. (2017). Adaptive spatial-spectral dictionary learning for hyperspectral image restoration. International Journal of Computer Vision, 122(2), 228-245. https://doi.org/10.1007/s11263-016-0921-6
Ghasrodashti, E. K., Karami, A., Heylen, R., & Scheunders, P. (2017). Spatial resolution enhancement of hyperspectral images using spectral unmixing and bayesian sparse representation. Remote Sensing, 9(6), 541. https://doi.org/10.3390/rs9060541
Hege, E. K., O'Connell, D., Johnson, W., Basty, S., & Dereniak, E. L. (2004, January). Hyperspectral imaging for astronomy and space surveillance. In Imaging Spectrometry IX (Vol. 5159, pp. 380-391). International Society for Optics and Photonics. https://doi.org/10.1117/12.506426
Lu, G., & Fei, B. (2014). Medical hyperspectral imaging: a review. Journal of biomedical optics, 19(1), 010901. https://doi.org/10.1117/1.JBO.19.1.010901
Loncan, L., De Almeida, L. B., Bioucas-Dias, J. M., Briottet, X., Chanussot, J., Dobigeon, N., ... & Tourneret, J. Y. (2015). Hyperspectral pansharpening: A review. IEEE Geoscience and remote sensing magazine, 3(3), 27-46. https://doi.org/10.1109/MGRS.2015.2440094
Mallat, S. (1999). A wavelet tour of signal processing. Elsevier. https://doi.org/10.1016/B978-012466606-1/50008-8
Mairal, J., Bach, F., Ponce, J., Sapiro, G., & Zisserman, A. (2009, September). Non-local sparse models for image restoration. In 2009 IEEE 12th ICCV (pp. 2272-2279) https://doi.org/10.1109/ICCV.2009.5459452
Middleton, E. M., Ungar, S. G., Mandl, D. J., Ong, L., Frye, S. W., Campbell, P. E., ... & Pollack, N. H. (2013). The earth observing one (EO-1) satellite mission: Over a decade in space. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6(2), 243-256. https://doi.org/10.1109/JSTARS.2013.2249496
Oliveira, J. P., Bioucas-Dias, J. M., & Figueiredo, M. A. (2009). Adaptive total variation image deblurring: a majorization–minimization approach. Signal processing, 1683-1693. https://doi.org/10.1016/j.sigpro.2009.03.018
Panasyuk, S. V., Yang, S., Faller, D. V., Ngo, D., Lew, R. A., Freeman, J. E., & Rogers, A. E. (2007). Medical hyperspectral imaging to facilitate residual tumor identification during surgery. Cancer biology & therapy, 6(3), 439-446. https://doi.org/10.4161/cbt.6.3.4018
Simoes, M., Bioucas‐Dias, J., Almeida, L. B., & Chanussot, J. (2014). A convex formulation for hyperspectral image super-resolution via subspace-based regularization. IEEE Transactions on Geoscience and Remote Sensing, 53(6), 3373-3388. https://doi.org/10.1109/TGRS.2014.2375320
Schaepman, M. E., Ustin, S. L., Plaza, A. J., Painter, T. H., Verrelst, J., & Liang, S. (2009). Earth system science related imaging spectroscopy—An assessment. Remote Sensing of Environment, 113, S123-S137. https://doi.org/10.1016/j.rse.2009.03.001
Schreiber, N. F., Genzel, R., Bouché, N., Cresci, G., Davies, R., Buschkamp, P., ... & Shapley, A. E. (2009). The SINS survey: SINFONI integral field spectroscopy of z∼ 2 star-forming galaxies. The Astrophysical Journal, 706(2), 1364. https://doi.org/10.1088/0004-637X/706/2/1364
Shaw, G. A., & Burke, H. K. (2003). Spectral imaging for remote sensing. Lincoln laboratory journal, 14(1), 3-28.
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267-288. https://doi.org/10.1111/j.2517-6161.1996.tb02080.x
Tosic, I., & Frossard, P. (2011). Dictionary learning. IEEE Signal Processing Magazine, 28(2), 27-38. https://doi.org/10.1109/MSP.2010.939537
Tropp, J. A., & Wright, S. J. (2010). Computational methods for sparse solution of linear inverse problems. Proceedings of the IEEE, 98(6), 948-958. https://doi.org/10.1109/JPROC.2010.2044010
Vargas, E., Espitia, O., Arguello, H., & Tourneret, J. Y. (2018). Spectral image fusion from compressive measurements. IEEE Transactions on Image Processing, 28(5), 2271-2282. https://doi.org/10.1109/TIP.2018.2884081
Vargas, E., Arguello, H., & Tourneret, J. Y. (2019). Spectral image fusion from compressive measurements using spectral unmixing and a sparse representation of abundance maps. IEEE Transactions on Geoscience and Remote Sensing, 57(7), 5043-5053. https://doi.org/10.1109/TGRS.2019.2895822
Wei, Q., Bioucas-Dias, J., Dobigeon, N., & Tourneret, J. Y. (2015). Hyperspectral and multispectral image fusion based on a sparse representation. IEEE Transactions on Geoscience and Remote Sensing, 53(7), 3658-3668. https://doi.org/10.1109/TGRS.2014.2381272
Wei, Q., Dobigeon, N., & Tourneret, J. Y. (2015). Bayesian fusion of multi-band images. IEEE Journal of Selected Topics in Signal Processing, 9(6), 1117-1127. https://doi.org/10.1109/JSTSP.2015.2407855
Wei, Q., Bioucas-Dias, J., Dobigeon, N., Tourneret, J. Y., Chen, M., & Godsill, S. (2016). Multiband image fusion based on spectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 54(12), 7236-7249. https://doi.org/10.1109/TGRS.2016.2598784
Yang, J., Wright, J., Huang, T. S., & Ma, Y. (2010). Image super-resolution via sparse representation. IEEE transactions on image processing, 19(11), 2861-2873. https://doi.org/10.1109/TIP.2010.2050625
Yin, H., Li, S., & Fang, L. (2013). Simultaneous image fusion and super-resolution using sparse representation. Information Fusion, 14(3), 229-240. https://doi.org/10.1016/j.inffus.2012.01.008
Zhao, Y., Yang, J., & Chan, J. C. W. (2013). Hyperspectral imagery super-resolution by spatial–spectral joint non-local similarity. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7(6), 2671-2679. https://doi.org/10.1109/JSTARS.2013.2292824
Zhao, Y., Yi, C., Yang, J., & Chan, J. C. W. (2014, July). Coupled hyperspectral super-resolution and unmixing. In 2014 IEEE Geoscience and Remote Sensing Symposium (pp. 2641-2644). IEEE.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 4 de marzo de 2020; Aceptado: 13 de agosto de 2020
Abstract
Context:
Systems that acquire hyperspectral (HS) images have opened a wide field of applications in different areas, such as remote sensing and computer vision applications. However, hardware restrictions may limit the performance of such applications because of the low spatial resolution of obtained hyperspectral images. In the state-of-the-art, the fusion of a HS image with low spatial resolution panchromatic (PAN) or multispectral (MS) images with high spatial resolution has been efficiently employed to computationally improve the resolution of the HS source. The problem of fusing images is traditionally described as an ill-posed inverse problem whose solution is obtained assuming that the high spatial resolution HS (HR-HS) image is sparse in an analytic or learned dictionary.
Method:
This paper proposes a non-locally centralized sparse representation model on a set of learned dictionaries to spatially regularize the fusion problem. Besides, we consider the linear mixing model that decomposes the measured spectrum into a collection of constituent spectra (endmembers) and a set of corresponding fractions (abundance) maps to take advantage of the intrinsic properties and low dimensionality of HS images. The spatial-spectral dictionaries are learned from the estimated abundance maps exploiting the spectral correlation between abundance maps and the non-local self-similarity in the spatial domain. Then, an alternating iterative algorithm is employed to solve the fusion problem conditionally on the learned dictionaries.
Results:
After using real data, the results show that the proposed method outperforms the state-of-the-art methods under various quantitative metrics: RMSE, UIQI, SAM, ERGAS, PSNR, and DD.
Conclusions:
This paper proposes a novel fusion model that includes a non-local Sparse representation of abundance maps by using spectral unmixing. The proposed model obtains better fused images than traditional fusion approaches based on sparcity.
Financing:
Project Vicerrectoría de Investigación y Extensión of Universidad Industrial de Santader (code VIE 2521).
Keywords:
Image fusion, dictionary learning, non-local sparse representation, spectral unmixing, abundance maps.Resumen
Contexto:
Los sistemas de adquisición de imágenes hiperespectrales (HS) son comúnmente usados en un rango diverso de aplicaciones que involucran tareas de detección y clasificación. Sin embargo, la baja resolución de imágenes hiperespectrales podría limitar el rendimiento de las tareas relacionadas con dichas aplicaciones. En los últimos años, fusionar la información de una imagen HS con imágenes multiespectrales (MS) o pancromáticas (PAN) de alta resolución espacial ha sido ampliamente usado para mejorar la resolución espacial de la imagen HS. La fusión de imágenes ha sido formulada como un problema inverso cuya solución es una imagen HS de alta resolución espacial, la cual se asume escasa en un diccionario analítico o aprendido. Por otra parte, el desmezclado espectral es un procedimiento en donde el espectro medido de un píxel mezclado es descompuesto en una colección de firmas espectrales que hacen referencia a las firmas puras de la imagen y mapas de abundancia que indican la porción de cada firma pura presente en un píxel especifico.
Método:
Este trabajo propone un modelo de representación escasa, centralizado y no local sobre un conjunto de diccionarios aprendidos para regularizar el problema de fusión convencional. Los diccionarios son aprendidos a partir de los mapas de abundancia estimados para explotar la correlación entre mapas de abundancia y la auto-similitud no local sobre el dominio espacial. Luego, condicionalmente sobre los diccionarios aprendidos, el problema de fusión es solucionado por un algoritmo numérico iterativo y alternante.
Resultados:
Después de usar datos reales, los resultados muestran que el método propuesto supera los métodos del estado del arte bajo diferentes métricas cuantitativas.
Conclusiones:
Este modelo permite incluir la redundancia no local en el problema de fusión de imágenes hiperespectral y multiespectral sobre los mapas de abundancia usando desmezclado espectral, mejorando los resultados de los métodos de fusión basados en el modelo de escasez tradicional.
Financiamiento:
Proyecto Vicerrectoría de Investigación y Extensión of Universidad Industrial de Santander (Código VIE 2521).
Palabras clave:
Fusión de imágenes, aprendizaje de diccionarios, representación escasa no-local, desmezclado espectral, mapas de abundancias.INTRODUCTION
Hyperspectral (HS) imaging acquires a real scene in hundreds of spectral bands, each associated with a specific wavelength (Medina et al., 2017). The analysis of spectral signatures of these images has allowed the advancement of many applications in the fields of medical imaging (Panasyuk et al., 2007; Lu and Fei, 2014), remote sensing (Schaepman et al., 2009; Bioucas-Dias et al., 2013; Velasco et al., 2016), and astronomy (Schreiber et al., 2009; Hege et al., 2004). However, due to hardware restrictions, HS images are limited by a low spatial resolution (Shaw and Burke, 2003). For example, the Hyperion imaging spectrometer has a spatial resolution of 30 meters-per-pixel (Middleton et al., 2013) that can degrade the performance for practical applications.
In order to increase the spatial resolution of HS images, a usual approach is to merge the HS image with high spatial resolution images. An example appropriate for this paper consists of merging the HS image (that has high spectral resolution) with a multispectral (MS) image (that has high spatial resolution) (Wei et al., 2015; Simoes et al., 2015). Another well-known example is HS pan-sharpening, which addresses the fusion of panchromatic and HS images (Loncan et al., 2015).
Image fusion is essential to find a suitable model considering the prior knowledge of natural images due to the ill-posed nature of the inverse problem. Thus, some effective regularizers that restrict the solution space have been employed in the state-of-the-art for image restoration (IR) problems with encouraging results (Dong, Zhang and Shi, 2011; Chan et al., 2015; Oliveira, Bioucas-Dias and Figueiredo, 2009; Vargas et al., 2018). In detail, under a super-resolution approach, employing previous total variations have achieved state-of-the-art performance for fusing HS and MS images (Simoes et al., 2015). Additionally, it has been demonstrated that assuming the sparcity of the signal of interest is a suitable regularization method in image restoration problems such as image de-blurring, image denoising, and image super-resolution (Dong et al. 2011, Wei et al., 2015; Yang et al., 2010). Formally, a sparce representation states that a signal 𝐱 ∈ ℝNp can be represented as a linear combination of a few atoms via 𝐱 = 𝚽𝜶x on the dictionary Φ (Cardon et al., 2015). If the target signals reconstructed are multi-dimensional images, the representation of smaller patches on an over-complete dictionary learned from the data successfully determines the underlying structure of the images (Mallat, 1999).
On the other hand, restoring the image x from a degraded image y = Hx + n under sparcity is challenging due to degradation during the acquisition process. The estimation of the sparce coefficient
cl
x
employing common optimization algorithms as Ba-yesian frameworks, iterative shrinkage/thresholding, Lasso, and basis pursuit (Tibshirani, 1996; Tropp and Wright, 2010; Beck and Teboulle, 2009; Bruckstein, Donoho and Elad, 2009; Chen, Donoho and Saun-ders, 2001) may not be an optimal estimation of the original sparce coefficient a
x
. Thus, the reconstruction
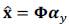 may lead to an inaccurate estimation (Mairal et al., 2009; Dong et al., 2012).
may lead to an inaccurate estimation (Mairal et al., 2009; Dong et al., 2012).
According to this limitation, we are interested on improving the estimated sparce representation, so non-local redundancy properties in natural scenes are studied to enhance the representation model. For instance, non-local self-similarities of natural scenes have been included in approaches for super-resolution or denoising leading to state-of-the-art performance (Elad and Aharon; 2006; Dian, Fang and Li, 2017; Mairal et al., 2009; Fu et al., 2017). Similarly, to enhance the accuracy of IR methods based on sparsity, a centralized non-local sparce representation (CNSR) model has been proposed in (Dong et al., 2012). Specifically, this representation intends to increase the quality of the reconstructed image
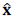 by reducing the error v
α
= α
x
- α
y
known as sparce coding noise (SCN). This goal is achieved by centralizing the sparce coefficient α
y
to α
x
that is estimated from the non-local redundancies in x.
by reducing the error v
α
= α
x
- α
y
known as sparce coding noise (SCN). This goal is achieved by centralizing the sparce coefficient α
y
to α
x
that is estimated from the non-local redundancies in x.
On the other hand, research on IR literature has included the unmixing spectral model on several IR problems to find a treatable connection between the distorted measurements and the original image, and to take advantage of intrinsic properties such as spectral non-local similarity (Wei et al., 2016; Vargas, Arguello and Tourneret, 2019; Zhao, Yang and Chan, 2013). Even sparcity assumptions in abundance (Vargas et al., 2018, Ghasrodashti et al., 2017; Zhao et al., 2014) and spatial non-local similarity (Zhao, Yang and Chan, 2013) have been taken into account on the hyperspectral image super-resolution and fusion problems showing promising results. Nonetheless, prior unified knowledge of spatial-spectral non-local similarity and sparcity has not been considered on the abundances.
This work introduces a multispectral and hyperspectral image fusion model that assumes a CNSR of abundance maps in a learned dictionary. More precisely, local and spectral non-local similarity assumptions on the abundances are included in the model by the spectral unmixing decomposition and the spatial non-local estimation from α y now associated with the sparse representation of the abundances α α , respectively. Additionally, the abundances are supposed to be sparce on an over-complete dictionary, which is constructed from available abundance and HS-MS data. The dictionary consists of several sub-dictionaries learned from groups of similar patches. Then, all patches of a cluster are sparsely represented and centralized to a good estimation of α α under its corresponding sub-dictionary (each cluster associates with a single sub-dictionary). Therefore, both the construction of a composite over-complete dictionary and the centralization are performed to exploit non-local redundancies in the abundances.
In the global optimization problem, the sparse codes and spatial-spectral dictionary are estimated jointly under an alternating approach. Once the dictionary has been updated, an iterative nonlinear shrinkage algorithm solves the resulting multi-band image fusion problem; this algorithm consists of projecting the solution of a quadratic problem on the thresholding operator in each iteration (Daubechies, Defrise and De Mol, 2004). Moreover, the regularization parameters underlying the optimization problem are adaptively adjusted from a Bayesian formulation (Dong et al. 2012). Non-local similarity and sparcity assumptions are favorable on abundance maps due to the large presence of soft regions. Additionally, the burden load decrease by data reduction compared to the original image. Considering experimental scenarios with real HS images, we show that the proposed fusion approach outperforms and achieves the performance of the competitive approaches gaining up to 1[dB] under the peak signal-to-noise ratio (PSNR) metric.
PROBLEM STATEMENT
For modeling the MS and HS images, it is commonly assumed that there is a linear degradation in the spectral and spatial domain of a HS image with higher resolution denoted by the vector
 with N
p
=NML (Wei et al., 2016; Wei, Dobigeon and Tourneret, 2015; Simoes et al., 2015). The acquired HS image denoted by the vector
with N
p
=NML (Wei et al., 2016; Wei, Dobigeon and Tourneret, 2015; Simoes et al., 2015). The acquired HS image denoted by the vector
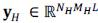 is assumed to be a blurred and down-sampled version of the high full-resolution image x. In contrast, the MS image
is assumed to be a blurred and down-sampled version of the high full-resolution image x. In contrast, the MS image
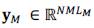 is obtained from a spectral degradation of the target image (Wei et al., 2015). Thus, the sensing models for the MS and HS images are given as
is obtained from a spectral degradation of the target image (Wei et al., 2015). Thus, the sensing models for the MS and HS images are given as

Where
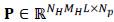 represents the down-sampling matrix,
represents the down-sampling matrix,
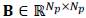 is a circular convolution operator described as blurring matrix,
is a circular convolution operator described as blurring matrix,
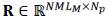 denotes the transfer function of the MS sensor, and the vectors
denotes the transfer function of the MS sensor, and the vectors
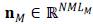 and
and
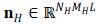 represent additive Gaussian noise for the MS and HS images.
represent additive Gaussian noise for the MS and HS images.
For notation convenience, the spatial-spectral tensor
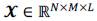 (L is the number of spectral bands and N x M represents the spatial dimension) is represented by the vector
(L is the number of spectral bands and N x M represents the spatial dimension) is represented by the vector
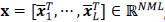 , where
, where
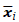 contains all the image intensities associated with the z'-th spectral band on X. Likewise, we can exploit intrinsic properties of the spectral unmixing model for the fusion problem in which each spectral signature of a multi-band image can be associated to a linear mixture of several pure spectral signatures known as endmembers. Under this model, the image x is decomposed as x =Ma, where
contains all the image intensities associated with the z'-th spectral band on X. Likewise, we can exploit intrinsic properties of the spectral unmixing model for the fusion problem in which each spectral signature of a multi-band image can be associated to a linear mixture of several pure spectral signatures known as endmembers. Under this model, the image x is decomposed as x =Ma, where
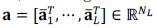 with N
L
=NML are the P abundane maps in a vector form denoting
with N
L
=NML are the P abundane maps in a vector form denoting
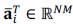 as the z'-th abundance map. The matrix
as the z'-th abundance map. The matrix
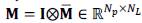 is a block-diagonal matrix on the endmembers' matrix
is a block-diagonal matrix on the endmembers' matrix
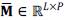 with P the number of materials. Thus, the acquisition models in equation (1) can be rewritten as
with P the number of materials. Thus, the acquisition models in equation (1) can be rewritten as

Considering the observation models in equation (2), the optimization problem formulated in this paper consists of estimating the vector of abundances from the observed measurements y M and y H . Since the resultant problem is ill-posed, this work proposes that the regularization strategy employed for the fused solution be a centralized non-local sparce model on the abundance maps.
METHODOLOGY
In this section, we describe the methodology for the fusion of hyperspectral and multispectral images based on the non-local sparse representation model. First of all, consider that the abundance data a is decomposed into overlapping image cubic patches. Dividing images in patches has obtained effective results in the image domain in many image processing applications (Tosic and Frossard, 2011). We start by defining
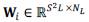 as the matrix extracting cubic patch at location
as the matrix extracting cubic patch at location
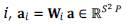 as the vectorized abundance cubic patch with dimensions S x S x P, and i indicating the position of the central pixel. Then, considering a sparce representation of the cubic patch in a fixed dictionary, i.e., = Φ α
α,i
, where α
α,i
is a sparce vector. Finally, considering the collection of sparce coefficients {α
α,i
}, the recovery of the abundances a can be computed by averaging all the patches
as the vectorized abundance cubic patch with dimensions S x S x P, and i indicating the position of the central pixel. Then, considering a sparce representation of the cubic patch in a fixed dictionary, i.e., = Φ α
α,i
, where α
α,i
is a sparce vector. Finally, considering the collection of sparce coefficients {α
α,i
}, the recovery of the abundances a can be computed by averaging all the patches
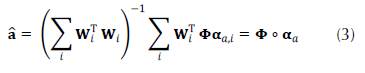
For notation simplicity, the estimated abundance ậ aforementioned is denoted as ậ =Φ o α α , where α α represents the collection of the set of sparce codes α α,i .
Non-local sparce representation model
In literature, different IR problems have employed sparcity-based regularization approaches to handle its ill-posed nature (Dong et al. 2011; Yang et al., 2010; Yin, Li and Fang, 2013). However, since the observed images are a degraded version of the target image, the obtained sparce coefficient αy is a degraded estimation of the sparce coefficient αα of the abundance maps, resulting in a degradation of the recovered image quality. To improve the sparce recovery results, an effective solution consists of employing non-local similarities of natural scenes (Mairal et al., 2009; Dong et al., 2012). Furthermore, this assumption of non-local similarity could also be satisfied with abundance maps since similar spatial structures in the image domain are present on the abundances. Therefore, the assumption of this work is that non-local similarities of the abundance maps could benefit the fused image results. Specifically, this work proposes a centralized non-local representation (Dong et al., 2012) of abundance maps to regularize the underlying high-resolution HS image. Based on the observation models in equation (2) and the CNSR model, the fusion problem is formulated as the following optimization problem
where the quadratic functions correspond to the data fidelity of the MS and HS images, the last function represents the CNSR prior model, β i is a close estimation of the sparce representation α α,i associated to the i-th abundance patch a i , and λ is a regularization parameter. The Term associated with the prior sparcity in equation (4) is removed because of the dictionary structure that implicitly promotes sparcity, this will be addressed later. Additionally, a ℓ1 -term is included to centralize α α,i to the non-local estimatio n β i suppressing the SCN α y - α x (Dong et al., 2012). Based on the non-locality of the abundances, the enhanced estimate β i of α α,i iscomputed as a weighted sum of sparse coefficients αy,p, so that pЄΩi, Ωi ⊆ {1,2, …}. In particular, the coefficients αy,p are the sparce vectors of non-local cubic patches similar toâi obtained from the abundance maps. Thus, β i can be computed as
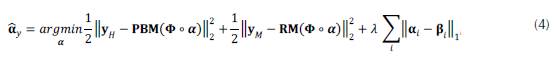
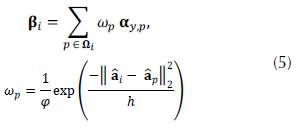
where ω p is the corresponding weight of the patch p, φ is a normalization factor, and h is a fixed constant. To distinguish the current patch and its similar neighboring patches, we employed the indexes i and p, respectively.
Bayesian interpretation
We developed a Bayesian analysis of the MS and HS image fusion based on the prior CNSR in order to provide an alternative to calculate the regularization parameter λ in equation (4). We define an auxiliary variable θ = α - β to obtain the relationship between maximum a posterior (MAP) estimator, and the SCN estimation. Thus, the MAP estimator of θ isgiven by
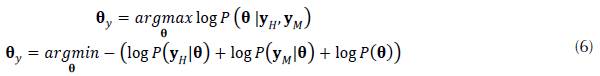
The likelihood terms P(yH|θ) and P(y M |θ) are characterized by the Gaussian distribution, and the prior probability term is characterized by the Laplacian distribution. According to the CNSR model for fusion in equation (4), the likelihood terms are formulated as

where
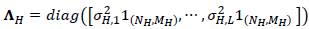 is the covariance matrix for the band-vectorized HS image with standard deviation per band σ
H,l
(l = 1, …, L) , (1α) denoting the vector of ones of size1
is the covariance matrix for the band-vectorized HS image with standard deviation per band σ
H,l
(l = 1, …, L) , (1α) denoting the vector of ones of size1
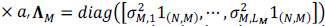 is the covariance matrix for the band-vectorized MS image with standard deviation per band
is the covariance matrix for the band-vectorized MS image with standard deviation per band
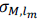 (l
m
= 1,…,L
M
), θi,j is they j-th element of the sparce code θ
i
, and Y
i,j
is the standard deviation of θ
i
(j). Now, substituting the P(yH|α,β),, P(yM|α,β) and P(θ) in equation (6) we obtain the MAP estimator of θ given by the following optimization problem
(l
m
= 1,…,L
M
), θi,j is they j-th element of the sparce code θ
i
, and Y
i,j
is the standard deviation of θ
i
(j). Now, substituting the P(yH|α,β),, P(yM|α,β) and P(θ) in equation (6) we obtain the MAP estimator of θ given by the following optimization problem
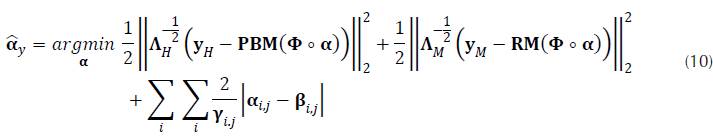
By observing equations (10) and (4) on the third term, we can see by comparison that the regularization parameter can be calculated as
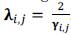 .
.
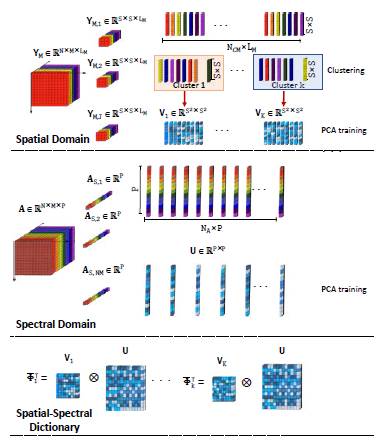
Dictionary learning
Basis functions extracted from learned or analytical dictionaries are able to represent basic structures of natural image and define sparcity domains. Let a given cubic patch a
i
be represented as a matrix
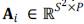 where the rows are the abundance coefficients. Under a sparce model of the abundances, A
i
, can be described by few atoms (Fu et al., 2017)
where the rows are the abundance coefficients. Under a sparce model of the abundances, A
i
, can be described by few atoms (Fu et al., 2017)

where {Φm} denotes a collection of atoms, α m are the corresponding sparce codes, and m « S 2 P. The selection of the dictionary elements is a relevant issue of sparcity-based methods. In this work, we propose a dictionary with tridimensional atoms that are constructed using separable abundance and spatial components as follows

where
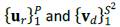 are orthonormal basis spanning the abundance maps and spatial subs-pace, respectively. Under this factorization of the dictionary, we are able to exploit the correlation in the abundances as well as in the spatial domain. Specifically, the basis for the abundance subspace domain U and the spatial domain V are extracted from the abundances data allowing to construct the atoms in equation (12) with correlation information between abundance maps and spatial information simultaneously. In the abundance subspace domain, the estimated abundance vector â isreorganized as a P x NM matrix via PCA the abundance basis U = [u
1
, -, Up]. Similarly, the spatial basis V = [v
1
, …, vS2] is calculated using PCA from spatial patches extracted along all the abundance maps.
are orthonormal basis spanning the abundance maps and spatial subs-pace, respectively. Under this factorization of the dictionary, we are able to exploit the correlation in the abundances as well as in the spatial domain. Specifically, the basis for the abundance subspace domain U and the spatial domain V are extracted from the abundances data allowing to construct the atoms in equation (12) with correlation information between abundance maps and spatial information simultaneously. In the abundance subspace domain, the estimated abundance vector â isreorganized as a P x NM matrix via PCA the abundance basis U = [u
1
, -, Up]. Similarly, the spatial basis V = [v
1
, …, vS2] is calculated using PCA from spatial patches extracted along all the abundance maps.
In the spatial domain, we learn different dictionaries for different clusters of the abundance training patches (Dong et al., 2011 ; Dong et al., 2012). Thus, the patches are clustered by spatial similarity of â pooled along with all the abundance maps employing the K-means method. This methodology lies on grouping patches spatially in different clusters C K , with k = 1, … ,K, by using the high frequency components of the abundance maps. This strategy is more suitable since clustering by intensity presents low performance discriminating images (Fu et al., 2017). The high frequency patterns ã of â can be calculated as

where G is a low pass filtering operator. It is worth noting that the high frequency of the abundance maps ã is employed only for clustering and the resultant clusters C
K
associates with a spatial basis
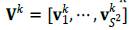 extracted from the estimated abundance maps â. Composing the PCA abundance and spatial basis following equation (12), the proposed structured spatial-spectral dictionary for a given abundance cubic patch a
i
in C
K
can be written as follow
extracted from the estimated abundance maps â. Composing the PCA abundance and spatial basis following equation (12), the proposed structured spatial-spectral dictionary for a given abundance cubic patch a
i
in C
K
can be written as follow

where
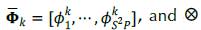 cienotes the Kronecker operator. It is important to note that a
i
only can be associated with a single spatial-spectral dictionary
cienotes the Kronecker operator. It is important to note that a
i
only can be associated with a single spatial-spectral dictionary
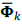 . A schematic representation of the spatial-abundance structure of the proposed adaptive dictionary is shown in Figure 1.
. A schematic representation of the spatial-abundance structure of the proposed adaptive dictionary is shown in Figure 1.
Figure 1: Schematic representation of the proposed adaptive spatial-spectral dictionary learned from the abundance maps.
Fusion algorithm based on a CNSR model
The strategy to solve the MS and HS image fusion problem based on a non-local sparce representation of the abundance maps in equation (4) is an iterative scheme that employs a shrinkage step in every iteration (Dong et al., 2012). The proposed algorithm is summarized in Algorithm 1.
Algorithm 1:: MS and HS Image Fusion based on CNSR

The algorithm consists of two main iterative loops. The external loop (whose iterations are indexed by t) is implemented to update the spatial-abundance dictionary
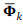 . Once the dictionary
. Once the dictionary
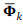 is computed, the internal loop (whose iterations are indexed by q) estimates an approximation of the abundances â by employing an alternating strategy of three steps. First, the solution of the problem associated with the forward model or the image fidelity term is found by a gradient descent algorithm. Second, a rough estimation of the abundance maps is obtained by the sparce unmixing algorithm via variable splitting and augmented Lagrangian (SUnSAL) introduced in (Bioucas et al., 2010). Third, a shrinkage operator (Dong et al., 2012; Daubechies, Defrise and De Mol, 2004) is employed to compute the sparce coefficients ây
. Thus, the solution ây in the q + 1-th iteration is given by
is computed, the internal loop (whose iterations are indexed by q) estimates an approximation of the abundances â by employing an alternating strategy of three steps. First, the solution of the problem associated with the forward model or the image fidelity term is found by a gradient descent algorithm. Second, a rough estimation of the abundance maps is obtained by the sparce unmixing algorithm via variable splitting and augmented Lagrangian (SUnSAL) introduced in (Bioucas et al., 2010). Third, a shrinkage operator (Dong et al., 2012; Daubechies, Defrise and De Mol, 2004) is employed to compute the sparce coefficients ây
. Thus, the solution ây in the q + 1-th iteration is given by
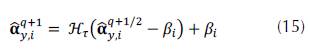
where
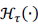 is the soft-thresholding proximal solution of the ℓ1 norm with a threshold parameter t.
is the soft-thresholding proximal solution of the ℓ1 norm with a threshold parameter t.
EXPERIMENTAL RESULTS
This section presents the performance of the proposed method on two target hyperspectral images fixed as ground truth for the simulations. The experimental scenarios are conducted on both data sets: the Pavia image with spatial resolution 128 x 128 and 93 spectral bands, and the Moffett image with spatial resolution 128 x 128 and 93 spectral bands. The high-resolution ground-truth images are degraded by spectral and spatial distortion operators to obtain the MS and HS images, respectively. Particularly, the HS image is obtained from the target image by filtering every band with a 5 x 5 filter sampled from a Gaussian distribution followed by a down-sampling operation on the vertical and horizontal directions with a scale factor d = 4. The MS image was calculated by applying a spectral filtering of the high-resolution ground-truth images with the LANDSAT g spectral response leading to a MS image with L M = 4 bands. Then, both degraded MS and HS images are perturbed band-by-band with additive Gaussian noise. The HS image is contaminated with SNR 30 = [db] in the last 50 bands and SNR 35 = [db] for the bands remaining while for the MS image is contaminated with a SNR 30 = [db]. The setting parameters for the fusion algorithm were selected as follows: K = 60 clusters; spatial patch size 6 x 6, 12 similar neighbors cubic patches are extracted to calculate β i (i.e., |Ωi|) in a neighborhood size of 50 x 50; the parameter δ is set on 1.25 while the thresholding for sparce representation is set on t = 1.841. In order to compare the proposed method, three different approaches known as (HMIF-SR), (HySure), and (HyMuXNol) (Wei et al., 2015; Simoes et al., 2015; Arias, Vargas and Arguello, 2019) are simulated on the same fusion scenario.
The MS and HS images and the full-resolution reconstructed images for the Pavia and Moffett images are shown in Figures 2 and 3. The results from the proposed fusion strategy show a better-quality estimation of the target image. Furthermore, the fused resultant images of adversary methods depict greater spectral and spatial degradation compared to the Pavia and Moffett ground-truth images.
Figure 2: Qualitative fused images (Pavia image). (Row 1, left) MS image. (Row 1, middle) MS image. (Row 1, right) Ground truth. (Row 2, left) HySure. (Row 2, middle) HMIF-SR. (Row 2, right) HyMuXNol. (Row 3) Proposed.
Figure 3: Qualitative fused images (Moffet image). (Row 1, left) MS image. (Row 1, middle) MS image. (Row 1, right) Ground truth. (Row 2, left) HySure. (Row 2, middle) HMIF-SR. (Row 2, right) HyMuXNol. (Row 3) Proposed.
The evaluation of the proposed fusion method is performed employing the PSNR (Peak Signal-to-Noise Ratio), UIQI (Universal Image Quality Index), RMSE (Root-Mean-Square error), ERGAS (Relative Dimensionless Global Error in Synthesis), SAM (Spectral Angle Mapper), and DD (Degree of Distortion) image fusion metrics (see (Wei et al., 2015) for more details). Tables 1 and 2 summarize the computed quantitative metrics of the proposed strategy compared to the competitive fusion strategies whose numerical values clearly favor the restored images from the suggested fusion method.
Source: Authors.
Table 1: Quantitative fusion results of the proposed method and the competitive algorithms on the Pavia image: PSNR [dB], UIQI, RMSE (102), ERGAS, SAM [degrees], DD (103)

Source: Authors
Table 2: Quantitative fusion results of the proposed method and the competitive algorithms on the Moffet image: PSNR [dB], UIQI, RMSE (102), ERGAS, SAM [degrees], DD (103)

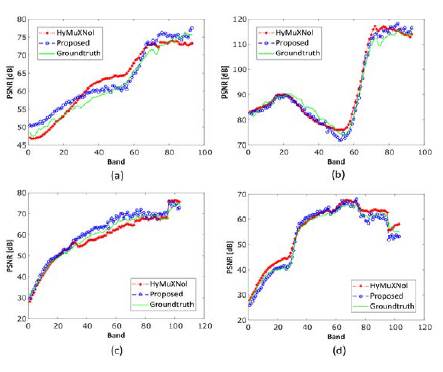
To further show the advantage of the proposed solution compared to the best method in the state-of-the-art HyMuXNol, we randomly extracted four spectral signatures on the Pavia and Moffett ground-truth images and evaluated them qualitatively (Figure 4). It is possible to see that the recovered spectral signatures using the prior CNSR on the abundances are closer to the ground-truth spectral signatures, indicating that the spectral information of the scenes is better fitted with the proposed model than the underlying model in the HyMuXNol method, and this happens for all the selected images.
Figure 4: Evaluation of the spectral performance: (Row 1) Ground-truth and recovered spectral signatures on the Pavia data set. (Row 2) Ground-truth and recovered spectral signatures on the Moffett data set.
CONCLUSIONS
This work proposed a MS and HS image fusion model solved under a sparce model on a set of learned dictionaries. By using the spectral unmixing decomposition, this model includes a non-local sparce representation of abundance maps on the fusion problem while taking advantage at the same time of the low dimensionality of the HS data. The estimated sparce representation is centralized for a better estimation obtained from the non-local redundancy of the abundances. These considerations lead to enhance the quality of fused images of state-of-the-art fusion methods based on sparce regularization. Additionally, a spatial-spectral dictionary is adaptively constructed, exploiting the low dimensionality of the abundance maps. The dictionary structure consists of K sub-dictionaries, each one estimated from a cluster of similar spatial features of abundance maps. Thus, an abundance patch is then sparcely represented in the appropriate dictionary. In order to obtain the full resolution image, the employed numerical strategy includes two main steps alternated iteratively: shrinkage thresholding operator for sparse regularization is used to solve the ℓ1 norm, and the execution of a gradient descent method to solve the quadratic fidelity problem. Restoration results show that the proposed image fusion model based on the abundance map analysis outperforms the competitive fusion methods based on sparse regularization in terms of the quantitative metrics PSNR, UIQI, RMSE, ERGAS, DD, and SAM.
Acknowledgements
ACKNOWLEDGMENTS
The authors gratefully acknowledge the Vicerrectoría de Investigación y Extensión of Universidad Industrial de Santader for supporting this work registered under the project titled: "Sistema óptico computacional compresivo para la adquisición y reconstrucción de información espacial, espectral y de profundidad de una escena, mediante modulaciones de frente de onda utilizando espejos deformables y aperturas codificadas" (VIE 2521 code).
REFERENCES
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.