Modelamiento de los niveles de contaminación en un tramo del río Sogamoso, mediante el acoplamiento de los métodos Lattice-Boltzmann y diferencias finitas

INTRODUCCIÓN

La contaminación tiene un impacto significativo (Cortes Zambrano et al., 2022, Cuadros Segura et al., 2021, Moyano Salcedo et al., 2021) en la gestión y el uso responsables de los recursos hídricos. Sin embargo, hace mucho tiempo el problema de la contaminación alcanzó una gran relevancia al sensibilizar a las personas para que fueran más responsables con el cuidado y uso de dichos recursos. Luego, en 2015, Naciones Unidas (ONU) aprobó diecisiete Objetivos de Desarrollo Sostenible (ODS) como parte de la Agenda de Desarrollo 2030. Entre ellos, el objetivo 6 consiste en garantizar la disponibilidad de agua, gestión sostenible y saneamiento para todos. El modelado de los fenómenos relacionados con los flujos (contaminantes) presenta aún desafíos y dificultades, entre las cuales se encuentra -por citar algunas-, la consideración de geometrías complejas y la convergencia del algoritmo partir del conjunto de parámetros físicos del modelo (Chen y Doolen, 1998,Krüger et al., 2017). Aunque estas dificultades definen el conjunto de ventajas y desventajas del método, nuevos avances significativos permiten establecer condiciones para simular sistemas que antes eran imposibles de modelar. El método LatticeBoltzmann permite simular la dinámica de un fluido a partir de un conjunto de ecuaciones, de las cuales se deduce la ecuación de Navier-Stokes, teniendo en cuenta la conservación de las ecuaciones de masa y momento.

En esta dirección, un sistema acoplado 1D y 2D simuló flujos de agua poco profunda en sistemas fluviales y lacustres a gran escala. Los resultados, comparables con datos experimentales de perfiles de velocidad para diferentes tiempos de relajación, evidencian una adecuada aproximación a los fenómenos reales.

Como es de conocimiento, la velocidad es un parámetro asociado a la viscosidad del fluido en Lattice-Boltzmann. Un caso interesante es el planteado por Meng et al. (2020), y Parmigiani et al. (2013), quienes simularon una sección del río Ródano, en Ginebra (Suiza) con Lattice-Boltzmann, mediante el cálculo de perfiles de velocidad y el establecimiento de límites computacionales en modelos con geometría 3D. Una contribución significativa fue la inclusión de sedimentación y procesos de erosión a lo largo de la ribera. Otros investigadores (Liu et al., 2015, Chen y Doolen, 1998) demostraron la fuerza del Lattice-Boltzmann para simular sistemas que permiten el cálculo del campo de velocidad en geometrías irregulares. En los fenómenos de difusión y advección de un contaminante, el campo de velocidad influye fuertemente en el comportamiento advectivo (Romero Suárez, 2011, García Sarmiento, 2019). Por tanto, la implementación de Lattice-Boltzmann para resolver la ecuación de Navier-Stokes proporciona una buena aproximación del campo de velocidad, según la geometría del río (Parmigiani et al. (2013). Por otro lado, la solución por diferencias finitas puede modelar el proceso de difusión/advección. Finalmente, Bermúdez y Juárez (2014) , y Ureña et al. (2009) analizaron la estabilidad y condiciones de convergencia, y comprobaron numéricamente el error global, según el número de nodos y el aumento del tiempo de simulación. Otros trabajos, como el de (Chen y Doolen, 1998), y (Liu et al., 2015) demostraron la fuerza del método de Lattice-Boltzmann para simular sistemas que permiten el cálculo del campo de velocidad en geometrías irregulares. En los fenómenos de difusión y advección de un contaminante, el campo de velocidad influye fuertemente en el comportamiento advectivo (García Sarmiento, 2019, Romero Suárez, 2011). Por consiguiente, la implementación de Lattice-Boltzmann para resolver la ecuación de Navier-Stokes proporciona una buena aproximación del campo de velocidades según la geometría del río (Parmigiani et al. (2013)). Por otro lado, la solución por diferencias finitas puede modelar el proceso de difusión/advección. Por último, Bermúdez y Juárez (2014), y Ureña et al. (2009) analizaron las condiciones de estabilidad y convergencia, y demostraron numéricamente el error global, según el número de nodos y el aumento del tiempo de simulación. Sus indicaciones garantizan la convergencia, ya que establece restricciones sobre algunos parámetros, así se evitan las inestabilidades asociadas a los modelos y discretización espaciotemporal.

Ecuación de advección/difusión

La ecuación de advección/difusión (ecuación (1)), describe el movimiento de partículas expuestas a un proceso difusivo, considerando el campo del vector de velocidad del fluido que los contiene:

C es la concentración (en porcentaje), D es el coeficiente de difusión en (m²/s) el cual representa la capacidad de propagación del material en el líquido, 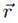es el vector posición en (m), 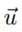es el vector velocidad del fluido en m/s. En la ecuación (1), 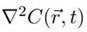representa el término difusivo, y 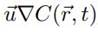, el término advectivo, que dependen del campo de velocidades del fluido.

Discretización

En la vecindad ∆t de un punto t una función f(t) se aproxima como:

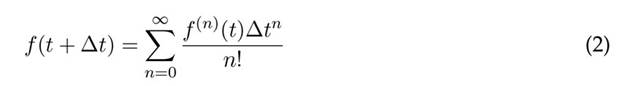
La sustracción de las ecuaciones (2) y (3) y el truncamiento a O(∆t) se obtiene la primera derivada:

Realizando el mismo procedimiento y el truncamiento a O(∆t²), se aproxima la segunda derivada:

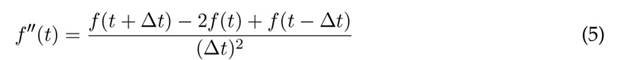
Reemplazando la discretización de las ecuaciones (4) y (5) en la ecuación (1) se obtiene la ecuación (6):

La ecuación (6) permite simular la evolución del proceso difusivo advectivo, el cual requiere conocer el campo de velocidad en cada punto del fluido, estimado mediante el método LatticeBoltzmann.

Ecuación de Navier-Stokes y el método de Lattice-Boltzmann

La ecuación de Navier-Stokes (ecuación (7)) describe el comportamiento de algunos fluidos debido a la conservación de la masa y el momento (Vazquez, 2004):

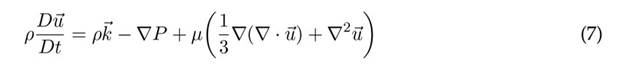
ρ es la densidad del fluido (kg/m3); 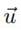el campo de velocidad (m/s); 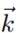aceleración creado por las fuerzas en el fluido; P, la presión del fluido (Pa), y µ, la viscosidad cinemática (m2/s).

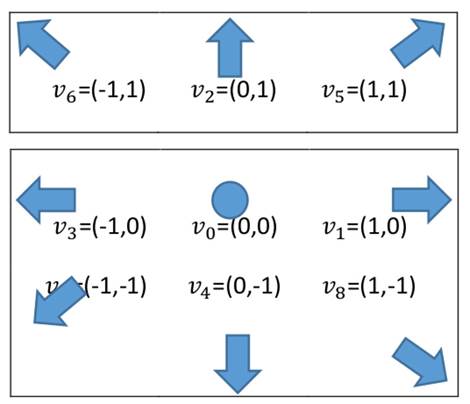
Actualmente, no existe solución analítica de la ecuación Navier-Stokes, excepto en casos específicos, por lo que el método de Lattice-Boltzmann proporciona una solución numérica aproximada de gran utilidad. Es un enfoque de simulación reciente, aplicado a sistemas de fluidos complejos, que atrae a investigadores en física computacional. Este método simula la dinámica de un fluido, resuelve el campo de flujo y lo discretiza en tiempo y espacio, pero sin hacer una discretización directa y explícita de la ecuación de Navier-Stokes. El método ofrece una ventaja numérica sobre otros, como diferencias finitas o volúmenes finitos (Krüger et al., 2017). Además, modela geometrías complejas o condiciones de contorno variables en el tiempo y que son ampliamente utilizadas para simular fenómenos con fluidos. En lugar de intentar resolver la ecuación (7), Lattic-Boltzmann imita una densidad de fluido en una celda que sufre continuos flujos y colisiones. El modelo 2DQ9 usado en la figura 1 representa el conjunto de velocidades de partículas en una celda que interactúa con las de las celdas vecinas.

Figura 1: Modelo de velocidad 2DQ9 para Lattice Boltzmann

El streaming step determina la dirección para transferir información de la función de distribución f hacia cada celda vecina. En el collision step, las celdas vecinas envían información sobre f a esta celda (celda central). La velocidad en la figura 1 tiene pesos que dependen del número de dimensiones espaciales y del modelo de velocidad utilizado. Estos pesos son:

Los pesos miden la importancia estadística de la información de la celda para cada una de las celdas vecinas, dependiendo del modelo de velocidad utilizado (Krüger et al., 2017). En las siguientes cantidades:

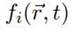es una función de distribución; ρ, la densidad de las partículas; 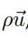, el momento por unidad de volumen; v _i = (v _ix , v _iy ), la velocidad de las partículas en un determinado instante y posición. La ecuación (11) es la función de equilibrio que calcula 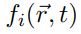, y es una aproximación en serie de Taylor de la función de distribución de velocidades de Boltzmann.

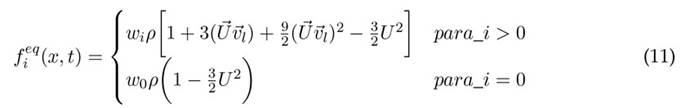
La ecuación de Boltzmann es (Chen y Doolen, 1998):

Ω _I es el operador de colisión. Esta investigación utilizó el operador Bhatnagar-Gross-Krook (BGK) (Krüger et al., 2017):

Donde τ es el tiempo de relajación, δt es el paso de tiempo entre dos procesos de pasos de transmisión. Finalmente, la ecuación de Boltzmann con el operador de colisión BGK (Bhatnagar Gross Krook) es:

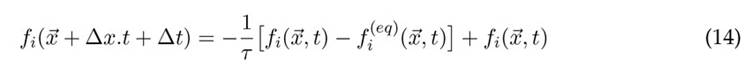
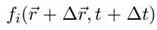es la función distribución de 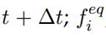, la función de equilibrio dado por la ecuación (11), y 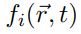, la función de distribución de las partículas con velocidad v _i para cada tiempo (t).

El error al usar el método de diferencias finitas mezcla el error espacial con el temporal. El error espacial está en el orden de ∆x² y el error en el tiempo está del orden del ∆t². Este ocurre por el truncamiento en los términos de la serie de Taylor. Las diferencias finitas son centradas, lo que permite mejorar el error y trabajarlo como parámetro, según la resolución espaciotemporal que se trabajó. Igualmente, se cumplen las condiciones de convergencia tanto para el modelamiento del campo de velocidades usando Lattice-Boltzmann, como para el modelamiento de la ecuación de difusión/advección. Con esto se garantiza que la propagación del error numérico no produce divergencias en los campos modelados (Krüger et al., 2017).

Metodología

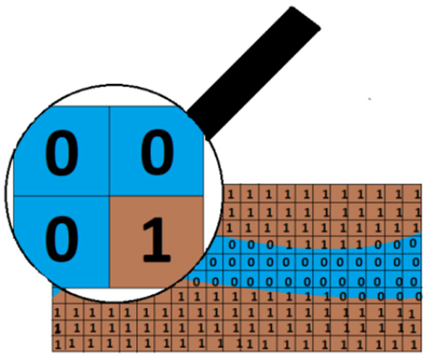
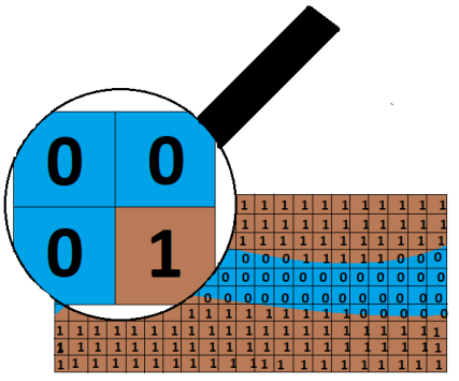
La metodología completa incluye dos códigos: el primero digitaliza la geometría para definir las áreas donde se encuentran el fluido y la roca; el segundo resuelve las ecuaciones de Navier-Stokes por el método de Lattice-Boltzmann y la ecuación de difusión/advección empleando diferencias finitas. La digitalización de la geometría y el mapeo de la fuente de agua proporciona un archivo de texto plano, donde cada pixel de la imagen tiene un valor de acuerdo con la frontera, la roca o el fluido. El código C++ inicializa todas las variables, crea las matrices que representan el espacio físico y carga la geometría en la variable celda. Esta variable tendrá la información sobre el tipo de medio almacenado en cada posición espacial de la matriz, determinando si es una roca (1) o un fluido (0) (figura 2).

Figura 2: Etiquetado de las celdas para definir roca y fluido dentro del espacio de la simulación

Validación del método

La validación del método implica la comparación de las soluciones analíticas con las obtenidas por modelado numérico. Para validar el proceso de difusión, en ausencia de un campo de velocidad uniforme, 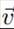la concentración C(x, y) tiene un perfil gaussiano, dado por:

Donde C₀ es el mayor valor en (x₀, y₀) y σ₀ es la desviación estándar, además la solución analítica es:

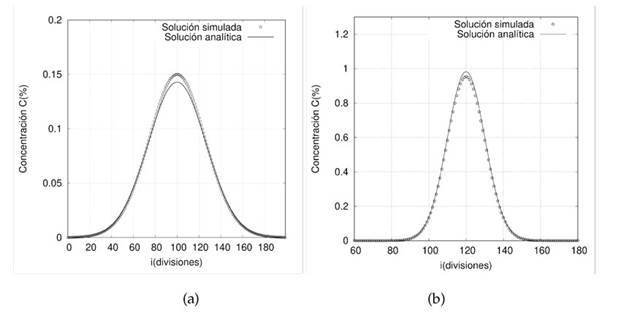
Con σ² _D = 2 · D · t, y D es el coeficiente de difusión. La tabla 1 contiene los parámetros usados, mientras que la figura 3 representa las soluciones analíticas y simuladas para cada uno de los procesos simulados.

Tabla 1: Parámetros usados en la validación de la componente difusiva

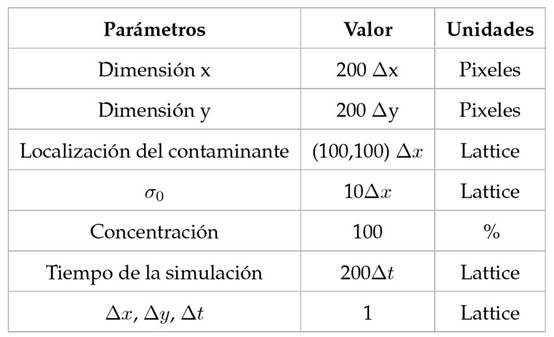
Figura 3: Distribución espacial de la concentración

a)Proceso difusivo, para un corte en j = 100, con un coeficiente de difusión D = 1, 5∆x²∆t (unidades de Lattice) y velocidad (0,0) ∆x/∆t (unidades de lattice). b) Proceso advectivo, para un corte en j = 120, con un coeficiente de difusión 0, 0043∆x²/∆t (unidades de lattice) y velocidad (v _x = 0, 1, v _y = 0, 1) ∆x/∆t (unidades de lattice).

La figura 3amuestra las soluciones analíticas y simuladas del fenómeno de difusión. La solución numérica es muy cercana a la analítica. El valor máximo de la concentración analítica es 0,1429 %, y el máximo está en el mismo punto arrojado por la solución simulada, 0,15 %. En la simulación del proceso advectivo se asume una velocidad de fluido homogénea. La solución analítica está dada por:

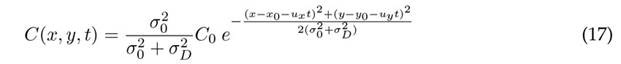
La figura 3b señala las soluciones analíticas y simuladas del fenómeno de advección después de pasos de 200∆t, t en unidades de la celda. La concentración analítica máxima es 0,98 % y el valor máximo para la simulación es 0,96 %, lo que indica la validez del enfoque de la solución.

RESULTADOS

En la figura 4 se ilustra la sección del río Sogamoso con su geometría utilizada en esta investigación. El área, ubicada en el departamento de Santander (Colombia), tiene coordenadas aproximadas entre 7°15’19,4"N 73°42’41,9"W y 7°15’06,1"N 73°43’19,8"W con una superficie estimada de 1,4 km (EW) a 0,9 km (NS).

Figura 4: Imagen satelital del tramo sobre el río Sogamoso

Fuente: Google Maps. (s. f.).

La figura 5 muestra el mapa de color digitalizado, donde cada color determina un tipo de material, agua o roca y condiciones de borde. El azul (0) corresponde al río, el azul (1) a la roca y el amarillo a los cuerpos sólidos dentro del canal. En su estado inicial, el modelo asume un fluido con velocidad cero.

Figura 5: Mapa de color del tramo del río Sogamoso

Nota: el color azul toma la etiqueta de 0, este valor corresponde al río. El verde toma el valor de 1, el cual corresponde a la región de frontera donde entra el río. Rojo es 2, y corresponde a la región de frontera donde finaliza el río. Negro es 3 y blanco es 4, corresponden a la orilla superior e inferior del río, es decir la roca que delimita el río. Finalmente, con amarillo que corresponde al 5, es la roca o sedimentos en medio del río, simulan obstáculos para el paso del fluido

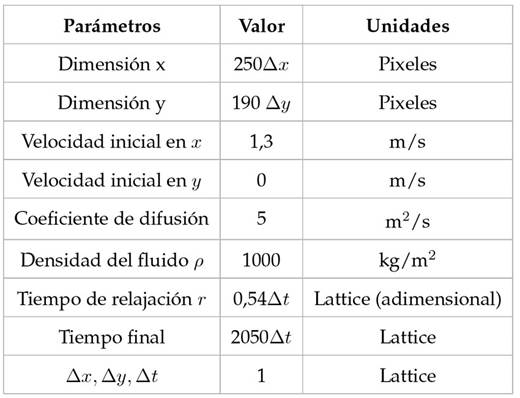
La condición en el borde izquierdo, el líquido entra, y la velocidad es de 1,3 m/s, mientras que el borde derecho por donde sale el líquido queda libre. El sistema evoluciona desde su estado inicial hasta alcanzar un estado estacionario; en adelante, se activa la fuente contaminante en el lado izquierdo dentro del río. La tabla 2 contiene los parámetros utilizados en la simulación.

Tabla 2: Parámetros del modelo

La figura 6 señala el resultado de la simulación, con la velocidad del fluido en el tiempo t=504 s. A la entrada del río, a la izquierda, la velocidad es de aproximadamente 1,3 m/s, según un informe proporcionado por el Instituto de Hidrología, Meteorología y Estudios Ambientales (Ideam). Las flechas amarillas indican la velocidad máxima de 1,3 m/s, las naranjas entre 0,6 m/s y 1,3 m/s. Los colores azul y gris son velocidades inferiores a 0,6 m/s. A la izquierda, el río viaja a 1,3 m/s y diverge en dos canales. En el canal superior, la velocidad disminuye a 1 m/s y luego 0,8 m/s hasta llegar a 0,6 m/s donde se divide en tres brazos. Posteriormente, los brazos se juntan y la velocidad aumenta entre 1,0 m/s y 1,3 m/s.

Figura 6: Campo vectorial de las velocidades en t = 504s

En la parte inferior del brazo, el río mantiene la velocidad a 1,3 m/s desde la entrada hasta donde diverge, donde cae a 1,0 m/s mientras que en el meandro inferior es 0,6 m/s. Desde el punto en el que los brazos se unen, la velocidad aumenta entre 1,0 m/s y 1,3 m/s. El número de Péclet está definido como Péclet =v/DL, dónde v es la velocidad en m/s, L es la longitud característica y D es el coeficiente de difusión cuyo valor es de 5 m2/s. Este valor muestra la relación entre la parte advectiva y difusiva. El río Sogamoso presenta dos tramos, el superior e inferior. En el superior se encuentran valores del número de Péclet del orden de 16,6 a 0,09. Esto significa que, empezando el tramo, el número de Péclet es mayor (la parte advectiva predomina) y luego disminuye drásticamente por la disminución de la velocidad (en este punto predomina la parte difusiva). En el brazo inferior, el número de Péclet es menor al empezar el tramo (Pe=36,4) y al finalizar, en el sector donde se unen los dos tramos (superior e inferior), el número de Péclet toma el valor de 89,2.

El río Sogamoso tiene aproximadamente 135 km de longitud, y una altitud que va desde 370 m en la fuente, hasta 70 m en su desembocadura en el río Magdalena. En la región de estudio, la elevación es de alrededor de 83 m (Topographic-map.com (s. f.)), y la pendiente de la topografía es de aproximadamente 0,00076 grados. La profundidad del río varía entre 2,5 m y 4,5 m (Ideam, 2019) de diciembre a abril, y puede aumentar hasta 7 m de mayo a junio (Ideam, 2017). El número de Froude proporcionado por la ecuación (18) representa la relación entre la inercia y la fuerza producida por la gravedad (Seizilles et al., 2013, Thual et al., 2015).

Donde v es la velocidad promedio del fluido, g es la gravedad y Dh es la profundidad hidráulica. En este punto del río Sogamoso, el número de Froude calculado de 0,22 señala un régimen subcrítico.

En el canal intermedio que intenta unir los dos brazos, parte central, el líquido permanece estancado. Un comportamiento similar ocurre en el área donde convergen los brazos. En una sección transversal del antebrazo, la velocidad cae de 1,3 m/s en la parte profundad, de 1,0; 0,8; 0,4; hasta estancarse en el banco de canales.

El comportamiento del fluido, mayor velocidad en áreas profundas y menor en bajíos y meandros, indica que el flujo es tipo Poiseuille a tan baja velocidad. Por otro lado, las direcciones de los vectores son consistentes con la geometría del río, colores más largos y cálidos (velocidades más altas) en los sectores más estrechos, y más cortos con colores más fríos (velocidades más bajas) cerca de la orilla. Según Krüger et al., 2017, en la ecuación de Lattice-Boltzmann de isotérmica básica, C _s determina la relación p = C ² _S ρ entre la presión p con la densidad ρ, constante estimada a través de/. Por tanto, p = C² _S ρ permite estimar la distribución de presiones en el río.

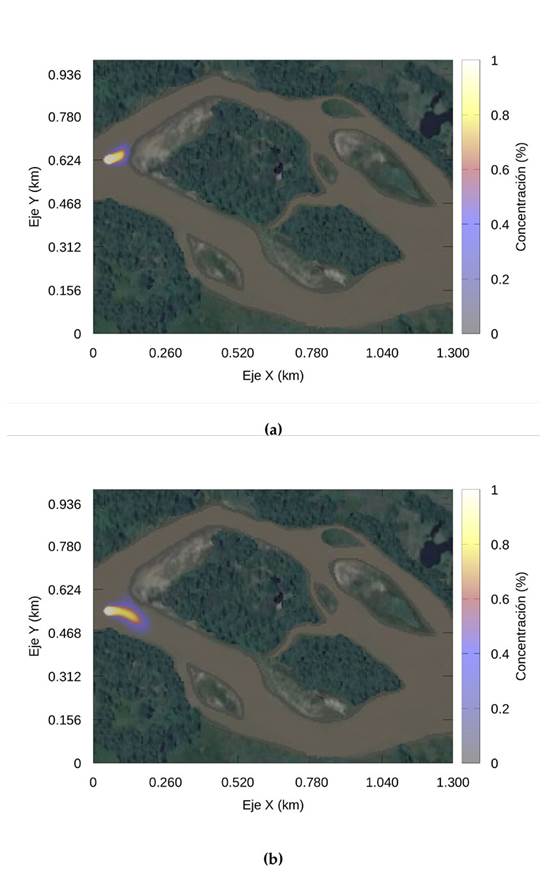
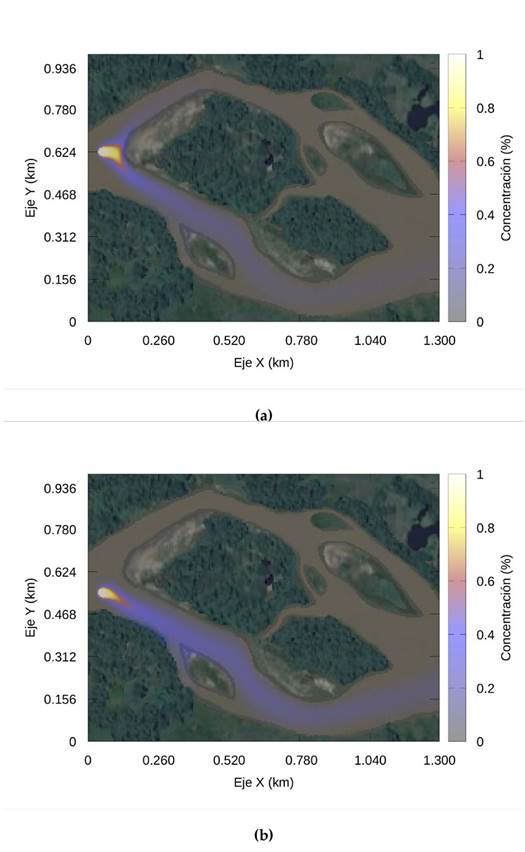
La figura 7 ilustra la distribución de la presión en el río en el tiempo t=504 s. La presión máxima es de alrededor de 24 kPa (blanco), 21 kPa (amarillo); y los colores más fríos, como el azul (17 kPa) y los grises (14 kPa), representan las presiones más bajas. La presión es mayor en la zona de entrada del flujo y menor en la zona de salida. El empuje ejercido por la alta velocidad de entrada hace que la presión disminuya cuando el volumen de entrada se distribuye sobre un área más grande. Después de alcanzar un estado estable, la simulación del contaminante comienza cuando la fuente se activa. La primera fuente se ubica cerca de las coordenadas x=0,087km para la longitud y para la latitud y=0,625 km. La figura 8A muestra el instante t=532 s, 28 s después de comenzar la contaminación. Allí la concentración es alta y se esparce lentamente.

Figura 7: Campo escalar de la distribución de la presión en t= 504 s

Nota: la escala de porcentaje está normalizada. a) t=532 s (28 s después de iniciada la contaminación).b) t = 1904 s (1400 s después de iniciada la contaminación)

Figura 8: Distribución de la concentración (a)

Nota: la escala de porcentaje está normalizada. a) t=532 s (28 s después de iniciada la contaminación). b) t = 1904 s (1400 s después de iniciada la contaminación)

La figura 8b muestra el estado de simulación 1400 s después de comenzar la contaminación. La mancha avanza más rápidamente a lo largo el brazo superior que en el inferior, alcanzando una distancia aproximada de 1,1 km. Sin embargo, 1400 s después de que comenzara la contingencia, la concentración más alta pasa por el brazo inferior (1904 s) (figura 8b), debido a que ese canal tiene mayor velocidad y capacidad de transporte. En ese momento, la mancha se agranda, y alcanza una distancia de 1,3 km. En una segunda simulación, la fuente contaminante está más cerca de la boca del antebrazo en las coordenadas x=0,087 km para la longitud y para la latitud y=0,546 km.

Posteriormente, en la figura 9a se indica la propagación del contaminante por el brazo inferior, 28 s después de activar la fuente, mientras que un flujo más débil avanza lentamente por la parte superior del brazo. El leve desplazamiento de la fuente contaminante perturba el régimen de propagación, de tal manera que el contaminante solo transita por un canal, es decir, predomina la advección y por tanto el campo vectorial de velocidad. Es necesario aclarar que la fuente vierte contaminante a una concentración constante que corresponde al valor máximo.

Figura 9: Distribución de la concentración

Nota: la escala de porcentaje está normalizada. a) t = 532 s (28 s después de iniciada la contaminación). b) t = 1904 s (1400 s después de iniciada la contaminación).

CONCLUSIONES

Esta investigación informa un enfoque acoplado de los métodos “Lattice-Boltzmann diferencias finitas” para resolver las ecuaciones de Navier-Stokes y simular difusión/fenómenos de advección, con flexibilidad de ajuste a geometrías irregulares. Las soluciones analíticas conocidas de modelos clásicos en comparación con los generados por el método numérico destacan la alta confiabilidad y estabilidad del método. Las simulaciones señalaron que la advección predomina sobre la difusión.

Por otro lado, el método permite medir el nivel de contaminación a lo largo del río en el tiempo, además de la velocidad de propagación, para tomar acciones correctivas. El enfoque permite analizar el comportamiento de una catástrofe ambiental, como la voladura de una tubería en un cuerpo de agua, variando la intensidad y posición de la fuente, la velocidad del flujo, la morfología del río, el tamaño del área modelada y el tiempo de evolución. El enfoque es aplicable y útil en otros campos de la ciencia.