Review of Charging Load Modeling Strategies for Electric Vehicles: a Comparison of Grid-to-Vehicle Probabilistic Approaches

INTRODUCTION

Due to the current debate around global warming, many countries have created numerous strategies to combat this issue. One of these strategies is the inclusion or penetration of electric vehicles (EVs) to the power grid (Alahyari et al., 2019). Nevertheless, the inclusion of this technology to the power grid is not only to fight against global warming; this penetration can also achieve an efficient operation of the power grid (Alahyari et al.,2019). All of this brings benefits to combat the aforementioned issue. However, this technology introduces new challenges that must be addressed. For example, with the penetration of EVs, it is not only evident that there is an increased electricity consumption in the power grid, along with the introduction of new load variations, but impacts have also been identified on transportation, manufacturing, and the economy (Li et al., 2019). These impacts depend on when EVs are connected for charging, where they are connected, and at which charging power (Grahn et al., 2011). Therefore, these factors must be considered in the operation, planning, and analysis of modern power grids such as active distribution networks or grid-connected microgrids (Alahyari et al., 2019). The penetration of EVs in studies on power network analysis has been widely addressed (Alahyari et al., 2019; Li et al., 2019; Kongjeen et al., 2019), and it can be supported by following several charging opportunities: unidirectional charging, bidirectional charging, uncontrolled charging, external charging strategies, and individual charging strategies (Grahn et al., 2011). Uncontrolled charging (UCC) means that EV users travel and park as they choose and connect their EVs when there is a need to recharge the battery. External charging strategies imply that the charging may somehow be controlled externally, based on the information of the power grid. Finally, individual charging strategies indicate that the individual can be seen within an UCC approach, but also that individuals may adjust their charging behavior based on economic incentives. For example, in the literature, it is commonly assumed that the penetration of EVs is modeled as a UCC unidirectional charging approach, which only considers the power flow in the grid-to-vehicle (G2V) direction. External charging strategies could be based on either unidirectional or bidirectional charging, which can consider a power flow in the vehicle-to-grid (V2G) direction. From the literature, one comes across reviews that organize their analysis about of EV charging technologies, EVs standards, charging infrastructure, or the impacts on power grid integration. However, there are few studies that focus on analyzing the different methodologies that have emerged using the G2V philosophy. In this article, we review different G2V approaches. Additionally, we perform an experimental comparison with three probabilistic models and evaluate their performance considering four levels of EV penetration.

EV CHARGING LOAD MODELING

Several approaches for modeling EV load have been proposed in the past. According to Yi and Scoffield (2018), we can find, for example, deterministic EV load modeling techniques (Kongjeen et al., 2019), Monte Carlo simulation approaches (MCS) (Li & Zhang, 2012), fuzzy methods (Shahidinejad et al., 2012), hybrid Fuzzy-MCS methods (Ahmadian et al., 2017) and many other techniques (Stiasny et al., 2021; Frendo et al., 2020) to model the EV load. In this paper, we intend to classify these methods into three groups: deterministic, data-driven, and uncertainty/variability approaches.

Deterministic approaches

In deterministic EV load modeling, several methods assume that EV parameters are known (Yi & Scoffield, 2018). For example, the available period, the arrival or departure times of vehicles, and the travelling distance are already known or fixed by the power grid operator, that is, EVs can be seen as stationary energy storage (Yi & Scoffield, 2018). On the other hand, it is possible to find studies that have used measurement-based load modeling approaches to estimate the load model for electric vehicle fast-charging stations (Gil-Aguirre et al., 2019). Basically, the authors estimate the parameters of the ZIP or polynomial load models, minimizing the discrepancy between the real measurement load and the simulated load responses (Gil-Aguirre et al., 2019). Kongjeen et al. (2019) implemented a modified backward and forward sweep method for analyzing the impact levels from EV load models on the grid based on constant current load and voltage-dependent loads. These deterministic EV load modeling approaches are also known as traditional methods.

Data-driven approaches

Due to the large amount of real-time driving data, by using these deterministic models, it is difficult to accurately capture the driving patterns (Li et al., 2019). These patterns show the usage behaviors of drivers and directly affect the energy consumption of EVs. Data-driven models are constructed from large historical data to model the underlying realistic EV charging behaviors. Based on these data-driven models, residential EV charging load profiles can be generated with regard to different numbers of households and charging rates. According to Li et al. (2019), these methods should be scalable and flexible frameworks. Some data-driven methods have been proposed to describe EV charging patterns and analyze EV driving data. For example, data mining methods such as clustering (Yi & Scoffield, 2018; Li et al., 2019), correlation analysis (Xydas et al., 2016), stochastic prediction (Ashtari et al., 2012), and time-series clustering (Zhou et al., 2017) are commonly employed to examine EV driving data. Specifically, Zhou et al. (2017) developed a time-series clustering with variable weights to analyze the driving cycle of hybrid-electric vehicles. On the other hand, Yi and Scoffield (2018) used historical residential charging behavior data to construct probability density functions for modeling the charging duration; and then they employed clustering based on the k-nearest neighbors (KNN) algorithm for charging decision-making. Li et al. (2019) proposed a two-level clustering model to determine the driving patterns of EVs. They identified five daily driving patterns and four multifaceted driving patterns that affect the daily load curve. However, the authors considered vehicle static parking patterns and did not take weather conditions into account. Crozier et al. (2019) introduced a probabilistic model based on K-means clustering for UCC of EVs to identify three distinct vehicle usage modes in the United Kingdom. However, the cluster number was included as a model parameter. To summarize, data-driven methods have a great potential for nonlinear system prediction, and the EV charging load can be computed considering different numbers of households and charging rates (Yi & Scoffield, 2018). However, these data-driven approaches have a weak performance against real-time driving data in low dimension. Although many studies mention differences between data-driven and machine learning techniques, we consider that both can be included into data-based approaches. We have found several approaches that use machine learning theory or concepts to model the EV load, charging behaviors, or driving patterns (Gerossier et al., 2019; Godde et al., 2015; Stiasny et al., 2021). Specifically, Gerossier et al. (2019) modeled the consumption profile of EVs from raw power measurements. From these measurements, the authors detected five kinds of plugs and EV batteries in order to determine the power drawn from the grid and the battery capacity using the random forest algorithm. On the other hand, Godde et al. (2015) proposed an approach for modeling the charging probability of electric vehicles as a Gaussian mixture model (GMM). This GMM comprehensively captures the charging profiles, assuming underlying assumptions about battery capacity, consumption, charging infrastructure, week day, and settlement structure. Stiasny et al. (2021) also used a GMM to distinguish seven aspects with respect to EV load modeling that influence the variables as flows and voltages in the grid. Frendo et al. (2020) proposed a data-driven regression model for predicting the EV charging demand from a large historical dataset of charging processes. Arias and Bae (2016) presented a forecasting model to estimate the EV charging demand using big data technologies. Specifically, the authors performed a cluster analysis to classify traffic patterns, a relational analysis to identify influential factors affecting the traffic patterns, and a decision tree to establish classification criteria, which determines the charging speed and power of an EV.

Uncertainty/variability approaches

After having discussed several deterministic, data-driven, and machine learning approaches, we would like to present the probabilistic, possibilistic, and stochastic methods that have been used to model the EV charging demand. We have decided to name them uncertainty/variability approaches due to the fact that these techniques deal with these two properties (uncertainty and variability) in the EV charging demand modeling process. In many research areas, these two fields are confused about their meaning and use.

In probabilistic methods, it is possible to find many studies that have used individual probabilistic distribution to model the EV charging demand. For example, these studies have employed Gaussian (Sun et al., 2015), Weibull (Li & Zhang, 2012), lognormal (Khoo et al., 2014), exponential distributions (Khoo et al., 2014), mixed probability distributions (i.e, a mixture of Gaussian distributions) (Flammini et al., 2019), or non-parametric methods (Chung et al., 2018; Chen et al., 2020) to determine the EV charging demand. However, the most common and used technique is Monte Carlo Simulation (MCS), which is conducted for a large number of samples generated using the probability density functions from several input variables (Li & Zhang, 2012; Su et al., 2019). These input variables can be home arrival/departure time, daily travelling distance/EV initial battery SoC, EV type, EV battery capacity, or EV recharge probability (Su et al., 2019). Many MCS applications can be found in the literature. For example, Grahn et al. (2011) analyzed the impact caused by the EV charging demand based on uncontrolled and controlled charging scenarios on the distribution transformer hot-spot temperature and loss of life by using a thermal model. Similarly, Tekdemir et al. (2017) also evaluated the effects of EVs on distribution grids. The authors used the MCS and Weibull probability distribution to model the EV charging demand, and they also assumed correlated loads on the grid. Under different conditions, Ul-Haq et al. (2018) employed MCS to develop an EV charging pattern model that considers the vehicle class, battery capacity, SoC, driving habit/need, plug-in time, mileage, recharging frequency per day, charging power rate, and dynamic EV charging price. In Ahmadian et al. (2015), a probabilistic approach is proposed to model the EV load demand considering home arrival time, home departure time, deriving distance, nonlinear characteristics of the battery charge, and different vehicle types. The authors used historical information from the National Household Travel Survey to obtain the probability distributions. On the other hand, in possibilistic approaches, we can find that authors such as Tan and Wang (2014) have proposed a load profile for EVs, which considers the arrival time, departure time, daily distance travelled, and vehicle parameters in order to obtain a stochastic model of driving patterns based on fuzzy logic theory. Hussain et al. (2019) introduced a fuzzy inference mechanism to determine an appropriate charging, discharging, or withholding decision for EVs. This scheme also considers the available power from the smart grid, arrival time, departure time, SoC, and the required stay time of EVs. Ali et al. (2017) proposed a hybrid fuzzy-MCS method where the parameters are modeled according to either probabilistic or possibilistic approaches. For example, the travelling distance is modeled using a fuzzy triangular membership function, while the arrival and departure times are modeled by Weibull probability distributions using MCS.

Finally, in uncertainty and variability approaches, different stochastic methods have been applied to model the EV charging demand. In these stochastic methods, we found approaches such as auto-regressive integrated moving average (ARIMA) processes (Amini et al., 2016), Markov chains (Sokorai et al., 2018), Poisson processes (Jiang et al., 2017), and queue theory-based Poisson processes (García-Valle & Vlachogiannis, 2009). A summary of these approaches can be seen in Table I.

ELECTRIC VEHICLE CHARGING PROBABILISTIC (EVCP) MODELING

In cases where the output variables are requested and the system is complex and includes uncertainty, probabilistic models of the system are advantageous to use in order to determine the behavior of some random variables. In our context, probabilistic modeling can be defined as a way of modeling a phenomenon that uses presumed probability distributions of certain input assumptions or variables to compute the involved probability distribution for chosen output variables (Pergler & Freeman, 2010). One way to achieve this probabilistic modeling is using MCS, which is the most commonly used technique for probabilistic modeling. This section presents three MCS-based EVCP models.

EVCP model 1

For model 1, we have considered the model presented by Su et al. (2019), where the authors assumed that the daily travel distance d and the plug-in time t _p of an EV are Gaussian and lognormal random variables. The authors also assumed that the state of charge SOC _ij after a daily travel distance (𝐷), can be computed from Equation (1) using the efficiency of battery power in driving cycles in EVs (η), as follows:

For each EV, the authors calculated the charging duration ( 𝑡 𝑑 ) to compute the total EV power using Equation (2), which is given by

where

Where P _c in Equation (3) is the rated charging power, j is the MCS iteration, and i represents the i-th EV in the specific predefined EV fleet, that is, where 𝑖={1,2,3,4,5}, which represents private EVs, utility EVs, commercial EVs (taxies), electric goods trucks, and electric buses, respectively.

EVCP model 2

For model 2, we propose an EVCP model that depends on the leaving time from home 𝑡_𝑙, the time that the EV user is away from home 𝑡_𝑎, and the charging efficiency 𝜂 of EVs as random variables to compute the energy consumption of EVs. 𝑡_𝑙 and 𝑡_𝑎 are modeled by Gaussian distributions, and 𝜂 is modeled as a uniform distribution. We also consider the five types of EVs, similarly to EVCP model 1. For our model, we approximate the minimum charging duration time 𝑡_𝑚𝑐𝑑 as a function of the initial SOC:

where 𝐶_𝑎𝑝 is the battery capacity, and the connecting time 𝑡_𝑐 and the fully charging time 𝑡_𝑓𝑐 are computed as

From the expressions shown in Equations (4) and (5), the total EV power is calculated from Equations (6) and (7), that is,

where

EVCP model 3

The third model was presented by Ahmadian et al. (2015), which we have modified to include the specific predefined EV fleet of the EVCP model 1. For this model, the home arrival time 𝑡_α, home departure time 𝑡_d, and travelled distance d are Gaussian random variables, and battery efficiency is uniformly distributed. The SOC is initially computed as in Equation (1). The rated charging power P _c is modelled as a nonlinear function of the SOC, where the SOC is recursively calculated as follows:

where η represents the efficiency of the EV during driving. Considering the random variables mentioned above and Equation (8), the total EV power is calculated using Equations (9) and (10).

where

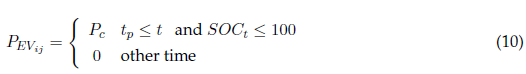
EXPERIMENTAL EVALUATION

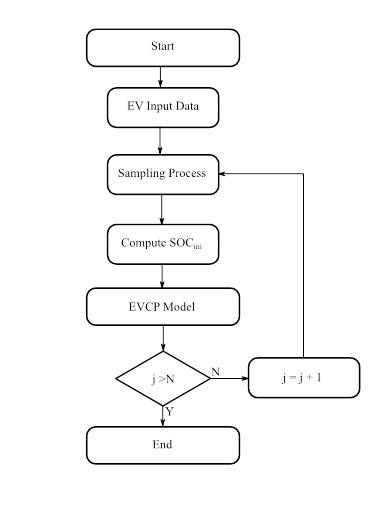
In this section, we compare the three aforementioned MCS-based EVCP models following the procedure shown in Figure 1. In the EV input data block, we use the information in Su et al. (2019) as the battery capacity, EV types, charging power, and full endurance mileages. On the other hand, for the sampling process block, we use the parameters of Table 2 to generate samples for all random variables that feed the three MCS-based EVCP models, and then to compute the total EV power. We repeat N = 5000 times the procedure shown in Figure 1 to obtain the histogram for the EV electric energy consumption. We adopt some assumptions about how to use the different EV types employed in Su et al. (2019). For example, we consider that 80% of private EVs are plugged into the power grid from 18 to 7 h, and the remaining 20% is recharged during working hours, that is, from 9 h to 17 h. We contemplate three penetration scenarios using 20, 200, 2.000 and 20.000 EVs. To determine the number of EVs, we use a Poisson distribution with an expected value 𝜆. For each level of penetration, we consider over 60% of private EVs, 20% of utility EVs, 10% of taxis, 5% of electric goods trucks, and 5% of electric buses.

Figure. 1: Flowchart for comparing the EVCP Models

Source: Authors

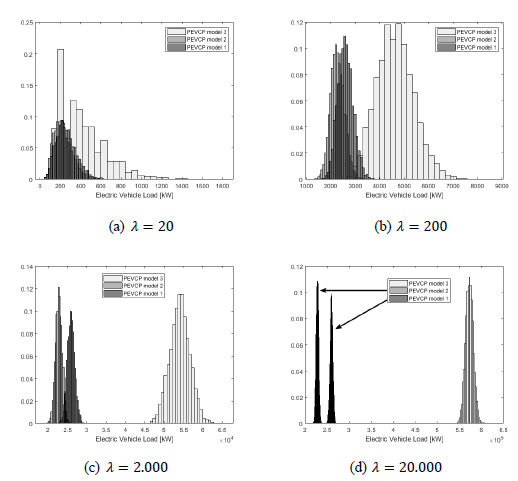
Figure 2 shows the results of the MCS applied to the three EVCP models considering a penetration of 20, 200, 2.000, and 2.0000 expected EVs. Note that the EVCP models 1 and 2 present similar results. On the contrary, EVCP model 3 obtained significant differences in the energy consumption of the EVs. On one hand, we observe that the EVCP models 1 and 2 keep coherence when the number of EVs increases. However, this can only be true if we are analyzing similar EVs. On the other hand, from EVCP model 3, note that the energy consumption gradually changes as the number of vehicles increases, but it is not consistent between one scenario and the other. From the above, it is necessary to improve EVCP models 1 and 2.

Figure 2: Two histograms of the EV charging demand when we apply MCS to the three EVCP models considering a penetration of 20, 200, 2.000, and 20.000 expected EVs

Source: Authors

We noticed that one of the great differences of models 1 and 2 with model 3 is that the latter, in addition to considering the non-linear characteristics of the battery charge, ensures that the battery is charged once it is connected to the power grid. From Figure 2, we also noticed that, when there is when low EV penetration, the behavior of the energy demand can be modeled using a probability distribution. However, when there is a high penetration of EVs, the probability that best adjusts to the behavior of EV demand can be a Gaussian or lognormal distribution. To this effect, we applied a similarity measure to determine how one probability distribution is different from the other, that is, we computed this distance between the real probability distribution (obtained by MCS) and a proposed distribution. Specifically, we computed the Wasserstein distance (Carrillo & Toscani, 2005) in order to measure the similarity between the true data distribution and some proposed distributions. We analyzed the Gaussian, lognormal, gamma, and Weibull distributions. To compute this distance, we repeated the experiment described above five times using only model 3, that is, we applied five times the procedure shown in Figure 1. From the obtained data, we fit the previously described distributions to the data. Then, we generated samples from these distributions and compared them, using the distance, with the data obtained by applying the MCS of each model. Table 3 shows the Wasserstein distance for modeling the EV demand considering the previous distributions. We particularly noticed that the gamma distribution can be a different modeling alternative for low EV penetration levels. On the other hand, note that the lognormal and Gaussian distributions are adequate options for modeling the demand of EVs when there is a high penetration.

CONCLUSION

A review of the state of the art of the modeling of electric vehicles under a G2V approach was presented, where three groups were identified: deterministic approaches, methods that deal with uncertainty and variability, and data-driven methods. Additionally, an experimental comparison was made with three probabilistic models based on Monte Carlo Simulation. From this comparison, we observed that EVCP model 3 and the gamma distribution can be appropriate for modeling the penetration of EVs in probabilistic load flow analysis or for stochastic planning studies for active distribution networks. As future works, it would be possible to consider smart charging strategies within these EVCP models, as well as to include more realistic scenarios.