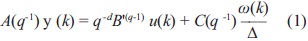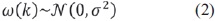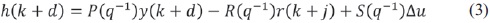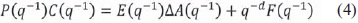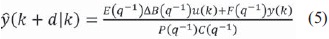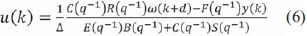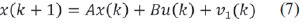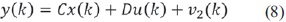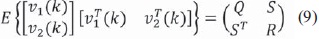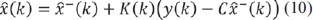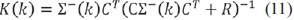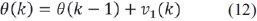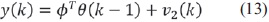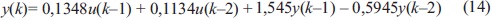DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2013.2.a03Published:
2013-04-01Issue:
Vol. 17 No. 36 (2013): April - JuneSection:
ResearchControl adaptativo basado en mínima varianza y filtro de Kaiman
Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Control adaptativo basado en mínima varianza y filtro de Kalman
Minimum variance and Kalman filter-based adaptive control
Carlos David Zuluaga Ríos1, Eduardo Giraldo2
1 Ingeniero Electricista, estudiante de Maestría en Ingeniería Eléctrica. Investigador de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: cardazu@utp.edu.co
2 Ingeniero Electricista, magister en ingeniería eléctrica. Docente de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: egiraldos@utp.edu.co
Fecha de recepción: 30 de noviembre de 2011 Fecha de aceptación: 27 de noviembre de 2012
Resumen
Este artículo presenta una metodología para el diseño de un control adaptativo basado en el control de mínima varianza (MVC) y el filtro de Kalman (KF). El control de mínima varianza es una técnica de mucho interés y ampliamente usada, ya que permite reducir el consumo de energía o material, o bien, incrementar el rendimiento de producción. El filtro de Kalman es un método recursivo que le da un soporte estocástico para el sistema adaptativo, mostrando que, para la identificación de sistemas dinámicos, es posible su utilización arrojando buenos resultados. La implementación de la metodología se realizó en un entorno de desarrollo integrado multiplataforma llamado Qt Creator basado en Qt 4,7, obteniendo óptimos resultados ante el problema de seguimiento de referencia; además, se puede observar que el esquema de control adaptativo presenta tiempos de establecimiento y sobrepasos notoriamente adecuados.
Palabras clave: control adaptativo, estimación de parámetros, filtro de Kalman.
Abstract
This paper presents a methodology for designing a minimum variance control- (MVC) and Kalman filter- (KF) based adaptive system. MVC is a technique of great interest, and it is widely used because it can reduce either energy or material consumption, or else, it can increase production performance. The Kalman filter is a recursive method that provides stochastic support for adaptive systems, showing feasibility and good results for dynamic system identification. The methodology implementation was conducted in a multiplatform integrated development environment called Qt Creator Qt 4.7-based, yielding good results when applied to the reference tracking problem. Moreover, it can be observed that the adaptive control scheme exhibits good settling times and notoriously appropriate overshoots.
Key words: adaptive control, parameter estimation, Kalman filter.
1. Introducción
Los controles autosintonizados ofrecen ciertas ventajas ante los controladores convencionales, de los cuales se pueden obtener una configuración óptima de su estructura para realizar etapas, igualmente, son capaces de resintonizarse ante perturbaciones o variaciones presentes en el proceso. La literatura pretende que los lectores y los investigadores se convenzan de que las técnicas de control adaptativos son una herramienta muy útil para el diseño de sistemas de control [1]. Dentro de este campo de los controles adaptativos, se pueden encontrar un número de técnicas que son empleadas para realizar la tarea de autosintonización, métodos como: lógica difusa [2], algoritmos de proyección [3], mínimos cuadrados recursivos [4], también existen la combinación de métodos como las redes neuronales y lógica difusa [5], y para aplicaciones no lineales se puede encontrar el filtro de Kalman extendido [5]. Todas estas técnicas han sido empleadas como herramientas para lograr un adecuado control de procesos. Este estudio se enfocará en el control de mínima varianza y el filtro de Kalman, ya que son métodos que brindan buenas características a la estructura adaptativa; algunas de estas particularidades son, por ejemplo, la recursividad del filtro de Kalman para estimar los parámetros de la planta en estudio, además el buen tiempo de cálculo para realizar estos estimados, ya que este método cuenta con cálculos matriciales, de forma que se obtengan las mínimas respuestas posibles; para el caso del control de mínima varianza, se puede mencionar la orientación para efectuar acciones de control de pequeñísima magnitud.
El control de mínima varianza (MVC) es una técnica de control efectivo para plantas que incluyen retardos en sus respuestas. En particular, el MVC tiene un control que intenta minimizar un término que penalice el esfuerzo de control.
El KF es una representación en modelo de espacio de estado de un sistema dinámico lineal, el cual entrega una solución recursiva al problema de estimación de parámetros, asumiendo que los ruidos presentados en el modelo de espacio de estado se distribuyen de manera gaussiana. Si esto se asegura, la literatura menciona que el KF es el mejor estimador de mínima varianza lineal [1].
El artículo se encuentra estructurado de la siguiente manera: en la segunda sección se muestra la metodología utilizada para realizar el esquema de control adaptativo, en la tercera sección se exponen los resultados al aplicar el control adaptativo a un caso simulado y a una aplicación real; y, finalmente, se presentan las conclusiones de la aplicación del esquema de control adaptativo.
2. Metodología
Para realizar el esquema de control adaptativo, se contará con técnicas que realizan la estimación del modelo de forma secuencial, el cual usa cada dato individual tan pronto esté disponible; así, se puede actualizar tanto la estimación del modelo como la señal que se quiere determinar, en este caso, la señal de salida del proceso. A continuación se detallarán las partes que contienen este esquema.
2.1 Control de mínima varianza
En esta sección se presenta de manera básica el método control de mínima varianza (MVC), donde se expone su estructura y cómo está compuesta la ley de control para un problema de seguimiento de referencia empleando MVC.
El MVC es equivalente al control de un paso adelante, discutido en [1], en el caso de sistemas estocásticos se utiliza el controlador de mínima varianza.
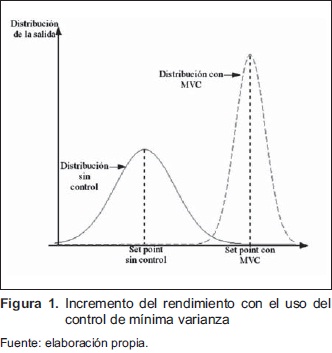
La motivación frecuente al usar el MVC, es que éste reduce la varianza de una variable dada, para el caso de la variable salida, en la Figura 1 se observa cómo la varianza se reduce, la literatura relacionada argumenta además que el rendimiento del controlador puede aumentar o su costo puede reducirse [1].
La Figura 1 es un ejemplo de la aplicación del control a un molino de viento, se observa que para el caso de MVC el rendimiento puede incrementarse para una probabilidad dada.
2.1.1 Diseño del control de mínima varianza
Considere un sistema SISO, descrito por la ecuación (1), como un modelo autorregresivo de media móvil con entrada auxiliar (ARMAX) [1]:
Donde
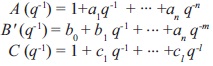
Donde {u(k)} y {y(k)} son la señal de entrada y de salida, respectivamente, q-d representa operador de retardo presente en la planta y {w(k)} es un "ruido blanco", el cual se distribuye normalmente, como se presenta en la ecuación (2) [1]:
Los polinomios A(q-1), B'(q-1) y C(q-1) son funciones del operador de retardo q-1. Δ es un operador diferencia ((1 - q-1)). La función de costo está dada por J = E{h(k + d)2)} en el caso de tener el problema de servo, el cual realiza el seguimiento de una señal de referencia; la expresión para la salida según el esquema empleado hasta ahora, se muestra en la ecuación (3) [6].
Donde
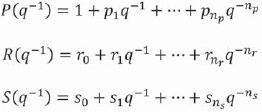
Donde r(k + j) es la señal referencia. Los polinomios P(q-1), R(q-1) y S(q-1) son las ponderaciones de la función de costo. Teniendo en cuenta la ecuación (3), y(k + d) es la salida del sistema, la cual debe ser predicha para el instante k. Para esto, se introduce la siguiente expresión Diofántina dada por la ecuación (4) [6]
Se nota que el filtro dado por de la ecuación (3) y ecuación (4) proporcionan características cuando se presentan perturbaciones. Si se multiplican ambos lados de la ecuación (1) por E(q-1)Δ y la ecuación Diofántina dada por la ecuación (4) es sustituida por E(q-1)Δ A(q-1), la predicción óptima para los d pasos adelante se puede obtener a partir de la forma ecuación (5) [6]
Sustituyendo la ecuación (5) en la ecuación (3) y minimizando la función de costo para proporcionar la señal de control ante el problema del servo MVC, se tiene la ecuación (6)
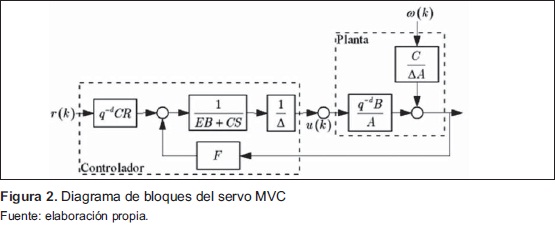
La Figura 2 muestra el diagrama de bloques en lazo cerrado aplicando MVC al sistema.2.2 Filtro de Kalman
El KF ofrece una forma de estimar el estado xk de un modelo en un sistema estocástico lineal de dimensión finita dado por la ecuación (7), ecuación (8) y ecuación (9), donde v1 y v2 representan entradas de ruido blanco. Si se remueven estas señales de ruido, el modelo se reduce a un sistema de espacio de estado determinístico [1], [7], [8].
La estimación del proceso se puede ver como una forma de control por realimentación: el filtro estima el estado en algún tiempo y luego obtiene la realimentación en la forma de las medidas (más ruido). Las ecuaciones para el KF se presentan en dos grupos: actualización de tiempo y actualización de la medida [9].
La señal v1 es el ruido de proceso y v2 es el ruido de la medida u observación, estos son procesos estacionarios de ruido blanco con media cero y no correlacionados.
Donde x(k) es una variable aleatoria y sus valores iniciales para el estado es 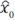 y covarianza es ∑0; los valores de las matrices de covarianza para los ruidos del proceso y medida están consignado en la ecuación (9).
y covarianza es ∑0; los valores de las matrices de covarianza para los ruidos del proceso y medida están consignado en la ecuación (9).
Donde E es el valor esperado. Las matrices de covarianza Q y R se asumen contantes y la matriz de covarianza es cero debido a que no existe correlación entre los ruidos del proceso y medida.
El filtro se basa en las dos interpretaciones siguientes [8]:
- Si el ruido es Gaussiano: el filtro presenta la estimación del estado de mínima varianza.
- Si se remueve la hipótesis: el filtro obtiene la estimación del estado de mínima varianza lineal.
El teorema de Kalman se basa en la obtención de una ecuación que estime el estado posterior 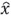 (k) como una combinación lineal del estado a priori
(k) como una combinación lineal del estado a priori 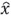 -(k), una ponderación de la diferencia entre la medida actual y(k) y una predicción de la medida C
-(k), una ponderación de la diferencia entre la medida actual y(k) y una predicción de la medida C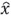 -(k), haciendo D= 0, lo anterior se muestra en la ecuación (10).
-(k), haciendo D= 0, lo anterior se muestra en la ecuación (10).
Donde K(k) es la ganancia de Kalman dada por la ecuación (11).
2.2.1 Estimación de parámetros utilizando el filtro de Kalman
El modelo del proceso se describe como se muestra en la ecuación (12) y ecuación (13).
Para este caso al aplicar el KF al sistema de la ecuación (7) y ecuación (8), 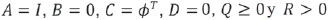 [7]. Se asume que el estado inicial no está correlacionado con los errores y con varianza finita.
[7]. Se asume que el estado inicial no está correlacionado con los errores y con varianza finita.
El filtro de Kalman para la estimación de parámetros se puede resumir de la siguiente forma:
- Inicializar
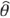 (0) y Σ(0)
(0) y Σ(0) - Realizar propagación a partir de
- Efectuar la actualización por medio de
Para k = 1 ...N
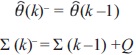
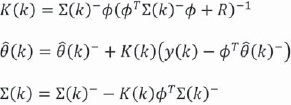
Donde 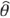 (k)- es la estimación a priori de los parámetros θ(k), Σ(k)- es la matriz de covarianza de la propagación del error de estimación,
(k)- es la estimación a priori de los parámetros θ(k), Σ(k)- es la matriz de covarianza de la propagación del error de estimación, 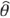 (k) es la actualización de la estimación de los parámetros θ(k), Σ(k) es la matriz de covarianza actualizada para error de estimación.
(k) es la actualización de la estimación de los parámetros θ(k), Σ(k) es la matriz de covarianza actualizada para error de estimación.
3. Resultados y discusión
Para dar a conocer los resultados al aplicar la estrategia de control adaptativo, se realizará primero una simulación de una planta que se ajusta a un modelo ARMA de segundo orden, luego se aplicará este esquema de control a un proceso real, como es el caso de un motor DC, específicamente el servomecanismo elaborado por Feedback con designación 33-100/110. Para la etapa de identificación de parámetros, se empleó un modelo ARMAX de tercer orden, es decir, para la ecuación (1) n=3, m=2 y l=3; la estimación de estos modelos fue realizada aplicando el filtro Kalman.
3.1 Simulación
Para aplicar lo anteriormente plasmado, se tomará un modelo ARMA de segundo orden, el cual es descrito por la ecuación (14), así:
La simulación fue realizada en un entorno de desarrollo integrado multiplataforma Qt Creator basado en Qt 4,7. Para esta simulación, la señal de referencia es cambiada a disposición del usuario, dándole un ambiente práctico. El retardo de la planta es considerado un paso. Además, los polinomios P(q-1) = R(q-1) = 1 los cuales son las ponderaciones de la función de costo, se asumen iguales a la unidad o, dicho de otra manera, de orden cero, debido a las restricciones hechas por [10] y [11]; la ponderación de la señal de control P(q-1) = λ se asume ser constante. En [6] recomiendan que esta ponderación tome un valor entre 2,41< λ < 11,55, este factor hace que la señal de control haga, o no, más esfuerzo para llevar la salida a su valor deseado, en nuestro caso a la señal de referencia.
Cuando se utiliza una ponderación constante del esfuerzo de control, lo que se logra con esto es la ubicación de los polos dentro de la zona de estabilidad, en este caso, dentro del círculo unitario. Existen diversos autores que han estudiado, de manera general, la elección de los polinomios de ponderación, mediante el análisis de los polos en la ecuación, característica del sistema de lazo cerrado. Nótese que, de esta forma, se establece una relación con el problema de asignación de polos [12]. Por otra parte, existen métodos que relacionan la elección con especificaciones típicas, como la eliminación del error en estado estacionario [13], o bien para que el controlador resultante tenga una estructura de un PID [14].
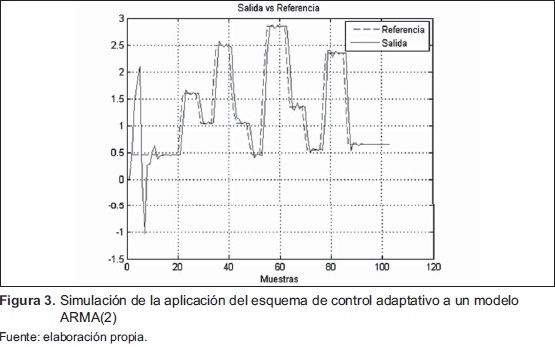
En la Figura 3 se observa que, en las primeras muestras, la señal de salida es un poco diferente, dado que el algoritmo de identificación está llegando a su convergencia; alrededor de la muestra 15 se nota que el algoritmo del filtro de Kalman estima, de manera adecuada, los parámetros del modelo que ajusta el sistema de simulación. Se observa además que el control de mínima varianza responde de manera apropiada, teniendo un tiempo de establecimiento aproximadamente de 10 muestras. De la aplicación del MVC al sistema simulado, se puede observar que se presenta un sobrepasó cerca del 5 %.
3.2 Ejecución practica
Mostrados lo resultados obtenidos ante el sistema simulado, se procederá a observar los resultados de la aplicación del MVC adaptativo a el motor DC (ambiente práctico).
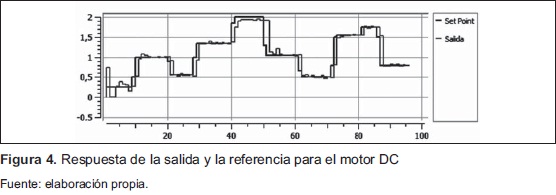
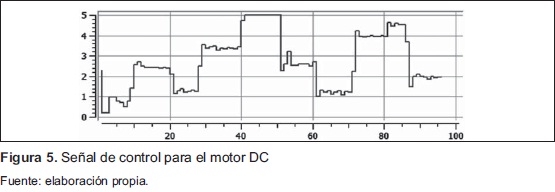
En la Figura 4 se observa, al igual que la simulación, que al principio el sistema está aprendiendo o estimando de manera adecuada y por ello se presentan cambios bruscos en las primeras muestras; se observa además que, para la muestra 8 se tiene, aproximadamente, una convergencia en los parámetros, por lo tanto, se tiene un establecimiento en la señal de salida; también de la Figura 4 se puede destacar que, ante los cambios hechos en la referencia, el control adaptativo se comporta adecuadamente haciendo que la salida siga constantemente la señal deseada. Alrededor de la muestra 42, se observa que la planta se satura y no puede llegar a el valor de referencia, esto se debe a que el sistema de adquisición solo tiene salida de 0 V a 5 V, en la Figura 5, cerca de la muestra 42, se tiene que la señal de control llega y se mantiene en 5 V, hasta que se presenta un nuevo cambio en la señal de referencia, cabe resaltar que ante este efecto el sistema adaptativo vuelve y retoma el seguimiento de la señal deseada, como se observa en la muestra 60.
4. Conclusiones
En este estudio se mostró la aplicación del control adaptativo basado en MVC y el filtro de Kalman, además, se expusieron las características del comportamiento de la estructura de control y del método que realiza la estimación de los parámetros del modelo ajustado a la planta de la simulación y del ambiente práctico. De las respuestas obtenidas, aplicando el esquema propuesto en este estudio, se observa que los tiempos de establecimiento y los valores de sobrepaso son adecuados, además, cabe resaltar que ante cualquier variación de la señal de referencia, la estrategia de control adaptativo lleva, de forma adecuada, la salida a el valor deseado.
En este artículo, se consideró un problema de control lineal óptimo-cuadrático gaussiano, obteniendo resultados notorios, poniendo de manifesto la relativa sencillez con que se resuelve el problema de síntesis, extendiendo la posibilidad de parametrizar el controlador con los parámetros del modelo del proceso. Esta propiedad hace que la estrategia de mínima varianza se utilizada en los sistemas de control adaptativo.
5. Financiamiento
Este trabajo se desarrolló en el marco del proyecto de investigación "Identificación de parámetros de un generador eólico doblemente alimentado basado en métodos recursivos bayesianos" en el programa de jóvenes investigadores "Virginia Gutiérrez de Pineda" y fue financiado por medio de Col-ciencias y la Universidad Tecnológica de Pereira.
Referencias
[1] G. Goodwin and K. Sin, Adaptive filtering, prediction and control, New York, NY, USA: Dover Publications, Inc., 2009.
[2] B. Lee, J. Peng and I. Chang, "A switching adaptivevss/fuzzy control", in Machine Learning and Cybernetics (ICMLC), 2011 International Conference, Vol. 3, pp. 1162-1167, July, 2011.
[3] M. Sawada and K. Itamiya, "A design scheme of model reference adaptive control system with using a smooth parameter projection adaptive law", in SICE Annual Conference (SICE) 2011, Sept. 2011, pp. 1704-1709.
[4] M. Delbari, K. Salahshoor and B. Moshiri, "Adaptive generalized predictive control and model reference adaptive control for cstr reactor", in Intelligent Control and Information Processing (ICICIP), 2010 International Conference, Aug. 2010, pp. 165-169.
[5] K. Szabat, "Direct and indirect adaptive control of a two-mass drivesystem - a comparison", in Industrial Electronics, 2008. ISIE 2008, pp. 564-569, July, 2008.
[6] M. Doi and Y. Mori, "Generalized minimum variance control for time varying systems without diophantine equation", in American Control Conference, 2002. Proceedings of the 2002, Vol. 4, pp. 3230-3235. 2002.
[7] L. Ljung, System identification: theory lor the user, 2nd ed. Prentice hall, Jan., 1999.
[8] S. Sánchez, y E. Giraldo, Sistemas de control en modelos de máquinas eléctricas, U.T.P. y ITM, Jan, 2009.
[9] B. Anderson and J. Moore, Optimal filtering, Dover publications, Jan., 2005.
[10] P. Tuffs and D. Clarke, "Self-tuning control of offset: a unifed approach", Control theory and applications, IEE Proceedings D, Vol. 132, No. 3, pp. 100-110, May 1985.
[11] W. Heath and P. Wellstead, "Self-tuning prediction and control for two-dimensional processes part 2: parameter estimation, setpoint tracking and offset handling", International Journal of control, Vol. 62, pp. 239-269, 1995.
[12] M. Ramos, E. Marquez and R. del Busto, "Generalised minimum variance with pole assignment controller modifed for practical applications" in Control Applications, 2004 Proceeding of the 2004 IEEE International Conference on, Vol. 2, pp. 13-18, Sept., 2004.
[13] A. Zayed, A. Hussain and L. Smith, "A modifed generalized minimum-variance stochastic self-tuning controller with pole-zero placement", in Multi Topic Conference, 2001. IEEE INMIC 2001, Technology for the 21st century. Proceedings. IEEE International, pp. 252-256, 2001.
[14] T. Yamamoto, A. Inoue and S. Shah, "Generalised minimum variance self-tuning pole-assignment controller with a PID structure", in Control applications, 1999. Proceedings of the 1999 IEEE International conference on, Vol. 1, pp. 125-130, 1999.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.