DOI:
https://doi.org/10.14483/22487638.19290Publicado:
01-10-2022Número:
Vol. 26 Núm. 74 (2022): Octubre - DiciembreSección:
Estudio de casoUbicación de un operador logístico para varios periodos de un horizonte de planeación mediante programación lineal
Location of a logistics operator for several periods of a planning horizon via linear programming
Palabras clave:
logística, operador logístico, programación lineal (es).Palabras clave:
logistics, logistic operator, linear programming (en).Descargas
Referencias
Airpharm Logistics Care. (10 de agosto de 2019). ¿Qué es un operador logístico? ¿Qué funciones tiene? https://www.airpharmlogistics.com/que-es-operador-logistico/
Ballou, Ronald H. (2013). Logística. Administración de la cadena de suministro. Pearson.
Carranza, O. et al. (2009). Logística, mejores prácticas en Latinoamérica. 2.ª ed. Editorial Thomson.
Chopra, S. y Meindl, P. (2013). Administración de la cadena de suministro: estrategia, planeación y operación. Editorial Pearson.
Christopher, M. (2010). Logistics and supply chain management. Pearson Education Inc.
Escalante Gómez, J. E. y Uribe Marín, R. (2014). Costos logísticos. Ecoe Ediciones.
García Cortes, J. G. (2019). Caracterización de una red de distribución para un operador logístico en Bogotá [Tesis de grado]. Repositorio de la Universidad Católica de Colombia. https://repository.ucatolica.edu.co/handle/10983/29
Guadarrama González, P. (2017). Dirección y asesoría de la investigación científica. Magisterio Editorial.
Guerrero Salas, H. (2010). Diseño de un modelo teórico de estructuración de redes vinculadas en logística para la distribución física [Tesis de maestría]. Repositorio de la Universidad Distrital Francisco José de Caldas. https://repository.udistrital.edu.co/handle/11349/3750
Guerrero Salas, H. (2017a). Inventarios, manejo y control. 2.ª ed. Ecoe Ediciones.
Guerrero Salas, H. (2017b). Programación lineal aplicada. 2.ª ed. Ecoe Ediciones.
Leiva Infante, E. y Velasco Cabrera, C. A. (2012). Propuesta de diseño de operación logística para una empresa que comercializa artículos para la línea hogar [Tesis de maestría]. Repositorio de la Universidad Icesi. https://repository.icesi.edu.co/biblioteca_digital/simple-search?filterquery=Trabajos+de+grado&filtername=subject&filtertype=equals
Pierre, D. (2016). Logística internacional. Administración de operaciones de comercio internacional. Cengage Learning.
Ragas Prat, I. (2019). Logística urbana: manual para operadores logísticos y administraciones públicas. Alpha Editorial S.A.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 20 de enero de 2022; Aceptado: 4 de julio de 2022
Resumen
Contexto:
La ubicación de los operadores logísticos se puede convertir en una ventaja competitiva para las organizaciones, ya que garantiza su respuesta efectiva frente a los cambios de la sociedad.
Método:
En este trabajo se presenta la formulación del modelo de programación lineal para la ubicación de un operador logístico en cada uno de los periodos de un horizonte de planeación.
Resultados:
Se garantiza el cumplimiento de la ubicación del operador logístico con sus respectivas restricciones a un costo mínimo; además, se conservan las funciones claras de programación dinámica en todo el horizonte de planeación.
Conclusiones:
La programación lineal es una técnica de investigación de operaciones muy utilizada en todos los campos empresariales. Esta aplicación es utilizada para garantizar la ubicación del operador logístico de un periodo a otro, con la causación única de los costos necesarios que garantizar un total mínimo para este; lo cual se puede visualizar en los datos específicos utilizados.
Palabras clave:
logística, operador logístico, programación lineal.Abstract
Context:
The location of logistics operators can become a competitive advantage for organizations as it guarantees their effective response to changes in society.
Method:
This paper presents the formulation of the linear programming model for the location of a logistics operator in each of the periods of a planning horizon.
Results:
Compliance with the location of the logistics operator with its respective restrictions at a minimum cost is guaranteed; in addition, to preserve the clear functions of dynamic programming throughout the planning horizon.
Conclusions:
Linear programming is an operations research technique widely used in all business fields; for which in this application it is used to guarantee the location of the logistics operator from one period to another with the sole causation of the necessary costs that guarantee a minimum total for it. This can be visualized based on the specific data used.
Keywords:
logistics, logistic operator, linear programming.Introducción
En la actualidad, uno de los factores de competitividad para las organizaciones es el desarrollo e integración de las redes de distribución que permiten satisfacer las necesidades de los clientes, en cuanto a cantidad, tiempo y lugar. Entre los aspectos que se requiere controlar está la distribución física, definida como el conjunto de operaciones necesarias para el desplazamiento de los productos que están organizados en diferentes cargas unitarias, desde el lugar de producción nacional o internacional, hasta el local del distribuidor en el país de destino, bajo el concepto de óptima calidad, costo razonable y entrega justo a tiempo (Chopra y Meindl, 2013). En este proceso, se requiere definir una investigación que debe estar determinada por factores de utilidad social, científica o cultural (Guadarrama, 2017); que para efectos de este proyecto se refiere a la utilidad científica de aplicación del modelo propuesto en empresas de producción, con el fin de reducir el costo total de la distribución física de los materiales y productos a través de la red logística.
Entre las ventajas de la formulación del modelo matemático están que no se requiere un gran volumen de información para poder establecer una solución óptima, y que permite evaluar el comportamiento en diferentes periodos de tiempo para establecer diferentes tendencias que tenga el mercado, lo que la convierte en una herramienta que contribuye en la toma de decisiones de las organizaciones.
Además, considerando la realidad de la información empresarial y más exactamente de los modelos generalizados, hay que enfatizar en que un modelo debe estar bien estructurado, a pesar de que hay información que difícilmente no va a estar bien determinada, pues es muy compleja su cuantificación (por ejemplo, un pronóstico exacto de demanda de un artículo en particular, la determinación de un costo de mantenimiento, costos causados por incumplimiento o niveles de satisfacción del cliente). En este sentido, se puede afirmar que el modelo planteado no debe ser estrictamente rígido, sino que debe considerar su flexibilidad para ejecutar análisis de sensibilidad de los parámetros involucrados, dado que los datos son dinámicos a través del tiempo.
También, hay que considerar los aspectos fortuitos que se puedan presentar y que son muy difíciles de establecer dentro del modelo; pero que las empresas deben tener la capacidad de respuesta rápida a fin de solucionar estos problemas. Dentro de estos aspectos casuales que se presentan se puede mencionar un cierre de una carretera, cierre o apertura de importaciones que permitan mejorar los precios de materias primas o componentes, entre otros. Estos aspectos han sido estudiados por varios autores, cuyas tendencias se esbozan a continuación.
Gerandin García (2019) caracteriza una red de distribución para un operador logístico en Bogotá (Colombia), a partir de la definición de la configuración óptima de una red de entrega, que busca garantizar el cumplimiento de los objetivos de la compañía a través del mejoramiento del servicio y del costo logístico, teniendo en cuenta el tipo de producto, la forma de entrega, el tipo de sector y de industria a la que pertenece. Se toma como referencia un operador logístico que distribuye artículos de telefonía móvil.
Se establece que, para la selección del diseño de una red de entrega, se deben considerar diferentes características del producto, los eslabones, el precio, entre otros. Es importante establecer los indicadores de desempeño para evaluar el funcionamiento del proceso logístico (García, 2019).
Leiva y Velasco (2012) proponen el diseño de una operación logística para una empresa que comercializa artículos para la línea hogar, acordes a las necesidades de los clientes, en las diferentes actividades (recepción, almacenamiento, alistamiento y despacho) que algunas organizaciones no tienen la capacidad de ofrecer en la ciudad de Santiago de Cali (Colombia).
Los autores hacen una revisión de las necesidades regionales y particulares, donde se establece que no hay la capacidad operativa frente al crecimiento del mercado. Se resaltan como factores de éxito la comunicación y la gestión entre el centro de distribución y las empresas.
Como se puede observar, la ubicación de los operadores logísticos se puede convertir en una ventaja competitiva para las organizaciones, ya que garantiza su respuesta efectiva frente a los cambios de la sociedad.
Estructura teórica
El desarrollo del marco teórico del presente trabajo inicia con el avance de la logística a través de los años, la cual surge en sus inicios para acompañar a las decisiones operativas de los altos mandos militares, primordialmente en Inglaterra, en la década de 1940 (Carranza, 2009). Allí, se realizan sus primeras aplicaciones, las cuales están ligadas estrechamente a la investigación de operaciones; y su estrategia vital consistía en evitar ataques de los enemigos. A partir de allí empezó a perfeccionarse con la conformación de equipos multidisciplinares. Luego, se hace un pequeño barrido con las generalidades de la programación lineal, tema fundamental en el modelo propuesto en el presente documento.
Logística
En las últimas dos décadas, el escenario de la logística ha cambiado con rapidez. Han surgido nuevas técnicas y pensamientos diferenciales que han sido aplicados con éxito por algunas empresas líderes de sectores. Los argumentos presentados inicialmente al respecto se orientaban a que era poco lo que los directivos de las empresas conocían sobre las oportunidades de éxito que existían para alcanzar grandes utilidades, mediante la aplicación de la logística.
Aunque, el avance y aplicación de la logística en los últimos años ha sido enorme, aún hace falta mucho en el medio colombiano, ya que falta sagacidad y emprendimiento por parte de algunos directivos de empresas. Esta área permite alcanzar resultados gerenciales de gran magnitud; pero, desafortunadamente para muchos es un territorio inexplorado.
Es importante tener en cuenta que muchas empresas (entre ellas, pymes) no han logrado integrar los procesos logísticos, sin embargo, para otras se ha convertido en un pilar para su desarrollo y crecimiento (Christopher, 2010).
Un aspecto esencial para el éxito competitivo de las empresas es el dominio de la logística, debido al acortamiento del ciclo de vida de los productos, cadenas de distribución cambiantes y tecnologías nuevas. Por tanto, el reto de la administración es atender las demandas que entran en conflicto en cada sistema y decidir si lo mejor es hacer el sistema más eficiente, equilibrarlo o rediseñarlo para un mejor funcionamiento.
Para una gran cantidad de gerentes, la logística está siendo considerada solo como el proceso desde cuando el producto sale de la firma, hasta cuando llega al consumidor final. En este enfoque se subestiman los costos de traslado (involucrados en el modelo de este proyecto) y almacenaje de productos semielaborados; además, de ignorar los gastos necesarios para la planeación o para operar sistemas de cómputo. Adicionalmente, se esconden las causas de entregas tardías o defectuosas, inventarios de productos terminados elevados y el hecho de que la transportación se encarece.
Todo lo expuesto, lleva a no tener en cuenta problemas de estructura como: una cantidad de almacenes mal surtidos y demoras en las entregas a los clientes.
Por ello, se debe considerar la logística como un sistema para el diseño, producción y entregas a los clientes; además de las actividades relacionadas con el movimiento de materiales, información y sistemas de control. Esto se debe realizar desde la obtención de la materia prima (proveedores) hasta la entrega final del producto al cliente. Existen dos formas de realizar el proceso: la logística convencional o tradicional, que se hace por la propia entidad; y el operador logístico, que se define como “la empresa que diseña, gestiona y controla los procesos de la cadena de suministro de otra empresa” (Airpharm Logistics Care, 2019).
Se puede entonces plantear que la logística es una actividad integral, a partir de la cual se deben tomar decisiones importantes como: producir de forma continua o por lotes, realizar una operación manual o automatizada de los almacenes, y ubicar almacenes centralizados o descentralizados. Con la aplicación de esto se obtiene un nivel de servicio alto y efectivo, el cual debe tener un costo adecuado o deseado.
Vale la pena anotar que la evaluación logística se debe realizar estratégicamente mediante la aplicación de todo tipo de métodos para la consecución de los objetivos. Debido a la complejidad, existen varios disponibles, cada uno de ellos apropiado para diferentes aspectos de la planeación estratégica de la logística.
Dentro de los aspectos primordiales a evaluar dentro de un proceso de planeación logística estratégica se pueden enumerar los siguientes:
-
Apalancamiento de la logística. Tiene que ver con la efectividad de una empresa para distinguirse en el mercado.
-
Evaluación del impacto de los planes estratégicos. Se relaciona con las mediciones de las consecuencias de planes logísticos alternativos.
Entre dichos métodos, se pueden mencionar el análisis de costos logísticos, modelos para toma de decisiones, instrumentos tradicionales de estrategias de manufactura, entre otros. Estos son útiles para medir el impacto de planes y soluciones propuestas, así como para determinar formas más eficientes de apoyo a la estrategia corporativa. Con ellos se pueden analizar problemas estratégicos como el número y ubicación de plantas, cantidad y ubicación de almacenes, patrones de suministro (cantidades de productos a fabricarse), métodos de transporte y niveles de inventario.
Los enfoques básicos de los modelos para toma de decisiones tienen que ver esencialmente con dos: simulación y modelos de optimización. Entre estos últimos se encuentra la programación lineal, asunto de aplicación en el presente proyecto.
La optimización es una aplicación del flujo, así como la ubicación de instalaciones de producción y operadores logísticos para una cadena de abastecimiento con todas sus restricciones y requerimientos. Para cada caso se modelan los costos de transporte, inventario y manejo. “La optimización es necesaria cuando hay un número significativo de restricciones o una red muy grande con interacciones complejas” (Christopher, 2010).
Este tipo de modelos permite adelantar análisis de sensibilidad para evaluar el impacto de posibles cambios en la información de los parámetros, sobre la estructura total del sistema.
Además, los costos de embarque, para las empresas en la actualidad, representan una proporción tan alta del costo total que las manufacturas, almacenes y otras instalaciones se ubican con un objetivo fundamental: reducción de costos.
Desarrollo de las redes logísticas
A comienzos de la década de 1960 (Carranza et al., 2009) surge la asociación nacional de logística y distribución física estadounidense, en donde se marca la adquisición de la importancia de la logística para las empresas. En 1986, esta asociación cambia el nombre a Council of Logistics Management, la cual implementa las definiciones más completas conocidas en la disciplina de la logística.
En la evolución de la logística, se evidencian cuatro eventos asociados al desarrollo y a los aportes a las organizaciones (Pierre, 2016).
En el primer evento, denominado fragmentación, en 1960, se desarrollaba el estudio con base en el pronóstico de la demanda, compras, planeación de requerimientos, planeación de la producción, inventario de manufactura, almacenamiento, manejo de materiales, empacado industrial, inventario de artículos terminados, planeación de la distribución, proceso de órdenes, transportación, servicio al cliente, planeación estratégica, tecnología de información, comercialización y ventas. A esta etapa se le denominó fragmentación debido al análisis independiente realizado a cada uno de los factores mencionados; lo cual redundaba en análisis aislados para cada factor.
Un segundo evento viene hacia el año 1980, en lo que se llamó integración envolvente, donde se desarrollaron los conceptos de administración de materiales y distribución física. En la administración de materiales se involucró pronóstico de la demanda, compras, planeación de requerimientos, planeación de la producción, inventario de manufactura, almacenamiento, manejo de materiales y empacado industrial; mientras que en distribución física se agrupó almacenamiento, manejo de materiales, empacado industrial, inventario de artículos terminados, planeación de la distribución, proceso de órdenes, transportación y servicio al cliente.
Un tercer evento se desarrolla en 1990, con la etapa denominada integración total, y bajo el nombre de logística, donde se incluye administración de materiales y distribución física.
Finalmente, en el cuarto evento, hacia el año 2000, emerge lo que hoy se conoce como administración de la cadena de abastecimientos, en donde se integra la logística con la planeación estratégica, tecnologías de información, comercialización y ventas.
Con base en los avances de la logística, no se puede dejar por fuera del inicio de este documento lo que hoy se conoce como logística. Según la definición promulgada por el Council of Logistics Management (Ballou, 2013) y el Concejo de Administración Logística (CLM),
[...] la logística es el proceso de planear, implementar y controlar el flujo y almacenamiento eficiente y a un costo efectivo de las materias primas, inventarios en proceso, de producto terminado e información relacionada, desde los puntos de origen hasta los de consumo; con el propósito de satisfacer las necesidades de los clientes. (p. 4)
Errores de la logística
A través del desarrollo y aplicación de la logística, se pretende evitar que se cometan errores, ya que el tiempo es oro para la logística. Dentro de los problemas más frecuentes en este aspecto se pueden mencionar los siguientes: espacio desaprovechado, falta de organización de mercancía, errores en el picking, falta de trazabalidad, inventario desactualizado, errores en la manipulación de la mercancía, demoras en las expediciones, señalización deficiente del almacén, kpi logísticos e incorrectos, integración con otros departamentos (ERP).
Para minimizar o evitar estos errores y generar una plataforma competitiva, se debe definir claramente los objetivos y las metas para establecer tiempos y flujos de las redes de distribución; además, tener conocimiento de las normas y programas de capacitación y unas tecnologías de información coherentes con la organización.
Algunas de las preguntas que debe contestar una buena gestión logística son:
-
¿Cuándo, dónde y cómo ampliar las instalaciones: almacenes, equipos, plantas, etc.?
-
¿Conviene centralizar o descentralizar el desarrollo de las operaciones?
-
¿Cuál es la combinación de productos y clientes que maximizan la utilidad?
-
¿Cuál es el escenario óptimo para maximizar el flujo de efectivo?
-
¿Cuál es el plan óptimo de abastecimiento, fabricación y distribución?
-
¿Cuántos centros de distribución se requieren?
-
¿En dónde deben estar ubicarlos los centros de distribución y plantas de producción?
-
¿Cuánto costará incrementar los niveles de servicio al cliente?
-
¿Para qué rutas tengo que contratar el transporte?
-
¿Cuánto inventario se necesita para abastecer la red?
Las respuestas a los anteriores interrogantes no obedecen a otra cosa que a la solución u optimización de los sistemas logísticos de las empresas, ya que durante todo el proceso debe existir un control de costos totales de la actividad de la empresa entre los cuales se pueden nombrar los siguientes (Escalante y Uribe, 2014): el costo del inventario, que incluye el costo del capital invertido y su costo financiero (además de la obsolescencia, roturas y seguros); costo de almacenaje o mantenimiento (Guerrero, 2017a); costos de preparación de pedidos, costos por transporte; costo de envase y embalaje, y los generados por todo el sistema de distribución o entrega al consumidor final.
Además, hay que tener en cuenta que en muchas empresas se trabaja con costos totales por naturaleza, mientras que el operador logístico trabaja con costos unitarios por operaciones.
Estructura de un canal logístico
Un operador logístico se define como
[...] aquella empresa que diseña, organiza, gestiona y controla los procesos de una o varias fases de la cadena de suministro como lo es el aprovisionamiento, transporte, almacenaje, distribución, e incluso algunas actividades del proceso productivo, utilizando para ello infraestructuras físicas, tecnología y sistemas de información, propios o ajenos. El operador logístico responde ante su cliente de los servicios acordados y es un interlocutor directo. (Ragas, 2019, p. 12).
Entonces, el canal logístico se debe analizar como una red integrada por nodos o eventos específicos que se interceptan entre sí, en donde cada evento viene a representar las áreas específicas de la empresa como almacenes, plantas de producción, puntos de venta; y las conexiones entre ellas que representan transportes a través de los cuales se genera el flujo de los materiales o productos. Además, integrados a esta red, se deben relacionar todos los entes externos que corresponden a los clientes y puntos de entrega de productos.
Según la figura 1, después de recibir las materias primas y materiales auxiliares, el producto es manufacturado en diferentes fábricas o plantas de producción, y enviado en medios de transporte a bodegas o almacenes intermedios (operadores logísticos); desde allí, y a través de diferentes medios de transporte, es trasladado a los consumidores o puntos de venta. Dentro de esta estructura se encuentra implícita la red del flujo de información referente a demandas, pedidos a proveedores, estadísticas, niveles de inventario, plazos de entrega y contabilización entre otros aspectos fundamentales.
Figura 1: Estructura de un canal logístico
Las dos redes deben estar interrelacionadas y de su adecuada comunicación depende el éxito del sistema logístico. Otro aspecto fundamental a considerar es la estructura de costos que se genera a través de toda la red, iniciando por los costos derivados de la administración de la demanda, continuando por los costos causados por el aprovisionamiento y seguidos por los costos de producción en planta, costos de transporte, costos de los inventarios y costos de distribución. (Guerrero, 2010, p. 23)
Cuando se realiza una correcta gestión en la red logística, se pueden obtener, entre muchos otros, los siguientes beneficios:
-
Disminución de los costos de distribución, tanto de las plantas de producción a los almacenes temporales, como de estos a los puntos de venta.
-
Minimización de costos por manejo de inventario, generados por una gestión adecuada de inventarios y la aplicación de modelos de optimización.
-
Niveles adecuados de producto terminado en los puntos de venta.
-
Cálculo adecuado del número de distribuidores en toda la red logística.
-
Solicitud y entrega de productos, materiales y materias primas en las cantidades necesarias, en el momento adecuado y en el punto de la cadena indicado.
Programación lineal
La programación lineal es una de las muchas técnicas de optimización de la investigación de operaciones. En esta, se realiza la distribución de una cantidad limitada de recursos entre la fabricación de los productos de una empresa. Obviamente, se persigue un máximo de utilidad o ingreso, o un mínimo de costos. Su estructura general tiene una función objetivo y las restricciones de recursos que tenga la empresa.
Modelo general de programación lineal
El modelo general de programación lineal supone la disponibilidad limitada de m recursos para la fabricación de n productos (Guerrero, 2017b).
Donde en forma generalizada se define lo siguiente:
bi = cantidad disponible del recurso i (i = 1, 2, 3, ..., m).
cj = costo o precio unitario del producto o actividad j (j = 1, 2, 3, ..., n).
Xj = cantidad a fabricar del articulo j (j = 1, 2, 3, ..., n).
aij = cantidad de recurso i (i = 1, 2, 3, ..., m) necesario para fabricar una unidad del artículo j (j = 1, 2, 3, ..., n).
Con base en lo anterior se obtiene el modelo generalizado, que en su forma estándar se expresa según las ecuaciones (1), (2) y (3):
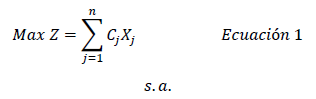
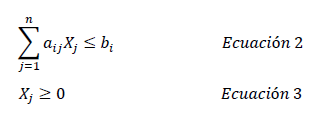
Componentes del modelo general
Los componentes del modelo general de programación lineal se describen a continuación:
- Matriz A: contiene todos los elementos de asignación unitaria de recursos.
- Vector X: contiene todas las variables del problema y está definido como vector columna.
- Vector b: en este se involucran todas las disponibilidades de recursos o términos independientes. Está definido como un vector columna.
- Vector C: en este vector fila se involucran todos los coeficientes de costo, utilidad, ingreso o precio, según sea el caso
- Vector 0: el vector columna cero contiene tantos ceros como variables involucre el problema, y garantiza las restricciones de no negatividad.
Desarrollo del modelo
El modelo que se plantea en el siguiente documento permite localizar operadores logísticos en un horizonte de planeación especifico, donde se establece un modelo generalizado del problema de localización dinámica de instalaciones que permite tomar decisiones óptimas en cuanto a la ubicación de operadores logísticos, garantizando la maximización de las utilidades y minimización de los costos de traslado.
Estructura general del modelo
El modelo generalizado establece la disponibilidad de m posibles alternativas de localización, para ubicar un operador logístico en una de ellas, en un horizonte de planeación de n periodos. La solución que arroja el modelo considera localizar de forma óptima un operador logístico en cada periodo del horizonte de planeación, mediante la utilización de la programación lineal; de tal forma que se consideren costos de traslado del operador logístico de un periodo al siguiente, para así obtener el máximo de utilidad en todo el horizonte de planeación.
En este problema se consideran los aspectos de recursividad a que obliga el algoritmo, ya que no se puede considerar la localización del operador logístico en una determinada ubicación sin tener en cuenta en qué sitio se encontraba en el periodo inmediatamente anterior.
El modelo realiza la ubicación óptima de un operador logístico en cada periodo del horizonte de planeación. Para ello se cuenta con m posibles sitios o ubicaciones y n posibles periodos en el horizonte de planeación.
Subíndices del modelo
Para el modelo se definen los siguientes subíndices:
i = subíndice que indica el posible sitio donde se ubicará el operador logístico. (i = 1, 2, ..., m).
j = subíndice que indica el periodo del horizonte de planeación en que se realizará la ubicación del operador logístico (j = 2, 3, ..., n).
k = subíndice que denota el sitio donde se ubicó el operador logístico en el periodo j-1. (periodo inmediatamente anterior) (k = 1, 2, ..., m).
Variables del modelo
Las variables involucradas en el modelo son las siguientes:
X i1 = variable que indica ubicar el operador logístico en el sitio i (i = 1, 2, ..., m) para el período 1 del horizonte de planeación.
X ijk = variable que indica ubicar el operador logístico en el sitio i (i = 1, 2, ..., m), para el período j (j = 2, 3, ..., n); habiendo ubicado en el período anterior (j-1) el operador logístico en el sitio k (k = 1, 2, ..., m).
Y ijk = variable que permite disparar ó no el costo de traslado de ubicar el operador logístico en el sitio i (i = 1, 2, ..., m), para el período j (j = 2, 3, ..., n); habiendo ubicado en el período anterior (j-1) el operador logístico en el sitio k (k = 1, 2, ..., m). Este costo de traslado se dispara si i≠k y no se dispara si i=k.
Y i1 = variable que dispara el costo de traslado por ubicar el operador logístico en el sitio i (i = 1, 2, ..., m), para el periodo 1.
Parámetros del modelo
Los parámetros que se involucran en el modelo son:
C i1 = utilidad bruta generada por ubicar el operador logístico en el sitio i (i = 1, 2, ..., m), para el período 1 del horizonte de planeación.
C ijk = utilidad bruta generada por ubicar el operador logístico en el sitio i (i = 1, 2, ..., m), para el período j (j = 2, 3, ..., n); habiendo ubicado en el período anterior (j-1), el operador logístico en el sitio k (k = 1, 2, ..., m).
F ijk = costo de traslado generado por ubicar el operador logístico en el sitio i (i = 1, 2, ..., m), para el período j (j = 2, 3, ..., n); habiendo ubicado en el período anterior (j-1) el operador logístico en el sitio k (k = 1, 2, ..., m).
F i1 = costo de traslado por ubicar el operador logístico en el sitio i (i = 1, 2, ..., m), para el periodo 1.
Modelo general
Función objetivo
La función objetivo del modelo tiene que ver con maximizar la utilidad neta generada por las ubicaciones del operador logístico a través de todo el horizonte de planeación, ya que se dispone de una utilidad bruta por ubicar en los diferentes sitios posibles y los costos de traslado de un periodo a otro, en el evento en que se causan. La función objetivo se establece mediante la ecuación (4):
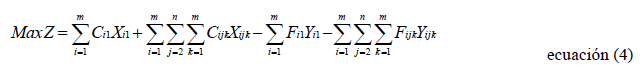
Restricciones del modelo
Para garantizar una solución óptima del modelo se deben considerar los siguientes tipos de restricciones:
Restricciones que garantizan una sola ubicación en cada período. Entre las que hay que considerar las siguientes:

Garantiza una ubicación para el periodo 1:

Garantiza una ubicación para los periodos j = 2, 3, 4, ..., n.
Restricciones que garantizan la recursividad.
Este tipo de restricciones garantiza la causación o no del costo de traslado y, además, permite tomar una ruta correcta; esto es, que asignado el operador i en el periodo j, para el periodo siguiente tome en cuenta esa ubicación. Por ejemplo, si la ubicación en el periodo 1 se realiza en el sitio 3, para ubicar en el periodo 2 no debe tener en cuenta ubicaciones diferentes al sitio 3 en el periodo 1. Dentro de estas restricciones hay que tener en cuenta las siguientes:
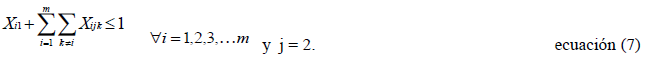
Garantiza la recursividad del periodo 1 con el 2.
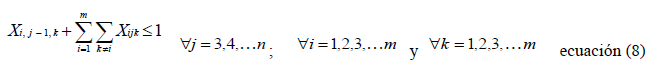
Garantizan la recursividad del periodo 2 con el 3, del periodo 3 con el 4, del periodo 4 con el 5, hasta el periodo n-1 con el n.
Restricciones que disparan o no el costo de traslado de un periodo a otro.

Dispara el costo de ubicación en el periodo 1.
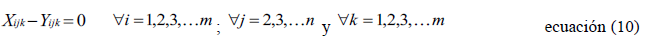
Dispara o no el costo de traslado de las ubicaciones en los periodos 2, 3, 4, ..., n-1 y n del horizonte de planeación.
Restricciones para variables binarias:
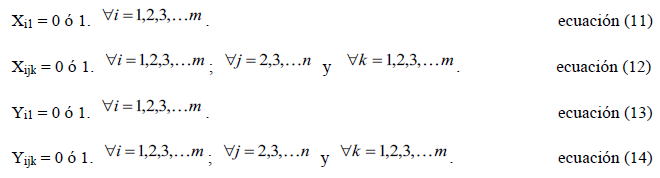
Modelo específico
Condiciones particulares
Supóngase que se tienen 4 posibles ubicaciones para realizar una ubicación en los próximos 4 años. El modelo específico para m= 4 sitios o posibles ubicaciones y n= 4 años queda de la siguiente manera (utilizando las ecuaciones 4 a 14):
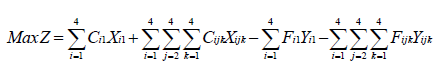 S.A.
S.A.
Restricciones que garantizan una sola ubicación en cada año.
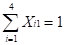 . Garantiza una ubicación para el año 1.
. Garantiza una ubicación para el año 1.
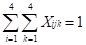 ∀j = 2,3y4. Garantiza una ubicación para los años 2, 3 y 4.
∀j = 2,3y4. Garantiza una ubicación para los años 2, 3 y 4.
Restricciones que garantizan la recursividad.
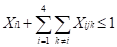 ∀i = 1,2,3y4 y j = 2. Garantiza la recursividad del año 1 con el año 2.
∀i = 1,2,3y4 y j = 2. Garantiza la recursividad del año 1 con el año 2.
 ∀j = 3y4; ∀i = 1,2,3y4 y ∀k = 1,2,3y4. Garantizan la recursividad del año 2 con el 3, y del año 3 con el 4.
∀j = 3y4; ∀i = 1,2,3y4 y ∀k = 1,2,3y4. Garantizan la recursividad del año 2 con el 3, y del año 3 con el 4.
Restricciones que disparan o no el costo de traslado de un año a otro.
X i1 - Y i1 =0 ∀i = 1,2,3y4. Dispara el costo de ubicación en el periodo 1.
X ijk - Y ijk =0 ∀i = 1,2,3y4; ∀j = 2,3y4 y ∀k = 1,2,3y4 . Dispara o no el costo de traslado de las ubicaciones en los años 2, 3 y 4 del horizonte de planeación.
Restricciones para variables binarias.
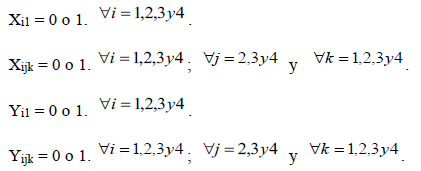
Resolviendo todas las sumatorias el modelo respectivo para m= 4 y n= 4 queda como aparece a continuación:
Max Z= C11X11 +C21X21 +C31X31 +C41X41 +C121X121 +C122X122 +C123X123 +C124X124 +C131X131 +C132X132 +C133X133 +C134X134 +C141X141 +C142X142 +C143X143 +C144X144 +C221X221 +C222X222 +C223X223 +C224X224 +C231X231 +C232X232 +C233X233 +C234X234 +C241X241 +C242X242 +C243X243 +C244X244 +C321X321 +C322X322 +C323X323 +C324X324 +C331X331 +C332X332 +C333X333 +C334X334 +C341X341 +C342X342 +C343X343 +C344X344 +C421X421 +C422X422 +C423X423 +C424X424 +C431X431 +C432X432 +C433X433 +C434X434 +C441X441 +C442X442 +C443X443 +C444X444 -F11Y11 -F21Y21 -F31Y31 -F41Y41 -F121Y121 -F122Y122 -F123Y123 -F124Y124 -F131Y131 -F132Y132 -F133Y133 -F134Y134 -F141Y141 -F142Y142 -F143Y143 -F144Y144 -F221Y221 -F222Y222 -F223Y223 -F224Y224 -F231Y231 -F232Y232 -F233Y233 -F234Y234 -F241Y241 -F242Y242 -F243Y243 -F244Y244 -F321Y321 -F322Y322 -F323Y323 -F324Y324 -F331Y331 -F332Y332 -F333Y333 -F334Y334 -F341Y341 -F342Y342 -F343Y343 -F344Y344 -F421Y421 -F422Y422 -F423Y423 -F424Y424 -F431Y431 -F432Y432 -F433Y433 -F434Y434 -F441Y441 -F442Y442 -F443Y443 -F444Y444.
S.A.
X11 +X21 +X31 +X41 = 1.
X121 +X122 +X123 +X124 +X221 +X222 +X223 +X224 +X321 +X322 +X323 +X324 +X421 +X422 +X423 +X424 = 1
X131 +X132 +X133 +X134 +X231 +X232 +X233 +X234 +X331 +X332 +X333 +X334 +X431 +X432 +X433 +X434 = 1.
X141 +X142 +X143 +X144 +X241 +X242 +X243 +X244 +X341 +X342 +X343 +X344 +X441 +X442 +X443 +X444 = 1.
X11 +X122 +X123 +X124 +X222 +X223 +X224 +X322 +X323 +X324 +X422 +X423 +X424 ≤ 1.
X21 +X121 +X123 +X124 +X221 +X223 +X224 +X321 +X323 +X324 +X421 +X423 +X424 ≤ 1.
X31 +X121 +X122 +X124 +X221 +X222 +X224 +X321 +X322 +X324 +X421 +X422 +X424 ≤ 1.
X41 +X121 +X122 +X123 +X221 +X222 +X223 +X321 +X322 +X323 +X421 +X422 +X423 ≤ 1.
X121 +X132 +X133 +X134 +X232 +X233 +X234 +X332 +X333 +X334 +X432 +X433 +X434 ≤ 1.
X122 +X132 +X133 +X134 +X232 +X233 +X234 +X332 +X333 +X334 +X432 +X433 +X434 ≤ 1.
X123 +X132 +X133 +X134 +X232 +X233 +X234 +X332 +X333 +X334 +X432 +X433 +X434 ≤ 1.
X124 +X132 +X133 +X134 +X232 +X233 +X234 +X332 +X333 +X334 +X432 +X433 +X434 ≤ 1.
X221 +X131 +X133 +X134 +X231 +X233 +X234 +X331 +X333 +X334 +X431 +X433 +X434 ≤ 1.
X222 +X131 +X133 +X134 +X231 +X233 +X234 +X331 +X333 +X334 +X431 +X433 +X434 ≤ 1.
X223 +X131 +X133 +X134 +X231 +X233 +X234 +X331 +X333 +X334 +X431 +X433 +X434 ≤ 1.
X224 +X131 +X133 +X134 +X231 +X233 +X234 +X331 +X333 +X334 +X431 +X433 +X434 ≤ 1.
X321 +X131 +X132 +X134 +X231 +X232 +X234 +X331 +X332 +X334 +X431 +X432 +X434 ≤ 1.
X322 +X131 +X132 +X134 +X231 +X232 +X234 +X331 +X332 +X334 +X431 +X432 +X434 ≤ 1.
X323 +X131 +X132 +X134 +X231 +X232 +X234 +X331 +X332 +X334 +X431 +X432 +X434 ≤ 1.
X324 +X131 +X132 +X134 +X231 +X232 +X234 +X331 +X332 +X334 +X431 +X432 +X434 ≤ 1.
X421 +X131 +X132 +X133 +X231 +X232 +X233 +X331 +X332 +X333 +X431 +X432 +X433 ≤ 1.
X422 +X131 +X132 +X133 +X231 +X232 +X233 +X331 +X332 +X333 +X431 +X432 +X433 ≤ 1.
X423 +X131 +X132 +X133 +X231 +X232 +X233 +X331 +X332 +X333 +X431 +X432 +X433 ≤ 1.
X424 +X131 +X132 +X133 +X231 +X232 +X233 +X331 +X332 +X333 +X431 +X432 +X433 ≤ 1.
X131 +X142 +X143 +X144 +X242 +X243 +X244 +X342 +X343 +X344 +X442 +X443 +X444 ≤ 1.
X132 +X142 +X143 +X144 +X242 +X243 +X244 +X342 +X343 +X344 +X442 +X443 +X444 ≤ 1.
X133 +X142 +X143 +X144 +X242 +X243 +X244 +X342 +X343 +X344 +X442 +X443 +X444 ≤ 1.
X134 +X142 +X143 +X144 +X242 +X243 +X244 +X342 +X343 +X344 +X442 +X443 +X444 ≤ 1.
X231 +X141 +X143 +X144 +X241 +X243 +X244 +X341 +X343 +X344 +X441 +X443 +X444 ≤ 1.
X232 +X141 +X143 +X144 +X241 +X243 +X244 +X341 +X343 +X344 +X441 +X443 +X444 ≤ 1.
X233 +X141 +X143 +X144 +X241 +X243 +X244 +X341 +X343 +X344 +X441 +X443 +X444 ≤ 1.
X234 +X141 +X143 +X144 +X241 +X243 +X244 +X341 +X343 +X344 +X441 +X443 +X444 ≤ 1.
X331 +X141 +X142 +X144 +X241 +X242 +X244 +X341 +X342 +X344 +X441 +X442 +X444 ≤ 1.
X332 +X141 +X142 +X144 +X241 +X242 +X244 +X341 +X342 +X344 +X441 +X442 +X444 ≤ 1.
X333 +X141 +X142 +X144 +X241 +X242 +X244 +X341 +X342 +X344 +X441 +X442 +X444 ≤ 1.
X334 +X141 +X142 +X144 +X241 +X242 +X244 +X341 +X342 +X344 +X441 +X442 +X444 ≤ 1.
X431 +X141 +X142 +X143 +X241 +X242 +X243 +X341 +X342 +X343 +X441 +X442 +X443 ≤ 1.
X432 +X141 +X142 +X143 +X241 +X242 +X243 +X341 +X342 +X343 +X441 +X442 +X443 ≤ 1.
X433 +X141 +X142 +X143 +X241 +X242 +X243 +X341 +X342 +X343 +X441 +X442 +X443 ≤ 1.
X434 +X141 +X142 +X143 +X241 +X242 +X243 +X341 +X342 +X343 +X441 +X442 +X443 ≤ 1.
X11 - Y11 = 0. X21 - Y21 = 0. X31 - Y31 = 0. X41 - Y41 = 0. X121 - Y121 = 0. X122 - Y122 = 0.
X123 - Y123 = 0. X124 - Y124 = 0. X131 - Y131 = 0. X132 - Y132 = 0. X133 - Y133 = 0.
X134 - Y134 = 0. X141 - Y141 = 0. X142 - Y142 = 0. X143 - Y143 = 0. X144 - Y144 = 0.
X221 - Y221 = 0. X222 - Y222 = 0. X223 - Y223 = 0. X224 - Y224 = 0. X231 - Y231 = 0.
X232 - Y232 = 0. X233 - Y233 = 0. X234 - Y234 = 0. X241 - Y241 = 0. X242 - Y242 = 0.
X243 - Y243 = 0. X244 - Y244 = 0. X321 - Y321 = 0. X322 - Y322 = 0. X323 - Y323 = 0.
X324 - Y324 = 0. X331 - Y331 = 0. X332 - Y332 = 0. X333 - Y333 = 0. X334 - Y334 = 0.
X341 - Y341 = 0. X342 - Y342 = 0. X343 - Y343 = 0. X344 - Y344 = 0. X421 - Y421 = 0.
X422 - Y422 = 0. X423 - Y423 = 0. X424 - Y424 = 0. X431 - Y431 = 0. X432 - Y432 = 0.
X433 - Y433 = 0. X434 - Y434 = 0. X441 - Y441 = 0. X442 - Y442 = 0. X443 - Y443 = 0.
X444 - Y444 = 0.
Xi1 = 0 o 1. ∀i = 1,2,3y4.
Xijk = 0 o 1. ∀i = 1,2,3y4; ∀j = 2,3y4 y ∀ik= 1,2,3y4.
Yi1 = 0 o 1. ∀i = 1,2,3y4.
Yijk = 0 o 1. ∀i = 1,2,3y4; ∀j = 2,3y4 y ∀ik= 1,2,3y4.
Supóngase que la información de utilidades brutas para la compañía Sigma, por la ubicación de un operador logístico en las 4 localizaciones posibles (A, B, C y D), en el horizonte de planeación de 4 años, es como se detalla en la tabla 1.
Tabla 1: Utilidades brutas por ubicación del operador logístico
Alternativas de localización
Utilidad proyectada en el horizonte de planeación
Año 1
Año 2
Año 3
Año 4
A
COP 500 000
COP 712 000
COP 900 000
COP 1 200 000
B
COP 525 000
COP 698 000
COP 897 000
COP 1 146 000
C
COP 486 000
COP 702 000
COP 901 000
COP 1 312 000
D
COP 512 000
COP 650 000
COP 917 000
COP 1 300 000
Además, se sabe que el costo de movilización o traslado del operador logístico es de COP 125 000, y que el costo del capital por año se ha avaluado en un 18 %. Con base en estos datos, los costos de traslado del operador logístico de un año a otro, calculados con base en flujos inversos netos en el horizonte de planeación, son los que se presentan en la tabla 2.
Tabla 2: Costos de traslado del operador logístico
Año
Costo del traslado
1
COP 125 000,00
2
COP 105 932,20
3
COP 89 773,05
4
COP 76 078,86
Llevando los datos de utilidad bruta y costos de traslado al modelo, se obtiene el siguiente planteamiento:
Max Z= 500000X11 +525000X21 +486000X31 +512000X41 +712000X121 +712000X122 +712000X123 +712000X124 +900000X131 +900000X132 +900000X133 +900000X134 +1200000X141 +1200000X142 +1200000X143 +1200000X144 +698000X221 +698000X222 +698000X223 +698000X224 +897000X231 +897000X232 +897000X233 +897000X234 +1146000X241 +1146000X242 +1146000X243 +1146000X244 +702000X321 +702000X322 +702000X323 +702000X324 +901000X331 +901000X332 +901000X333 +901000X334 +1312000X341 +1312000X342 +1312000X343 +1312000X344 +650000X421 +650000X422 +650000X423 +650000X424 +917000X431 +917000X432 +917000X433 +917000X434 +1300000X441 +1300000X442 +1300000X443 +1300000X444 -125000Y11 -125000Y21 -125000Y31 -125000Y41 -0Y121 -105932.2Y122 -105932.2Y123 -105932.2Y124 -0Y131 -89773.05Y132 -89773.05Y133 -89773.05Y134 -0Y141 -76078.86Y142 -76078.86Y143 -76078.86Y144 -105932.2Y221 -0Y222 -105932.2Y223 -105932.2Y224 -89773.05Y231 -0Y232 -89773.05Y233 -89773.05Y234 -76078.86Y241 -0Y242 -76078.86Y243 -76078.86Y244 -105932.2Y321 -105932.2Y322 -0Y323 -105932.2Y324 -89773.05Y331 -89773.05Y332 -0Y333 -89773.05Y334 -76078.86Y341 -76078.86Y342 -0Y343 -76078.86Y344 -105932.2Y421 -105932.2Y422 -105932.2Y423 -0Y424 -89773.05Y431 -89773.05Y432 -89773.05Y433 -0Y434 -76078.86Y441 -76078.86Y442 -76078.86Y443 -0Y444.
S.A.
X11 +X21 +X31 +X41 = 1.
X121 +X122 +X123 +X124 +X221 +X222 +X223 +X224 +X321 +X322 +X323 +X324 +X421 +X422 +X423 +X424 = 1
X131 +X132 +X133 +X134 +X231 +X232 +X233 +X234 +X331 +X332 +X333 +X334 +X431 +X432 +X433 +X434 = 1.
X141 +X142 +X143 +X144 +X241 +X242 +X243 +X244 +X341 +X342 +X343 +X344 +X441 +X442 +X443 +X444 = 1.
X11 +X122 +X123 +X124 +X222 +X223 +X224 +X322 +X323 +X324 +X422 +X423 +X424 ≤ 1.
X21 +X121 +X123 +X124 +X221 +X223 +X224 +X321 +X323 +X324 +X421 +X423 +X424 ≤ 1.
X31 +X121 +X122 +X124 +X221 +X222 +X224 +X321 +X322 +X324 +X421 +X422 +X424 ≤ 1.
X41 +X121 +X122 +X123 +X221 +X222 +X223 +X321 +X322 +X323 +X421 +X422 +X423 ≤ 1.
X121 +X132 +X133 +X134 +X232 +X233 +X234 +X332 +X333 +X334 +X432 +X433 +X434 ≤ 1.
X122 +X132 +X133 +X134 +X232 +X233 +X234 +X332 +X333 +X334 +X432 +X433 +X434 ≤ 1.
X123 +X132 +X133 +X134 +X232 +X233 +X234 +X332 +X333 +X334 +X432 +X433 +X434 ≤ 1.
X124 +X132 +X133 +X134 +X232 +X233 +X234 +X332 +X333 +X334 +X432 +X433 +X434 ≤ 1.
X221 +X131 +X133 +X134 +X231 +X233 +X234 +X331 +X333 +X334 +X431 +X433 +X434 ≤ 1.
X222 +X131 +X133 +X134 +X231 +X233 +X234 +X331 +X333 +X334 +X431 +X433 +X434 ≤ 1.
X223 +X131 +X133 +X134 +X231 +X233 +X234 +X331 +X333 +X334 +X431 +X433 +X434 ≤ 1.
X224 +X131 +X133 +X134 +X231 +X233 +X234 +X331 +X333 +X334 +X431 +X433 +X434 ≤ 1.
X321 +X131 +X132 +X134 +X231 +X232 +X234 +X331 +X332 +X334 +X431 +X432 +X434 ≤ 1.
X322 +X131 +X132 +X134 +X231 +X232 +X234 +X331 +X332 +X334 +X431 +X432 +X434 ≤ 1.
X323 +X131 +X132 +X134 +X231 +X232 +X234 +X331 +X332 +X334 +X431 +X432 +X434 ≤ 1.
X324 +X131 +X132 +X134 +X231 +X232 +X234 +X331 +X332 +X334 +X431 +X432 +X434 ≤ 1.
X421 +X131 +X132 +X133 +X231 +X232 +X233 +X331 +X332 +X333 +X431 +X432 +X433 ≤ 1.
X422 +X131 +X132 +X133 +X231 +X232 +X233 +X331 +X332 +X333 +X431 +X432 +X433 ≤ 1.
X423 +X131 +X132 +X133 +X231 +X232 +X233 +X331 +X332 +X333 +X431 +X432 +X433 ≤ 1.
X424 +X131 +X132 +X133 +X231 +X232 +X233 +X331 +X332 +X333 +X431 +X432 +X433 ≤ 1.
X131 +X142 +X143 +X144 +X242 +X243 +X244 +X342 +X343 +X344 +X442 +X443 +X444 ≤ 1.
X132 +X142 +X143 +X144 +X242 +X243 +X244 +X342 +X343 +X344 +X442 +X443 +X444 ≤ 1.
X133 +X142 +X143 +X144 +X242 +X243 +X244 +X342 +X343 +X344 +X442 +X443 +X444 ≤ 1.
X134 +X142 +X143 +X144 +X242 +X243 +X244 +X342 +X343 +X344 +X442 +X443 +X444 ≤ 1.
X231 +X141 +X143 +X144 +X241 +X243 +X244 +X341 +X343 +X344 +X441 +X443 +X444 ≤ 1.
X232 +X141 +X143 +X144 +X241 +X243 +X244 +X341 +X343 +X344 +X441 +X443 +X444 ≤ 1.
X233 +X141 +X143 +X144 +X241 +X243 +X244 +X341 +X343 +X344 +X441 +X443 +X444 ≤ 1.
X234 +X141 +X143 +X144 +X241 +X243 +X244 +X341 +X343 +X344 +X441 +X443 +X444 ≤ 1.
X331 +X141 +X142 +X144 +X241 +X242 +X244 +X341 +X342 +X344 +X441 +X442 +X444 ≤ 1.
X332 +X141 +X142 +X144 +X241 +X242 +X244 +X341 +X342 +X344 +X441 +X442 +X444 ≤ 1.
X333 +X141 +X142 +X144 +X241 +X242 +X244 +X341 +X342 +X344 +X441 +X442 +X444 ≤ 1.
X334 +X141 +X142 +X144 +X241 +X242 +X244 +X341 +X342 +X344 +X441 +X442 +X444 ≤ 1.
X431 +X141 +X142 +X143 +X241 +X242 +X243 +X341 +X342 +X343 +X441 +X442 +X443 ≤ 1.
X432 +X141 +X142 +X143 +X241 +X242 +X243 +X341 +X342 +X343 +X441 +X442 +X443 ≤ 1.
X433 +X141 +X142 +X143 +X241 +X242 +X243 +X341 +X342 +X343 +X441 +X442 +X443 ≤ 1.
X434 +X141 +X142 +X143 +X241 +X242 +X243 +X341 +X342 +X343 +X441 +X442 +X443 ≤ 1.
X11 - Y11 = 0. X21 - Y21 = 0. X31 - Y31 = 0. X41 - Y41 = 0. X121 - Y121 = 0.
X122 - Y122 = 0. X123 - Y123 = 0. X124 - Y124 = 0. X131 - Y131 = 0. X132 - Y132 = 0.
X133 - Y133 = 0. X134 - Y134 = 0. X141 - Y141 = 0. X142 - Y142 = 0. X143 - Y143 = 0.
X144 - Y144 = 0. X221 - Y221 = 0. X222 - Y222 = 0. X223 - Y223 = 0. X224 - Y224 = 0.
X231 - Y231 = 0. X232 - Y232 = 0. X233 - Y233 = 0. X234 - Y234 = 0. X241 - Y241 = 0.
X242 - Y242 = 0. X243 - Y243 = 0. X244 - Y244 = 0. X321 - Y321 = 0. X322 - Y322 = 0.
X323 - Y323 = 0. X324 - Y324 = 0. X331 - Y331 = 0. X332 - Y332 = 0. X333 - Y333 = 0.
X334 - Y334 = 0. X341 - Y341 = 0. X342 - Y342 = 0. X343 - Y343 = 0. X344 - Y344 = 0.
X421 - Y421 = 0. X422 - Y422 = 0. X423 - Y423 = 0. X424 - Y424 = 0. X431 - Y431 = 0.
X432 - Y432 = 0. X433 - Y433 = 0. X434 - Y434 = 0. X441 - Y441 = 0. X442 - Y442 = 0.
X443 - Y443 = 0. X444 - Y444 = 0.
Xi1 = 0 ó 1. ∀i = 1,2,3y4.
Xijk = 0 o 1. ∀i = 1,2,3y4; ∀j = 2,3y4 y ∀k = 1,2,3y4.
Yi1 = 0 o 1. ∀i = 1,2,3y4.
Yijk = 0 o 1. ∀i = 1,2,3y4; ∀ij= 2,3y4 y ∀k = 1,2,3y4.
Solución del modelo específico
El desarrollo del presente documento no pretendía generar ningún software, sino un modelo para la ubicación de operadores logísticos a través de un horizonte de planeación. Por tanto, en este aspecto se recomienda utilizar el paquete WINQSB para obtener las soluciones de los diferentes planteamientos, con base en el número de localizaciones disponibles para ubicar los operadores logísticos y la cantidad de periodos del horizonte de planeación; así como la información de utilidades brutas y costos de traslado que se deben establecer con antelación.
A partir del reporte generado con WINQSB para el ejemplo de la compañía Sigma utilizado en el ítem anterior, se interpreta lo siguiente:
X 31 = 1. Indica que en el año 1 el operador logístico se debe ubicar en el sitio C.
X 323 = 1. Indica que en el año 2 el operador logístico se debe ubicar en el sitio C, y que en el año 1 se ubicó en el sitio C.
X 333 = 1. Indica que en el año 3 el operador logístico se debe ubicar en el sitio C, y que en el año 2 se ubicó en el sitio C.
X 343 = 1. Indica que en el año 4 el operador logístico se debe ubicar en el sitio C, y que en el periodo 3 se ubicó en el sitio C.
Y 31 = 1. Hace causar el costo de ubicar en el año 1, el operador logístico en el sitio C.
Y 323 = 1. Hace causar el costo de traslado del operador logístico del sitio C en el año 1, al sitio C en el año 2. Como se puede observar, realmente no hay traslado, porque el operador no cambia de sitio del año 1 al año 2; por lo tanto, no hay costo de traslado. Esto se puede verificar con base en la función objetivo del modelo, pues esta variable tiene como coeficiente “cero”.
Y 333 = 1. Hace causar el costo de traslado del operador logístico del sitio C en el año 2, al sitio C en el año 3. Como se puede observar, realmente no hay traslado porque el operador no cambia de sitio del año 2 al año 3; por tanto, no hay costo de traslado. Esto se puede verificar con base en la función objetivo del modelo, pues esta variable tiene como coeficiente “cero”.
Y 343 = 1. Hace causar el costo de traslado del operador logístico del sitio C en el año 3, al sitio C en el año 4. Como se puede observar, realmente no hay traslado porque el operador no cambia de sitio del año 3 al año 4; por tanto, no hay costo de traslado. Esto se puede verificar con base en la función objetivo del modelo, pues esta variable tiene como coeficiente “cero”.
A partir de la solución anterior, se observa que el único costo que se causa es el de la ubicación del primer año, pues de ahí en adelante no se cambia la ubicación del operador logístico. En la tabla 3 se detalla la ubicación óptima del operador logístico en los cuatro años del horizonte de planeación, junto con la utilidad bruta generada.
Tabla 3: Ubicación óptima del operador logístico
Año
Ubicación
Utilidad bruta
1
C
COP 486 000
2
C
COP 702 000
3
C
COP 901 000
4
C
COP 1 312 000
Total
COP 3 401 000
La utilidad neta total para la ubicación del operador logístico en el horizonte de planeación es de COP 3.276.000 que se obtiene de COP 3 401 000 menos COP 125 000. Este último dato es el único costo de ubicación o traslado que se causa. El valor de utilidad neta total es justamente el mismo arrojado como máximo valor de la función objetivo por el WINQSB.
Conclusiones
El desarrollo del presente proyecto permite concluir lo siguiente:
-
El modelo aplicado sí garantiza tener en cuenta las restricciones de recursividad de la localización de los operadores logísticos a través de todo el horizonte de planeación. Con base en la solución de la aplicación realizada, se puede observar este hecho, pues X 31 indica ubicar en el sitio C para el año 1; X 323 especifica la ubicación en el sitio C para el año 2, habiendo ubicado en el año 1 en el sitio C (esto lo indica el tercer subíndice de la variable); X 333 establece ubicar en el año 3 en el sitio C (primer subíndice de la variable), dado que en el año 2 se ubicó en C (tercer subíndice de la variable y lo mismo ocurre con la ubicación del cuarto año). Todo lo anterior se hizo para un ejemplo específico; pero se garantiza el modelo sin importar la cantidad de ubicaciones disponibles y el número de periodos del horizonte de planeación.
-
El modelo propuesto permite concluir que solo se causan los costos de traslado en el evento que haya cambio de ubicación del operador logístico de un año a otro. En caso contrario, como en la aplicación realizada, causará costo de “cero”.
Referencias
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.