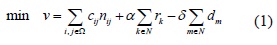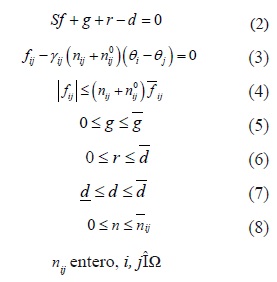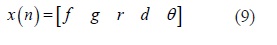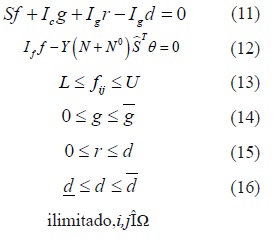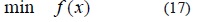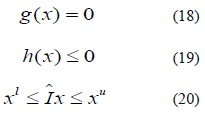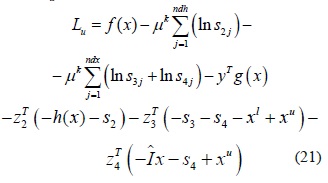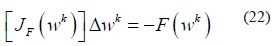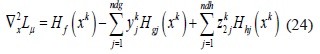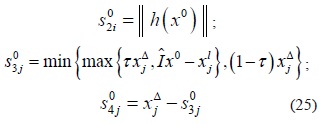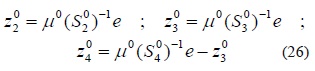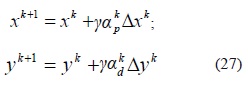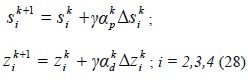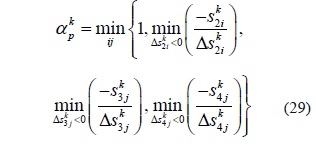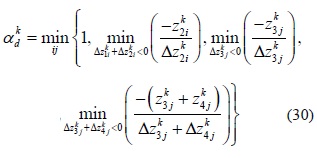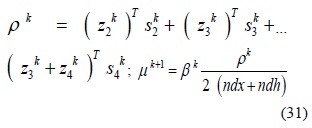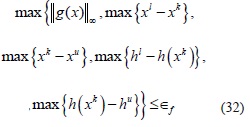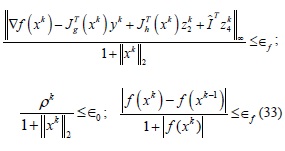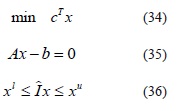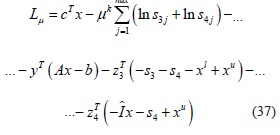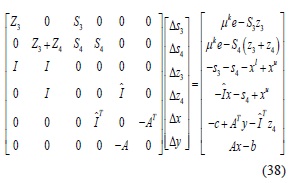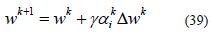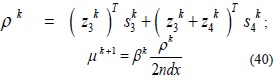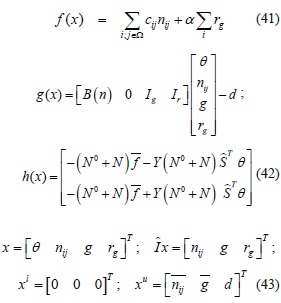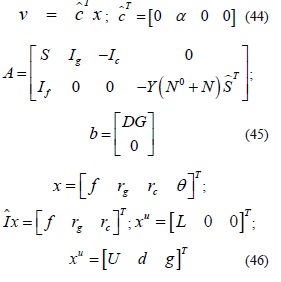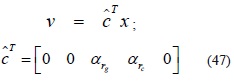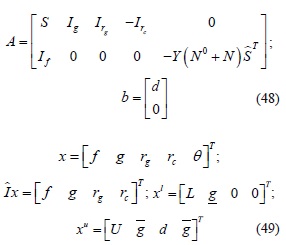DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2014.1.a05Publicado:
19-12-2013Número:
Vol. 18 Núm. 39 (2014): Enero - MarzoSección:
InvestigaciónPlaneamiento de la transmisión considerando seguridad e incertidumbre en la demanda empleando programación no lineal y técnicas evolutivas
Transmission planning considering security and demand uncertainty through non-linear programming and evolutionary techniques
Palabras clave:
Genetic algorithm, contingencies, demand uncertainty, interior point method, optimization. (en).Palabras clave:
algoritmo genético, contingencias, incertidumbre en la demanda, método de puntos interiores, optimización (es).Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Planeamiento de la transmisión considerando seguridad e incertidumbre en la demanda empleando programación no lineal y técnicas evolutivas
Transmission planning considering security and demand uncertainty through non-linear programming and evolutionary techniques
Ricardo Andrés Bolaños Ocampo1, Carlos Adrián Correa Flórez2
1Ingeniero Electricista, magíster en Ingeniería Eléctrica. Analista Coordinación
de Operación de XM Filial de ISA. Bogotá, Colombia.
Contacto: rabolanos@xm.com.co
2Ingeniero Electricista, magíster en Ingeniería Eléctrica. Profesor asistente de la
Universidad de La Salle. Bogotá, Colombia.
Contacto: carcorrea@unisalle.edu.co
Fecha de recepción: 29 de agosto de 2012 Fecha de aceptación: 21 de mayo de 2013
Clasificación del artículo: investigación
Financiamiento: XM ISA - Universidad de La Salle
Resumen
En este trabajo se presenta una metodología de solución para el problema de planeamiento de la expansión de redes de transmisión de energía eléctrica considerando contingencias simples (N1) e incertidumbre en la demanda futura. Para resolver el problema se utiliza un algoritmo genético especializado de Chu & Beasley (AGCB) para realizar las propuestas de inversión cuyos flujos de carga son resueltos mediante programación lineal con un método de punto interior de alto orden o método predictor corrector (MPC). Adicional-mente, es implementada una inicialización de la población mediante un método de punto interior no lineal. La metodología propuesta es validada utilizando 3 sistemas de prueba de la literatura especializada: el sistema del Sur Brasilero de 46 barras, el sistema IEEE de 24 barras y el sistema Garver de 6 nodos. Los resultados mostrados demuestran la validez del enfoque para solucionar el problema del planeamiento de la transmisión considerando contingencias, al encontrar planes de expansión de mínimo costo.
Palabras clave: algoritmo genético, contingencias, incertidumbre en la demanda, método de puntos interiores, optimización.
Abstract
This paper proposes a methodology for solving the Transmission Expansion Planning Problem considering single contingencies (N-1) and future demand uncertainty. To solve this problem, a specialized Chu-Beasley Genetic Algorithm (CBGA) is used so that investment plans can be suggested. These plans are evaluated through a Higher Order Interior Point Method for Linear Programming or through a Predictor Corrector Method. Additionally, initialization of the CBGA is carried out using Non-linear Interior Point. The methodology is validated using three test systems from the specialized literature: 46-Bus South-Brazilian, IEEE 24-Bus, and a 6-Bus Garver system. Results demonstrate the validity of this approach to solving the transmission planning problem when contingencies are considered; which is attained by finding expansion plans of minimum cost.
Keywords: genetic algorithm, contingencies, demand uncertainty, interior point method, optimization.
1. Introducción
El problema del planeamiento de la transmisión consiste en determinar el plan de expansión de mínimo costo teniendo en cuenta las restricciones de la red. De hecho, la red eléctrica exige mantener altos índices de calidad, seguridad y eficiencia, y un adecuado plan de expansión de la transmisión permite que estas características sean factibles ante el crecimiento de las demandas en los diferentes centros de consumo.
El plan debe dar respuesta en cuanto a cantidad, ubicación y tiempo para la construcción de los diferentes equipos de transmisión, hecho que permite abordar el problema desde diversos puntos de vista: el modelo estático [1], [2] presenta un único horizonte de planeamiento, mientras que el modelo multietapa [3], [4] realiza propuestas en el tiempo para varias etapas interdependientes. El modelamiento se puede clasificar también de acuerdo al grado de complejidad, a saber: modelos de transportes [5], DC [1] - [7], híbridos [3] y modelo AC [8]. Las diferencias entre cada modelo se reflejan en la forma en que se consideran las restricciones de Kirchhoff para sistemas de potencia. En este artículo se aborda el problema de la expansión de la transmisión mediante el modelo DC, que resulta en un problema de optimización del tipo no lineal entero mixto (PNLEM) de gran tamaño. Existen múltiples propuestas para resolver dicho problema empleando métodos exactos [4] o algoritmos combinatoriales[9]. No obstante, estos algoritmos son aprovechados para minimizar la inversión. El presente desarrollo lleva asociada la seguridad, evaluada mediante el criterio de contingencias simples (N – 1) similar al enfoque planteado en [10] - [12]. Adicionalmente se introduce el concepto de incertidumbre en la demanda con el fin de encontrar soluciones de menor costo o a lo sumo iguales, pero con mayor atención de demanda en cada nodo [1], [2], [10].
Este artículo está dividido de la siguiente forma: en la primera parte se presentan los conceptos de seguridad, incertidumbre y el modelo de planeamiento utilizado, posteriormente se describe el método de solución del problema operativo y la inicialización no lineal mediante el método de puntos interiores de alto orden [1], [13], [14], posteriormente se presenta el algoritmo de solución del problema de inversión implementando un algoritmo especializado de Chu & Beasley [15] y finalmente se presentan los resultados obtenidos de la aplicación a los sistemas de prueba de Garver, IEEE-24 y Sur Brasil.
2. El problema de planeamiento De la transmisión
El modelo matemático usado para el planeamiento de la transmisión considerando incertidumbre en la demanda y generadores ficticios para evitar infactibilidad, basado en el modelo DC [1], [2] [6], [16], asume la siguiente forma para minimizar costos de inversión:
s.a.
Donde: ij Corredor entre los nodos i – j.
cij Costo de inversión por instalación de equipos en el corredor ij.
f Vector de flujos fij de potencia activa entre los nodos i – j.
f ij Máximo flujo de potencia activa por línea entre los nodos i – j.
γij Susceptancia de línea entre los nodos i – j.
nij, nij 0 Número de circuitos adicionados y del caso base en el corredor ij.
nij Número máximo de circuitos permitidos en el corredor ij.
g, d Vectores de generadores y demandas del sistema.
g, g Vectores de generaciones mínimas y máximas del sistema.
rg,rc Vectores de generadores y demandas ficticias.
θ Vector de los ángulos nodales θi.
Ω Conjunto de ramas candidatas.
S Matriz de incidencia nodo elemento.
El modelo dado por las ecuaciones (1) a (8), es idéntico al modelo implementado en [6] para el modelo 2 allí descrito. Suele considerarse α=10δ, que indica que se penalice con mayor severidad la no desatención de demanda (corte de carga), sin embargo, el signo menos en la función objetivo reduce el costo de inversión cuando las configuraciones intenten atender mayor cantidad de demanda haciéndolas más atractivas dado que el problema es de minimizar el costo de inversión. Si se considera el vector f que contiene los flujos fij, se puede definir el conjunto de variables dependientes del número de líneas por corredor dado por:
Las ecuaciones (2) y (3) representan la primera y segunda ley de Kirchhoff de la red DC equivalente. El modelo DC, suele dividirse en 2 sub-problemas donde un algoritmo combinatorial realiza una propuesta de inversión (número de líneas a ser adicionadas:nij), y el subproblema operativo es convertido en un problema de Programación Lineal (PL) [3].
El objetivo es ahora minimizar el corte de carga y maximizar la demanda atendible en cada nodo.
s.a.
Donde IfIge Ifson matrices identidad apropiadas y -Y(N+N0 )SˆTes una matriz que agrupa las variables de (3) reduciéndola a la forma que se presenta en la ecuación (12); U=-L=(nij+ nijo) fij son los límites inferiores y superiores de los flujos, respectivamente. El objetivo del problema se convierte en determinar dónde y cuántos circuitos se deben adicionar para que el corte de carga r sea nulo (sub-problema operativo) con un costo de inversión mínimo (problema de inversión).
2.1 Seguridad en sistemas eléctricos de potencia
Los sistemas eléctricos de potencia deben operar con criterios de calidad, confiabilidad y seguridad. No obstante, la seguridad es uno de los elementos más importantes de la operación debido a que se debe garantizar la atención de la demanda aún ante condiciones anormales de operación. Los sistemas altamente enmallados en teoría son más seguros porque existen muchos caminos para atender la demanda desde los principales centros de generación; sin embargo, no es conveniente instalar equipos que produzcan amarres eléctricos o paralelos remotos entre diferentes niveles de tensión limitando el transporte de potencia a la capacidad de los equipos de menor nivel de tensión. Por esto, es conveniente introducir el concepto de seguridad desde el planeamiento mismo del sistema para una adecuada operación futura. En este trabajo se evalúa la seguridad del sistema mediante el criterio de contingencias simples (N – 1) que es de obligatorio cumplimiento para la operación de un sistema eléctrico de potencia. Para cada configuración se calcula el corte de carga o demanda no atendida que resulta de someterlas a la salida forzada de un elemento a la vez.
2.2 Incertidumbre en la demanda
Los estudios de planeamiento de largo plazo tienen intrínsecamente asociadas incertidumbres debido a que se hacen proyecciones matemáticas de las condiciones de operación futuras, y estas dependen de factores exógenos como son las condiciones ambientales, implementación de nuevas tecnologías, variables econométricas, entre otras, que hacen que el problema no sea medible en el largo plazo de forma determinista [20]. En [6] se plantean 2 modelos que consideran la incertidumbre en la demanda, en este trabajo se implementa el modelo 2 que mide la incertidumbre en cada uno de los nodos del sistema para el escenario futuro. Por tanto, un posible escenario para el i-ésimo nodo proyectado durante un período de tiempo de n años, comprendido entre el año actual t0 y final tf, tiene valores de demanda esperada diy una posible desviación de ± 5 % de di.
3. Método De Puntos Interiores (MPI)
3.1 Programación no lineal
El método de puntos interiores (MPI) se ajusta bastante bien a la solución de problemas de programación lineal (PL) y programación no lineal (PNL) [6], [13], [14]. Para el caso del modelo relajado del planeamiento de la expansión de la transmisión [7], [17] se describe a continuación el método primal dual implementado.
3.1.1 Método Primal - Dual (MPD)
Un problema de PNL con restricciones de desigualdad puede ser escrito en forma canónica como sigue:
s.a.
Donde f(x), g(x), h(x),Îx,xuy xlson la función de costos (1), el conjunto de restricciones de igualdad (2-3) y de desigualdad (4-8), el conjunto de variables canalizadas (9) y los límites superior e inferior de estas últimas, respectivamente. Si al conjunto de restricciones de desigualdad se adicionan las variables de holgura (si> 0) para transformarlas en restricciones de igualdad y se introducen las condiciones de no negatividad en la función objetivo como términos de barrera logarítmica y se llevan todas las restricciones a la función objetivo, se obtiene una función Lagrangiana Lu dada por:
Donde μk es un parámetro de barrera que decrece en forma monótona a cero en el proceso iterativo. Se definen además las cantidades nx, ndx,ndg, ndh, como el número de variables del problema, número de variables canalizadas, número de restricciones de igualdad y el número de restricciones de desigualdad, respectivamente.
Aplicando las condiciones necesarias de optimalidad de primer orden de Karush-Kuhn-Tucker (KKT), (∇Lµ=0), a la función lagrangiana, se obtiene un conjunto de ecuaciones comúnmente denominado F(w)=0, que resuelto mediante el método de Newton, se obtiene:
La matriz JF (wk) de (22) se obtiene de las derivadas parciales de segundo orden de F(w), así:
Donde Si y Zison matrices diagonales con las componentes si. yzi,∇fεRnx es el gradiente de la función objetivo, Jg εRndgYJhεRnhg, son las matrices jacobianas de las restricciones de igualdad y desigualdad respectivamente. Además:
es el término complicante del problema tipo PNL, dado que exige el cálculo de ndg + ndh + 1 matrices hessianas en cada iteración, incrementando la dificultad del ya complicado problema PNL.
3.1.2 Inicialización y actualización de variables
El punto inicial debe cumplir con la condición de no negatividad S20, Z20, S30, S40, Z30, (Z30+Z40) >0. Para este propósito, dado que el proceso de convergencia es sensible al punto inicial, una manera de inicializar las variables primales del problema consiste en tomar el punto medio entre los límites superior e inferior de aquellas variables canalizadas y ceros para las variables libres. Las variables yj son 0 o -1 al inicio del proceso y para las variables de holgura primales se tiene:
Típicamente, τ=0.25 , además, xΔ= xu-x1 y las variables de holgura duales son inicializadas como:
Después de obtener las direcciones Δwk de la solución de (22), los nuevos valores de las variables primales, duales y de holgura para la iteración k+1 son obtenidos como sigue:
el valor de γε(0,1) y es un parámetro de seguridad para garantizar que el próximo punto satisfaga las condiciones de no negatividad. Un valor típico tanto para PL como para PNL es γ = 0,99995. Los escalares αkp y αdk ε(0, 1], son las longitudes de paso primal y dual, respectivamente para la iteración k. En PNL, se acostumbra elegir α=min {αkp y αdk }. Estos valores son obtenidos así:
3.1.3 Reducción del parámetro de barrera
El valor residual de la condición de complementariedad tiende monótonamente a cero durante el proceso iterativo y llamado gap de complementariedad pk , que junto con el parámetro de barrera µk son calculados en cada iteración k, como:
donde βε(0,1) es un parámetro de centralización. Para compensar los objetivos de reducir µk y mejorar la dirección central, βk se escoge dinámicamente como βk+1 =max {0,95 βk,0.1}, con β0 =0.2. Generalmente µ0 =0.1,1 o 10.
3.1.4 Criterios de convergencia
El sistema (22) es resuelto hasta que cada uno de los siguientes criterios de convergencia sea cumplido:
Factibilidad primal
Factibilidad dual, condición de optimalidad y desvío de la función objetivo
3.2 Método de puntos interiores para programación lineal
A continuación se presenta un método de puntos interiores de alto orden (MPIAO), en este caso es el predictor corrector (MPC) para programación lineal usado en la solución de los problemas operativos con y sin redespacho del problema tratado.
3.2.1 Método Predictor-Corrector (MPC)
El problema del planeamiento de la transmisión tal como fue descrito en (10)-(16) puede expresarse de la siguiente forma canónica:
donde, cTx, Ax -b, Ix, xu , xl son las funciones objetivo (6) y (10), el conjunto de restricciones de igualdad (7, 8) y (11, 12), el conjunto de variables canalizadas (9) y (13), y los límites superior e inferior de las variables canalizadas respectivamente. En este caso, la función lagrangiana Lµ[1] es:
Siguiendo el mismo procedimiento descrito en el numeral 4.1, se obtiene el siguiente sistema de Newton para el cálculo de las direcciones de búsqueda Δwk :
3.2.2 Inicialización y actualización de las variables
Como el punto inicial debe cumplir con: S20, Z20, S30, S40, Z30, (Z30+Z40) >0 las variables del problema, al igual que las variables de holgura primales y duales son inicializadas de la misma forma reportada en [1], [2], [3] y [4]. Después de obtener las direcciones Δwk de (38), los nuevos valores de las variables para la iteración k+1 son actualizados de:
El escalar αik toma valores αpk y αdk ε(0, 1], para las longitudes del paso primal y dual, respectivamente, que son obtenidos con el mismo enfoque de [1] - [3].
3.2.3 Reducción del parámetro de barrera
En este caso, el gap de complementariedad pk y el parámetro de barrera µk+1 , son calculados en cada iteración k mediante:
3.2.4 Criterios de convergencia
El sistema (38) debe ser resuelto hasta que los mismos criterios de convergencia descritos ampliamente en [2] y [3] sean cumplidos.
4. Metodología
4.1 Adaptación del modelo DC al método de puntos interiores
Para el caso no lineal, el modelo DC (Direct Current), de las ecuaciones (1)-(5) puede ser reescrito, matricialmente, de la siguiente forma:
Donde: 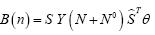
Para el caso del modelo lineal DC sin redespacho, se tiene:
Para el sistema con redespacho, se tiene:
4.2 Algoritmo genético de Chu-Beasley
Los algoritmos genéticos (AG) han sido ampliamente usados en problemas de optimización de diferentes disciplinas, y en caso de los problemas eléctricos caracterizados por tener una alta explosión combinatorial han sido muy exitosos [3], [18]. Los AG tradicionales tienen asociado un alto costo computacional por el hecho de tener que evaluar la función objetivo en cada ciclo generacional para un número de hijos igual al tamaño de la población, y de esta manera la población es modificada ciclo tras ciclo. Los AG básicos y sus respectivos operadores de selección, cruzamiento y mutación, se explican ampliamente en [19].
El AG modificado de Chu-Beasley (AGCB) propuesto en este trabajo posee varias ventajas con respecto al AG tradicional, como mantener el tamaño de la población constante para analizar solamente un hijo por cada ciclo generacional, disminuyendo el número de evaluaciones de la función objetivo, que en este caso se traduce en PL para encontrar el corte de carga. Además de lo anterior, un hijo es aceptado dentro de la población solamente cuando cumple con criterios de diversidad. Esto restringe la homogenización de la población y garantiza la búsqueda de soluciones en diferentes puntos.
En el presente trabajo se utilizó la codificación decimal, por ser apropiada para el problema del PST [3]. A continuación se describen las principales etapas del AG propuesto.
4.2.1 Inicialización de la población
Esta etapa es clave para el éxito de todo el proceso, debido a que una inicialización inteligente puede guiar el algoritmo por espacios que estén cercanos a configuraciones de buena calidad. El proceso comienza con la evaluación de un PNL que tiene como red base el estado actual del sistema que se esté analizando, entonces el PNL arroja valores continuos de nij que corresponden a circuitos que seguramente son importantes y que con una alta probabilidad puedan estar presentes en la solución del problema. Por la forma del problema relajado, dichos circuitos tienen la característica de tener un bajo costo con relación a la cantidad de potencia que pueden transportar o que sean indispensables para aliviar los problemas de corte de carga. Es importante tener en cuenta que uno de los factores que garantiza el éxito del AGCB es la diversidad, por tanto, si bien las propuestas nij son un buen indicador de los caminos importantes, no es seguro que absolutamente todos los caminos estén presentes en la solución final, entonces, dicha solución relajada se utiliza para generar solo algunos individuos, donde la decisión de adicionar una línea en los caminos con nij¹ 0 se toma de manera aleatoria, de esta forma un individuo tiene adiciones únicamente en algunos de los caminos con nij¹ 0.
Después de lo anterior, el mecanismo de generación del resto de individuos se realiza mediante el bloqueo de los corredores que en el caso base tuvieron nij¹ 0. Lo que se busca con esto es que el PNL se abstenga de ubicar circuitos en algunos de los corredores que ya se utilizaron para generar algunos individuos. Esto hace que el problema relajado se vea forzado a buscar nuevas soluciones que también son de buena calidad y que pueden arrojar corredores con nij¹ 0, que sean importantes en el proceso del planeamiento. La generación del resto de individuos pasa entonces por un proceso cíclico de bloqueo y asignación de circuitos, que se repite un número de veces determinado.
4.2.2 Verificación de diversidad
Después de la generación de la población es posible que algunos individuos tengan un alto grado de similitud, hecho que reduce la diversidad de la población y que disminuye las posibilidades de éxito del AG (ya se ha mencionado que la diversidad es una de las características que hace que el AG pueda converger a respuestas de buena calidad). Para afrontar esta situación se emplea un mecanismo para verificar la diversidad de la población que consiste en realizar una comparación de cada uno de los individuos con el resto para determinar en cuantos corredores (bits) son iguales 2 configuraciones. En este caso la similitud de una configuración con otra se establece por la existencia o no de circuitos en un corredor; de acuerdo con lo anterior, si en una posición de la configuración 1 hay una propuesta de 2 líneas, y para la misma posición la configuración 2 tiene un valor de 3, el proceso de diversidad concibe esta posición como no diversa. Cuando se verifica la diversidad de una configuración con otra el número de casillas similares no debe sobrepasar un valor predeterminado (ρdiv) no demasiado alto ya que esto modificaría sustancialmente la población haciendo que se pueda perder información valiosa otorgada por el PNL. Un valor común de ρdiv puede ser 2.
4.2.3 Selección
En el proceso de selección se realizan 2 torneos para escoger 2 padres. Dentro de cada torneo puede existir un número variable de padres, si dicho número es alto, es claro que se prioriza el elitismo y viceversa. En cada torneo gana un derecho como padre el individuo que mejor función fitness posea. Así, después de 2 procesos de torneo se tienen 2 padres listos para entrar en la etapa de cruzamiento.
4.2.4 Cruzamiento
El cruzamiento se realiza de manera tradicional, teniendo en cuenta que solo se elige un único punto para su implementación. Es de aclararse que en la implementación del AGCB no hay necesidad de definir una trasa de cruzamiento por el hecho de que la población se mantiene intacta y solo cambia en una configuración cuando un individuo cumple ciertos criterios de diversidad y optimalidad, a diferencia del AG convencional que realiza un cambio de toda la población en cada ciclo generacional y resulta interesante que algunas configuraciones padre tengan la posibilidad de sobrevivir completamente. Después del cruzamiento de los padres se generan 2 hijos que deben ser evaluados con el fin de descartar el hijo con peor función fitness.
4.2.5 Mutación
En la etapa de mutación se prioriza la adición de circuitos cuando la configuración tiene un alto corte de carga y viceversa cuando la configuración tiene un corte de carga bajo o nulo. También se puede incluir la posibilidad de realizar un intercambio o swap cuando la configuración es factible.
4.2.6 Mejoramiento
Otro de los elementos que diferencian el AGCB implementado del AG tradicional es la inclusión de una etapa de mejoramiento en la cual la configuración resultante de la mutación es sometida a un minucioso análisis para determinar qué circuitos se encuentran en calidad de sobrantes, es decir, cada uno ellos es retirado temporalmente para encontrar el corte de carga bajo esta nueva condición, y si dicho corte se mantiene igual o disminuye, entonces el circuito es definitivamente retirado; de esta manera se logra encontrar configuraciones con igual o menor grado de infactibilidad pero con menor costo. Este proceso de mejoramiento aumenta de manera considerable el esfuerzo computacional, ya que necesita de la solución de tantos PL como caminos con circuitos haya en el individuo analizado.
El individuo que resulte del proceso anterior solo se introduce a la población si mejora la incumbente o si cumple con criterios de diversidad.
5. Resultados
La metodología propuesta fue implementada usando Matlab 7.8.0® aplicada a los sistemas de prueba de Garver de 6 nodos y 15 corredores, IEEE-24 de 24 nodos y 41 corredores y Sur Brasil 46 nodos y 79 corredores. Los resultados obtenidos considerando seguridad en todos los sistemas de prueba se listan a continuación.
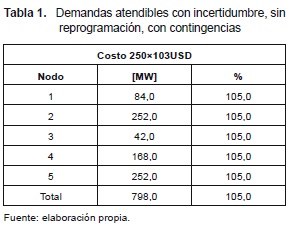
5.1 Sistema Garver considerando incertidumbre sin reprogramación de la generación
Para el sistema Garver, la mejor solución encontrada cuando se considera como ±5 % de incertidumbre en la demanda y la generación, sin reprogramación de la generación, tiene costo de inversión de 250×103USD, cuya configuración responde al siguiente conjunto de adición de circuitos: n2–6=4; n3–5=2 y n4–6=2. La tabla 1 resume las demandas atendibles y la tabla 2 la generación en cada nodo por cada una de las configuraciones encontradas. En ambas se puede apreciar demanda y generación en el 105,0 % en cada nodo.
5.2 Sistema Garver considerando incertidumbre y reprogramación de la generación
Cuando se considera reprogramación de la generación e incertidumbre en la demanda, se obtienen 2 soluciones óptimas alternativas de costo de inversión 160×103USD, dadas por el siguiente conjunto de adición de circuitos. Configuración 1: =2; n3–5=2 y n4–6=2, Configuración 2: n2–6=2; n2–6n=2 y n=3. La tabla 3 muestra la generación 3–54–6 en cada nodo. Las demandas atendibles, son idénticas a las presentadas en la tabla 1 con un total de 798,0 MW (105,0%) en cada uno de los nodos del sistema.
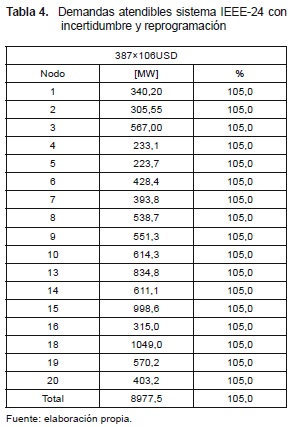
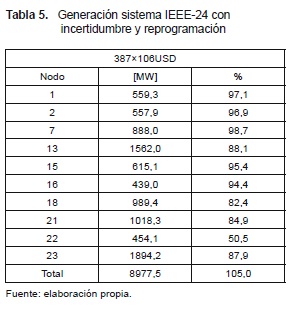
5.3 Sistema IEEE-24 considerando incertidumbre y reprogramación de la generación
En las tablas 4 y 5 se observan las demandas atendibles y la generación en cada nodo para la mejor solución encontrada de costo de 387×106USD cuando se considera el ±5 % de incertidumbre en la demanda en cada nodo del sistema. El número de líneas que se deben adicionar en este caso y su ubicación son:n1–5=1; n3–24=1 ; n4–9=1 ; n6–10=2 ; n7–8 =3 ; n10–12=1 ; n15–24=1.=1 y n14–23=1
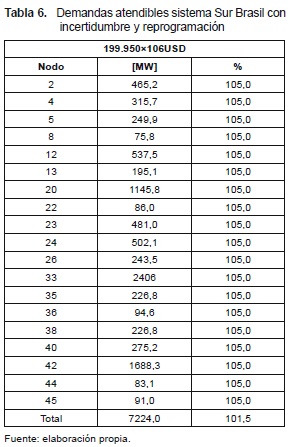
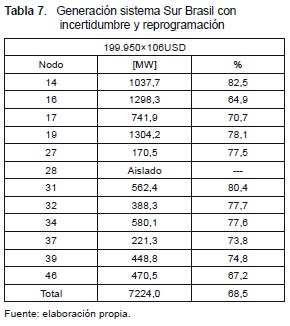
5.4 Sistema Sur Brasil considerando incertidumbre y reprogramación de la generación
En la tabla 6 se observan las demandas atendibles y en la tabla 7 la generación, para la mejor solución encontrada de costo de 199.950×106USD con el enfoque del modelo de [6] cuando se considera el ± 5 % de incertidumbre en la demanda en cada nodo del sistema. El número de líneas que se deben adicionar en este caso y su ubicación son:n2-5=1; n5-11=4; n12-14=4; n19-21=1; n20-21=3; n20-23=2; n31-32=1; n32-43=1; n40-45=1; n42-43=2; y n46-11=3.
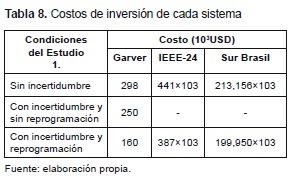
La tabla 8 muestra comparativamente los costos de inversión de cada sistema y el efecto de considerar la seguridad y la incertidumbre en la demanda. Los resultados presentados sin considerar incertidumbre se pueden encontrar en [1].
6. Conclusiones
El problema de planeamiento considerando la seguridad del sistema mediante el criterio de contingencias simples (N – 1), que es de obligatorio cumplimiento en la operación de SEP, incrementa considerablemente los costos de inversión en equipos comparado con el esquema básico de planeamiento.
Considerar la incertidumbre en la demanda permite obtener soluciones de igual costo que las del esquema de planeamiento básico pero con mayor atención de demanda o en su defecto soluciones de menor costo de inversión, que es un factor importante para los estudios de planeamiento, lo que redunda en un mejor uso de los activos del sistema (líneas, transformadores y generadores).
La combinación de seguridad e incertidumbre en la demanda representa un importante aporte para los estudios de planeamiento, dado que son aspectos propios de los sistemas de potencia y de las técnicas de proyección de demanda.
El método de puntos interiores como propuesta de solución del problema operativo es bastante robusto, hecho que es de suma importancia en este tipo de problemas que calcula miles de flujos de carga para múltiples configuraciones.
Se implementó un algoritmo especializado de Chu & Beasley que permite evaluar el costo de las diferentes propuestas de inversión en equipos, que cuenta con una etapa de mejoramiento que potencia su proceso de convergencia.
En general, los criterios de seguridad tienen un importante efecto sobre el mercado debido a que los agentes pueden llegar a identificar ventajas competitivas con generaciones de seguridad o atrapamientos de generación, por lo que podrían ajustar sus precios de oferta para incrementar sus márgenes de ganancia. Mediante un esquema de planeamiento que considere la seguridad, se evita que los agentes aprovechen esta situación y así se menguan estas ventajas inherentes al esquema de mercado imperante.
Referencias
[1] R. Bolaños, Planeamiento de la Expansión de Sistemas de Transmisión de Energía Considerando Seguridad e Incertidumbre Mediante Optimización Multiobjetivo, Tesis de Maestría, Universidad Tecnológica de Pereira, 2008.
[2] C. Correa, Planeamiento Multiobjetivo de la Expansión de la Transmisión Considerando Múltiples Escenarios de Generación, Tesis de Maestría, Universidad Tecnológica de Pereira, 2008.
[3] A. Escobar, Planeamiento Dinámico de la Transmisión en Sistemas de Transmisión Usando Algoritmos Combinatoriales, Tesis de Maestría, Universidad Tecnológica de Pereira, 2002.
[4] E. Asada, E. Carreño, R. Romero and A. V. García, "ABranch-and-Bound Algorithm for the Multi-StageTransmission Expansion Planning", IEEE Power Engineering Society General Meeting, vol. 1, pp. 171-176, 2005.
[5] L.Garver, "Transmission network estimation using linear programing", IEEE Transactions on Power Apparatus and Systems, vol. 89, pp. 1688-1697, Sep./Oct. 1970.
[6] I. Silva, M. Rider, R. Romero and C. Murari, "Transmission Network Expansion Planning Considering Uncertainty In Demand", IEEE Transactions on Power Systems, vol. 21, no. 4, pp. 1565-1573, Nov. 2006.
[7] M. Rider, R. Romero and J. Mantovani, "Transmission Expansion Planning Using the DC Model and Nonlinear-Programming Technique", IEEE Proceedings on Generation Transmission and Distribution. vol. 152, issue 6, pp. 763-769, Nov. 2005.
[8] M. Rider, R. Romero, L. Gallego and A. García, "Heuristic Algorithm Solve the Short Term Transmission Network Expansion Planning", IEEE Power Engineering Society General Meeting, vol.1, pp. 1-7, Jun. 2007.
[9] A. Monticelli, R. Gallego and R. Romero, "Comparative Studies on Non-Convex Optimization Methods for Transmission Network Expansion Planning", IEEE Transactions on Power Systems, vol. 13, Issue 3, pp. 822-828, Aug. 1998.
[10] I. J. Silva, Planejamento da Expansao de Sistemas de Transmissao Considerando Seguranca e Planos de Programacao da Geracao, Tesis Doctoral, Universidad de Campinas, 2005.
[11] A. Kazerooni, and J. Mutale, "Transmission Network Planning Under Security and Environmental Constraints", IEEE Transactions on Power Systems, vol. 25, Issue 2, pp. 1169-1178, May 2010.
[12] H. Zhang, V. Vittal, G. Thomas and J. Quintero, "A Mixed-Integer Linear Programming Approach for Multi-stage Security Constrained Transmission Expansion Planning", IEEE Transactions on Power Systems, vol. 27, Issue 2, pp. 1125-1133, May 2012.
[13] L. Xie, H.-D. Chiang, "An enhanced multiple predictor-corrector interior point method for optimal power flow", IEEE Power and Energy Society General Meeting, pp. 1-8, 2010.
[14] I. Farhat, M. El-Hawary, "Interior point methods application in optimum operational scheduling of electric power systems", Generation, Transmission Distribution, IET,vol. 3, issue 11, pp. 1020-1029, 2009.
[15] J. Beasley, P. C. Chu, "A Genetic Algorithm for the Generalized Assignment Problem", Computers Operations Research, vol.24, issue 1, pp. 17-23, Jan.1997.
[16] R.A. Bolaños, C.A. Correa and A. Escobar, "Planeamiento de la transmisión considerando incertidumbre en la demanda y reprogramación de la generación", Scientia Et Technica, año XIV, no. 40, Nov. 2008.
[17] I. Sanchez, R. Romero, J. Mantovani and M. Rider, "Transmission-expansion Planning using the DC model and non-linear programming technique", IEEE Proceedings on Generation, Transmission and Distribution, vol. 152, issue 6, pp. 763-769, Nov. 2005.
[18] R. Gallego, A. Monticelli and R. Romero, "Transmission System Expansion Planning by an Extended Genetic Algorithm", IEEE Proceedings of Generation, Transmission and Distribution, vol. 145, issue 3, pp. 329-335, May 1998.
[19] R.A. Gallego, R. Romero, y A. Escobar, Técnicas de Optimización Combinatorial, Pereira: Universidad Tecnológica de Pereira, abril de 2006.
[20] H. Fan, H. Zhong, L. Gao and J. Tan, "Study on transmission network expansion planning considering uncertainties", IEEE Power Engineering and Automation Conference (PEAM), vol. 3, pp. 82-85, 2011.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.