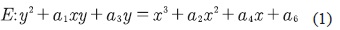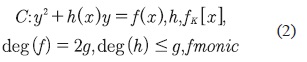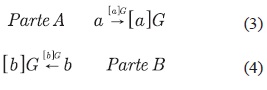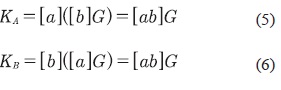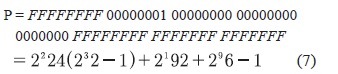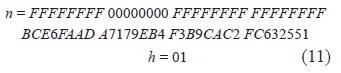Modelo test-bed de simulación y evaluación de criptografía de curva elíptica en redes IPv6 de próxima generación

Modelo test-bed de simulación y evaluación de criptografía de curva elíptica en redes IPv6 de próxima generación

Simulation test-bed for the evaluation of elliptic curve cryptography on next generation wireless IPv6-enabled networks

Nelson Enrique Vera Parra¹, Danilo Alfonso López², Héctor Cristyan Manta Caro³

¹Ingeniero Electrónico, magíster en Teleinformática. Docente e investigador de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: neverap@udistrital.edu.co
²Ingeniero Electrónico, magíster en Teleinformática. Docente e investigador de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: dalopezs@udistrital.edu.co
³Ingeniero Electrónico, magíster en Teleinformática. Investigador de la Universidad de Granada. Granada, España. Contacto: cristyan.manta@gmail.com

Fecha de recepción: 2 de marzo de 2013-Fecha de aceptación: 23 de noviembre de 2013

Clasificación del artículo: investigación
Financiamiento: Universidad Distrital Francisco José de Caldas

Resumen

En la actualidad, las redes móviles e inalámbricas de nueva generación, tales como las redes de área personal IPv6 de baja potencia (6LoWPAN), redes de sensores inalámbricos sobre IPv6 y redes móviles IPv6 jerárquicas se encuentran bajo rigurosa investigación y desarrollo, pues representan el paso por seguir en la evolución de las redes Machine-to-Machine (M2M), al tiempo que apoyan el acceso de banda ancha de la próxima generación de tecnologías y sistemas inteligentes sobre Internet futuro.

Estas redes de nueva generación imponen restricciones en cuanto al poder de procesamiento, ancho de banda y recursos de energía, lo que representa una gran limitante en la implementación de mecanismos de seguridad. En este sentido, en lo últimos años han surgido diversas propuestas para la administración de claves, procedimientos de firma digital y cifrado de datos basados en curvas elípticas e híper-elípticas, que logran niveles de seguridad equivalentes a los algoritmos convencionales basados en algoritmos Dffie-Hellman y Rivest-Shamir-Adleman (RSA), pero que reducen la longitud de clave y, por ende, los recursos computacionales y de red asociados.

Este artículo examina los algoritmos basados en criptografía de curvas elípticas (ECC) y su aplicación a redes móviles e inalámbricas de nueva generación habilitadas para IPv6. Así mismo, describe un modelo de simulación para la evaluación de ECC, donde se comparan los recursos computacionales necesarios y las limitaciones en mecanismos ligeros de seguridad.

Palabras clave: criptografía, curvas elípticas, redes móviles e inalámbricas, seguridad informática.

Abstract

Currently, mobile networks and next generation wireless networks such as, IPv6 low-power Wireless Personal Area networks 6LoWPAN, wireless sensor networks and hierarchical mobile networks in IPv6, are under rigorous research and development, thereforethose networks represent the next step in the evolution of the Machine-to-Machine M2M networks, while supporting broadband access for the next generation of intelligent systems, technologies and future Internet.

These next generation networks impose restrictions on the processing power, bandwidth and energy resources, which represents a major constraint in the implementation of security mechanisms. In this regard, in recent years there have been various proposals for key management, digital signature procedures and data encryption based on elliptic and hyper-elliptic curves, to achieve levels of safety equivalent to conventional algorithms based on Diffie-Hellman and Rivest-Shamir-Adleman RSA, but reducing the key length and thus the computational and network resources.

This paper reviews algorithms based on Elliptic Curves Cryptography ECC and their application to IPv6-enabled new generation wireless networks. This paper also describes a simulation test-bed for the evaluation of ECC, where we compare computational resources required and limitations for lightweight security mechanisms in secure neighbor discovery, and DNS security extensions.

Key words: Cryptography, elliptic curves, information security, wireless networks.

Introducción

Los avances en matemática aplicada, matemática discreta aplicada, criptografía de curva elíptica e híperelíptica han permitido a lo largo de los últimos años el desarrollo y la estandarización de novedosos protocolos de seguridad y marcos de referencia (Blade et al., 2005; Cohen et al., 2006).

La criptografía de curva elíptica puede proveer el mismo nivel y tipo de seguridad que los algoritmos convencionales RSA o Diffie-Hellman pero con claves mucho más cortas. A causa del tamaño de claves más cortas, los protocolos con base en ECC pueden ser implementados en hardware especializado como FPGA (Gwalani et al., 2009) o tarjetas inteligentes sin el uso de coprocesadores matemáticos y empleando a cambio aceleradores computacionales. La longitud corta de las claves se traduce directamente a mecanismos de seguridad ligeros, a su vez, ECC se puede convertir en un elemento para la próxima generación de comunicaciones inalámbricas habilitadas con soporte a IPv6.

Desde la definición de IPv6, el esquema de direccionamiento para la Internet del futuro, múltiples investigaciones se han llevado a cabo en el tema. Algunos de ellos han estudiado específicamente las aplicaciones de la ECC a IPv6 (Huang, 2008); sin embargo, donde ECC desempeña un papel clave en la seguridad es en entornos de recursos limitados y restringidos. En los últimos años, el escenario móvil de IPv6 ha sido objeto de continua investigación. Mobile IPv6 trae a la sociedad de la información un amplio espectro de posibilidades y aplicaciones, desde el comercio electrónico móvil, e-salud hasta los sistemas de gobierno electrónico.

Los sistemas inteligentes sobre IP, así como las redes de comunicación inalámbrica con el apoyo de Mobile IPv6 requieren estudios de vulnerabilidad en la etapa de implementación (Seo et al, 2008), además de asegurar todos los principios y factores de autenticidad e identidad (Ehmke et al., 2008), integridad, confidencialidad y demás. Como ejemplo, se encuentra un sistema de cifrado basado en identidad aplicada al control de la señalización en Mobile IPv6 (Ehmke et al., 2008). Otros investigadores se han centrado en el análisis comparativo de los sistemas criptográfieos para redes jerárquicas móviles IPv6 (Kan-dikattu etal, 2008).

Este trabajo se organiza de la siguiente forma.En la sección I se presenta una revisión de los principales cripto-sistemas elípticos e hiper-elípticos, comenzando con una breve reseña de los aspectos matemáticos tras las curvas elípticas y luego describiendo los protocolos criptográficos basados en ECC, estrechamente relacionados con los mecanismos ligeros discutidos en este documento. En la sección II se presentan aplicaciones específicas de ECC en la definición de mecanismos de seguridad ligeros. En la sección III se describe el planteamiento propuesto de modelo de simulación y evaluación. En la sección IV se describen las herramientas y procedimientos realizados. Finalmente, en la sección V se presentan y discuten los resultados y en la sección VI se concluye.

Sistemas criptográficos Con base en curvas elípticas E hiperelípticas

Fundamentos en aritmética de curvas elípticas e hiper-elípticas

Las curvas elípticas son una clase específica de curvas algebraicas (Cohen etal., 2006).

Definición 1: una curva elíptica Ε sobre un cuerpo K denotado por E/K está dada por la ecuación (1) (ecuación de Weierstrass).

Donde los coeficientes a₁,a₂,a₃,a₄,a₆ εK tal que para cada punto (x₁,v₁) con coordenadas en K satisfacen la ecuación (1), las derivadas parciales 2v₁+o₁x₁+o₃ y 3x²₁+a₂x₁+a₄-a₁v₁ no desaparecen simultáneamente. Para propósitos criptográficos se presentan curvas hiperelípticas cuadráticas.

Definición 2: una curva dada por la forma de la ecuación (2):

Se conoce como curva hiper-elíptica de Genus g sobre Κ si no hay punto de la curva sobre la clausura algebraica de 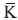de K que satisfaga ambas derivadas parciales 2y+h=0 y f-h'y=0. Las curvas elípticas pueden ser definidas sobre cualquier campo finito GF(q), conocido como campo de Galois, donde q es referido como la característica del campo. Considerando solo campos primos GF(q), donde ρ es un número primo, y GF(2^m), donde la característica es un polinomio primitivo binario de grado m. Una curva elíptica definida sobre un campo finito describe un conjunto finito de puntos, referidos como puntos en la curva.

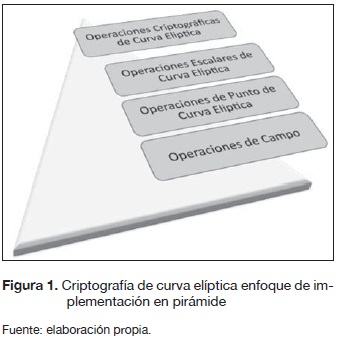
En relación con la implementación de la criptografía de curva elíptica, esta puede ser descrita en un acercamiento de forma piramidal (Victorovich, 2010). Ver figura 1. En el segundo nivel de la pirámide se encuentran varios tipos de operaciones de punto de curva elíptica que permiten la manipulación de los puntos de la curva. La definición de la curva elíptica sobre un campo finito implica que por parte de las operaciones aritméticas de punto se emplea aritmética de campo finito, que se encuentra en el primer nivel. Las operaciones de punto de curva elíptica se pueden utilizar de tal manera que permitan la aritmética entre los puntos de curvas elípticas y los factores escalares, lo cual permite la creación del nivel de operaciones escalares de curva elíptica, a pesar de que solo una de esas operaciones se utiliza realmente en el ECC: multiplicación punto de curva elíptica.

En el nivel superior se encuentran las operaciones criptográficas de curva elíptica; esto es, los protocolos y algoritmos de cifrado, los cuales proporcionan mecanismos de seguridad y servicios como cifrado de datos, autenticación, y la generación y verificación de firmas digitales. Todos ellos se basan en la multiplicación punto.

Protocolos criptográficos con base en curvas elípticas

Con base en la criptografía de curvas elípticas se ha propuesto un número significativo de algoritmos y protocolos, con el fin de direccionar principios de seguridad convencionales. Además, múltiples esfuerzos de normalización han tenido lugar, y muchos de estos estándares han reducido las opciones disponibles para la aplicación por medio de recomendación de ciertos parámetros, tales como curvas específicas o campos finitos específicos (Blade et al, 2005). La idea detrás de las recomendaciones y los estándares es permitir la interoperabilidad entre sistemas criptográficos, y al mismo tiempo definir adecuadamente un conjunto de parámetros. El primer estándar ECC fue desarrollado en ANSI X9.62. Algunos de los estándares más importantes en el área del campo de ECC son:

• ANSI X9.62
• ANSI X9.63
• FIPS 186.2
• IEEE 1363
• ISO 15946-2
• SECG

ECC tiene también un papel clave en la internet futura, y de esta manera la Fuerza de Tarea de Ingeniería de Internet (IETF) ha publicado varios Request for Comments (RFC) en los que especifican lo siguiente: los roles de la criptografía de curva elíptica en la seguridad de capa de transporte TLS (Blake etal., 2006; Badra etal, 2009), ECC y su rol en Kerberos (Zhu et al, 2008), ECC e esquemas de información de clave pública (Turner et al, 2009), el algoritmo de firma digital con base en curva elíptica ECDSA y su papel en infraestructura de clave pública (Dang et al, 2010). Recientemente, la IETF publicó en febrero de 2011 una descripción de temas fundamentales de criptografía de curva elíptica contenidos en la RFC 6090 (McGrew etal, 2011).

Algoritmo de firma digital de curva elíptica ECDSA

En 1992, el algoritmo ECDSA fue por primera vez propuesto por Scott A. Vanstone en respuesta a una solicitud de comentarios del Instituto Nacional de Estándares y Tecnología y luego fue definido en la norma ANSI X9.62. ECDSA es un esquema de firma de variante ElGamal Para ECDSA los parámetros del dominio están dados por (H, K, E, q, G), donde H es una función hash. Ees una curva elíptica sobre un campo finito K, y G es un punto en la curva de orden primo q. Por lo tanto, los parámetros de dominio definen una función hash, un grupo de orden q, y un generador de este grupo. El algoritmo de firma ECDSA se describe en la tabla 1. El algoritmo de verificación ECDSA se presenta en la tabla 2.

Algoritmo Diffie-Hellman de curva elíptica ECDH

El protocolo Diffie-Hellman DH permite el intercambio de llaves a dos pares de una comunicación sobre un canal no seguro con el fin de acordar una llave secreta (McGrew et al, 2011). El algoritmo DH fue originalmente definido en términos de operaciones en el grupo multiplicativo de un campo con característica prima. Una primera modificación fue realizada por Massey, quien definió el algoritmo en términos de un grupo cíclico arbitrario y, más tarde, se analizó el protocolo DH sobre un grupo de curva elíptica (Koblitz, 1987).

El algoritmo puede ser descrito así: primero las dos partes acuerdan en un conjunto de parámetros de dominio (K,E, q, h, G) de forma similar a ECDSA; luego, el protocolo sigue como se describe en las ecuaciones (3) y (4).

En segunda instancia, la parte A de la comunicación computa K_A, y la parte B computa K_B Ver ecuaciones (5) y (6).

Puesto que K_A= K_B y ambas partes han acordado en la misma clave privada. Los mensajes transferidos son frecuentemente referidos como llaves públicas efímeras, ephemeralpublickeys, ya que toman la forma de llaves públicas con base en logaritmos discretos, pero solo existen por un periodo corto. Dado [a]G y [b]G, el problema de recuperar [ab]G se denomina el problema Diffie-Hellman de curva elíptica, ECDHP. El protocolo ECDH particularmente consume un ancho de banda bajo si se emplea un punto de compresión; además, este es muy eficiente si se compara con la base estándar, el protocolo DH con base en campo finito.

Aplicaciones ecc: mecanismos De seguridad ligeros

Descubrimiento seguro ligero de vecinos

El descubrimiento de vecinos de IPv6 definido por el IETF y la configuración automática de direcciones sin estado, en adelante denominados conjuntamente protocolos de descubrimiento de vecinos (NDP), no son adecuados en referencia a aspectos de seguridad y requieren optimizaciones para ambientes de recursos limitados de baja potencia, que operan en enlaces inalámbricos con alta probabilidad de pérdida como 6LoWPAN (Kushalnagar et al., 2007; Sarikaya et al, 2011). Las optimizaciones para el descubrimiento de Vecino en 6LoWPAN incluyen optimizaciones que deben ser simples (Kandikattu etal., 2008).

Los protocolos NDP no son seguros, especialmente cuando la seguridad física en el enlace no está asegurada y es vulnerable a ataques (Kushal-nagar et al., 2007). El protocolo de descubrimiento de vecinos seguro (SEND) es definido para asegurar NDP. Las direcciones criptográficamente generadas CGA se utilizan en SEND. SEND exige el uso del algoritmo de firma RSA que es computacionalmente intenso y no es adecuado utilizarlo para nodos de bajo consumo de energía y de recursos limitados (Sarikaya et al, 2011). Por consiguiente, el uso de algoritmos de firma y clave pública RSA conllevan a tamaños de mensajes poco adecuados para su uso en enlaces de baja tasa de bits, de corto alcance, asimétricos y no transitivos, como 6LoWPAN.

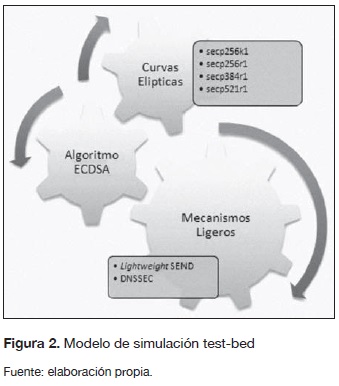
En Sarikaya et al. (2011) se propone una ampliación del protocolo de descubrimiento de vecinos con CGA para 6LoWPAN. Los nodos generan CGA y registran estas direcciones con el enrutador por defecto. La generación de CGA se basa en ECC y la firma se calcula utilizando el algoritmo ECDSA con P-256. La curva por utilizar es la recomendación secp256r1 correspondiente al OID 1.2.840.10045.3.1.7. (Shelby etal, 2010) y el cálculo de la función hash de la clave se basa en SHA-2. El protocolo resultante se denomina protocolo de descubrimiento de vecinos seguro ligero LSEND; la figura 2 ilustra el intercambio de mensajes en el protocolo LSEND.

Extensiones de seguridad a DNS

Las extensiones de seguridad para el servicio de nombres de dominio (DNSSEC) han sido ampliamente definidas por la IETF. DNSSEC utiliza cifrado de claves y firmas digitales para proporcionar autenticación de datos DNS. En Hoffman et al. (2011) se propone la extensión y la aplicación de la ECC para DNSSEC y la definición de dos nuevos algoritmos de firma: ECDSA con la curva P-256 (seguridad aproximada equivalente a RSA con llaves de 3072 bits) y SHA-256, y ECDSA con la curva P-384 y SHA-384, así como el empleo de registros de recursos RR, DNSKEY y RRSIG.

Modelo test-bed de simulación Y evaluación

El objetivo principal de cualquier banco de pruebas o modelo test-bed es facilitar el estudio y la evaluación de las ideas que tienen una visión promisoria en aplicaciones reales. De hecho, en una plataforma real existen también una o varias restricciones físicas de hardware y tal vez de otro tipo. Estas restricciones afectan al rendimiento de los algoritmos implementados. Con el fin de simular y evaluar nuevas ideas en el área de la seguridad informática en escenarios móviles, se ha diseñado e implementado un modelo test-bed de simulación realista. Este modelo permite la evaluación preliminar de nuevos paradigmas y sirve como base para extensiones y futuras investigaciones en el área de la criptografía de curva elíptica e hiperelíptica en escenarios con restricciones de procesamiento y memoria.

El modelo test-bed de simulación y evaluación está construido sobre los pilares de cuatro curvas elípticas secp256kl, secp256rl, secp384rl y sec-p521r (Certicom Research, 2010), cuyos parámetros fundamentales han sido seleccionados según normatividad y su discusión se encuentra en la siguiente subsección "Propiedades de los parámetros recomendados de curva elíptica de dominio sobre". Con base en estos se implementa el algoritmo de firma digital ECDSA descrito en la subsección "Algoritmo de firma digital de curva elíptica ECDSA". Como trabajo futuro de investigación se plantea el desarrollo de mecanismos ligeros de seguridad de acuerdo con el modelo propuesto. Los aspectos principales del modelo test-bed de simulación y evaluación se muestran en la figura 2.

Propiedades de los parámetros recomendados de curva elíptica de dominio sobre 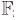_P

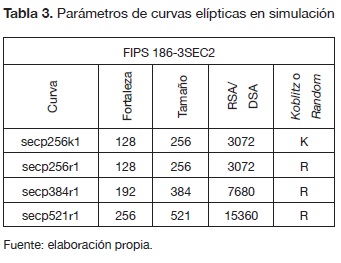
Un elemento clave de la propuesta de modelo simulación test-bed es la selección de la(s) curva(s) elíptica(s) base del criptosistema por evaluar; en este trabajo se emplea la recomendación de curvas y parámetros en Sarikaya et al. (2011); Certicom Research (2010). En la tabla 3 se listan las propiedades de los parámetros de dominio de curva elíptica recomendados y al mismo tiempo la situación con respecto a su alineación con otras normas.

Los parámetros de dominio de curva elíptica aleatorios verificables sobre 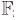p secp256r1 están especificados por la séxtupla T = (p;a;b;G;n;h) donde el campo finito 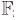p se define por la ecuación (7).

La curva E = y²=xⁱ + ax + b sobre 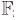_P se define por la ecuación (8).

E fue seleccionada verificable y aleatoria como se especifica en la norma ANSI X9.61 de la semilla. Ver ecuación (9).

El punto base G en forma comprimida es como se muestra en la ecuación (10).

Finalmente, el orden n de G y el co-factor se expresan en la ecuación (11).

Herramientas Y Procedimientos

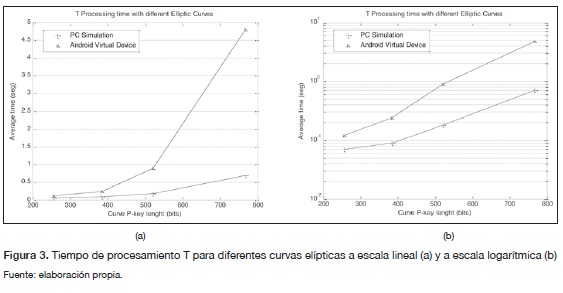
En este modelo se emplea el ambiente de desarrollo Eclipse IDE para desarrolladores Java como base para el sistema de simulación test-bed, en conjunto con el kit de desarrollo de software Android y Herramientas de desarrollo ADT con el fin de emular dispositivos móviles virtuales con restricción de recursos. Para fines comparativos y para establecer una línea base se utiliza MAT-LAB® como una herramienta de simulación de rendimiento en PC del cómputo de las curvas elípticas seleccionadas y el algoritmo de firma digital ECDSA. Estos se utilizan para la evaluación de ECC, donde se comparan los recursos computacionales necesarios y las limitaciones. La figura 3 ilustra el tiempo de procesamiento T para diferentes curvas elípticas empleando longitud de clave desde 256 bits hasta claves de 521 bits. El presente trabajo se centra en la medición del tiempo del algoritmo ECDSA, en los procesos de firma y verificación (tipo aleatorio).

Resultados Y Discusión

Existe una dependencia directa entre el aumento de tiempo de procesamiento en relación con la longitud de la clave, tanto en PC como en el dispositivo de simulación virtual de Android. Sin embargo, para mejorar la seguridad del algoritmo ECDSA por medio de la utilización de una clave de 521 bits, el costo en tiempo aumenta un 87,5 % en el dispositivo Android virtual respecto a la simulación de PC. Así mismo, en los resultados se proyecta el costo en tiempo para una clave hipotética de 768 bits como se muestra en los gráfieos de la figura 3. Existen fuertes limitaciones en las herramientas computacionales del modelo de simulación test-bed, en cuanto a los dispositivos Android virtuales, puesto que no es posible realizar restricción de recursos de memoria en la simulación. En ese sentido, las limitaciones de potencia de procesamiento no se pueden simular con la herramienta seleccionada. El próximo objetivo del estudio es establecer las limitaciones del procesador y de la energía en entornos reales.

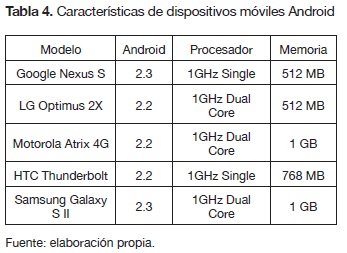
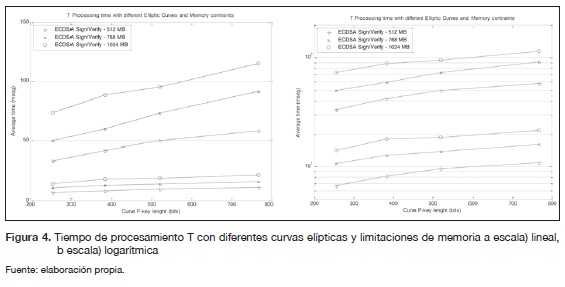
En la tabla 4 se listan las principales características de los dispositivos móviles Android reales, a fin de seleccionar las restricciones de memoria en la evaluación de la simulación. La figura 4 ilustra el tiempo de procesamiento T con diferentes curvas elípticas de longitud de clave de 256 bits de longitud de clave hasta 521 bits y al mismo tiempo con limitaciones en el tamaño de la memoria RAM en el dispositivo Android virtual. Las medidas tomadas son discriminadas por tipo de proceso, es decir, firma (gráficos de la parte inferior) y verificación (gráficos de la parte superior).

Conclusiones Y Trabajo Futuro

La criptografía con base en curva elíptica es cada vez más importante para la nueva generación de tecnologías inalámbricas de comunicaciones hablitadas con IPv6. En este contexto el algoritmo ECDSA es un esquema de firma de la variante ElGamal que se ha propuesto como base de nuevos mecanismos de seguridad de caracter ligero. En este trabajo se midió el costo en tiempo requerido por parte de algoritmos criptográficos ECDSA, que se constituye como base de mecanismos ligeros nuevos; el costo de tiempo aumenta exponencialmente en relación directa con la longitud de la clave y hay un esfuerzo del 85 % adicional para aplicar un esquema de seguridad de mayor fortaleza.

Un elemento clave del modelo de simulación test-bed es la selección de las curvas elípticas, como base del sistema de cifrado. Un aspecto importante a tener en cuenta es el uso de curvas y parámetros estándar tales como los recomendados en FIPS 186-3, normas ANSI. Es importante señalar que el proceso de verificación dentro del algoritmo ECDSA tiene un costo de tiempo más grande que el proceso de registro, además de que se encuentra una relación directa entre la longitud de la clave y el coste de tiempo. El siguiente paso en la investigación es la implementación de los algoritmos criptográficos en un escenario de banco de pruebas reales en dispositivos ligeros basados en hardware, y también la inclusión de otros algoritmos de cifrado en el modelo.

Referencias

Badra, M. y Hajjeh, I. (2009). ECDHEPSK Cipher Suites for Transport Layer Security (TLS). Internet Engineering Task Force RFC 5489.

Blake, G., y Seroussi, N. (2005). Advances in elliptic Curve Cryptography. USA: Cambridge University Press.

Blake, S., Bolyard, N., Gupta, V., Hawk, C. y Moeller, B. (2006). Elliptic Curve Cryptography (ECC) Cipher Suites for Transport Layer Security (TLS). Internet Engineering Task Force RFC 4492.

Certicom Research. (2010). SEC 2: Recommended Elliptic Curve Domain Parameters. Standards for Efficient Cryptography Version 1.0.

Cohen, H., Frey, G., Avanzi, R., Doche, C., Lange, T., Nguyen, K. y Vercauteren, F. (2006). Handbook of Elliptic and Hyperelliptic Cryptography. France: Chapman & Hall/ CRC Taylor & Francis Group.

Dang, Q., Santesson, S., Moriarty, K., Brown, D. y Polk, T. (2010). InternetX.509 Public Key Infrastructure: Additional Algorithms and Identifiers for DSA and ECDSA. Internet Engineering Task Force RFC 5758.

Ehmke, M., Forsgren, H., Grahn, K., Karlsson, J., Karvi, T. y Pulkkis, G. (2009). Securing Control Signaling in Mobile IPv6 with Identity-Based Encryption. Issues in Informing Science and Information Technology, 6, 649-667.

Gwalani, K. y Elkeelany, O. (2009). Design and Evaluation of FPGA Based Hardware Accelerator for Elliptic Curve Cryptography Scalar Multiplication. WSEAS Trans. on Computers, 8(5), 47-53.

Hoffman, P. y Wijngaards, W. (2011). Elliptic Curve DSA for DNSSEC", Internet-Draft (draft-ietf-dnsext-ecdsa-00). Unpublished.

Huang, P. (2008 ) A Research of the Elliptic Curve Cryptology Applies to the IPv6 Protocol. Int. Conf. on Mathematical Methods and Computational Techiniques in Electrical Engineering, 3, 108-115.

Kandikattu, R. y Jacob, L. (2008). A Secure IPv6 based Urban Wireless Mesh Network. Journal on Computer Communications, 37(15), 112-120.

Kandikattu, R. y Jacob, L. (2010). Comparative Analysis of Different Cryptosystems for Hierarchical Mobile IPv6-based Wireless Mesh Network. International Journal of NetworkSecurity, 10(3), 190-203.

Koblitz, N. (1987). Elliptic Curve Cryptosystems. Mathematics of Computation, 48, 203-209.

Kushalnagar, N., Montenegro, G. y Schumacher, C. (2007). IPv6 over Low-Power Wireless Personal Area Networks (6LoWPANs): Overview, Assumptions, Problem Statement, and Goals. Internet Engineering Task Force RFC 4919.

McGrew, D., Igoe, K. y Salter, M. (2011). Fundamental Elliptic Curve Cryptography Algorithms. Internet Engineering Task Force RFC 6090.

Sarikaya, B. y Xia, F. (2008). LightweightSecure Neighbor Discovery for Low-power and Lossy Networks. Internet-Draft (draft-sari-kaya-6lowpan-cgand-00). Unpublished.

Seo, K., Balitanas, M., Cho, E. y Kim, S. (2009). Mobile Network Protocol Vulnerabilities in Advent of IPV6. Journal of Security Engineering, 6, 91-98.

Shelby, Z., Chakrabarti, S. y Nordmark, E. (2010). Neighbor Discovery Optimization for Low-power and Lossy Networks", Internet-Draft (draft-ietf-6lowpan-nd-15). Unpublished.

Turner, S., Brown, D., Yiu, K., Housley, R. y Polk, T. (2009). Elliptic Curve Cryptography Subject Public Key Information. Internet Engineering Task Force RFC 5480.

Victorovich S. (2010). Elliptic Curve Cryptography on Heterogeneous Multicore Platform. M.Sc. Computer Engineering Thesis.Virginia Polytechnic Institute and State University.

Zhu, L., Jaganathan, K. y Lauter, K. (2008). Elliptic Curve Cryptography (ECC) Support for Public Key Cryptography for Initial Authentication in Kerberos (PKINIT). Internet Engineering Task Force RFC 5349.