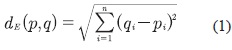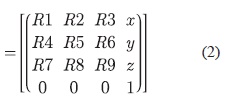Modelos urbanos tridimensionales generados a partir de nubes de puntos de un escáner láser terrestre

Modelos urbanos tridimensionales generados a partir de nubes de puntos de un escáner láser terrestre

Three-dimensional urban models generated from point clouds of a terrestrial laser scanner

Hernán Porras Díaz¹, Jhon Jairo Cáceres Jiménez², Elver Omar Gallo Lancheros³

¹Ingeniero Civil, doctor en Ingeniería Telemática. Docente e investigador de la Universidad Industrial de Santander. Bucaramanga, Colombia. Contacto: hporras@uis.edu.co
²Ingeniero de Sistemas, doctor en Ingeniería Civil. Docente e investigador de la Universidad Industrial de Santander. Bucaramanga, Colombia. Contacto: jcaceres@uis.edu.co
³Ingeniero de Sistemas, candidato a magíster en Ingeniería de Sistemas e Informática. Investigador de la Universidad Industrial de Santander. Bucaramanga, Colombia. Contacto: omga27@gmail.com

Fecha de recepción: 22 de noviembre de 2012-Fecha de aceptación: 23 de noviembre de 2013

Clasificación del artículo: revisión
Financiamiento: Universidad Industrial de Santander

Resumen

En este artículo se presenta una revisión del estado del arte de las diferentes metodologías que se han desarrollado para el tratamiento digital de nubes de puntos tridimensionales, recolectadas mediante un escáner láser terrestre. Este instrumento tiene la capacidad de capturar información topográfica y geométrica de cualquier estructura con precisiones hasta el orden de los milímetros, y en algunos casos también captura la información radiométrica de los objetos escaneados. Esta información recolectada se representa en forma de nubes de puntos que se utilizan en una amplia variedad de aplicaciones como la planeación del crecimiento urbano, el análisis estructural de construcciones, el modelado de fenómenos de erosión y deforestación, la documentación de patrimonio histórico y la navegación virtual a través de los sitios turísticos mediante modelos tridimensionales de edificaciones. Por lo tanto, el propósito de este trabajo es proveer una revisión en el estado del conocimiento acerca de las técnicas desarrolladas en las diferentes fases que se llevan a cabo con el tratamiento de estas nubes de puntos, como el registro y georreferenciación, la segmentación, clasificación y modelado tridimensional.

Palabras clave: clasificación, escáner terrestre, modelo 3D, segmentación.

Abstract

The state of the art of the processing methods for TLS (terrestrial laser scanner) digital point clouds is shown in this paper. The TLS is an instrument able to capture topographic and geometric information of any structure at millimeter accuracy. Also, in some cases, they capture radiometric information of the scanned objects. The collected information is represented by point clouds that are used on a wide range of applications such as planning of urban development, structural analysis, erosion and deforestation modeling, cultural heritage preservation and virtual navigation. The purpose of this work is to offer a review of the state of the art on the methods used through the several steps of the point cloud processing workflow: relative and absolute registration, segmentation, classification and three dimensional modeling.

Key words: classification, model 3D, segmentation, terrestrial scanner.

Introducción

El escaneo a través del láser surgió inicialmente como una respuesta al problema de cómo hacer mediciones sobre la superficie de la tierra con el fin de generar cartografía y modelos digitales de elevación de forma rápida y precisa. Estas mediciones empezaron a ser una realidad con el invento del primer instrumento llamado Electronic Distance Measurement (EDM) (Carter, 1973), el cual posteriormente dio paso a la técnica basada en la medición a través del láser. Con respecto al principio de operación del láser los escáneres se puede clasificar en los basados en tiempo de vuelo y en diferencia de fase, mientras que, con respecto a la plataforma donde se monta el dispositivo, existe el escáner láser aéreo (ALS), el terrestre (TLS) y recientemente el móvil (MLS). El ALS fue introducido comercialmente a comienzos de los años setenta (Fernández Díaz, 2007; Laefer, Truong Hongy Fitzgerald, 2011), con el fin de generar modelos digitales de elevación y de ciudades a gran escala. Posteriormente, a finales de los años noventa es lanzado comercialmente el TLS (Laefer et al., 2011), con el fin de obtener mediciones con alta precisión de los elementos que conforman el mobiliario urbano. El ALS genera baja densidad de puntos, por lo tanto, es ideal para capturar información de grandes áreas en corto tiempo y con precisiones del orden de los centímetros; por su parte, el TLS es usado para capturar información de los objetos a corta distancia, lo que genera una alta cantidad de puntos con precisiones del orden de los milímetros.

La información recolectada por el escáner corresponde a un conjunto de puntos que representan las coordenadas XYZ de la superficie de cualquier objeto con respecto al sistema de referencia del escáner. Adicionalmente, varios de estos dispositivos también pueden capturar la información espectral del objeto, así como su porcentaje de reflectancia que comúnmente se le denomina "valor de intensidad del pulso".

Una de las aplicaciones más importantes que se le ha dado a la nube de puntos generada por el TLS es la creación de modelos digitales tridimensionales de los elementos que conforman un entorno urbano, tales como fachadas de edificios, puentes. vías y señales de tránsito, entre otros. Este artículo presenta una revisión general sobre las metodologías que algunos investigadores han llevado a cabo para la generación de modelos tridimensionales a partir de una nube de puntos. En la sección dos se muestra un estudio más detallado sobre las características y el funcionamiento del TLS. En la sección tres se presentan las técnicas que existen para llevar a cabo el procesamiento de la nube de puntos, como el registro, la georreferenciación, la segmentación, la clasificación y el modelado 3D. Finalmente, en la sección cuatro se exponen las conclusiones con respecto al estado del arte de la tecnología del escáner laser terrestre.

Recolección De Datos

Escáner láser terrestre (TLS)

Es un sistema basado en la tecnología láser que permite obtener una muestra de la superficie de un objeto de diferente forma y tamaño (Van Gen-chten, 2008; Bornaz y Rinaudo, 2004). El resultado es una nube de puntos con gran detalle en la geometría y con un alto grado de precisión, que se captura de una manera rápida y eficiente (Yan, Liy Xie, 2010). Estos instrumentos han sido ampliamente usados en la adquisición de información en las áreas urbanas, con el fin de generar modelos tridimensionales de las ciudades (Sithole y Vos-selman, 2003; Vosselman y Dijkman, 2001). Así mismo, son utilizados en la planeación urbana, la navegación virtual de los sitios turísticos, el análisis del estado estructural de los edificios, la detección de posibles zonas de inundación mediante el análisis de la topografía del terreno, la evaluación y análisis de seguridad de vías y puentes, la documentación de áreas de desastre cuando el evento ya ha ocurrido, el registro de la escena del crimen para evitar alteraciones de las evidencias y el suministro de información para los mapas de los Sistemas de Información Geográfica (SIG), entre otros (Van Genchten, 2008).

Principios de operación

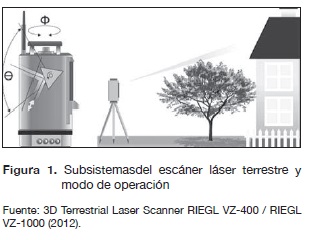
El TLS está compuesto por dos subsistemas básicos: el primero es un dispositivo electrónico de emisión del rayo láser comúnmente llamado Light Detection and Ranging (LIDAR), y el segundo es un dispositivo mecánico y óptico capaz de dirigir el haz de láser en forma de escaneo sobre el área de interés (Fernández Díaz, 2007), como se muestra en la figura 1. Con respecto al principio de operación del láser, los dos tipos más comunes de escáneres son los de tiempo de vuelo (TOF), y los de diferencia de fase (PD) (Van Genchten, 2008; Fernández Díaz, 2007).

El tipo de escáner TOF calcula el tiempo transcurrido desde el momento en que sale el pulsodel láserhasta que retorna; con este valor calcula la distancia del objetivo.Lapropiedad de pulso permite obtener una buena señal de retorno a pesar deque existan condiciones de ruido en el ambiente. Algunos escáneres comerciales basados en esta tecnología son: Optech ILRIS-3D (Optech, 2012), Leica ScanStation C10 (Leica, 2012a), Riegl (toda la gama) (Riegl, 2012), Trimble VX (Trimble, 2012a), Callidus CP3200 (Van Genchten, 2008), entre otros. El tipo de escáner PD calcula la distancia mediante la diferencia de fase entre las formas de las ondas enviadasy de las retornadas. El láser emitido por este tipo de escáner es contínuo y de potencia modulada. Algunos escáneres comerciales disponibles basados en esta tecnología son:

Z+F Imager 5010 (Z+F, 2012), Trimble FX (Trimble, 2012b), Leica HDS7000 (Leica, 2012b), Faro Focus 3D (Faro, 2012), entre otros.

Características técnicas

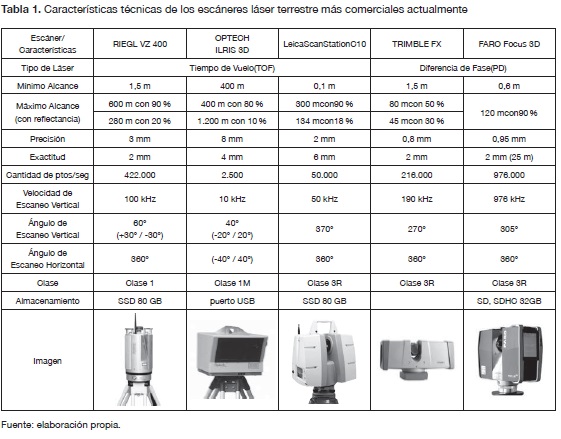
Actualmente existe en el mercado un amplio rango de TLS, donde cada uno posee especificaciones técnicas de acuerdo con la necesidad del usuario final, ver tabla 1. Las características técnicas más importantes que se deben tener en cuenta al momento de adquirir un TLS son: el alcance mínimo y el máximo que se mide en metros; la precisión, que hace referencia al grado de dispersión de un conjunto de mediciones sobre la media de ese valor; la exactitud, que es la cercanía de una medición respecto a su valor real; el campo de visión, que se expresa en grados y describe el ángulo d barrido vertical que realiza el escáner; la clase de láser, que depende de su potencia y su longitud de onda y que indica el grado de peligro para el ojo humano basado en la exposición máxima permisible (MPE) al rayo; la velocidad de escaneo y la cantidad de puntos por segundo que es capaz de recolectar (Van Genchten, 2008; Fernández Díaz, 2007). Los tipos de escáner TOF tienen mayor alcance y velocidad de escaneo que los de tipo PD, mientras que estos últimos poseen mayor precisión y recolectan más cantidad de puntos por escaneo que los escáneres basados en TOF.

Procesamiento De Los Datos

El resultado del escaneo a través del TLS es un conjunto de puntos generalmente llamado "nube de puntos", cuya definición fue propuesta por el Dr. Jon Mills y David Barberen en 2003, "la nube de puntos es un conjunto de coordenadas XYZ en un sistema de referencia común, que le muestra al espectador una comprensión de la distribución espacial de un objeto en el sitio. También se puede incluir información adicional como un valor de intensidad o un valor RGB" (Reshetyuk, 2009, p.4).

El formato en que se almacena la nube de puntos depende del software del fabricante; algunos formatos solo contienen la información de las coordenadas XYZ del punto, mientras que otros, además de las coordenadas, contienen otro tipo de información como el porcentaje de intensidad del pulso láser, el valor del vector normal de cada punto y la posición del escáner, entre otros. Los formatos más comunes para el almacenamiento de nube de puntos son: XYZ, PTX, PTS, XYZRGB, LAS y FLS.

Para la generación de modelos tridimensionales a partir de los datos de un TLS, se requiere hacer un tratamiento especializado de la nube de puntos que consiste en varias etapas entre las cuales se destacan: el registro y la georreferenciación, la segmentación, la clasificación de los objetos contenidos dentro de la nube de puntos y el modelado 3D de estos objetos.

Registro de la nube de puntos

En la mayoría de los casos, los objetos que se van escanear son demasiado grandes o poseen formas muy complejas para que puedan ser escaneados desde una sola posición: por esta razón, es necesario ubicar el escáner desde diferentes lugares con el fin de obtener la información completa del objeto. Cada posición de escaneo posee sus propias coordenadas locales cuyo origen está en el escáner. Por lo tanto, para obtener una representación completa del objeto escaneado, las nubes de puntos deben ser transformadas a un sistema de coordenadas común o al sistema de coordenadas de algunas de las posiciones de escaneo. Existen varios enfoques para el registro de nube de puntos:

• Registro basado en puntos artificiales {targets): son elementos fabricados con material reflectante con el fin de ser identificados más fácilmente dentro de la escena y así poder determinar con alto grado de exactitud sus posiciones en el sistema de coordenadas usado para el registro. En la práctica, se necesita tener al menos tres targets con sus posiciones dentro de un sistema de coordenadas conocido.
• Registro usando puntos naturales: para el caso que no sea posible colocar los targets debido a las condiciones de la escena, se utilizan diferentes puntos con características naturales que sean visibles dentro de la nube de puntos, por ejemplo, bordes de acero o esquinas de edificios. Después del escaneo, estos puntos naturales son usados como puntos de enlace que se identifican manualmente en la nube de puntos o se escanean separadamente con una alta resolución para una mejor identificación. En la práctica se recomienda usar al menos cuatro puntos naturales.
• Registro mediante emparejamiento de superficies: consiste en alinear las nubes de puntos por medio de las superficies geométricas de dos escaneos. Este algoritmo estima la distancia euclidiana entre fragmentos de superficies por mínimos cuadrados e intenta minimizar las distancias de forma iterativa.

Georreferenciación de la nube de puntos

Es el proceso de transformación de la nube de puntos registrada con el sistema de coordenadas del escáner, a un sistema de coordenadas externas (geodésicas) que pueden ser de ámbito local o global (Reshetyuk, 2009). Actualmente existen diferentes técnicas para llevar a cabo este proceso y se pueden clasificar en dos grandes grupos:

• Georreferenciación indirecta: en esta técnica los targets poseen un sistema de coordenadas geodésicas conocido, lo que permite la transformación de las coordenadas de una nube de puntos al sistema de coordenadas de ellos. Estos targets son llamados puntos de control y sus coordenadas pueden ser determinadas mediante un levantamiento topográfico con una estación total o con equipos de posicionamien-to global (GPS). Otra técnica de georreferen-ciación indirecta consiste en alinear la nube de puntos recolectada con otra que ya tenga un sistema de coordenadas establecido y, mediante el algoritmo llamado Iterative Closest Point (ICP), se determina el mejor emparejamiento entre las dos mediante la minimización de una función de distancia. Como el ICP usa la información geométrica (XYZ) de la nube de puntos, cuenta con seis grados de libertad (traslación y rotación en los tres ejes de coordenadas) para realizar el ajuste. En cada iteración el ICP realiza los siguientes pasos:

□ Encuentra los puntos más cercanos usando la distancia euclidiana entre las dos nubes de puntos. Ver ecuación (1).



□ Después calcula la alineación de la nube de puntos mediante una transformación geométrica, que consiste en encontrar la mejor matriz de rotación/traslación necesaria para lograr el ajuste mediante métodos como el de descomposición de valores singulares (SVD) (Wall, Andreasy Rocha, 2003) o mediante Quaterniones (Kuipers, 2002). Esta matriz está compuesta por una matriz interior de rotación de 3x3 y su cuarta columna corresponde al vector de traslación. Ver ecuación (2).



□ Después de aplicar la matriz de transformación a la nube de puntos se regenera en una nueva nube con un sistema de coordenadas diferente. Este proceso se realiza iterativamente hasta que se minimice la función de error o se cumpla el criterio de parada definido por el usuario.

• Georreferenciación directa: en este método se establece el sistema de referencia geodésico directamente sobre el TLS al momento de realizar el escaneo. Esto se puede realizar de dos maneras: con la ubicación del escáner sobre un punto con sistema de coordenadas geodésicas conocido o mediante el montaje de un equipo GPS sobre el TLS. Comparado con el método de georreferenciación indirecta, este enfoque es más económico y menos costoso en tiempo, ya que no requiere de una estación total, ni de puntos de control en la escena.

Segmentación de la nube de puntos

La segmentación puede definirse como el proceso de etiquetado de cada uno de los puntos, donde los que pertenecen a una misma superficie o región se les asigna la misma etiqueta (Rabbani, Van den Heuvely Vosselman, 2005). En otras palabras, es el proceso de agrupar espacialmente dentro de regiones homogéneas (segmentos), puntos que contengan características similares. Un segmento es un subconjunto cerrado dentro de la nube de puntos, en donde cada punto pertenece solo a un segmento y no hay dos segmentos que tengan puntos en común.

Selección y extracción de características

La selección de características tiene como objetivo principal la elección de los atributos más relevantes de cada punto o segmento, con el fin de disminuir ⁽²⁾ su cantidad y eliminar información redundante para el proceso de segmentación o clasificación (Dash y Liu, 1997). Este procedimiento en muchos casos es subjetivo y se consigue mediante técnicas de prueba y error, aunque también existen algunos métodos para realizar este proceso (Kira y Rendell, 1992; Narendra y Fukunaga, 1971).

La extracción de características consiste en la transformación del espacio de características formado por los atributos de los puntos o segmentos, en un nuevo espacio que resalte mejor la información relevante y remueva la redundante. En algunos casos, esta transformación conlleva a una reducción en la dimensión del espacio de características. Entre las técnicas más usadas se encuentran: el análisis de factores, el análisis de discriminantes lineales y el Principal Component Analysis (PCA) (Sithole, 2005; Leal y Leal, 2006). Algunos trabajos han utilizado este último método para la detección de postes (Liberge, Soheilian, Chehata y Paparoditis, 2010;Yokoyama, Date, Kanai y Take-da, 2011), o para la detección de elementos urbanos (El-Halawany, Moussa, Licht, y El-Sheimy, 2011; El-Halawany y Lichti, 2011).

Las características más importantes de cada punto o segmento que se utilizan en el proceso de segmentación o de clasificación están definidas de la siguiente manera (Pu y Vosselman, 2006; Pu y Vosselman, 2009a; Pu, Rutzinger, Vosselman, y Oude Elberink, 2011):

• Características geométricas: a) El tamaño: es la característica más distintiva y hace referencia a la longitud, ancho, altura, área y volumen. Por ejemplo, en las fachadas, las paredes o puertas se pueden distinguir fácilmente de otros objetos por su tamaño. b) La posición: algunos objetos se esperan que se encuentren en cierta posición con respecto a la escena. Por ejemplo, las ventanas y puertas siempre se encuentran sobre la pared, mientras que el techo siempre se encuentra en la parte superior. c) La orientación: esta característica generalmente puede ser predecible en los objetos. Por ejemplo, las paredes siempre se encuentran en forma vertical, mientras que la superficie del terreno es horizontal, d) La densidad: en el caso de las ventanas, el pulso del láser penetra el vidrio y difícilmente retorna la información, produciendo una muy baja densidad de puntos dentro estas áreas. Otras características importantes son: el perímetro, la dispersión y la forma geométrica.
• Características radiométricas: son las que están asociadas con el valor del porcentaje de intensidad del pulso retornado. Algunos TLS también pueden capturan imágenes, lo que permite asociar la información espectral a cada punto de la nube.
• Características topológicas: tienen que ver con la relación espacial que existe entre los segmentos, que puede ser definida por la adyacencia y conectividad que existen entre ellos. Por ejemplo, el terreno y el techo siempre se interceptan con las paredes.

Las características más importantes a nivel del punto son: el valor de intensidad del pulso láser, el ancho del pulso (Rutzinger, Hófle, Hollaus y Pfeifer, 2008), y la información espectral obtenida de imágenes digitales tomadas con una cámara (Rottensteiner, Trinder, Clode y Kubik, 2005). Por su parte, en el segmento se encuentran: la altura promedio, el volumen estimado, la desviación estándar, la cantidad de puntos por segmento y el porcentaje de puntos del último eco (Vosselman, 2009). Existen varios métodos para la segmentación de nube de puntos que se pueden clasificar de la manera en que se expone a continuación.

Segmentación basada en la detección de bordes

Este método detecta discontinuidades en las superficies que se forman cerca de los límites de los objetos contenidos en la nube de puntos; por lo tanto, este proceso inicia con la identificación de la extensión de la superficie que está determinada por los bordes y las intersecciones, donde los puntos que se localizan dentro de la frontera se consideran que pertenecen a una misma región (Belton, 2008). El desempeño de este tipo de segmentación está determinado por el detector de bordes (Sithole, 2005; Wang y Shan, 2009; Canny, 1986). La detección de bordes consiste en estimar una superficie plana dentro del vecindario alrededor de un punto de interés, para determinar el valor de la normal de esta superficie (Hoppe, De-Rose, Dumpchamp, McDonald y Stuetzle, 1992). Este proceso comúnmente se realiza a través del método PCA (Johnson y Wichern, 2002) o mediante regresión de mínimos cuadrados (Shakarji, 1998). Por lo tanto, la variación en la dirección de la normal de la superficie proporciona un indicador del nivel de curvatura o de cambio de la superficie local que permite identificar los bordes (Pauly, Gross y Kobbelt, 2002).

Segmentación basada en el crecimiento de regiones

Esta técnica consiste en detectar superficies continuas que tengan propiedades geométricas similares (Woo, Kang, Wangy Lee, 2002). El proceso comienza examinando un punto semilla que se asocia a un segmento que va creciendo mediante la inspección de los demás puntos alrededor de este punto semilla. El crecimiento se inicia a partir del punto más cercano hasta que se agoten los demás puntos candidatos, ya sea por eliminación de ellos o por la inclusión dentro de un segmento (Vosselman, Gorte, Sitholey Rabbani, 2004;Sa-pkota, 2008;Pu y Vosselman, 2006). El trabajo presentado en Hoover et al. (1996) proporciona una comparación de métodos de segmentación para encontrar superficies planas. En Rabbani et al. (2005) presenta un método que consiste en dos pasos: estimación de la normal de la superficie local mediante los k-vecinos más cercanos y el crecimiento de regiones que se ejecuta usando las normales de los puntos estimados; en esta fase los puntos son agregados al segmento mediante una medida de proximidad y un criterio de suavidad de la superficie.

Segmentación basada en la agrupación de características (clustering)

En este método cada punto es asociado a un vector que contiene las mediciones de sus propiedades geométricas y radiométricas comúnmente llamadas "características" (Sapkota, 2008) (ej. las coordenadas XYZ, el vector normal de la superficie local, el valor de intensidad y la información espectral del objeto). Esas características son representadas en un sistema de coordenadas de n-dimensiones (Sithole, 2005), en el que los puntos se agrupan en regiones compactas y separadas, comúnmente llamadas "clústeres". En Filin (2002) se define un vector de características de siete dimensiones. El espacio formado por estos vectores es agrupado usando un algoritmo de modo de búsqueda que permite identificar las superficies de los segmentos; finalmente, estos segmentos son agrupados en el espacio de objetos con base en una medida de proximidad.

Otro método es el basado en grafos, que consiste en la implementación de un grafo de atributos G(V, ΕJ de una nube de puntos V y las aristas E_A que están basadas en medidas de proximidad. En Zahan ( 1971) se usa un grafo llamado Minimum Spanning Tree (MST) y define que las aristas que no cumplen con un criterio de proximidad son aquellas cuyos pesos son significativamente más grandes que el promedio de los pesos de las aristas más cercanas. En Klasing, Wollherr y Buss (2008) cada nodo es conectado a los vecinos que se encuentren dentro de un radio predefinido. La principal ventaja de esta técnica es que es com-putacionalmente menos costosa que los demás algoritmos basados en grafos, ya que no hace una búsqueda sobre todos sus vecinos cada vez que está examinando algún nodo en particular, sino que la búsqueda la realizan solamente en los vecinos que se encuentran dentro del radio definido.

Segmentación basada en la línea de escaneo

Esta técnica adopta la estrategia de división y unión, donde la nube de puntos es dividida en líneas de escaneo a lo largo de una dirección (Wang y Shan, 2009). Estas líneas son divididas de forma recursiva e independiente en segmentos de líneas rectas, hasta que la distancia perpendicular de los puntos a su correspondiente segmento de línea esté por debajo de un umbral definido. Posteriormente, los segmentos de líneas de escaneo son unidos basados en alguna medida de similitud mediante el método de crecimiento de regiones (Jiang y Bunke, 1994). En Sithole y Vosselman (2003) se describe un método de segmentación que agrupa puntos de líneas de escaneo basado en una medida de proximidad. Estos grupos no necesitan corresponder a una secuencia de puntos en la línea de escaneo; por lo tanto, todos los puntos están presentes en cada conjunto de líneas de escaneo y varios de ellos tendrán diferente orientación. Esta propiedad es usada para unir estos segmentos de líneas en regiones.

Segmentación mediante el ajuste a un modelo

Este tipo de segmentación se basa en la premisa de que los objetos hechos por el hombre pueden ser escaneados y se pueden descomponer en primitivas geométricas tales como planos, cilindros y esferas (Schnabel, Roland, Wessel y Klein, 2007). Este enfoque intenta ajustar formas geométricas en la nube de puntos; por lo tanto, aquellos puntos que se ajusten a la representación matemática de alguna forma geométrica son etiquetados como pertenecientes a un segmento. Entre los métodos para la estimación de parámetros que permiten la extracción de formas geométricas dentro de una nube de puntos se destacan la Transformada de Hough 3D (Vosselman y Dijkman, 2001; Pu y Vosselman, 2009a; Vosselman et al., 2004) y el Random Sample Consensus (RANSAC) (Schnabel, Roland et al., 2007; Schnabel, Wahly Klein, 2007).

Otros métodos de segmentación

La segmentación basada en "voxels" convierte la nube de puntos en una malla 3D, donde las celdas que conforman esta malla son pequeños cubos llamados "voxels" (volumen elements), que es similar al concepto de los pixeles (picture elements) para el caso 2D. El algoritmo propuesto en Gorte y Pfeifer (2004) inicia con la conversión de la nube de puntos a un raster 3D. El siguiente paso es el proceso de "esqueletonización", que consiste en la remoción iterativa de voxels que no hacen parte del objeto, con el fin de dejar al descubierto los componentes que conforman su estructura y las relaciones topológicas entre ellos. Posteriormente, la segmentación se hace sobre los esqueletos de los objetos para luego hacerla transformación, pero esta vez de voxels segmentados a nube de puntos segmentada.

La segmentación es una etapa importante aunque no necesaria (Velizhev, Shapovalovy Schindler, 2012) para el siguiente paso, que consiste en la clasificación de los objetos, ya que permite identificar los segmentos claves y reducir el ruido en los datos. Así, logra un mejor desempeño en los algoritmos de clasificación. Sin embargo, en otras investigaciones la etapa de clasificación se realiza antes de la segmentación (Belton, 2008).

Clasificación de objetos en nube de puntos

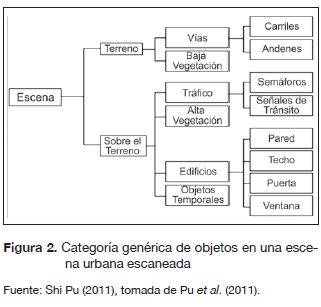
La clasificación consiste en la separación de puntos o segmentos, según sea el caso, en diferentes clases que han sido previamente definidas (ej. edificaciones, vegetación, terreno, etc.), mediante la evaluación de sus características intrínsecas o naturales, donde para cada clase existe un conocimiento previo sobre su naturaleza (Fernández Díaz, 2007). Para el caso de los elementos que conforman un entorno urbano, los objetos poseen un número de rasgos distintivos y organizados de manera jerárquica dentro de cualquier escena, tal como se visualiza en la figura 2. La mayoría de los trabajos realizados con datos de un TLS se han enfocado en el reconocimiento de fachadas de edificios (Pu y Vosselman, 2006; Pu y Vossel-man, 2009a; Pu y Vosselman, 2009b), mientras que otros se han orientado más en la detección de elementos de las vías (Liberge et al., 2010; El-Halawany y Lichti, 2011; Pu et al., 2011). Con base en los tipos de características, la clasificación se puede categorizar basada en las propiedades radiométricas o geométricas de los puntos (Belton, 2008):

Clasificación basada en las características radiométricas

Este tipo de clasificación se basa en la información espectral de cada punto (intensidad del pulso o color)que depende de las propiedades de cualquier superficie, como su reflectancia, textura, el ángulo de incidencia, así como de las especificaciones del escáner (Lichti y Harvey, 2002; Pfeifer, Dorninger, Haring y Fan, 2007). En Gordon, Li-chti y Stewart (2001) se utiliza el valor de intensidad para la clasificación de superficies continuas, ya que permite la diferenciación entre los elementos que conforman las fachadas. Otros trabajos se han concentrado en combinar la información de color de imágenes 2D con la nube de puntos 3D (Lichti, 2005; Jansa, Studnicka, Forkert, Haring y Kager, 2004).

Clasificación basada en las características geométricas

Este tipo de clasificación se basa en la información geométrica derivada de las coordenadas 3D de los puntos. Como esta información es común para todas las nubes de puntos independientemente del TLS que se use o de la configuración que tenga el dispositivo, es el tipo de clasificación más usado.

En Vosselman et al. (2004) se presenta una vista general de las diferentes técnicas para la extracción de superficies planas, cilindricas y esféricas en nubes de puntos, con base en los parámetros de cada una de estas formas geométricas. En Pu et al. (2011) se presenta un trabajo basado en la técnica de detección de forma para la localización de señales de tránsito, que inicia con una segmentación mediante el crecimiento de regiones (Vosselman et al., 2004). Luego, se extraen las características con base en el enfoque propuesto en Pu y Vosselman (2009a) y en Pu y Vosselman (2009b) y finalmente, cada segmento es ajustado a una envolvente convexa, con el fin de comparar su área con las áreas de las señales de tránsito en estudio (rectangular, triangular y circular) y realizar el proceso de clasificación.

En Pu y Vosselman (2006) se presenta un enfoque automático para la extracción de objetos de las fachadas dentro de una nube de puntos. Inicialmente se definen las clases que conforman las fachadas de las edificaciones (pared, puerta, ventana, techo, salientes y entrantes). Después se aplican algoritmos de segmentación para agrupar las superficies planas. Luego se extraen las características más relevantes de cada segmento y se establecen sus restricciones basadas en el conocimiento humano. Cada segmento es ajustado a una envolvente convexa con el fin de definir los rangos de valores de las características. Finalmente, el proceso de clasificación confronta cada segmento mediante las restricciones de las características para determinar la clase a la cual pertenece (Pu y Vosselman, 2009a).

Una técnica para la detección de múltiples objetos en un entorno urbano fue presentado en Golov-inskiy, Kim y Funkhouser (2009). Este algoritmo inicia con la localización potencial de los objetos, basándose en la alta densidad de puntos que estos poseen; después se aplica un método de segmentación para remover los puntos del terreno. La extracción de características se lleva a cabo con base en la forma y el contexto. Y en la etapa de clasificación, cada vector de características del objeto candidato es clasificado con respecto a un conjunto de entrenamiento etiquetado manualmente.

En la tesis presentada en Belton (2008) se realiza un proceso de clasificación a nivel de punto. Basado en las características geométricas, los puntos füeron etiquetados en tres clases: superficie, frontera y borde. Esta clasificación se llevó a cabo con base en las propiedades algebraicas de continuidad y de diferencial de los segmentos de las superficies, mediante algoritmos del vecindario más cercano y varianza de la curvatura del vecindario (Belton y Lichti, 2006).

El trabajo presentado en Velizhev et al. (2012) se basa en la detección y el reconocimiento de objetos pequeños y compactos de un entorno urbano (ej. carros, señales de tránsito y lámparas). El proceso inicia con el filtrado de los puntos del terreno mediante el algoritmo de RANSAC, luego, se extraen grupos de puntos llamados "componentes conectados", los cuales se consideran como potenciales objetos. Después se evalúan las características de cada componente (ej. altura, volumen, descriptor spin-image) y, finalmente, se aplica un algoritmo de clasificación supervisada llamado Implicit Shape Models (ISM), que reconoce los objetos mediante un sistema de votación de las localizaciones de sus centros.

Otro tipo de clasificación de nubes de puntos está basado en el enfoque estadístico (Luo y Sohn, 2012), donde los parámetros del modelo y las probabilidades a posteriori son estimadas mediante el ajuste de un modelo Gaussiano mixto usando el algoritmo Expectation Maximization (EM). En la fase de análisis de características se detectaron tres tipos de objetos en el entorno urbano: los objetos hechos por el hombre, que generalmente son superficies planas o cilíndricas con algún valor de reflectancia (ej. edificaciones y postes de luz); los objetos naturales, que son superficies irregulares con poca reflectancia (ej. los árboles, el suelo); finalmente, los objetos dinámicos, tales como los peatones y vehículos, que generalmente son de pequeña altura y obstruyen a los dos tipos de objetos anteriores.

Generación de modelos tridimensionales

Una vez identificados los objetos dentro de la nube de puntos en la fase de clasificación, se lleva a cabo el proceso de visualización mediante la generación de un modelo tridimensional con las dimensiones extraídas de los objetos. Aunque existen aplicaciones comerciales para la transformación de la nube de puntos en modelos sólidos, muchos de los procesos tienen limitaciones significativas como la dependencia de geometrías preestablecidas que no reflejan suficientemente la geometría de una edificación, la dependencia de un programa basado en dibujo asistido por computador (CAD) y la incapacidad de operar de manera óptima con datos dispersos e información faltante (Laefer et al., 2011). Existen dos enfoques dominantes que se nombran a continuación.

Geometría sólida constructiva- Constructive Solid Geometry (CSG)

En este enfoque se construyen los modelos a partir de una serie de sólidos primitivos simples (caja, esfera, cilindro y aros) y de operaciones booleanas como: unión, intersección y diferencia (Laefer et al., 2011; Hoffman y Rossignac, 1996). El proceso de construcción de los modelos tridimensionales se realiza en forma de árbol llamado CSG-Tree, donde los sólidos primitivos simples son las hojas y las operaciones booleanas se almacenan como nodos interiores (Goldman, 2009).

Representación de fronteras - B-rep (Boundary Representation)

En este enfoque la estructura geométrica consta de vértices, curvas y superficies junto con los datos numéricos que describen la posición, el tamaño y la orientación, mientras que la estructura topológica de los modelos adyacentes consta de vértices, aristas y caras, junto con punteros que almacenan la información de la conectividad (Hoffman y Rossignac, 1996; Goldman, 2009).

Un trabajo basado en el enfoque B-rep para la reconstrucción de superficies se presenta en Loren-sen y Cline (1987) denominado Marchin gCubes. El proceso inicia con la subdivisión del espacio de coordenadas en voxels; aquellos voxels que contengan algún elemento de la superficie son remplazados con una serie de triángulos alrededor de los puntos hasta formar polígonos. Después se realiza la unión de los cubos adyacentes a través de sus vértices vecinos para producir la malla poligonal de la superficie. Otro trabajo presentado en Azernikov y Fischer (2004) se basa en la aproximación de la conectividad de grafos a partir del modelo Hierarchical Space Decomposition Model (HSDM) y la reconstrucción de caras. El proceso se divide en las siguientes etapas: construcción del HSDM a partir de la nube de puntos, extracción de superficie mediante la conectividad de grafos, la reconstrucción de caras y, finalmente, la reconstrucción de la malla y su extensión mediante la incorporación de los vectores normales.

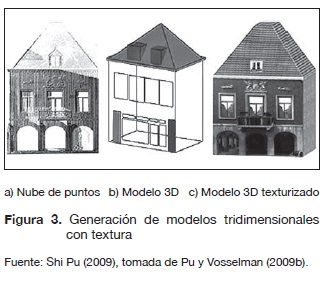
Otro enfoque para la reconstrucción de superficies está basado en la triangulación de Delaunay, que consiste en la generación de una red irregular de triángulos (TIN) a partir de todos los puntos de la escena. El trabajo presentado en Pu y Vosselman (2007) para la detección de ventanas inicia con la generación de un TIN para los segmentos de la fachada; como las ventanas presentan menor densidad de puntos entonces los triángulos son más grandes en esa área, y esta característica permite detectar estos segmentos más fácilmente para luego ser ajustados a un rectángulo mínimo delimitante. En Pu y Vosselman (2009a) y Pu (2007) se presenta un enfoque para la generación automática de modelos de edificaciones mediante ajuste a polígonos. En su etapa de modelado los objetos reconocidos son ajustados directamente a polígonos convexos mediante los métodos: Quick Hull (Barber, Dobkiny Huhdanpaa, 1996), mínimos cuadrados o transformada de Hough (Vosselman et al, 2004). En las partes ocultas de las edificaciones se hacen suposiciones a partir de las partes visibles y del conocimiento acerca de estas y luego se completa el modelo mediante la combinación de los polígonos ajustados y las suposiciones de las partes ocultas. En Pu y Vosselman (2009b) se da un toque más real a los modelos tridimensionales, con la ejecución de un método para la aplicación de color y textura a partir de imágenes digitales, tal como se visualiza en la figura 3.

En Boissonnat (1984) se propone un método para reconstruir una malla mediante la triangulación de superficies a partir del vecindario de un conjunto de puntos aplicando el método de mínimos cuadrados. Esta triangulación se propaga hasta que no existan más puntos libres de manera similar a la técnica de crecimiento de regiones.

Actualmente, existen en el mercado algunas herramientas comerciales de software para la transformación de nube de puntos en superficie en modelos sólidos. Estas aplicaciones se pueden clasificar en dos categorías: las que dependen de un software intermediario CAD o comúnmente llamado "Add-on" para plataformas CAD y las aplicaciones independientes (Bradley y Currie, 2005). Los tipos de archivos de salida de estas aplicaciones son: DXF, SAT, STEP, STL, entre otros. A pesar de que estas aplicaciones facilitan la construcción de un modelo, aún presenta varias desventajas como el consumo considerable de tiempo, ya que no se puede generar un modelo satisfactorio sin algún grado de posprocesamiento manual (Young et al., 2008; Viceconti, Zannoni y Pierotti, 1998).

Tendencias Y Trabajos Futuros

En Batty, Chapman y Evans (2000) se presenta un estado del arte sobre las diferentes aplicaciones que se la han dado a los modelos de ciudades en 3D, entre las que se destacan: los servicios de emergencia, la planeación urbana, las telecomunicaciones, la arquitectura, el turismo, entre otros.

Una de las tendencias más importantes que se está llevando a cabo con el uso de estos modelos es para el análisis SIG 3D. En Moser, Al-brecht y Kosar (2010) se basaron en estudios de casos reales para resaltar las capacidades de análisis 3D, las cuales fueron estructuradas en categorías como: funciones de análisis espacial (Tomlin, 1991) y operaciones con datos en 3D (Moser, 2010). Las categorías que se plantearon para el análisis SIG 3D fueron: a) el análisis de proximidad, usada para el cálculo de distancias, buffer e intersecciones entre objetos 3D; b) el análisis de propagación de volumen o dinámica de flujos, utilizada para modelar la dinámica de las corrientes de aire a través de las edificaciones con el fin de evaluar la distribución de la contaminación en la ciudad; c) la densidad en 3D, para examinar las posibles ubicaciones de antenas para la cobertura de la telefonía móvil y el análisis de visibilidad, que permite identificar las áreas que son visibles desde alguna posición del observador sin tener que generar vistas con perspectiva (Moser et al. 2010).

Recientes investigaciones están conduciendo al enriquecimiento semántico de los modelos de ciudades 3D para el desarrollo urbano sostenible. CityGML (Gróger, Kolbe, Czerwinski y Nagel, 2008) es la primera norma estándar relacionada con este tipo de modelos, donde se intenta proporcionar una descripción de las propiedades geométricas, topológicas y semánticas de los objetos 3D, que permiten enriquecer estos modelos con información importante relacionada con los diferentes temas urbanos. En Métral, Ghoula, y Falquet (2012) se aborda el problema relacionado con la visualización de modelos de ciudades 3D enriquecidos, y proponen una representación formal de las técnicas de visualización existentes en forma de una ontología de técnicas de visua-lización 3D. Igualmente, en Billen, Zaki, Ser-vi�res, Moreau, y Hallot (2012) se propone una ontología del espacio para fortalecer el diseño de modelos de ciudades 3D basados en el estándar CityGML. Otras investigaciones acerca de la reconstrucción urbana se llevan a cabo en la Sociedad Internacional de Fotogrametría y Sensores Remotos (ISPRS) en la comisión III, grupo de trabajo 4 (ISPRS, 2013) y en la Cooperación Europea en Ciencia y Tecnología (European COST Action, 2013).

Conclusiones

El desarrollo de la tecnología del escáner láser ha revolucionado la forma del levantamiento de la información topográfica tanto en el área urbana como en la rural. La gran ventaja que tiene esta tecnología es la rapidez y la precisión con la que captura los datos que se representan en forma de una nube de puntos que implícitamente contiene las coordenadas XYZ, el porcentaje de reflectancia y el color de las superficies escaneadas.

El gran volumen de datos recolectados mediante TLS ha impulsado el desarrollo de investigaciones para llevar a cabo el tratamiento de dicha nube de puntos; algunos de ellos se han enfocado en el desarrollo de algoritmos para el registro, filtrado, segmentación y visualización de nube de puntos, mientras que otros trabajos han hecho énfasis en el reconocimiento y clasificación de objetos.

Financiamiento

Este trabajo forma parte el proyecto de investigación "Herramienta para automatizar la generación de un modelo tridimensional de elementos urbanos", financiado por la Universidad Industrial de Santander (UIS) y por el grupo de investigación Geomática adscrito a la Escuela de Ingeniería Civil de la UIS.

Referencias

Azernikov, S. y Fischer, A. (2004). Efficient surface reconstruction method for distributed CAD. Computer-AidedDesign, 36(9), 799-808.

Barber, C. B., Dobkin, D. y Huhdanpaa, H. (1996). The Quickhull Algorithm for Convex Hulls. ACM Transactions on Mathematical Software (TOMS), 22 (4), 469-483. DOI: 10.1145/235815.235821

Batty, M., Chapman, D. y Evans, S. (2000). Visualizing the City: Communicating Urban Design to Planners and Decision Markers. London.

Belton, D. (2008). Classification and Segmentation of3D TLSPoint Clouds. Tesis de Doctorado no publicada, Curtin University of Technology, Perth, Australia.

Belton, D. y Lichti, D. (2006). Classification and segmentation of terrestrial laser scanner point clouds using local variance information. The International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 36(5), 44-49.

Billen, R., Zaki, C, Servi�res, M., Moreau, G. y Hallot, P. (2012). Developing an ontology of space: Application to 3D city modeling. In T. Leduc, G. Moreau, y R. Billen (Eds.). Usage, Usability, and Utility of 3D City Models - European COST Action TU0801, 02007, 14. DOI: 10.1051/3u3d/201202007.

Boissonnat, J. (1984). Geometric Structures for Three Dimensional Shape Representation. ACMTransactions on Graphics (TOG), 3 (4), 266-286. DOI: 10.1145/357346.357349.

Bornaz, L. y Rinaudo, F. (2004). Terrestrial laser scanner data processing. Proceedings of XX ISPRS Commission V Congress (vol. 45, pp. 514-519).

Bradley, C. y Currie, B. (2005). Advances in the Field of Reverse Engineering. Computer-Aided Design and Applications, 2 (5), 697-706.

Canny, J. (1986). A computational approach to edge detection. IEEE transactions on pattern analysis and machine intelligence, 8(6), 679-98. Retrieved from. http://ncbi.nlm.nih.gov/pubmed/21869365. DOI: 10.1109/TPAMI.1986.4767851.

Carter, W. (1973). The Lunar Laser Ranging Pointing Problem. University of Arizona.

Dash, M. y Liu, H. (1997). Feature Selection for Classification. Intelligent Data Analysis, 1 (3), 137-156.

El-Halawany, S. I. y Lichti, D. (2011). Detection of Road Poles from Mobile Terrestrial Laser Scanner Point Cloud. International Workshop on Multi-Platform/ Multi-Sensor Remote Sensing and Mapping (M2RSM) (pp. 1-6). IEEE. DOI: 10.1109/ M2RSM.2011.5697364.

El-Halawany, S. I., Moussa, A., Lichti, D. y El-Sheimy, N. (2011). Detection of road curb from mobile terrestrial laser scanner point cloud. ISPRS workshop, Laser scanning 2011, 38(5), 6.

European COST Action, T. (2013). Usage, Usability and Utility of 3D City Models. Recuperado de http://3u3d.edpsciences.org/

Faro. (2012). Faro Laser Scanner Focus 3D. Junio. Recuperado de http://www.faro.com/focus/es.

Fernández Díaz, J. C. (2007). Scientific Applications of the Mobile Terrestrial Laser Scanner System. Tesis de Maestría no publicada, University of Florida, USA.

Filin, S. (2002). Surface clustering from airborne laser scanning data. International Archives of Photogrammetry, Remote Sensing and Spa-tiallnformation Sciences, 34 (3), 119-124.

Goldman, R. (2009). An Integrated Introduction to Computer Graphics and Geometric Modeling (1st ed., p. 543).USA: CRC Press.

Golovinskiy, A., Kim, V. G. y Funkhouser, T. (2009). Shape-based recognition of 3D point clouds in urban environments. International Conference on Computer Vision - ICCV (pp. 2154-2161). IEEE. DOI: 10.1109/ICCV.2009.5459471.

Gordon, S., Lichti, D. y Stewart, M. (2001). Application of a high-resolution, ground-based laser scanner for deformation measurements. In Proceedings of 10th International FIG Symposium on Deformation Measurements, 23-32.

Gorte, B. y Pfeifer, N. (2004). Structuring Laser-Scanned Trees using 3D Mathematical Morphology. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 35 (B5), 929-933.

Gróger, G., Kolbe, T., Czerwinski, A. y Nagel, C. (2008). OpenGIS ® City Geography Markup Language ( CityGML ) Encoding Standard. Open Geospatial Consortium Inc. Recuperado de www.opengeospatial.orgstandards/citygml/.

Hoffman, C. y Rossignac, J. (1996). A Road Map to Solid Modeling. IEEE Transaction on Visualization and Computation Graphics, 2(1), 3-10. DOI: 10.1109/2945.489381.

Hoover, A., et. al. (1996). An Experimental Comparison of Range Image Segmentation Algorithms. IEEE Transactions on Pattern Analysis and Machine Intelligence Archives, 18(7), 673-689. DOI: 10.1109/34.506791.

Hoppe, H., DeRose, T., Dumpchamp, T., McDonald, J. y Stuetzle, W. (1992). Surface reconstruction from unorganized points. ACM SIGGRAPH Computer Graphics, 26(2), 71-78.DOI: 10.1145/142920.134011.

ISPRS. (2013). International Society for Photo-grammetry and Remote Sensing. Recuperado de http://www2.isprs.org/commissions/comm3/wg4.html.

Jansa, J., Studnicka, N., Forkert, G., Haring, A. y Kager, H. (2004). Terrestrial laserscan-ning and photogrammetry - acquisition techniques complementing one another. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 35.

Jiang, X. y Bunke, H. (1994). Fast Segmentation of Range Images into Planar Regions by Scan Line Grouping. Machine Vision and Applications, 7(2), 115-122. DOI: 10.1007/BF01215806.

Johnson, R. y Wichern, W. (2002). Applied Multivariate Statistical Analysis (5th ed.). New Jersey, USA: Prentice Hall.

Kira, K. y Rendell, L. (1992). The feature selection problem: Traditional methods and a new algorithm. Proceedings of Ninth National Conference on Artificial Intelligence (pp. 129-134).

Klasing, K., Wollherr, D. y Buss, M. (2008, May). A clustering method for efficient segmentation of 3D laser data. Conference on Robotics and Automation, ICRA 2008. IEEE International, pp. 4043-4048. Munich, Alemania: IEEE. DOI: 10.1109/RO-BOT.2008.4543832.

Kuipers, J. (2002). Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality (p. 400). Princeton: Princeton University Press.

Laefer, D., Truong Hong, L. y Fitzgerald, M. (2011). Processing of terrestrial laser scanning point cloud data for computational modelling of building facades. Recent Patents on Computer Science, 4 (1), 16-29. DOI: 10.2174/1874479611104010016.

Leal, E. y Leal, N. (2006). Point Cloud Denoising Using Robust Principal Component Analysis. Proceedings of the First International Conference on Computer Graphics Theory and Applications (pp. 51-58). Setúbal, Portugal.

Leica. (2012a). Leica ScanStation C10. Junio. Recuperado de http://www.leica-geosystems.es/es/Leica-ScanStation-C10_79411.htm.

Leica. (2012b). HDS7000 Laser Scanner. Junio. Recuperado de http://www.leica-geosys-tems.es/es/HDS7000_90337.htm.

Liberge, S., Soheilian, B., Chehata, N. y Papa-roditis, N. (2010). Extraction of Vertical Posts in 3D Laser Point Clouds acquired in Dense Urban Areas by a Mobile Mapping System. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences (vol. 38, pp. 126-130). Saint-Mandé, Francia.

Lichti, D. (2005). Spectral filtering and classification of terrestrial laser scanner point clouds. The Photogrammetric Record, 20(111), 218-240. DOI: 10.1111/j.1477-9730.2005.00321.x.

Lichti, D. y Harvey, B. (2002). Effects of refleeting surface material properties on time-of-flight laser scanner measurements International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 34 (4).

Lorensen, W. y Cline, H. (1987). Marching Cubes: A High Resolution 3D Surface Construction Algorithm. ACM SIGGRAPH Computer Graphics, 21 (4), 163-169. DOI: 10.1145/37402.37422.

Luo, C. y Sohn, G. (2012). Terrestrial Laser Scanning Data Classification Using Expectation Maximization Algorithm. The XXII Congress of the International Society for Photogrammetry and Remote Sensing. Melbourne, Australia.

Métral, C., Ghoula, N. y Falquet, G. (2012). An ontology of 3D visualization techniques for enriched 3D city models. (T. Leduc, G. Moreau, y R. Billen, Eds.) Usage, Usability, and Utility of 3D City Models-European COST Action TU0801, 02005, 15. DOI: 10.1051/3u3d/201202005.

Moser, J. (2010). Potential of3D GIS Models for Municipalities - The case of study of Salzburg. Proceeding of the Geoinformatics Forum Salzburg.

Moser, J., Albrecht, F. y Kosar, B. (2010). Beyond visualisation - 3D GIS Analyses for virtual city models. International Archives of Photogrammetric, Remote Sensing and Spatial Information Sciences, XXXVIII (4/ W5), 143-146.

Narendra, P. y Fukunaga, K. (1971). A branch and bound algorithm for Feature Subset Selection. IEEE Transactions on Computers, C-26 (9), 917-922. DOI: 10.1109/TC.1977.1674939.

Optech. (2012). ILRIS Terrestrial Laser Scanner. Junio. Recuperado de http://www.optech.

Pauly, M., Gross, M. y Kobbelt, L. (2002). Efficient simplification of point sampled surfaces. Proceedings of the conference on Visualization, IEEE Computer Society (pp. 163-170). Massachusetts, USA. DOI: 10.1109/VISUAL.2002.1183771.

Pfeifer, N., Dorninger, P., Haring, A. y Fan, H. (2007). Investigating terrestrial laser scanning intensity data: Quality and functional relations. In Optical 3-D Measurement Techniques VIII, 328-337.

Pu, S. (2007). Automatic building modeling from terrestrial laser scanning. Advances in 3D Geoinformation Systems (pp. 147-160). Springer Berlin Heidelberg.

Pu, S., Rutzinger, M., Vosselman, G. y Oude El-berink, S. (2011). Recognizing basic structures from mobile laser scanning data for road inventory studies. Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 66(6), S28-S39. DOI: 10.1016/j.isprsjprs.2011.08.006.

Pu, S. y Vosselman, G. (2006). Automatic extraction of building features from terrestrial laser scanning. Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 35 (6). Recuperado de http:// www.isprs.org/proceedings/XXXVI/part5/paper/1219_Dresden06.pdf.

Pu, S. y Vosselman, G. (2007). Extracting windows from terrestrial laser scanning. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 36(3), 320-325.

Pu, S. y Vosselman, G. (2009a). Knowledge based reconstruction of building models from terrestrial laser scanning data. ISPRS Journal of Photogrammetry and Remote Sensing, 64(6), 575-584. DOI: 10.1016/j.isprsjprs.2009.04.001.

Pu, S. y Vosselman, G. (2009b). Building facade reconstruction by fusing terrestrial laser points and images. Sensors (Basel, Switzerland), 9(6), 4525-4542. DOI: 10.3390/s90604525.

Rabbani, T., Van den Heuvel, F. y Vosselman, G. (2005). Segmentation of point clouds using smoothness constraint. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 36(5), 248-253.

Reshetyuk, Y. (2009). Self-calibration and direct georeferencing in terrestrial laser scanning. Tesis de Doctorado no publicada. Royal Institute of Technology - KTH, Estocolmo, Suecia.

Riegl. (2012). Riegl Laser Measurement System. Junio. Recuperado de http://www.riegl.com/nc/products/terrestrial-scanning.

Rottensteiner, F., Trinder, J., Clode, S. y Kubik, K. (2005). Using the Dempster-Shafer method for the fusion of LIDAR data and multi-spectral images for building detection. Information fusion, 6(4), 283-300. DOI: 10.1109/ICPR.2004.1334203

Rutzinger, M., Hõfle, B., Hollaus, M. y Pfeifer, N. (2008). Object-Based Point Cloud Analysis of Full-Waveform Airborne Laser Scanning Data for Urban Vegetation Classification. Sensors, 8(8), 4505-4528. DOI: 10.3390/ s8084505.

Sapkota, P. P. (2008). Segmentation of Coloured Point Cloud Data. Tesis de Maestría no publicada. International Institute for Geo-Information Science and Earth Observation. Enschede. Holanda.

Schnabel, R., Roland, W., Wessel, R. y Klein, R. (2007). Shape Recognition in 3D Point Clouds (p. 9). Bonn, Alemania.

Schnabel, R., Wahl, R. y Klein, R. (2007). Efficient RANSAC for Point-Cloud Shape Detection. Computer Graphics Forum, 26(2), 214-226.

Shakarji, C. (1998). Least-squares fitting algorithms of the NIST algorithm testing system. Journal of Research of the National Institute of Standard and Technology, 6(106), 633-641.

Sithole, G. (2005). Segmentation and Classification of Airborne Laser Scanner Data (p. 203): NCG, Nederlandse Commissie voor Geodesie. Delft, Holanda.

Sithole, G. y Vosselman, G (2003). Automatic structure detection in a point-cloud of an urban landscape. Proceedings 2nd GRSS/ IPRS joint workshop on Remote Sensing and Data Fusion over Urban Areas, pp. 67-71. Berlín, Alemania.DOI: 10.1109/ DFUA.2003.1219959.

Tomlin, D. (1991). Cartographic Modelling. En D. Maguire, M. Goodchild y D. Rhind (Ed.). Geographical Information Systems: Principles and Applications (I, pp. 631374). Harlow. Inglaterra: Wiley.

Trimble. (2012a). Trimble VX Spatial Station. Junio. Recuperado de http://trl.trimble.com/docushare/dsweb/Get/Docu-ment-348124/022543-261F_TrimbleVX_DS_0110_lr.pdf.

Trimble. (2012b). Trimble FX Scanner Datasheet. Junio. Recuperado de http://trl.trimble.com/docushare/dsweb/Get/Docu-ment-397918/022504-105B_TrimbleFX_DS_0610_LR.pdf.

Van Genchten, B. (2008). Theory and practice on Terrestrial Laser Scanning. M. Santana Quintero, J. L. Lerma, y E. Heine (Eds.) Learning tools for advanced three-dimensional surveying in risk awareness project (pp. 1-241). Valencia: Universidad Politécnica de Valencia: Editorial UPV.

Velizhev, A., Shapovalov, R. y Schindler, K. (2012). Implicit Shape Models for Object Detection in 3D Point Clouds. ISPRS of the Photogrammetry, Remote Sensing and Spatial Information Sciences (vol. 1). Melbourne, Australia. DOI: 10.5194/isprsan-nals-I-3-179-2012.

Viceconti, M., Zannoni, C. y Pierotti, L. (1998). TRI2SOLID: An Application of Reverse Engineering Methods to the Creation of CAD Models of Bone Segments. Computer Methods and Programs in Biomedicine, 56(3), 211-220. DOI: 10.1016/S0169-2607(98)00011-X.

Vosselman, G. (2009). Advanced Point Cloud Processing. In Photogrammetric Week'09.

Vosselman, G. y Dijkman, S. (2001). 3D building model reconstruction from point clouds and ground plans. International Archives of Photogrammetric, Remote Sensing and Spatial Information Sciences, 34 (3/W4), 37-44.

Vosselman, G., Gorte, B. G. H., Sithole, G. y Rabbani, T. (2004). Recognising Structure in Laser Scanner Point Clouds. The International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 46(8/W2), 33-38.

Wall, M., Andreas, R. y Rocha, L. (2003). Singular value decomposition and principal component analysis. A Practical Approach to Microarray Data Analysis, 02(4001), 91-109.

Wang, J. y Shan, J. (2009). Segmentation of Lidar Point Clouds for Building Extraction. American Society Photogrammetric Remote Sensing Annual 2009. American Society for Photogrammetry and Remote Sensing.

Woo, H., Kang, E., Wang, S. y Lee, K. H. (2002). A new segmentation method for point cloud data. International Journal of Machine Tools and Manufacture, 42 (2), 167-178. DOI: 10.1016/S0890-6955(01)00120-1.

Yan, L., Li, Z. y Xie, H. (2010, June). Segmentation of unorganized point cloud from terrestrial laser scanner in urban region. 18th International Conference on Geoinformatics, pp. 1-5. Beijing, China: IEEE. DOI: 10.1109/GEOINFORMATICS.2010.5567982.

Yokoyama, H., Date, H., Kanai, S. y Takeda, H. (2011). Pole-like objects recognition from mobile laser scanning data using smoothing and principal component analysis. ISPRS Workshop, Laser Scanning 2011, 38 (W12), 115-120.

Young, P., Beresford-West, T., Coward, S., Notar-berardino, B., Walker, B. y Abdul-Aziz, A. (2008). An efficient approach to converting three-dimensional image data into highly accurate computational models. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 366(1878), 3155-3173. DOI: 10.1098/rsta.2008.0090.

Z+F. (2012). Z+F Profiler 5010 Technical Data. Junio. Recuperado de http://www.zf-uk.com/downloads/5010_Specs.pdf.

Zahan, C. (1971). Graph-theorical methods for detecting and describing gestalt clusters. IEEE Transactions on Computers, 20(1), 68-86. DOI: 10.1109/T-C.1971.223083.