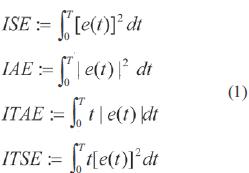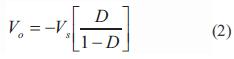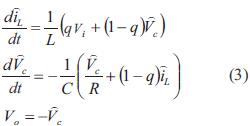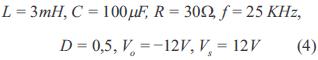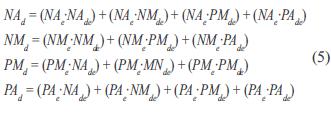DOI:
https://doi.org/10.14483/22487638.7237Published:
2013-09-18Issue:
Vol. 17 (2013): Special EditionSection:
ResearchDiseño de un controlador proporcional derivativo difuso para un conversor reductor-elevador empleando el defuzificador basado en relaciones booleanas
Keywords:
control difuso, convertidores CC-CC, relaciones booleanas. (es).Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Diseño de un controlador proporcional derivativo difuso para un conversor reductor-elevador empleando el defusificador basado en relaciones booleanas
A proportional derivative fuzzy controller design for a buck-boost converter using a method based on boolean relations
Lina Cristina Morales Laguado1, Helbert Eduardo Espitia Cuchango2, José Jairo Soriano Méndez3
1Ingeniera Electrónica, Estudiante de Maestría en Ingeniería Industrial. Project
Manager de Motorola Solutions. Bogotá, Colombia.
Contacto: lina.morales.laguado@gmail.com
2Ingeniero Electrónico, Ingeniero Mecatrónico, Especialista en Telecomunicaciones
Móviles, Magíster en Ingeniería Industrial, Magíster en Ingeniería Mecánica. Docente de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: heespitiac@udistrital.edu.co
3Ingeniero Químico, Ingeniero Electrónico, Magíster en Ingeniería Industrial. Docente
de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: jairosoriano@udistrital.edu.co
Fecha de recepción: 16 de abril de 2012 Fecha de aceptación: 27 de noviembre de 2012
Resumen
En este documento se presenta el diseño de un sistema de control para la regulación del voltaje de salida de un conversor de corriente continua del tipo reductor-elevador. En particular para el diseño del controlador se emplea un esquema de control no lineal conocido como defusificador basado en relaciones booleanas. Para el desarrollo del trabajo, en primer lugar se revisa el modelo del conversor evidenciando la no linealidad del sistema. Posteriormente se diseña un controlador proporcional derivativo, el cual incorpora en su arquitectura el defusificador basado en relaciones booleanas. Este controlador es optimizado de acuerdo con el criterio de la integral del error cuadrado ponderado en el tiempo. Los resultados obtenidos en simulación muestran el comportamiento del sistema con el controlador diseñado. Con los resultados se analiza el desempeño del sistema considerando el criterio de optimización y el consumo de potencia.
Palabras clave: control difuso, convertidores CC-CC, relaciones booleanas.
Abstract
This paper presents the design of a controller to regulate the output voltage of a direct current converter of the type buck-boost. The design relies on a nonlinear control scheme known as defuzification, which is based on boolean relations. To develop the scheme, we first review the converter model, highlighting the nonlinearity of the system. Subsequently, we design a proportional derivative controller that incorporates boolean-relation-based defuzification in its architecture. This controller is optimized according to the criterion of integral square error weighted in time. Simulation results show the behavior of the system with the design controller. In the last part of the paper we analyze the system performance considering optimization metrics and power consumption.
Key words: fuzzy control, DC-DC power converters, boolean relations.
1. Introducción
Los conversores de tipo reductor-elevador o buck-boost, son usados generalmente como fuente de alimentación con voltaje de salida ajustable que puede ser mayor o menor al voltaje de alimentación del conversor. Este tipo de sistemas muestran una estructura variable, ya que las ecuaciones diferenciales que describen su comportamiento dependen del estado del elemento de conmutación presentando características dinámicas no lineales, tal como se observa en [1], [2], [3] y [4]. Además, en aplicaciones prácticas, se evidencian comportamientos no lineales tales como saturaciones y zonas muertas, causadas por las limitaciones físicas de los elementos del conversor.
Para este tipo de sistemas se han aplicado diversas técnicas de control tanto convencional como no linealenfocadas a desarrollar controladores adecuados para este tipo de plantas [5], [6], [7]. Un ejemplo de esta situación es la aplicación de inteligencia computacional, tal como se observa en [8] y [9].
En este documento se utiliza un modelo promediado, el cual es obtenido usando el modelo instantáneo [4]. Con el modelo definido, se procede a diseñar el controlador de regulación Proporcional Derivativo (PD), el cual incorpora en su arquitectura el Defusificador Basado en Relaciones Booleanas (DBR). Para realizar el diseño se consideran trabajos anteriores, donde se utilizan controladores PD difusos para conversores de corriente continua. De esta manera, se pretende mostrar las características del DBR como un nuevo esquema de control difuso. El controlador PD DBR es optimizado mediante la minimización del criterio Integral del Error Cuadrado Ponderado en el Tiempo (ITSE) [10]. Las figuras de mérito empleadas para establecer la eficiencia del controlador diseñado son el índice de desempeño ITSE y el consumo de potencia.
2. Metodología
Para el desarrollo del trabajo presentado en este documento en primer lugar se analizó el modelo del sistema a controlar, el cual consiste en un Circuito Conversor de Corriente Continua (CC-CC) del tipo reductor elevador. Posteriormente se propone el sistema de control y se realiza el ajuste de parámetros empleando optimización. Como paso final se obtienen los resultados de la propuesta mediante simulación, observando de esta forma el desempeño del controlador diseñado.
Para la implementación de la aplicación y simulaciones se empleó Matlab con las herramientas de simulación Simulink y SimPowerSystems, adicionalmente se emplea la caja de herramientas para la solución de ecuaciones diferenciales ordinarias ODE y la herramienta de optimización OPTIM (OptimizationToolbox).
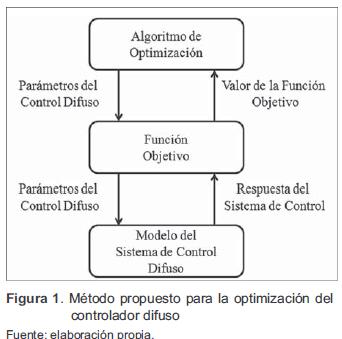
Con el fin de realizar la optimización, se sigue el proceso que se muestra en la figura 1, donde primero se implementa el modelo de la planta y el respectivo sistema de control. En este caso se toman como variables de optimización los parámetros del controlador difuso, de tal forma que luego de realizar la simulación del sistema con una respectiva configuración de parámetros se determina el correspondiente valor de la función objetivo, la cual es empleada en el proceso de optimización.
Considerando que se requiere realizar varias simulaciones del sistema de control con el fin de efectuar su optimización, para tener un tiempo de simulación corto se emplea un método de Runge-Kutta de segundo y tercer orden, el cual se encuentra implementado en Matlab mediante la función ode23 [11].
Por otro lado, cuando se realiza la optimización de sistemas de control se pueden considerar diferentes índices de control óptimo, los cuales, según lo descrito en [12], pueden ser: ISE (Integral Square Error), IAE (Integral Absolute Error), ITAE (Integral of Time Absolute Error), ITSE (Integral of Time Weighted Squared Error). Los anteriores índices de desempeño se pueden observar en la ecuación (1).
Tal como se mencionó anteriormente, se emplea el índice de desempeño ITSE para la optimización del controlador difuso buscando de esta forma una penalización fuerte del error para tiempos grandes.
En esta propuesta se emplea optimización sin restricciones, un tipo de optimización donde se pueden tener estrategias de búsqueda de línea o de región de confianza para determinar el punto siguiente en una iteración. En la estrategia de búsqueda de línea se escoge una dirección sobre la cual se busca un punto que proporcione un mejor valor de la función objetivo, en cada iteración se busca una nueva dirección y un nuevo punto. Por otro lado, en la estrategia de región de confianza se construye una función modelo que se aproxime a la función objetivo. Puesto que el modelo para ciertos puntos difiere de la función objetivo, se establece una región donde esta aproximación sea buena, la cual se llama región de confianza. Como ejemplo de un algoritmo con estrategia de búsqueda de línea se tiene el método de Newton. Por otro lado, como ejemplos de métodos basados en región de confianza se tienen los que emplean formas cuadráticas como aproximación de la función objetivo [13].
En el método de Newton, tanto el vector gradiente como la matriz hessiana se determinan mediante aproximaciones numéricas de primeras y segundas derivadas respectivamente [13]. Sin embargo, existe otra orientación en la que se realizan aproximaciones sucesivas de la inversa del hessiano, ya que el cálculo de esta inversa puede ser costoso desde el punto de vista computacional. Este conjunto de métodos se llama cuasi-Newton, entre los cuales se tienen los métodos de DFP (Davidon-Fletcher-Powell) y BFGS (BroydenFletcher-Goldfarb-Shanno) [13].
3. SISTEMA POR CONTROLAR
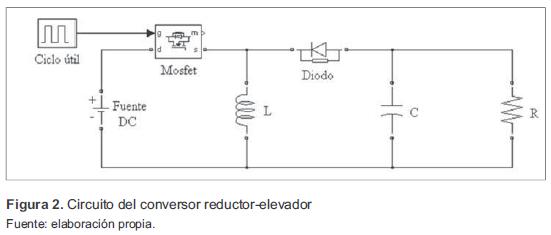
El sistema a controlar es un conversor CC-CC reductor-elevador, que opera en dos modos diferentes. Cuando el interruptor está cerrado, la corriente en la bobina L aumenta linealmente cargando la bobina. Cuando el interruptor está abierto, la corriente en la bobina L disminuye, descargándose de esta forma la bobina. Para efectos del documento, se considera que la corriente en la bobina es permanente [2], [3]. El circuito correspondiente se muestra en la figura 2 y la relación de voltajes entrada-salida del conversor se tiene en ecuación (2), donde D corresponde al ciclo útil de conmutación, VO al voltaje de salida y VS al voltaje de entrada.
El modelo matemático del conversor depende no solo de los diferentes componentes de su estructura, sino también de la configuración que adquiere el circuito al cambiar de estado de conmutación. Típicamente, dos modelos son usados en la literatura; uno es el denominado modelo instantáneo, el cual considera la dinámica relacionada con la operación del interruptor; el otro es el modelo promediado que no considera la dinámica del interruptor, sino el comportamiento dominante causado por los otros elementos [4]. El modelo promediado considerado se presenta en ecuación (3).
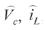 , Vi y R corresponden al voltaje en el condensador, C representa corriente en la bobina y L voltaje de entrada y resistencia o carga. Adicionalmente, q es definida como una señal que caracteriza el comportamiento dinámico promediado del interruptor. Para el caso en consideración, los valores de operación del conversor se tienen en la ecuación (4).
, Vi y R corresponden al voltaje en el condensador, C representa corriente en la bobina y L voltaje de entrada y resistencia o carga. Adicionalmente, q es definida como una señal que caracteriza el comportamiento dinámico promediado del interruptor. Para el caso en consideración, los valores de operación del conversor se tienen en la ecuación (4).
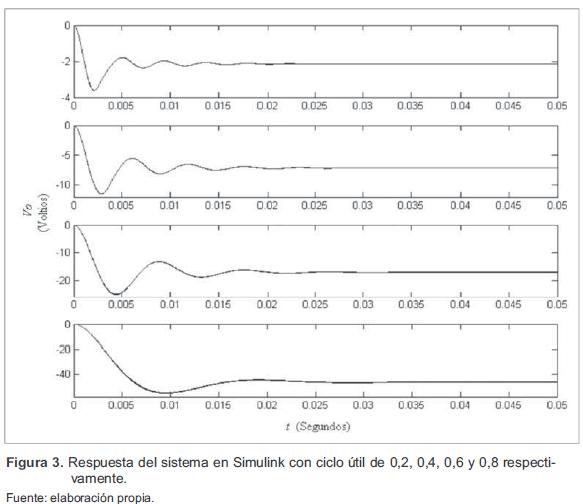
Utilizando Simulink, se puede observar la respuesta del conversor reductor-elevador cuando el ciclo útil D (entrada al conversor) cambia. En la figura 3 se evidencia el comportamiento no lineal del sistema debido a no tener respuestas en la misma proporción al variar el ciclo útil.
4. Controlador Pd DBR
El DBR (Defuzification Based on Boolean Relations) propone un mecanismo de implementación para los sistemas de lógica difusa, tomando como referencia el diseño de automatismos, ya que estos sistemas son muy empleados en control de procesos por su facilidad de implementación. Esta técnica de diseño considera los sensores, actuadores y las relaciones booleanas empleadas como estrategias de control [14]. Con esta orientación se espera facilitar la implementación computacional de los sistemas de inferencia difusa (FIS), teniendo un mejor desempeño en cuanto al tiempo de procesamiento del FIS.
El DBR consiste en la reducción de los procesos de implicación y agregación en una sola operación, de forma que se facilite su implementación. Puede considerarse como un caso intermedio de los sistemas de inferencia difusa tipo Mamdani y Takagi-Sugeno, no normalizados. Sin embargo, no se podría suponer estrictamente de esta manera, ya que el DBR tiene asociada una metodología de diseño. Esta metodología propuesta con el DBR muestra una transición de la lógica booleana a la lógica difusa, aprovechando los mecanismos de diseño de lógica booleana para extenderlos a la lógica difusa.
El fundamento del DBR corresponde a una extrapolación de los sistemas bivalentes a la teoría del control difuso. La propuesta parte de analizar el problema como si se tuvieran valores de entrada difusos bivaluados (la variable pertenece o no a la etiqueta difusa). A partir de las reglas de inferencia, se obtienen las relaciones booleanas entre los diferentes conjuntos difusos de cada universo de discurso y las salidas virtuales del sistema. El nombre virtual indica que no es una relación con respecto a un conjunto de salida descrito previamente, sino una asociación lingüística, con el ánimo de asignar una acción de control apropiada.
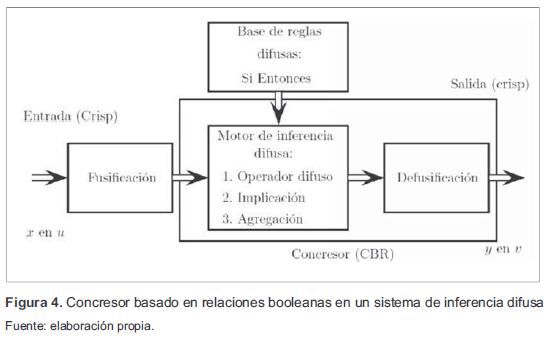
Los bloques estructurales del DBR son en esencia la fusificación y la concreción de la información difusa. En este caso el proceso de la defusificación es una tarea intrínseca al concresor. Un esquema de dicho proceso se puede observar en la figura 4.
5. Diseño Del Controlador
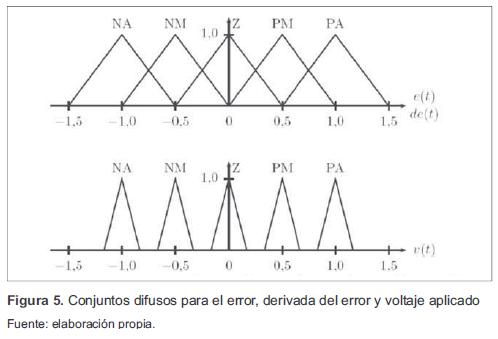
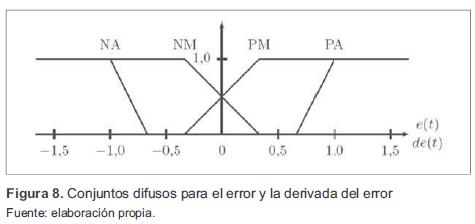
Para el desarrollo del controlador PD DBR se toma como referencia los trabajos presentados en [4] y [7], donde se realiza el diseño de controladores difusos para convertidores de corriente continua. Para un sistema de inferencia difusa tipo Mamdani, se consideran los conjuntos difusos de la figura 5 que tienen como universos de discurso el error y la derivada del error, donde el error corresponde a un problema de regulación del sistema cuando la salida de voltaje difiere de la deseada. Por otro lado, la salida corresponde al voltaje aplicado.
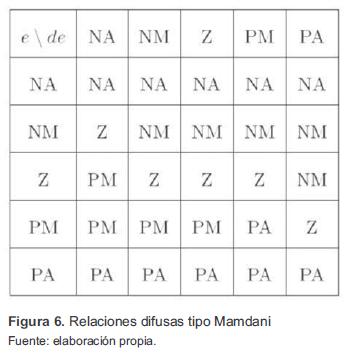
La relación entre conjuntos difusos convencionalmente se realiza mediante la figura 6. En este cuadro, para una acción de control se relacionan 2 conjuntos difusos considerando que los otros no intervienen, similar al caso cuando se simplifican variables de tipo booleano en una tabla de verdad donde se tiene la relación de todos los posibles valores de las entradas. La primera columna corresponde a los posibles conjuntos del universo de discurso del error y la primera fila a los posibles conjuntos del universo de discurso de la derivada del error, los cuales se pueden observar en la figura 6. La intersección en el cuadro entre estos dos universos de discurso indica la respuesta del sistema difuso.
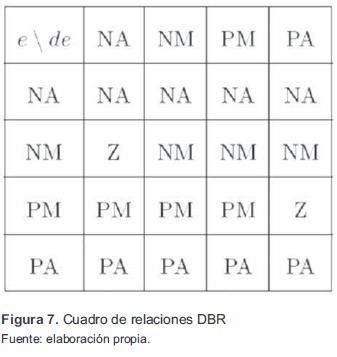
En la figura 6 se puede observar que el conjunto cero en la derivada del error tiene tres acciones iguales a cero, por lo tanto, para el controlador PD DBR este conjunto puede ser eliminado, ya que tiene una acción de cero en la salida total. Para mantener las mismas regiones de acción en los dos universos de discurso, también se omite el conjunto cero en el universo de discurso del error. Dadas las anteriores consideraciones, se tiene el cuadro de relaciones que se presenta en la figura 7.
Bajo el enfoque de un sistema de lógica difusa tipo Mamdani y considerando la t-norma como (·) y la s-norma como (+), se obtienen las relaciones difusas mostradas en ecuación (5) para las funciones de pertenencia asociadas al universo de discurso de salida.
Analizando los anteriores resultados, se observa que el cuadro de relaciones tiene una interpretación muy parecida a una tabla de verdad, donde las salidas se encuentran ya simplificadas.
Para los conjuntos difusos del controlador PD DBR, se considera que la acción de control está ligada al sensor empleado, por lo que se obtienen conjuntos de la forma como se muestra en la figura 8. Esta forma de conjuntos supone una conmutación entre los actuadores virtuales correspondientes a cada región.
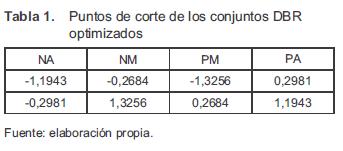
Para la optimización del controlador, se eligió el criterio Integral del Error Cuadrado Ponderado en el Tiempo (ITSE), debido a que este no solo tiene en cuenta la minimización del error sino también el tiempo de establecimiento (tS) del sistema [15]. Luego de realizar la optimización del controlador difuso, se obtienen los puntos de corte de los conjuntos DBR optimizados,los cuales se pueden observar en la tabla 1.
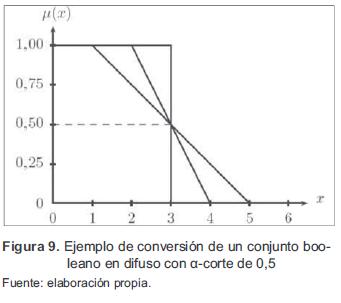
Las acciones virtuales (controlador PD DBR) quedan determinadas como: -1,7459, -1,2679, 1,2679 y 1,7459. Para establecer los puntos de corte y acciones virtuales iniciales se utilizó un criterio de conversión de conjuntos booleanos basándose en α-corte de 0,5, el cual se puede apreciar en la figura 9.
6. Resultados En Simulación
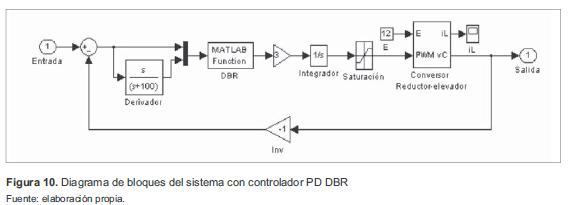
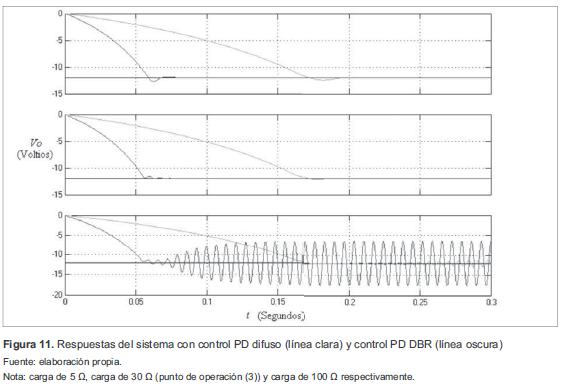
En la figura 10 se muestra el diagrama de bloques del sistema con el controlador PD DBR. Se observa que el sistema en el punto de operación tiene una buena respuesta con los 2 controladores planteados. El controlador PD DBR en comparación con el PD difuso, presenta un tiempo de establecimiento menor. Al variar la carga del sistema, el controlador PD difuso presenta una respuesta similar en todos los casos (figura 11). Sin embargo, con carga 100 Ω se presenta un pequeño rizado (aproximadamente del 8,33 %) en estado estacionario. El controlador PD DBR, de la misma manera que el PD difuso, con carga de 100Q presenta un rizado en estado estacionario, pero mucho mayor (aproximadamente del 41,66 %). Este rizado genera un consumo de energía para la fuente de alimentación; además, puede llegar a producir daños o desgaste de los elementos que constituyen la planta, tal como se presenta en [3] y [16].
Debido a que los controladores fueron propuestos de acuerdo a un punto de operación, al variar la carga se modificará este también, ocasionando que el comportamiento del sistema no sea lo esperado. Lo anterior evidencia la existencia de una dependencia directa del comportamiento del sistema con respecto a los conjuntos con los cuales se diseñan los controladores. Es necesario notar que a mayor cantidad de relaciones establecidas, se abarca y se hace una mejor distribución del universo de discurso mejorando la respuesta del sistema al variar parámetros de la planta como lo es la carga del sistema.
7. Resultados Obtenidos
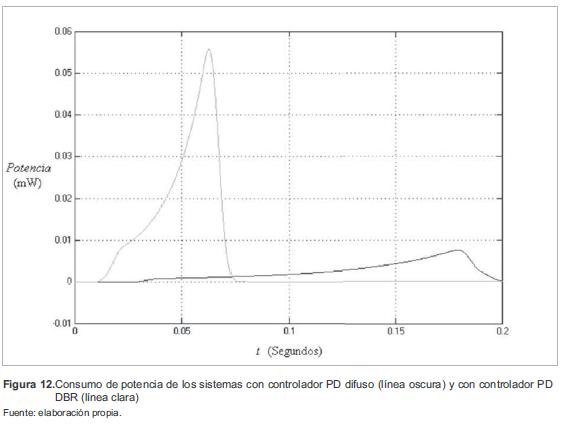
Luego de realizar las respectivas simulaciones, las curvas de potencia de los 2 sistemas se muestran en la figura 12. Tal como se aprecia, el sistema con controlador PD DBR presenta una respuesta con mayor consumo de potencia (integral bajo la curva de potencia) correspondiente a 1,311 mW, mientras que el sistema PD difuso tiene un consumo de 0,4639 mW.
La curva de potencia del sistema con controlador PD DBR presenta un sobrepico pero menor tiempo en su establecimiento (que equivale a una respuesta más rápida del sistema). Por el contrario, la curva de potencia con el controlador PD difuso presenta un sobrepico menor, pero su consumo dura más tiempo, generando un mayor tiempo de establecimiento.
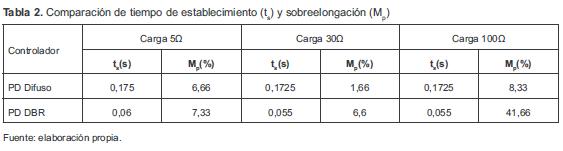
Las características de tiempo de establecimiento (2 %) y sobreelongación de las respuestas de los sistemas con los dos controladores se muestran en la tabla 2. La respuesta con el controlador PD DBR presenta menor tiempo de establecimiento en los tres casos, pero mayor sobreelongación. En contraste con la respuesta del controlador PD difuso, el tiempo de establecimiento es mayor, pero con menor sobreelongación. Se observa que el sistema del controlador PD DBR con carga 5Ω y 30Ω a pesar de que muestra mayor sobreelongación en comparación con el PD difuso, presenta una diferencia pequeña (aproximadamente 0,67 para 5Ω y 4,94 para 30Ω).
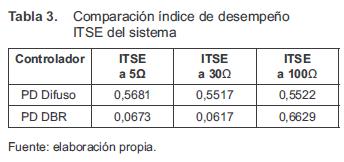
Por otro lado, en la tabla 3 se presentan los resultados obtenidos para la figura de mérito ITSE.
Al minimizar el índice de desempeño ITSE se obtiene que para el punto de operación considerado ecuación (4) y el sistema con carga de 5Ω, el controlador PD DBR presenta un menor valor de ITSE en comparación con el controlador PD difuso. El controlador PD DBR presenta un mayor valor de ITSE en comparación con el PD difuso cuando el sistema tiene una carga de 100Ω.
8. Conclusiones
Se evidencia la capacidad del controlador PD DBR para ser aplicado en plantas no lineales con las características que tiene un conversor reductor-elevador.
Reduciendo la carga del conversor, la respuesta del sistema es satisfactoria, mostrando un tiempo de establecimiento y sobre-impulso tolerables.
Teniendo en cuenta que el índice de desempeño propuesto para evaluar el comportamiento del sistema fue el criterio ITSE, se observó un resultado favorable, ya que el criterio es menor para el controlador PD DBR en comparación con el diseño del controlador PD difuso originalmente planteado en la literatura.
En trabajos futuros se propone explorar la metodología asociada al DBR en otras topologías de conversores CC-CC, como también el uso de diferentes figuras de mérito para evaluar los diseños con DBR.
9. Financiamiento
El presente trabajo se desarrolló en el marco de la investigación de los sistemas de inferencia difusa basados en relaciones booleanas, el cual es un proyecto realizado en el grupo de investigación Laboratorio de Automática, Microelectrónica e Inteligencia Computacional (LAMIC) de la Universidad Distrital Francisco José de Caldas.
Referencias
[1] N. Díaz, and J. Soriano,"Study of two Control Strategies based in Fuzzy Logic and Artificial Neural Network compared with an Optimal Control strategy applied to a Buck Converter", IEEE Fuzzy Information Processing Society, NAFIPS'07, pp. 313318, june 2007.
[2] D. Hart, Electrónica de Potencia, Madrid: Pearson, 2001.
[3] H. Rashid, Electrónica de Potencia: Circuitos, Dispositivos y Aplicaciones, Naucalpan de Juárez, México: Prentice Hall Hispanoamericana S.A., 1993.
[4] M. Pomar, J. Normey, and E. Camponogara, "Nonlinear Model based Predictive Controller of a Buck Boost Converter", 16th IFAC World Congress ,vol. 16, part 1, july 2005.
[5] B. Lin, and C. Hua, "Buck/Boost Converter Control with Fuzzy Logic Approach", IEEE Proceedings of the International Conference on Industrial Electronics, Control, and Instrumentation IECON, vol. 2, pp. 1342-1346, noviembre 1993.
[6] L. Morales, H. Chamorro, J. Soriano, y N. Díaz, "Control Óptimo para un Conversor BuckBoost",IEEE 7º Encuentro de Energía, Potencia, Instrumentación y Medidas, EPIM'2008, pp. 168-173, octubre 2008.
[7] H. Park, and H. Kim, "Simultaneous Control of Buck and Boost DC-DC Converter by Fuzzy Controller", IEEE, Proceedings International Symposium on Industrial Electronics ISIE, vol. 2, pp. 1021-1025, june 2001.
[8] J. Mendel, "Fuzzy Logic Systems for Engineering: A tutorial", Proceedings of IEEE, vol. 83, pp. 345-377, March 1995.
[9] L. Wang, A Course in Fuzzy Systems and Control, Upper Saddle River, NJ, USA: Prentice Hall, 1997.
[10] C. Smith, y A. Corripio, Control automático de procesos: teoría y práctica, México, D.F.: Limusa, 1991.
[11] P. Bogacki, and L. Shampine, "A 3(2) pair of Runge–Kutta formulas", Applied Mathematics Letters, vol. 2, no. 4, pp. 321-325, 1989.
[12] O. Arrieta, y V. Alfaro, "Sintonización de controladores PI y PID utilizando los criterios Integrales IAE e ITAE", Ingeniería, vol. 13, no. 1-2, pp. 31-39, 2003.
[13] H. Mora, Optimización no lineal y dinámica, Bogotá: Universidad Nacional de Colombia, Editorial UNIBIBLOS, segunda edición, 2001.
[14] J. Soriano, "Propuesta de Concresor basado en Relaciones Booleanas", Revista de Ingeniería Universidad Distrital FJC, vol. 6, no. 2, pp. 44-50, 2001.
[15] C. Chen, Analog and Digital Control System Design: Transfer-Function, State Space and Algebraic Method, Fort Worth: Saunders College, 1993.
[16] B. Bose, Modern Power Electronics and AC Drives, Singapore: Pearson Education, 2002.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.