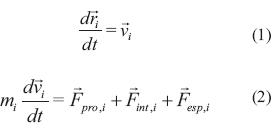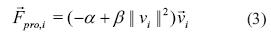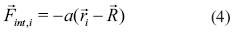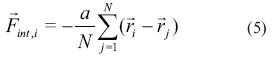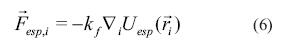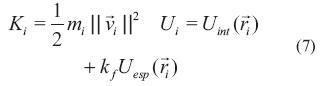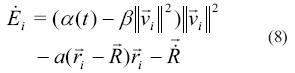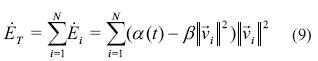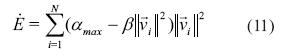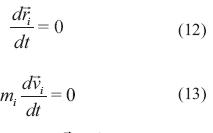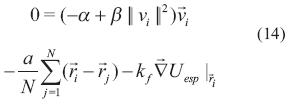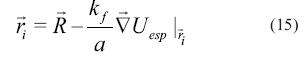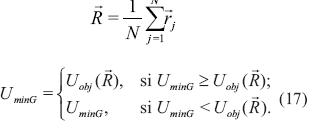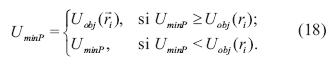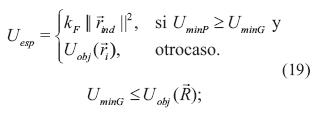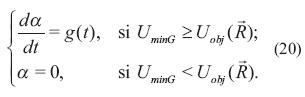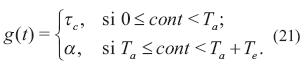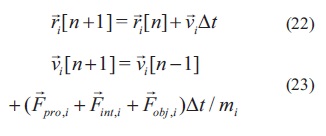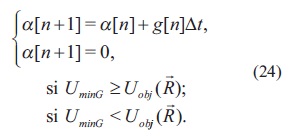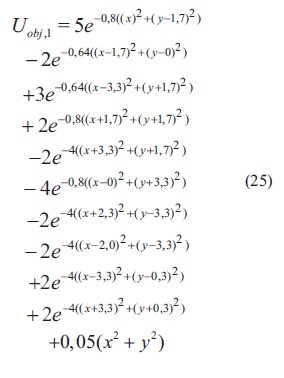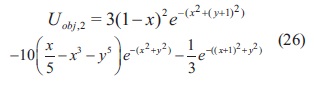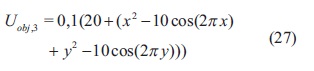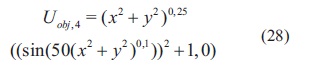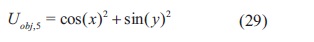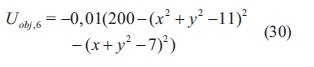DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2014.4.a02Publicado:
01-10-2014Número:
Vol. 18 Núm. 42 (2014): Octubre - DiciembreSección:
InvestigaciónAlgoritmo de optimización basado en enjambres de partículas con comportamiento de vorticidad y búsqueda individual y grupal
Vortex Particle Swarm Optimization with Individual and Group Search
Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Algoritmo de optimización basado en enjambres de partículas con comportamiento de vorticidad y búsqueda individual y grupal
Vortex Particle Swarm Optimization with Individual and Group Search
Helbert Eduardo Espitia Cuchango1, Jorge Iván Sofrony Esmeral2
1Ingeniero electrónico, ingeniero mecatrónico, especialista en Telecomunicaciones Móviles, magíster en Ingeniería Industrial, magíster en Ingeniería Mecánica, docente de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Contacto: heespitiac@udistrital.edu.co
2Ingeniero eléctrico, magíster en Sistemas de Control, doctor en Sistemas de Control, docente de la Universidad Nacional de Colombia, Bogotá, Colombia. Contacto: jsofronye@unal.edu.co
Fecha de recepción: 31 de agosto de 2013 Fecha de aceptación: 16 de mayo de 2014
Clasificación del artículo: Investigación
Financiamiento: Universidad Nacional de Colombia
Resumen
En este documento se realiza la propuesta de un algoritmo de optimización basado en un enjambre de partículas con características de vorticidad, donde se considera una búsqueda grupal asociada al punto medio del enjambre y una búsqueda individual dada por la mejor posición de cada individuo. Con la búsqueda grupal se espera lograr la convergencia de todo el enjambre, mientras que la búsqueda individual permite una mejor exploración del espacio de búsqueda. El algoritmo presenta fases de convergencia y exploración dadas por el modelo seleccionado, el cual se encuentra basado en el comportamiento de un enjambre de individuos. Para establecer el desempeño del algoritmo se emplea un conjunto de funciones de prueba en dos dimensiones.
Palabras clave: algoritmo, comportamiento animal, optimización.
Abstract
In this document, it will be introduced the proposal for optimization algorithm based on particle swarms vorticity features, where a search group is considered through the association to the midpoint of the swarm and an individual search is given for the best position of each individual. The search group seeks to achieve the convergence of the whole swarm, whereas the individual search allows better exploration in pursuant of space.
The algorithm has convergence and exploration behavior given by the selected model which is based on the behavior of a swarm of individuals. For establishing the algorithm performance, a set of test functions in two dimensions is used.
Keywords: algorithm, animal behaviour, optimization.
Introducción
La descripción del comportamiento de muchos seres vivos se caracteriza por presentar movimiento cooperativo coordinado, tal como bandadas de aves, cardúmenes de peces e incluso microorganismos. Uno de los comportamientos de interés consiste en el movimiento circular de partículas alrededor de un punto denominado vórtice (Ebeling, 2002), ya que esta forma de locomoción puede ser una buena estrategia para la búsqueda de alimento y evasión de obstáculos y depredadores (García, 2007). Por las anteriores características estos comportamientos pueden ser empleados en la propuesta de algoritmos de optimización.
Comportamientos de enjambres
En la naturaleza se pueden apreciar diferentes comportamientos los cuales han sido estudiados y representados de forma analítica. En particular, las congregaciones de individuos son una temática interesante por los comportamientos emergentes que surgen (Sumpter, 2006). Entre los trabajos que se pueden resaltar se encuentra el presentado por Vicsek (1995), donde se desarrolla un modelo básico para representar un enjambre de individuos. Este último autor lleva a cabo una extensión de su trabajo (Vicsek, 2008), donde describe algunos patrones representativos de los enjambres. Por otro lado, Sumpter (2006) hace una revisión del comportamiento colectivo para la formación de enjambres observando propiedades de autorregulación y principios de comportamiento colectivo como: integridad, variabilidad, realimentación positiva, realimentación negativa, umbrales de respuesta, dirección, inhibición, redundancia, sincronización y egoísmo.
Sobre los diferentes enfoques considerados para modelos de enjambres, Couzin (2005) analiza el efecto que tiene el liderazgo de un individuo, Ba-jec (2009) considera las diferentes formas de organización que presentan las aves y Zhang (2008) observa el efecto que tiene incorporar mecanismos de predicción en un modelo de enjambre.
Modelos de partículas con comportamiento de vorticidad
La vorticidad es un comportamiento que se presenta con frecuencia en los fluidos y se debe al acoplamiento que existe entre las fuerzas inercia-les y las fuerzas viscosas (número de Reynolds [Berg, 1983]). El análisis de este comportamiento se realiza mediante las ecuaciones de Navier Stokes, las cuales suelen ser difíciles de resolver de forma analítica en casos generales (Çengel, 2003). El comportamiento de vorticidad se caracteriza por el movimiento de forma rotacional de partículas alrededor de un punto, el cual se denomina vórtice. Además de los fluidos, este tipo de comportamiento se presenta en enjambres de individuos como peces, aves y bacterias, entre otros. Existen dos modelos que son los más empleados para representar este comportamiento, uno consiste en el modelo de partícula autopropulsada (Levine, 2000; D'Orsogna, 2006) y el otro corresponde al de partícula activa brownia-na (Ebeling, 2006). Este último, a diferencia del primero, considera una componente estocástica. Por lo general, estos modelos suelen emplear potenciales de Morse para representar la interacción entre individuos; sin embrago, en el trabajo de Erdmann (2005) se puede observar un modelo que emplea un potencial parabólico.
Algoritmos de enjambres de partículas con estrategias para evasión de mínimos locales
De los diferentes algoritmos de optimización bioinspirados, según Bratton (2007) los algoritmos PSO (particle swarm optimization) de enjambres de partículas son una buena alternativa; sin embargo, tienden a presentar convergencia temprana en mínimos locales (Evers, 2009; Schutte, 2002), y adicionalmente, son susceptibles de una mala selección de sus parámetros, tal como lo muestran Hvass (2010) y Van den Bergh (2001). Por lo anterior, se han desarrollado modificaciones y propuestas con las cuales se busca evadir mínimos locales, teniendo una mejor exploración del espacio de soluciones.
Una estrategia general para el escape de mínimos locales consiste en realizar un proceso de dispersión (explosión), luego de tener una convergencia a un mínimo local. Un ejemplo de este concepto se pueden apreciar en el trabajo de Mesa (2010) con el algoritmo de optimización Supernova, en el trabajo de Krishnanand (2009) para el algoritmo de optimización Glowworm y en el trabajo de Passino (2005) con el algoritmo de optimización basado en forrajeo de bacterias.
En particular, para el algoritmo PSO una primera modificación consiste en adicionar un factor de inercia modulada tal como lo proponen Feng (2007) y Yin (2009). Con este enfoque se busca controlar la exploración del algoritmo sobre el espacio de búsqueda. Los citados autores exponen que un factor grande de inercia acelera la convergencia mientras que un valor pequeño mejora la capacidad de búsqueda. Una modificación adicional del algoritmo PSO consiste en reiniciarlo cuando se considera que hay un estancamiento de este (García, 1997).
Adicionalmente al enfoque de inercia modulada, Hendtlass (2005) propone un método denominado olas de enjambres de partículas (Waves of Swarm Particles WoSP), con el cual se busca impulsar el enjambre para que pueda escapar de un mínimo local y así continuar con el proceso de exploración. Por otro lado, Parsopoulos (2004) propone emplear técnicas de repulsión para cada mínimo local encontrado, así espera evadir soluciones encontradas previamente. Asimismo, Liang (2006) presenta una variante del algoritmo PSO denominada aprendizaje integral, la cual consiste en emplear la información histórica de las partículas para actualizar su velocidad. Este enfoque busca conservar la diversidad del enjambre evitando la convergencia prematura.
Finalmente, entre los algoritmos de optimización que emplean el concepto de vorticidad se encuentra el presentado por Menser (2006), donde se desarrolla un algoritmo basado en el comportamiento de un fluido en un sumidero (drenaje). A este se le denomina Particle Swirl Algorithm (PSA). Aunque emplea el concepto de vorticidad, difiere de la propuesta realizada en este documento, donde se busca emplear el concepto de vorticidad para lograr que el enjambre de partículas escape de un mínimo local y de esta forma pueda continuar el proceso de búsqueda. Un primer trabajo donde se plantea un algoritmo de optimización basado en comportamiento de enjambres con características de vorticidad es el de Espitia (2013), quien no considera la búsqueda individual para mejorar las características de exploración el enjambre. Con anterioridad este mismo concepto fue empleado para la planeación de trayectorias de robots móviles (Espitia, 2011a, 2011b).
Metodología
La metodología empleada para el desarrollo del algoritmo de optimización consiste, en primera instancia, en la selección y revisión de un modelo de enjambre de partículas, seguida por su respectivo análisis matemático. Después se realiza la propuesta del algoritmo y por último se valida con funciones de prueba ampliamente conocidas en la literatura.
Modelo Empleado
El modelo seleccionado para realizar la propuesta del algoritmo de optimización se basa en la forma de locomoción de zooplancton Daphnia (Ebeling, 2006). Con este modelo se busca aprovechar el comportamiento de vorticidad, ya que tal como lo muestra Abdel (2008) esta puede ser una buena estrategia para evadir mínimos locales. El modelo seleccionado se encuentra dado por las ecuaciones (1) y (2).
La ecuación (1) permite establecer la posición 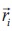 de la i-ésima partícula conociendo su velocidad
de la i-ésima partícula conociendo su velocidad 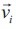 . La ecuación (2) relaciona la velocidad de las partículas con las fuerzas presentes sobre esta.
. La ecuación (2) relaciona la velocidad de las partículas con las fuerzas presentes sobre esta.
La fuerza de autopropulsión considerada corresponde a la ecuación (3).
La fuerza de interacción de las partículas está dada por la ecuación (4).
En este modelo 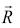 corresponde al centro de masa del enjambre. La información del ambiente (en este caso la función objetivo) está dada por Uesp La fuerza sobre cada partícula que se produce por el potencial Uesp se encuentra dada por la ecuación (6).
corresponde al centro de masa del enjambre. La información del ambiente (en este caso la función objetivo) está dada por Uesp La fuerza sobre cada partícula que se produce por el potencial Uesp se encuentra dada por la ecuación (6).
Donde Kfes una constante que pondera la influencia de la función objetivo.
Análisis del enjambre de partículas
El algoritmo propuesto utiliza dos tipos de comportamiento. El primero corresponde a movimientos de traslación del enjambre hacia un punto (óptimo) y el segundo a un comportamiento de vorticidad. La estrategia principal consiste en lograr la convergencia del enjambre a un estado de equilibrio (posiblemente un mínimo) con velocidad baja y, una vez que se ha encontrado un mínimo, se incrementa la fuerza de propulsión para lograr un comportamiento de vorticidad, aumentando así la dispersión. Este comportamiento se espera que proporcione buenas capacidades de exploración y que permita que el enjambre escape de mínimos locales. El parámetro autopropulsión α se utiliza para cambiar el comportamiento de enjambre y se considera como una función del tiempo, de tal manera que 0<a(t)<amax. Para el siguiente análisis se presentan dos casos extremos; estos son: a (t)=0 y a(t)=amax.
Análisis de energía
Siendo Ki y Ui la energía cinética y potencial de la i-ésima partícula, respectivamente. Estas cantidades están dadas por la ecuación (7).
La energía total de la i-ésima partícula se define como Ei=Ki+Ui y la energía total del enjambre ET corresponde a la suma de la energía total de todas las partículas. Tomando la derivada de tiempo de la energía total de cada partícula se tiene la ecuación (8).
Mediante la adición de las contribuciones de cada partícula y empleando la igualdad 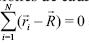 entonces se tiene la ecuación (9).
entonces se tiene la ecuación (9).
A partir de la ecuación (9) es posible observar que un estado constante de energía (ET=0) se logra cuando 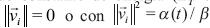 . Se consideran particularmente dos casos para a(t): (i) a(t)=0 y (i) a(t)=amax, donde amaxes un valor positivo grande acotado. En el primer caso el enjambre converge a un punto de equilibrio, mientras que en el segundo caso el enjambre presenta un comportamiento de vorticidad.
. Se consideran particularmente dos casos para a(t): (i) a(t)=0 y (i) a(t)=amax, donde amaxes un valor positivo grande acotado. En el primer caso el enjambre converge a un punto de equilibrio, mientras que en el segundo caso el enjambre presenta un comportamiento de vorticidad.
En el primer caso (i), con a(t)=0, de la ecuación (9) se tiene la ecuación (10).
Dado que la energía del sistema tiene derivada en el tiempo definida negativa para todos vi#0, el sistema tiende a un estado de energía mínima con 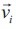 = 0.
= 0.
En el caso (i), el parámetro a(t) se fija en un valor grande, pero acotado amaxtal que se tiene la ecuación (11).
Si ÉT=0, el sistema permanece en un estado de energía constante. Con 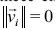 las partículas deben encontrarse estáticas, en tanto que con
las partículas deben encontrarse estáticas, en tanto que con 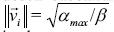 se logra el movimiento del enjambre con energía constante. Finalmente, al incrementar amax se aumenta la velocidad máxima de las partículas y por lo tanto hay una mayor dispersión del enjambre.
se logra el movimiento del enjambre con energía constante. Finalmente, al incrementar amax se aumenta la velocidad máxima de las partículas y por lo tanto hay una mayor dispersión del enjambre.
Puntos de equilibrio
Los puntos de equilibrio se pueden establecer con las ecuaciones (12) y (13).
Por consiguiente, se tiene 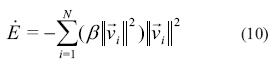 =0 y la ecuación (14).
=0 y la ecuación (14).
Considerando 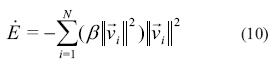 = 0 , la ecuación (14) se reduce a la condición de equilibrio dada por la ecuación (15).
= 0 , la ecuación (14) se reduce a la condición de equilibrio dada por la ecuación (15).
En ecuación (15) si 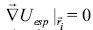 entonces
entonces 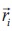 =
= 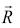 , por lo tanto, el enjambre converge a un mínimo local. En otros casos cuando
, por lo tanto, el enjambre converge a un mínimo local. En otros casos cuando 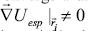 , se logra un equilibrio en función de la posición de las partículas y la función objetivo.
, se logra un equilibrio en función de la posición de las partículas y la función objetivo.
Simulación del modelo
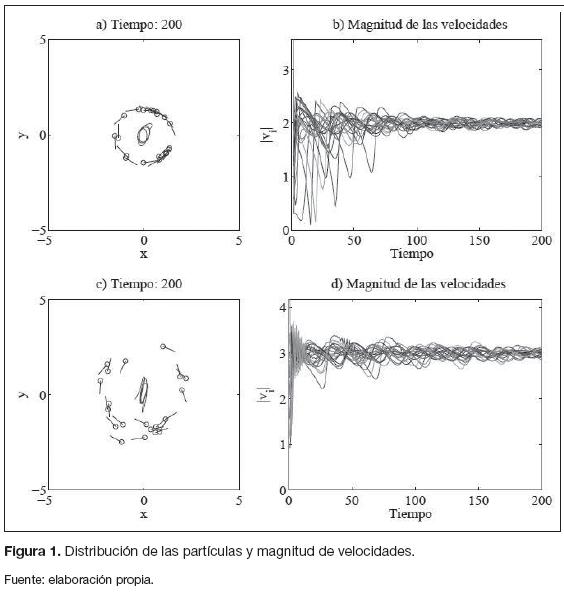
Con el fin de observar las características del modelo se realiza un conjunto de simulaciones con un potencial parabólico Uesp=0.5(x2+y2) y parámetros K=1, mi=1, a=1, N=20 y ß=1, con α igual a 4 y 9. En la figura 1 se presentan los resultados para 200 iteraciones y condiciones iniciales aleatorias para la posición.
Esta figura muestra el comportamiento de vorticidad y la magnitud de la velocidad de las partículas, la cual tiende a ser 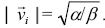 . Para α=4 se tienen las figuras a y b mientras que para α=9 se tienen las figuras cyd.
. Para α=4 se tienen las figuras a y b mientras que para α=9 se tienen las figuras cyd.
Estrategia de búsqueda basada En dispersión
Con la estrategia propuesta se espera tener una exploración adecuada del espacio de búsqueda, de tal forma que después de encontrar un mínimo local se pueda escapar de este para seguir el proceso de búsqueda. Con el fin de lograr lo anterior se propone aumentar la energía de propulsión del enjambre α cuando se alcanza un mínimo local, y sólo se disminuye cuando el enjambre es capaz de escapar de este punto.
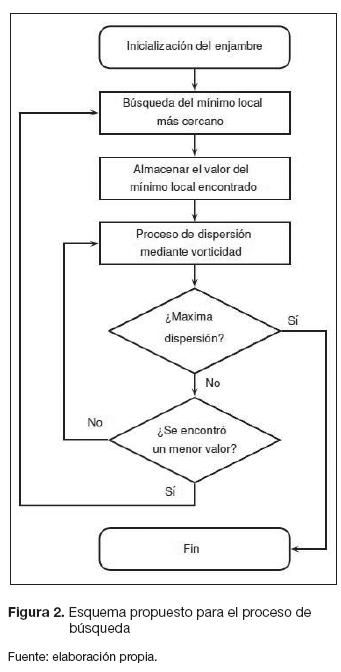
La propuesta de búsqueda emplea el comportamiento de vorticidad como un mecanismo de dispersión para lograr una búsqueda global. En la figura 2 se puede apreciar el diagrama de flujo para la estrategia de búsqueda propuesta. En un primer lugar se inicializa el enjambre y se procede a encontrar el mínimo local más cercano almacenando el valor del mínimo encontrado. Posteriormente, para lograr que el enjambre escape del mínimo encontrado, se realiza el proceso de dispersión, empleando para esto el comportamiento de vorticidad. Con el anterior proceso, mediante la búsqueda grupal e individual se espera encontrar un valor mínimo menor al encontrado previamente. En caso de que no se encuentre un valor tal se detiene el algoritmo, considerando para esto una dispersión máxima de las partículas sobre el espacio de búsqueda.
Para lograr lo anterior el algoritmo presenta tres etapas:
- Convergencia de búsqueda grupal: en esta etapa el algoritmo converge al punto de equilibrio de las partículas, el cual puede ser el mínimo local más cercano. En esta etapa el comportamiento del enjambre está dado por la función objetivo, observando para esto la posición media del enjambre.
- Dispersión y búsqueda: cuando el enjambre encuentra un mínimo local se realiza el proceso de dispersión, buscando tener movimientos circulares de las partículas. En esta misma etapa se realiza la búsqueda de un mejor valor al encontrado previamente. Esta búsqueda se realiza tanto individual como grupalmente. En el caso de que se encuentre un mejor valor grupal o individual, se procede a realizar la respectiva convergencia.
- Convergencia de búsqueda individual: en este caso una de las partículas encuentra un mejor valor, por lo cual el potencial de la función objetivo se reemplaza por un potencial de atracción hacia el mejor punto encontrado, de tal forma que el enjambre pueda converger a este punto.
Valor mínimo individual y grupal
Con el fin de establecer la fase del algoritmo se considera el valor mínimo encontrado por la posición media de las partículas U minG y un valor mínimo dado por la mejor posición de las partículas de forma individual U minP . Estos valores se determinan considerando la función objetivo Uobj.
El mejor valor del grupo se determina conociendo el promedio de las posiciones del enjambre 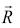 mediante las ecuaciones (16) y (17).
mediante las ecuaciones (16) y (17).
La mejor posición de la partícula está dada por la evaluación de cada partícula de la ecuación (18).
Identificación de las fases del algoritmo
Para identificar la fase en la cual se encuentra el algoritmo existen las siguientes condiciones:
- Convergencia de búsqueda grupal: UminG ≥ Uobj(
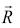 ). En este caso α=0 y Uesp corresponde al potencial de la función objetivo Uobj.
). En este caso α=0 y Uesp corresponde al potencial de la función objetivo Uobj. - Dispersión: UminG≤ Uobj (
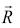 ). En este caso se incrementa la energía mediante a(t) y Uespcorresponde al potencial de la función objetivo Uobj
). En este caso se incrementa la energía mediante a(t) y Uespcorresponde al potencial de la función objetivo Uobj - Convergencia de búsqueda individual: UminP ≥ UminG y UminG≤ U obj(
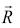 ). En este caso a=0 y Uespcorresponde a un potencial cuadrático asociado a la mejor posición encontrada.
). En este caso a=0 y Uespcorresponde a un potencial cuadrático asociado a la mejor posición encontrada.
Función objetivo
Considerando que 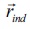 es la mejor posición encontrada por algún individuo, entonces Uespse puede determinar con la ecuación (19).
es la mejor posición encontrada por algún individuo, entonces Uespse puede determinar con la ecuación (19).
Incremento de energía
La adición de energía se realiza mediante el factor de propulsión, el cual está dado por la ecuación (20).
Para la función g(t) se considera un tiempo Ta asociado al incremento de energía y un tiempo Te para la espera, momento en el cual las partículas se dispersan de forma circular sobre el espacio de búsqueda. El número total de iteraciones que toma este ciclo es Ta+Te, donde se emplea la variable cont para realizar la cuenta de las iteraciones. La función g(t) está dada por la ecuación (21).
Con la anterior estrategia se espera que la energía de propulsión aumente hasta que las partículas logren evadir el mínimo local. El aumento de la energía está dado por el parámetro τc, el cual corresponde a la tasa con la cual se incrementa la energía de autopropulsión.
Criterio de parada del algoritmo
Como se ha mencionado previamente, el algoritmo utiliza la dispersión para escapar de mínimos locales y explorar de manera eficiente el espacio de búsqueda. Por lo tanto, el nivel de dispersión se emplea como criterio de parada del algoritmo. Considerando lo anterior, el criterio de parada propuesto establece que si el número de partículas en el espacio de búsqueda es menor que un valor específico, entonces el algoritmo se detiene.
Implementación del algoritmo
Para implementar el modelo dinámico del enjambre en el algoritmo, las ecuaciones diferenciales se convierten a tiempo discreto considerando un intervalo de tiempo Δt, de tal forma que se tienen las ecuaciones (22) y (23).
El cálculo de α en tiempo discreto se realiza con la ecuación (24).
Finalmente, el algoritmo de optimización propuesto se puede apreciar en la figura 3.
Análisis cualitativo del algoritmo
De los diferentes parámetros involucrados en el algoritmo de optimización se puede hacer la siguiente descripción:
- ß: Factor de frenado de las partículas. Al aumentar, las partículas tienden a ir más lento.
- α: Factor de propulsión. Al incrementarse, las partículas aumentan su energía cinética, elevándose de esta forma su velocidad.
- a: Factor de interacción. Al aumentar, el enjambre de partículas tiende a unirse más y al disminuir se dispersan más.
- Kf: Factor de ponderación de la función objetivo. Al incrementarse, las partículas convergen rápidamente a un mínimo local, y al disminuir, estas se pueden mover, sobre todo el espacio de búsqueda.
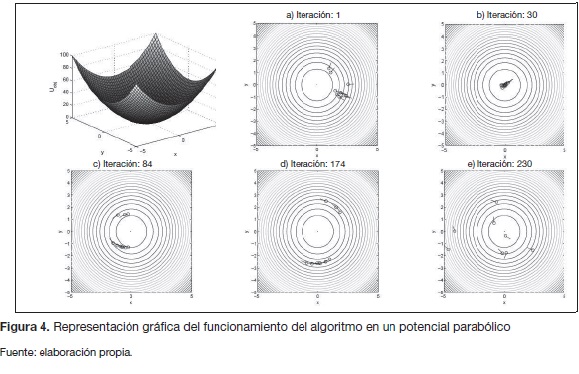
Para mostrar el funcionamiento del algoritmo se realiza una simulación, considerando un potencial cuadrático de la forma Uobj=2(x2+y2). En la figura 4 se puede apreciar el potencial y la evolución que tiene la posición de las partículas en la medida que pasan las iteraciones. Es de apreciar que luego de encontrar el mínimo local, las partículas inician el proceso de dispersión realizando un movimiento circular.
Resultados
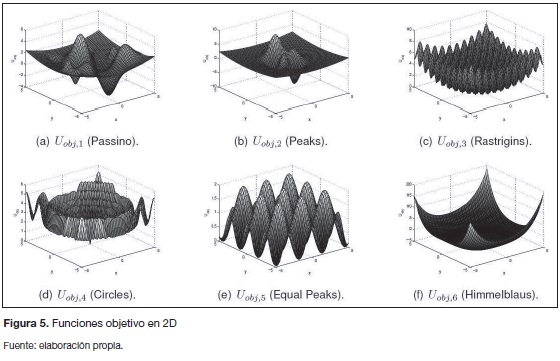
Para ilustrar el desempeño del algoritmo propuesto se considera un conjunto de funciones de prueba de 2 dimensiones, las cuales se pueden observar en Passino (2002) y Krishnanand (2009). En la figura 5 se puede apreciar la representación gráfica de las funciones objetivo empleadas.
Passino: esta función de prueba es una adaptación de la presentada en Passino (2002). En este caso la función tiene un mínimo global en (0,113,-3,2597), cuyo valor es -3,4354 Esta función de prueba se encuentra descrita por la ecuación (25).
Peaks: esta función tiene dos mínimos locales y un mínimo global en (0,2282,-1,6199) que es igual a -6,4169. La ecuación (26) describe esta función de prueba.
Rastrigins: esta función representa un problema bastante difícil debido a su gran número de locales mínimos y máximos. El mínimo global se encuentra en (0,0) con un valor de 0. Esta función se encuentra dada por la ecuación (27).
Circles: esta función presenta varios círculos concéntricos como regiones de máximos y mínimos locales. El mínimo global se encuentra en (0,0) con un valor de 0. La ecuación (28) describe esta función de prueba.
Equal Peaks: esta función tiene varios mínimos con un valor de 0 y situados periódicamente en x y y. Esta función se encuentra descrita por la ecuación (29).
Himmelblaus: consiste en una adaptación de la función representada en Krishnanand (2009),la cual tiene cuatro mínimos con valor de -2 situados en (-1,5616,2,29260), (2,5616,2,1068), (2,5615,-2,1068) y (1,5616,-29260). La ecuación (30) describe esta función de prueba.
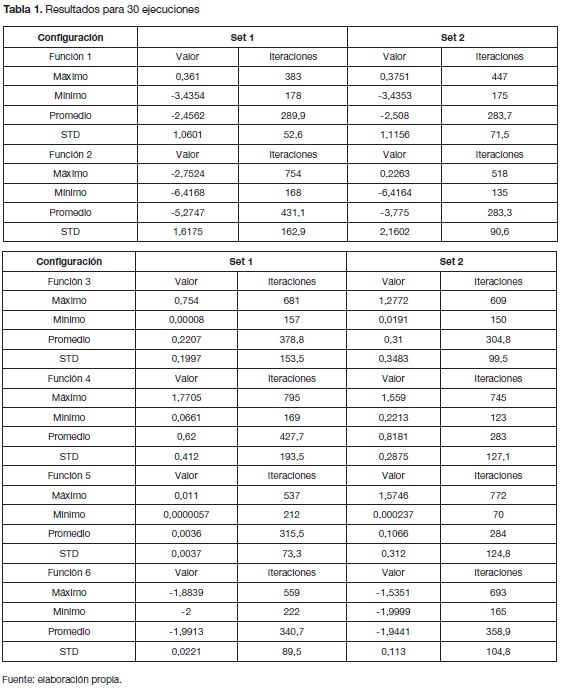
Para la ejecución del algoritmo se toma: mi=1, ß=1, amax=20 y At= 0,1. El rango del espacio de búsqueda considerado es (-6< x <6) y (-6< y <6). Las condiciones iniciales de las partículas son aleatorias en posición y cero en velocidad. Dos configuraciones de parámetros consideradas son: Set 1 a=1, K=1; Set 2 a=0,5, KK),5. Por último, se realizan 30 ejecuciones para cada conjunto de configuraciones. La tabla 1 muestra los valores máximos y mínimos encontrados durante el proceso de optimización (mejores y peores resultados), el valor medio y la desviación estándar (STD) de los resultados. También se aprecia el número de iteraciones empleadas por el algoritmo con cada función de prueba.
Conclusiones
El modelo empleado fue seleccionado buscando tener una expresión compacta con pocos términos y que permita describir comportamientos de enjambre como desplazamientos uniformes y movimientos circulares, los cuales se observan en diferentes grupos de seres vivos.
El algoritmo propuesto es un proceso de optimización basado en un comportamiento emergente que utiliza la vorticidad de un enjambre de partículas para mejorar las capacidades de búsqueda y escapar de los mínimos locales. Los resultados que se presentan muestran la eficacia de la estrategia propuesta, donde el enjambre fue capaz de evitar los mínimos locales y encontrar una solución global (aproximada) de las funciones propuestas.
En los resultados de la tabla 1 se puede apreciar que hay un mejor desempeño del algoritmo para la primera configuración de parámetros (Set 1). Adicionalmente, en estos resultados se observa que en promedio el mayor número de iteraciones se encuentra en esta misma configuración de parámetros. También es de notar que en la mayoría de la funciones objetivo el algoritmo logra encontrar el mínimo global.
En particular la función objetivo Circles resulta de interés, debido a la simetría circular que presenta, lo cual puede dificultar el escape de las partículas de los mínimos locales. En la tabla 1 se puede observar que para esta función objetivo el algoritmo emplea el mayor número de iteraciones.
Financiamiento
El financiamiento del presente proyecto se encuentra en el marco del proyecto con código 16332 de la Dirección de Investigación Sede Bogotá - Universidad Nacional de Colombia.
Agradecimiento
Los autores manifiestan su agradecimiento a la Universidad Distrital Francisco José de Caldas y a la Universidad Nacional de Colombia por el apoyo en el desarrollo de este trabajo.
Referencias
Abdel, M. y McInnes, C., "Wall Following to Escape Local Minima for Swarms of Agents Using Internal States and Emergent Behavior", International Conference of Computational Intelligence and Intelligent Systems ICCIIS, 2008.
Bajec, I. y Heppner, F., "Organized Flight in Birds", Animal Behaviour, Vol. 78, No. 4, 2009, pp. 777-89.
Berg H., Random Walks in Biology, Princeton University Press, 1983.
Bratton, D. y Kennedy, J., "Defining a Standard for Particle Swarm Optimization", Proceedings of IEEE Swarm Intelligence Symposium SIS, 2007.
Çengel, Y., Mecánica de fluidos, McGraw-Hill, 2003.
Couzin, I., Krause, J., Franks, N. y Levin, S., "Effective Leadership and Decision Making in Animal Groups on Themove", Letters to Nature, Vol. 433, 2005, pp. 513-16.
D'Orsogna, M., Chuang, Y., Bertozzi, A. y Chayes, L., "Self-Propelled Particles with SoftCore Interactions: Patterns, Stability, and Collapse", Physical Review Letters, Vol. 96, 2006.
Ebeling, W. y Erdmann, U., "Nonequilibrium Statistical Mechanics of Swarms of Driven Particles", Physica A: Statistical Mechanics and its Applications, Vol. 314, No. 1-4, 2002, pp. 92-96.
Erdmann, U., Ebeling, W. y Mikhailov, A., "Noise-Induced Transition from Translational to Rotational Motion of Swarms", Physical Review E, Vol. 71, No. 5, 2005.
Espitia, H. y Sofrony J., "Path Planning of Mobile Robots Using Potential Fields and Swarms of Brownian Particles", IEEE Congress on Evolutionary Computation (CEC), 2011, pp. 123-129.
Espitia H. y Sofrony J., "Vortex Particle Swarm Optimization", IEEE Congress on Evolutionary Computation (CEC), 2013.
Espitia, H., Sofrony, J. y González C., "Vortex Swarm Path Planning Algorithm", IEEE Electronics, Robotics and Automotive Mechanics Conference (CERMA), 2011,pp. 184-90.
Evers, G., An Automatic Regrouping Mechanism to Deal with Stagnation in Particle Swarm Optimization (Master Thesis), University of Texas-Pan American, 2009.
Feng, C., Cong, S. y Feng, X., "A New Adaptive Inertia Weight Strategy in Particle Swarm Optimization", IEEE Congress on Evolutionary Computation (CEC), 2007.
García, J. y Alba, E., "Restart Particle Swarm Optimization with Velocity Modulation: A Scalability Test", Springer, Soft Computing - A Fusion of Foundations, Methodologies and Applications, Vol. 1, 1997.
García, R., Moss, F., Nihongi, A., Strickler, R., Gõller, S., Erdmann, U., Schimansky, L. y Sokolov, I., "Optimal Foraging by Zoo-plankton within Patches: The Case of Da-phnia", Elsevier, Mathematical Biosciences, Vol. 2, 2007, pp. 165-88.
Hendtlass, T., "A Particle Swarm Algorithm for High Dimensional, Multi-Optima Problem Spaces", IEEE Swarm Intelligence Symposium, 2005.
Hvass, M., Tuning & Simplifying heuristical optimization (Ph.D. Thesis), University of Southampton, UK, 2010.
Krishnanand, K. y Ghose, D., "Glowworm Swarm Optimization for Simultaneous Capture of Multiple Local Optima of Multimodal Functions", Springer Science, Swarm Intelligence, Vol. 3, No. 2, 2009, pp. 87-124.
Levine, H., Rappel, W. y Cohen, I., "Self-Organization in Systems of Self-Propelled Particles", Physical Review E, Vol. 63, No. 1, 2000.
Liang, J., Qin, A., Suganthan, P. y Baskar, S., "Comprehensive Learning Particle Swarm Optimizer for Global Optimization of Mul-timodal Functions", IEEE Transactions on Evolutionary Computation, Vol. 10, 2006.
Menser, S. y Hereford, J., "A New Optimization Technique", Proceedings of the IEEE Digital Object ldentifier Southeast Con, 2006.
Mesa, E., Supernova: un algoritmo novedoso de optimización global (tesis de maestría), Universidad Nacional de Colombia, Sede Medellín, 2010.
Parsopoulos, K. y Vrahatis, M., "On the Computation of all Global Minimizers through Particle Swarm Optimization", IEEE Transactions on Evolutionary Computation, Vol. 8, 2004.
Passino, K., "Biomimicry of Bacterian Foragin for Distributed Optimization and Control", IEEE Control Systems Magazine, 2002.
Passino, K., Biomimicry for Optimization, Control, and Automation, Springer-Verlag, London, UK, 2005.
Schutte, J., Particle Swarms in Sizing and Global Optimization (Master's Dissertation), University of Pretoria, 2002.
Sumpter, D., "The Principles of Collective Animal Behaviour", Philosophical Transactions of the Royal Society B, Vol. 361, No. 1465, 2006, pp. 5-22.
Van den Bergh, F., An Analysis of Particle Swarm Optimizers (PhD. Thesis), University of Pretoria, Pretoria, 2001.
Vicsek T., "Universal Patterns of Collective Motion from Minimal Models of Flocking", Second IEEE International Conference on Self-Adaptive and Self-Organizing Systems, 2008.
Vicsek, T., Czirók, A., Ben, E., Cohen, I. y Sho-chet, O., "Novel Type of Phase Transition in a System of Self-Driven Particles", Physical Review Letters, Vol. 75, No. 6, 1995.
Yin, L. y Liu, X., "A PSO Algorithm Based on Biology Population Multiplication (PMP-SO)", Proceedings of the Second Symposium International Computer Science and Computational Technology (ISCSCT '09), 2009.
Zhang, H., Chen, M., Stan, G., Zhou, T. y Maciejowski, J., "Collective Behavior Coordination with Predictive Mechanisms", IEEE Circuits and Systems Magazine, 2008.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.