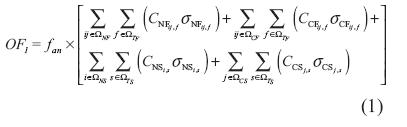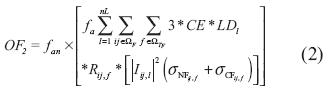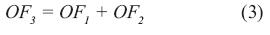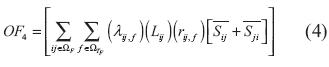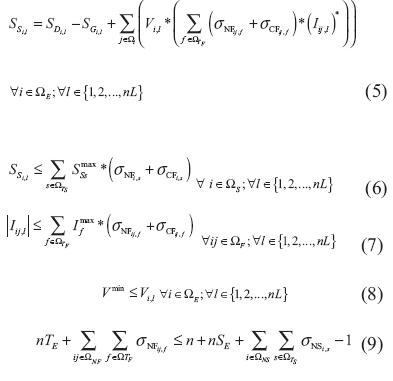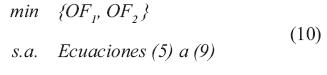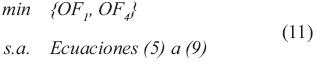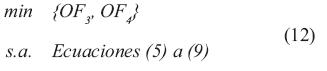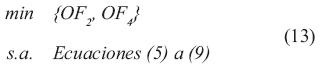Planeación óptima de sistemas de distribución considerando múltiples objetivos: costo de inversión, confiabilidad y pérdidas técnicas

Planeación óptima de sistemas de distribución considerando múltiples objetivos: costo de inversión, confiabilidad y pérdidas técnicas

Optimal planning of distribution systems considering multiple objectives: investment cost, reliability and technical losses

Ana María Mejía Sülanilla¹, Ricardo Alberto Hincapié Isaza², Ramón Alfonso Gallego Rendón³

¹Ingeniera electricista, magíster en Ingeniería Eléctrica, ingeniera de Diseño Eléctrico de Transformadores de Potencia, ABB Ltda., Pereira, Colombia. Contacto: ana.mejia@co.abb.com
²Ingeniero electricista, magíster en Ingeniería Eléctrica, estudiante de doctorado en Ingeniería, docente del Programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira, Pereira, Colombia. Contacto: ricardohincapie@utp.edu.co
³Ingeniero electricista, magíster en Sistemas de Potencia, doctor en Ingeniería Eléctrica, docente del Programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira, Pereira, Colombia. Contacto: ragr@utp.edu.co

Fecha de recepción: 4 de febrero del 2014-Fecha de aceptación: 6 de mayo del 2014

 Clasificación del artículo: Investigación
Financiamiento: Vicerrectoría de Investigaciones, Innovación y Extensión Universidad Tecnológica de Pereira

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.1.a08

Resumen

En este artículo se propone una metodología para solucionar el problema del planeamiento multiobjetivo de sistemas de distribución de energía eléctrica, empleando un algoritmo elitista de ordenamiento no dominado (NSGA-II). Esta metodología considera cuatro modelos matemáticos, donde las funciones objetivo son costos fijos, costos variables, costos fijos y variables, y confiabilidad de la red; como conjunto de restricciones se tienen criterios técnicos y operativos. Al solucionar cada uno de estos modelos se identifican los elementos comunes, los cuales son fijados para la siguiente etapa del proceso; esto se repite hasta hallar una configuración final del sistema. De esta forma, en cada paso del algoritmo se generan especies de cortes, los cuales reducen el espacio de solución. La metodología es verificada con un sistema de distribución de la literatura especializada y se obtienen resultados que muestran la efectividad del método al encontrar un punto de equilibrio entre todos los objetivos considerados.

Palabras clave: algoritmo genético, confiabilidad, optimización, planeamiento de sistemas eléctricos.

Abstract

In this article, a method to solve the multi-objective planning problem of electric power distribution systems is proposed by means of using a non-dominated sorting elitist algorithm (NSGA-II). This method considers four mathematical models, where fixed costs, variable costs, fixed and variable costs, and network reliability are considered as objective functions. The set of constraints is comprised of technical and operational criteria. When all mathematical models are solved common elements to the solutions with each model are found. This process is repeated until a final configuration of the system is found. In this manner, in each step of the algorithm, sorts of cuts are generated, which reduce the solution space of the problem. The method is verified with a distribution system from the specialized literature, obtaining results that show the effectiveness of the method when an equilibrium point is found among all the objectives considered.

Keywords: genetic algorithm, optimization, power system planning, reliability.

Introducción

El aumento del consumo de energía eléctrica de cargas existentes y la aparición de nuevas zonas, debido a la construcción de sectores residenciales, comerciales e industriales, son factores que ocasionan que los operadores de red tengan que realizar acciones de una forma adecuada, con el fin de abastecer la cantidad de energía requerida. El estudio del crecimiento de la demanda de energía eléctrica y el conjunto de estrategias planteadas para abastecer esta demanda se conoce como el planeamiento de sistemas de distribución (PSD) (Bernal-Agustín, 1998). Si estas estrategias no son apropiadas, se pueden presentar problemas tales como regulación de tensión por fuera de límites permitidos, incremento de pérdidas técnicas, sobrecargas en elementos, pérdida de confiabilidad de la red, sobrecostos en los proyectos y empeoramiento de índices de continuidad y calidad del servicio. Para evitar estos inconvenientes, en el PSD se deben tener en cuenta los siguientes aspectos: aumento del calibre de los alimentadores existentes, ampliación de las subestaciones existentes, ubicación y dimensionamiento de nuevas subestaciones de distribución, ubicación y dimensionamiento de nuevos tramos de red, reconfiguración de la topología de la red, reubicación de transformadores de distribución y ubicación de elementos de protección y control para mejorar la confiabilidad en la red.

Adicionalmente, en la vida real el problema del planeamiento de sistemas de distribución involucra varios objetivos; sin embargo, tradicionalmente se ha planteado un modelo matemático con una única función objetivo que incluye los costos del proyecto. En los modelos matemáticos propuestos para este problema se consideran funciones multiobjetivo, las cuales tienen en cuenta costos de inversión, operación y criterios de confiabilidad. La importancia de emplear dos o más objetivos en la solución del problema radica en una mejor aproximación del modelo matemático empleado para describir los sistemas reales.

Para solucionar el problema de la planeación multiobjetivo de sistemas de distribución, se han publicado diversos artículos en la literatura especializada, con diferentes modelos matemáticos y técnicas de solución. Con respecto a las funciones objetivo consideradas se tienen: costos y confiabilidad (Ramírez y Bernal, 2001); costos, confiabilidad y riesgo de inversión (Ramírez y Domínguez, 2004); costos e índices de fallas del sistema (Carrano, Soarez, Takahashi, Saldanha y Neto, 2006); costos, pérdidas y caída de tensión (Mori y Yamada, 2007); costos y caída de tensión (Mantway y Al-Muhaini, 2008); costos, pérdidas e interrupción del servicio (Kong et ál., 2008); costos y consumo de energía (Kayu y Ooka, 2009); costos, confiabilidad, pérdidas y caída de tensión (Ganguly, Sahoo y Das, 2011); costos de inversión y costos de interrupción del servicio (Ganguly, Sahoo y Das, 2013). Para solucionar el problema se han considerado diversas técnicas multiobjetivo, entre las que se destacan: algoritmos evolutivos (Ramírez y Bernal, 2001; Carrano, Soarez, Takahashi, Saldanha y Neto, 2006; Mori y Yamada, 2007; Kong et ál., 2008; Kayu y Ooka, 2009); búsqueda tabú (Ramírez y Domínguez, 2006); cúmulo de partículas (Mantway y Al-Muhaini, 2008; Sahoo, Ganguly y Das, 2012).

Con el fin de solucionar el problema planteado, se propone una metodología en la que se emplea como técnica de solución un algoritmo genético de ordenamiento no dominado (Nondominated sorting genetic algorithm - NSGA-II). Esta metodología emplea cuatro modelos matemáticos, todos con dos funciones objetivo. Con la aplicación de estos modelos se busca tener más herramientas al momento de tomar decisiones, para así involucrar funciones objetivos que impacten directamente en la solución del problema. Las funciones objetivo consideradas son: costos fijos, costos variables, costos fijos y variables y confiabilidad de la red (energía no servida [ENS]).

El conjunto de restricciones está compuesto por las ecuaciones de balance nodal, capacidades máximas permitidas para los elementos del sistema, máxima caída de tensión permitida y radialidad de la red. Con la aplicación de la metodología se encuentran elementos comunes a las soluciones halladas con cada modelo, los cuales son definidos en cada paso del proceso; esto se repite hasta hallar una configuración final del sistema que satisfaga los requerimientos de energía eléctrica de los usuarios de forma confiable y segura. De esta forma en cada paso del algoritmo se generan especies de cortes (tendencias), los cuales reducen el espacio de solución del problema. La respuesta encontrada en un sistema de distribución refleja la importancia de considerar la metodología propuesta en el planeamiento de estos sistemas.

Este artículo está organizado de la siguiente forma: la primera sección (la presente) corresponde a la introducción; en la segunda sección se describe la formulación del problema; en la tercera sección se ilustra la metodología propuesta; en la cuarta sección se presenta la aplicación de la metodología propuesta y los resultados obtenidos, finalmente, se encuentran las conclusiones y recomendaciones derivadas de este artículo.

Formulación del problema

Para describir el problema del planeamiento de sistemas de distribución de energía eléctrica empleamos cuatro modelos matemáticos del tipo no lineal entero mixto, los cuales consideran dos funciones objetivo cada uno. Inicialmente, se ilustra la nomenclatura empleada. Luego se presentan las funciones objetivo y el conjunto de restricciones de los modelos matemáticos propuestos. Por último, se describen en forma detallada estos modelos.

Formulación general

Funciones objetivo

Función objetivo 1 (OF). Representa los costos de inversión del sistema (ecuación (1)).

Los dos primeros términos representan los costos de inversión de nuevos tramos de red y reconductorización de tramos de red existentes, respectivamente. Los dos últimos términos son los costos de instalación de una nueva subestación y ampliación de la existente, respectivamente.

Función objetivo 2 (OF). Considera los costos de operación del sistema (ecuación (2)), los cuales llevan en cuenta el costo de las pérdidas de energía activa en todos los tramos de red del sistema.

Función objetivo 3 (OF₃). Involucra los costos de inversión y operación del sistema (ecuación (3)), en forma conjunta. Por lo tanto:

Función objetivo 4 (OF₄). Representa la confiabilidad del sistema de distribución por medio de la ENS (ecuación (4)), mediante las tasas de falla y los tiempos de reparación, de acuerdo con el tipo de conductor y la longitud de cada tramo de red considerado. Para su evaluación se emplea el criterio de contingencias n-1 (Billinton y Allan, 1996).

Conjunto de restricciones

El conjunto de restricciones se presenta en las ecuaciones (5) a (9). Estas corresponden a balance nodal, capacidad máxima de subestaciones, capacidad máxima de tramos de red, límites de tensión del sistema y radialidad de la red, respectivamente.

Modelos matemáticos empleados

Los cuatro modelos matemáticos empleados se ilustran en las ecuaciones (10) a (13).

Modelo matemático 1

Modelo matemático 2

Modelo matemático 3

Modelo matemático 4

Metodología propuesta

En esta sección se describe la metodología propuesta para solucionar el problema del planeamiento de sistemas de distribución de energía eléctrica, empleando como técnica de solución el algoritmo NSGA-II.

Codificación empleada

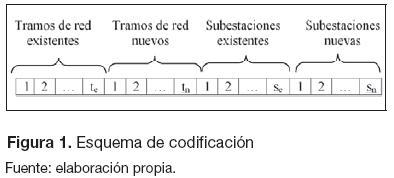
Se emplea un vector con variables enteras que representa una configuración del sistema (figura 1), donde t_e, t_n, s_e y s_n representan el número de tramos de red existentes y nuevos, así como el número de subestaciones existentes y nuevas, respectivamente. En este vector cuando una posición tiene asociado un cero, eso quiere decir que este elemento no se propone en dicha solución. Cuando tiene un valor diferente de cero, quiere decir que ese elemento es propuesto con el tipo descrito en su posición.

Técnica de solución

Los aspectos del algoritmo se describen a continuación (Deb, 2004; Gallego, Escobar y Toro, 2008).

Generación de la población inicial: puede generarse usando una técnica heurística constructiva o de forma aleatoria. En este artículo se genera de forma aleatoria.

Selección: se emplea la selección por torneo considerando apilamiento. En esta etapa se comparan dos soluciones y se retorna el ganador, asumiendo que cada solución i tiene un rango de no dominancia y una distancia de apilamiento. Una solución i gana un torneo con otra solución j si la solución i tiene mejor rango (mejor frente de Pareto), o si tienen el mismo rango pero la solución i tiene mayor distancia de apilamiento.

Recombinación y mutación: se aplica la recombinación sobre dos padres, generando dos descendientes directos y seleccionando el de mejor calidad, el cual es sometido a mutación. Esto se realiza hasta completar la población descendiente. Las tasas de recombinación y de mutación se encuentran por pruebas de ensayo y error.

Evaluación de configuraciones e infactibilidades: para la evaluación de las configuraciones los modelos son transformados de restrictos a irrestrictos; de esta forma las violaciones de las restricciones (en caso de que existan) son llevadas a la función objetivo como un valor de penalización, multiplicados por un factor con el fin de unificar unidades de la función objetivo. Para evaluar las configuraciones se emplea un flujo de carga radial de barrido iterativo (Shirmohammadi, Hong, Semlyeny Luo, 1988).

Criterio de parada: el criterio de parada se basa en dos aspectos: si la solución incumbente no mejora después de un número predefinido de iteraciones, o si se alcanza un número máximo de iteraciones del algoritmo.

Selección de una solución del frente

Para seleccionar una solución del frente de Pareto se emplea el criterio maxmin, el cual consiste en normalizar para cada solución los valores de ambas funciones objetivo con respecto a los valores extremos encontrados en el frente (Deb, Amrit, Agarwaly Meyarivan, 2000). Una vez normalizadas ambas funciones objetivo, se selecciona el menor valor para cada solución. Luego se obtiene el máximo valor de todos los valores mínimos encontrados previamente. El valor final definido está asociado a la solución encontrada con el criterio maxmin, es decir, pertenece a una solución que tiene en cuenta la importancia de cada objetivo considerado, llevando a soluciones centradas en el frente óptimo de Pareto.

Determinación de tendencias de las configuraciones

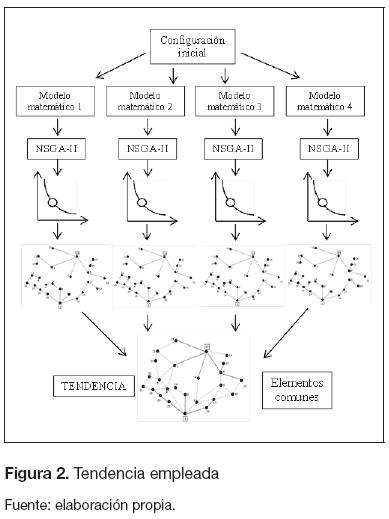
Al aplicar la técnica de solución a los modelos matemáticos propuestos (ecuaciones (10) a (13)) y luego de seleccionar la mejor solución del frente de Pareto, se comparan las configuraciones encontradas con el fin de hallar una tendencia entre estas (elementos comunes). Una vez se determina esta tendencia, se fijan sus posiciones en el vector codificación y se ejecuta nuevamente el algoritmo con todos los modelos matemáticos propuestos. Este proceso se repite hasta que se encuentra una topología final (tendencia final) que tenga elementos comunes a todas las soluciones de los modelos matemáticos (ver figura 2). Al final de cada tendencia se pueden encontrar tramos de red propuestos que generan anillos en el sistema, por lo que estos elementos no forman parten de los elementos definidos en la siguiente fase del proceso. Adicionalmente, se pueden encontrar tramos de red comunes a los modelos matemáticos que no están conectados al resto del sistema (islas), razón por la cual estos elementos (al igual que los anteriores), tampoco forman parte de los elementos que son definidos en la siguiente fase del proceso; es decir, quedan nuevamente como tramos propuestos para la siguiente iteración (tendencia).

Una vez definida la topología del sistema, se seleccionan los calibres de los conductores. Inicialmente se fijan los calibres que son iguales en los modelos matemáticos. Luego, para los tramos de red con calibres diferentes se define su calibre escogiendo el mayor valor obtenido en los modelos; esto con el fin de dar cumplimiento a los resultados de todos los modelos matemáticos empleados.

Algoritmo

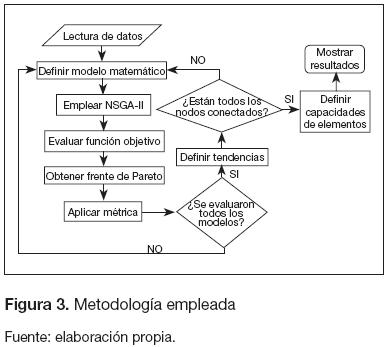
La metodología propuesta se ilustra en la figura 3.

Con el fin de probar la metodología propuesta en este artículo, se empleó un sistema de distribución de 25 nodos (Nahman y Peric, 2008).

Resultados obtenidos

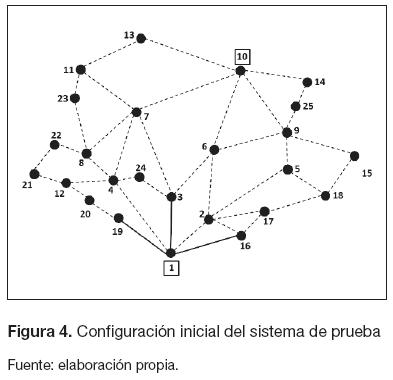
La implementación y aplicación de la metodología se realizó en Matlab R2009b®. En la figura 4 se ilustra la configuración inicial del sistema, cuyo voltaje nominal es 13,2 kV. El nodo con el número 1 corresponde a la subestación existente y el número 10 a la subestación propuesta. Se consideran cuatro tipos de calibres para los conductores y cuatro tipos de subestaciones, los cuales se ilustran en la tabla 1, donde los términos CI y CR corresponden a costos de instalación y repotenciación, respectivamente. Los tramos de red existentes (1-3, 1-16, 1-19) y la subestación existente son del tipo 1.

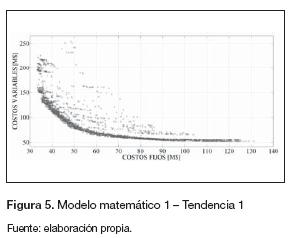
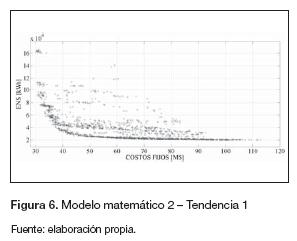
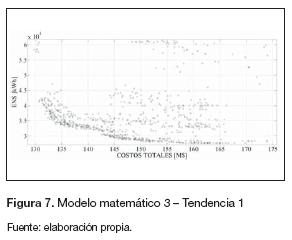
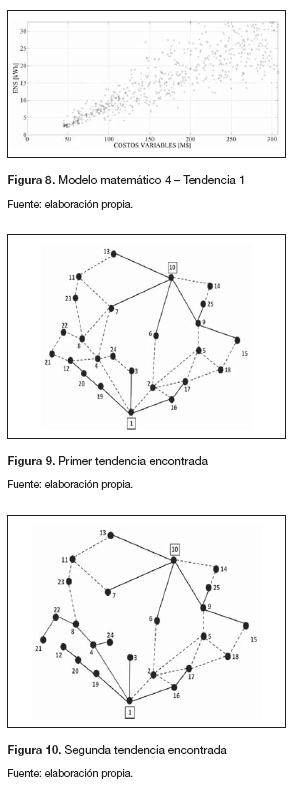
Los parámetros empleados por el algoritmo son: 60 individuos en la población, 300 generaciones y tasas de recombinación y mutación de 0,9 y 0,05, respectivamente. El comportamiento del algoritmo cuando se emplean los cuatro modelos matemáticos propuestos se presenta en las figura 5 a 8. En estas figuras se observa cómo el algoritmo converge a regiones de buena calidad, al partir de una población inicial generada aleatoriamente. De las figuras 5 a la 7 se observa que las funciones objetivo están en conflicto, ya que el mejoramiento de uno de ellos empeora al otro objetivo. Esta situación no ocurre con el cuarto modelo matemático (figura 8), pues se observa que ambos objetivos están en la misma dirección. De acuerdo con esto para las próximas iteraciones (tendencias) no se considera el cuarto modelo matemático, pues este no considera objetivos en conflicto.

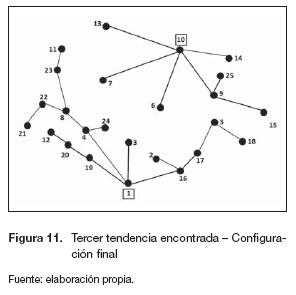
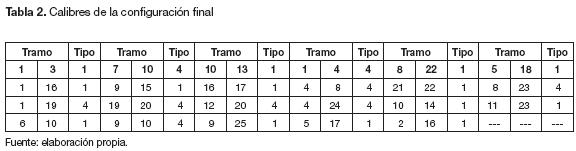
De cada frente de Pareto encontrado con los primeros tres modelos matemáticos se selecciona una configuración, usando la métrica descrita en la subsección "Selección de una solución del frente". Posteriormente, se determinan los elementos comunes, los cuales son definidos para el siguiente paso del proceso. Esto se repite hasta que se encuentra una configuración común a todos los modelos y en la cual no hay nodos desconectados. En la figuras 9 a 11 se presentan las configuraciones encontradas después de evaluar tres tendencias. La topología de la figura 11 corresponde a la configuración final del sistema encontrada por la metodología. Para esta configuración las dos subestaciones son de igual capacidad (tipo 2).

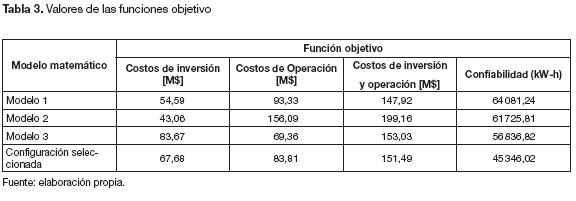
Los calibres de cada tramo de red se presentan en la tabla 2. A la configuración seleccionada se le evalúan los tres modelos matemáticos, con los cuales se obtienen: costos de inversión, costos de operación, costos totales y confiabilidad (ENS). Estos valores se ilustran en la tabla 3.

Discusión de los resultados

Al resolver el modelo matemático 4 (costos de operación vs. confiabilidad), se observa que ambos objetivos están en la misma dirección (figura 8). Esto se debe a que las tasas de falla y los tiempos de reparación vienen dados por calibres de conductor, los cuales disminuyen a medida que aumenta el calibre. Dado que a mayor calibre se tienen menores pérdidas técnicas (disminuye la resistencia) y considerando el aspecto descrito previamente, el algoritmo tiene una tendencia por seleccionar siempre calibres de gran tamaño, pues de esta forma disminuye el nivel de ENS (mejorando la confiabilidad) y reduce el costo de pérdidas de energía (costos operativos).

Con respecto a los costos de inversión, se observa que la configuración seleccionada tiene un valor mayor que los modelos matemáticos 1 y 2 y menores al modelo 3. Los valores mayores de costos operativos se obtienen con los modelos 1 y 2. Adicionalmente, los costos totales del proyecto ($ 151,49 millones) son menores que los costos encontrados con los tres modelos matemáticos.

El mayor nivel de ENS se encuentra en el modelo 1, ya que este solamente considera costos en sus funciones objetivo (inversión vs. operación). Sin embargo, cuando en los modelos matemáticos se considera la minimización de criterios de confiabilidad, se observa que este valor es menor que el caso en que no se consideran. Adicionalmente, se observa que la configuración seleccionada presenta menores valores de ENS que los tres modelos matemáticos.

Si se considera solamente el modelo 1, la energía no servida sería alta en comparación con los otros modelos, por lo cual la confiabilidad del sistema sería baja; si se considera exclusivamente el modelo 2, los costos totales serían elevados, con un gran porcentaje representado en los costos de operación; en el caso del modelo 3 se tienen los mayores costos de inversión, lo cual reduce los costos de operación y mejora la confiabilidad, aunque requiere una mayor inversión inicial. Esto demuestra que la metodología permite encontrar un punto de equilibrio entre todos los objetivos, generando una inversión moderada, con costos de operación cerca de la mitad de los costos totales y un nivel de ENS inferior al que puede establecerse solamente considerando costos de inversión y operación.

Una ventaja de manejar tendencias considerando varios modelos matemáticos es que se puede reducir el espacio de solución, con algoritmos más eficientes y estableciendo diferentes alternativas que permiten la evaluación y la búsqueda de los parámetros óptimos de acuerdo con el interés sobre cada objetivo en particular.

De los resultados obtenidos en el sistema de prueba se observa que las subestaciones son de igual tamaño en todos los modelos matemáticos (tipo 2). De acuerdo con esto, se nota que la selección de las subestaciones solamente se ve afectada por los costos de inversión, pues selecciona siempre el menor tipo (más económico), pero no se ve influenciada por los costos de operación o confiabilidad. Se puede deducir entonces que los elementos que más tienen peso a la hora de definir una tendencia son los tramos de red, ya que varían dependiendo del objetivo tratado.

Conclusiones

En este artículo se propuso e implementó un algoritmo NSGA-II aplicado a la solución del problema de la expansión de sistemas de distribución de energía eléctrica usando modelos de optimización multiobjetivo. Los modelos matemáticos empleados consideran dos funciones objetivo: el primero usa costos de inversión vs. costos de operación; el segundo emplea costos de inversión vs. confiabilidad; el tercero considera costos de inversión y operación vs. confiabilidad y el cuarto modelo usa costos de operación vs. confiabilidad. Los cuatro modelos tienen en cuenta el mismo conjunto de restricciones: ecuaciones de balance nodal, capacidades máximas en subestaciones y alimentadores, regulación máxima permitida y radialidad de la red. Esta metodología fue verificada con un sistema de prueba de la literatura y se encontraron soluciones que reflejan su validez al aportar al estado del arte en esta temática, dado que las configuraciones halladas encuentran un punto de equilibrio con respecto a todos los objetivos considerados, lo que demuestra la importancia de tenerlos en cuenta.

En el sector eléctrico se presentan fluctuaciones en los proyectos de inversión, dado que pueden tenerse diferentes prioridades dependiendo de los rubros que se tengan asignados, de los reglamentos internos o códigos que se deban cumplir en un periodo específico, o de las sanciones que se tengan a nivel nacional por ENS o pérdidas en la red. Esta condición genera que las prioridades de las empresas del sector eléctrico puedan cambiar, lo que genera cambios en sus inversiones o planeamiento de la red. Establecer una metodología que pueda evaluar diferentes parámetros y conocer el comportamiento que se presenta ante una determinada condición, permite tomar decisiones basadas en diferentes criterios y da la flexibilidad necesaria para elegir cuál condición requiere priorizar la empresa de acuerdo con su contexto y la condición en que se encuentre.

De los resultados obtenidos se aprecia que existe una tendencia en las topologías y capacidades de las subestaciones, independiente de las funciones objetivo empleadas. Encontrar este tipo de tendencias permite disminuir el espacio de solución mediante especies de cortes generados.

La gran diferencia en la tendencia obtenida a partir de los tres modelos matemáticos, se encuentra en los calibres de los conductores. La selección de los calibres de los tramos de red puede ser realizada a partir del interés específico de cada electrificadora por los objetivos considerados, o empleando una técnica que permita encontrar un punto de equilibrio entre estos. En este artículo se considera el mayor calibre obtenido de los tres modelos, con el fin de dar cumplimiento a todos los objetivos.

El algoritmo NSGA-II es una herramienta efectiva y poderosa para solucionar problemas multiobjetivo. Se puede observar el comportamiento adecuado del algoritmo, dado que sin importar el modelo matemático empleado, el tamaño del sistema de prueba y la generación aleatoria de la población inicial, este siempre converge a regiones de buena calidad.

La metodología propuesta es general y flexible y puede ser empleada en la solución del problema del planeamiento de sistemas de distribución realizando un planeamiento estático o por etapas y empleando dos o más objetivos, con la ventaja de obtener soluciones con buenas condiciones operativas sin importar el tamaño o la topología del sistema empleado.

Financiamiento

Este artículo es producto del proyecto "Planeamiento integrado de redes de distribución de energía eléctrica de media y baja tensión" (Código 6-13-4), el cual ha sido financiado por la Universidad Tecnológica de Pereira.

Referencias

Bernal-Agustín, J. (1998). Application of Gene-tic Algorithms To the Optimal Design of Power Distribution Systems. Zaragoza, España: Universidad de Zaragoza.

Billinton, R. y Allan, R. (1996). Reliability Evaluation of Power Systems. Nueva York: Plenum.

Carrano, E., Soarez, L., Takahashi, R., Saldanha, R. y Neto, O. (2006). Electric Distribution Network Multiobjective Design Using a Problem-Specific Genetic Algorithm. IEEE, 21 (2), 995-1005.

Deb, K. (2004). Multi-Objective Optimization using Evolutionary Algorithms. Nueva York: John Wiley y Sons.

Deb, K., Amrit, P., Agarwal, S. y Meyarivan, T. (2000). A Fast and Elitist Multiobjective Genetic Algorithm. Nueva Delhi: Kanpur Genetic Algorithms Laboratory, Indian Institute of Technology.

Gallego, R., Escobar, A. y Toro, E. (2008). Técnicas metaheurísticas de optimización. Pereira: Textos Universitarios Universidad Tecnológica de Pereira.

Ganguly, S., Sahoo, N. y Das, D. (2011). Multi-Objective Planning of Electrical Distribution Systems Incorporating Shunt Capacitor Banks. International Conference on Energy, Automation, and Signals (ICEAS) (pp. 1-6). Bhubaneswar, India.

Ganguly, S., Sahoo, N. y Das, D. (2013). Multi-Objective Planning of Electrical Distribution Systems Using Dynamic Programming. Electrical Power and Energy Systems, 46, 65-78.

Kayu, G. y Ooka, R. (2009). Application Multi-Objective Genetic Algorithm for Optimal Design Method of Distributed Energy System. Eleventh Intenational IBPSA Conference (pp. 162-172). Glasgow, Escocia.

Kong, T., Cheng, H., Hu, Z., Wang, C., Chen, C. y Gao Y. (2008). Multiobjective Planning of Open-Loop mv Distribution Networks Using ComGIS Network Analysis and MOGA. Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (pp. 1340-1346). NanJing, China.

Mantway, A., y Al-Muhaini, M. (2008). Multi-Objective BPSO Algorithm for Distribution System Expansion Planning Including Distributed Generation. Transmission and Distribution Conference and Exposition. T&D. IEEE/ PES, (pp. 1-8). Chicago, Estados Unidos.

Mori, H. y Yamada, Y. (2007). An Efficient Multi-Objective Meta-Heuristic Method for Distribution Network Expansion Planning. Ponencia presentada en la conferencia IEEE Lausanne Power Tech Conference, Lausana, Suiza, 1-5 de julio de 2007 (pp. 374-379).

Nahman, J. y Peric, D. (2008). Optimal Planning of Radial Distribution Networks by Simulated Annealing Technique. IEEE Transactions on Power Systems, 23 (2), 790-795.

Ramírez, I. y Bernal, J. (2001). Reliability and Costs Optimization for Distribution Network Expansion Using an Evolutionary Algorithm. IEEE Transactions on Power Systems, 16 (1), 111-118.

Ramírez, I. y Domínguez, J. (2004). Possibilistic Model Based on Fuzzy Sets for the Mul-tiobjective Optimal Planning of Electric Power Distribution Networks. IEEE Transactions on Power Systems, 19 (4), 1801-1810.

Ramírez, I. y Domínguez, J. (2006). New Mul-tiobjective Tabu Search Algorithm for Fuzzy Optimal Planning of Power Distribution Systems. IEEE Transactions on Power Systems, 21 (1), 224-233.

Sahoo, N., Ganguly, S. y Das, D. (2012). Multi-Objective Planning of Electrical Distribution Systems Incorporating Sectionalizing Switches and Tie-Lines Using Particle Swarm Optimization. Swarm and Evolutionary Computation, 3, 15-32.

Shirmohammadi, D., Hong, H., Semlyen, A. y Luo, G. (1988). A Compensation-Based Power Flow Method for Weakly Meshed Distribution and Transmission Networks. IEEE Transactions on Power Systems, 3 (2), 753-762.