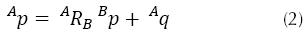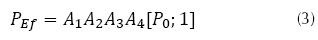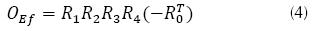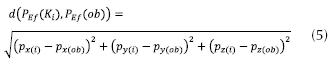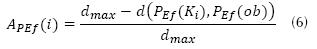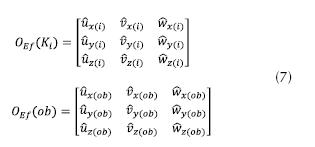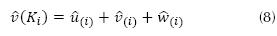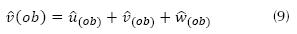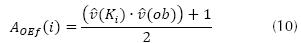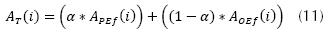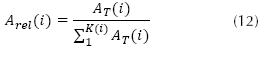DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2015.2.a02Published:
2015-04-01Issue:
Vol. 19 No. 44 (2015): April - JuneSection:
ResearchCinemática inversa de robot serial utilizando algoritmo genético basado en MCDS
Inverse kinematics of a serial robot using SDKM- based genetic algorithm
Downloads
References
Aguilar, O. A., & Huegel, J. C. (2011). Inverse Kinematics Solution for Robotic Manipulators Using a CUDA-Based Parallel Genetic Algorithm. In I. Batyrshin & G. Sidorov (Eds.), Advances in Artificial Intelligence (Vol. 7094, pp. 490-503): Springer Berlin Heidelberg.
Albert, F. Y. C.; Koh, S. P.; Chen, C. P.; Tiong, S. K., & Edwin, S. Y. S. (2011). S.Y.S. Paper presented at the International Conference on Computer Engineering and Applications, Singapore.
Araujo, L., y Cervigon, C. (2009). Algoritmos evolutivos: Un enfoque práctico (Vol. 1). Madrid: Ed. RaMa.
Barrientos, A.; Peñín, L. F.; Balaguer, C., & Santoja, R. A. (2007). Fundamentos de robótica (Vol. 2). Aravaca, Madrid: McGraw-Hill.
Bravo, S. Á. (2012). Evaluación de técnicas evolutivas en el cálculo de la cinemática inversa de robots manipuladores. Ingeniería Técnica en Electrónica, Universidad Carlos III de Madrid.
Carvalho, L., & Gaspar, E. (1991). The solution of the inverse kinematic problem of robot arm with neural networks. Paper presented at the IX Brazilian Congress on Mechanical Engineering, Brasil.
Denavit, J., & Hartenberg, R. S. (1955). A kinematic notation for lower-pair mechanisms based on matrices. Journal of Applied Mechanics, 22, 215-221.
Duffy, J., & Crane, C. (1980). A displacement analysis of the general spatial 7-link, 7R mechanism. Mechanism and Machine Theory, 15(3), 153-169.
Gibbs, J. (1996). Easy inverse kinematics using genetic programming. Paper presented at the GP-96 Conference.
Giraldo, L.; Delgado, E., y Castellanos, G. (2006). Cinemática Inversa de un Brazo Robot Utilizando Algoritmos Genéticos. Revista Avances en Sistemas e Informática, 3(1), 29-34.
Gonzálvez, B. A., e Iglesias, J. I. C. (2002). Identificación de parámetros cinemáticos de un robot industrial mediante un sistema de rastreo láser. PhD, Universidad Politécnica de Valencia.
Guez, A., & Ahmad, Z. (1988). Solution to the inverse kinematics problem in robotics by neural networks. Paper presented at the International Conference on Neural Networks, San Diego, Ca.
Jamshidi, M., S., C. d.; Krohling, A. R., & Fleming, J. P. (2005). Robust Control systems with genetic algorithms. International Journal of Robust and Nonlinear Control, 15(7), 210.
Kalra, P., & Prakash, N. R. (2003). A Neuro-genetic Algorithm Approach for solving the inverse kinematics of Robotic Manipulators. Systems, Man and Cybernetics, 2003. IEEE International Conference, 2, 1979-1984.
Khalil, W., & Dombre, E. (2004). Chapter 6 - Inverse kinematic model of serial robots. In W. Khalil & E. Dombre (Eds.), Modeling, Identification and Control of Robots (pp. 117-144). Oxford: Butterworth-Heinemann.
Khwaja, A. A.; Rahman, M. O., & Wagner, M. G. (1998). Inverse Kinematics of Arbitrary Robotic Manipulators Using Genetic Algorithms. In J. Lenarčič & M. Husty (Eds.), Advances in Robot Kinematics: Analysis and Control (pp. 375-382): Springer Netherlands.
Köker, R. (2013). A genetic algorithm approach to a neural-network-based inverse kinematics solution of robotic manipulators based on error minimization. Information Sciences, 222, 528-543.
Lee, C., & Ziegler, M. (1984). Geometric approach in solving inverse kinematics of puma robots. IEEE Transactions on Aerospace and Electronic Systems, 20(5), 1-27.
Murray, R. M.; Li, Z., & Sastry, S. S. (1994). A Mathematical Introduction to Robotic Manipulation (Vol. 2): CRC Press.
Oyama, E.; Chong, N.; Agah, A.; Maeda, T., & Tachi, S. (2001). Inverse kinematics learning by modular architectore neural networks with performance perdiction networks. Paper presented at the International Conference on Robotics and Automation.
Parker, J.; Khoogar, A., & Goldberg, D. (1989). Inverse kinematics of redundant robots using genetic algorithms. Paper presented at the International Conference on Robotics and Automation.
Pieper, L. D. (1968). The kinematics of manipulators under computer control. PhD, Stanford University (457).
Primrose, E. J. F. (1986). On the input-output equation of the general 7R-mechanism. Mechanism and Machine Theory, 21(6), 509-510.
Siciliano, B.; Sciavicco, L.; Villani, L., & Oriolo, G. (2009). Robotics: Modelling, Planning and Control (Vol. 1). London: Springer-Verlag.
Tabandeh, S.; Clark, C., & Melek, W. (2006). A Genetic Algorithm Approach to solve for Multiple Solutions of Inverse Kinematics using Adaptive Niching and Clustering. Paper presented at the IEEE Congress on Evolutionary Computation, Sheraton Vancouver Wall Centre Hotel, Vancouver, BC, Canada.
Tsai, L. W. (1999). Robot Analysis: The Mechanics of Serial and Parallel Manipulators (Vol. 1). New York: John Wiley & Sons, Inc.
Zomaya, A. (1994). Transputer Ensembles for Embedded Robotics Computations. Transputer Communications, 2, 151-170.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a02
Cinemática inversa de robot serial utilizando algoritmo genético basado en MCDS
Inverse kinematics of a serial robot using SDKM- based genetic algorithm
Juan Jairo Vaca González*
Cristhian Andrés Peña Caro**
Harold Vacca González***
* Ingeniero de Diseño y Automatización Electrónica, especialista en Diseño Mecatrónico PLM; magíster en Ingeniería Biomédica, estudiante de doctorado en Ingeniería – Ciencia y Tecnología de los Materiales, Universidad Nacional de Colombia, Bogotá. Contacto: jjvacag@unal.edu.co
** Ingeniero de Diseño y Automatización Electrónica, especialista en Diseño Mecatrónico PLM, estudiante de maestría en Ingeniería Mecánica en la Universidad Nacional de Colombia, Bogotá, Colombia. Contacto: crapenaca@unal.edu.co
*** Licenciado en matemáticas, magíster en Matemáticas Aplicadas, docente de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Contacto: hvacca@udistrital.edu.co
Fecha de recepción: 12 de junio de 2013 Fecha de aceptación: 5 de diciembre de 2014
Citation / Para citar este artículo: Vaca-González, J. J., Peña Caro, C. A., & Vacca-González, H. (2015). Cinemática inversa de robot serial utilizando algoritmo genético basado en MCDS. Revista Tecnura, 19(44), 33-45. doi: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a02
Resumen
Los robots manipuladores seriales son herramientas eficaces para realizar tareas repetitivas y de precisión en la industria, siempre que se comprenda la cinemática involucrada en el posicionamiento y orientación del efector final. Este artículo presenta una metodología para resolver el problema cinemático inverso de un robot serial (Melfa RV-2A) utilizando un algoritmo genético (AG) a partir del modelo cinemático directo Screws (MCDS). Para esto, se obtienen los parámetros Screw que modelan el robot, se calcula el espacio de trabajo asociado y se diseña el AG contemplando una función multi-objetivo de alcance de posición y orientación en que se sitúa el efector final, con respecto a una coordenada y orientación de un punto objetivo establecido. La validación del AG se realiza según la aptitud, el tiempo de convergencia y la cantidad de generaciones usadas por la función para alcanzar el objetivo. Por tanto, la implementación de un AG basado en un MCDS es una herramienta que podría utilizarse para calcular la cinemática inversa de robots seriales. Esta implementación permite establecer por primera vez la exposición matricial de un sistema cinemático directo para obtener la solución cinemática inversa de un robot serial. En consecuencia, se demuestra que esta es una metodología factible y eficiente para solucionar la cinemática inversa de cualquier tipo de robot manipulador.
Palabras clave: algoritmo genético, cinemática directa, cinemática inversa, espacio de trabajo, robot serial, Screws.
Abstract
Serial robotic manipulators are efficient tools to carry out repetitive and precision tasks in industry, as long as there is understanding of the involved kinematics in the positioning and orientation of the final effector. This article presents a methodology to the solution of an inverse kinematic serial robot (Melfa RV-2A) problem through genetic algorithm (GA) implementation using the Screws direct kinematic model (SDKM). In order to do this, the Screws parameters that model the main four robot joints are obtained, the related workspace is calculated and the GA is designed considering a multi objective function of position and orientation located in the final effector, with respect to a coordinate and orientation of an established target point. The GA validation is carried out according to aptitude, convergence time and number of generations used in order to reach the main objective. Therefore, the implementation of a SDKM-based AG is a tool that could be used to calculate the inverse kinematic of serial robots. This implementation allows to establishing for the first time the matrix exhibition of a direct kinematic system to obtain the inverse kinematic solution of a serial robot. In consequence, it is demonstrated that this methodology is feasible and efficient to solve the inverse kinematic of any manipulator robot.
Keywords: direct kinematic, genetic algorithm, inverse kinematic, screws, serial robot, workspace.
Introducción
El creciente uso de robots manipuladores seriales en la industria, como herramienta para tareas repetitivas y de precisión, hace necesario comprender la cinemática involucrada en torno al posicionamiento y orientación del efector final. Cuando esto se tiene, es posible realizar el control y programación de trayectorias para tareas como soldadura, pintura, ensamblaje, entre otras. Así mismo, el estudio del movimiento permite seleccionar la clase de robot manipulador según el tipo y la cantidad de eslabones necesarios para efectuar una tarea específica.
Un robot serial puede ser modelado como una cadena abierta de elementos (eslabones) unidos por ejes de revolución o traslación (articulaciones), en donde cada par eje-eslabón tiene asociada una matriz homogénea con componentes de rotación, traslación, perspectiva y escalamiento (Barrientos, Peñín, Balaguer, & Santoja, 2007). El posicionamiento y orientación del efector final resulta del movimiento relativo de cada eslabón respecto a un sistema de referencia fijo en la base del robot. A partir de un arreglo de parámetros articulares de traslación y/o rotación (cantidad definida por el número de articulaciones), el robot efectúa movimientos que determinan la solución cinemática directa, la cual se puede interpretar como una transformación lineal de vectores en el espacio que se desplazan desde el sistema de referencia origen, superponiéndose hasta alcanzar el sistema de referencia del efector final. A partir de este análisis se implementan métodos matriciales, como el propuesto por Denavit & Hartenberg en 1955, para identificar los diferentes ejes articulares de cada eslabón del robot. El método de desplazamientos sucesivos Screw, en tanto, establece una solución paramétrica al problema cinemático directo a partir del teorema Chasles y la fórmula de Rodrigues (Murray, Li, & Sastry, 1994); allí se determinan ejes de movimiento, relacionados únicamente con el sistema de referencia base, que una vez acoplados producen los movimientos articulares de donde se deducen la ubicación y orientación del efector final; el método tiene como ventaja poder aplicar el análisis tanto en robots seriales como paralelos (Tsai, 1999).
Por otra parte, la cinemática inversa consiste en obtener las variables articulares necesarias para alcanzar una combinación de posición y orientación deseadas del efector final. La solución ha sido abordada analíticamente por métodos basados en sistemas matriciales 4X4 (Pieper, 1968), o por solución geométrica (Lee & Ziegler, 1984). Es conocido, además, que para robots seriales que sobrepasan una cadena abierta de más de 3 eslabones se pueden obtener sistemas de ecuaciones hasta el orden 32 (Duffy & Crane, 1980), en los cuales existen al menos 16 soluciones complejas (Primrose, 1986). Así mismo, se han presentado métodos de solución iterativos basados en redes neuronales (Carvalho & Gaspar, 1991; Guez & Ahmad, 1988; Oyama, Chong, Agah, Maeda, & Tachi, 2001); algoritmos evolutivos para un manipulador de puntos individuales (Gibbs, 1996; Khwaja, Rahman, & Wagner, 1998; Parker, Khoogar, & Goldberg, 1989); y algoritmos genéticos (Siciliano, Sciavicco, Villani, & Oriolo, 2009), en los cuales se plantean soluciones a variables específicas de cinemática inversa; más recientemente Giraldo, Delgado, & Castellanos, 2006, han aplicado algoritmos genéticos en un brazo robot Scorbot VR plus. Por otro lado, con el objeto de dar solución a las ecuaciones no lineales derivadas del cálculo de la cinemática inversa de robots seriales, la implementación de algoritmos neuro-genéticos ha evidenciado ser una herramienta prometedora (Kalra & Prakash, 2003).
El uso de algoritmos genéticos para la solución de la cinemática inversa de robots seriales se ha enfocado en mejorar la precisión del efector final para alcanzar un punto dado en el espacio. Por ejemplo Köker, en 2013, implementó un algoritmo genético en combinación con una red neuronal para minimizar el error del efector final. Los resultados obtenidos muestran que el modelo implementado mejora la posición del efector final, obteniendo una precisión de micrómetros. Dado que los eslabones de un robot serial pueden tener diferentes orientaciones para llegar al objetivo final, la solución analítica de este problema no lineal se dificulta. En este sentido, el uso de algoritmos genéticos puede tener en cuenta todas las posibles combinaciones y soluciones que hacen que el robot guie el efector final para alcanzar un punto dado (Tabandeh, Clark, & Melek, 2006; Aguilar & Huegel, 2011; Albert, Koh, Chen, Tiong, & Edwin, 2011).
Como se mencionó antes, se han implementado diferentes algoritmos genéticos para desarrollar la cinemática inversa de robots seriales; sin embargo, los trabajos han basado el análisis del algoritmo genético a partir de sistemas matriciales y geometría tradicional para calcular la orientación del efector final. El presente artículo presenta la implementación de un algoritmo genético para calcular la cinemática inversa de robots seriales utilizando el modelo cinemático directo Screws (MCDS). Esta novedad permite establecer, por primera vez, la implementación matricial de un sistema cinemático directo para obtener la solución cinemática inversa de un robot serial. Utilizando esta metodología se obtiene de manera más eficiente la solución del problema cinemático inverso de un robot serial (Melfa RV-2A), teniendo en cuenta el alcance y la orientación del efector final. Para llevarla a cabo se analizan cuatro de las seis articulaciones que realizan la tarea establecida y que cumplen con las dimensiones y estructura del robot, descartando las articulaciones que causan redundancia cinemática (Zomaya, 1994), con el objetivo de limitar la cantidad de soluciones posibles (Khalil & Dombre, 2004).
La estructura del artículo se dispone así: MCDS y espacio de trabajo; Materiales y Métodos: Implementación de AG; Pruebas y Resultados de validación del algoritmo; Conclusiones y recomendaciones.
Modelamiento cinemático directo screw (mcds) y espacio de trabajo
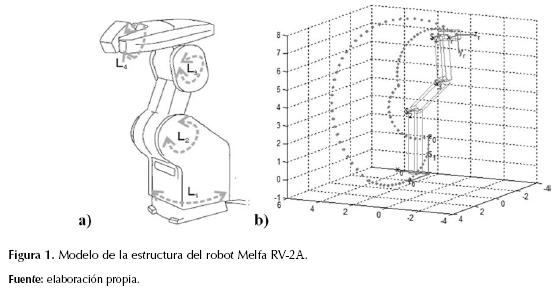
Los fabricantes de robots industriales proveen en sus catálogos las dimensiones y características necesarias para su modelado cinemático o, en su defecto, estas pueden obtenerse a través de medición directa sobre el robot. Si se requiere un grado importante de precisión en los parámetros cinemáticos, estos pueden estimarse mediante técnicas de calibración de robots, tema suficientemente abordado por Gonzálvez & Iglesias, 2002, y Jamshidi, S., Krohling, & Fleming, 2005, entre otros. En el caso que nos ocupa, a partir de las dimensiones del robot dadas por el fabricante (figura 1a), se modela una estructura a escala que representa las distancias entre las diferentes articulaciones. De este modo, se igualan los valores asociados a las dimensiones, rangos de operación y las cuatro articulaciones rotativas, que permiten alcanzar las coordenadas objetivo de acuerdo con el área de trabajo del robot (figura 1b) para los cuatro eslabones que deben cumplir con la tarea principal establecida (posicionarse y orientarse en una coordenada establecida). En consecuencia, los parámetros obtenidos del modelo del robot permiten representarlo matemáticamente mediante matrices homogéneas, como indica la ecuación (1).
La matriz homogénea reúne dos componentes: primero la rotación del sistema de referencia ligado a un eslabón B respecto al sistema anterior A, siendo 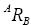 una matriz 3X3; y segundo, la coordenada de origen de un sistema de referencia respecto al anterior A (traslación), siendo
una matriz 3X3; y segundo, la coordenada de origen de un sistema de referencia respecto al anterior A (traslación), siendo 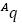 un vector 3X1; los demás componentes: el vector de perspectiva s y constante de escalamiento K, no se utilizan en el modelo, por lo que se asignan los valores arbitrarios señalados en la ecuación (1).
un vector 3X1; los demás componentes: el vector de perspectiva s y constante de escalamiento K, no se utilizan en el modelo, por lo que se asignan los valores arbitrarios señalados en la ecuación (1).
Luego de la anterior modelación, puede ilustrarse que el método de desplazamientos sucesivos de Screw está basado en dos resultados: el teorema de Chasles y la fórmula de Rodrigues. El primero establece que sin importar cómo el cuerpo rígido sea desplazado de un punto a otro, tal desplazamiento puede considerarse como la suma de una rotación y una traslación alrededor y a lo largo de un eje. El segundo establece que para el desplazamiento general de un cuerpo rígido, dados un ángulo de rotación, una coordenada de traslación y un eje de desplazamiento, es posible encontrar el vector resultante. Esta fórmula se representa matricialmente mediante un vector desplazado 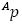 que resulta de la suma entre la rotación
que resulta de la suma entre la rotación 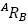 de un vector
de un vector 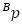 y una traslación
y una traslación 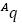 , como indica la ecuación (2).
, como indica la ecuación (2).
Esta expresión describe la transformación homogénea Ap = ABp donde A es una matriz de transformación 4X4.
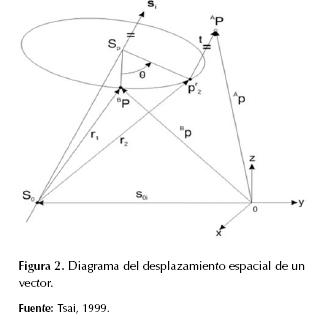
Cada elemento de esta matriz es derivado de la fórmula de Rodrigues y requiere cuatro parámetros para describir un Screw (parámetros Screw): un vector de posición de origen Soi, un vector unitario de dirección Si, una variable de ángulo de rotación θ y una magnitud variable de desplazamiento t. De este modo, un Screw se describe de acuerdo con la teoría espacial de desplazamiento de un vector (figura 2).
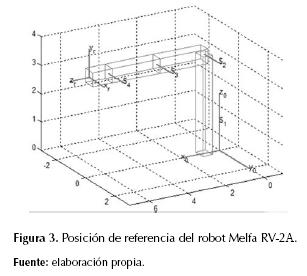
La cinemática directa del brazo robot analizado parte de encontrar los parámetros Screw (tabla 1) asociados a cada uno de los eslabones Li desde una posición de referencia inicial (Home) del robot (figura 3); estos parámetros involucran la desviación d1 entre la base y la segunda articulación del robot. La magnitud t para todos los eslabones es cero, debido a que no hay articulaciones prismáticas.
Los parámetros Screw para el Ef especifican únicamente la coordenada de posición en la que este se situará con respecto al sistema de referencia origen. Para conocer la posición del centro del efector final PEf se considera la ecuación (3).
Las matrices A1, ..., A4 son matrices homogéneas Screw asociadas a cada uno de los eslabones, con parámetros (Si, Soi, ti, θi). El vector Po corresponde a la posición Home (Pox, Poy, Poz) del centro del Ef. De este modo los tres primeros elementos de PEf indican la coordenada (Px, Py, Pz) en la que se ubica el centro del Ef después de un desplazamiento. Para obtener la orientación OEf del efector final, se considera la ecuación (4).
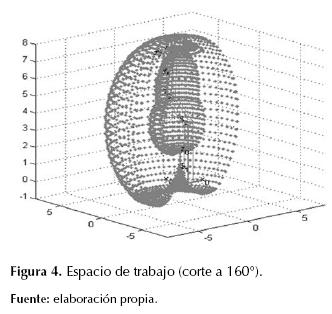
Las matrices R1, ..., R4 corresponden a las matrices de rotación Screw de los eslabones tomadas de las matrices homogéneas 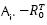 corresponde a la inversa de la matriz de rotación asociada al sistema de referencia del Ef en la posición Home. Con base en los rangos de operación (tabla 2), dados por el fabricante del robot, se obtienen las posibles posiciones (Px, Py, Pz) que puede tomar el Ef, generando de este modo el arreglo de coordenadas que forman el espacio de trabajo (figura 4).
corresponde a la inversa de la matriz de rotación asociada al sistema de referencia del Ef en la posición Home. Con base en los rangos de operación (tabla 2), dados por el fabricante del robot, se obtienen las posibles posiciones (Px, Py, Pz) que puede tomar el Ef, generando de este modo el arreglo de coordenadas que forman el espacio de trabajo (figura 4).
Materiales y métodos: diseño e implementación del AG
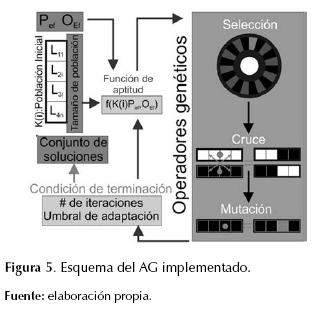
Un AG es un método de optimización basado en los principios de selección natural y modificación genética, con una estructura que consta de: una población inicial de individuos, una función de aptitud y operadores genéticos (selección, cruce y mutación) (Araujo & Cervigon, 2009). La estructura del AG implementado (figura 5) evidencia el flujo de trabajo seguido para conseguir una solución al problema cinemático inverso a partir de los parámetros de cinemática directa (PEf y OEf ) que serán las condiciones de la función de aptitud.
A continuación se especifica cada uno de los componentes del esquema para el AG implementado.
Población inicial (representación de los individuos)
Cada uno de los arreglos de variables articulares desde L1 a L4 son los individuos K(i) de la población inicial, los cuales se definen, en este caso, como una cadena de números enteros que se representan literalmente dentro de los rangos de operación (tabla 2) para cada eslabón. Usualmente se toma una cadena binaria que representa el genotipo del problema, pero debido a que el espacio de búsqueda es equivalente al espacio de trabajo que contiene un número infinito de posibles coordenadas (fenotipo), se selecciona esta representación de individuos, brindando suficiente variedad y precisión para poder explorar todas las zonas del espacio de búsqueda (Araujo y Cervigón, 2009). El tamaño de la población fija se establece de 200 individuos, el cual es un tamaño pequeño que cubre de manera objetiva el espacio de búsqueda.
Función de evaluación
La función de aptitud multi-objetivo debe encontrar un conjunto de respuestas que alcancen condiciones óptimas de posición y orientación del Ef. Inicialmente se obtienen las variables de cinemática directa (PEf y OEf ) para cada uno de los individuos K(i) de la población en curso para ser evaluadas de acuerdo con la posición y orientación objetivo (PEf(ob) y OEf (ob)) dados del Ef. La aptitud de un individuo i según la componente de posición (APEf), se calcula a partir de la distancia euclidiana (ecuación (5)) entre la posición del Ef de un individuo PEf (Ki) y PEf(ob).
Entonces APEf para un individuo i se describe en la ecuación (6).
Donde dmax será la distancia máxima posible entre dos puntos dentro del espacio de trabajo y corresponde a 2(L2+L3+L3) que es el diámetro máximo del espacio de trabajo. De este modo APEf se define como una función de maximización en el rango 0 < APEf < 1, donde 0 representa el individuo menos apto (punto más lejano de PEf(ob)) y 1 el más apto (punto más cercano de PEf(ob)).
La aptitud de un individuo según su orientación AOEf se obtiene a partir de la comparación entre la orientación del i-ésimo individuo de la población en curso OE f (Ki ) y OE f (ob). Entonces AOEf se define a partir de las matrices de orientación asociadas a cada individuo (ecuación (7)).
Para OE f (Ki ) se obtiene a partir de la ecuación (8).
Para OE f (ob) se obtiene a partir de la ecuación (9).
A partir de la suma vectorial de las componentes de las matrices de rotación 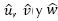 según las ecuaciones (8) y (9), se obtiene AOEf para un individuo i-ésimo según la ecuación (10).
según las ecuaciones (8) y (9), se obtiene AOEf para un individuo i-ésimo según la ecuación (10).
De este modo, la función de AOEf se define como una función de maximización en el rango 0 < AOEf (i)< 1, donde 0 representa el individuo menos apto 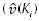 paralelo opuesto a
paralelo opuesto a 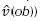 , y 1 el mejor individuo apto
, y 1 el mejor individuo apto 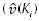 colineal a
colineal a  pasando por la condición de ortogonalidad cuando AOEf = 0.5.
pasando por la condición de ortogonalidad cuando AOEf = 0.5.
Por último, la función de aptitud total AT se define usando las ecuaciones (6) y (10) y se describe en la ecuación (11).
Donde α es una variable asignada en el rango 0 < α < 1, que indica el peso que se asigna al objetivo (posición y orientación) dentro de la función de aptitud multi-objetivo. Adicionalmente, se halla la aptitud relativa, ecuación (12), para emplearla en los operadores genéticos.
Operadores genéticos
A continuación se describen los operadores genéticos implementados.
La selección se compone de los métodos de la ruleta y elitismo donde, a partir de la clasificación descendente de la de la Arel población en curso, 10% de individuos más aptos siempre pasan a la siguiente generación, los individuos restantes se someten a selección por el método de la ruleta según estos pasos:
- Generación de un número aleatorio p que determina la posición de parada de la ruleta.
- Si
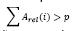 la ruleta se detiene y el individuo K(i) asociado es seleccionado.
la ruleta se detiene y el individuo K(i) asociado es seleccionado.
El cruce es de tipo mono-punto, realizado a partir de la población seleccionada, y consiste en escoger al azar una posición en la cadena de cada par de individuos padre e intercambiar las partes divididas por dicha posición, de tal modo que los individuos generados tengan propiedades combinadas, lo que puede llevar a mejorar la aptitud en las generaciones posteriores.
La mutación consiste en cambiar el valor de una de las posiciones de cada individuo (Ki) solo si la probabilidad de mutación establecida de 10% (umbral) es superada; este método se ejecuta de manera similar al operador de mutación bit a bit, pero en este caso la posición remplazada depende del rango de operación de la articulación Li que representa, siendo cada nueva posición un número aleatorio comprendido en el rango de operación de la posición seleccionada para mutar.
Pruebas y análisis de resultados
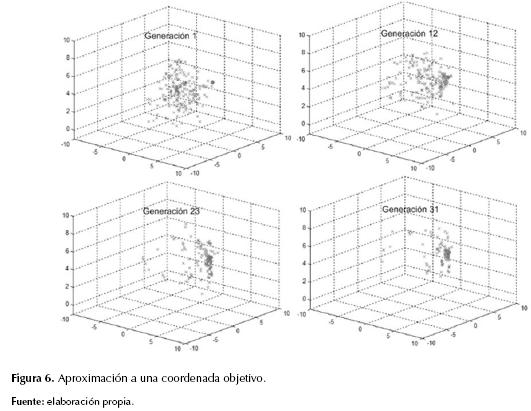
Con el objetivo de evaluar el fenotipo del AG, gráficamente en la figura 6 se evidencia cómo, generación tras generación de individuos, el arreglo de coordenadas obtenidas de la implementación del AG (puntos claros) cubre el espacio de búsqueda y confluye en la coordenada objetivo (punto oscuro).
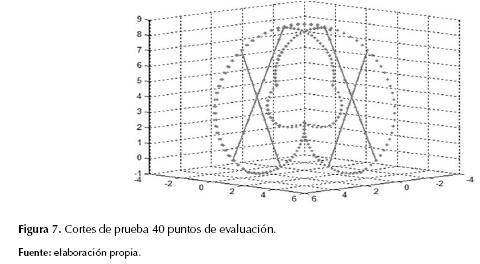
Para comprobar la efectividad del AG implementado, se extrae una muestra de cuarenta coordenadas fijas encerradas dentro del espacio de trabajo, distribuida en dos cortes, como se muestra en la figura 7, de tal modo que se logre cubrir de manera objetiva los rangos de operación del robot. Además, estas coordenadas están ubicadas de modo acorde con una distribución lineal con el objetivo de evaluar la eficiencia del AG.
Como la función de aptitud evalúa paralelamente la orientación de una coordenada para cada individuo, se establece una orientación estándar, según la matriz de rotación de la coordenada objetivo OE f (ob) para el Ef, que consiste en una rotación en torno al eje X de -125°, de tal modo que el sistema de coordenadas del efector final sea comparado con el sistema de referencia objetivo basado en AOEf (i).
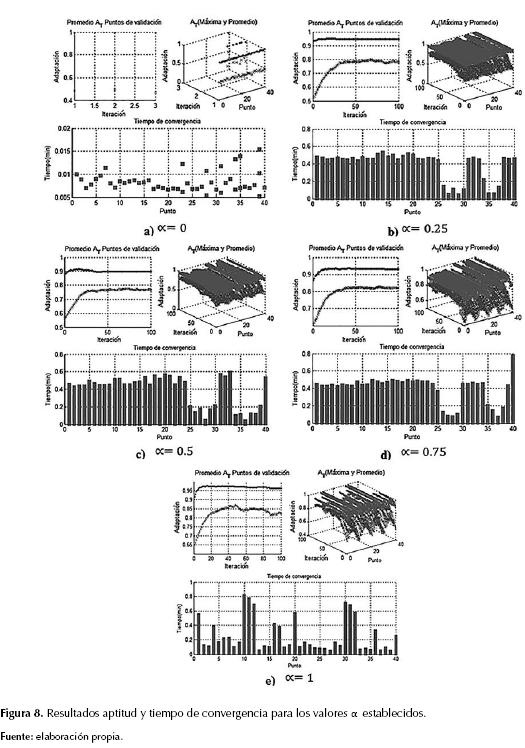
Una vez obtenidas las coordenadas y su orientación, cada una se evalúa en el AG para diferentes valores α de peso de la función de aptitud. La pruebas de aptitud, tiempo de convergencia y resumen de aptitud para la muestra de puntos seleccionados de validación se evalúa para los valores α = 0, 0.25, 0.5, 0.75 y 1. Las condiciones de parada del algoritmo se basan en un umbral de aptitud superior a 95% o cuando se alcance un total de cien iteraciones. En la figura 8 se muestran las gráficas de la aptitud y tiempo de convergencia resultantes de la variación del peso en la función de aptitud. Allí se indican los valores de aptitud máxima, los cuales son la población solución del problema, y la aptitud promedio que indicará la eficiencia de convergencia del AG en cada generación.
Los resultados demuestran que la evaluación de un solo parámetro (cuando α =0 evalúa solo orientación (figura 8a); y cuando α =1 evalúa solo precisión (figura 8e)); el tiempo de convergencia es, en promedio, el menor de todos los casos debido a que la función de aptitud solo busca un parámetro y el otro parámetro es nulo. Los puntos de mayor dificultad de alcance según el tiempo de convergencia se pueden constatar en la figura 8e. Así mismo al evaluar únicamente la orientación, esta puede hallarse rápidamente, como lo demuestra el tiempo de convergencia en la figura 8a. Se puede concluir que estos valores de α no resuelven el problema conjunto debido a la parcialidad en los resultados, porque al evaluar solo la orientación el Ef puede tomar la orientación objetivo en cualquier coordenada; análogamente, si se evalúa solo el posicionamiento este puede resolverse sin orientar debidamente el Ef. Cuando la función de aptitud tiene un α = 0.25 se observa que la componente de orientación aún sigue tomando dominio en la solución, lo que indica que no es un buen equilibrio ponderado para la función de aptitud, porque aunque la tendencia de dicha función es buena, el Ef no alcanzará el correcto posicionamiento del Ef.
En las gráficas de la figura 8c y la figura 8d se evidencia que en el rango 0.5 < α < 0.75 puede haber un equilibrio justo entre posicionamiento y orientación ya que en los datos relacionados con estas gráficas, el error promedio es inferior a 6%, lo que indica que el AG encuentra mejores soluciones ponderadas para los objetivos planteados. Las gráficas de promedio de aptitud AT de los puntos de validación son la muestra de aptitud máxima y promedio para las coordenadas establecidas, lo que indica la eficiencia del AG. La tendencia de las líneas oscura y clara indica cómo converge el AG, demostrando que se pueden reducir los valores de condición de parada del algoritmo debido a la rapidez en la obtención de una solución viable y establecer nuevas condiciones en torno a la aptitud y el tiempo de convergencia.
Conclusiones y recomendaciones
Un AG es un método dinámico de optimización para el cual no se han establecido parámetros fijos que garanticen su funcionamiento para cualquier tipo de problema; sus parámetros de entrada y funcionamiento, en efecto, son adaptados de acuerdo con las necesidades de cada problema; en este caso se comprueba que para el problema cinemático inverso, un AG puede resolver de manera eficaz el problema conjunto de precisión y orientación. En comparación con los métodos tradicionales de solución del problema cinemático inverso, un AG, al ser un método iterativo aleatorio, no incrementa su dificultad a medida que aumenta el número de eslabones en serie en el robot manipulador, pudiendo de esta forma resolver rápida y efectivamente el problema cinemático inverso para una cadena abierta de n-eslabones. Así mismo, se puede comprobar la convergencia del AG evaluando varias coordenadas en donde se evidencia que pueden hallarse singularidades de pares posición-orientación, que equivalen a coordenadas alcanzables por el Ef pero que no son plenamente orientables, lo que indica que antes de efectuar una búsqueda conjunta de coordenada-orientación óptimas, se debe conocer la autonomía del robot para determinar de manera efectiva un punto y ser orientado en el mismo. Con la implementación de este AG se puede destacar que se reducen las posibles soluciones a una coordenada específica, ya que el cálculo de la orientación en conjunto con el posicionamiento implica que se reduzcan las posibles combinaciones de variables articulares.
Como trabajo futuro se propone la programación de trayectorias a partir de la interpolación de coordenadas resueltas de cinemática inversa obtenidas de la implementación del AG. Además, se propone establecer un espacio de trabajo que contemple las singularidades resultantes del análisis de autonomía del robot.
Por otra parte, (Bravo, 2012) examina el rendimiento de un algoritmo de búsqueda directa a partir del problema de cinemática inversa de robots manipuladores de diferentes grados de libertad a través de un enfoque evolutivo denominado Differential Evolution. Este trabajo sugiere a futuro insistir en la comparación de resultados obtenidos mediante diferentes métodos de inversión cinemática; así como en la implementación, simulación y comparación de algoritmos de cálculo de la cinemática inversa de robots manipuladores redundantes, móviles, o con mayor número de grados de libertad. Todos caminos válidos a seguir basados en el algoritmo genético aquí presentado.
Financiamiento
Grupo de investigación en Ciencias Básicas -SciBas-, de la Universidad Distrital Francisco José de Caldas.
Referencias
Aguilar, O. A., & Huegel, J. C. (2011). Inverse Kinematics Solution for Robotic Manipulators Using a CUDA-Based Parallel Genetic Algorithm. In I. Batyrshin & G. Sidorov (Eds.), Advances in Artificial Intelligence (Vol. 7094, pp. 490-503): Springer Berlin Heidelberg.
Albert, F. Y. C.; Koh, S. P.; Chen, C. P.; Tiong, S. K., & Edwin, S. Y. S. (2011). S.Y.S. Paper presented at the International Conference on Computer Engineering and Applications, Singapore.
Araujo, L., y Cervigon, C. (2009). Algoritmos evolutivos: Un enfoque práctico (Vol. 1). Madrid: Ed. RaMa.
Barrientos, A.; Peñín, L. F.; Balaguer, C., & Santoja, R. A. (2007). Fundamentos de robótica (Vol. 2). Aravaca, Madrid: McGraw-Hill.
Bravo, S. Á. (2012). Evaluación de técnicas evolutivas en el cálculo de la cinemática inversa de robots manipuladores. Ingeniería Técnica en Electrónica, Universidad Carlos III de Madrid.
Carvalho, L., & Gaspar, E. (1991). The solution of the inverse kinematic problem of robot arm with neural networks. Paper presented at the IX Brazilian Congress on Mechanical Engineering, Brasil.
Denavit, J., & Hartenberg, R. S. (1955). A kinematic notation for lower-pair mechanisms based on matrices. Journal of Applied Mechanics, 22, 215-221.
Duffy, J., & Crane, C. (1980). A displacement analysis of the general spatial 7-link, 7R mechanism. Mechanism and Machine Theory, 15(3), 153-169.
Gibbs, J. (1996). Easy inverse kinematics using genetic programming. Paper presented at the GP-96 Conference.
Giraldo, L.; Delgado, E., y Castellanos, G. (2006). Cinemática Inversa de un Brazo Robot Utilizando Algoritmos Genéticos. Revista Avances en Sistemas e Informática, 3(1), 29-34.
Gonzálvez, B. A., e Iglesias, J. I. C. (2002). Identificación de parámetros cinemáticos de un robot industrial mediante un sistema de rastreo láser. PhD, Universidad Politécnica de Valencia.
Guez, A., & Ahmad, Z. (1988). Solution to the inverse kinematics problem in robotics by neural networks. Paper presented at the International Conference on Neural Networks, San Diego, Ca.
Jamshidi, M., S., C. d.; Krohling, A. R., & Fleming, J. P. (2005). Robust Control systems with genetic algorithms. International Journal of Robust and Nonlinear Control, 15(7), 210.
Kalra, P., & Prakash, N. R. (2003). A Neuro-genetic Algorithm Approach for solving the inverse kinematics of Robotic Manipulators. Systems, Man and Cybernetics, 2003. IEEE International Conference, 2, 1979-1984.
Khalil, W., & Dombre, E. (2004). Chapter 6-Inverse kinematic model of serial robots. In W. Khalil & E. Dombre (Eds.), Modeling, Identification and Control of Robots (pp. 117-144). Oxford: Butterworth-Heinemann.
Khwaja, A. A.; Rahman, M. O., & Wagner, M. G. (1998). Inverse Kinematics of Arbitrary Robotic Manipulators Using Genetic Algorithms. In J. Lenarčič & M. Husty (Eds.), Advances in Robot Kinematics: Analysis and Control (pp. 375-382): Springer Netherlands.
Köker, R. (2013). A genetic algorithm approach to a neural-network-based inverse kinematics solution of robotic manipulators based on error minimization. Information Sciences, 222, 528-543.
Lee, C., & Ziegler, M. (1984). Geometric approach in solving inverse kinematics of puma robots. IEEE Transactions on Aerospace and Electronic Systems, 20(5), 1-27.
Murray, R. M.; Li, Z., & Sastry, S. S. (1994). A Mathematical Introduction to Robotic Manipulation (Vol. 2): CRC Press.
Oyama, E.; Chong, N.; Agah, A.; Maeda, T., & Tachi, S. (2001). Inverse kinematics learning by modular architectore neural networks with performance perdiction networks. Paper presented at the International Conference on Robotics and Automation.
Parker, J.; Khoogar, A., & Goldberg, D. (1989). Inverse kinematics of redundant robots using genetic algorithms. Paper presented at the International Conference on Robotics and Automation.
Pieper, L. D. (1968). The kinematics of manipulators under computer control. PhD, Stanford University (457).
Primrose, E. J. F. (1986). On the input-output equation of the general 7R-mechanism. Mechanism and Machine Theory, 21(6), 509-510.
Siciliano, B.; Sciavicco, L.; Villani, L., & Oriolo, G. (2009). Robotics: Modelling, Planning and Control (Vol. 1). London: Springer-Verlag.
Tabandeh, S.; Clark, C., & Melek, W. (2006). A Genetic Algorithm Approach to solve for Multiple Solutions of Inverse Kinematics using Adaptive Niching and Clustering. Paper presented at the IEEE Congress on Evolutionary Computation, Sheraton Vancouver Wall Centre Hotel, Vancouver, BC, Canada.
Tsai, L. W. (1999). Robot Analysis: The Mechanics of Serial and Parallel Manipulators (Vol. 1). New York: John Wiley & Sons, Inc.
Zomaya, A. (1994). Transputer Ensembles for Embedded Robotics Computations. Transputer Communications, 2, 151-170.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.