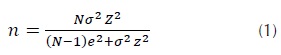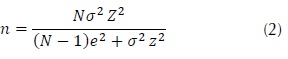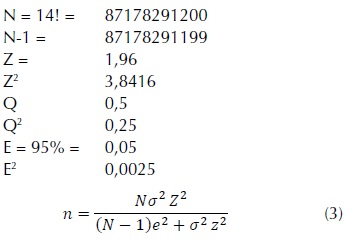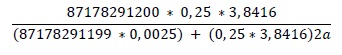Optimización de un ruteo vehicular usando algoritmo genético simple chu-beasley

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a07

Optimization of a vehicular routing using simple genetic chu-beasley algorithm

Optimización de un ruteo vehicular usando algoritmo genético simple chu-beasley

Guillermo Roberto Solarte Martínez^*
Andrés Gaspar Castillo Sanz^**
Guillermo Rodríguez Gahona^***

^* Ingeniero de Sistemas. Magíster en Investigación de Operativa y Estadística; candidato a doctor en Informática. Docente Investigador, Universidad Tecnológica de Pereira, Pereira, Colombia. Contacto: roberto@utp.edu.co
^** Ingeniero Informático. Doctor en Ingeniería del Software. Docente Investigador, Universidad Pontificia de Salamanca, Madrid, España. Contacto: andres.castillo@upsam.es
^*** Estudiante de Sistemas y Computación, Universidad Tecnológica de Pereira, Pereira, Colombia. Contacto: guiro4321@gmail.com

Fecha de recepción: 21 de enero de 2014 Fecha de aceptación: 19 de enero de 2015

Citation / Para citar este artículo: Solarte Martínez, G. R., Castillo Sanz, A. G., & Rodríguez Gahona, G. (2015). Optimization of a vehicular routing using simple genetic chu-beasley algorithm. Revista Tecnura, 19(44), 93-108. doi: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a07

Abstract

The research presented in the article is geared towards the area of genetic algorithms in the optimization of resources and processes, and then a case study is set based on vehicular routing and optimization of the same, applying the genetic algorithm of Chu-Beasley. This study, which started on November 2013 and finished on March 2014, was applied in Bogotá city, as it is the capital of Colombia. This metropolis counts with many industrial areas, gathering centers, warehouses and other commercial activities. Likewise, the growing of the capital in the last years has been significant, which has generated an exponential territorial extension, causing mobility problems and transport. For that reason, it is imperative for some warehouses that have to distribute their products, to optimize the routes and guarantee effectiveness and efficiency in delivery.

Keywords: chromosomes, genetic algorithms, mutation, probability, process, recombination theory, routing, species, vehicular.

Resumen

La investigación presentada en el artículo está orientada hacia el área de los algoritmos genéticos en la optimización de recursos y procesos; a continuación se establece un estudio de caso fundamentado en el ruteo vehicular y la optimización del mismo, aplicando el algoritmo genético de Chu-Beasley. Este estudio, que inició en noviembre de 2013 y terminó en marzo de 2014, se aplicó en la ciudad de Bogotá, D.C., por ser la capital de Colombia. Esta metrópoli cuenta con innumerables zonas industriales, centros de acopio, almacenes y demás actividades comerciales. De la misma manera, el crecimiento de la capital en los últimos años ha sido significativo, lo que ha generado una extensión territorial exponencial, causando problemas de movilidad y transporte. Por ello es imperioso para algunas empresas que deben distribuir sus productos optimizar los recorridos y garantizar efectividad y eficiencia en las entregas.

Palabras clave: algoritmos genéticos, cromosomas, enrutamiento, especies, mutaciones, probabilidad, proceso, recombinación, teoría, vehicular.

Introduction

The natural selection of the species is considered one of the most important theories in recent times since it determines the evolutionary character of the living beings, specially of the human beings; starting from this, some sciences and disciplines have been benefited their discursive structure to implement various explanatory strategies of the own problems of those disciplines. In this sense, appears the well-known genetic algorithms, and its creator Jhon Holland (1962), comprehends the importance of the evolutionary theory specially the related with the adaptive systems, starts the process for the creation of such algorithms that search fundamentally to design artificial systems that give account of the mechanisms and working of the natural systems. After the creation of the genetic algorithms by Holland, one of his students David Goldberg (1972) decided to introduce the algorithms designed by his teacher to the plane of the industrial problems, although he did not account with the support of his mentor, Golderg could have success in his enterprise establishing the algorithms in the optimization of the industrial process. In this way, the evolutionary theory and selection of the species become in a method that as engineering as other disciplines adapt to transform and improve the industrials and entrepreneurial process.

This work intends to apply the genetic algorithms (Rondon Villareal, 2010)in the optimization of the particular case of vehicular routing, potentiating its effects and improving the industrial conditions. It is very important to point out that for the application of this specific situation, the Chu-Beasley genetic algorithm will be used, since this allowed a particular management of the object population of study. The following research pretends to realize a conceptual routing by the genetic algorithms, their classifications and advantages of the applications, showing from a concrete case the importance of its use in determinate situations.

Genetic algorithms

Genetic algorithms can be defined as

The AG are adaptive methods that can be used to resolve seeking and optimization problems. These methods are based in the genetic process of the live organisms. Along the generations, the populations evolve in the nature according to the principles of the natural selections and the survival of the strongest, postulated by Darwin (1859). (Cerón, 2012).

It means, the genetic algorithms intend to make use of the genetic development of the living beings to implement mathematically systems which allow the optimization of diverse process. (Pessoa Artut, 2011). This work is inspired particularly in the selection of the species theory, by Darwin and the genetic, this offers an adaptive optimization mechanism on the basis of probability, the survival and the adaptation. The principles of the biology that guide fundamentally the genetic algorithms (Gestal, RiveRo, Rabuñal, & DoRaDo, 2010, p. 30) can be considered the following:

1. The evolution process that operates over the chromosomes.

2. The natural selection is the union between the chromosomes and the actuation of the decoded structures.

3. The reproduction process occurs when the evolution take place, maybe through mutations, where the chromosomes of the children change slightly of the parents or by recombination process. (M. Cerrolaza). These principles began to be decoded on computerized simulations, which allow starting the adaptability process for the algorithms. One of the first investigations that gave the denomination of genetic algorithms is the one made by Bagley, who developed a test to control the game of six peons watching their tasks; this test allow to find the necessary conditions to use in an assessment function of the game, this way discovering that the algorithm can be used in different ambits. On the other hand, the contribution of Rosemberg is the application of the algorithms in engineering, which process provides substantially the optimization of functions on industrials works. To solve problems using genetic algorithms is indispensable make use of the chromosomal representation of the population.

• The way to create the initial population.
• An assessment function.
• The genetic operators.

The assessment of the parameters that the algorithm uses (M. Cerrolaza).

The first item refers to the importance to code the design of variables of strings in finite length, as resemble in the genetic the chromosome strings, but in the algorithms must be realized from any kind of alphabet, which in this case the binary code is used. The second aspect is about the election of the population, this selection should be random. The third ambit in the genetic algorithms is the linking of the algorithm with the problem to be solved, it means, the exposition of one of the chromosomes to the function of merit, which indicates the reaction that is the reason of the success or the failure of the algorithm, and its applicability. The fourth aspect is the genetic operators that can be considered especially with the crossings, mutations and generations, which produce a variation in the result. And the last factor in the algorithms is the assessment, which involves different elements that compose the algorithm and the process to be solved (size of the population, reproduction probability, etc.) Genetic algorithms are an adaption of the laws of the biology in the optimization and solution of several problems using the changes and the variations of the environment, where the situation is executed. The basic genetic algorithm needs fundamentally the following requirements to work:

Generation of the initial population

This is the starter element to elaborate a genetic algorithm, therefore it is very important to obtain the results. The selection of the population is random commonly, that is to say, choosing some characters of the string, it is important that the population is enough big or long to and so is diverse and nurtured; but it cannot be too long because can produce problems in the code. It is very important to understand that the size of the population affect the successful of the algorithm, due to the fact that a small population or a big one do not guarantee diverse solutions, for many theoretical the perfect size would be between 1 to 21. The population use to be chosen generating randomly bunches, but also can be chosen through a specific function or generate a portion of an individual an after that, create the search. The operator for selection is used for the selection to choose the best adapted individuals keeping the characteristics of the valuable solutions and hence the possibilities of reproduction are bigger, but in some situations the operator select those individuals that are not enough adapted because these ones can contain useful information necessary for the solution. In the selection operator, exist two selection ways: By ranking “Developed by Whitley (1989) which consist in calculate the reproduction probabilities attending the ordination of the population by the adaptive value. And the selection by Tournament reports a computational value very low due to its simplicity. A group of t individuals are selected (commonly t = 2, binary tournament) and a random number between 0 and 1 is generated. If this number is less than certain threshold k (usually 0.75), the individual with the best adaptation is selected to reproduce and if the number is less than K, the individual with the worst adaptation is selected.

Representation of the individuals

The main types of representation can be classified as follows:

• Binary: where each gen of the chromosome is a bit (0 or 1).
• Example: 010011000. Integer: Where each gen of the chromosome is an integer.
• Example: 106-107-108. Real: Where each gen is a real number.
• Example: 1.28-3.26-5.23

Permutation: Where each gen is an integer number but cannot be repeated in the chromosome. Codification scheme: The genetic algorithms are codified as the genetic strings; with the purpose of generate genotypes and phenotypes (rizar Mesa, 2014)

The genotype of an organism is the total sum of all the genes it inherited, it is a pattern or a kind of model designed to serve as a guide for the development of the organism, so that it becomes the same kind of being the parent or parents of the proceeding. At the cellular level, the genotype is the model that guides the development and activities of the cell and is transmitted to daughter cells when the cell divides more. The phenotype of an organism includes factors such as physical appearance, biochemical processes occurring in the body and behavior, and living in a world and interact with others. In summary, the phenotype of an organism is how it looks to observers.It means, give possible solutions to several problems, optimizing such solutions, transmitting it from generation to generation looking for the most suitable, that is the reason why the genetic algorithm needs to use a simple alphabet –that generally is the binary code– and

The variables that represent the parameters of the problem must be discretized to represent it with string bits. It must be used enough resolution able to ensure that the output has a suitable level of precision. It is assumed that the discretization is representative of the objective function. (Zimmermann, 2013).

The crossing: it is a mechanism of analysis and interpretation of data, which is used to obtain a screening of the information of the populations and makes multiples mixtures until create better individuals, each time more adapted to the conditions. There are many methods for those combinations:

The crossing point, where a point is selected in the string of the parents, the genes are crossed to the left. In the n point crossing, many positions in the string of the parents are chosen and the genes in each side of the position are crossed. In the uniform crossing, it is decided which of the parents assume each position of the string. It is important taking into account in the crossings, that the good features must be inherited or such crossings must not leave that the children have worst features that their parents.

Mutation

Mutation intends to produce fundamentally innovating solutions since the alteration of some genes in an existent solution to promote the variability in the population, creating an element of randomness in the environment of the population. To realize mutations, it can be since the most elemental way in which each gen mutates randomly with totally freedom and independence, until complex configurations where the mutation is realized taking into account some characteristics of the genes.

Schaffer & col. find that the effect of the crossing in the search is lower than the expected. They use the well-known primitive evolution, where the evolutional process consists only of the selection and mutation. They also find that such primitive evolution exceeds to an evolution based on exclusively in the selection and crossing. (Goldberg, 2011).

The mutation is constituted in one of the fundamental elements in order to prevail the population and even that the conditions of adaptability are higher and better, some people consider the mutations fundamental for the heuristic exercise of the genetic algorithms.

Substitution of the population: With the crossings and the mutations, appear new populations that are denominated the lineage or descendants that will create the new populations, such creation of new populations have three different ways:

• “When the numbers of individuals reach certain number, a subset of the population is removed containing the less adapted individuals.
• Each time a new individual is created in the population, the less adapted is erased and the new one takes its place.
• Each time a new individual is created in the population, a solution is deleted randomly independently of its adaptation”.
• Referent to the stop criterion, this respond to a maximum number of descendants or to the resolution time, or with the situation and condition of the population.

The conditions mentioned before constitute the simple genetic algorithms, but exist certain modifications to the same that will be described as follows:

Chu-beasley algorithm

The use of genetic algorithms in the solutions of determinate problems is a case of the metaheuristic (canarias, 2013), General strategies to build algorithms that are above heuristics, and extend somewhat beyond, called metaheuristics, i.e., to solve a kind of general computational problem, using the parameters given by the user on generic and abstract procedures waiting a manner efficient. Typically, these procedures are heuristic. Due to the fact that it works under the computational system, that is why we talked about the simple genetic algorithms described previously; however, it appears new modification in these algorithms, which are not going to be described in this research. This work is focused in a specific algorithm due to the features of the problem and its optimization, the algorithm is known as the Chu-Beasley algorithm. This algorithm consists fundamentally, in a modification of the simple genetic algorithm with some additional considerations that allow a higher optimizing of the possible solutions.

The algorithm must satisfice some characteristics:

• The initial population must be totally heterogeneous.
• The selection process is by tournament.
• The recombination generates two children; one of them will be selected through any criteria.
• The Chu-Beasley algorithm must have two alternative parents for the selection by random lottery, these two alternatives are crossed, obtaining a child alternative, if is possible, the mutation is applied, if not, it must be repaired with a reparation method to acquire an observable alternative that achieve the necessary number of zeros in the population.
• In each insistence, only one individual is entered to the population, taking into account the next parameter: The current alternative or resultant will be replaced by a worse alternative of the existent population. Moreover, if the resultant alternative is not better than the worse alternative of the existent population, this one will not be taking into account and will be discarded.

Optimizing of the vehicular routing using the chu-beasly genetic algorithm

The case of Super Almacenes Olímpica (SAO), Bogotá, D.C.

Taking into account the importance of the genetic algorithms in the optimizing of the resources and process, following, it is established a case based on the vehicular routing (Pessoa Artut, 2011)and the optimizing of it, applying the Chu-Beasley genetic algorithm.

Geographical framework

The case of study will be applied in the Bogotá city because is the capital of Colombia, this metropolis counts with many industrial areas, gathering centers, warehouses and other commercial activities; in the same way, the growing of the capital in the last years has been significant, which has generated an exponential territorial extension, causing mobility problems and transport (Claudia Archetti , Martin W. P. Savelsbergh , M. Grazia Speranza, 2006), for that reason it is imperative for some warehouses that have to distribute their products, to optimize the routes and guarantee effectiveness and efficiency in delivery.

Bogotá D.C is divided in twenty locations (See figure 1), such division allows to establish travels and measure the distances, and also set up routes due to the distances and the security and mobility problems.

Taking into account the amplitude of the Colombian capital, for the case that is going to be developed in the present work, the vehicular routing is going to be executed in three of the twenty locations, supporting them in the distribution of the products of one of the most important chain warehouses of the city. In this sense, the optimizing of the vehicular routing (Gruttner & Pinninghoff, 2009) will be realized in the distribution of products of Olímpica warehouses that have the mission of: The Olympic Stores born in the Colombian Atlantic Coast in the hands of the Char family, which starts especially drugstores that quickly become chain are one of the first stores to build the format superstore, i.e., in one place offer all kinds of items needed for homes, drugstore, fruits, vegetables, food, restaurant, appliances, etc. Today it is one of the few stores that do not have foreign capital in Bogotá, is from the eighties offering service. The Super Almacenes Olímpica (SAO) are very appreciated in the capital, for the monthly promotions that realize a their low prices that are specially offered to the people who are joined to Compensar; likewise, the mall of food, which is very concurrent, therefore, every day, the restaurants should receive supplies coming from other regions, and they are distributed by trucks in routes by localities (See figure 2).

As it was mentioned before, for the concrete case of the application of the Chu-Beasley algorithm in the vehicular routing of the SAO warehouses, fourteen (14) warehouses (See figure 3) are going to be used, which are located in Chapinero, Barrios Unidos and Teusaquillo as follows:

Research methodologies

Description of the problem

The Super Almacenes Olímpica (SAO) must do many daily routs to carry the products to the warehouse, the drugwarehouse, the restaurants by all the city, such products are delivered by trucks that supply the warehouses of the different locations. Only one truck distributes the products to the localities of Chapinero, Teusaquillo and Barrios Unidos, this starts from a X central, these centric locations have the majority of the offices, malls, and also have two difficulties, by one side is the mobility and in the other hand the concentration of the population; for that reason it is necessary to optimize the vehicular routing, improving the times and realizing faster deliveries. The SAO enterprise count with vehicles for the distribution of their own brand (Brand Olympic), in the entirely city of Bogotá, D.C., due to the huge size of the warehouses, the distribution in the urban area and taking into account the problematic of the transport in Bogotá, it is indispensable to divide the delivery of the products, nevertheless, due to these measures taken, the delivery process remains slow in the delivery of their products to the warehouses, and there is not any standard to follow, and that is why their deliveries still are unsuccessful.

To achieve the optimizing of the vehicular routing, the Chu-Beasley genetic algorithm will be used to find the best route and in this way improves the times in the deliveries.

For the problem of the vehicular routing, the traveling salesman problem will be taking into account, thus:

The vehicular routing problem (VRP) has several applications in many industries. Some of these applications can be seen in the enterprises that distribute perishable foods and drinks, in the public services, logistic operators, garbage collection, postal service, etc. In concrete, the VRP came up as a generalization of the traveling salesman problem. In this problem, a traveler has to visit a group of cities, crossing for each one exactly one time, in order that the salesman returns to the city where he started in a shorter distance. When exist more than one traveler, we are taking about the m-traveling salesmen problem. (Quintero, 2012).

Apparently, the distribution should be by locations, but it is not very efficiently doing it in that way, this is because the distribution of the warehouses is not uniformly distributed in each location, for example, in the location of Chapinero exists 10 supermarkets, meanwhile in the location of Teusaquillo there are only 2. As a probe case, a sector guided by the map is going to be taken and the location of the different warehouses. The sector is taken by parts from the locations of Chapinero, Barrios Unidos and Teusaquillo with 14 headquarters in total.

Procedures and algorithms

To reach the optimizing of the vehicular routing of the Super Almacenes Olímpica in the locations of Chapinero, Teusaquillo and Barrios Unidos, the process will begin making the measures of the distance between each one of the 14 warehouses, where the optimizing of the vehicular routing will be implemented. To measure the approximately distances between the different headquarters, it was used the “Distance Measurement Tool” from Google, which allow to measure an approximately distance between two points (See figure 4). For this specific case, it has to be taking into account the routes of the Bogotá city, it is established that the distance [A-B] is different to the distance [B-A], for this reason, the number of possible combinations for this case is given by n, where n is the number of headquarters.

Codification

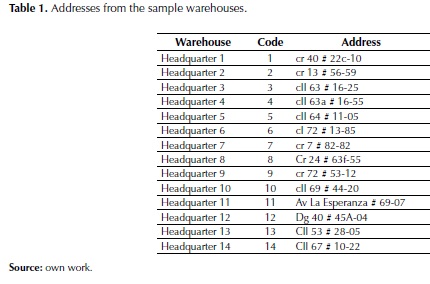
Generally, it is used the binary code to realize the codification of the population, however, for the Travelling Salesman Problem (TSP), this kind of representation it is not very suitable. An entirely codification is use for each one of the headquarters that goes from the 1^st until the 14^th , that is way the chromosome would have 14 genes (14 headquarters), each number represents the name of the warehouse or headquarter, according to table 1.

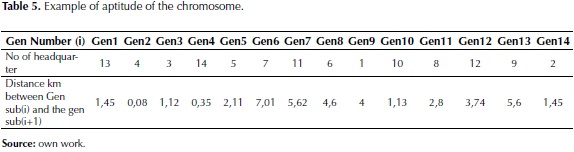
Table 2 presents an example of one of the chromosomes or possible solution for the proposed case. Each gen# indicates the order of the headquarter within the route (chromosome), and the associated number indicates the number of the headquarter from the chromosome.

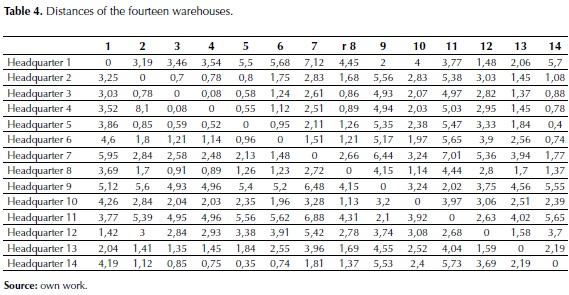
You must take into account that when you analyze the aptitude assessment of the chromosome as a feasible solution, you should add the routes that are between each of the headquarters according to the order described in the chromosome. This can be done using the data from table 3.

Distances table

Table 4 presents the distance between each of the headquarters, the data is represented in kilometers. You must take into account as stated before, for this case the distance of [A,B] is different to the distance [B,A], this is due to the different conditions of transport in the city, where most of the times differ in big size these two distances. The data provided in table 4 was extracted using GoogleMaps (“Distance Measurement Tool”) to approximate the distances among the geographical locations of each warehouse.

Selection method

As a selection method we use the selection tournament method, for this case were selected randomly couples of individuals to compete against each other and the most suitable according to the aptitude assessment will be able to be part of the next generation with their genes intact.

Size of the sample

It is used the probabilistic sampling method "simple random sampling", as a method for sample selection. Equations (1), (2) and (3) are used to compute the size of the sample. All of them rely on the finite property of the population.

The possible combinations are given by the factorial of n (i.e., n!) Therefore it is not feasible to compute the total population (N), so we have that N = n! , where n corresponds to the number of headquarters of the case to analyze.

Where

Replacing

N = size of the sample

N = 85, 1204

Now, the work will be realized with a sample of 386 individuals from a population of 87178291200. (Condori, 2014).

Chromosome

According to the size for the calculation of the sample, 386 chromosomes are selected randomly, and we will call it as the initial population (P0). P0 is referred in the file PoblacionesGeneradas.xlsx on the sheet Poblacion Inicial.

The calculation of the aptitude for each individual is realized. This is achieved using the data distance indicated in table 4. For this, we take the number of the gen1 (that represents a headquarter) and the distance from gen2, the distance of the gen2 with the gen3 and thus successively until gen14, where is set the distance with the gen1, and at the end, the entirely of the distances between the genes are summed up, this result indicates the total distance traveled by a vehicle X for all the headquarters, returning to the headquarter where it started. An example of this is presented in table 5.

As a method of selection, we will use the tournament deterministic method, where after having the initial population (P0), we will select random couples that will compete against each other to determine who will pass to conform the next population (P1), the criterion to define the winner of the tournament is by the adding between each of the genes, and it is selected that one, which distance is the shorter, that is to say, calculating the aptitude of each one of the genes, the most suitable will be the one of lower DTR (Granada, 2014).

Step followed, the genetic operator of crossing will be used. Given the big multitude of algorithms of crossing and after the assessment of the most relevant, it is decided to initially use the algorithm of crossing of 1 point. In this step and taking into account the essence of the algorithm used for the crossing of a point, came up the need of adding a new method of reparation, which guarantee that after the crossing, the resultant chromosome cover all the headquarters without exception, which would guarantee the uniqueness of their genes.

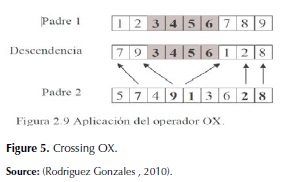
Crossings in order (OX)

This crossing consists of randomly selecting a substring of a parent A. That substring will be given to the equal son, that is, same genes, same order. The genes of the substring of the parent A are removed from the parent B, the remaining genes of the parent B will be those that are missing in the son. See figure 5 for an explanation.

Mutation operator

The mutation operator will be applied at a rate of 1.04% of the population, which is equivalent according to the population P to 4 individuals, this value will be constant in each generation (yciencia, 2014).

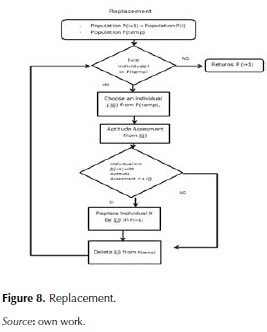
Replace of the population

Now, it will be obtained a population P(temp), with a number of individuals equal to the P(0) (current population), for this, is applied a replacing, taking into account the population obtained during the application of the different operators that we will call P(temp) and the current population P(0) which we will call P(i). The replacement will be used to obtain the new population P(i+1), taking into account the following restriction:

Each individual from P(temp) will be part of the new population P(i+1) if and only if, its aptitude assessment is better than the aptitude assessment of an individual from P(i), otherwise it will not be taken into account. After analyzing the totality of the individuals from P(temp), we will obtain the new population P(i+1), this population will return to the beginning of the iteration and thus until the stop criterion.

Stop criterion

As stop condition, it is established a condition of number of iterations, which is composed as follows:

• In each iteration is saved the individual whose aptitude assessment will salient (in the case when more than one individual exist with the best assessment, only one will be selected randomly). This individual will be maintained until another one with better aptitude assessment replaces it.
• After 1000 iterations the process will end, and displays the chromosome with better aptitude.

Flowchart

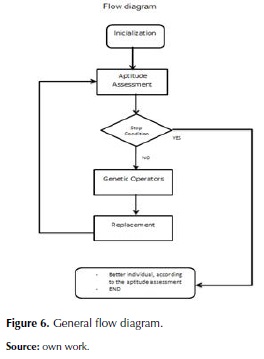
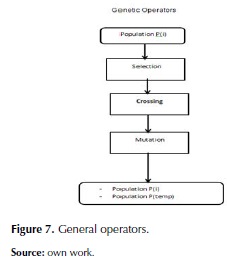
The following are the steps taken by the G.A. A flowchart representation is provided in figures 6, 7 and 8.

1. Start with an initial population, which is randomly generated.
2. Aptitude assessment of each individual.
3. Apply the operators (Selection, crossing and mutation).
4. Generate the new population.
5. Go to step 2 until the stop condition be satisfied.
6. When the stop condition is accomplished, return to the best individual found.

Results

Developed software

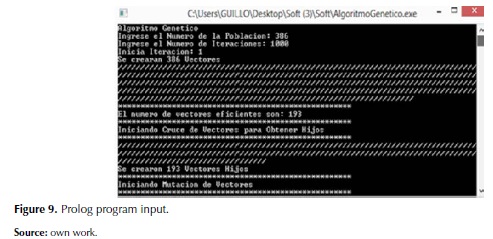
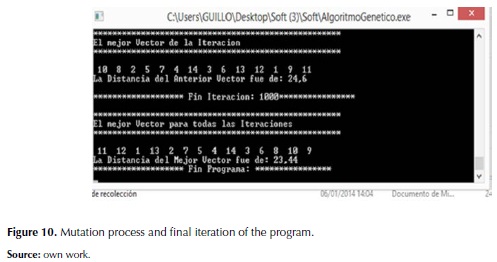
To automate the process, a console application in .NET with framework 3.5 was developed. Although there are specialized software for this kind of problems such as Prolog and Lisp that were the first choice consulted, but the first one was selected because of the names of the authors of the work to the syntax of the same. Figures 9 and 10 show screenshots of the software. Following data were entered into the program genetic Algorithm.

Enter the number of population: 386. Enter the number of iterations: 1000 Please iteration: 1. 386 vectors were created.

Conclusions

For a vehicle routing problem, the traveling salesman case, we have that for a number of 14 headquarters, the possible combinations of the problem is given by n!, Where n is the number of headquarters. So we have that the time cost to evaluate the problem fully, it would take according to an analysis approximately about 45,336 years. This is taking into account the language used. For a sample of the population of 386 we have that the chromosome with better aptitude assessment after 1000 iterations is. As shown in table 6.

Given the initial population, where big part of the population has an attitude assessment superior to 40 km, and only 3 chromosomes less than 0.08%, hardly are below 30 km can be considered acceptable this mechanism, even we cannot guarantee that it is the best option, but undoubtedly, considering the cost, it is very acceptable.

Acknowldge

The project was authorized by Supermercados Olímpica and Universidad Tecnológica de Pereira. Supermercados Olímpica was in charge of providing the information about the routes and location of the stores and the Universidad Tecnológica de Pereira supported the project with the tools and knowledge.

References

Bogotá, A. M. (24 de enero de 2014). Alcaldía Mayor de Bogotá Portal oficial. Recuperado el 3 de abril de 2014, de Alcaldía Mayor de Bogotá Portal oficial.

Canarias, U. d. (2013). Recuperado en 2014, de Universidad de Las Palmas de Gran Canaria. http://www.ulpgc.es/.

Cerón, S. M. (2012). Algoritmos Geneticos. Recuperado en 2013, de noticias umg chiquimula.com /: http://www.noticiasumgchiquimula.com/index.php/.

Claudia Archetti, Martin W. P. Savelsbergh, M. Grazia Speranza (2006). An optimization based heuristic for the split delivery vehicle routing problem. Georgia Institute of Technology, School of Industrial and Systems Engineering, Atlanta, U.S.A., 56- 65.

Condori, D. J. (2014). Análisis de Datos Clínicos y Epidemiológicos. bioestadistico.com.

Gestal, M.; RiveRo, D.; Rabuñal, J. R., & DoRaDo, J. (2010). Introducción a los Algoritmos Genéticos y la Programación Genética. A Coruña, 2010, 30 -68.

Goldberg, D. M. (2011). http://eddyalfaro.galeon.com/. Obtenido de http://eddyalfaro.galeon.com/: http://eddyalfaro.galeon.com/geneticos.html.

Google (8 de febrero de 2005). Google Maps. Recuperado el 3 de abril de 2014, de: https://www.google.com/maps/dir/Supermercado+Olimpica,+BogotA

Granada, C. d. (2014). Algoritmos geneticos. Ciencias de la Computación e Inteligencia Artificial de la Universidad de Granada. http://decsai.ugr.es/index.php.

Gruttner, E., & Pinninghoff, M. A. (2009). Algoritmos Genéticos en Recorridos Óptimos de Líneas de Transporte Público. Universidad de Concepción, Chile, 34 -32.

M. Cerrolaza, W. A. (s.f.). Algoritmos de optimización estructural basados en simulación genetica . En W. A. M. Cerrolaza, Algoritmos de optimización estructural basados en simulación genetica. Venezuela: Carraza.

Pessoa Artut, U. E. (2011). A Robust Branch-Cut-and-Price Algorithm for the Heterogeneous Fleet Vehicle Routing Problem. Universidad Federal Fluminen, 56.

Pinninghoff J., M. A., Matthews D., E., & Díaz C., H. (2005).

Quintero, T. (2012). Problema del ruteo Vehicular. 34- 56.

Ravindra K. Ahuja, Ö. E. (2009). Estudio de técnicas de búsqueda por vecindad a muy gran escala. Departamento de ingeniería industrial y de sistemas, 23-32.

Rizar Mesa, M. I. (2014). La Revista Cubana de Computación. GIGA. Obtenido de: Algoritmos Genéticos: Evolución, Genética y Computación: http://www.ecured.cu/index.php/Algoritmo_gen%C3%A9tico

Rodríguez Gonzáles, V. B. (4 de marzo de 2010). Manipulacion genética aplicada a problemas de viajero. Recuperado el 3 de abril de 2014, de: Instituto Politécnico Nacioan Mexico: http://tesis.ipn.mx:8080/xmlui/bitstream/handle/123456789/.

Rondon Villareal, Nydia Paola; Delgado Quintero, Darío José; Mendoza Castellanos, Alfonso; Quintero, Andrés Felipe; Serna Suárez, Iván David. (2010). Algoritmos Genéticos en la solución de problemas de ruteo de vehículos con capacidad CVRP.

Sánchez Medina, J. J. (2007). Optimización del tráfico rodado mediante el ajuste de ciclos de semáforos por algoritmos genéticos en dispositivos de computación paralela usando modelación discreta. Universidad de Las Palmas de Gran Canaria, España, 67-74.

Tiendeo.com Gran Vía 395, 0. B. (2013). Súper Almacenes Olímpica. Recuperado el 3 de abril de 2014, de Súper Almacenes Olímpica: http://www.tiendeo.com.co.

Zimmermann, D. (2013). ehowenespanol.com. Obtenido de: ehowenespanol.com: http://www.ehowenespanol.com/definicion-genotipo-fenotipo-info_184970/