Modelos matemáticos para la definición del layout de las celdas de manufactura. Revisión de literatura

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.4.a03

Revisión

Modelos matemáticos para la definición del layout de las celdas de manufactura. Revisión de literatura

Mathematical models for the definition of cell manufacturing layout. Literature review

Gustavo Andrés Romero Duque¹
Camilo Mejía Moncayo²
Johanna Alexandra Torres Martínez³

¹ Ingeniero de producción, magister en innovación, candidato a magister en ingeniería industrial. Docente tiempo completo de la Fundación Universitaria Los Libertadores. Bogotá, Colombia. Contacto: garomerod@libertadores.edu.co
² Ingeniero Mecánico, magister en Ingeniería Mecánica. Profesor Asociado Facultad de Ingeniería, Universidad EAN, Bogotá, Colombia. Contacto: cmejiam@ean.edu.co
³ Ingeniera de producción, especialista en logística y producción, estudiante de maestría en Finanzas. Docente cátedra de la Fundación Universitaria Los Libertadores. Bogotá, Colombia. Contacto: jatorresm2@libertadores.edu.co

Como citar: Romero Duque, G. A., Mejía Moncayo, C., & Torres Martínez, J. A. (2015). Modelos matemáticos para la definición del layout de las celdas de manufactura. Revisión de literatura. Revista Tecnura, 19(46), 135-147. doi:10.14483/udistrital.jour.tecnura.2015.4.a11

Fecha de recepción: 28 de febrero de 2014 Fecha de aceptación: 24 de agosto de 2015

Resumen

El presente artículo de revisión aborda el planteamiento del problema del layout de las celdas de manufactura (LCM) de una forma descriptiva, considerando primero el problema y sus variaciones, luego los elementos de los modelos matemáticos, y posteriormente los métodos de solución empleados; y por último se concluye con algunas perspectivas futuras alrededor de este tema.

Palabras clave: Celdas de manufactura, Formación de celdas, Layout, Métodos de solución.

Abstract

This review article discusses the approach to the layout problem of cell manufacturing (LCM) in a descriptive form; considering at first the problem and its variations, then the elements of the mathematical models, subsequently presenting solution methods used; and finally some future perspectives about this topic are considered.

Keywords: Cell formation, Layout, Manufacturing cells, Solution methods.

Introducción

Las celdas de manufactura y la tecnología de grupos son una expresión tecnológica de la manufactura esbelta que se ha difundido por todo el mundo por las mejoras en productividad que genera para una organización, en especial para aquellas con volúmenes bajos de producción y productos variados, como sucede en la economía colombiana.

El proceso general de implementación de celdas de manufactura (Singh, 1996) consiste en solucionar dos problemas: la formación de las celdas de manufactura y la determinación del layout al interior de ellas y entre ellas.

La formación de las celdas de manufactura consiste en agrupar las partes a fabricar en familias y las máquinas que las procesan, en celdas de manufactura, en virtud de las similitudes existentes en sus procesos de fabricación. La métrica para determinar la optimalidad de las soluciones es la minimización de los movimientos de las partes a fabricar al interior de las celdas y entre estas. Existen diferentes métodos para solucionar este problema (Kusiak, 1990; Singh, 1996; Hassam, 1998;Yin, 2006).

La determinación del layout al interior de las celdas y entre ellas consiste en la asignación de cada una de las máquinas a una determinada ubicación al interior de la celda y la definición de la posición relativa entre las celdas (Drira, 2007). Generalmente, este proceso se ha realizado secuencialmente, lo cual genera soluciones óptimas particulares para cada problema por separado, pero no una solución integral para el sistema de manufactura, ya que la sola formación de las celdas no soluciona problemas críticos para el sistema, como los transportes excesivos, los almacenamientos y las esperas que derivan de la configuración del layout de la planta y las celdas de manufactura; por lo tanto, es indispensable solucionar los dos problemas simultáneamente con un enfoque metodológico basado en optimización.

Adicionalmente, los cambios en los productos y las demandas del mercado hacen que los volúmenes de producción y las características de los productos cambien, lo cual genera un escenario dinámico que modifica las operaciones y los tiempos de operación de estas, y disminuye el desempeño del layout y del sistema de manufactura.

Análisis de la información

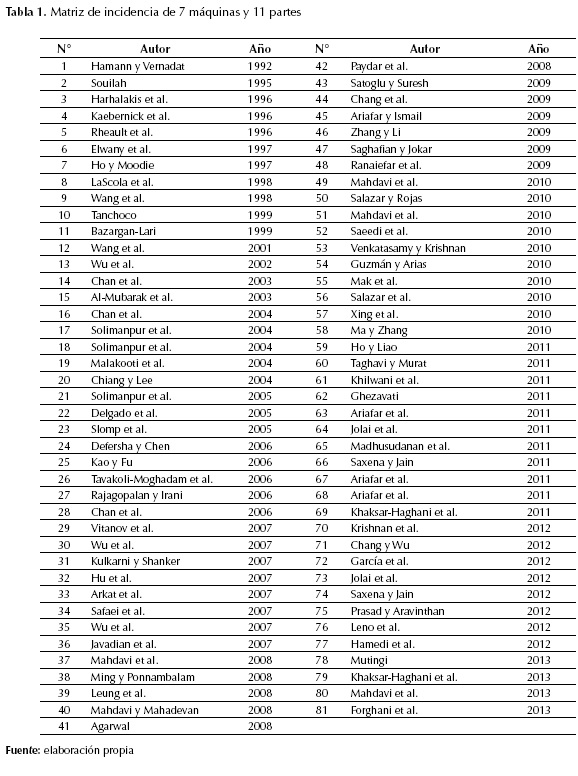
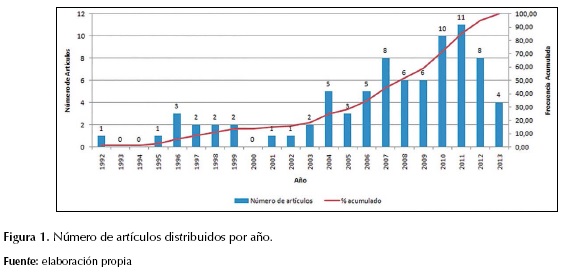
Se presenta una relación de algunos de los principales trabajos relacionados con la formación y definición del layout de celdas de manufactura (tabla 1), los cuales se han venido incrementando con el paso de los años (figura 1).

Definición del modelo para la formación y layout de celdas

La determinación del espacio físico y su distribución para realizar una actividad productiva es un problema frecuente en la historia de la producción, en especial para la industria de manufactura, donde recursos como el espacio, los materiales y el tiempo son limitados y costosos (Tompkins, 2006). Este problema fue planteado formalmente por Koopmans & Beckmann (1957), quienes definieron el problema del layout como un asunto industrial enfocado a la ubicación de las plantas de producción para minimizar el costo del transporte entre estas y lograr la mayor rentabilidad o ganancia.

Posteriormente, y en un sentido más general, Askin y Standridge (1993) plantean este problema como la asignación de cada departamento de una fábrica a una ubicación específica en ella, lo cual concuerda con el planteamiento posterior de Singh y Sharma (2005). Para ellos, el problema consiste en encontrar el arreglo más eficiente para n fábricas en n ubicaciones.

Una definición más detallada del problema del layout fue planteada por Drira, Pierreval y Hajri-Gabouj (2007), quienes presentan las múltiples variaciones que este puede asumir, las cuales dependen de factores como los volúmenes de producción, las características de los productos, la geometría del espacio, los sistemas de manejo de materiales, el uso de múltiples pisos o niveles en la construcción y la consideración estática o dinámica del problema. A partir de estos factores es posible realizar una taxonomía general de las diferentes variaciones del problema en el cual se encuentra el layout de las celdas de manufactura.

El concepto de celdas de manufactura se fundamenta en la filosofía de tecnología de grupos (Singh, 1996), la cual se basa en la agrupación de partes y máquinas a partir de las similitudes en procesos de fabricación entre ellas, e implica una mezcla entre las distribuciones por proceso y producto. Esta se caracteriza por la generación al interior de la planta de pequeñas minifábricas o celdas de manufactura donde se fabrican, en un conjunto de máquinas, un grupo de piezas llamado familia de partes.

Tal tipo de configuración es el apropiado para sistemas de manufactura con diversidad de productos y volúmenes de producción variables. De esto se desprende el problema del layout interceldas (Elwany et al. 1997; Maghsud Solimanpur, Vrat, & Shankar 2004), intraceldas (Hamann & Vernadat, 1992) e inter e intraceldas, lo cual implica solucionar el problema de la formación de las celdas y luego determinar la posición relativa de las máquinas (intra cell layout problem) y de estas entre sí (inter cell layout problem) (Kaebernick, Bazargan-Lari, & Arndt, 1996; Wu et al., 2007; Maghsud Solimanpur, Vrat, & Shankar, 2004; Wu et al., 2007; Ariafar et al., 2011a; Ming & Ponnambalam, 2008; Ariafar et al., 2011a; Ho & Liao, 2011; Kia et al., 2012; Iraj Mahdavi et al., 2009).

Formación de celdas de manufactura

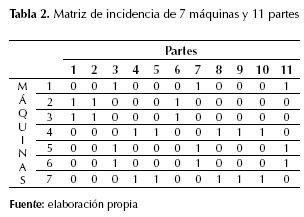
La definición del layout de las celdas de manufactura requiere formar las celdas y definir el layout inter- e intraceldas. El proceso de formación de las celdas de manufactura inicia con la generación de los grupos de máquinas y familias de partes. En este proceso se agrupan las partes en familias a partir de las similitudes que tienen en sus procesos de fabricación, y las máquinas se agrupan en celdas siguiendo las similitudes en las piezas que en ellas se fabrican. Dicho proceso puede realizarse de forma secuencial o simultánea para obtener las celdas de manufactura y las familias de partes. Este proceso comúnmente se basa en matrices de incidencia (a_ij) (tabla 1) que relacionan las partes con las máquinas, donde a_ij = 1 si la parte J es procesada por la máquina i, en otro caso a_ij = 0) (tabla 2). Estas matrices se construyen a partir de las rutas de fabricación de los productos.

Selim, Askin y Vakharia (1998) clasifican los procedimientos de formación de las celdas en: métodos descriptivos, análisis de agrupamiento, partición gráfica, programación matemática e inteligencia artificial. Papaioannou y Wilson (2010) añaden los métodos con algoritmos heurísticos y metaheurísticos; de forma similar, Yin y Yasuda (2006) describen y clasifican las propuestas basadas en coeficientes de similitud, que son uno de los tipos de técnicas basadas en análisis de agrupamiento.

Problema de layout intraceldas

Posteriormente a la formación de las celdas de manufactura, es necesario resolver el problema del layout intra- e interceldas de manufactura, que consiste en la asignación de las máquinas o procesos que conforman las celdas a una posición determinada dentro de estas, las cuales deben ser también asignadas a una determinada posición respecto al resto de celdas. El planteamiento general se basa principalmente en la minimización del costo del transporte mediante la definición del sistema de manejo de materiales debido a que ; este aspecto es importante, ya que de él depende la forma que puede tomar el layout al interior de la celda (Hamann &Vernadat, 1992).

Las características de las piezas como su material, forma, dimensiones, peso, cantidad, entre otras, restringen la forma como deben ser manipuladas, pasando de un sistema con manipulación manual realizada por los operarios al uso de conveyors, vehículos AGV, robots u otros. El sistema de manejo de materiales determina cómo se tratan los casos de retrocesos, si son o no permitidos, y los movimientos entre celdas o secciones, que se relacionan directamente con los puntos de carga y descarga de los materiales a la celda (Tavakoli-Moghadam et al., 2006).

Finalmente, la posición que ocupará cada máquina en la celda puede manejarse considerando el espacio discreto, caso en el cual cada máquina se asigna a una posición determinada previamente, o manejando el espacio de forma continua, donde se determinan las coordenadas de la posición de cada máquina.

Problema de layout interceldas

El problema del layout entre celdas puede ser planteado considerando las relaciones existentes entre las celdas (que pueden ser cuantitativas o cualitativas) como lo plantean Elwany et al. (1997), quienes emplean un algoritmo de mejora que trabaja en serie con un algoritmo de recocido simulado para establecer la posición de las celdas entre sí. Otra forma es plantearlo considerando los flujos de materiales entre las celdas como un problema de asignación (Solimanpur, Vrat, & Shankar, 2005), que se soluciona mediante un algoritmo basado en colonia de hormigas (ACO) un problema de asignación cuadrática (QAP).

Solución simultánea inter e intraceldas

La solución simultánea de la formación de las celdas de manufactura y el layout intra e interceldas, forma en la cual se puede apreciar la naturaleza multiobjetivo del problema, puede plantearse de dos maneras: (a) la primera consiste en llevar el problema multiobjetivo a uno monoobjetivo, integrando en la función objetivo la formación de las celdas y la definición del layout, lo cual se logra a través de la minimización del costo de transporte y manipulación de materiales, como lo presentan Ming y Ponnambalam (2008), quienes emplean un algoritmo híbrido PSO-GA, Ariafar et al.,(2011), que emplean recocido simulado, Ho y Liao (2011), quienes emplean programación lineal, y Wu et al. (2007), que plantean un modelo que minimiza el costo del transporte y maximiza el agrupamiento de las celdas de manufactura empleando algoritmos genéticos con codificación jerárquica; (b) la segunda es plantear cada función objetivo por separado, como lo presentan Maghsud Solimanpur, Vrat, & Shankar (2004), quienes emplean algoritmos genéticos multiobjetivo, considerando las similitudes entre partes, el costo y tiempo de procesamiento, y el costo de adquisición de las máquinas.

En términos generales se pueden identificar dos planteamientos matemáticos para la definición del layout de las celdas de manufactura: uno se fundamenta en asignar posiciones a las máquinas en las celdas minimizando el costo de transporte y manipulación de materiales (LaScola Needy, Billo, & Warner 1998; Wang, Lin, & Wu, 1998; Ariafar et al., 2011b; Mahdavi et al., 2010), lo cual implica que no se evalúa de forma explícita el agrupamiento de las celdas; (b) el otro planteamiento considera de forma explícita la formación de las celdas en la función objetivo conjuntamente con el costo de transporte y manipulación de materiales (Krishnan et al., 2012; Mutingi, 2013; Iraj Mahdavi et al., 2013). Las variables empleadas son de asignación de las máquinas a las celdas y a las posiciones dentro de estas, así como de las partes a las celdas para formar las familias; manejan además restricciones de unicidad y pueden incluir diversos parámetros que se integran a los modelos.

Tipos y métodos de solución

Entre las diversas técnicas y métodos para definir el layout de celdas de manufactura están los heurísticos (Vitanov, 2007; Mahdavi, 2008; Kulkarni, 2007), los metaheurísticos (Krishnan, 2012; Solimanpur, 2004) y, en algunos casos, probabilísticos (Defersha, 2006).

Un método ampliamente difundido entre los autores son los algoritmos genéticos, prueba de ello son los trabajos de Chan (2006), Krishnan (2012), Wu (2007) y Kulkarni (2007), a los cuales se les han implementado diferentes esquemas de cruce y mutación para mejorar su desempeño.

Propuestas como la de Ming (2008) plantean soluciones híbridas empleando un algoritmo genético AG y optimización de enjambre de partículas PSO. Otros ejemplos de hibridación lo presentan Saeedi (2010) y Ghezavati (2011), quienes combinan un algoritmo genético AG y de recocido simulado SA.

La optimización basada en colonia de hormigas ACO también ha sido empleada en este problema, como lo presentan Solimanpur (2004) Kao (2006) y Saghafian (2009). Hamann (1992) utiliza algoritmos de ramificación y acotamiento y planos de corte, con los cuales resuelve de forma simultánea o secuencial la definición del layout de las celdas, primero seleccionando el sistema de manejo de material, luego la disposición de la planta y por último su localización.

Autores como Defersha (2006) partieron de un modelo probabilístico para dar solución al problema de FC mediante el método de descomposición de Benders, mientras que Ho (2011) emplea programación matemática; Mahdavi (2010), programación lineal entera, mientras que Safaei (2007) genera una posible solución mediante programación difusa.

Algunos de los métodos de solución menos comunes, son reportados por Saghafian (2009), con el método de proceso analítico jerárquico, Bazargan-Lari (1999) plantea un algoritmo PSO (optimización por enjambre de partículas), Tanchoco (1999) propone el método de flujo segmentado topología (SFT), y Jolai (2012) concibe el método de electromagnetismo como algoritmo (EM-like).

Manejo de variables y parámetros en el modelo

En este apartado se analizan los tipos de variables utilizados (enteras, binarias o continuas); para ello se revisaron las variables planteadas en la bibliografía consultada.

Tipos de variables

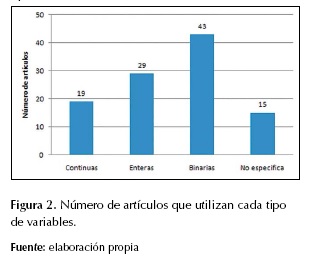
Los modelos matemáticos planteados utilizan diferentes tipos de variables, siendo frecuentes las variables binarais y las enteras. En la figura 2 se presenta el número de artículos que maneja cada tipo de variables.

En los artículos evaluados, la mayoría de modelos (56%) maneja un solo tipo de variable, ya sean binarias (o booleanas), enteras o continuas. Sin embargo, también es común encontrar modelos que trabajan dos tipos de variables (21%) o hasta tres tipos (5%). Por esta razón algunos artículos son contados dos o tres veces y la suma total es mayor al total de artículos revisados.

Variables binarias

Las variables binarias están presentes en el 53% de los artículos y corresponden básicamente a variables de asignación. Estas variables de decisión son por lo general:

• Si una celda es asignada a una determinada posición
• Si una máquina es asignada a una determinada celda o determinada posición
• Si una pieza es asignada a determinada máquina o a determinada celda.

Otras variables binarias se utilizan para determinar si debe crear o activar una celda o la asignación de otro tipo de elementos como herramientas o trabajadores.

Variables enteras

Las variables enteras se utilizan cuando las variables se definen como el número de elementos asignados a determinada celda o máquina. Las variables enteras comunes plantadas son:

• Número de celdas creadas
• Número de máquinas de determinado tipo asignadas cada celda
• Número de piezas procesadas en determinada máquina o celda

Otras variables enteras utilizadas son por ejemplo el número de máquinas adicionadas o quitadas de cada celda en cada periodo, para el caso de modelos dinámicos.

Variables Continuas

Las variables continuas tienen diferentes usos en los modelos de formación de celdas de manufactura y distribución de planta. Los usos frecuentes de este tipo de variables son:

• Coordenadas de ubicación de cada celda o máquina cuando la localización no se hace mediante la asignación de estas a locaciones preestablecidas. Estas coordenadas corresponden a un extremo de la celda o máquina.
• Distancia resultante entre celdas o máquinas después de realizada la localización.
• Flujo resultante entre celdas o máquinas después de realizada la formación de celdas y la distribución de planta.

Parámetros

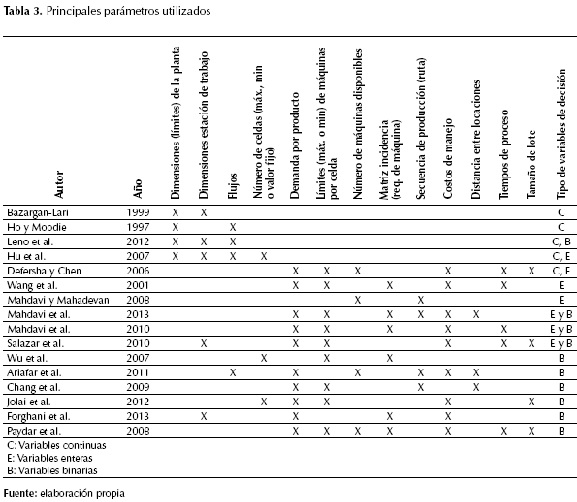
Para el análisis de los parámetros utilizados en los modelos, se tomaron en cuenta aquellos artículos que los definían explícitamente en modelos de programación matemática. En la tabla 3 se muestran los principales parámetros utilizados, relacionados con el tipo de variable de decisión utilizada.

La tabla 3 se ordenó de acuerdo con el tipo de variables de decisión utilizadas, iniciando por los modelos que utilizan variables continuas, siguiendo con los de variables enteras y terminando con los de variables binaras. Los modelos con variables continuas resultaron enfatizar más en el uso de un tipo de parámetros que los modelos con variables de decisión enteras y binarias.

En el caso de modelos matemáticos con variables de decisión continuas, como los de Bazargan-Lari (1999), Ho (1997), Leno et al. (2012) y Hu et al. (2007), cuyas decisiones principales se basan en la determinación de las coordenadas de localización de las máquinas o de las celdas, los parámetros más utilizados fueron las dimensiones de la planta, las dimensiones de las máquinas o estaciones de trabajo y flujos entre celdas y máquinas ya definidos.

En los modelos cuyas variables de decisión son enteras o binarias, los parámetros en orden de utilización de mayor a menor son:

• Demanda por producto
• Requerimientos de máquina. La representación de si una parte requiere de una máquina se hace mediante una matriz de incidencia parte-máquina (donde el parámetro toma el valor de 1 si una parte requiere ser procesada en determinada máquina y 0 si no es el caso), o mediante la definición de la ruta o rutas de proceso de cada parte.
• Límites máximos o mínimos de máquinas por celda
• Costos de manejo de material intracelda e intercelda
• Tiempos de proceso
• Número de máquinas disponibles de cada tipo
• Tamaño de lote
• Distancia entre locaciones
• Dimensiones estación de trabajo
• Número de celdas, las cuales podían ser dadas por un límite máximo, un límite mínimo o un valor fijo previamente determinado.
• Nivel de flujo intercelda para el caso en que los modelos que parten de una formación de celdas ya definida.

Software de apoyo

Dentro de los programas más utilizados como soporte informático en la literatura consultada, se encuentran los siguientes lenguajes de programación:

Pruebas o estudio de casos

Entre las principales estrategias para evaluar el desempeño de las propuestas se encontró la utilización de estudios de caso y los problemas de prueba.

El estudio de caso como método de investigación es muy útil para estudiar problemas prácticos o situaciones determinadas; es a la vez un método descriptivo e inductivo. Así lo utilizan para mostrar y respaldar su investigación Tanchoco (1999), Chiang (2004), Chan (2003), Malakooti (2004), Vieira Conceizao (2005), Rajagopalan (2006), Chan, T. S (2006), Salazar (2010), García (2012) y Prasad (2012).

Los problemas de prueba son casos específicos de desarrollo a partir de especificaciones o restricciones que tiene cada problema. Entre otros autores que utilizan esta tipología para probar sus modelos se encuentran Kaebernick (1996), Zolfaghari (2006), Ariafar (2009), Saeedi (2010), Venkatasamy (2010) y Madhusudanan Pillai (2011).

Perpectivas y tendencias a futuro

Es necesario realizar trabajos que permitan indagar con más detalle la relación entre los parámetros de diseño tales como el número de celdas, el tamaño del sistema y su impacto en el rendimiento. También se requiere incluir otros factores, como la capacidad de las máquinas y rutas alternativas en la herramienta de soporte de decisiones como lo propone Vitanov (2007).

En problemas de gran tamaño, los modelos propuestos se pueden resolver utilizando métodos heurísticos (Suresh, 2009) y encontrar la secuencia óptima de producción sin tener en cuenta como restricción el número de estados (operaciones) (Guzmán, 2010).

Otros escenarios propuestos a futuro son la elaboración de directrices relativas al medio ambiente (Al-Mubarak, 2003), estudios de esquemas de asignación de más de un elemento a la vez en una celda, considerando múltiples objetivos (Madhusudanan Pillai, 2011).

Por otra parte , en lugar de una comparación de pares de máquinas y de selección basados en el flujo máximo entre ellos, vale la pena diseñar algoritmos que consideran más de dos máquinas a la vez (Mahdavi, 2008), así como la consideración de tiempo de transporte con capacidades finitas (Malakooti, 2004).

Una línea de investigación por desarrollar sería la del estudio de cómo la cultura organizacional afecta el proceso de implementación de un sistema de fabricación celular, especialmente en el caso de las pequeñas y medianas empresas (Vieira Conceizao, 2005).

Referencias

Al-Mubarak F, C. C. (2003). A simulation study of focused cellular manufacturing as an alternative batch-processing layout. International Journal of Production Economics, 83(2), 123-138.

Ariafar S, N. I. (2009). An improved algorithm for layout design in cellular manufacturing systems. Journal of Manufacturing Systems, 132-139.

Ariafar S, N. I. (2011a). A stochastic facility layout model in cellular manufacturing systems. International Journal of the Physical Sciences, 3754-8.

Ariafar S, N. I. (2011b). Inter-cell and intra-cell layout design in a cellular manufacturing system. in Business, Engineering and Industrial Applications (ISBEIA), 28-33.

Bazargan-Lari, M. (1999). Layout designs in cellular manufacturing. European Journal of Operational Research, 258-272.

Chan F, T. S. K. W. (2006). Two-stage approach for machine-part grouping and cell layout problems. Robotics and Computer-Integrated Manufacturing, 217-238.

Chan W, M. C. Y. (2003). A heuristic algorithm for machine assignment in cellular layout. Computers & industrial engineering, 49-73.

Chiang C-P., S.-D. L. (2004). Joint determination of machine cells and linear intercell layout. Computers & Operations Research, 1603-1619.

Defersha F, M. M. C. (2006). A comprehensive mathematical model for the design of cellular manufacturing systems. International Journal of Production Economics, 767-783.

Delgado E. A., C. J. (2005). Applying genetic algorithms for programming manufacturing cell tasks. Ingeniería e Investigación, 24-31.

Drira A, P. H. (2007). Facility layout problems: A survey. Annual Reviews in Control, 31(2), 255-267.

Elwany M, H., A. B.-A. (3 de Enero de 1997). A Combined Multicriteria Approach for Cellular Manufacturing Layout. Alejandría, Egipto.

García C, E. G. (2012). Algoritmo Evolutivo Eficiente Aplicado a la Planeación de la Expansión de Sistemas de Distribución. Información tecnológica, 3-10.

Ghezavati, V. R. (2011). A new stochastic mixed integer programming to design integrated cellular manufacturing system: A supply chain framework. International Journal of Industrial Engineering Computations, 563-574.

Guzmán L, E. S. J. S. (2010). Modelo con redes de Petri e implementación con grafcet de un sistema de manufactura flexible con procesos recurentes y recursos compartidos. Ciencia e Ingeniería Neogranadina, 61-75.

Hamann T, F. V. (1992). The Intra-cell layout problem in automated manufacturing systems.

Hamedi H, N. I. (2012). Virtual cellular manufacturing system based on resource element approach and analyzing its performance over different basic layouts. International Journal of Industrial Engineering Computations, 3(2), 265-276.

Hassam, M. S. (1998). Cell formation in group technology: review, evaluation and directions for future research. Computer ind. Engng, 3-20.

Ho Y.-C., C. L. (1997). Locating IO points of flexible manufacturing cells with the consideration of within-cell and inter-cell flow distance. Computers & Industrial Engineering, 33(3-4), 665-668.

Ho Y.-C., T.-W. L. (2011). A concurrent solution for intra-cell flow path layouts and I/O point locations of cells in a cellular manufacturing system. Computers & Industrial Engineering, 614-634.

Jolai F, M. T. (2011). A variable neighborhood binary particle swarm algorithm for cell layout problem. Int J Adv Manuf Technol, 327-339.

Jolai F, R. T.-M. (2012). An Electromagnetism-like algorithm for cell formation and layout problem. Expert Systems with Applications, 2172-2182.

Kaebernick H, M. B.-L. (1996). An Integrated Approach to the Design of Cellular Manufacturing. CIRP Annals-Manufacturing Technology, 421-425.

Kao Y., S. C. (2006). An ant-based clustering algorithm for manufacturing cell design. Int J Adv Manuf Technol, 1182-1189.

Khaksar-Haghani F, R. K. (2011). Multi-floor layout design of cellular manufacturing systems. International Journal of Management Science and Engineering Management, 6(5), 356-365.

Koopmans & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(53).

Krishnan K, K. S. M. (2 de Agosto de 2012). A comprehensive approach to facility layout design and cell formation. The International Journal of Advanced Manufacturing Technology, 737- 753.

Kulkarni P, C. K. S. (2007). A genetic algorithm for layout problems in cellular manufacturing systems. in Industrial Engineering and Engineering Management.

Kusiak A. (1990). Intelligent manufacturing systems. Prentice-Hall International.

LaScola K., Needy R. E. Billo, and R. C. Warner, "A cost model for the evaluation of alternative cellular manufacturing configurations," Computers & industrial engineering, vol. 34, no. 1, pp. 119-134, 1998.

Leno I, J. S. S. (2012). Integrated Layout Design Approach for Cellular Manufacturing System Environment. Journal of Applied Sciences, 2411-2417.

Madhusudanan V. Pillai, I. B. (2011). Design of robust layout for Dynamic Plant Layout Problems. Computers & Industrial Engineering, 813-823.

Mahdavi I, B. M. (2008). CLASS: An algorithm for cellular manufacturing system and layout design using sequence data. Robotics and Computer-Integrated Manufacturing, 488-497.

Mahdavi I, B. S. (2008). A flow matrix-based heuristic algorithm for cell formation and layout design in cellular manufacturing system. Int J Adv Manuf Technol, 943-953.

Mahdavi I, M. M. (2010). Designing a mathematical model for intra-cell layout of dynamic cellular manufacturing systems considering production planning and system reconfiguration. Computers and Industrial Engineering, 1-6.

Malakooti, B, N. R. (2004). Integrated group technology, cell formation, process planning, and production planning with application to the emergency room. International journal of production research, 1769-1786.

Ming L, C. S. G. (2008). A hybrid GA/PSO for the concurrent design of cellular manufacturing system. in Systems, Man and Cybernetics, 1855-1860.

Paydar M, M. I. M. (2008). Solving a new mathematical model for cellular manufacturing system: fuzzy goal programming. IEEE International Conference, 1224-1228.

Prasad P, S. S. G. A. (2012). Development of Cellular Layout for a Pump Manufacturing Industry. Social Science Research Network, Rochester, NY, SSRN Scholarly Paper ID 2012951.

Rajagopalan R, S. A. (2006). Some comments on Malakooti et al. 'Integrated group technology, cell formation, process planning, and production planning with application to the emergency room. International Journal of Production Research, 2265-2276.

Renna P, M. A. (s.f.). Evaluation of cellular manufacturing configurations in dynamic conditions using simulation. Int J Adv Manuf Technol, 56, 9-12.

Saeedi S, M. S. (2010). Heuristic Approaches for Cell Formation in Cellular Manufacturing. JSEA, 674-682.

Safaei N, M. S.-M. (2007). Designing cellular manufacturing systems under dynamic and uncertain conditions. J Intell Manuf, 383-399.

Saghafian S, M. R. (2009). Integrative cell formation and layout design in cellular manufacturing systems. Journal of Industrial and Systems Engineering, 97-115.

Salazar A, F. L. C. (2010). Propuesta de distribución en planta bietapa en ambientes de manufactura flexible mediante el proceso analítico jerárquico. Revista EIA, 161-175.

Saxena L, K. P. K. (2012). An integrated model of dynamic cellular manufacturing and supply chain system design. Int J Adv Manuf Technol, 385-404.

Singh N. (1996). Systems approach to computer-integrated design and. New York, John Wiley, 643.

Slomp J, B. V. (2005). Design of virtual manufacturing cells: a mathematical programming approach. Robotics and Computer-Integrated Manufacturing, 21(3), 273-288.

Solimanpur M, P. V. (2004). A multi-objective genetic algorithm approach to the design of cellular manufacturing systems. International Journal of Production Research, 1419-1441.

Solimanpur M, P. V. (2004). Ant colony optimization algorithm to the inter-cell layout problem in cellular manufacturing. European Journal of Operational Research, 592-606.

Suresh S. I. (2009). A goal-programming approach for design of hybrid cellular manufacturing systems in dual resource constrained environments. Computers & Industrial Engineering, 560-575.

Tanchoco J. M. (1999). Cellular machine layout based on the Segmented Flow Topology. International journal of production research, 1041-1062.

Tompkins J. (2006). Planeación de instalaciones ( 3ra ed.). Thomson.

Venkatasamy V, K. K. (2010). Integrating Group Technology and Facility Layout for Reduced Intercellular Flow. IIE Annual Conference. Proceedings.

Vitanov V, B. T. (2007). A decision support tool to facilitate the design of cellular manufacturing layouts. Computers & Industrial Engineering. Vol. 52, 380-403.

Vieira Conceizao, S. (2005). Optimizacao do fluxo de materiais através da manufatura celular. Revista producao, 15(2), 235-250.

Wang T, Y. K. B. (2001). A simulated annealing algorithm for facility layout problems under variable demand in Cellular Manufacturing Systems. Computers in Industry, 181-188.

Wu X., C.-H. C. (2007a). A genetic algorithm for cellular manufacturing design and layout. European Journal of Operational Research, 156-167.

Wu X., C.-H. C. (2007b). Genetic algorithms for integrating cell formation with machine layout and scheduling. Computers & Industrial Engineering, 277-289.

Yin, Y. (2006). Similarity coefficient methods applied to cell formation problem: a taxonomy and review. International Journal of Production Economics 101, 329-352.

Zhang, H. M. (2010). The Dynamics Facility Layout Study Based on Cellular Manufacturing. 862-865.

Zolfaghari S, E. V. (2006). Cellular manufacturing versus a hybrid system: a comparative study. Journal of Manufacturing Technology Management, 17(7), 942-961.