DOI:
https://doi.org/10.14483/23448393.13247Published:
2018-11-05Issue:
Vol. 23 No. 3 (2018): September - DecemberSection:
Computational IntelligenceA Meta-Optimization Approach to Solve the Set Covering Problem
Un Enfoque de Meta-Optimización para Resolver el Problema de Cobertura de Conjunto
Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 16 de abril de 2018; Revisión recibida: 9 de agosto de 2018; Aceptado: 14 de septiembre de 2018
Abstract
Context:
In the industry the resources are increasingly scarce. For this reason, we must make a good use of it. Being the optimization tools, a good alternative that it is necessary to bear in mind. A realworld problem is the facilities location being the Set Covering Problem, one of the most used models. Our interest, it is to find solution alternatives to this problem of the real-world using metaheuristics.
Method:
One of the main problems which we turn out to be faced on having used metaheuristic is the difficulty of realizing a correct parametrization with the purpose to find good solutions. This is not an easy task, for which our proposal is to use a metaheuristic that allows to provide good parameters to another metaheuristics that will be responsible for resolving the Set Covering Problem.
Results:
To prove our proposal, we use the set of 65 instances of OR-Library which also was compared with other recent algorithms, used to solve the Set Covering Problem.
Conclusions:
Our proposal has proved to be very effective able to produce solutions of good quality avoiding also have to invest large amounts of time in the parametrization of the metaheuristic responsible for resolving the problem.
Keywords:
Artificial Bee Colony Algorithm, Meta-Optimization, Set Covering Problems..Resumen
Contexto:
En la industria los recursos son cada vez más escasos, por esta razón se debe hacer un buen uso de ellos y las herramientas de optimización son una buena alternativa que se debe tener presente. Un problema del mundo real lo constituye la ubicación de instalaciones, siendo el problema de cobertura de conjuntos uno de los modelos más utilizados. El presente interés es encontrar alternativas de solución a este problema de la vidareal, utilizando metaheurísticas.
Método:
Uno de los principales problemas que se enfrentan al utilizar metaheurísticas es la dificultad de realizar una correcta parametrización con el objetivo de encontrar buenas soluciones. Esta no es una tarea fácil, por lo cual la propuesta es utilizar una metaheurística que permita proporcionar buenos parámetros a otra metaheurística que será la encargada de resolver el problema de cobertura de conjuntos.
Resultados:
Para probar la propuesta, se utiliza el set de 65 instancias de OR-Library, el cual fue comparado con otros recientes algoritmos que son usados para resolver el problema de cobertura de conjuntos.
Conclusiones:
La propuesta ha demostrado ser muy efectiva, logrando producir soluciones de buena calidad y evitando, además, que se tenga que invertir gran cantidad de tiempo en la parametrización de la metaheurística encargada de resolver el problema.
Palabras clave:
Algoritmo colonia de abejas artificiales, metaoptimización, problema de cobertura..Introduction
The Set Covering Problem (SCP), introduced in [1], is an important problem NP-Hard present in the current industry. The following applications for covering problems were mentioned in [2]: Bus stop location, Fire equipment allocation, Fire company relocation, Fire service sitting and Terrain visibility. Also, in [3] were presented some general applications of the gradual covering problem: The delivery problem; Competitive location; Dense competition; The radio, TV, or cellular transmitter problem and Medical facility location problem.
Mathematically SCP can be defined as: Let A = (a
ij
) be an m-row, n-column, zero-one matrix. We say that a column j can cover a row i if aij = 1. Each column
j
is associated with a non-negative real cost c
j
. 
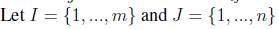be the row set and column set, respectively. The SCP calls for a minimum cost subset 
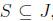, such that each row 
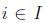is covered by at least one column
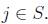. A mathematical model for the SCP is stated in the following:
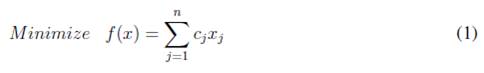
subject to
If the costs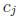 
are equal for each 
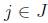, the problem is referred to as the unicost SCP, otherwise, the problem is called the weighted or non-unicost SCP, where 
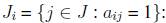the subset of columns covering row 
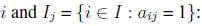the subset of rows covered by column
j
.
The goal is to minimize the sum of the costs of the selected columns, where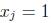 
if the column j is in the solution, 0 otherwise. The constraints ensure that each row i is covered by at least one column.
Different solving methods have been proposed in the literature for the Set Covering Problem. The use of metaheuristics is a good alternative to tackle this problem as can be swarm intelligence continuous metaheuristic. Because they are continuous metaheuristics and SCP is a combinatorial problem, these metaheuristics must be accompanied by a binarization mechanism. In the literature, we find the main binarization technique used to solve SCP corresponds to transfer functions, for more details on binarization techniques see gas [4], [5]. Among the main algorithms that use this technique we found a cat swarm [6], a binary Firefly Optimization [7], a Binary Cuckoo Search (BCS) [8] and artificial bee colony [9]. Specific binarization techniques have also been developed to solve SCP, among the most efficient are: a Teaching-learning binarization [10], a Binary Black Hole (BBH) [11], and a specific Jumping Particle Swarm Optimization (JPSO) method [12].
Depending on the algorithm that has been used, the quality of the solution wanted and the complexity of the SCP chosen, it is defined the amount of customization effort required. Being of paramount importance the determination of the values that are given to the parameters. Conveniently, this work proposes a meta-optimization approach where the task of customization is transferred to another metaheuristic (a “high level”metaheuristic) which can handle the task of parameters adjustment for a low level metaheuristic [13].
Our proposal considers a Genetic Algorithm (GA) for parameter setting and an ABC algorithm at a lower level using an Automatic Parameter Tuning approach. The Automatic Parameter Tuning is carried by the GA which searches for the best parameters in the parameter space in order to tune the solver automatically.
This approach is considered as meta-optimization since there are two metaheuristics covering tasks of parameter setting, for the former, and problem solving, for the latter [14]. This work is an extension of[15] where emphasis is given to the percentage of improvement of the different instances.
The rest of this paper is organized as follows. In Section 2, we briefly survey the ABC algorithm. In section 3 we present the meta-optimization approach. In Section 4, we present the experimental results obtained. The analysis of the results of comparing our proposal with a constructive metaheuristic is presented in section 5. Finally, in Section 6 we conclude the paper and give some perspectives for further research.
Artificial Bee Colony Algorithm
ABC is one of the most recent algorithms in the domain of the collective intelligence [16]. Created by Dervis Karaboga in 2005, who was motivated by the intelligent behavior observed in the domestic bees to take the process of foraging [17]. ABC is an algorithm of combinatorial optimization based on populations, in which the solutions of the problem of optimization, the sources of food, are modified by the artificial bees, that fungen as operators of variation. The aim of these bees is to discover the food sources with major nectar.
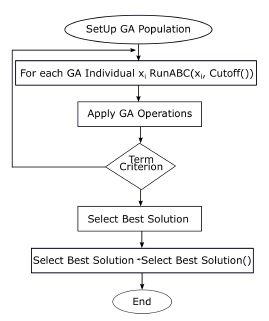
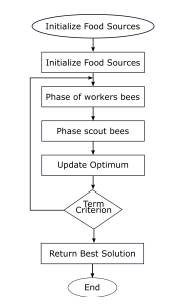
In the ABC algorithm, the artificial bees move in a multidimensional search space choosing sources of nectar depending on its past experience and its companions of beehive or fitting his position. Some bees (exploratory) fly and choose food sources randomly without using experience. When they find a source of major nectar, they memorize his position and forget the previous one. Thus, ABC combines methods of local search and global search, trying to balance the process of the exploration and exploitation of the space of search. The Flow chart of Artificial Bee Colony is showed in Fig. 1.
Figure 1: Flow Chart of ABC Algorithm.
The procedure for determining a food source in the neighbourhood of a particular food source which depends on the nature of the problem. Karaboga [18] developed the first ABC algorithm for continuous optimization. The method for determining a food source in the neighbourhood of a particular food source is based on changing the value of one randomly chosen variable while keeping other variables unchanged. This is done by adding to the current value of the variable the product of a uniform value in [-1, 1] and the difference in values of this variable for this food source and some other randomly chosen food source. This approach can not be used for discrete optimization problems for which it generates at best a random effect.
Singh [19] subsequently proposed a method, which is appropriate for subset selection problems. In his model, to generate a neighbouring solution, an object is randomly dropped from the solution and in its place another object, which is not already present in the solution is added. The object to be added is selected from another randomly chosen solution. If there are more than one candidate objects for addition then ties are broken arbitrarily. In this work we use the ABC algorithm described in [20] and extending the work presented in [14].
A Meta-Optimization Approach to Solve the SCP
Metaheuristics, in their original definition, are solution methods that orchestrate an interaction between local improvement procedures and higher level strategies. Thus, metaheuristics create a process capable of escaping from local optima and performing a robust search of a solution space.
Over time, these methods have also come to include any procedures that employ strategies for overcoming the trap of local optimality in complex solution spaces. The use of one or more neighborhood structures as a means of defining admissible moves to transition from one solution to another, or to build or destroy solutions in constructive and destructive processes are examples of such procedures.
Parameter setting
The selection of an adequate set of values for parameters improves the performance of metaheuristic methods. This configuration can be realized of two ways:
Offline configuration
It consists of finding the appropriate configuration of parameters of the algorithm before the algorithm is executed. It is mostly done in the form of trial and error. This makes tuning process a very high consuming time task. There depends much of the intuition and the experience of the creator of the algorithm. They are typically undocumented and therefore not reproducible driving often to an unequal adjustment of different algorithms. An alternative to find good values for the parameters shown in [21]. Within this group are the racing methods where it is evaluated iteratively different candidate configurations for a certain number of instances [22];Also this Sequential Model-Based Optimisation, this approach, consists of improving the initial values of the parameters alternating .the experiment design and the identification of the parameters [23] and Graphic Radial Method, in this approach radar chart curve is used to define the best configuration [5].
Online configuration
It is an important research area, since the algorithms can adapt themselves better to the characteristics of a particular instance. In the search process, it is essential to identify the phases of exploration and exploitation of the algorithm since the adjustment of parameters can be different in each stage allowing to achieve a better performance. Can improve results in cases of algorithms that are used in situations which are very different to those that were built.
Different techniques exist, being the most simple to define the rule variation of parameters before executing the algorithm.
The on-line approaches can be classified in dynamic and adaptive. Dynamic approaches are those where the updating of the parameters is performed in a random or deterministic way. On the other hand in adaptive approaches the memory is used and the change of value is made according to the progress in the search process. One special case is the autonomous search concept where internal and external information is used for adjustment. Find a correct configuration of parameters constitutes an optimization problem for which we can use a meta-Level optimizer.
Meta-Optimization
A meta-optimization approach can be considered as two or more metaheuristics where a higher level metaheuristic controls the parameters of a lower level one, which is at charge of dealing more directly to the problem. Our ABC algorithm employs four control parameters which are: number of food sources, the value of limit,% of Columns to add, and% of Columns to eliminate. On a higher level GA allows to evaluate different parameter configurations avoiding manual configuration. Each GA individual encodes the parameters of an ABC algorithm generating an ABC instance. The detail of the proposed approach is presented below:
Higher level metaheuristic
GA has been successfully used in various algorithm configurations, a particular case is the presented by Grefenstette [24], that used it to find the parameter values of another genetic algorithm. Another example is [25] where several subpopulations are used and a specialized cross-over operator to generate new candidate configurations. On the other hand it was recently used by Senthilkumar in [26] to find the parameters of the arc welding process with flux core. Using a proven algorithm in the search for configurations, allows us to validate our proposal.
In the GA component, the chromosome genes are: “Food sources”, it is the number of initial solutions for ABC (which is equal to the number of workers or onlookers bees), it will take values between 50 and 500. The second gene, “Limit”, it takes values between 0 and 100. Similarly, the third and fourth genes, “% Columns to Add” and “% Columns to Eliminate”, they take values between 0.01 and 10.
During each generation of the GA algorithm, in order to produce offsprings, a tournament selection method is used to select a set of individuals from the population as follows. Given the size k of the tournament group and a probability p, the k individuals are sorted using their fitness value and a random value r is generated. If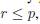 
, the best individual is choosen, otherwise the probability p is incremented, a new random value is generated and the tournament group is reduced by one. This process is repeated at most k times. If no individual is chosen after k attempts, the worst individual belonging to the tournament group is selected. To select n individuals this selection procedure is carried out n times.
The operator randomly selects two chromosomes from the population and performs the crossover as follows. It generates randomly a binary crossover mask with the same length as the chromosomes. If the value of a bit is 1, chromosome information is copied from the first parent. If the value is 0, the genes from the second parent are used and vice-versa for the second offspring.
The mutation operator is applied with a certain rate replacing the value of a gene with a value drawn uniformly from its domain.
Lower level Metaheuristic
In the ABC component, a first step is performed in order to initialize the parameters of ABC as size of the colony, number of workers and onlookers bees, limit of attempts and maximum number of cycles (iterations). To generate the initial population we cross every row of the counterfoil of constraints and by every row a column is selected at random. This column is part of the solution which is represented by means of an entire vector. This vector considers the columns chosen in one solution. To complete this vector a procedure is performed for all the rows in such a way that the generated solution complies with all the constraints. Then, the evaluation of the population fitness is performed using the objective function, see (1). Afterwards, the modification of the position and selection of sites for worker bees is performed as follows. A hard-working bee modifies its current position selecting a food source randomly. If a hard-working bee duplicates a solution, it is transformed to an explorer bee. Otherwise, it proceeds to add a certain random number of columns between 0 and the maximum number of columns to be added. Then, it proceeds to eliminate a certain random number of columns between 0 and the maximum number of columns to be eliminated. If the new solution does not meet the constraints, it is repaired.
We use repair method where all rows not covered are identified and the columns required are added. So in this way all the constraints will be covered. The search of these columns are based in the relationship showed in the Equation 4.
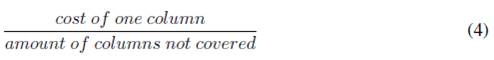
Once the columns are added and the solution is feasible, a method is applied to remove redundant columns of the solution. A redundant column are those that are removed, the solution remains a feasible solution.
After this, the fitness of the solution is evaluated by means of the objective function of the SCP and if the fitness is minor that the solution previously obtained, the solution is replaced. Otherwise, the number of attempts for improving this solution is increased and the algorithm continues evaluating another hard-working bee.
Integrating Components
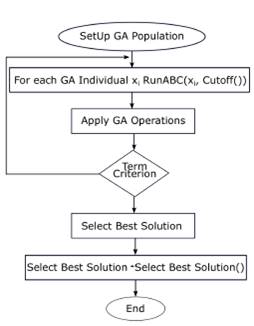
The Figure 2 shows the meta-optimization approach developed to solve the SCP. Once the GA population is generated, each individual is taken to run the ABC algorithm until a certain cut-off. Then, the genetic operators are applied and a termination criterion is evaluated in order to stop the parameter setting. Once the termination criterion is achieved, the best individual from the GA contains the best parameter set which is selected to run the ABC algorithm.
Figure 2: Tuning ABC().
Results
In this section we detail the behaviour of our approach. To solve the different SCP instances, a Computer with Windows 7, 2.5 GHz Dual Core processor and 4GB in RAM was used.
The ABC algorithm was executed 30 times for each instance, where the main features are shown in the Table I,where the density corresponds to the percentage of non-zero in the matrix.
In the top level Java Package was used1 (jgap) 3,5 version to implement the genetic algorithm using the parameters shown in the Table II. The GA implementation has 3 main phases: configuration, initial population and evolution of the population.
Table I: Features of the 65 instances [20].
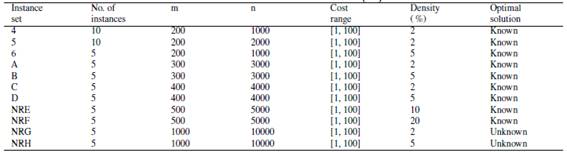
Table II: Parameters used in GA
The best parameters settings for each instance were found using GA, since these may vary because the search space can change very much of one instance to another. In the table IIIshows the values of the parameters of the best chromosomes obtained.
Table III: Parameters values from best chromosome
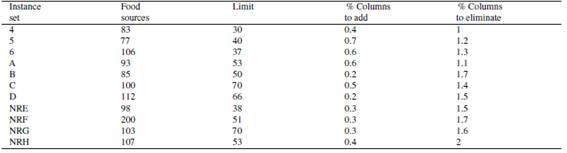
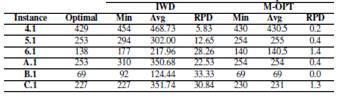
Table IV: Results obtained for IWD - Meta-Optimization
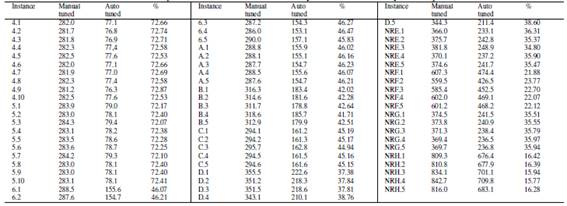
In order to compare our proposal with other works and given information available, we use the relative percentage deviation (RPD) which quantifies the deviation of the target value Z of Zopt. We report the optimal value, the best found value using our proposed and its average. The results are shown in the Tables V, VIand VII.
Table V: Results obtained for Set 4
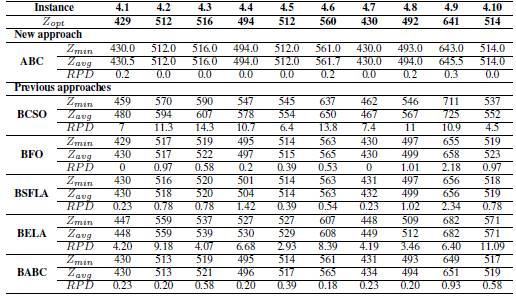
Table VI: Results obtained for Set 5
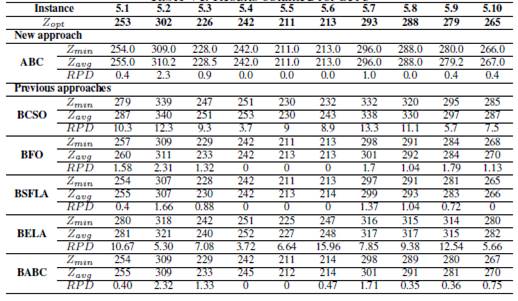
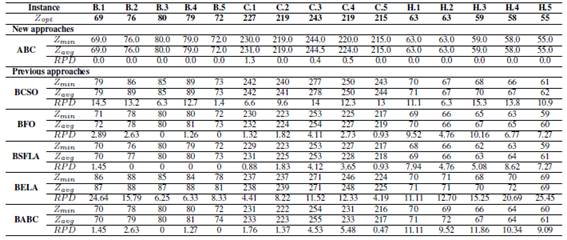
Table VII: Results obtained for Set B, C and H
To validate our proposal were resolved the 65 instances of OR-Library and were compared with published results of recent approaches: Binary Cat Swarm Optimization (BCSO) [6]; Binary Firefly Optimization (BFO) [27]; Binary Shuffled Frog Leaping Algorithm (BSFLA) [28]; Binary Electromagnetism - Like Algorithm (BELA) [29]; and Binary Artificial Bee Colony (BABC) [30]. The comparison is done using relative percentage deviation (RPD).
The table Vshow the results obtained for instances from group 4, where ABC had the best optimal values compared to the results by the previous approaches, only BFO exhibit a good performance for this data with two global optimums.
In the group 5, ABC, BFO, BSFLA AND BABC obtained optimal values, detailed as follows: ABC, four optimal values; BFO, three optimal values; BSFLA, four optimal values; BABC, two optimal values. BELA and BCSO did not achieve some optimum. The results are shown in the Table VI.
The results of groups B, C and H are shown in the Table VIIwhere it is visualized that ABC achieves all the optimals for groups B and H, also achieving 2 optimal for group C. In relation to the other techniques used in the comparison, BFO finds two optimal values, BSFLA finds four optimal values. In the case of BABC, there are two optimal values. BCSO not get optimal as well as BELA.
Additionally, our proposal was compared with the constructive Metaheuristic called Intelligent Water Drops presented by [31]. For this comparison was used the first instances of the groups 4, 5, 6, A, B y C. The results are shown in the table IV.
In order to demonstrate that our approach helps to improve the overall time to solve a problem, to contribute to the search for a good configuration parameters in less time, we use the table VIIIit shows the times used for the configuration of each instance. Manually we used 5 hours, in contrast with GA we use 720 seconds for each group of instances.
In the Table VIIIwe can see that the biggest instances the percentage of progress of the time diminishes what it makes necessary to incorporate in the future other techniques to improve this behavior.
Table VIII: Comparison of ABC with manually and automatically tuned parameters
In tables IXto XI we analysed the difference of RPD of the different techniques with respect to the RPD obtained by ABC. We can observe that for Set 4 table Xin average the lowest percentage of improvement corresponds to 36,41 %, however low to 27.84% for set 5. For the most complicated groups, our proposal also presents important improvement with respect to the other techniques.
Table IX: Comparison RPD Set 4 with ABC
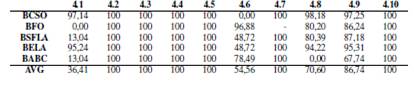
Table X: Comparison RPD Set 5 with ABC
Table XI: Comparison RPD Set B, C and H with ABC
Statistical Analysis
To perform the statistical analysis in this study, we use the following tests:
-
Kolmogorov-Smirnov-Lilliefors 32 is used to determine the independence of samples.
-
Wilcoxons Signed Rank 33 is used to verify superiority of the strategy of resolution using Meta-optimization in relation to the IWD algorithm
For both tests, we use a significance level of 0.05, that is, values smaller than 0.05 indicate that the corresponding hypothesis cannot be assumed. For the first test, the following hypothesis is used:
H0 = The data follow a normal distribution.
H1 = The data do not follow a normal distribution.
Given the P-values obtained in the tests, the hypothesis is rejected.
The Wilcoxon-Mann-Whitney [33] test is then applied. To verify the superiority of the resolution strategy using Meta-Optimization in relation to the IWD Algorithm, fitness is used, and the following hypotheses are defined:
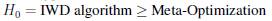
H1 = IWD algorithm < Meta-Optimization
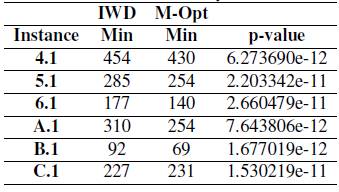
It is obtained p-value < 0.05; therefore, the hypothesis H0 is rejected, and H1 is accepted, which implies that Meta-optimization provides better results. This procedure extends to each instance of the benchmark (Table XII). The results of this analysis are coincident with those verified by RPD.
Table XII: Statistical Analysis Results.
Conclusions
In our work we use a metaheuristics with a meta-optimization approach to solve the SCP. The results revealed, once again, the importance of the parametrization of the algorithms. The results were very good in comparison with the other proposals used. Clearly the use of the automation in the parameters, allows to significantly improve the results in relation to the manual parameterization. In theis work, was possible to observe that the time of instances of the groups 4 and 5, considering the time used in the process of configuration, was greater than 50 percent. As future work, we propose the use of other metaheuristics with different parameters with the order to improve the results and also to facilitate the use by simplifying the parametrization of the metaheuristic of top level. In addition you can use this approach to other problems of the real world as is the problem of routing of school buses with time windows [34].
Acknowledgements
Acknowledgment
Broderick Crawford is supported by grant CONICYT / FONDECYT / REGULAR 1171243 and Ricardo Soto is supported by Grant CONICYT / FONDECYT / REGULAR / 1160455, Gino Astorga is supported by Postgraduate Grant, Pontificia Universidad Católica de Valparaíso, 2015 and José Garcia is supported by INF-PUCV 2016. This research was partially funded by CORFO Program Ingeniería 2030 PUCV - Consortium of Chilean Engineering Faculties.
Referencias
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.
2.jpg)
