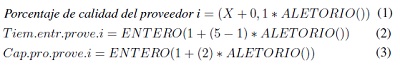
DOI:
https://doi.org/10.14483/23448393.13316Publicado:
2018-10-05Número:
Vol. 23 Núm. 3 (2018): Septiembre - DiciembreSección:
Ingeniería IndustrialProcedimiento de Evaluación y Selección de Proveedores basado en el Proceso de Análisis Jerárquico y en un Modelo de Programación Lineal Entera Mixta
Evaluation and Selection of Providers Procedure Based on the Hierarchical Analysis Process and a Mixed Integer/Linear Programming
Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 21 de mayo de 2018; Revisión recibida: 7 de agosto de 2018; Aceptado: 5 de octubre de 2018
Resumen
Contexto:
Las organizaciones en la actualidad deben seleccionar proveedores de forma eficaz para dar una respuesta oportuna a las necesidades de sus clientes y, de esta manera, garantizar su competitividad. El objetivo de este estudio fue establecer un procedimiento para la selección de proveedores vinculando el Proceso de Análisis Jerárquico (AHP, por sus siglas en inglés) y un modelo de Programación Lineal Entera Mixta (MILP, por sus siglas en inglés).
Método:
Se efectúo una revisión de literatura en las bases de datos Science Direct, Engineering Information, ProQuest y Scopus, la cual permitió identificar las técnicas más utilizadas por los académicos, empresarios e investigadores para la selección de proveedores. Se seleccionaron los modelos matemáticos para el AHP y el MILP. El AHP se realizó por medio de simulación con el método de Montecarlo y el MILP se validó a través de análisis de sensibilidad. En el MILP se usaron los parámetros proporcionados por Ruiz, Mendoza y Ablanedo, el cual se modificó para diferentes cantidades de lotes.
Resultados:
Los parámetros que alimentan el modelo MILP se cambiaron por los simulados al realizar el AHP, los cambios realizados a los parámetros demostraron que el modelo matemático es válido. Se logró proponer un procedimiento para la selección de proveedores que mejore la eficacia en la toma de decisiones.
Conclusiones:
La selección de proveedores es un aspecto esencial para garantizar la calidad de los productos y servicios proporcionados por las organizaciones, por lo tanto, el procedimiento propuesto proporciona criterios para la toma decisión de los proveedores considerando unidades, capacidades, costos y número de lote.
Palabras clave:
Gestión de proveedores, gestión logística y operaciones, optimización multicriterio, programación lineal entera mixta, proveedores..Abstract
Context:
Organizations today must select suppliers effectively to provide a timely response to the needs of their customers and thus ensure their competitiveness. The objective of this study was to establish a systematic procedure for the selection of suppliers linking the hierarchical analysis process (AHP) and a mixed integer/linear programming (MILP).
Method:
A literature review was carried out in the Science Direct, Engineering Information, ProQuest and Scopus databases, which allowed identifying the most used techniques by academics, businessperson and researchers, for the selection of suppliers. The mathematical models for the AHP and the MILP were selected. The AHP was performed by means of simulation with the Montecarlo method and the MILP was validated through sensitivity analysis. In the MILP the parameters provided by Ruiz, Mendoza and Ablanedo were used, from which it was modified for different lots quantities.
Results:
The parameters that feed the MILP model were changed by the simulations when performing the AHP, the changes made to the parameters showed that the mathematical model is valid. It was possible to propose a procedure for the selection of suppliers that improves the effectiveness in decision making.
Conclusions:
The selection of suppliers is an essential aspect to guarantee the quality of the products and services provided by the organizations, therefore, the proposed procedure provides criteria for the decision of the suppliers considering units, capacities, costs and lot number.
Keywords:
Mixed integer/linear programming, multicriteria optimization, operations and logistics management, suppliers, supply chain management..Introducción
En la actualidad las organizaciones se enfrentan a altos niveles de competitividad, por consiguiente, deben estar preparadas para enfrentarla, para lo cual se requiere satisfacer las necesidades de sus clientes, entre ellas proveer los productos solicitados en las cantidades demandadas, al precio justo y con la calidad específica, con las características deseadas, entre otros; en este sentido, uno de los aspectos que se requiere fortalecer en la gestión de las organizaciones es la selección de los proveedores, quienes tienen un papel prioritario por ser los que proveen de materias primas e insumos.
Las características de los proveedores se ven modificadas de acuerdo con la gestión del cambio que adelante la organización tanto en sus procesos como en sus productos, por ello, es necesario modificar la política de inventarios debido a aspectos relacionados con la cultura organizacional, la capacidad de producción, el costo del producto, el porcentaje de calidad, la velocidad de respuesta, el servicio posventa, el número de unidades que puede suministrar o el tamaño de lote que puede proporcionar. En relación con el tamaño de lote se puede identificar que la cantidad de unidades por lote puede variar, dando oportunidades para que el cliente acceda a promociones, descuentos, rebajas del costo por unidad; por tal razón, se debe evaluar a los proveedores que presentan diferentes tamaños de lotes con el objetivo de acceder a estos descuentos por unidad, se debe identificar qué tamaño de lote se debe solicitar para satisfacer la demanda.
Este artículo presenta un procedimiento para el problema de selección de proveedores, en el cual se relacionan dos técnicas, a saber: Proceso Análisis Jerárquico (AHP, por sus siglas en inglés) y Programación Lineal Entera Mixta (MILP, por sus siglas en inglés). Se afronta este problema con dos técnicas, una de aproximación y un modelo de programación entera mixta, la primera como una herramienta de tamizaje con la técnica de optimización multicriterio [1] y la segunda de optimización [2], con las cuales se busca mejorar la eficiencia en la toma de decisiones al momento de elegir un proveedor.
La investigación surgió de la necesidad de dar respuesta a las organizaciones en el SSP, puesto que en la actualidad estas deben adquirir materias primas, componentes, servicios, insumos, entre otros, en el momento preciso, en las mejores condiciones de calidad, precio, disponibilidad, transporte, en fin, una cantidad diversa de criterios por evaluar. Los bienes deben ser obtenidos fuera de la empresa, con el fin de garantizar el aprovisionamiento de los recursos para poder atender los requerimientos de sus clientes [3]; lo anterior garantiza que si se compra bien se vende bien, es por esto que SSP es un problema que se debe optimizar.
En la revisión de la literatura se encontró que algunos autores describen cómo se puede optimizar esta decisión [4] - [10], también afirman que el SSP es problema multicriterio que incluye factores cualitativos y cuantitativos [1], [5], [11]-[13]; se pueden utilizar dos técnicas multicriterio que ayudan a tomar esta decisión: programación matemática y minería de datos. Otros autores, con el fin de seleccionar los mejores proveedores, realizan comparaciones entre factores tangibles e intangibles, algunos de los cuales pueden producir conflicto [11]. Algunas de las técnicas que se identificaron en la solución del problema SSP son minería de datos, técnicas de optimización, técnicas de decisión multicriterio como: Proceso de Análisis en Red (ANP, por sus siglas en inglés), AHP, Análisis Envolvente de Datos (DEA, por sus siglas en inglés), análisis de conglomerados (CA, por sus siglas en inglés), inteligencia artificial (AI, por sus siglas en inglés), modelos de ponderación lineal, simulación de Montecarlo, la teoría de conjuntos difusos, modelos de costo total de propiedad (TCO,por sus siglas en inglés), números difusos, método Electre, método Moora, Modelo Lineal Aditivo (MLA), Topsis, Vikor, Promethee y Análisis de Elección Discreta (DCA, por sus siglas en inglés).
Además de lo anterior, se reconoce que la aplicación de métodos híbridos como es la programación matemática (PM) y DEA permiten generar información que facilita la toma decisiones frente al problema de selección de proveedores, puesto que se requiere no solo elegir el producto, sino también las unidades de acuerdo con las diferentes cantidades de lotes según cada proveedor; asimismo, se revisaron modelos estadísticos, los cuales se refieren a la incertidumbre de la demanda estocástica, identificando que los modelos estudiados únicamente presentan un solo criterio a través de Redes Bayesianas (BN, por sus siglas en inglés). Por otra parte, se identificaron modelos basados en inteligencia artificial, como Algoritmos Genéticos (AG), Redes Neuronales (NN, por sus siglas en inglés) y sistemas expertos. Dada la complejidad del SSP en el mundo real, la investigación actual tiende a integrar múltiples técnicas de toma de decisiones en el establecimiento de un modelo de decisión en el SSP [14].
Al efectuar la revisión de literatura, se detectaron veintiún artículos relacionados, sin embargo, no se encuentran investigaciones que aborden la selección de proveedores cuando estos ofertan diferentes tamaños de lotes o cuando el comprador exige que le envíen diferentes tamaños de lotes paraacceder a las promociones, descuentos y rebajas de las unidades. En el estudio de Ghaniabadi y Mazinani [15] se identificó que la cantidad de unidades por lote puede variar a diferentes tamaños; por tal razón, se debe evaluar a los proveedores que presentan diversas cantidades de lotes con el objetivo de acceder a estos descuentos por unidad. Es de señalar que, a partir de esta revisión, se detectó AHP y MILP, dos metodologías ampliamente utilizadas para el SSP [2]. El AHP fue introducido por Saaty en 1980, como respuesta a problemas de toma de decisiones en el Departamento de Defensa de los EE.UU.
AHP es un método de selección de alternativas (estrategias, inversiones, proveedores, etc.), que está en función de una serie de criterios, los cuales no se pueden optimizar al mismo tiempo por estar en conflicto, para ello, se debe ponderar tanto los criterios como las alternativas utilizando matrices de comparación pareadas y la escala propuesta por Saaty. El empleo del AHP permite generar el conjunto más apropiado de pesos que representan con precisión la importancia relativa de los criterios y alternativas según la subjetividad del tomador de decisiones, en pro de soluciones más razonables [16].
El MILP es una técnica que se utiliza para optimizar una función sujeta a restricciones, esto con el objetivo de identificar los posibles resultados o combinaciones para la mejor decisión. Investigadores como [11], [17], [18] han utilizado estas técnicas de optimización para solucionar el SSP.
Sin embargo, estas dos metodologías no han sido usadas para elegir proveedores con múltiples tamaños de lotes. Cabe precisar que para una organización es importante saber cuántos lotes diferentes de cada producto requiere y en qué periodo de tiempo debe adquirirlos, es por ello que el objetivo de este artículo es establecer un procedimiento de evaluación y selección de proveedores basado en el proceso de análisis jerárquico y en un modelo de programación lineal entera mixta.
Metodología
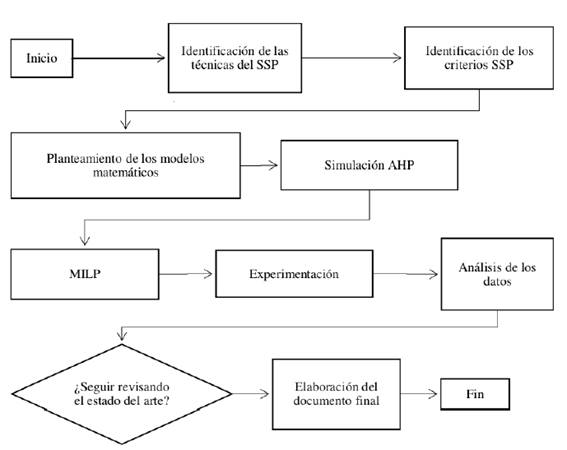
El alcance de este trabajo es proponer un procedimiento para la selección de proveedores, el cual mejore la eficiencia en la toma de decisiones involucrando estas dos técnicas dentro del proceso. La validación se realizó utilizando la estadística descriptiva e inferencial y el análisis de sensibilidad. En la Figura 1 se presenta el paso a paso que se desarrolla, inicia con la identificación de las técnicas del SSP y de los criterios de selección de proveedores, posteriormente se identificaron los modelos matemáticos y a través de la simulación APH y MILP se efectuó la experimentación; finalmente, se define el procedimiento para la evaluación y selección de proveedores.
Figura 1: Diagrama de Flujo de la Metodología de Investigación.
Según la revisión de la literatura, se identificaron los modelos matemáticos para el AHP y, al mismo tiempo, para el MILP. El proceso de análisis jerárquico se realizó por medio de simulación con el método de Montecarlo, el cual alimenta al modelo de programación lineal por medio de parámetros también simulados por esta técnica.
La validación de la simulación del AHP se efectuó por medio de estadística tanto descriptiva como inferencial, además, se realizó por medio de simulación con el método de Montecarlo. En el MILP se usaron los parámetros proporcionados por Ruiz, Mendoza y Ablanedo [17], del cual semodificó para diferentes cantidades de lotes y se validó el modelo matemático mediante el análisis de sensibilidad.
Posteriormente, los datos fueron analizados para dar respuesta a la hipótesis: H0. El procedimiento de evaluación y selección de proveedores es eficiente en la toma de decisiones cuando se incluye AHP y un MILP.
Maximizar Eficiencia
E = Eficiencia
MAX. E= f(procedimiento sistemático)
MAX. E = f(AHP; MILP)
Resultados
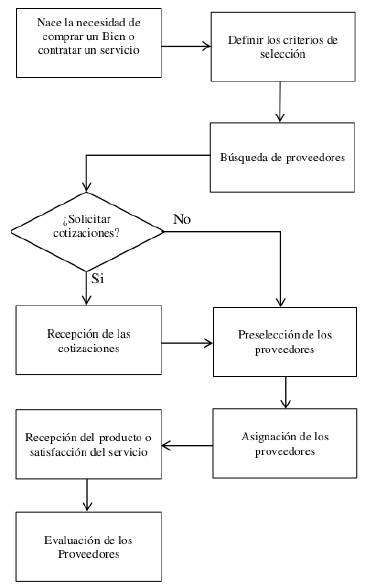
La investigación establece un procedimiento para el SSP usando dos técnicas, una de aproximación y otra de optimización. Este procedimiento se estructura en ocho pasos como se aprecia en la Figura 2. Cabe destacar que el procedimiento propuesto se diferencia de los demás publicados en esta área del conocimiento en que vincula el AHP y un MILP en las etapas de preselección y asignación de los proveedores. Con la aplicación de estos pasos se mejora la eficiencia en la toma de decisiones al momento de elegir un proveedor, dado que se optimizan los siguientes tipos de costos como es el inventario, órdenes pendientes, adquisición por proveedor y de administración por proveedor; además, este procedimiento constituye un aporte en el conocimiento según literatura revisada, puesto que en las investigaciones reportadas el modelo de programación lineal entera mixta, aunque ha sido utilizado para la selección de proveedores, no ha incluido la condición de diferentes cantidades de lotes; en este sentido, el modelo matemático que soporta el procedimiento propuesto toma como referencia el modelo de Ruiz, Mendoza y Ablanedo [17]. Se identifica que el modelo matemático que se trabaja [17] no cierra los flujos de inventarios al finalizar el horizonte de planeación y no considera los costos de producción de las unidades pendientes por satisfacer (backorder); por tal razón, se propone la modificación del modelo matemático, la reproducción del ejemplo numérico expuesto por los autores del artículo en cuestión se presenta con el fin comprobar si funciona para diferentes cantidades de lotes y se complementa dos nuevas restricciones: la eliminación de los inventarios y del backorder al final del horizonte de planeación. Los resultados obtenidos son más aceptables y coherentes al satisfacer la demanda en todo el horizonte de planeación.
Figura 2: Procedimiento para la evaluación y selección de proveedores.
Procedimiento para la evaluación y selección de proveedores
Se presenta un estudio de caso, en el cual se desea seleccionar a los proveedores idóneos para proveer los recursos que necesita la empresa, esto se realiza utilizando el procedimiento que se propone para la evaluación y selección de proveedores; se inicia con la necesidad de solventar unos requerimientos, los cuales son cuatro productos que se deben satisfacer en un horizonte de planeación de seis meses, en unas cantidades determinadas.
En este caso de estudio se aborda el SSP con la aplicación de un método híbrido, llamado así por la unión de dos métodos, que incluye el AHP y MILP, siguiendo las recomendaciones del estudio de Ho, Xu y Dey [2]. Los autores aluden a la complejidad del proceso en el mundo real y señalan que los resultados tienden a integrar múltiples técnicas de toma de decisiones en el establecimiento de un modelo de decisión en el SSP como AHP, MILP, MP, ANP, entre otros. Según estos mismos autores, el híbrido más beneficioso para el proceso de toma de decisiones es AHP y MILP, por ser el AHP la técnica de aproximación que entrega ponderaciones o la importancia de las alternativas y en la técnica de optimización MILP donde el tomador de decisiones debe tener en consideración las capacidades de los proveedores, el presupuesto del comprador y los productos que el proveedor puede proporcionar.
Necesidad de contratar un producto o servicio
La persona encargada de seleccionar los proveedores que la organización necesita para satisfacer las necesidades de sus clientes se enfrenta a dos o más alternativas, cuando se habla de estas alternativas se hace referencia a los proveedores de un producto o un servicio.
Definir los criterios de selección
Es un error seleccionar a un proveedor por solo un criterio, pues en las condiciones de competitividad actuales este único criterio no satisface los requerimientos de los clientes, un ejemplo es el costo; en la actualidad existe variedad de criteritos utilizados para resolver el SSP [19]. Estos criterios generalmente se encuentran en conflicto, por ejemplo, un proveedor que presenta el costo más bajo del mercado, pero la calidad no satisface la exigida por el cliente, o cuando la calidad del proveedor se ajusta a los requerimientos del cliente, pero las entregas de este proveedor pueden ser extemporáneas, lo que genera retrasos en los procesos de la organización. A lo cual se debe buscar un equilibrio adecuado entre estas.
Búsqueda de los proveedores
Se puede realizar con diferentes mecanismos, esta se hace para identificar los posibles proveedores del producto o servicio. Los mecanismos tradicionales para la búsqueda de proveedores son: solicitud de cotizaciones, consulta de base de datos interna y externa, referencias personales, licitaciones, cámaras de comercio, internet, ferias empresariales, exposiciones, asociaciones, etc. En la actualidad, las TIC han potencializado el espectro de posibilidades para acceder a una gran cantidad de posibles proveedores. Según Keskin, İlhan y Özkan [13], la globalización del comercio y la ampliación del internet han cambiado la preferencia de los clientes, con respecto a muchos factores, por consiguiente, se requiere una mayor y más rápida selección de proveedores, es por ello, que estos mecanismos deben adecuarse a las necesidades de las empresas; lo anterior genera un espacio de mucha competencia en un escenario altamente competitivo, en el cual los proveedores juegan un papel vital en organizaciones exitosas [20].
Solicitud y recepción de cotizaciones
Para lograr el aprovisionamiento se debe buscar en el mercado quién pueda proveer estos productos, bienes o servicios con calidad, precio justo, con la mayor confiabilidad de entrega, en fin, con un sin número de criterios.
Después de la búsqueda de las empresas proveedoras se debe identificar cuántos proveedores son nuevos y cuántos llevan una trayectoria en la organización; del primer grupo se requiere solicitar información por medio de visitas del representante de ventas, visitas a las empresas de los proveedores y cotizaciones, esto para conocer los aspectos de calidad, de costo, plazos de validez de las ofertas, plazos de entrega, tamaños de lotes, empaques del producto, posibles devoluciones, etc. Del segundo grupo se comprende que dada la trayectoria del proveedor se cuenta con la información necesaria.
Preselección de los proveedores
Esta actividad obedece a la identificación de los mejores proveedores que cumplan con todos los criterios preestablecidos por parte de la empresa.
Se utiliza AHP como técnica de aproximación o como un proceso de tamizado para el procedimiento SSP. Se definieron un conjunto de criterios para el AHP relacionados con calidad, tiempos de entrega y capacidad de producción. La razón principal al considerar estos criterios es porque un solo criterio no proporciona la mejor decisión de elección para este problema, por consiguiente, se debe tener en cuenta múltiples criterios a la hora de seleccionar los mejores proveedores [21]. Se definió el criterio costo para la etapa de asignación de forma óptima a los proveedores con MILP según el procedimiento propuesto, todos estos criterios son también utilizados por los investigadores en el SSP.
Siguiendo el procedimiento de selección de proveedores expuesto, como un ejemplo del modelo propuesto, se presentan siete oferentes, los cuales cumplen con los criterios de calidad, tiempos de entrega y capacidad de producción. Los elementos de interacción del problema en cuestión es la selección de los mejores tres oferentes, cuyos criterios son calidad, capacidad de producción y tiempos de entrega; las alternativas son los siete oferentes que cumplieron con las exigencias planteadas por la organización.
Según Ruiz, Mendoza y Ablanedo [17], para garantizar la confiabilidad del flujo de aprovisionamiento se debe utilizar una política de proveedores múltiples, con los cuales se minimiza la probabilidad de escasez y los efectos producidos al interior de la empresa cuando un proveedor falle; por tal razón, el AHP se realiza para preseleccionar los tres mejores proveedores de los siete presentados como ejemplo, esto se logra calculando y generando de forma simulada el conjunto de pesos o la importancia relativa de los criterios y las alternativas.
El siguiente paso al aplicar AHP es construir y ordenar las matrices de comparaciones pareadas, estas matrices se obtuvieron por medio de simulación de variables discretas y con ayuda del método de Montecarlo; la razón principal para utilizar este método es porque el elemento tiempo no es factor pertinente [22]. Igualmente Montgomery, Runger y Maisel [23] definen una variable aletoria X discreta uniforme si cada uno de los n valores que están en el rango de esta, X1, X2 , ldots, Xn, tienen la misma probabilidad de ser escogidos f(X) = 1/n, por tal razón, se define que la escala que suguiere Saaty (Tabla I) tiene este tipo de distribución; por consiguiente, a las puntuaciones de esta se les asignan una probabilidad de f(X) = 1/9, donde Yi presenta los posibles valores de la variable, hi presenta la frecuencia relativa y Hi la frecuencia relativa acumulada.
Tabla I: Distribución de probabilidad para la escala de Saaty.
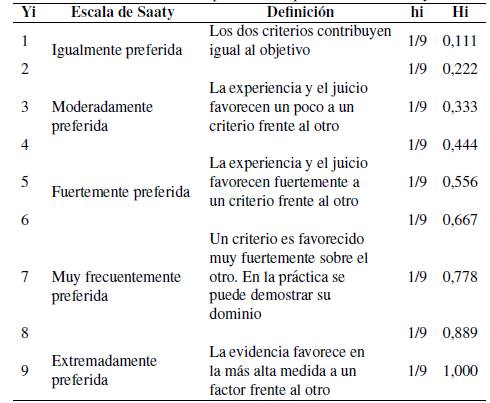
Los valores 2, 4, 6 y 8 se utilizan cuando no se puede definir con claridad la preferencia entre los factores, pero se les puede asignar probabilidad. Estos son valores intermedios de preferencia.
Con ayuda de números pseudoaleatorios se construyeron las matrices de comparaciones por pares (A), esto con el objetivo de estimar el peso o la importancia de los criterios (calidad, capacidad de producción y tiempos de entrega) en función de seleccionar los mejores tres proveedores de los siete tomados como ejemplo.
Se generaron porcentajes de calidad para cada proveedor i por medio de la expresión (1), el cual se definió como porcentaje mínimo el 90% de calidad de cualquier proveedor.
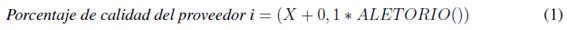
Donde:
X = Representa el porcentaje mínimo de calidad.
También se simularon los tiempos de entrega y se valoraron en unidades de tiempo (semanas). Los datos solo pueden tomar valores enteros de uno a cinco, para la simulación de estas variables se utiliza la expresión (2).
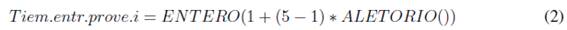
La capacidad de producción se valoró con respecto a la cantidad de lotes que puede suministrar cualquier proveedor g. En la simulación de esta variable se estima que cualquier proveedor puede solo suministrar uno o más tamaños de lotes; se empleó la expresión (3) para simular datos.
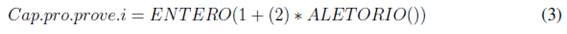
Los parámetros del MILP se simularon para cada uno de los proveedores, entre estos, se simuló si el proveedor g provee el artículo k, el número de unidades por lote del artículo k del proveedor g, capacidad utilizada del artículo k del proveedor g del lote l, costo del lote l del artículo k del proveedor g, capacidad de producción del proveedor g en el tiempo t y costo de administración por tener el proveedor g activo durante un periodo de tiempo.
Un supuesto para el ejemplo propuesto, el cual consiste en disponer de cinco personas encargadas de tomar la decisión de seleccionar los mejores tres oferentes del grupo propuesto de siete, en un caso en particular estas personas pueden ser: el gerente de producción, el gerente de compras, el contador de la compañía, entre otros. Las cuales, al presentárseles las matrices de comparaciones pareadas y realizar el procedimiento de comparación, llegan a un consenso; este conceso da cuenta de la subjetividad mediante el cálculo del cociente de consistencia y definiendo una sola tabla que representan las preferencias del grupo. La subjetividad de la evaluación de las matrices de comparaciones pareadas se podría mejorar por medio de los resultados de la evaluación a los proveedores en periodos anteriores al de la asignación, a través de los criterios (porcentaje de calidad, tiempo de entrega del proveedor y capacidad de producción). En la Tabla IIse presenta un ejemplo de la simulación de las comparaciones entre el proveedor i y el proveedor j en función del criterio calidad, obteniendo los elementos a ij simulados. En esta replica consignada en la tabla se evidencia que el proveedor tres fue mejor calificado o tiene más importancia con respecto a los demás proveedores con un 33.22 %.
Tabla II: Comparaciones pareadas de proveedor versus proveedor en función de la calidad.
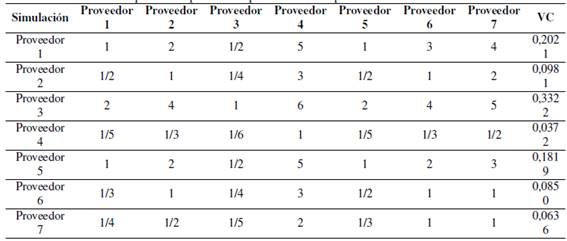
Para un mayor entendimiento del lector se presenta una explicación breve de esta réplica simulada, en la cual el proveedor cinco es fuertemente preferido con respecto al proveedor cuatro, por lo tanto, el elemento a54 = 5 como se instituye en la escala sugerida por Saaty (Tabla I), como también se establece que el proveedor uno está entre moderadamente preferida y fuertemente preferido con respecto al proveedor siete, por tal razón, el elemento a17 = 4, y como último ejemplo se evidencia el proveedor dos y el proveedor seis son igualmente preferidos, por tal motivo el elementos a26 = 1. Los demás elementos de la matriz se establecen con las propiedades que establece Saaty, las cuales son: (a) reciprocidad, la cual establece que si aij * aji = 1 entonces aij =  donde
donde 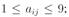 (b) homogeneidad, si las alternativas i = j son aij consideradas igualmente importantes por lo tanto aij = aij = 1, se realizaron veintiún comparaciones por tabla, los demás elementos de la matriz se obtienen aplicando estas propiedades.
(b) homogeneidad, si las alternativas i = j son aij consideradas igualmente importantes por lo tanto aij = aij = 1, se realizaron veintiún comparaciones por tabla, los demás elementos de la matriz se obtienen aplicando estas propiedades.
La simulación de los pesos de los criterios en función del problema se obtuvo generando números aleatorios por cada criterio, al sumar estos pesos y dividir el número de generado aleatoriamente entre la suma se obtiene el peso o la importancia relativa de cada criterio en función del problema (Tabla III).
Tabla III: Peso simulados de los criterios
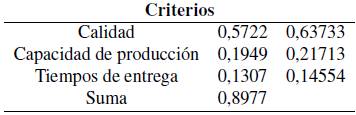
Los siguientes pasos al aplicar el AHP son obtener las matrices normalizadas y medir la consistencia, la cual calcula los juicios que los tomadores de decisiones ha tomado con firmeza o coherencia en el transcurso de la serie de comparaciones pareadas; en la simulación las matrices que se obtuvieran el cociente de consistencia (CR) mayor a 10% se rechazan, la razón principal para realizar esta acción es que los juicios no son coherentes, por el contrario las matrices con CR < 10% se tienen presentes.
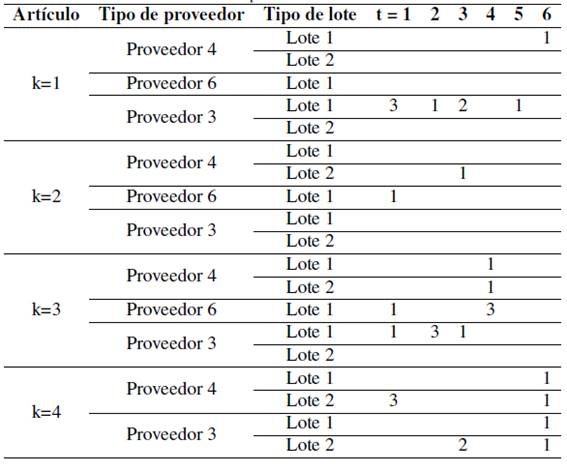
Se realizaron 30 réplicas de estas matrices, con sus correspondientes parámetros por cada proveedor g. El número de veces que cualquier proveedor ocupa alguno de los tres primeros puestos de las 30 réplicas se presenta en la columna de la frecuencia absoluta (ni) como se ve en la Tabla IV, donde se demuestran que se deben de elegir en el AHP los proveedores tres, cuatro y seis. La razón principal para escoger a estos tres proveedores es porque tienen mayores reiteraciones en cualquiera de los tres puestos, el porcentaje de apariciones de cada uno de los proveedores en cualquier puesto son: 18.89% proveedor tres y 17,78% proveedor cuatro y seis, sumando entre ellas se obtiene más de la mitad de las veces. Cabe recordar que el AHP se aplica como una técnica de tamizaje para seleccionar a tres proveedores de siete prestablecidos al comienzo, los cuales se utilizaran en el siguiente paso, este tamizaje es importante para el siguiente método, en el cual se asignarán de forma óptima estos para satisfacer los requerimientos de cuatro productos en un horizonte de planeación constituido por seis períodos.
Tabla IV: Número de veces que el proveedor g ocupó los primeros puestos
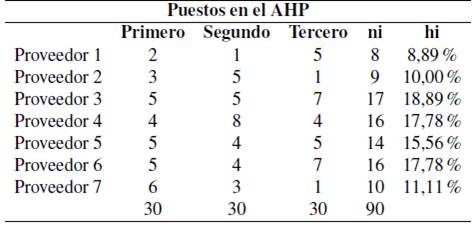
Al realizar las 30 réplicas por medio de la simulación de Montecarlo al AHP, se establece que esta simulación entrega diferentes posibilidades de tamizaje, en la Tabla IVse presenta el número de veces que cualquier proveedor ocupó el primero, el segundo y el tercer puesto. Al analizar la Tabla IVse evidencia que el proveedor siete ocupa seis veces el primer puesto, el segundo puesto el proveedor cuatro con ocho veces y el tercer puesto lo comparten el proveedor tres y el proveedor seis con siete veces.
La validación de este proceso se realizó por medio de la estadística, se realizó este análisis a los pesos ( Wi ) de los proveedores que ocuparon los primeros tres puestos de las 30 réplicas que arrojó el AHP, donde se demuestra que el error estadístico está en el orden del 3 al 2 %.
La media de cada criterio se puede usar como estimador puntual del parámetro poblacional, pero con la construcción de un intervalo alrededor del estadístico de muestra se atrapa el parámetro poblacional [24], es por esto que se calcula el intervalo de confianza para la media poblacional de estos pesos con la ayuda de la expresión (4). Se obtuvo que el parámetro poblacional para el criterio calidad de esta simulación tiene un peso de 26; 2% < µ < 38;26% con un nivel de confianza del 95 %, para el criterio capacidad de producción con la misma confianza se espera se encuentre entre 31;41% < µ < 44;76% y para el tiempo de entrega se espera que la importancia para esta simulación de este criterio se encuentre entre 22;95% < µ < 36; 46%:
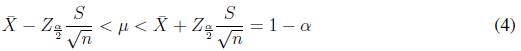
Al simular la preselección de los proveedores se obtuvieron que los mejores tres proveedores eran: el proveedor tres, proveedor cuatro y proveedor seis. Para evitar confusiones o malentendidos, a partir de este momento se denotan estos tres proveedores como el proveedor uno, dos y tres respectivamente.
Asignación de proveedores
La aplicación de MILP como complemento de la primera o como técnica de optimización para el procedimiento de asignación de los proveedores. La aplicación de esta técnica se realiza con el fin de proporcionar un sustento eficiente en la toma de decisiones
En la simulación del AHP se obtuvieron los parámetros del modelo MILP, propuesto por Ruiz, Mendoza y Ablanedo [17]. El modelo de estos autores incluye la selección y asignación de proveedores en lotes fijos; en este sentido, la mejora del modelo se incorporó en el uso de múltiples cantidades de lotes. Los autores definieron unos parámetros que se consideraron en la optimización del ejemplo propuesto, adicionalmente, se incorpora un análisis de sensibilidad y a la vez se alimenta el modelo con los parámetros simulados en el AHP.
Para continuar con este procedimiento a continuación se expresa la denotación, en ella se enuncian los parámetros, las variables y el modelo matemático.
Parámetros
qkgl Número de unidades por lote l del artículo k del proveedor g.
Ukgl Capacidad utilizada del artículo k del proveedor g del lote l.
Ckgl Costo del lote l del artículo k del proveedor g.
pgt Capacidad de producción del proveedor g en el tiempo t.
dkt Demanda del artículo k el tiempo t.
hk Costo de mantener el artículo k.
Vk Costo por unidades pendientes del artículo k.
bkt Unidades sin satisfacer del artículo k en el tiempo t.
ikt Unidades en el inventario del artículo tipo k en el tiempo t.
bk0 Unidades sin satisfacer del artículo k en el tiempo t = 0.
ik0 Unidades en el inventario del artículo tipo k en el tiempo t = 0:
mg Costo de administración por tener al proveedor g activo durante un período de tiempo.
ɸ Un valor muy grande.
Variables
Xkglt Número de lotes a ser requerido del artículo k del proveedor g del tamaño de lote l en el tiempo t
ikt Inventario en el tiempo t del artículo tipo k.
bkt Unidades insatisfechas en el tiempo t del artículo tipo k.
agt Variable binaria que indica si el proveedor g se encuentra activo durante el período t.
Modelo matemático
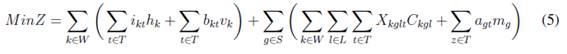
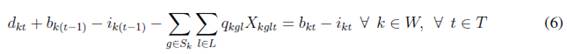
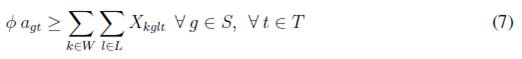
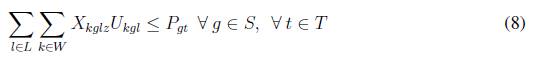


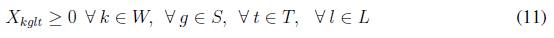
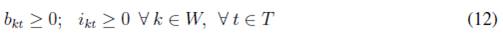


La función objeto (5) tiene como objetivo minimizar los costos de inventario y los costos de las órdenes pendientes por artículo, costos de adquisición y costos de administración por proveedor. Las restricciones en (6) determinan el flujo de unidades para el artículo k en todo los períodos de tiempo t; en estas se tienen presentes todos los tamaños diferentes de lotes recibidos del proveedor g que puede producir el artículo k, en (7) son restricciones que determinan si un proveedor g está activo o no durante el período t, las restricciones en (8) limitan los lotes asignados al proveedor g para todo el producto hasta el período t, las restricción en (9) determinan el inventario al final del horizonte de planeación el cual debe ser igual a cero para cada artículo k, o igual a una constante K que representa un inventario de seguridad. Las restricciones en (10) determinan que no se permiten unidades pendientes al finalizar el horizonte de planeación, lo cual demuestra que se debe satisfacer la demanda en todo el horizonte de planeación, las demás restricciones (11), (12), (13) y (14) representan las restricciones de no negatividad de las variables, variables binarias y variables enteras.
Con esta técnica se espera identificar cuántos lotes se deben comprar del artículo k, del proveedor g, en qué período t y qué tamaño de lote l, con el objetivo de minimizar los costos de inventario, órdenes pendientes, administración de los proveedores y el costo de compra de los productos.
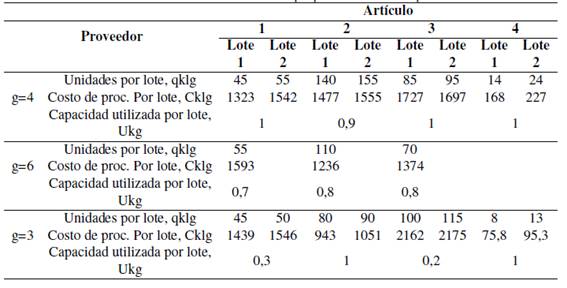
Por tal razón se presenta en la Tabla V, la información por artículo, en la Tabla VI, se presenta la información por proveedor y en la Tabla VII, se expone información de los artículos por proveedor.
Fuente: Ruiz, Mendoza y Ablanedo (2013)
Tabla V: Información por artículo.
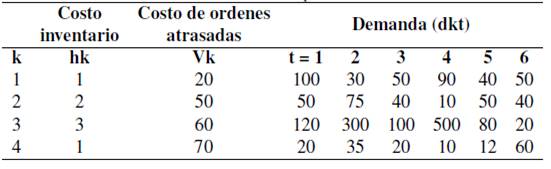
Fuente: Ruiz, Mendoza y Ablanedo (2013).
Tabla VI: Información del proveedor. Fuente: Ruiz, Mendoza y Ablanedo (2013).
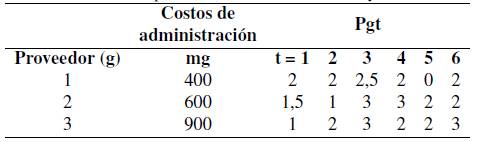
Tabla VII: Información de los artículos por proveedor
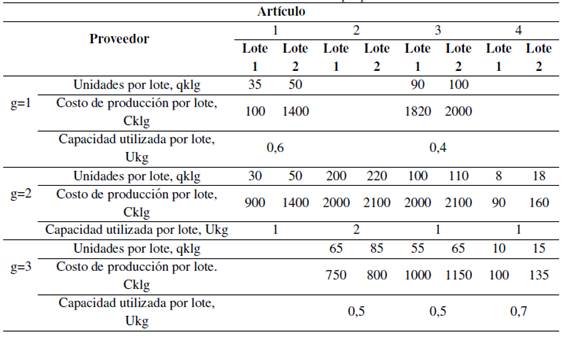
En la Tabla VIII, se presenta el costo por unidad del artículo tipo k, suministrado por el proveedor tipo g del tamaño de lote tipo l, en ella se formula el costo de una unidad de un artículo si se compra a un determinado proveedor, con un tamaño de lote específico, por ejemplo, si se observa la Tabla VIIIse evidencia que el precio más económico para el artículo tres lo proporciona el proveedor tres con el tamaño de lote dos.
Tabla VIII: Costo por unidad del artículo tipo k suministrado por proveedor tipo g del tamaño de lote tipo l.
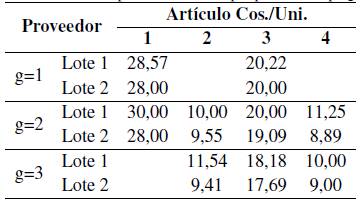
Los supuestos de este modelo son: la demanda de los artículos es determinística, algunos de los proveedores solo pueden suministrar unos productos, cada producto debe ser ofertado por lo menos por dos proveedores, el inventario inicial y final como también las órdenes pendientes para cualquier producto son cero y los proveedores presentan dos tamaños de lote con diferentes cantidades por cada producto.
El modelo matemático tiene que evaluar 208 variables entre enteras y binarias, las enteras compuestas por 144 variables que proporcionan en número de lotes a ser requiero del artículo k del proveedor g del tamaño de lote l en el tiempo t, veinticuatro variables que representan el nivel de inventario del artículo k al final del período t, veinticuatro variables proporcionan las unidades pendientes del articulo k al final del período t. Las binarias compuestas por dieciocho variables que identifican si el proveedor g se encuentra activo durante el período t, y un total de 68 restricciones.
Con los parámetros propuestos por los autores
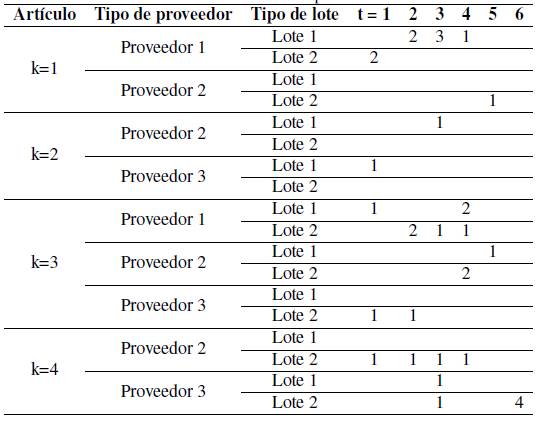
En la Tabla IXse presentan de forma óptima la asignación de los tres proveedores preseleccionados, teniendo en cuenta los parámetros que Ruiz, Mendoza y Ablanedo [17] propusieron, en la cual se establece que el primer artículo lo satisfacen los proveedores uno y dos. El costo total de esta asignación es $47 667, constituido de la siguiente forma: el costo de inventario fue de $902, el costo por órdenes pendientes es $3140, $7300 el costo de administración por proveedores y $36 325 el costo de adquisición de los diferentes productos.
En la Tabla IXse observa también que el proveedor uno, al satisfacer el producto tres, debe de entregar dos diferentes cantidades de lote en el cuarto período, con un costo por unidad de $20,22 y $20 respectivamente; también se observa que el proveedor dos debe entregar dos lotes de 110 unidades por lote para el mismo producto y periodo de tiempo, lo cual corresponde a 220 unidades de este proveedor, con un costo por unidad $19,09, por lo tanto se esperan recibir 500 unidades en el cuarto período, para satisfacer la demanda de este periodo.
Al realizar los análisis correspondientes, se observa que el costo más bajo por unidad del producto tres lo proporciona el proveedor tres (Tabla VIII), el modelo indica que este proveedor no es utilizado para proporcionar este producto en el período cuatro, esto se debe a que las unidades por lote son muy pequeñas (Tabla VII) en comparación con los otros dos proveedores, como también la capacidad de producción del proveedor es muy baja en el horizonte de planeación.
Tabla IX: Solución óptima.
El análisis de sensibilidad consiste en medir el efecto que tiene sobre la solución óptima el hecho de hacer cambios en los valores en los parámetros del modelo [25], por tal razón, se ilustra la sensibilidad del modelo aumentándole una unidad a la capacidad al proveedor tres; en la Tabla Xse evidencia la solución óptima realizando este cambio en los parámetros.
Tabla X: Solución óptima del análisis de sensibilidad.
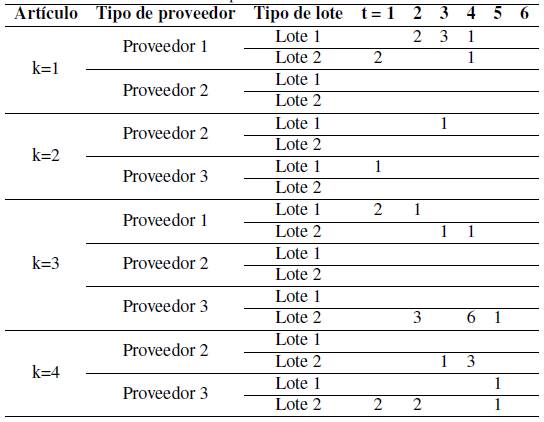
El nuevo costo total es $46 230, el cual se desglosa así: $1505 el costo de inventario, $3000 el costo órdenes pendientes, $6400 el costo de administración de los proveedores activos en algún periodo de tiempo y el costo de compra o de adquisición de $35 325.
Como también se evidencia en la Tabla IXel proveedor tres solo entregaba un lote en el periodo uno y en el periodo dos del artículo tres, con una cantidad por cada lote de 65 unidades; por otro lado, en la Tabla X, este mismo proveedor debe entregar el mismo artículo de la siguiente forma: tres lotes en el periodo dos, seis lotes en el periodo cuatro y un lote en el periodo cinco, con la misma cantidad de unidades por lote, esto se debe al costo más bajo por unidad del producto y al aumento de la capacidad del proveedor.
Al comparar los resultados se evidencia que el costo total disminuye en 3 %, al aumentar en una unidad la capacidad del proveedor tres, contrastando las dos soluciones óptimas se establece: el costo de inventario subió de $902 a $1505, el costo de ordenes pendientes disminuyó de $3140 a $3000, el costo de administración de los proveedores disminuyo de $7300 a $6400 y el costo de adquisición disminuyó $36 325 a $35 325.
De acuerdo con el análisis hecho anteriormente sobre el costo por unidad del producto tres, donde lo provee el proveedor tres con el lote dos, el cual es igual a $17,69 por unidad y es el costo más barato, el cual no se tiene presente en la respuesta anterior; se evidencia en la Tabla 10 que esta situación cambia al aumentarle la capacidad a este proveedor en una unidad en todo el horizonte de planeación, está en la posibilidad de oferta y entregar seis lotes, con un tamaño de lote de 65 unidades en el período cuatro, por consiguiente, está en la capacidad el proveedor de entregar 390 unidades con un costo de producción de $2000 en este periodo.
Con los parámetros simulados AHP
En este apartado se realizará la optimización de la preselección de los proveedores con los parámetros simulados con el AHP, los resultados esperados de esta simulación indican que se debe escoger al proveedor tres, proveedor cuatro y proveedor seis, por fortuna de las 30 réplicas que se realizaron se presentó una con estos tres proveedores ocupando los primeros puestos, se hace referencia a la réplica veintidós, en primer lugar se encuentra el proveedor cuatro, en segundo lugar el proveedor tres y en el tercer lugar el proveedor seis. Se presentan los parámetros de esta réplica (Tabla XI y Tabla XII), los demás parámetros permanecen sin cambio. En esta réplica se evidencia que el proveedor tres y cuatro distribuye los cuatros productos, en cambio el proveedor seis no suministra el producto cuatro, los proveedores tres y cuatro suministran dos tamaños de lotes, pero el proveedor seis solo un tamaño de lote.
Tabla XI: Información por proveedor simulada por AHP.
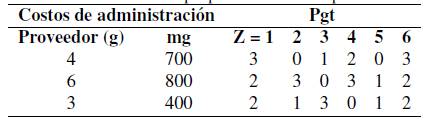
Tabla XII: Información de los artículos por proveedor simulados por AHP.
En la Tabla XIII, se presenta la tabla óptima con los parámetros simulados, con un costo total de esta asignación de $47 219.70.
Tabla XIII: Solución óptima del análisis de sensibilidad
Recepción del producto o satisfacción del servicio
La satisfacción del servicio es una muestra de la confianza que tienen las organizaciones por sus proveedores [26]. En este procedimiento se espera que los proveedores seleccionados y asignados para uno o varios productos en el tiempo previsto cumplan con los requerimientos solicitados por la organización.
Evaluación de proveedores
La calificación de desempeño se realiza proporcionado una evaluación al servicio prestado por cada proveedor, esta calificación puede variar desde 0 hasta 100 puntos.
La calificación final de cada uno de los proveedores se obtiene realizando un promedio de las calificaciones obtenidas por cada criterio en el horizonte de planeación, lo anterior con el objetivo de evaluar a los proveedores para continuar con sus servicios, para futuras contrataciones y suspender o eliminar las relaciones con alguno de ellos.
Conclusiones
El modelo matemático propuesto corresponde a una versión mejorada del modelo de Ruiz, Mendoza y Ablanedo [17], puesto que incorpora dos nuevas restricciones que permiten cerrar los flujos de inventarios y backorder al final del horizonte de planeación en tanto se satisface la demanda y no se dejan unidades pendientes. Además, incluye las diferentes cantidades de lotes al momento de seleccionar los proveedores, aspectos que contribuyen a mejorar la toma de decisiones ya que optimiza costos de inventario, órdenes pendientes, adquisición por proveedor y administración por proveedor. Igualmente es relevante mencionar que un elemento adicional que se tuvo que considerar sobre el modelo propuesto [17] es el cálculo de la oferta del producto tipo k en el periodo t, con el objetivo de determinar si los proveedores cubren la demanda, es decir, sin la incorporación de las restricciones nueve y diez (inventario y backorder final =0) el modelo no es viable para el escenario estudiado.
Además, se identificaron 117 criterios, los cuales se clasificaron en ocho grupos: calidad, producción, costo, financieros, administrativos, logísticos, servicio posventa y otros criterios. Los criterios con mayor utilización en los artículos científicos revisados son: sistema de gestión de la calidad con 33 %, costo 23 %, entrega del producto o servicio 21 %, capacidad del proveedor 18 %, aseguramiento en las políticas ambiéntales 17,5 %, entre otros.
Se propuso y se estableció un procedimiento, descrito en la sección de resultados, para la evaluación y selección de proveedores que mejore la eficacia en la toma de decisiones en la cual intervinieran AHP Y MILP, el primero (AHP) como técnica de aproximación y el segundo (MILP) como técnica de optimización que permita la disminución de los costos, y contempla diferentes cantidades de lotes por cada proveedor.
En el modelo de programación lineal entera mixta inicialmente se aplicaron los parámetros que proporciona el referente teórico [17], y así obtener un punto de comparación al momento de analizar los resultados que se desarrollaron con la modificación del modelo propuesto, además de incorporar los nuevos parámetros que se obtuvieron al aplicar el AHP (simulados), en la que se lograron buenos resultados según el proceso de validación. La validación de la simulación del AHP se realizó por medio de la estadística descriptiva y estadística inferencia. La validación de la técnica de optimización en que se empleó el MILP se realizó por medio de un análisis de sensibilidad.
Se recomienda en futuras investigaciones agregar parámetros al modelo matemático y relacionarlos con otras variables, entre ellas, el nivel de calidad deseado, el tiempo de entrega del producto y la ponderación o calificación de los proveedores para incluir la evaluación de estos cuando son proveedores antiguos. Adicionalmente, estudiar un híbrido entre una aproximación estadística que disminuya la incertidumbre de la demanda y la incorporación de una técnica de optimización matemática, es decir, que los resultados de la disminución de la incertidumbre de la demanda sean una entrada en la técnica de optimización.
Referencias
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.




2.jpg)