DOI:
https://doi.org/10.14483/23448393.13760Published:
2019-01-30Issue:
Vol. 24 No. 1 (2019): January - AprilSection:
Special Number Renewable Energy Sources, Systems and IntegrationOptimized Hierarchical Control for an AC Microgrid Under Attack
Control Jerárquico Optimizado para una Microrred de CA Bajo Ataque
Downloads
References
R. H. Lasseter, “Microgrids,” in IEEE Power Engineering Society winter Meeting, pp. 305–308, 2002 ".
J. M. Guerrero, J. C. Vasquez, J. Matas, L. G. De Vicuña, and M. Castilla, “Hierarchical control of droopcontrolled AC and DC microgrids - A general approach toward standardization,” IEEE Transactions on Industrial Electronics, vol. 58, no. 1, pp. 158–172, 2011 ".
M. C. Chandorkar, D. M. Divan, and R. Adapa, “Control of parallel connected inverters in standalone ac supply systems,” IEEE Transactions on Industry Applications, vol. 29, no. 1, pp. 136–143, 1993 https://doi.org/10.1109/28.195899
F. L. Lewis, Z. Qu, A. Davoudi, and A. Bidram, “Secondary control of microgrids based on distributed cooperative control of multi-agent systems,” IET Generation, Transmission and Distribution, vol. 7, pp. 822–831, 2013 https://doi.org/10.1049/iet-gtd.2012.0576
F. Dörfler, J. W. Simpson-Porco, and F. Bullo, “Breaking the Hierarchy : Distributed Control and Economic Optimality in Microgrids,” vol. 3, no. 3, pp. 241–253, 2016.
S. Abhinav, H. Modares, F. L. Lewis, F. Ferrese, and A. Davoudi, “Synchrony in networked microgrids under attacks,” IEEE Transactions on Smart Grid, vol. 9, no. 6, 2017 https://doi.org/10.1109/TSG.2017.2721382
J. M. Guerrero, M. Chandorkar, T. Lee, and P. C. Loh, “Advanced Control Architectures for Intelligent Microgrids; Part I: Decentralized and Hierarchical Control,” IEEE Transactions on Industrial Electronics, vol. 60, no. 4, pp. 1254–1262, 2013 https://doi.org/10.1109/TIE.2012.2194969
F. Pasqualetti, F. Dorfler, and F. Bullo, “Attack detection and identification in cyber-physical systems,” IEEE Transactions on Automatic Control, vol. 58, pp. 2715–2729, Nov 2013 https://doi.org/10.1109/TAC.2013.2266831
J. M. Guerrero, P. C. Loh, T. L. Lee, and M. Chandorkar, “Advanced control architectures for intelligent microgridsPart II: Power quality, energy storage, and AC/DC microgrids,” IEEE Transactions on Industrial Electronics, vol. 60, no. 4, pp. 1263–1270, 2013
M. S. Mahmoud, M. Saif Ur Rahman, and F. M. A.L.-Sunni, “Review of microgrid architectures – a system of systems perspective,” IET Renewable Power Generation, vol. 9, no. 8, pp. 1064–1078, 2015 https://doi.org/10.1049/iet-rpg.2014.0171
A. Nedić and A. Ozdaglar, “Subgradient methods for saddle-point problems,” Journal of Optimization Theory and Applications, vol. 142, no. 1, pp. 205–228, 2009 https://doi.org/10.1007/s10957-009-9522-7
F. Guo, C.Wen, J. Mao, J. Chen, and Y. Song, “Hierarchical decentralized optimization architecture for economic dispatch: A new approach for large-scale power system,” IEEE Transactions on Industrial Informatics, vol. 14, pp. 523–534, Feb 2018 https://doi.org/10.1109/TII.2017.2749264
F. Guo, C. Wen, J. Mao, J. Chen, and Y.-D. Song, “Hierarchical Decentralized Optimization Architecture for Economic Dispatch: A New Approach for Large-scale Power System,” IEEE Transactions on Industrial Informatics, 2017
E. Baron-Prada, C. A. Uribe, and E. Mojica-Nava, “A Method for Distributed Transactive Control in Power Systems based on the Projected Consensus Algorithm,” IFAC-PapersOnLine, vol. 51, pp. 379–384, jan 2018 https://doi.org/10.1016/j.ifacol.2018.12.065
C. A. Macana and H. R. Pota, “Optimal energy management system for strategic prosumer microgrids: An average bidding algorithm for prosumer aggregators,” in 2017 11th Asian Control Conference (ASCC), pp. 705–710, Dec 2017 https://doi.org/10.1109/ASCC.2017.8287256
C. A. Macana, S. M. Mohiuddin, H. R. Pota, and M. A. Mahmud, “Online energy management strategy for islanded microgrids with feedback linearizing inner controllers,” in IEEE Innovative Smart Grid Technologies (ISGT-Asia), pp. 1–6, Dec 2017
E. Mojica-Nava, S. Rivera, and N. Quijano, “Distributed dispatch control in microgrids with network losses,” in IEEE Conference on Control Applications (CCA), pp. 285–290, Sep. 2016 https://doi.org/10.1109/CCA.2016.7587850
N. Quijano, C. Ocampo-Martinez, J. Barreiro-Gomez, G. Obando, A. Pantoja, and E. Mojica-Nava, “The role of population games and evolutionary dynamics in distributed control systems: The advantages of evolutionary game theory,” IEEE Control Systems Magazine, vol. 37, pp. 70–97, Feb 2017 https://doi.org/10.1109/MCS.2016.2621479
A. J.Wood and B. F.Wollenberg, Power generation, operation, and control. New Jersey: J.Wiley & Sons, 1996
Z. Li, C. Zang, P. Zeng, H. Yu, and S. Li, “Agent-based distributed and economic automatic generation control for droop-controlled AC microgrids,” IET Generation, Transmission and Distribution, vol. 10, no. 14, pp. 3622–3630, 2016 https://doi.org/10.1049/iet-gtd.2016.0418
J. N. Webb, Game theory: decisions, interaction and Evolution. Berlin: Springer, 2007.
J. Hofbauer and K. Sigmund, Evolutionary Games and Population Dynamics. Cambridge University Press, 1998 https://doi.org/10.1017/CBO9781139173179
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 30 de agosto de 2018; Revisión recibida: 9 de noviembre de 2018; Aceptado: 22 de enero de 2019
Resumen
Contexto:
Una microrred de CA (corriente alterna) basada en inversores y que funciona en modo isla puede ser v´ıctima de ciberataques, estos pueden ir contra el controlador o contra el sistema de comunicaciones entre los nodos; el control secundario puede rechazar el ataque, sin embargo, la acción de un controlador terciario es necesaria para estabilizar el flujo de potencia en la microrred.
Método:
La técnica basada en factores de confianza permite repeler ataques a la microrred actuando directamente sobre el controlador secundario, sin embargo, esta técnica omite factores de optimización; en este caso, las sen˜ales de control generadas a partir de los factores de confianza fueron complementa- das en un controlador terciario para incluir criterios de optimizacio´n.
Resultados:
Se simula una microrred en Matlab para diferentes escenarios y ataques, permitiendo verificar la acertada respuesta del controlador ante ataques ciberne´ticos.
Conclusiones:
El control terciario permite estabilizar la potencia del sistema ante el rechazo de un ciberataque por parte del control secundario. Cada inversor entrega potencia de acuerdo con su rango ma´ximo de potencia, sin afectar la establidad de todo el sistema.
Palabras clave:
Ciberataque, control distribuido, control jerárquico, microrred..Abstract
Context:
An inverter-based microgrid working in islanded mode can suffer cyber-attacks, these can be done against either the local controller or the communication links among the inverters. Secondary control is able to reject those attacks, however, a tertiary control action is necessary in order to stabilize the power flow among the microgrid.
Method:
Confidence factor technique allows to reject attacks in a microgrid acting directly over the secondary control, however, this technique omits other factor related to the power available. In this case, secondary control was complemented with a tertiary control that includes optimization criteria.
Results:
An inverter-based microgrid is simulated in Matlab for different scenarios and under cyber- attack, this allows checking the correct response of the controller under attacks and the effective power- sharing among inverters.
Conclusions:
The tertiary control allows stabilizing the active power of the system after the rejection of a cyber-attack by the secondary control. Each inverter supplies active power according to its maximum power rating without affecting the stability of the whole system.
Keywords:
Microgrid, cyber-attack, distributed control, hierarchical control, Language: English..Introduction
A microgrid consists of a set of distributed generators and energy storage devices connected to a common DC or AC bus, where loads can be connected with the distributed generators or directly to the common bus [1]. Additionally, a microgrid can work either connected to a distribution network or in an islanded mode. A microgrid, based on inverters, is controlled by a three-level hierarchical scheme, usually, assuming a decoupling between active and reactive power, and a highly inductive output impedance at each inverter. Thus, a direct relation between active power and frequency can be assumed [2]. Primary control is usually decentralized and based on droop control, this allows to avoid high circulating current and the power-sharing condition (the condition in which each inverter supply power according to its maximum power rating) is guaranteed [3]. Secondary control is in charge to return voltage and frequency to its reference values, this can be done either in a centralized or distributed manner [4]. Finally, tertiary control is generally centralized and allows solving optimization problems and economic dispatch [5].
A microgrid controlled in a distributed way can be prone to cyber-attacks. Those can be done over an inverter controller or actuator, and attacks over a communication link [6]. Attacks can be repelled including a variable gain term in the frequency secondary control which includes reliability factors such as confidence factor related with the information measured at each inverter, and trust factor related with the reliability of the data received from the other inverters. These factors use a distance measure through a Euclidean norm given by the error between the measured frequency and the frequency of reference, compared with an already defined threshold value.
Dynamic gains are included directly over the secondary control of each inverter. However, those factors do not consider the power availability of each one, and there is not an optimization criteria to repeal the cyber-attack without saturating some of the inverters. These optimal references not only guarantee that the cyber-attack is repelled but also, keep the signal inside the limits allowed by the system.
This document is organized as follows: Section 2 presents the equation for primary and secondary control and the equations for attack rejection. Section 3 presents the basics of tertiary control, the economic dispatch problem and the design of the controller based on the population games approach. Simulation results are presented in Section , and finally, conclusions are shown in Section 5.
Hierarchical Control and Cyber-Attacks Over an AC Microgrid
This section shows the design of primary and secondary controllers for an AC microgrid. Assuming a linear relationship between frequency and active power secondary control is designed following a distributed scheme in which two consensus equations are used: one for achieving power sharing, and the other for synchronization purposes. Next, the equation for cyber-attack rejection [6] is considered.
Distributed frequency control
An inverter based AC microgrid is controlled following a hierarchical frame. In the first level, the primary control avoids the appearing of high circulating currents when inverters are connected in parallel. Primary control drops the frequency according to the active power demanded by loads [3], this linear relation is represented by (1)

where fref is the frequency of reference in Hz, mi is the droop coefficient, Pi is the medium power at inverter i, and Pi * is the active power reference for inverter i.
The power reference value Pi * can be modified based on the requirements of each inverter or some programmed event. However, reference values cannot be achieved only by primary control, because in an isolated microgrid not always the power generated equals the power demanded [7]. In fact, those values are better generated by a tertiary control capable of optimize them according to power availability criteria.
Primary control also assures that each inverter supplies power according to its maximum active power value, a condition known as power-sharing presented in (2)
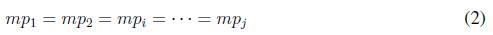
Then, the equation that represents the frequency for inverter i in an a.c microgrid with primary droop control, and secondary frequency control [4] is given by

where δ fi is the secondary control term.
The secondary control shifts the droop control function returning the frequency to its reference value. Secondary frequency control can include a leader node (not necessarily unique) that knows the reference value. So, consensus problem changes into a synchronization problem. Secondary control is given by (4)
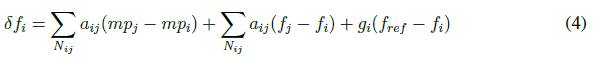
where Nij is the set of neighbors of agent i, aij represents the ij-th elements of the adjacency matrix, fi y fj are the frequencies measured in the inverters i and j, respectively. gi represent the elements of the pinning vector, and fref represents the frequency reference value.
Cyber-attacks over an AC microgrid
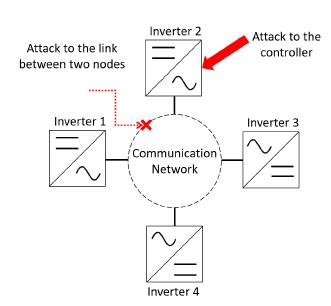
A distributed control gathers data from neighbors through a local communication system, becau- se of this is more susceptible to cyber-attacks. According to Figure 1 attacks can be classified as attacks to local controllers, and attacks to the communications links between nodes [8].
Figure 1: Types of attacks in a microgrid
If the attack occurs over the controller of the i-th inverter, the frequency at inverter i is given by (5)

where fi c is the corrupted frequency at inverter i after the attack, ηi indicates if there is an attack or not, and f i a is a perturbation injected by the controller.
Similarly, if the attack occurs in the link between two nodes this is model as it is shown in (6)

where fi j is the frequency measured between inverters i and j, and ηi indicates the presence of the attack [8].
The error in inverter i is given by (7)
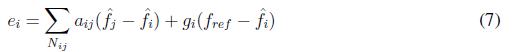
where the values fˆ i and fˆ j correspond to the observed values in the nodes i and j, respectively.
So, it is defined as the norm of the error (7) as

and the sum of the norms of the errors as
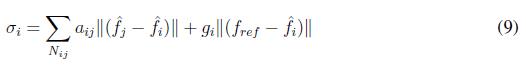
Then, the following factor is defined

where ∆ i represents a threshold value that considers the effect of other factors rather than attacks. Having into account this factor, the confidence factor is defined as

The confidence factor only can take values between zero and one (0 ? Ci ? 1). The control of frequency is modified as it is shown in (12)
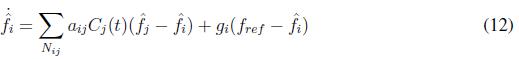
The trust factor is another coefficient that determines the reliability of the measures that a node received from its neighbors. The measurements that exceed the threshold value are rejected. First, it is calculated the factor defined in (16)
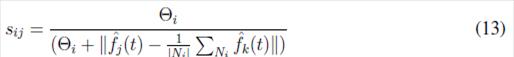
where Θ i corresponds to a threshold value, and ? Ni ? is the number of neighbors of the inverter. The trust factor is defined as


The control of frequency is modified as it is shown in (16)
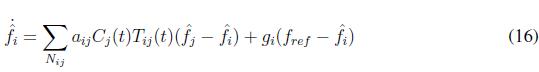
Assuming an AC microgrid with predominantly inductive transmission lines, the instantaneous active power exchange is given by the following expression
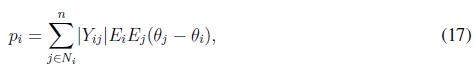
where ? Yij ? is the magnitude of the line admittance between inverter i and j, Vi and Vj are the bus voltages at inverters i and j, respectively.
Taking the first derivative of p along time, and considering the relation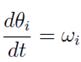 expression (17) becomes
expression (17) becomes
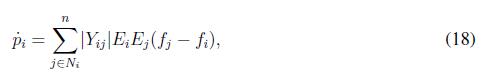
Taking the first derivative of (3) along time expression is written as
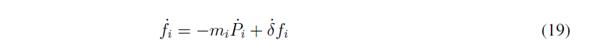
Then replacing (18), and (16) in (19) the following expression is obtained
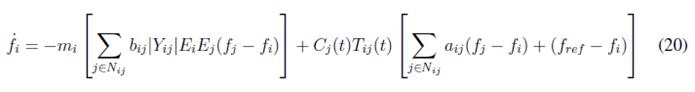
Expression (20) is written in matrix form as follows
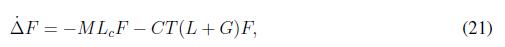
where M is a diagonal matrix with the droop coefficients, Lc is a Laplacian matrix for the physical connection among inverters whose values are given by ωij = EiEj ? Yij ?, F is the vector that contains the frequency measured at each inverter, C and T are diagonal matrices whose values are the coefficient and trust parameters, respectively. L is the Laplacian matrix who represents the connections among agents. G is the diagonal matrix that determines if an agent is a leader or not.
Expression (21), can be written as ∆˙F = ( M Lc +CT (L+G))F , the solution of this differential equation is of the form F(t) = Ae − t ( MLc +CT (L+tt)). This expression is asymptotically stable if term M Lc + CT (L + G) remains positive. Notice that, Laplacian matrices are positive defined, as matrices M ,C, T , and G are diagonal matrices whose values are real and positive, the product of those matrices is positive defined too, then the expression holds.
Tertiary Control for Active Power Control
In this section, the design of the tertiary control is presented. The economic dispatch problem is introduced, and then a population game approach is studied. Tertiary control gathers information of power consumption from the whole microgrid, and based on this data, generates the signal for each inverter according to optimization criteria.
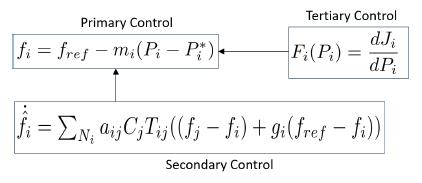
Tertiary control sends the set-point values for primary control at each inverter. As it is shown in Figure 2 primary control uses the frequency droop control with power reference Pi*, this value is sent by tertiary control after an optimization process represented by functional Fi ( Pi ). Additionally, secondary control sends the frequency reference value to the droop control and receive the information of frequency and active power value from each inverter.
Figure 2: Hierarchical control layers
Next, an economic dispatch control strategy is presented. This control algorithm sets the optimal power values for each generator based on economic criteria. Then some basics concepts of the proposed population games approach are shown.
Economic Dispatch Problem
Tertiary control is considered the last layer in hierarchical control, and it is related with the optimization of the dispatch of the resources available in the power system, which is also called economic dispatch [9], [10]. Economic dispatch is a highly studied problem, some approaches use convex optimization methods, principally derived from the work of Nedicét al. in [11], based on this work several approaches have been made [12] - [14]. Moreover, other approaches using game theoretical approaches have been made [15]-[18] proving the effectiveness of game theory to handle economic dispatch problems. Tertiary control can be either centralized or distributed, distributed controllers are used in large-scale systems where centralized controllers often suffer from computation and communication overheads. However, instead of several advantages of distributed controllers, centralized controllers are highly used due to their robustness and easily configured and maintained under operation.
Economical dispatch denotes the problem of determining the optimum output power of a set of generators in a power system in order to satisfy loads and fulfill power system requirements. Economic dispatch problem consists of minimizing the total generation cost [18), [19]. Here, the cost of the power supplied by each generator is minimized using an utility function based on a quadratic function [12], [13], [20] such as

where F ( pi ) is the utility function of generator i, pi is the power generated by generator i. Moreover, αi, βi, ζ ? R≥0 are utility coefficients. Using the utility function of all agents in the power system we can formulate the economic dispatch problem as follows
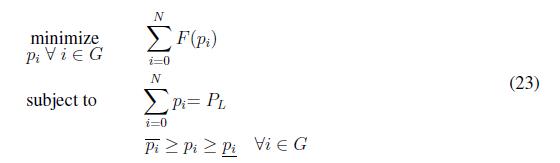
where PL is the power demanded by the load in the system, N is the number of generators in the power system, pi and pi are the maximum and minimum power capacity respectively. Economic dispatch problem in (23) is solved when constraints (23) and (23) are fulfilled, moreover the economic dispatch criterion states that all agents should operate with the same marginal utilities as follows
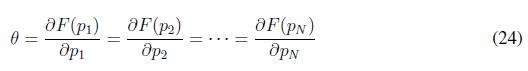
where θ ? R > 0. In order to solve (23) a game theoretical method based on population games is used, specifically, replicator dynamics solve iteratively the economic dispatch problem using criterion (24). The before statement can be summarized in the following lemma
Lemma 1 A solution of problem (23), P* belonging to the feasible set ∆, is an optimal solution if and only if ? iSW (Pi*) = ? jSW (Pj *) for all i, j.
Population Games Approach
One of the main contributions of this work is to optimize, through a tertiary control, the respon- se of a microgrid against an attack. In order to reach this contribution, a centralized population dynamics control based on game theory is proposed. Population dynamics represent how a pure population strategy progress over time. In population games, replicator dynamics have been used in several engineering applications such as economic power dispatch, lighting systems, and urban drainage systems [18]. These applications have been made considering some implementation be- nefits, such as robustness to dynamic environmental uncertainties.
The replicator dynamics solves the economic dispatch problem as a resource allocation problem. Replicator dynamics considers G = {1, 2, 3 . . . N} finite number of generators, who adopt a i-th strategy from a finite set of pure strategies. Accordingly, to achieve an appropriate performance in the steady state, the power demanded by the load should be the sum of all power set points. The payoff function ( Fi ) is associated with the chosen strategy, therefore, a continuous time implemen- tation is also used. In its general form, the replicator dynamics can be represented as

where β is a parameter that permits modify the convergence speed [21]. The average payoff in the population F¯(p) is given by

The results in [22] are used to guarantee the power balance, the choice of (26) guarantees the invariance of the constraint set ∆ defined as
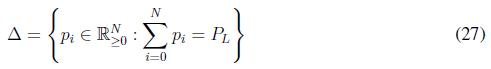
This result ensures that if pi (0) ? ∆, ?θυοτ;i ? G, all pi (t) ? ∆ with t ³ 0. In other words, the power demanded by the loads in the system always is dispatched i.e, the replicator dynamic algorithm guarantees a perfect balance between the power demanded and the power generated. One of the characteristics of the replicator dynamics algorithm is that in the stationary state the fitness function of all agents is equal to the average fitness (F¯). This condition allows solving the problem of economic dispatch through the replicator dynamics since the fitness function is derived from the utility function. In order to include the constraints in (23), we use Lagrange Multipliers as
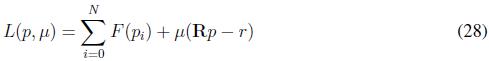
where µ is the Lagrange Multipliers, the fitness functions are defined as
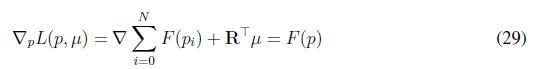
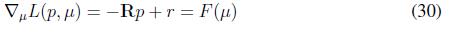
Finally, the fitness functions for this replicator dynamics are
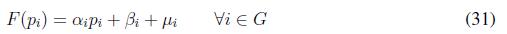
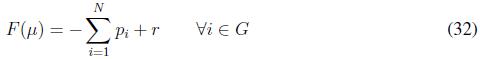
Notice that ? stands for the Jacobian of a function. Now, we state the following theorem in order to characterize the optimality of the proposed algorithm
Theorem 1 Assume a convergence constant β ? R . Furthermore, let Pi (k), with i ? Ν , being the set points generated by executing (25), with fitness functions defined as in (31) and (32) . Then, Pi (k) with i converges to the optimal solution Pi∗ that belongs to the feasible set of power, that is
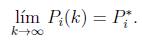
Proof.
Since we have defined fitness functions as (31) and (32), by definition a potential function for the population game (25) is h(P, µ) = L = SW (P) µ T(R P - r) and considering the form of the economic dispatch in (23), it can be shown that the game satisfies the external symmetry (24). When the optimality condition in Lemma 1 is reached then Fi ( pi ) = Fj ( pj ) for all i, j and it is noticed that in the replicator dynamics (25) we have
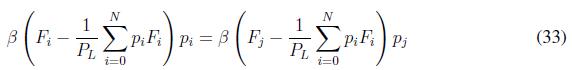
To reach optimality, both sides of the equation must be equal. At the optimal point, this only can be equal to zero. It is possible to see through Lemma 1, that

Then, it is possible to see that

Then, (33) is


which implies that (25) reaches an optimal point.
Simulation Results
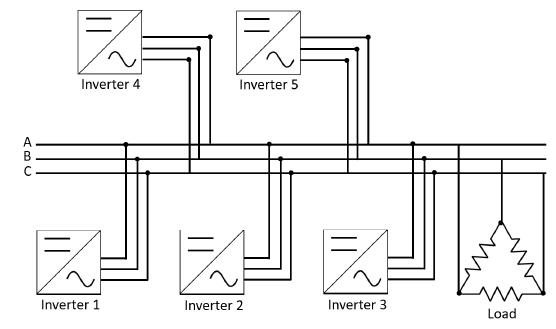
A five inverter-based microgrid is simulated using Simulink?, inverters are considered as con- trolled three-phase voltage sources. Each inverter is connected to a common bus in parallel as it is shown in Figure 3. Three different scenarios are simulated: the first one shows the performance of tertiary control without any attack; the second one shows the performance of controllers when the controller of inverter one is attacked, and finally, the third one shows the performance of the system when false data is added to the measured frequency at inverter one.
Figure 3: Microgrid Schematic
Microgrid parameters are presented in Table I. Each inverter has a different nominal active power value, and a different low-pass filter constant. Transmission lines among inverters are considered similar to visualized clearly the changes introduced by tertiary and secondary control.
Table I: Microgrid Parameters
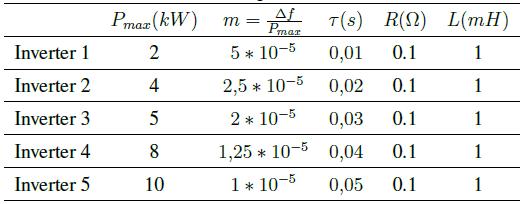
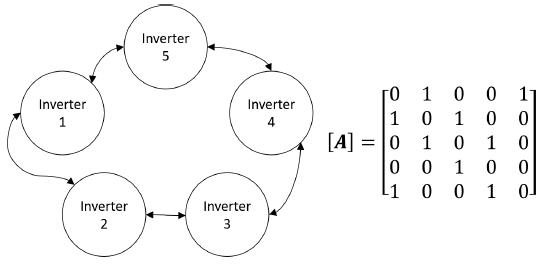
The five inverter microgrid has a communication system defined by an undirected graph with its related adjacency matrix as it is shown in Figure 4.
Figure 4: Graph representation and adjacency matrix of the communication links between nodes
The nominal power for each inverter is set at the tertiary control: Pnom 1 = 1000W, Pnom 2 = 2000W, Pnom 3 = 4000W, Pnom 4 = 6000W, Pnom 5 = 7000W.
First case A load Pload = 20000W is connected at t = 1s and a similar load is connected at t = 4s.
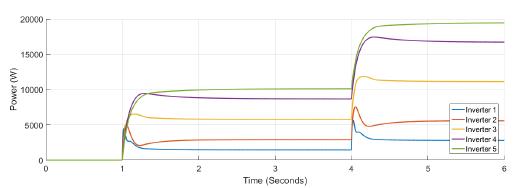
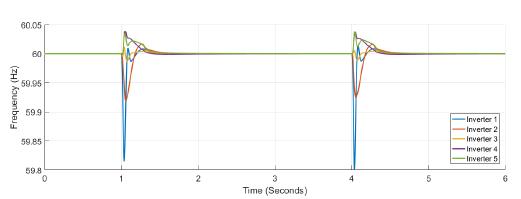
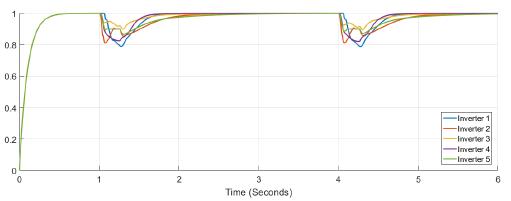
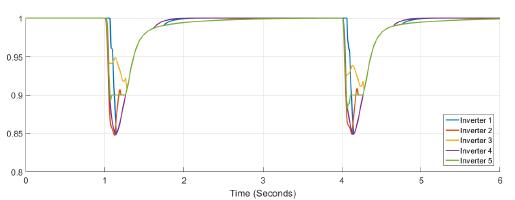
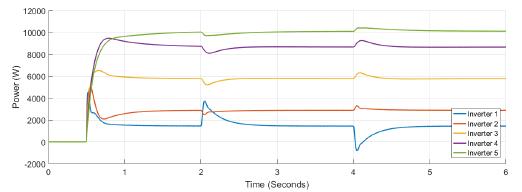
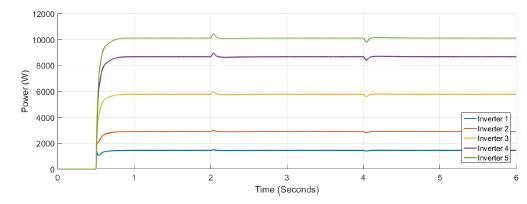
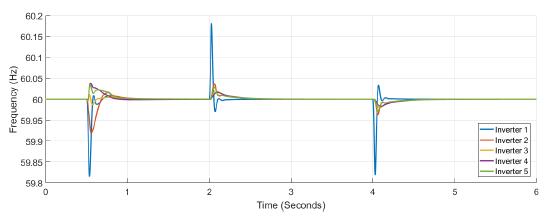
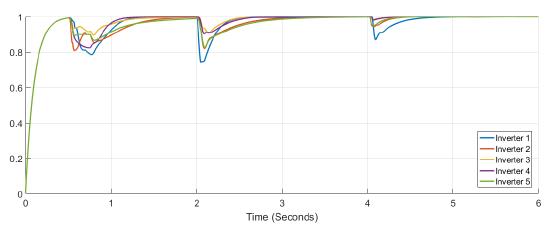
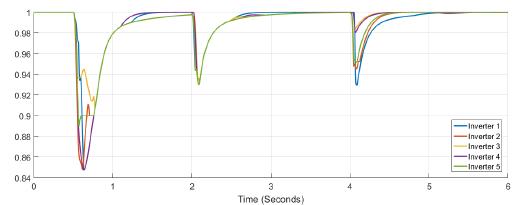
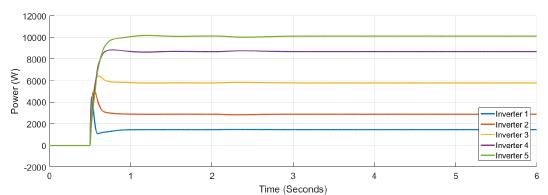
Figure 5 shows the power at each inverter when loads are connected at t = 1s and t = 4s. The action of tertiary control is implicit in the behavior of power-sharing at each inverter, so its power capacity is taken into account. Tertiary control action is depicted in Figure 6 while Figure 7 shows the behavior of frequency at each inverter, notice that the changes at t = 1s and t = 4s when loads are connected are similar, and frequency reference value is achieved in steady state. Figure 8 and Figure 9 show the behavior of confidence and trust values when the microgrid is not under attack. Trust and confidence values drop to less than 0.2 when their threshold values are set at 0.9.
Figure 5: Active power for each inverter
Figure 6: Output from tertiary controller
Figure 7: Frequency measured at each inverter
Figure 8: Confidence factor Figure 8. Confidence factor
Figure 9: Trust factor
Second case A load Pload = 20000W is connected at t = 0,5s and a false data signal is introduced controller of inverter 1 between t =2s and t =4s.
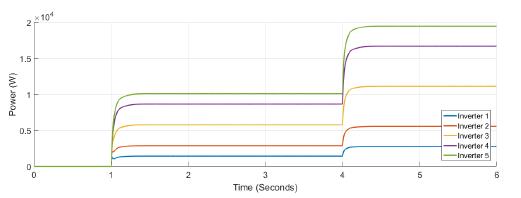
Figure 10 and Figure 11 show the active power supplied by each inverter, and the tertiary control response, respectively. Inverter 1 is able to supply or to absorb active power. At Figure 12 frequency variations appears at t = 0,5s when the load is connected, and at t = 2s and t = 4s when false data is introduced at the controller of inverter one. Finally, in Figure 13 and Figure 14 a variation of less than 0.2 for confidence and 0.1 for trust is shown. Notice that only for the trust coefficient the threshold value of 0.9 is achieved.
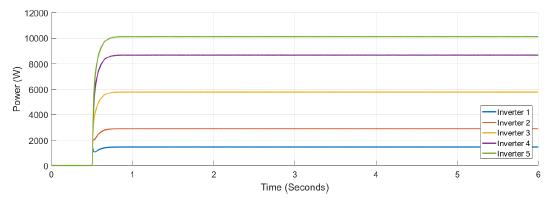
Figure 10: Active power for each inverter under attack in case 2
Figure 11: Output from tertiary controller when is under attacks in case 2
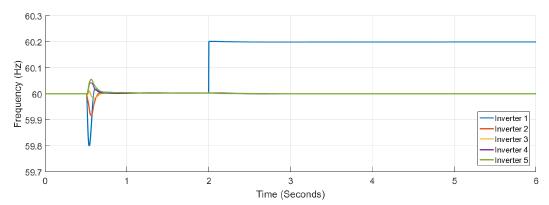
Figure 12: Frequency measured at each inverter when under attack
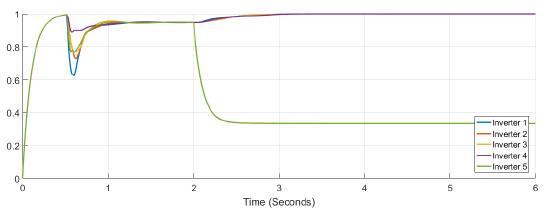
Figure 13: Confidence factor when inverter 1 is under attack
Figure 14: Trust factor when inverter 2 is under attack
Third case A load Pload = 20000W is connected at t = 0,5s and a false data signal is introduced at the communication channel of inverter at t =2s.
Figure 15 and Figure 16 present the power variation at each inverter after the attack, there is a little variation in the power at each inverter, and no much variation at the tertiary controller respon- se. In Figure 17 the frequency response is shown, notice the attack over the frequency measurement at inverter one; a constant signal of 0.2 Hz is added at t = 2s. Figure 18 shows the frequency at inverter one, the variation of frequency after a load variation is larger than the variation after the attack. Figure 19 shows the confidence factor variation after cyber-attack, this factor drops below 0.4 for inverter five, while Figure 20 shows the variation for trust factor, trust factor drops below 0.75 for inverter five while other inverters do not drop below the threshold value of 0.9.
Figure 15: Active power for each inverter under attack in case 3
Figure 16: Output from the tertiary controller when is under attacks in case 3
Figure 17: Frequency measured at each inverter when under attack
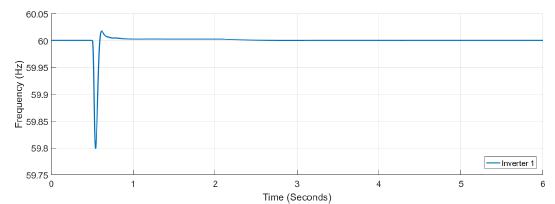
Figure 18: Frequency measured at inverter 1 under attack
Figure 19: Confidence factor when inverter 1 is under attack
Figure 20: Trust factor when inverter 3 is under attack
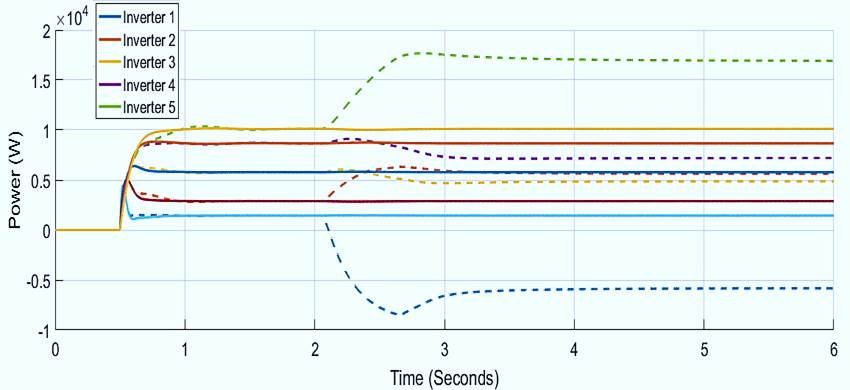
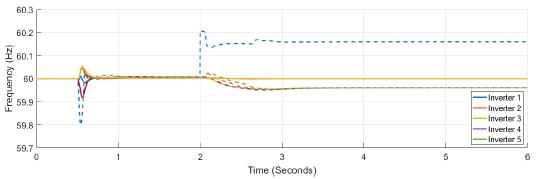
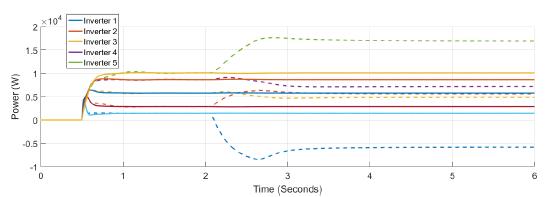
Finally, the comparison between the active power and frequency responses with and without confidence and trust factors are presented in Figure 21, and Figure 22. The frequency without those factors deviates from the reference value, not only in the inverter that suffers the attack but in all the other inverters. The active power varies abruptly when the system is under attack. Notice that the inverter that is attacked change from supply to absorb power. In contrast, active power has not changed when confidence and trust factors are used.
Figure 21: Frequency response of the system with (complete line) and without (dash line) trust and confidence factors
Figure 22: Active power response of the system for all the inverters with (complete line) and without (dash lines) trust and confidence factors
Conclusions
The distributed tertiary control is able to stabilize the active power flow in the microgrid after the cyber-attack. The power references for the primary control are modified to overcome the perturbation created by the cyber-attack without changing the frequency at steady state. Attacks on local controller and communication channels are simulated and the effectiveness of attack rejection is proved. The tertiary control shows its effectiveness to avoid inverters saturation and to keep the necessary conditions for optimal economical dispatch; such as maximum active power ratings, and maximum frequency deviation.
References
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










