DOI:
https://doi.org/10.14483/23448393.2288Publicado:
1998-11-30Número:
No 1 (1999)Sección:
Ciencia, investigación, academia y desarrolloDiseño de Antenas Cassegrain con Sublefectores Conformados
Descargas
Referencias
[ 1 ] Pokras, A. M., Somov, A. M. et al. Antenas de las Estaciones Terrenas de Comunicaciones por Satélites. Capitulo 7. Edit. Radio. Moscú 1985.
[ 2 ] Pino, Antonio G. Contribución al Estudio de las Antenas de Superficies Reflectoras Conformadas. Tesis Doctoral. E.T.S.I.T. Universidad Politécnica de Madrid. 1989.
[ 3 ] Collins, G. W. Shaping of Subreflectors in Cassegrainian Antennas for Maximum Aperture Efficiency. I.E.E.E. Transaction on Antennas and Propagation. Vol. 21. No. 3. May 1973.
[ 4 ] Calvo, M. y Besada, J. L. Diseño Avanzado de Antenas. Editado por E.T.S.I. Telecomunicación. Universidad Politécnica de Madrid. Noviembre. 1993.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Investigación y Ciencia
Ingeniería, 1999-00-00 vol: nro:1 pág:49-51
Diseño de Antenas Cassegrain con Subreflectores Conformados
Rafael Pérez
Alfonso Francisco Lee Tenorio
INTRODUCCIÓN
La conversión de las antenas Cassegrain clásicas en antenas Cassegrain con subreflectores conformados permite de una forma sencilla y poco costosa elevar la eficiencia de estas antenas. El presente trabajo muestra los resultados obtenidos con un Software, que dado el mismo reflector parabólico original y en ciertos casos la misma bocina alimentadora, permite, variando la superficie del subreflector, obtener una configuración Cassegrain más eficiente y por tanto de mayor ganancia. En el mismo se usa el método de la Optica Geométrica para lograr una iluminación uniforme en la abertura del reflector parabólico dado un patrón de radiación específico de la bocina excitadora.
El programa permite el análisis y determinación de los principales parámetros a la frecuencia de operación; determinándose de esta forma el lugar geométrico del nuevo subreflector conformado y los fundamentales parámetros de la antena, tales como: eficiencias esperadas, ganancia, patrón de radiación del sistema cercano al lóbulo principal, ancho del haz entre puntos de mitad de potencia, relación Delante/Detrás, la razón de onda estacionaria en el sistema alimentador, etc.
CONFORMACIÓN DEL SUBREFLECTOR
Como se ha demostrado [1] [2], cuando se conforman ambos reflectores en un sistema Cassegrain, el reflector principal conformado puede ser cercanamente aproximado a una parábola equivalente con una distancia focal ligeramente menor. Debido a que un desenfoque axial en un paraboloide produce solo un error de fase cuadrático, es evidente que la conformación especial del subreflector introduce errores de fase cuadráticos primarios que son corregidos al conformar el reflector principal. De este modo, todas las conformaciones requeridas pueden ser hechas en el subreflector, ajustando el punto focal de este como el punto alrededor del cual la mayoría de la energía dispersa sea lo más cercanamente un frente de ondas esférico. Esta técnica llevaría a determinar el contorno del subreflector requerido para obtener una distribución de amplitud uniforme y luego experimentalmente determinar el punto focal de la superficie resultante.
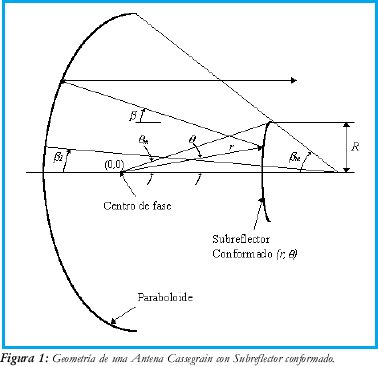
La geometría a considerar se ilustra en la Figura 1. El centro de fase del excitador primario que radia un patrón de potencia F(θ), está ubicado como muestra la figura. Los requerimientos a imponer en esta configuración es que la función patrón disperso I(β) (potencia relativa) sea constante o uniforme dentro del sector angular β1 ≤ β ≤ βm y cero en cualquier otro punto (Optica Geométrica). Esto dará la primera ecuación de dos que se necesitan para obtener la superficie del subreflector (r,θ). La otra ecuación se obtendrá al aplicar al Ley de Snell a la superficie reflectante del subreflector.
La potencia incidente es proporcional a 2π.F(θ)θ.sin.θd. Similarmente la potencia reflejada es proporcional a 2πI(β).sin β.d β. Igualando la potencia dentro de un ángulo β que se reflejará dentro de un ángulo , se tiene que:
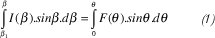
haciendo el limite inferior β1 para considerar los efectos del bloqueo por el alimentador primario. Normalizando respecto a la potencia total e integrando:
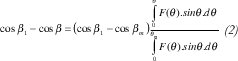
Aplicando la Ley de Snell a la superficie del subreflector, perfectamente conductor, se obtiene una relación entre el ángulo dado y la primera derivada de la superficie.
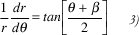
Las ecuaciones (2) y (3) son suficientes para especificar completamente el contorno del subreflector [3], y pueden ser fácilmente programadas para un patrón del alimentador primario dado y una configuración reflectora deseada (β1,βm,θm,2R).
El procedimiento sería; primero, es necesario diseñar una bocina que radie un patrón de potencia F(θ) apropiado. Luego el diseño del subreflector puede ser realizado usando los valores β1, βm,βm , el diámetro del subreflector derivado del diseño general de la antena, (2) y (3). El paso que queda es experimentalmente determinar el punto focal del subreflector midiendo patrones de fase. Al encontrar este punto, se hace coincidir con el foco del reflector principal cuando el sistema alimentador es instalad. Estos pasos completados correctamente deben dar un sistema altamente eficiente con una ganancia cercana a la óptima.
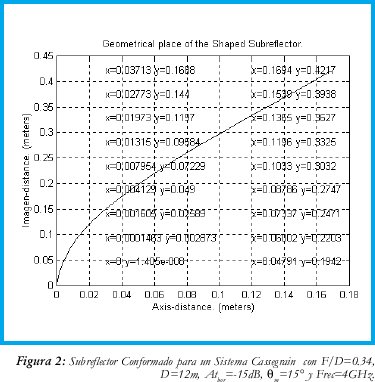
Este procedimiento de diseño está incluido en el Software CSSGRN1. En la Figura 2 se puede observar un subreflector conformado, para una iluminación con bocina cónica lisa que radia un patrón de potencia modelado según Calvo [4], obtenido con este instrumento de diseño.
En estos casos, como el diseño se realiza para un alto ahusamiento, gran cantidad de la energía radiada por la bocina, ahora de mayor directividad, estará en la zona central del subreflector; por le que una conformación adicional se necesitará en esta zona para mejorar la Razón de Onda Estacionaria.
Si se diseña un Sistema Clásico Cassegrain con estos parámetros (Ver Figura 2) se obtiene una Eficiencia de Iluminación (ηi) del orden de 0,74 y una Eficiencia de Desbordamiento (ηi) de 0,97; lo que resultaría en una Ganancia Directiva (Gd) de 50,56dB. En cambio con el subreflector conformado se obtiene una i η1 y una ηi=0,97 resultando en una Gd= 51,84 dB; apreciándose las ventajas de este último.
CONCLUSIONES
Se comprobó como conformando el subreflector, como método más ecónomico, se puede lograr un aumento apreciable de la eficiencia del sistema alimentador en un sistema Cassegrain; lográndose un aumento de ganacia del orden de 1,5 dB, pudiendose utilizar esto en sistemas clásicos ya instalados otorgándosele un valor agregado a los mismos.
REFERENCIAS
[1] Pokras, A. M., Somov, A. M. et al. Antenas de las Estaciones Terrenas de Comunicaciones por Satélites. Capitulo 7. Edit. Radio. Moscú 1985.
[2] Pino, Antonio G. Contribución al Estudio de las Antenas de Superficies Reflectoras Conformadas.Tesis Doctoral. E.T.S.I.T. Universidad Politécnica de Madrid. 1989.
[3] Collins, G. W. Shaping of Subreflectors in Cassegrainian Antennas for Maximum Aperture Efficiency. I.E.E.E. Transaction on Antennas and Propagation. Vol. 21. No. 3. May 1973.
[4] Calvo, M. y Besada, J. L. Diseño Avanzado de Antenas. Editado por E.T.S.I. Telecomunicación. Universidad Politécnica de Madrid. Noviembre. 1993.
Rafael Pérez Alfonso
Msc. Ing. Telecomunicaciones, Universidad Central de Las Villas
Francisco Lee Tenorio
Ing. en Telecomunicaciones, Universidad Central de Las Villas Doctor en Ciencias Técnicas, Universidad Central de Las Villas Vicerrector y Profesor titular Facultad de Ingeniería Eléctrica Universidad Central de Las Villas.
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.





2.jpg)