DOI:
https://doi.org/10.14483/22484728.5504Publicado:
2013-12-09Número:
Vol. 7 Núm. 2 (2013)Sección:
Visión InvestigadoraOptimizacion basada en un modelo de particulas con comportamiento de vorticidad
Optimization based on a model of particles with vorticity behavior
Palabras clave:
optimization, particle swarm, vorticity (en).Palabras clave:
Optimización, enjambres de partículas, vorticidad (es).Descargas
Referencias
P. Kevin, “Biomimicry of bacterian foragin for distributed optimization and control”, ieee Control Systems magazine, 2002.
B. Mauro, P. Paola y D. Marco, “On the invariance of ant colony optimization”, ieee Transactions on evolutionary computation, vol. 11, no. 6, 2007.
D. Marco y G. Luca, Ant algorithms for discrete optimization, Massachusetts Institute of Technology, Artificial Life 5, pp. 137-72, 1999.
D. Marco, B. Mauro y S. Thomas, “Ant colony optimization. Artificial ants as a computational intelligence technique”, IEEE Computational Intelligence Magazine, 2006.
Z. Aaron, S. Angus, M. Holger y N. John, “Parametric study for an ant algorithm applied water distribution system optimization”, ieee Transactions on Evolutionary Computation, vol. 9, no. 2, 2005.
K. Dervis, An idea based on honey bee swarm for numerical optimization, Technical Report-TR06, 2005.
T. Sarita, M. John, J. Chahl, H. Butler y Z. Steve, Bees: exploring Mars with bioinspired technologies, ieee computer Society, 2004.
A. Russell y C. Michael, “Hans J. Bremermann, A pioneer in mathematical biology”, BioSystems, vol. 34, no. 1, pp. 1-10, 1995.
R. Eberhart y J. Kennedy, “Particle swarm optimization”, ieee Proceedings Neural Networks, 1995.
C. Leandro, A quantum particle swarm optimizer with chaotic mutation operator, Elsevier Chaos Solitons and Fractals, 2006.
C. Leandro y C. Viviana, Particle swarm approach based on quantum mechanics and harmonic oscillator potential well for economic load dispatch with valve-point effects, Elsevier Energy Conversion and Management, 2008.
S. Davoud y M. Ellips, “Particle swarm optimization methods, taxonomy and applications”, International Journal of Computer Theory and Engineering, vol. 1, no. 5, 2009.
Y. Xin-She, “A new metaheuristic bat-inspired algorithm”, Nature Inspired Cooperative Strategies for Optimization (NICSO), 2010.
Y. Xin-She, Firefly algorithm, Lévy flights and global optimization, Londres: Springer, Research and Development in Intelligent Systems XXVI, 2009.
M. Antonio y S. Onur, “Monkey search: a novel metaheuristic search for global optimization”, aip Conference Proceedings, Data mining systems analysis and optimization in biomedicine, 2007.
A. Kaveh y S. Talatahari, “A novel heuristic optimization
method: charged system search”, Acta Mechanica, vol. 213, no. 3-4, pp. 267-89, 2010.
Y. Xin-She, “Harmony search as a metaheuristic algorithm”, Springer Berlin, Music-Inspired Harmony Search Algorithm, 2009.
S. Hamed, “Problem solving by intelligent water drops”, ieee Congress on Evolutionary Computation, 2007.
D. J. T. Sumpter, The principles of collective animal behaviour, Philosophical Transactions of the Royal Society B, 2006.
V. Tamás, C. András, B. Eshel, C. Inon y S. Ofer, “Novel type of phase transition in a system of self-driven particles”, Physical Review Letters, vol. 75, no. 6, 1995.
V. Tamás, “Universal patterns of collective motion from minimal models of flocking”, Second ieee International Conference on Self-Adaptive and Self-Organizing Systems, 2008.
C. Iain, K. Jens, F. Nigel y L. Simon, “Effective leadership and decision making in animal groups on themove”, Letters to Nature, vol. 433, no. 3, pp. 513-15, feb. 2005.
B. Iztok y H. Frank, “Organized flight in birds”, Animal Behaviour, 78, 2009.
Z. Hai, C. Michael, S. Guy, Z. Tao y M. Jan, “Collective behavior coordination with predictive mechanisms”, ieee Circuits and Systems Magazine, third quarter, pp. 67-85, 2008.
B. Howard, Random walks in biology, Princeton University Press, 1983.
Ç. Yanus, Mecánica de fluidos, McGraw-Hill, 2003.
L. Herbert, R. Wouter-Jan y C. Inon, “Self-organization in systems of self-propelled particles”, Physical Review E 63, 2000
M. R. D’Orsogna, Y. L. Chuang, A. L. Bertozzi y L. S. Chayes, “Self-propelled particles with soft-core interactions: patterns, stability, and collapsel”, Physical Review Letters, PRL 96, 2006.
E. Werner y E. Udo, “Nonequilibrium statistical mechanics of swarms of driven particles”, Physica A: Statistical Mechanics and its Applications, vol. 314, 2002.
E. Udo, E. Werner y M. Alexander, “Noise-induced transition from translational to rotational motion of swarms”, Physical Review E, no. 71, p. 051904, 2005.
A. Wahid y M. Colin, “Wall following to escape local minima for swarms of agents using internal states and emergent behavior”, International Conference of Computational Intelligence and Intelligent Systems icciis, 2008.
E. Helbert y S. Jorge, “Path planning of mobile robots using potential fields and swarms of Brownian particles”, ieee Congress on Evolutionary Computation (cec), pp. 123-29, 2011
E. Helbert, S. Jorge y G. Cesar, “Vortex swarm path planning algorithm”, IEEE Electronics, Robotics and Automotive Mechanics Conference (cerma), pp. 184-190, 2011.
S. Menser y J. Hereford, “A new optimization technique”, Proceedings of the ieee Digital Object Identifier Southeast Con, 2006.
E. Udo, E. Werner, S. Lutz, O. Anke y M. Frank, “Active Brownian particle and random walk theories of the motions of zooplankton: application to experiments with swarms of Daphnia”, Journal of Theoretical Biology, 9, 2008.
M. Robert y S. Frank, “Modeling vortex swarming in Daphnia”, Bulletin of Mathematical Biology, vol. 69, pp. 539-62, 2007.
E. Werner, Nonequilibrium statistical mechanics of swarms of driven particles, Elsevier Physica, 2002
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
OPTIMIZACIÓN BASADA EN UN MODELO DE PARTÍCULAS CON COMPORTAMIENTO DE VORTICIDAD
OPTIMIZATION BASED ON A MODEL OF PARTICLES WITH VORTICITY BEHAVIOR
Fecha de envío: marzo de 2013
Fecha de recepción: marzo de 2013
Fecha de aceptación: octubre de 2013
Helbert E. Espitia C.
Ingeniero electrónico,ingeniero mecatrónico, especialista en Telecomunicaciones Móviles, magíster en Ingeniería Industrial, magíster en Ingeniería Mecánica, Universidad Distrital “Francisco José de Caldas” (Colombia). Correo electrónico: heespitiac@udistrital.edu.co
Jorge I. Sofrony E.
Ingeniero eléctrico, MSc.en Sistemas de Control, Ph.D. en Sistemas de Control, Universidad Nacional de Colombia (Colombia). Correo electrónico:jsofronye@unal.edu.co
Resumen:
En la naturaleza se pueden observar diferentes comportamientos en enjambres, los cuales pueden ser fuentes de inspiración en la propuesta de algoritmos de optimización. En particular, el comportamiento que es de atención en este trabajo consiste en el movimiento circular de partículas, con la formación de un vórtice, ya que se considera que esta estrategia de locomoción que emplean algunos seres vivos para buscar alimento y evadir obstáculos puede ser útil en procesos de optimización. Para el desarrollo del algoritmo de optimización se toma como referencia un modelo que permite describir el comportamiento de vorticidad. Considerando este modelo se propone la estrategia de optimización. Para mostrar el concepto se emplea una función de prueba en dos dimensiones y se varían los parámetros del modelo, con el fin de observar las características del proceso de búsqueda propuesto.
Palabras Clave:
Optimización, enjambres de partículas, vorticidad
Abstract:
In nature we can see different behaviors for swarms which can be sources of inspiration to perform the proposal of optimization algorithms. In particular, the behavior observed in this paper is the circular motion of particles with the formation of a vortex. Due to this, the strategy of locomotion may be useful in optimization processes. For the development of the optimization algorithm is taken a model which describing the behavior of vorticity. Considering this model the optimization strategy is proposed. To show the concept is used a test function in two dimensions. Additionally were considered different values of parameters to observe the characteristics of the proposed search process.
Keywords:
optimization, particle swarm, vorticity
1. Introduccion
La naturaleza es una buena fuente de inspiración para el desarrollo de algoritmos de optimización, ya que es posible observar diferentes comportamientos de seres vivos que pueden ser útiles en procesos de optimización. Algunos de estos comportamientos se encuentran relacionados con los procesos asociados a la búsqueda de alimento, como también a la evasión de depredadores [1]. Un comportamiento interesante presente en la naturaleza ocurre cuando un grupo de individuos (enjambre) realiza movimientos circulares alrededor de un punto (comportamiento de vorticidad). En el presente documento se realiza la propuesta de un algoritmo de optimización considerando este tipo de comportamiento, el cual se emplea para escapar de mínimos locales y de esta forma ampliar las capacidades de exploración sobre el espacio de búsqueda.
En la primera parte del documento se revisan conceptos sobre modelos de enjambre y optimización bioinpirada. Posteriormente, se presenta el modelo considerado, el cual se toma como referencia para implementar el algoritmo de optimización. El modelo seleccionado permite emular el comportamiento de vorticidad, por lo cual se realiza una simulación donde se puede observar la formación del vórtice para un grupo de partículas. En la siguiente sección se describe la estrategia planteada para el proceso de optimización y se observa el comportamiento del algoritmo sobre una función objetivo de dos dimensiones. Finalmente, se presentan las conclusiones y trabajos futuros que se esperan tener al respecto, ya que la propuesta realizada en este documento se considera como un primer acercamiento.
1.1 Optimización bioinspirada
Sobre técnicas de optimización que emulan el comportamiento de seres vivos se tienen los algoritmos basados en colonias de hormigas, tal como se puede apreciar en [2-5]. Bajo esta misma orientación, el comportamiento de abejas ha permitido el desarrollo de algoritmos tanto de optimización como de búsqueda y exploración [6,7]. Adicionalmente, se tiene la optimización basada en quimiotaxis bacteriana, la cual emula el comportamiento que presenta una bacteria para buscar alimento y evadir zonas tóxicas [1,8].
Otra fuente de inspiración biológica para el desarrollo de algoritmos de optimización consiste en el estudio de los comportamientos colectivos o de enjambres. Al respecto, algunas investigaciones han indicado que estos tipos de comportamiento obedecen a simples reglas de interacción entre individuos.
En relación con el desarrollo de aplicaciones que involucran enjambres de individuos, originalmente su implementación en procesos de optimización fue propuesta por James Kennedy y Russell Eberhart [9]. Otros trabajos consisten en el desarrollo de algoritmos de optimización basados en enjambres de partículas que emplean elementos de mecánica cuántica [10], como también la aplicación del oscilador armónico [11].
Sobre otros algoritmos bioinspirados se pueden apreciar propuestas basadas en el comportamiento de murciélagos (bat algorithm: BA) [12,13], luciérnagas (firefly algorithm: FA) [14] y primates [15]. También existen enfoques bajo principios y leyes físicas como la ley de Coulomb para partículas cargadas (charged system search: CSS) [16], la sintonía en frecuencia de una nota musical (harmony search HS) [17] y la caída de agua en una cascada (intelligent water drops IWD) [18].
1.2 Comportamientos de enjambres
En la naturaleza se pueden apreciar diferentes comportamientos, los cuales han sido estudiados y representados de forma analítica. En particular, las congregaciones de individuos son una temática interesante por los comportamientos emergentes que surgen [19]. Entre los trabajos por resaltar se encuentra el presentado en [20], donde se desarrolla un modelo básico para representar un enjambre de individuos. Una extensión del anterior trabajo se realiza en [21], donde se describen algunos patrones representativos de los enjambres. Por otro lado, en [19] se realiza una revisión del comportamiento colectivo para la formación de enjambres, observando las propiedades de la autorregulación y principios del comportamiento colectivo como lo son: integridad, variabilidad, realimentación positiva, realimentación negativa, umbrales de respuesta, dirección, inhibición, redundancia, sincronización y egoísmo.
Sobre los diferentes enfoques considerados para modelos de enjambres, en [22] se analiza el efecto que tiene el liderazgo de un individuo, en [23] se consideran las diferentes formas de organización que presentan las aves y en [24] se observa el efecto que tiene incorporar mecanismos de predicción en un modelo de enjambre.
En particular, el comportamiento emergente que es de atención en este documento consiste en el movimiento circular de partículas, con la formación de un vórtice, ya que se considera que esta estrategia de locomoción que emplean ciertos seres vivos para buscar alimento y evadir obstáculos puede ser útil en procesos de optimización.
1.3. Modelos de partículas con comportamiento de vorticidad
La vorticidad es un comportamiento que se presenta con frecuencia en los fluidos y se debe al acoplamiento que existe entre las fuerzas inerciales y las fuerzas viscosas (número de Reynolds [25]). El análisis de este comportamiento se realiza mediante las ecuaciones de Navier Stokes, las cuales suelen ser difíciles de resolver de forma analítica en casos generales [26].
El comportamiento de vorticidad se caracteriza por el movimiento de forma rotacional de partículas alrededor de un punto, el cual se denomina vórtice. Además de los fluidos, este tipo de comportamiento se presenta en enjambres de individuos como peces, aves y bacterias, entre otros. Existen dos modelos que son los más empleados para representar este comportamiento: el de partícula autopropulsada [2,28] y el de partícula activa browniana [29]. Este último, considera una componente estocástica, a diferencia del primero. Por lo general, estos modelos suelen emplear potenciales de Morse para representar la interacción entre individuos; sin embrago, en [30] se puede observar un modelo que emplea un potencial parabólico.
1.4. Aplicaciones de enjambres con características de vorticidad
Es importante señalar que sobre aplicaciones que emplean modelos de enjambres con características de vorticidad, uno de los trabajos más representativos es el desarrollado por Colin McInnes y Wahid Abdel [31], donde se propone un método para la planeación de trayectorias de robots móviles que permite evadir mínimos locales. Este algoritmo es denominado local minimal avoidance (LMA), o también local minimal escape (LME). Propuestas similares para la planeación de trayectorias de robots móviles se pueden apreciar en [32] y [33], donde se emplea un modelo de partícula activa y se desarrolla el algoritmo de planeación de trayectorias VSPP (vortex swarm path planning algorithm)
>Finalmente, entre los métodos de optimización que emplean el concepto de vorticidad se encuentra el presentado en [34], donde se desarrolla un algoritmo que considera una analogía con el comportamiento de un fluido en un sumidero (drenaje). Este algoritmo se denomina particle swirl algorithm (PSA). Aunque el algoritmo PSA emplea el concepto de vorticidad, difiere de la propuesta que presentamos en este documento, con la cual se busca emplear el concepto de vorticidad para lograr que el enjambre de partículas escape de un mínimo local y de esta forma pueda continuar el proceso de búsqueda.
2. Modelos de enjambres
Un modelo de enjambre consiste en la descripción del movimiento de un conjunto de individuos. En términos generales, se puede expresar la posición de un individuo como:
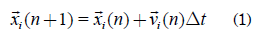
Donde i(n + 1) es el punto siguiente de la
posición del individuo i,la cual se determina
con el punto actual
i(n) considerando la velocidad
i del individuo
Adicionalmente, para un total de N individuos, la velocidad de un individuo se puede calcular como:
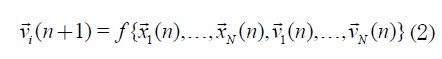
Siendo esta última ecuación aquella en la cual se presentan las variaciones de los diferentes algoritmos que buscan emular el comportamiento de los enjambres [12].
2.1. Modelo empleado
El modelo seleccionado para realizar la propuesta del algoritmo de optimización se encuentra basado en la forma de locomoción de zooplancton Daphnia [35-37]. Con este modelo se busca aprovechar el comportamiento de vorticidad, ya que tal como se presenta en [31], esta puede ser una buena estrategia para evadir mínimos locales. El modelo seleccionado es el siguiente:
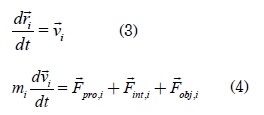
La primera ecuación corresponde al cálculo de
posición de la partícula, conociendo su velocidad
i. La segunda ecuación corresponde
al cálculo de la velocidad de la partícula, donde mi es la masa de la i-èsima particula. La
fuerza de autopropulsión se considera como:
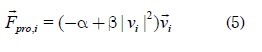
El anterior término es muy similar al presente
en la ecuación de Rayleigh, la cual describe
un comportamiento de ciclo límite. Cuando
actúa solamente esta fuerza, la velocidad de
las partículas en estado estable tiende a ser 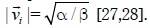
La fuerza de interacción de las partículas está dada por:
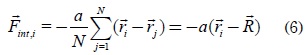
Donde corresponde al centro de masa del
enjambre:
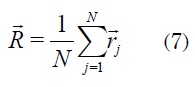
La información de la función objetivo está dada por Uobj. La fuerza sobre cada partícula que se produce por el potencial Uobj es:
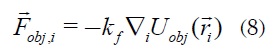
Donde ki es una constante que pondera la influencia de la función objetivo.
3. Simulación del modelo
Con el fin de observar las características del modelo se realizó un conjunto de simulaciones con diferentes valores de sus parámetros. Los parámetros considerados son mi, N, a, β
En primer lugar, tomando Fdis= -Faut en la figura 1 (a)
se puede observar el comportamiento de la fuerza de autopropulsión para diferentes valores de α, donde los valores negativos representan la fuerza de propulsión suministrada a la partícula, mientras que los valores positivos corresponden a la fuerza de frenado.
El comportamiento de Fdis para diferentes valores de β, la fuerza de autopropulsión disminuye, mientras que el efecto de la fuerza de frenado aumenta.
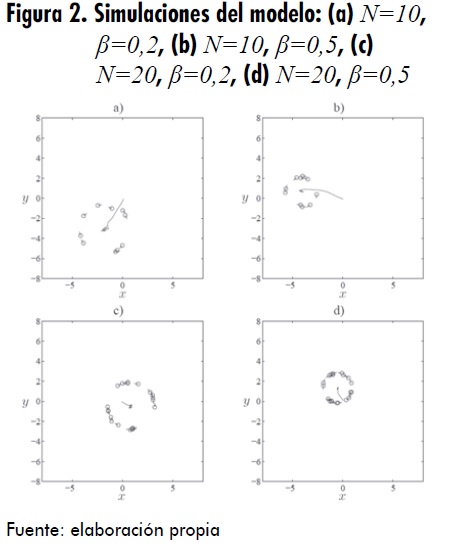
Con el fin de realizar la simulación del modelo se tomó mi=1, a =1, y N para 10 y 20 partículas. Además, considerando la relación
y teniendo en cuenta el efecto de β en la fuerza de autopropulsión según la figura 1, entonces se toma fijo α= 1 y β con 0,2 y 0,5 Adicionalmente, para esta simulación se considera que no existe ningún potencial asociado a la función objetivo Uobj.
La simulación se realiza para 300 iteraciones, tomando condiciones iniciales aleatorias para la posición y cero para la velocidad. La distribución final de las partículas se presenta en la figura 2, donde se puede observar el vórtice formado.
En la figura 2, se puede apreciar que el parámetro β asociado a la fuerza de frenado tiene un efecto mayor en el radio del enjambre que el parámetro N asociado al número de partículas. Por otro lado, también se observa que en la ausencia de un potencial externo Uobj, el centro del vórtice está sujeto a las condiciones iniciales del modelo
el parámetro N asociado al número de partículas. Por otro lado, también se observa que en la ausencia de un potencial externo Uobj el centro del vórtice está sujeto a las condiciones iniciales del modelo.
4. Estrategia de optimización propuesta
Con la estrategia propuesta se busca tener
una exploración adecuada del espacio de búsqueda,
de tal forma que en la medida que se
encuentra un mínimo local se pueda escapar
de este para seguir el proceso de búsqueda.
Con el fin de lograr lo anterior, se propone aumentar
la energía de propulsión del enjambre cuando se alcanza un mínimo local y solo
se disminuye cuando el enjambre escapa de
este punto. Para establecer cuándo incrementar
la energía de propulsión, se considera una
variable Umin que se actualiza con el valor
mínimo de la función objetivo Uobj
. Esto
puede ser expresado como:
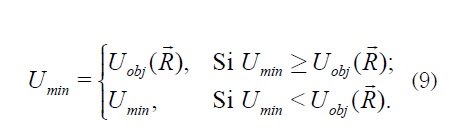
La adición de la energía se logra con el factor de propulsión α, el cual en esta propuesta se calcula como:
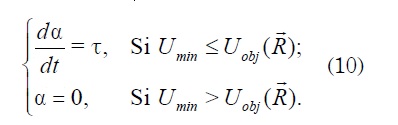
Es de notar que al llegar el enjambre a un mínimo
local (Umin ≥ Uobj ) el término α aumenta, incrementándose de esta forma la
energía de propulsión. Esta acción continuará
sucediendo hasta que las partículas escapen
del mínimo local. El aumento de la energía
viene dado por el parámetro τ.
Como se aprecia en (10), en el momento en que el enjambre encuentra otro punto con un valor menor de Umin al establecido previamente, la energía de propulsión es cero por lo cual el enjambre presenta un comportamiento de descenso hacia otro mínimo local.
Para emplear el modelo dinámico del enjambre, las ecuaciones diferenciales se convierten a tiempo discreto, tomando un intervalo de tiempo Δt, de tal forma que se tiene:
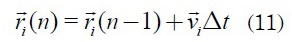
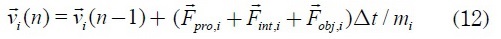
La ecuación de α en tiempo discreto es:
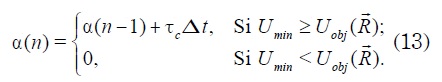
Finalmente, el algoritmo de optimización propuesto se puede apreciar en la Figura 3.
5. Análisis cualitativo de parámetros
Sobre los diferentes parámetros involucrados en el algoritmo de optimización se tiene la siguiente descripción cualitativa:
β: Factor de frenado de las partículas. Al aumentar, las partículas tienden a ir más lento.
α: Factor de propulsión. Al incrementarse, las partículas aumentan su energía cinética y de esta forma elevan su velocidad.
a: Factor de interacción. Al aumentar, el enjambre de partículas tiende a unirse más.
kf : Factor de ponderación de la función objetivo. Al incrementarse, las partículas convergen rápidamente a un mínimo local, y al disminuir, las partículas se pueden mover sobre todo el espacio de búsqueda.
6. Función de prueba
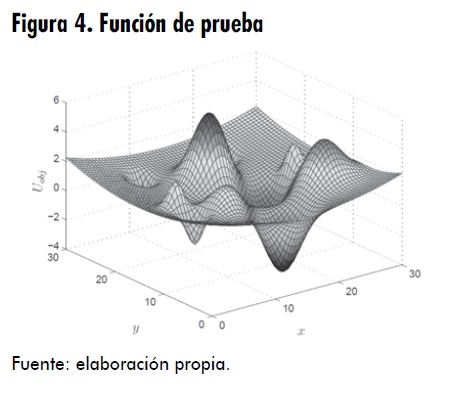
Con el fin de observar el comportamiento del algoritmo para la variación de sus parámetros se emplea la función objetivo propuesta en [1]. Esta función presenta varios mínimos y máximos los cuales se pueden apreciar en la figura 4.
La expresión para la función mostrada en la figura 4. es:
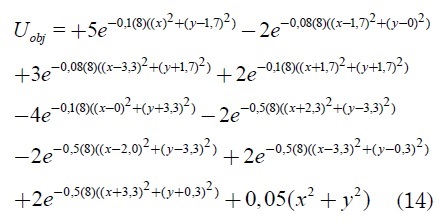
7. Resultados experimentales
Para observar el comportamiento del algoritmo se realizaron variaciones sobre β, kf y &a En la figura 5 se pueden apreciar las trayectorias de las partículas y la trayectoria media recorrida para β=1, kf=3 y &a. Con estos mismos parámetros, en la figura 6 se aprecia la energía suministrada al enjambre, como también el valor de Umin obtenido. En este caso se observa que el enjambre de partículas logra encontrar el mínimo global, pero se queda estancado en este.
Para lograr que el enjambre escape del mínimo y continúe el proceso de búsqueda, se puede disminuir el factor de frenado β. Considerando lo anterior, se toma β=0,7, kf=3 y a=1. En la figura 7 se presentan las trayectorias de las partículas y la trayectoria media realizada por estas. En la figura 8 se aprecia la energía suministrada y el valor de Umin. En este caso se observa que el enjambre logra escapar del mínimo para continuar el proceso de búsqueda, aunque no existe como tal otro valor menor al encontrado. Una alternativa adicional para lograr un resultado similar al anterior, es disminuir el factor de ponderación de la función objetivo kf . En este caso se toma β=1, kf=2,4 y a=1.
En la figura 9 se observan las trayectorias de las partículas y la trayectoria media, donde se aprecia que el enjambre en la parte final de la simulación presenta una alta dispersión de las partículas, cubriendo así buena parte del espacio de búsqueda. Esta característica es la que se espera lograr con el proceso de búsqueda propuesto.
En la figura 10 se presenta la energía adicionada y el valor de Umin . En este caso fue necesario incrementar el número de iteraciones para lograr que el enjambre escape del mínimo.
Por otro lado, para controlar la dispersión de las partículas se puede incrementar o disminuir el factor de interacción a. Para mostrar esto se β=1, kf=3 y a=0,5. En la figura 11 se presentan las trayectorias de las partículas y la trayectoria media, mientras que en la figura 12 se puede observar la energía adicionada y el valor mínimo encontrado de la función objetivo. En este caso se aprecia que se tiene una mayor dispersión de las partículas.
8. Conclusiones
Se apreció que es posible proponer una estrategia de optimización basada en un modelo de enjambre que describe el comportamiento de partículas con movimientos circulares.
La selección del modelo se realizó buscando tener una expresión compacta, con pocos términos, y que permita describir comportamientos de enjambre como desplazamientos uniformes y movimientos circulares, los cuales se aprecian en diferentes grupos de seres vivos.
Para la variación de parámetros se consideraron análisis reportados del modelo y simulaciones previas de este.
En esta propuesta se tiene como criterio de parada el número máximo de iteraciones, por lo cual es necesario en una nueva versión incluir un criterio de parada más general, como lo es la dispersión de las partículas, por ser esta una característica importante del comportamiento de las partículas cuando logran escapar del mínimo local.
En futuros desarrollos se puede proponer una estrategia de control para el factor de propulsión con la cual se pueda evadir mínimos locales de forma más eficiente. Una alternativa adicional para mejorar el algoritmo consiste en modificar de forma dinámica el factor asociado al campo potencial, de tal forma que el enjambre pueda escapar rápidamente de mínimos locales.
En un trabajo futuro, luego de tener una versión mejorada del algoritmo propuesto se espera comparar su desempeño con otros algoritmos bioinspirados, considerando el número de iteraciones, la cantidad de mínimos locales identificados y la capacidad de encontrar el mínimo global.
Referencias
[1] P. Kevin, “Biomimicry of bacterian foragin for distributed optimization and control”, ieee Control Systems Magazine, 2002.
[2] B. Mauro, P. Paola y D. Marco, “On the invariance of ant colony optimization”, ieee Transactions on evolutionary computation, vol. 11, no. 6, 2007.
[3] D. Marco y G. Luca, Ant algorithms for discrete optimization, Massachusetts Institute of Technology, Artificial Life 5, pp. 137- 72, 1999.
[4] D. Marco, B. Mauro y S. Thomas, “Ant colony optimization. Artificial ants as a computational intelligence technique”, IEEE Computational Intelligence Magazine, 2006.
[5] Z. Aaron, S. Angus, M. Holger y N. John, “Parametric study for an ant algorithm applied water distribution system optimization”, ieee Transactions on Evolutionary Computation, vol. 9, no. 2, 2005.
[6] K. Dervis, An idea based on honey bee swarm for numerical optimization, Technical Report-TR06, 2005.
[7] T. Sarita, M. John, J. Chahl, H. Butler y Z. Steve, Bees: exploring Mars with bioinspired technologies, ieee Computer Society, 2004.
[8] A. Russell y C. Michael, “Hans J. Bremermann, A pioneer in mathematical biology”, BioSystems, vol. 34, no. 1, pp. 1-10, 1995.
[9] R. Eberhart y J. Kennedy, “Particle swarm optimization”, ieee Proceedings Neural Networks, 1995.
[10] C. Leandro, A quantum particle swarm optimizer with chaotic mutation operator, Elsevier Chaos Solitons and Fractals, 2006.
[11] C. Leandro y C. Viviana, Particle swarm approach based on quantum mechanics and harmonic oscillator potential well for economic load dispatch with valve-point effects, Elsevier Energy Conversion and Management, 2008.
[12] S. Davoud y M. Ellips, “Particle swarm optimization methods, taxonomy and applications”, International Journal of Computer Theory and Engineering, vol. 1, no. 5, 2009.
[13] Y. Xin-She, “A new metaheuristic bat-inspired algorithm”, Nature Inspired Cooperative Strategies for Optimization (NICSO), 2010.
[14] Y. Xin-She, Firefly algorithm, Lévy flights and global optimization, Londres: Springer, Research and Development in Intelligent Systems XXVI, 2009.
[15] M. Antonio y S. Onur, “Monkey search: a novel metaheuristic search for global optimization”, aip Conference Proceedings, Data mining systems analysis and optimization in biomedicine, 2007.
[16] A. Kaveh y S. Talatahari, “A novel heuristic optimization method: charged system search”, Acta Mechanica, vol. 213, no. 3-4, pp. 267-89, 2010.
[17] Y. Xin-She, “Harmony search as a metaheuristic algorithm”, Springer Berlin, Music-Inspired Harmony Search Algorithm, 2009.
[18] S. Hamed, “Problem solving by intelligent water drops”, ieee Congress on Evolutionary Computation, 2007.
[19] D. J. T. Sumpter, The principles of collective animal behaviour, Philosophical Transactions of the Royal Society B, 2006.
[20] V. Tamás, C. András, B. Eshel, C. Inon y S. Ofer, “Novel type of phase transition in a system of self-driven particles”, Physical Review Letters, vol. 75, no. 6, 1995.
[21] V. Tamás, “Universal patterns of collective motion from minimal models of flocking”, Second ieee International Conference on Self-Adaptive and Self-Organizing Systems, 2008.
[22] C. Iain, K. Jens, F. Nigel y L. Simon, “Effective leadership and decision making in animal groups on themove”, Letters to Nature, vol. 433, no. 3, pp. 513-15, feb. 2005.
[23] B. Iztok y H. Frank, “Organized flight in birds”, Animal Behaviour, 78, 2009.
[24] Z. Hai, C. Michael, S. Guy, Z. Tao y M. Jan, “Collective behavior coordination with predictive mechanisms”, ieee Circuits and Systems Magazine, third quarter, pp. 67-85, 2008.
[25] B. Howard, Random walks in biology, Princeton University Press, 1983.
[26] Ç. Yanus, Mecánica de fluidos, McGraw-Hill, 2003.
[27] L. Herbert, R. Wouter-Jan y C. Inon, “Self-organization in systems of self-propelled particles”, Physical Review E 63, 2000.
[28] M. R. D’Orsogna, Y. L. Chuang, A. L. Bertozzi y L. S. Chayes, “Self-propelled particles with soft-core interactions: patterns, stability, and collapsel”, Physical Review Letters, PRL 96, 2006.
[29] E. Werner y E. Udo, “Nonequilibrium statistical mechanics of swarms of driven particles”, Physica A: Statistical Mechanics and its Applications, vol. 314, 2002.
[30] E. Udo, E. Werner y M. Alexander, “Noise-induced transition from translational to rotational motion of swarms”, Physical Review E, no. 71, p. 051904, 2005.
[31] A. Wahid y M. Colin, “Wall following to escape local minima for swarms of agents using internal states and emergent behavior”, International Conference of Computational Intelligence and Intelligent Systems icciis, 2008.
[32] E. Helbert y S. Jorge, “Path planning of mobile robots using potential fields and swarms of Brownian particles”, ieee Congress on Evolutionary Computation (cec), pp. 123-29, 2011.
[33] E. Helbert, S. Jorge y G. Cesar, “Vortex swarm path planning algorithm”, IEEE Electronics, Robotics and Automotive Mechanics Conference (cerma), pp. 184-190, 2011.
[34] S. Menser y J. Hereford, “A new optimization technique”, Proceedings of the ieee Digital Object Identifier Southeast Con, 2006.
[35] E. Udo, E. Werner, S. Lutz, O. Anke y M. Frank, “Active Brownian particle and random walk theories of the motions of zooplankton: application to experiments with swarms of Daphnia”, Journal of Theoretical Biology, 9, 2008.
[36] M. Robert y S. Frank, “Modeling vortex swarming in Daphnia”, Bulletin of Mathematical Biology, vol. 69, pp. 539-62, 2007.
[37] E. Werner, Nonequilibrium statistical mechanics of swarms of driven particles, Elsevier Physica, 2002.


.png)




.jpg)





