Behavioral model of a basic trabecular-bone multi-cellular unit using cellular automaton

BEHAVIORAL MODEL OF A BASIC TRABECULAR-BONE MULTI-CELLULAR UNIT USING CELLULAR AUTOMATON

submitted date: October 2013
received date: November 2013
accepted date: December 2013

Aldemar Fonseca Velásquez

.Sc. In Electronic Engineer, Universidad Distrital Francisco José de Caldas (Colombia). M.Sc. In Biomedical Engineering, Universidad Nacional de Colombia (Colombia). INTEGRA Research Group, Universidad Distrital Francisco José de Caldas (Colombia). Current position: professor at Universidad Distrital Francisco José de Caldas (Colombia). E-mail: afonseca@udistrital.edu.coo

Abstract

Bone remodeling is the biological process through which old bone tissue is transformed into new bone through the action of a basic unit of bone remodeling (BMU). This paper presents a computational model to determine the variation of cell population caused by the presence of micro-fractures within the BMU during the remodeling process, also determines the spatial evolution at particular points of the trabecular bone surface. The remodeling process presented is governed by a twodimensional cellular automaton that evolves according to a set of rules and states, based on biological processes that occur in bone remodeling. The simulation of the remodeling process, programmed in MATLAB® performed in time intervals of 0.3 seconds, in the model showed a ratio of 20 osteoclasts to 190 osteoblasts. On the other hand, an approximate resorption time of 34 days and 150 days for formation was obtained. Bone mass showed a maximum percentage loss of 19%.

Key words

bone remodeling, cellular automaton, osteoclasts, osteoblasts, resorption.

Introduction

Bone remodeling is the biological process through which old bone tissue is transformed into new bone through the action of a basic unit of bone remodeling (BMU). In these units, two types of cells are involved, namely osteoclast lineage resorbing bone cells and osteoblast lineage cells, which form new bone. Some of most common bone-remodeling causes are: 1) Bone mass increase to resist additional mechanical loads, 2) Bones micro- cracks or microfissures and 3) fractures.

This paper focuses on bone remodeling caused by micro-cracks or micro-fissures, which takes place in the trabecular surface due to various types of efforts and also to natural attrition of the tissue [1]. Micro-cracks are detected by the osteocytes and so the remodeling process starts with a BMU formation that moves onto the surface of a trabecula segment [2] [3] [4]. Within the BMU formation, osteoclasts and osteoblasts coexist through a mechanism known as coupling, which is the balance between bone resorption and bone formation [5]. This coupling is mediated by a set of interrelated factors that may be of genetic, mechanical, vascular, nutritional, hormonal and/or local nature.

Different studies have proposed models, with specific approaches, in order to explain, verify, analyze and make assumptions about the process of bone remodeling. Some of these models include those based on cell population dynamics, or a set of static-mechanicals models, biochemical models and mechanical-biological models, among others [2] [3] [4] [6] [7] [8] [9]. However, despite the studies available, it is still required to integrate knowledge of cell populations along with their spatial and temporal actions at a specific trabecular remodeling site, so the biological, spatial and temporal aspects of the remodeling process caused by a microfracture in normal bone can be verified.

The aim of this paper is to develop a computational model based on histomorphometric data and so obtain quantitative estimates (in the process of bone remodeling) of cell populations and their activity within the BMU on the a trabecular surface. This model can be taken as the basis for future studies and simulations involving some factors that play a particular role in the remodeling process and may cause an imbalance between resorption and formation.

Various models that explain the remodeling process at a specific trabecular-bone site have been formulated. Some of the currently known models include that of Pivonka [10], who investigated the influence of the available bone surface for remodeling using representative bone volume units as well as defining that, just as there is a mechanical control, there may be a geometric regulation to the remodeling process that affects the porosity of the bone tissue. The work of Fazzalari [11] provided a model of the effect of the remodeling process on the local structure of spongy bone when there are several active BMUs. Meanwhile, Buenzli proposed a model, based on an automaton, for explaining the resorption phase in cortical bone from the osteoclasts part [12]. In another work, Buenzli [13] also proposes a space-time continuum model based on cell populations, which integrates some signs of interaction between the osteoblast and osteoclast cell lineages involved in the remodeling process model; as results, the model indicates that cell populations behave as traveling waves moving across the surface of the cortical bone. In Wang’s work [14], a new 3D simulation method to resemble the trabecular-bone remodeling process is developed to quantitatively study the dynamic evolution of bone mass and of the trabecular microstructure as a response to different mechanical loading conditions.

This paper presents a computational model to determine the variation of cell population caused by the presence of micro-fractures within the BMU during the remodeling process. The model also determines the spatial evolution at particular points of the trabecular bone surface. The remodeling process presented in this model is governed by a twodimensional cellular automaton that evolves according to a set of rules and states, based on biological processes that occur in bone remodeling. The parameters used in the model were derived from case studies, case reports and specialized literature.

The simulation of the remodeling process in the model showed a ratio of 20 osteoclasts to 190 osteoblasts. On the other hand, an approximate resorption time of 34 days and 150 days for formation was obtained. Bone mass showed a maximum percentage loss of 19%. The results indicate there is a tradeoff between the spatial configuration of the trabecular surface and how the BMU cell changes its cell-population spatial and temporal features. Ergo, these characteristics are dependent on the size of the trabecular segment and also on the depth of the crack. These features are known from research studies that show how dimensions of the micro-fracture behave when changing stress conditions and therefore provide an insight into the remodeling device response [13], [15], and [16].

1. Materials and Methods

The proposed model is an exemplification of targeted remodeling on biological processes as a result of the existence of micro-fractures in the trabecular surface. The model is aware of phenomenological aspects such as cell populations and their part on the remodeling site, and is developed through a cellular automaton in a two-dimensional domain which represents a surface segment. Therefore, for the automaton approach, the evolution rules and the set of states were defined based on the characterization of the biological process found in previous studies and reports.

The definition, specification and development of the automaton are presented below. The whole construction was completed by considering models based on automata, especially those with applications to biological systems [17] [18] [19].

1.1 D efining the cellular automaton for the model

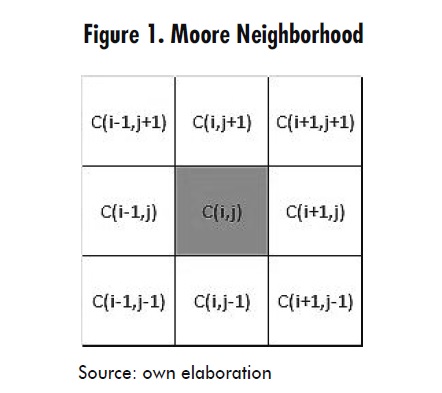
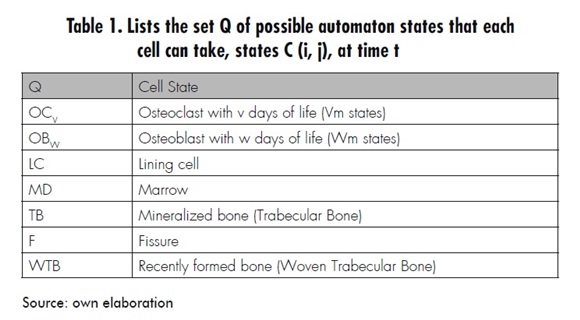
For the present model, a Moore neighborhood was used as shown in Figure 1, where C(i,j) represents the state of a generic cell on which evolution rules that depend on the state of its eight neighbors are applied.

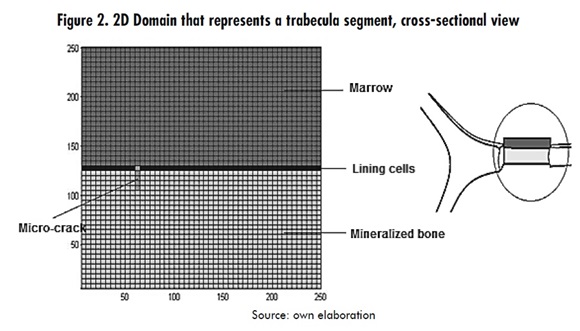
A two dimensional domain, which represents a cross section of a trabecular segment, was defined. The domain dimensions are 250μmx125μm in a 50x25 cell array, as shown in Figure 2.

The cellular automaton allows the validation of biological models because the evolution rules can be modified according to the temporal evolution [19]. In this case, it is necessary to establish several stages in the bone remodeling process that is being represented. To this end, each stage will have its own set of rules for the time evolution of the automaton.

Then the cellular automaton model is defined by the quadruple array C = ‹A,Q α, N› where A is the two-dimensional domain (according to Figure 2), Q is the set of states that each cell may take (according to Table 1), α is the transition function defined by the set of evolution rules (which will be presented next), and N defines a neighborhood of eight neighbors (as shown in Figure 1), namely a Moore neighborhood.

1.1.1 Evolution rules

Canopy Phase:

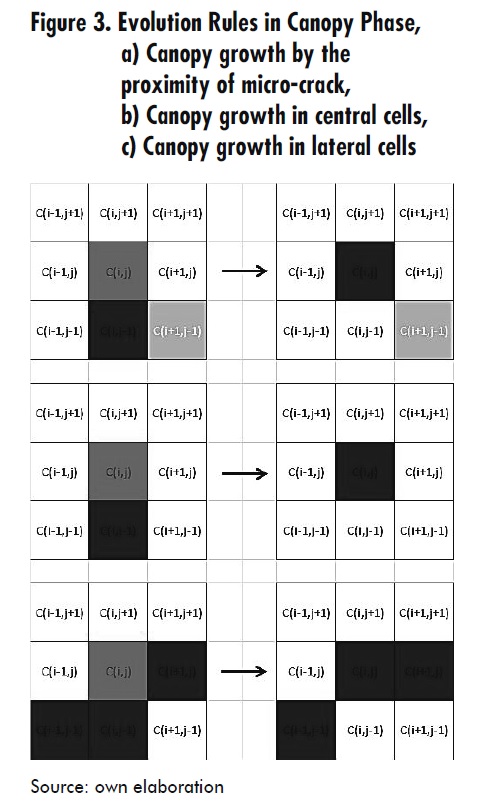
1. When a cell C_i,j is in an MD state (marrow), its neighbor C_i,j-1 is in LC state (lining cell) and another neighbor is in F state (micro-crack), or else, its neighbors C_i-1,j-1 y C_i+1,j-1 are in a different state from LC, then C_i,j switches to LC state. This is true in the range, x − a < i < x + a and holds for the cells whose vertical range is

   

   where a and b determine the horizontal and vertical radius of the hemi- ellipse representing the canopy, x_o corresponds to the horizontal location of the micro-crack and m is the height of the domain, i.e. the canopy formed by LC cells (lining cells) has growth limits which are related to the size of the fissure (Figure 3).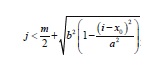



2. When a C_i,j cell has turned into the MD state (marrow) and its neighbors C_i-1,j-1, C_i,j-1 y C_i+1,j have the LC state, then C_i,j switches to LC state. This is valid in the range, x − a < i < x + a and holds for the cells whose vertical range is

   

Osteoclast differentiation phase

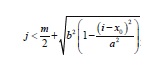
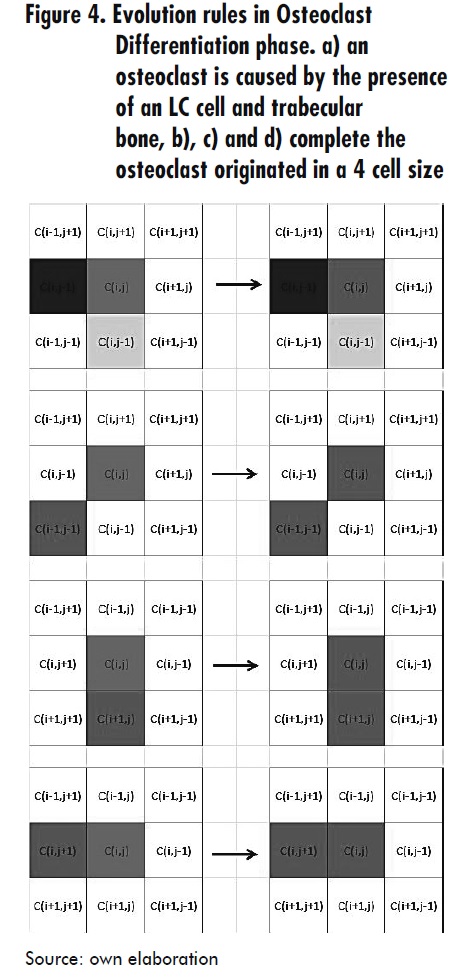
3. When a cell C_i,j is in MD (marrow) status, its neighbor C_i-1,j is in the LC state and its neighbor C_i,j-1 is in TB (trabecular bone) state, or any of its neighbors C_i-1,j-1, C_i,j-1 or C_i-1,j is in OC1 (osteoclast) state, then C_i,j changes into OC1 state. This is always true if u (t) < u (t −1) + d_u1 with du₁ = α₁u₁^g11u₂^g21 - β₁u₁ i.e. a restriction of the osteoclasts population is imposed, which depends on time; in this expression, u₁ represents the osteoclasts population, u₂ is the osteoblasts population, and g11 and g21 represent autocrine and paracrine factors that affect osteoclast differentiation [2]. See Figure 4.



Resorption and osteoclast movement Phase

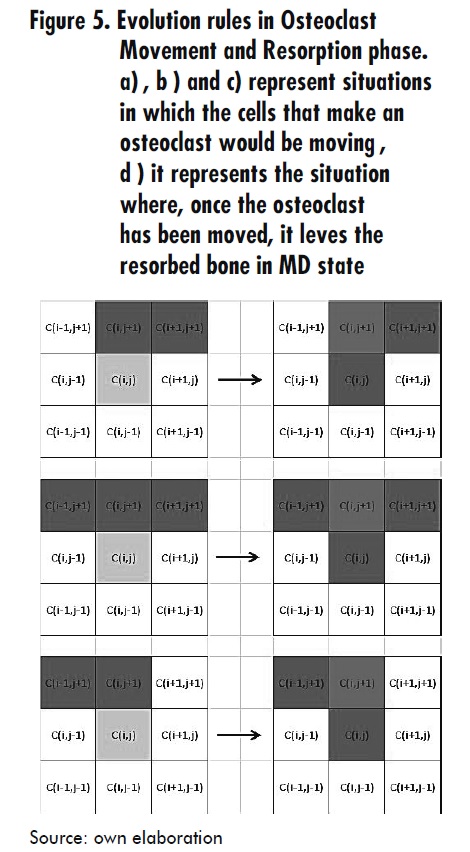
4. When a cell C_i,j is in TB state, its neighbor C_i,j+1 is in OCV (Osteoblast with Vday) state and any of its neighbors C_i-1,j+1 or C_i+1,j+1 is in OCV state, then C_i,j switches to OC_V+1 state. With this rule both the osteoclasts movement and the advancement of its lifetime is shown.
5. When a cell C_i,j is in OC_V state (osteoclast) and its neighbor C_i,j-1 is in OC_V+1 state, then C_i,j switches to MD state.
6. When a cell C_i,j is in OC_Vm state, then C_i,j switches to MD state, with Vm as the average life of osteoclasts. See Figure 5.



Osteoblast differentiation Phase

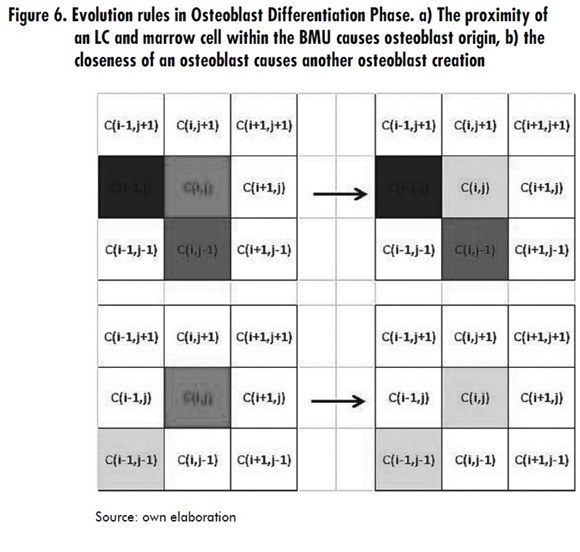
7. When a C_i,j cell is in MD state, its neighbor C_i-1,j-1 is in LC state, its neighbor C_i,j-1 is in MD state and its neighbor C_i,j-1 is in OC4 state; then C_i,j switches to OB1 state. This is always valid if u₂ (t ) < u₂ (t −1) + du₂, with du₂= α₂u₁^g12 u₂^g12 - β₂u₂ i.e. a restriction of the osteoclasts population is imposed, which is time dependent, where g₁₂ and g₂₂ are autocrine and paracrine factors that influence the osteoblasts differentiation [2].
8. When a _Ci,j cell is in MD state and its neighbor C_i-1,j-1 is in OB1 state, then C_i,j switches to OB1 state. This is always valid if u₂ (t) < u₂ (t-1)+ du₂ with du₂= α₂u₁^g12 u₂^g22 - β₂u₂ see Figure 6.



Osteoblasts Formation and Movement Phase

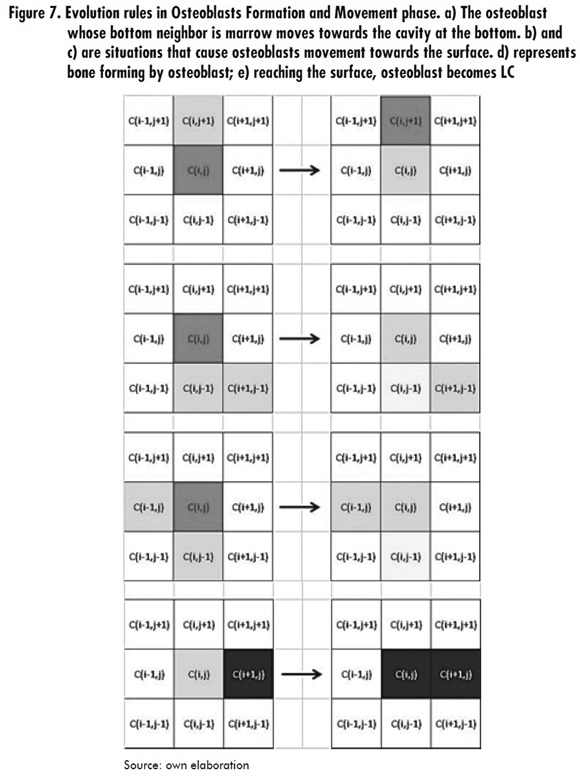
9. When a C_i,j cell is in MD state and its neighbor C_i,j+1 is in OB_W state, then C_i,j switches to OB_W+1 state. With this rule both osteoblasts movement and lifetime progress are represented.
10. When a C_i,j cell is in OB_W state, then C_i,j switches to MD state. This is always true if W < 6, where W represents the osteoblast lifetime since its activation for the formation task.
11. When a C_i,j cell is in O_BW state, then C_i,j switches to WTB state. This is always true if 6 < W < Wm, where Wm is the osteoblast average life.
12. When a C_i,j cell is in OB_W state, then C_i,j switches to LC state. This holds whenever W=Wm. See Figure 7.

2. Results

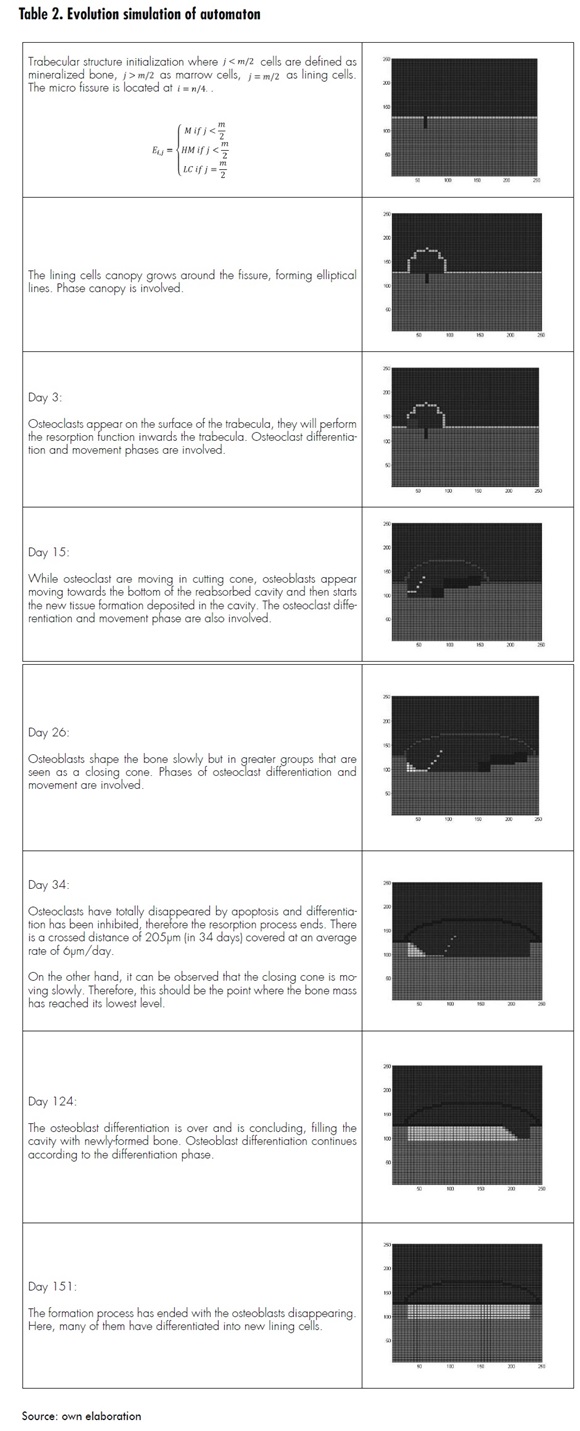
The automaton algorithm, programmed using Matlab, was run for simulations in time intervals of 0.3 seconds. Each interval represents one day in the remodeling process. Table 2 describes the process evolution along whit a graphic representation of the automatons simulation

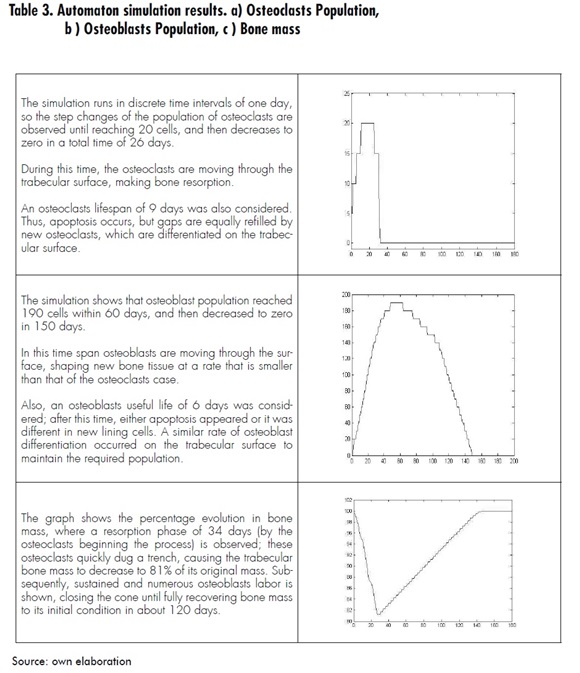
Measurements were also obtained during automaton evolution, representing the remodeling process evolution in terms of osteoclasts population, osteoblasts population and bone mass. The results of these measurements are described in Table 3.

3. C onclusions and Discussion

According to the simulations, it was observed that there is a tradeoff between spatial configuration of the trabecular surface and cell populations in the BMU within the remodeling process, i.e. the cavity dimensions of resorption are dependent on the micro-crack proportions. Also, the amount of cells and time involved in the process depend on the dimensions of the micro-crack. For instance, the simulation was performed with a 25μm-depth micro-crack, which implied a cavity depth of 30μm [16].

The model presented in this paper explains the process of bone remodeling at the trabecular surface level for both spatial and temporal evolution. Using the cellular automaton it is possible to achieve coupling populations of osteoclasts and osteoblasts along with the cells movement at the remodeling site. For the simulation conditions established, it was observed that the remodeling cycle occurs over a period of 151 days, during which resorption takes around 34 days and formation 120 days. It was also possible to verify that the osteoclast population reaches 20 cells, while the osteoblast population reaches 190 cells. These results are comparable with references such as Eriksen [20]thyroid hormone, sex steroids etc.

The model has been developed assuming particular conditions as well as a set of temporal, spatial and biological parameters such as the factors implied in the differentiation of the cells involved in the bone remodeling process, the average lives of these cells, and bone microenvironment conditions. All these conditions are representative of the trabecular bone remodeling case in a healthy bone. Similarly, the model may consider abnormal situations of the remodeling process that may affect both the cell populations involved and the time and spatial dimensions resulting from the remodeling cycle in a specific site.

References

[1] D. B. Burr, “Targeted and nontargeted remodeling.,” Bone, vol. 30, no. 1, pp. 2-4, Jan. 2002.

[2] S. V. Komarova, R. J. Smith, S. J. Dixon, S. M. Sims, and L. M. Wahl, “Mathematical model predicts a critical role for osteoclast autocrine regulation in the control of bone remodeling,” Bone, vol. 33, no. 2, pp. 206-215, Aug. 2003.

[3] V. Lemaire, F. L. Tobin, L. D. Greller, C. R. Cho, and L. J. Suva, “Modeling the interactions between osteoblast and osteoclast activities in bone remodeling.,”Journal of theoretical biology, vol. 229, no. 3, pp. 293-309, Aug. 2004.

[4] S. C. Manolagas, “Birth and death of bone cells: basic regulatory mechanisms and implications for the pathogenesis and treatment of osteoporosis.,” Endocrine Reviews, vol. 21, no. 2, pp. 115-137, 2000.

[5] J. Roberto and B. Evia, “Marcadores de remodelado óseo y osteoporosis,” vol. 58, pp. 113-137, 2011.

[6] A . Moroz, M. C. Crane, G. Smith, and D. I. Wimpenny, “Phenomenological model of bone remodeling cycle containing osteocyte regulation loop.,” Bio Systems, vol. 84, no. 3, pp. 183-190, 2006.

[7] D. I. Wimpenny and A. Moroz, “On allosteric control model of bone turnover cycle containing osteocyte regulation loop.,” Bio Systems, vol. 90, no. 2, pp. 295-308, 2007.

[8] I. F. Hernández-gil, M. Angel, A. Gracia, C. Pingarrón, L. Blanco, R. J. Carlos, and D. I. F. Hernández-gil, “Bases fisiológicas de la regeneración ósea II . El proceso de remodelado FASES :,” pp. 151-157, 2005.

[9] I. Fernández-Tresguerres-Hernández-Gil, M. A. Alobera-Gracia, M. del-Canto-Pingarrón, and L. Blanco-Jerez, “Physiological bases of bone regeneration I. Histology and physiology of bone tissue.,” Medicina Oral Patologia Oral Y Cirugia Bucal, vol. 11, no. 1, pp. E47- E51, 2006.

[10] P. Pivonka, P. R. Buenzli, S. Scheiner, C. Hellmich, and C. R. Dunstan, “The influence of bone surface availability in bone remodelling—A mathematical model including coupled geometrical and biomechanical regulations of bone cells,” Engineering Structures, vol. 47, pp. 134- 147, Feb. 2013.

[11] N . L. Fazzalari, B. L. Martin, K. J. Reynolds, T. M. Cleek, A. Badiei, and M. J. Bottema, “A model for the change of cancellous bone volume and structure over time.,” Mathematical biosciences, vol. 240, no. 2, pp. 132-40, Dec. 2012.

[12] P. R. Buenzli, J. Jeon, P. Pivonka, D. W. Smith, and P. T. Cummings, “Investigation of bone resorption within a cortical basic multicellular unit using a latticebased computational model.,” Bone, vol. 50, no. 1, pp. 378-89, Jan. 2012.

[13] P. R. Buenzli, P. Pivonka, and D. W. Smith, “Spatio-temporal structure of cell distribution in cortical bone multicellular units: a mathematical model.,” Bone, vol. 48, no. 4, pp. 918-26, Apr. 2011.

[14] H. Wang, B. Ji, X. S. Liu, X. E. Guo, Y. Huang, and K.-C. Hwang, “Analysis of microstructural and mechanical alterations of trabecular bone in a simulated three-dimensional remodeling process.,” Journal of biomechanics, vol. 45, no. 14, pp. 2417-25, Sep. 2012.

[15] Velandia and A. Pérez, “Estudio computacional de las microgrietas, la apoptosis y el envejecimiento en el remodelamiento óseo”, 2008, disponible en: http://revistabm.eia.edu.co

[16] M . G. Goff, C. R. Slyfield, S. R. Kummari, E. V Tkachenko, S. E. Fischer, Y. H. Yi, M. G. Jekir, T. M. Keaveny, and C. J. Hernandez, “Three-dimensional characterization of resorption cavity size and location in human vertebral trabecular bone.,” Bone, vol. 51, no. 1, pp. 28-37, Jul. 2012.

[17] O. R. López Vaca, A. Tovar Pérez, and D. A. Garzón Alvarado, “Aplicación de los autómatas celulares en análisis estructural bajo esfuerzo plano,” Intekhnia, vol. 6, no. 2, 2012.

[18] I. Tecnológico, D. E. C. Rica, D. D. E. Computación, and C. Rica, “Un Lenguaje para la Especificación de Autómatas Celulares con Aplicaciones en Biología,” 2000.

[19] L. Y. Maza, “Modelado de bosques con autómatas celulares de dos dimensiones,” pp. 1-4, 2008.

[20] E . F. Eriksen, “Cellular mechanisms of bone remodeling.,” Reviews in endocrine & metabolic disorders, vol. 11, no. 4, pp. 219-27, Dec. 2010.