DOI:
https://doi.org/10.14483/22484728.5512Published:
2013-12-09Issue:
Vol. 7 No. 2 (2013)Section:
A Research VisionSubcategorias reflexivas y correflexivas de la categoria de los espacios topologicos
Reflective and coreflective subcategories of the topological spaces category
Keywords:
Reflective subcategory, coreflective subcategory, topological space, functor (en).Keywords:
Subcategoría reflexiva, subcategoría correflexiva, espacio topológico, funtor (es).Downloads
References
R. Montañez y C. Ruiz, “Elevadores de estructura”, Boletín de Matemáticas, Nueva serie, XIII, no. 2, pp. 111-35, 2006.
J. Hernández, Sobre las subcategorías reflexivas y correflexivas de la categoría de los espacios topológicos, tesis de Maestría, Universidad Nacional de Colombia, Bogotá, 2012.
J. Adamek, Theory of Mathematical Structures, Boston: Lancaster: D. Reidel Publishing, 1983.
S. Mac Lane e I. Moerdijk, Sheaves in Geometry and Logic, A first introduction to topos Theory, New York: Springer-Verlag, 1992.
R. Montañez, Funtores elevadores y coelevadores de estructuras, tesis de doctorado, Universidad Nacional de Colombia, Bogotá, 2007.
J. Adamek, H. Herrlich y G. Strecker, Abstract and Concrete Categories, New York: John Wiley & Sons, 1990.
J. Hernández, R. Montañez y C. Ruiz, “Nociones de mejoramiento en la categoría de los espacios topológicos”, Revista Visión Electrónica, Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, año 5, no. 1, pp. 56-67, enero-junio 2011.
R. Montañez, Fibraciones categóricas, tesis de maestría, Universidad Nacional de Colombia, Bogotá, 1994.
S. Willard, General topology, Adisson Wesley Publishing Company, 1970.
L. Español, M. García y C. Minguez, “On Proper and Exterior Sequen-tiality”, Applied Categorical Structures, vol. 18, no. 6, pp. 653-668, doi: 10.1007/s10485-009-9201-8.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
SUBCATEGORÍAS REFLEXIVAS Y CORREFLEXIVAS DE LA CATEGORÍA DE LOS ESPACIOS TOPOLÓGICOS
REFLECTIVE AND COREFLECTIVE SUBCATEGORIES OF THE TOPOLOGICAL SPACES CATEGORY
Fecha de envío: febrero de 2012
Fecha de recepción: febrero de 2012
Fecha de aceptación: septiembre de 2013
Jorge A. Hernández P.
Matemático. MSc. en Matemáticas, Universidad Nacional de Colombia (Colombia). Docente de la Universidad Distrital Francisco José de Caldas (Colombia), investigador de los grupo SciBas y Vialtopo. Correo electrónico: jahernandezp@udistrital.edu.co
José R. Montañez P.
Lic. en Matemáticas, Ph.D. en Matemáticas, Universidad Nacional de Colombia (Colombia). Docente de la Universidad Nacional de Colombia (Colombia), investigador del grupo Vialtopo. Correo electrónico: jrmontanezp@unal.edu.co.
Resumen:
Es frecuente en el trabajo de ciertas áreas de las matemáticas, y en sus aplicaciones en otras ramas de la ciencia y la ingeniería, construir objetos enriquecidos con propiedades universales, a partir de objetos dados. Estas ideas motivan las definiciones de subcategorías reflexivas y correflexivas, nociones que expresan mejoramiento, optimización y densidad. En este artículo se hace una revisión de la teoría relacionada con las subcategorías reflexivas y correflexivas de la categoría de los espacios topológicos, y a este respecto se proponen nuevos métodos de construcción de dichas categorías en las categorías de los espacios topológicos y en la de los espacios topológicos punteados.
Palabras Clave:
Subcategoría reflexiva, subcategoría correflexiva, espacio topológico, funtor
Abstract
Often working in certain areas of mathematics and its applications in other branches of science, fortified building objects from universal properties of given objects. These ideas motivate the definitions of coreflective and reflective subcategories, expressing notions improvement, optimization and density. In this article we review the theory of reflective and coreflective subcategories of the category of topological spaces and proposes new methods of construction of these categories in the category of topological spaces and in the category of topological spaces with base point.
Keywords:
Reflective subcategory, coreflective subcategory, topological space, functor
1. Introducción
Es frecuente en el trabajo de ciertas áreas de las matemáticas construir objetos enriquecidos con propiedades universales, a partir de objetos dados. Estas ideas motivan las definiciones de subcategorías reflexivas y correflexivas, nociones que expresan mejoramiento, optimización y densidad.
Para citar algunos ejemplos relacionados con el área de la topología, que será el centro de atención en este trabajo, la categoría de los espacios compactos Hausdorff es una subcategoría reflexiva de la categoría de los espacios completamente regulares. En este caso el proceso de optimización es precisamente la compactificación de Stone-C*ech, que define un funtor adjunto a izquierda del funtor de inclusión de los compactos Hausdorff en los completamente regulares. Para citar otro ejemplo, la categoría de los espacios métricos es una subcategoría reflexiva de la categoría de los espacios pseudométricos, lo cual significa que todo espacio pseudométrico determina un espacio métrico con cierta propiedad universal.
En este artículo se hace una revisión bibliográfica de la teoría relacionada con las subcategorías reflexivas y correflexivas, en particular de la categoría de los espacios topológicos. Se muestran algunos métodos de construcción de subcategorías reflexivas y correflexivas en la categoría de los espacios topológicos Top, así como también en la categoría de los espacios topológicos punteados Top*. En particular, en los ejemplos anotados anteriormente, el objeto y su mejorado cambian de conjunto subyacente. En [1], a través de endofuntores denominados elevadores y coelevadores, que se construyen a través de topologías iniciales y finales, se muestran algunas formas de construir subcategorías reflexivas y correflexivas en Top sin cambiar el conjunto subyacente, de tal manera que sus puntos fijos forman una subcategoría reflexiva o una subcategoría correflexiva de Top. En este trabajo, esta teoría se complementa, de manera original, con un proceso similar, pero partiendo de funciones continuas en lugar de espacios topológicos.
Un tema que consideramos central en este trabajo es el estudio de la categoría Top*, en la cual se estudian y se complementan, entre otros, los métodos dados en [2], en aspectos relacionados con la topología general, la teoría de categorías y la topología categórica.
2. Conceptos básicos
En este apartado se presenta la teoría básica relacionada con subcategorías reflexivas y correflexivas y se ejemplifica en las áreas del álgebra y la topología, siendo esta última el contexto de interés de la investigación aquí presentada.
2.1. Subcategorías reflexivas y correflexivas
Definición 1: sea C una categoría y H una subcategoría de C. Se dice que H es reflexiva en C, si para todo objeto V de C , existe un objeto V * en H y un morfismo rv: V → V* llamado la reflexión de V , tales que para todo objeto U de H y todo morfismo f :V → U , existe un único morfismo f * :V * → U en H tal que f* ° rv = f [3].
Puede observarse, fácilmente, que la reflexión de cada objeto es única, salvo isomorfismos, y que el morfismo rv: V → V* es un epimorfismo. Además, si H es reflexiva en C y K es reflexiva en H, entonces K es reflexiva en C.
Definición 2: dados los funtores F: C → D y G: D → C se dice que F es adjunto a izquierda de G y que G es adjunto a derecha de F , si para todos los objetos X de C y Y de D se tiene el isomorfismo natural de clases [F(X), Y]D ≅ X ,G(Y)]C1
Proposición 1: H es una subcategoría reflexiva de una categoría C, si y solamente si el funtor inclusión I: H → C tiene adjunto a izquierda [3]. De manera dual, se tiene el concepto de subcategoría correflexiva y su correspondiente caracterización en términos de la adjunción.
Ejemplos
- La subcategoría plena de Top formada por los espacios completamente regulares, es una subcategoría reflexiva de Top. En efecto, sea (X, τ) un espacio topológico y sea (X, τc ), donde una base para τc está formada por la familia {A| A = X \ f -1 (0), f:(X, τ) → R en tal caso, ((X, τc), f) es la reflexión de (X, τ) [1, 5].
- Sea Top0 la subcategoría de los espacios T0 entonces, Top0 es subcategoría reflexiva
en Top. En efecto, sea (X, τ) un espacio
topológico sobre el conjunto X, se
define la relación de equivalencia: , así:
entonces, se construye el espacio X/: y se considera la aplicación canónica j: X → X/: y sobre X/ se define la topología cociente, que denotamos por β, entonces, el morfismo j:(X, τ) → (X/:,β) es continua y además se cumple que si (Z, α) es un espacio topológico T0 y f:(X, τ) → (Z, α) es continua. El morfismo Φ (X/:,β) → (Z, α) definido por Φ ([x])=f(x) es el único que hace Φ° j = f; en efecto (Φ ° j)(x)=Φ (j(x))=Φ ([x])=f(x) [6].
- Sea u C = Metu la categoría de los espacios métricos, cuyos morfismos son funciones uniformemente continuas, y H = la subcategoría plena de los espacios métricos completos. Entonces, si (X, d) es un objeto de Metu se construye el espacio (X*,d*), donde X* es completación del espacio métrico (X,d). Así, ((X*,d*),i) es la reflexión de (X,d). En efecto, sea (Z,η) un espacio métrico completo y sea f:(X,d)→(Z,η) una función uniformemente continua. De esta manera, el morfismo Φ(X*,d*)→(Z,η) definido por Φ(x)=f(x), es uniformemente continuo y cumple Φ ° i=f
- Sea X un conjunto no vacío y ℘ 2(X)
el conjunto de partes de X. Sea C la
categoría que determina la relación
de contenencia en el conjunto ℘(X). Sean: τ una topología sobre X y H la
categoría que determina la relación de
contenencia en τc. Entonces, H es una
subcategoría reflexiva en C. En efecto,
sea A ∈ ℘ (X). Asi
contiene a A (
es la adherencia de A), y
∈ τc. Ahora bien, si existe un conjunto B en τc, tal que B contiene a A, por ser Ā el menor conjunto cerrado que contiene a A, se tiene que B contiene a
, de lo cual se induce la reflexión de A.
- Sea C=HComp la categoría de los espacios compactos Hausdorff y sea H = Tych la categoría de los espacios Tychonoff (o espacios completamente regulares). Entonces, mediante la compactación de Stone-Ĉ ech, para cada espacio completamente regular (X, τ) su compactificación es B(X), y (B(X),i) es la reflexión de (X, τ) [6].
- Sea X un conjunto no vacío y ℘(X) el conjunto de partes de X. Sea C la categoría que determina la relación de contenencia en el conjunto ℘(X). Sean τ una topología sobre X y H la categoría que determina la relación de contenencia en τ. Entonces, H es una subcategoría correflexiva en C. En efecto, sea A ∈ ℘ (X). De esta manera, A0 es subconjunto de A (A0 es el interior de A) y A0 ∈ τ. Si existe un conjunto B en τ tal que B es subconjunto de A, por ser A0 el mayor conjunto abierto contenido en A, B es un subconjunto de A0 de lo cual se induce la correflexión de A [7].
- Sea C la categoría de los espacios topológicos punteados. Los objetos de esta categoría son los espacios topológicos en los cuales se ha fijado un punto base y los morfismos son las funciones continuas que preservan el punto base [7]. Sea H la subcategoría plena de C formada por los espacios topológicos conexos punteados. H es reflexiva en C. En efecto, sea (X, τX, x0 ) un espacio topológico punteado cualquiera y sea X* la componente conexa de x0 Entonces, se determina el espacio topológico (X*, τX*, x0 ) donde τX* es la topología relativa a X*. El espacio topológico (X*, τX* ) es conexo y la inclusión i: (X* → X ) es continua y es la correflexión de X.
- Sea C=Top y K = la categoría de los espacios secuenciales (es decir, espacios en los que todo subconjunto secuencialmente cerrado es cerrado). Si (X, τ ) es un objeto en C, se define τ' ={A ⊆ X | X\A es secuencialmente compacto en (X, τ)}. De esta manera, (X, τ) es una topología sobre X; teniéndose que ((X, τ')idx ) es la correflexión (X, τ) En efecto, sea (ψ, α ) un espacio topológico secuencial y sea f=(Z, α) → (X, τ) una función continua. Entonces, la función φ=(Z, α) → (X, τ); definida por φ(x):= f(x) es continua en K [6]. Además, es la única función continua que cumple id ° φ = f . Otra demostración, haciendo uso de funtores elevadores, puede encontrarse en [8] y [5].
3. Un método de construcción de subcategorías reflexivas y correflexivas en la categoría Top
En algunos de los ejemplos considerados en la sección anterior, en particular en los relacionados con el área de la topología, dados en los ejemplos 2, 3, 5 y 7, un espacio y su reflexión no tienen en general el mismo conjunto subyacente, lo que sí sucede en el ejemplo 8. Siguiendo a [5], en esta sección se muestra un método de construcción de subcategoras de Top donde el espacio de partida y su reflexión (correflexión) tienen el mismo conjunto subyacente; es de anotar que el método en cuestión está relacionado con las topologías iniciales y finales. Consideramos interesante el hecho de que las subcategorías construidas son además categorías topológicas, en el sentido de [3]. Adicionalmente, se presentan algunos resultados que complementan lo desarrollado en [5].
3.1. Topologías iniciales y finales
En la categoría de los espacios topológicos, la colección de topologías sobre un conjunto i > X
tiene estructura de retículo completo, con el orden inducido por la inclusión, siendo la topología grosera el mínimo y la discreta el máximo. Dada un familia de topologías sobre X, el ínfimo está dado por la intersección y el supremo por la topología generada por la reunión.Por otra parte, en la categoría de los espacios topológicos Top se resuelve el siguiente problema: dada una función f: X → Y y τy una topología sobre Y, se puede construir sobre el conjunto X la topología "τx" llamada topología inicial, de la siguiente manera: τx={f-1(B)|B ∈ τY }. De esta forma, la función f:(X, τX )→ (Y, τX ) resulta continua y τx es la menor topología sobre X que hace de f una función continua. Además, para todo espacio topológico (Z, τz ) y cualquier función g: Z → X tal que h: (Z, τz ) → (Y, τy ) sea continua y h=f ° g entonces, g: (Z, τx ) → (X, τx ) es continua. En forma dual, dada una función f: X → Y y τx una topología sobre X, se construye la topología sobre Y:τY ={B⊆Y | f-1(B) ∈ τX }; llamada topología final. De esta forma, la función f:(X, τX )→ (Y, τY ) es continua y τY es la mayor topología sobre Y que hace de f una función continua. Además, para todo espacio topológico (Z, τz ) y cualquier función g: (Y → Z ) tal que h= g ° f sea continua, la función g: (Y, τx ) → (Z, τz ) es continua. En particular, cuando la f es sobreyectiva, se dice que τx es una topología cociente.
Un caso particular de una topología final es el siguiente: dados un espacio topológico (X, τx ) y una relación de equivalencia R sobre X, se construye el conjunto cociente X/R; adicionalmente, se tiene de manera natural la función:
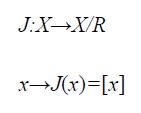
Entonces, se puede construir la topología cociente sobre (X/R).
El cilindro, el toro, la cinta de Möbius y la botella de Klein son subespacios de R3 que se obtienen mediante la construcción anterior, definiendo para cada caso una relación adecuada en un rectángulo, considerando este como subespacio de R2 (ver [9]).
De forma más general, ver [3] o [6] en Top sea S=(fλ,X) un sumidero cuyo dominio es la familia (Xλ, τλ) para todo λ ∈ A. Entonces, la topología final para X, correspondiente a la familia {τλ}λ∈A y {fλ}λ∈A es: τ={U ⊆ X} | f λ-1 (∪) ∈ τx, ∀ λ ∈ A} Así, las funciones fλ:(Xλ, τλ)→ (X, τ) son continuas y cumplen la propiedad universal a derecha, para todo λ ∈ A. Dicha topología se llama topología final para el sumidero. De manera dual, se tiene la estructura inicial para la fuente: F: (X, fλ ) cuyo codominio es la familia (Xλ, τλ ). Entonces, la topología inicial para X, correspondiente a {τλ}λ∈A {fλ}λ∈A es la topología τ generada por la familia: A:{fλ-1 (u)λ ⊆ X | uλ∈ τλ }, donde las funciones fλ: (X, τ)→ (Xλ, τλ ) son continuas y cumplen la propiedad universal a izquierda para todo λ ∈ A
3.2 Construcción de subcategorías reflexivas y correflexivas a través de topologías iniciales y finales
Haciendo uso de topologas iniciales y finales, veremos la forma de construir una clase de endofuntores de Top, a los que denominamos funtores elevadores y coelevadores de estructura, los cuales generan mediante sus puntos fijos reflexivas y correflexivas de Top.
Definición 3: sea E:Top → Top un funto. Decimos que E es un elevador de estructura o simplemente un elevador, si cumple: 1.O ° E=O, donde O es el funtor olvido de Top en Conj, siendo Conj la categoría de los conjuntos y 2. X ≤ E((X)
Análogamente, se dice que un endofuntor C es un coelevador de estructura, si cumple (1) y C(X) ≤ X para todo X ∈ Top,[5].
Definición 4: un funtor E:Top → Top se llama idempotente si E ° E = E En tal caso, los puntos fijos de E coinciden con su imagen E(Top). En adelante E(Top) será la subcategoría plena de Top
Proposición 2: si E:Top → Top es un elevador idempotente, entonces E(Top) es una subcategoría correflexiva de Top [5].
En efecto: sea X ∈ Top. Como E es elevador, entonces X ∈ E(X) es decir, la función: ix : E(X) → X es continua y E(X) es la correflexión de X.
De forma dual, si C:Top → Top es un coelevador idempotente, entonces C(Top) es una subcategoría reflexiva de Top. Es fácil ver que los elevadores preservan la propiedad de ser Hausdorff y los coelevadores preservan la conexidad y la compacidad. Se verá enseguida una forma de construir elevadores y coelevadores a partir de espacios topológicos.
Sean W y X espacios topológicos. En la colección de funciones continuas f: W → X, al olvidar la topología de X se tiene el sumidero que notamos: s(W,X)={f : W → X | f ∈ [W,X]Top} la estructura final para s(W,X) se escribe Fs(W,X)=X [5].
De la definición de topología final para un sumidero, se tiene que
- X≤(W,X)
- [W,X]Top ≅[W,Fs(W,X)]Top.
En adelante, por simplicidad en la escritura se escribirá [W,X], en vez de [W,X]Top Como consecuencia de la observación anterior se tiene de inmediato el siguiente teorema.
Teorema 1: sea W un espacio topológico. La aplicación
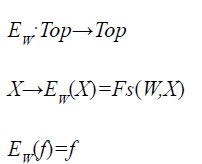
define a EW como un elevador idempotente en Top
Observaciones:
- EW (W)=W
- EW (Top) es una categora topológica, noción que puede ser consultada en [5].
- EW (Top) es correflexiva en Top.
De manera dual, haciendo uso de estructuras iniciales, un espacio topológico da origen a un coelevador idempotente C.
Ejemplos
- Sea N el conjunto de los números naturales N∞=N ∪{∞}, τN ∞= P(N) ∪ {A ∪{∞}|N\A}. La subcategoría plena de Top formada por los espacios secuenciales corresponde a EN ∞(Top). Por lo tanto, EN ∞(Top) es una subcategoría correflexiva de Top (un espacio X es secuencial si cada subconjunto secuencial abierto de X es abierto. Un subconjunto A ⊆ X es secuencialmente abierto si cada sucesión en X que converge a un punto de A, está eventualmente en A. En otras palabras, por fuera de A hay un número finito de elementos de la sucesión).
- La subcategoría plena de Top, formada por los espacios completamente regulares, corresponde a CI (Top), donde I=[0,1] y CI es el coelevador correspondiente a I, de Top en Top. Por lo tanto, CR es una subcategoría reflexiva de Top.
- Si W={.}, sobre este conjunto se puede definir una única topología. Ahora, la imagen del elevador EW corresponde a la subcategoría plena de Top, formada por los espacios discretos.
- Si W={.}, la imagen del coelevador CW corresponde a la subcategoría plena de Top, formada por los espacios con topología grosera.
3.3. Elevadores idempotentes a partir de funciones continuas
Los elevadores y coelevadores construidos a partir de un espacio topológico dado pueden considerarse como construidos a partir de la función identidad de dicho espacio. Con esta idea, esta sección generaliza este hecho, de manera que los resultados obtenidos son originales y de carácter más general. Su importancia radica en que de acuerdo con la proposición 3, se generan métodos de construcción de subcategorías correflexivas de Top.
Sea h: W1 → W2 una función continua para cada espacio topológico X, sea SX={g:W2 → X;g ∈[W2,X]Top} y sea SX◦h={g◦h:W1 → X;g ∈ SX}.
Considérese en Top la aplicación Eh que asigna a cada espacio topológico X el espacio Eh(X)=Fs , y a cada función continua f la función Eh (f)=f
Dada una función f: X → Y la función f : Eh(X)→Eh(Y) resulta continua. Esto determina el funtor
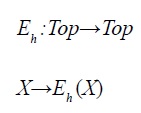
Observaciones
- El funtor Eh : Top → Top es un elevador idempotente y, por tanto, Eh (Top) es una subcategoría correflexiva de Top [2].
- Para cada espacio topológico W se cumple EW = EIW. Por tanto, un espacio y su función identidad generan la misma subcategoría correflexiva de Top.
- Si h : W1 → W2 es una función continua, entonces FS(W2 , X)Fsx° h es decir,
- Sean h : W1 → W2 y h : W2 → W3 funciones continuas, entonces,
- Sean f,g ∈ [W,W]Top y A={f,g}. Entonces, A ⊆ [W,W]Top. Considerando EA el elevador correspondiente al conjunto A, definido de manera natural, se cumple EA=Ef ∩ Eg; es decir, EA (X)= Ef(X) ∩ Eg(X), para ε todo espacio topológico X.
- Si A={f,g}, B={f}, B ⊆ [W,W], B ⊆ A, entonces, EB(X) ≤ EA(X).
- Si A ⊂ B; A,B⊆ [W,W] entonces, EA(X) ≤ EB(X).
- Si g ∈ [W,W]Top es un homeomorfismo, entonces, Eg(X) ≅ EW. Por tanto, un espacio topológico y cualquiera de sus homeomorfismos generan la misma subcategoría correflexiva de Top.
- Sea entonces, Iiso ⊆ [W,W]. Luego, existe Eiso y se tiene Eiso ≅ EW.
- Si A={f,g}; g es isomorfismo. Entonces EA=Ef , es decir, EA(X)=Ef(X) para todo espacio topológico X.
- Si Λ ⊆ [W,W]Top y Iso ⊆ A entonces, EA(X)=E(A\ Iso)(X), es decir, EA(X)=E(A\Iso)(X) para todo espacio topológico X.
- Si f ∈ [W,W]Top y f es constante, entonces Ef(X)=(X,D), donde D es la topología discreta.
- Si Eg(X)=Ef(X); no necesariamente f=g. En efecto, sean f,g:W → W funciones constantes de valores w0 y w1 respectivamente, con w0 ≠ w1. Entonces, Eg(X)=Ef(X) y f ≠ g.
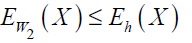
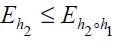
Definición 5: Sean f,g ∈[W,W]Top se define f:g, si y solamente si ∃h homeomorfismo, tal que f=g◦h. Claramente, esta relación es de equivalencia.
Proposición 3: si f:g, entonces Eg ≅ Ef , y por lo tanto, las funciones f y g generan la misma subcategoría correflexiva de Top.
En efecto: como f:g, existe un homeomorfismo h tal que g=f◦h entonces Ef ≤ Ef◦h, es decir, que Ef ≤ Eg(1). Como g=f◦h y h es isomorfismo g◦h-1=f, por tanto Eg◦h-1=Ef , nuevamente usando la propiedad Eg ≤ Eg◦h-1=Ef , es decir, Eg ≤ Ef (2). De (1) y (2) Ef ≅ Eg.
4. Espacios topológicos punteados
En esta sección se muestran nuevas formas de construir subcategorías reflexivas y correflexivas, usando una técnica muy particular, como lo es el agregar o quitar abiertos a un espacio topológico punteado usando su punto base. Estas construcciones dan origen a elevadores y coelevadores definidos en Top* y, por tanto, a subcategorías correflexivas y reflexivas de Top*. Es de anotar que estas nuevas técnicas no se pueden utilizar en Top y, en consecuencia, amplían la teoría expuesta en [5] y, en general, en la sección anterior. Al final se muestra la manera de generalizar los espacios topológicos punteados y, por consiguiente, la categoría Top*.
4.1 Algunos métodos de construcción de subcategorías reflexivas y correflexivas en Top*
Consideraremos la categoría de los espacios topológicos punteados Top*, cuyos objetos son ternas (X,τ,x0), donde X es un conjunto, τ una topología sobre X y x0 ∈ X, y un morfismo f entre dos espacios punteados f:(X,τ,x0) → (Y,τ,y0), es una función continua y f(x0)=y0. Es de anotar que trabajaremos con una definición un poco más fuerte.
Definición 6: la categorÍa de los espacios topológicos punteados Top* se define así:
- Los objetos son ternas (X,τ,x0), X es un conjunto, Τ una topología sobre X y x0 es un punto de X.
- Los morfismos en Top* son funciones f:X → Y continuas y tales que f-1(y0)=x0. Es de anotar que de la teoría de elevadores y coelevadores en [5], y tratando de encontrar métodos distintos a los allí expuestos, se proponen nuevos métodos de construcción de elevadores y coelevadores que no usan topologías iniciales y finales. No obstante, es necesario anotar que las nociones de elevador y coelevador en Top* son las mismas que las dadas para Top*, partiendo en cada caso de un endofuntor definido en Top*; y en forma análoga a lo considerado en Top*, se tiene que la subcategoría plena de Top* formada por los puntos fijos o la imagen de un elevador idempotente definidos en Top*, es correflexiva en Top*; y la subcategoría plena de Top*, formada por los puntos fijos o la imagen de un coelevador idempotente definidos en Top*, es reflexiva en Top*.
A continuación se ilustra la manera de ampliar una topología agregando nuevos abiertos, los cuales se construyen agregando el punto base de un espacio topológico punteado a cada uno de sus abiertos iniciales. Enseguida se muestra cómo esta construcción genera un elevador y, por tanto, una subcategoría correflexiva de Top*.
Si (X,τ,x0) es un objeto de Top*, se define τ*= τ ∪ {A ∪ {x0}|a ∈ τ}. Es claro que τ* es una topologa sobre X.
Proposición 4: dada la aplicación E:Top* → Top* definida por E(X,τ,x0)=(X,τ,x0) y E(f)=f un elevador idempotente, entonces la subcategoría plena de Top*, E(Top*) formada por sus puntos fijos, forma una subcategoría correflexiva de Top*.
- Si (X,τ,x0) ∈ Top* es claro que (X,τ,x0) ∈ Top*.
- Si f:(X,τ,x0) → (Y,τ,y0) es una función continua, E(f)= f:(X,&tau*;,x0) →(Y,τ,y0) es continua. En efecto, sea A ∈ (Y,τ,y0) entonces puede suceder que A ∈ τ o que A=A ∪{y0}, en el primer caso f-1(A) ∈ (X,τ,x0) pues f es continua; en el segundo caso f-1(A)= f-1(A ∪ {y0})=f-1(A1) ∪ f-1({y0})=f-1(A1)∪ {x0}. Luego E:Top* → Top* es un funtor.
- Claramente, (X,τ,x0) ≤ E(X,τ,x0)
- De la definición 6 se obtiene de inmediato que E es idempotente.
- E(Top*)es una subcategorÍa correflexiva de Top*. Aunque este hecho se sigue de la nota de la sección 4.1., aquí se hace la prueba particular de este hecho. En efecto, la función i: (X,τ,x0) → (X,τ,x0) es continua. Ahora bien, sea (Y, β,y0) un elemento de E(Top*) y sea g:(Y, &beta*;,y0)→ (X,τ,x0) una función continua. Entonces, la función g: (Y, &beta*;,y0) → (X,τ*,x0) definida por ḡ(y)=g(y) es la única que hace el siguiente diagrama conmutativo. Luego, E(Top*) es una subcategoría correflexiva de Top*.
Observación: con respecto al funtor E se tiene que:
- Los espacios groseros no son puntos fijos de E.
- Si {x0} es abierto, entonces X=X* es decir, τ = τ*.
- Si {x0} es cerrado, entonces (X,τ,x0) es no conexo.
Proposición 5: sea (X,τ,x0) un espacio topológico y sea (xn)n ∈N una sucesión convergente en dicho espacio; entonces, la sucesión (xn)n ∈N en (X,τ,x0) no necesariamente es convergente, como lo muestra el siguiente ejemplo:
Ejemplo: en (R, µ ,0), donde R es el conjunto de los números reales y µ es la topología usual. La sucesión 1/n converge a 0, 1/n → 0 En τ*= τ ∪{A ∪ {0}|A ∈ τ} el abierto (-∞ 0) ∪ {0} no contiene elementos de la sucesión.
Proposición 6: sean (X,τ,x0) un espacio topológico y (xn)n ∈ N una sucesión que converge a l, l ≠ x0, entonces la sucesión (xn)n ∈ N en (X,τ,x0) también converge a l.
En efecto, sea V un abierto de τ* tal que l ∈ V. Debemos encontrar n0 ∈ N, de tal forma que si n ≥ n0 entonces xn ∈ V. Hay dos posibilidades: i) si V ∈ τ, puesto que xn converge a l en τ, entonces existe n0 ∈ N tal que si n ≥ n0; n ∈ V; ii) si V=A ∪{x0}, A ∈ τ, entonces l ∈ A y estamos en el caso anterior.
Teorema 2: si (X,τ,x0) es conexo y {x0} no es cerrado en τ entonces (X,τ,x0) es conexo.
En efecto, supongamos que (X,τ,x0) es no conexo, es decir, existen abiertos N y M tales que N∪M=X y N ∩ M=ϕ como τ*= τ ∪ {A∪ {x0}|A ∈ τ} entonces, se tienen los siguientes casos:
- N, M ∈ τ en este caso (X,τ,x0) sería no conexo.
- N ∈ τ, M=A ∪{x0} entonces puede suceder:
- x0 ∈ N y x0 ∉ A entonces N ∩ M ≠ ϕ, lo cual es imposible.
- x0 ∈ N y x0 ∈ A y como M=A ∪ {x0}; N ∩ M≠ϕ
- x0 ∉ N y x0 ∉ A entonces N ∪ M=N ∪(A ∪ {x0}=X, es decir, N ∪ A=X\{x0}, en este caso X\{x0} es abierto, lo cual es imposible.
Las siguientes dos proposiciones ilustran la manera de reducir una topología, en el sentido de quitar abiertos, eliminando los abiertos que contienen al punto base de un espacio topológico punteado. Enseguida se muestra cómo esta construcción genera un coelevador y, por tanto, una subcategoría reflexiva de Top*.
Si (X, τ,x0) es un espacio topológico punteado, la colección τ*=( τ{A ∈ τ|x ∈ A}) ∪ {X} es una topología sobre X.
Proposición 7: la aplicación C:Top* → Top*, definida por C(X, τ,x0)=(X, τ*,x0) y C(f)=f es un coelevador y, por tanto, la imagen de dicho funtor es una subcategoría reflexiva en Top*. La prueba es inmediata.
Proposición 8: todo espacio topológico punteado (X, τ,x0) se puede sumergir en un espacio topológico conexo.
En efecto, sea (X, τ,x0) un espacio topológico y, considerando (X, τ*, x0) donde τ*=(τ\ {A;A ∈ τ;x0 ∈ A}) ∪ {X}, entonces τ* ⊆ τ. Por tanto, i: (X, τ, x0) → (X, τ*, x0) es continua. Nótese que (X, τ*, x0) es conexo, pues la única forma de obtener X como unión de dos abiertos es que uno de ellos sea el mismo X.
Proposición 9: todo espacio topológico punteado se puede sumergir en un espacio topológico compacto.
En efecto, sea (X, τ, x0) un espacio topológico. Si consideramos el espacio topológico (X, τ*, x0)) donde τ*=(τ\{A∈ τ|x0 ∈ A}) ∪ {X}, entonces, como antes, τ* ⊆ τ y así la función i:((X, τ, x0) → (X, τ*, x0) es continua. Nótese que (X, τ*, x0) es un espacio topológico compacto, pues la única forma de escribir X como unión de abiertos, es si uno de ellos es el mismo espacio X.
Observación: en Top* no todo coelevador preserva la disconexión. Si C:Top*→Top* es un coelevador, entonces no necesariamente C(Top*) es disconexo, lo cual se muestra en el siguiente ejemplo de carácter general.
Ejemplo: sea C el coelevador
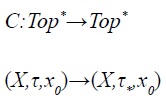
(X,τ,x0) puede ser disconexo y (X,τ*;,x0) siempre es conexo. Para finalizar esta sección, se muestra un endofuntor en Top* cuya imagen está formada por espacios que son a la vez compactos y conexos. Si (X,τ,x0) es un espacio topológico y si X0=X\{x0}, entonces τ1={A ∩ X0|A ∈ τ} ∪ {X} es una topología sobre X.
Proposición 10: la aplicación F:Top* → Top*, F(X,τ,x0)=(X,τ1,x0) y F(f)=f, es un funtor. Por tanto, la subcategoría plena formada por sus puntos fijos forma una subcategoría reflexiva en Top*.
C:Top* → Top* es un funtor, en efecto:
- F(X,τ,x0)=(X,τ1,x0) ∈ Top*
- Sea f:(X,τ,x0) → (Y,α,y0) una función continua, entonces f:(X,τ1,x0)→(Y,α1,y0) es continua. En efecto, sea A1 ∈ α, entonces, A1=A\{y0}. Luego, f-1(A\{y0})=f-1(A) ∩ f-1({y0}c). Como f:(X,τ,x0) → (Y,α,y0) es continua, entonces f-1(A) ∈ τ y f-1(A) ∩ f-1({y0}c)= B ∩{x0}c=B\{x0}c. Por ende, F:Top* → Top* es un funtor.
Proposicion 11: si (X,τ,x0) es un espacio topológico, entonces (X,τ1,x0) es conexo.
En efecto, sean A,B ∈ τ tales que A1 ∩ B1=ϕ entonces,
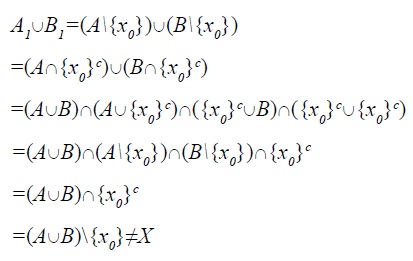
para todo A,B ∈ τ y, por tanto, X es conexo.
Puesto que todo recubrimiento abierto de X debe contener a {X}, la prueba de la siguiente proposición es inmediata.
Proposición 12: (X,τ1,x0) es compacto.
4.2. Una generalización de los espacios topológicos punteados
Proposición 13: si (X,τ) es un espacio topológico X+=X ∪ {x1}; {x1} ∈ X definimos τ*=τ∪ {A ∪ {x0}|A ∈ τ}, entonces τ* es una topología de X+.
- Como Ø ∈ τ* y X+=X ∪ {x1}, entonces Ø y X+ ∈ τ*.
- Sean C,D ∈ τ*, vemos que C ∪ D ∈ τ*. En efecto, si C,D ∈ τ* entonces pueden darse varios casos :
- C,D ∈ τ, por tanto C ∩ D ∈ τ ⊆τ*.
- C ∈ τ y D=A ∪ {x1}, con A∈ τ, entonces,
- Sea {Bα}α ∈ H una familia de elementos de τ’. Si todo Bα está en τ, entonces
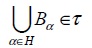 de donde
de donde 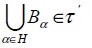 . Si para algún α’ ∈ H
se tiene que B=A ∪ {x1}, A ∈ τ, entonces,
. Si para algún α’ ∈ H
se tiene que B=A ∪ {x1}, A ∈ τ, entonces,
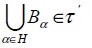 . En consecuencia, la siguiente
proposición es inmediata.
. En consecuencia, la siguiente
proposición es inmediata.
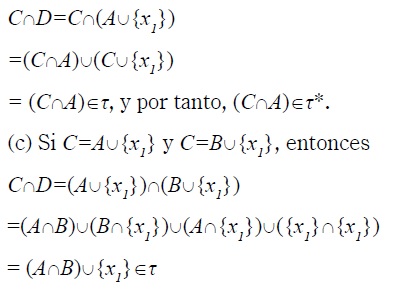
Proposición 14: sean (X,τ) un espacio topológico y x0,x1 ∈ X, x0 ≠ x1. Se define τ**= τ ∪ τ0 ∪ τ1 ∪ τ2, donde τ0={A ∪ {x0}|A ∈ τ}, τ1={A ∪ {x1}|A ∈ τ}, τ2={A ∪ {x0,x1}|A ∈ τ}. Entonces, τ’ es una topología.
La categoría de los espacios topológicos bipunteados, notada Top**, tiene por objetos a las ternas de la forma (X,τ,{x0,x1}), x0 ≠ x1 y un morfismo f entre dos objetos (X,τ,{x0,x1}) x0 ≠ x1; y (Y, α,{y0,y1}) y0 ≠ y1 es una función f:X → Y tal que f:(X,τ) →(Y,α) es continua, f:{x0,x1} → {y0,y1} es biyectiva y además f-1({y0,y1})= {x0,x1}.
Proposición 15: si f:(X,τ,{x0,x1}) → (Y,α,{y0,y1}) es un morfismo de Top**, entonces f:(X,τ**,{x0,x1}) → (Y,α**,{y0,y1}), es continua. En efecto:
- Si B ∈ α entonces, f-1(B) ∈ τ.
- Sea C=B ∪ {y0}, B ∈ τ, entonces f-1(C)= f-1(B ∪ {y0})=f-1(B) ∪ f-1{y0}=A ∪ {x0} o f-1(C)= A ∪ {x1}.
- C=B ∪ {y1}, B ∈ τ, entonces, f-1(C)= f-1(B ∪ {y1})=f-1(B) ∪ f-1{y1}=A ∪ {x0} o f-1(C)= A ∪ {x1}.
- Si C=B ∪ {y0,y1}, B ∈ τ, entonces, f-1(C)= f-1(B ∪ {y0,y1})=f-1(B) ∪ f-1(B ∪ {y0,y1})=A ∪ {x0,x1}, es decir, f es continua.
En forma análoga a como se hizo en Top*, se definen elevadores y coelevadores en Top**; de igual manera, los puntos fijos de elevadores y coelevadores idempotentes de Top* dan origen a subcategorías correflexivas y reflexivas de Top**, respectivamente.
Proposición 16: la aplicación E:Top** → Top** definida por E(X,τ,{x0,x1})=(X,τ**,{x0,x1}) y E(f)=f, es un elevador y E(Top**) es correflexiva en Top**.
En efecto, de las proposiciones 14 y 15 y el hecho que τ ⊆ τ**, se tiene que E es un elevador idempotente y que E(Top**) es correflexiva de Top**.
A continuación se consideran conjuntos con un subconjunto distinguido, es decir, parejas de la forma (X,A), donde X es un conjunto y A un subconjunto finito de X.
Es de anotar que si (X,τ) es un espacio topológico y A ⊆ X, entonces, τA={C ∪ E|C ∈ τ, y, E ∈ ℘ (A)}; claramente, τA es una topología sobre X.
Por otra parte, si (X,τ) es un espacio topológico y B ⊂ X, se define el conjunto τE={A ∪ E|E ∈ P(B), y, A ∈ τ}, entonces
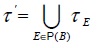
es una topología sobre X.
Definición 7: sea n un entero positivo. La categoría Conjn tiene por objetos a las parejas de la forma (X,A), donde X es un conjunto y A ⊂ X, de cardinal n, esto es, |A|=n. Los morfismos entre dos objetos (X,A) y (Y,B), son funciones f : X → Y, tal que f-1(C)=A y f |A:X → B, es biyectiva.
Definición 8: sea n un entero positivo. La categoría Topn tiene por objetos a las ternas de la forma (X,τ,A), donde X es un conjunto, τ una topología sobre X y A un subconjunto finito de X, de cardinal n, |A|=n. Los morfismos entre dos objetos (X,τ,A) (Y,α,B) son funciones f:X → Y tal que f es continua, f-1(B)=A y f |A:X → B es biyectiva.
En forma análoga a como se hizo en Top*, se definen elevadores y coelevadores en Topn , y de igual manera los puntos fijos de elevadores y coelevadores idempotentes en Top* dan origen a subcategorías correflexivas y reflexivas de Topn, respectivamente.
Proposición 17: sobre Topn se define la aplicación E:Topn → Topn de la siguiente forma: E(X,τ,A)=(X,τA,A) donde τA={C ∪ E| A ∈ τ, y, E ∈ P(B)} y E(f)=f. Entonces, E es un funtor, elevador idempotente y ETopn es correflexiva en Topn.
En efecto, la aplicación E:Topn → E:Topn es claramente una aplicación entre objetos. Sea
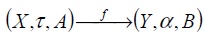
un morfismo en Topn, es decir, f:X → Y una función f |A:X → B biyectiva y f:(X,τ) → (Y,α) es continua, luego: E(f):(X,τA,A) → (Y,αB,B) es continua. En efecto, sea D ∈ αB entonces, D ∈ α, ó, D=C∪ E, C ∈ α y E ⊆ B; y f-1(D) ∈ τ si D ∈ α. Ahora bien, si D=C ∪ E entonces, f-1(C ∪ E)=f-1(D) ∪ f-1(E) ∈ τ, pues f-1(C) ∈ τ y f-1(E) ∈ ℘(A).
Puesto que claramente E es elevador idempotente, E(Topn) es una subcategoría correflexiva de (Topn)
5. Conclusiones: los espacios exteriores
La categoría formada por los espacios topológicos y las funciones propias determina la categoría propia, que ha resultado útil para el estudio de los espacios no compactos y su homotopía propia. En [10] se presenta la categoría de los espacios exteriores E como una extensión de la categoría propia y una potente herramienta para el estudio de los espacios no compactos. En particular, se muestra que E es una categoría equivalente a una subcategoría de los espacios punteados en donde los puntos son cerrados. Se considera importante citar estos resultados, a manera de conclusiones.
- Una externología sobre un espacio topológico (X,τ) es una colección no vacía ε de subconjuntos abiertos, es decir, ε ⊆ τ que satisface las siguientes propiedades: i) si E1,E2 ∈ ε entonces, E1 ∩ E2 ∈ ε; ii) si E ∈ ε, U ∈ ε y E⊆U, entonces, U ∈ ε [10]. Los elementos de ε se llaman abiertos-externos, o ε– abiertos; un espacio exterior es una terna (X,ε,τ) donde X es un conjunto, τ es una topología sobre X y ε es una externología sobre X. Se define la categoría de los espacios exteriores E. Los objetos de esta categoría son ternas de la forma (X,ε,τ), donde τ es una topología sobre X y ε una externología. Los morfismos f entre dos espacios exteriores (X,εX,τX) y (Y,εY,τY) son funciones f:X → Y tales que: f:(X,τX) → (Y,τY) son continuas. f: (X,εX) → (Y,εY) es tal que f-1(A) ∈ εX si A ∈ εY [10].
- Dado un espacio exterior (X,ε,τ) se determina un espacio topológico (X,τ∞), donde τ∞=τ ∪ {A ∪{∞}|A ∈ ε}. Nótese que {∞} es cerrado, ∞ es un elemento que no está en X [10]. Dado un morfismo f:(X,εx,τx)→(Y,εY,τY) en E, la función f:(X,τx ∞) → (Y,τY∞) resulta continua. Por tanto, se ha determinado un funtor F:E → Top, ver [10], la imagen de F, la notaremos Top∞. Cada espacio (X,τ∞) se puede ver como un objeto de la categoría Top*. A continuación se mencionan algunos resultados que se consideran interesantes dentro de la teoría en cuestión.
- Top∞ es una subcategora de Top* cuando {x0} es cerrado [10].
- La categoría de los espacios exteriores E es equivalente a la categoría Top∞ [10].
1. En general,[A, B]C corresponde a los morfismos de A en B de una categoría C
2. En la categoría de los espacios topológicos los isomorfismos corresponden a los homeomorfismos.
Referencias
R. Montañez y C. Ruiz, “Elevadores de estructura”, Boletín de Matemáticas, Nueva serie, XIII, no. 2, pp. 111-35, 2006.
[2] J. Hernández, Sobre las subcategorías reflexivas y correflexivas de la categoría de los espacios topológicos, tesis de Maestría, Universidad Nacional de Colombia, Bogotá, 2012.
[3] J. Adamek, Theory of Mathematical Structures, Boston: Lancaster: D. Reidel Publishing, 1983.
[4] S. Mac Lane e I. Moerdijk, Sheaves in Geometry and Logic, A first introduction to topos Theory, New York: Springer-Verlag, 1992.
[5] R. Montañez, Funtores elevadores y coelevadores de estructuras, tesis de doctorado, Universidad Nacional de Colombia, Bogotá, 2007
[6] J. Adamek, H. Herrlich y G. Strecker, Abstract and Concrete Categories, New York: John Wiley & Sons, 1990.
[7] J. Hernández, R. Montañez y C. Ruiz, “Nociones de mejoramiento en la categoría de los espacios topológicos”, Revista Visión Electrónica, Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, año 5, no. 1, pp. 56-67, enero-junio 2011.
[8] R. Montañez, Fibraciones categóricas, tesis de maestría, Universidad Nacional de Colombia, Bogotá, 1994.
[9] S. Willard, General topology, Adisson Wesley Publishing Company, 1970.
[10] L. Español, M. García y C. Minguez, “On Proper and Exterior Sequen-tiality”, Applied Categorical Structures, vol. 18, no. 6, pp. 653-668, doi: 10.1007/s10485-009-9201-8.


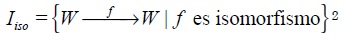
1.png)




.jpg)