DOI:
https://doi.org/10.14483/udistrital.jour.colomb.for.2014.1.a03Publicado:
01-01-2014Número:
Vol. 17 Núm. 1 (2014): Enero-JunioSección:
Artículos de investigación científica y tecnológicaEvaluación de MDE para la estimación de volúmenes por procesos de erosión aplicando análisis de autocorrelación espacial en una cuenca de los andes venezolanos. Caso de estudio: microcuenca torrencial La Machirí
Evaluation of digital elevation models for estimating erosion volumes by using spatial autocorrelation analysis in a catchment of the Venezuelan Andes, a case study in the torrential micro-watershed La Machirí
Palabras clave:
Exploratory spatial data analysis -ESDA, multiple- point geostatistics, digital elevation model (DEM), La Machirí, volume (en).Palabras clave:
análisis exploratorio de datos espaciales (ESDA), geoestadística de puntos, MDE, La Machirí, volumen (es).Descargas
Referencias
Adediji, A., Ibitoye, M., & Ekanade, O. (2008). Generation of digital elevation models (DEMs) for gullies in Ondo-State, Nigeria. Journal of Environmental Hydrology, 16, 1-11.
Anton, C., & Martínez-Casasnovas (2001). Cartografía de la erosión por barrancos mediante restitución fotogramétrica y modelos digitales de elevación en El Penedès (Cataluña). Teledetección, medio ambiente y cambio global.
Bosque, J. (1992). Sistemas de información geográfica. Madrid: Ediciones Rialp. 451 p.
Camargo, C. (2012). Evaluación multitemporal de procesos de erosión en laderas mediante el uso de sensores remotos. Caso de estudio: micro-cuenca torrencial “La Machirí” San Cristóbal, Edo. Táchira (Trabajo de Maestría, Manejo de Cuencas Hidrográficas). Mérida: Universidad de Los Andes. 146 p.
Casalí, J., López, J., & Giráldez, J. (1999). Erosión por cárcavas efímeras en el sur de Navarra (España): descripción y cuantificación. Ingeniería del Agua, 6, 251-258
Conrad, O. (2010). Description module SAGA: Mínimun distance analysis, Spattial point pattern analysis, Variogram surface. Revisado el 3 de junio de 2012.
Enviromental Systems Research Institute (ESRI) (2008). ArcGis Versión 9.3.
Derose, R., Gómez, B., Marden, M., & Trustrum, N. (1998). Gully erosion in Mangatu forest, New Zealand, estimated from digital elevation models. Earth Surf. Process. Landforms, 23, 1045-1053.
Felicisimo, A. (1994). Modelos digitales del terreno. Introducción y aplicaciones en las ciencias ambientales. Oviedo: Pentalfa Ediciones. 118 p.
Ferrer, C. (1977). Estudio geomorfológico detallado de la cuenca media-inferior del río Torbes Estado Táchira. Mérida: Universidad de los Andes. 180 p.
Finol, U. (1972). En la micro-cuenca “La Machirí”, el hombre perdió la batalla. Mérida: Universidad de Los Andes. 23 p.
Giraldo, R. (2002). Introducción a la geoestadística: Teoría y aplicación. Bogotá: Universidad Nacional de Colombia. 94 p.
González, A. (1982). diagnóstico físico conservacionista de la cuenca del río Torbes. Mérida: Universidad de los Andes. 72 p.
Hernández, L. (2008). Proyecto fotogramétrico digital. Bogotá: Universidad Distrital Francisco José de Caldas. 179 p.
Hopf, J. (1972). Proyecto conservacionista y corrección de la cuenca La Machirí, San Cristóbal Edo. Táchira. Mérida: Corporación de los Andes. 44 p.
James, l., Watson, D., & Hansen, W. (2007). Using LiDAR data to map gullies and headwater streams under forest canopy: South Carolina, USA. Catena, 71, 132-144.
Junior, J., Cruz, L., Nogueira, T., & Rodriguez, S. (2008). Monitoramento de processos erosivos em parcelas experimentais no município de uberlândia, mg. Revista Geográfica Académica, 2 (3), 5-18.
Larsson, R., & Strömquist, L. (1995). Monitoreo del medio ambiente con análisis de imágenes satelitarias. Tryckkontakt, Uppsala. 97 p.
Laboratorio de Fotogrametría y Sensores Remotos (2007). Sistemas de información geográfica, ejercicio número 04: Escaneo y georeferenciación. Laboratorio de Fotogrametría y Sensores Remotos. Mérida: Universidad de los Andes. 9 p.
Leica Geosystems Geospatial Imaging (2008). Erdas Imagine 9.2. Leica Photogrammetry Suite 9.2.
Lobo, J., & Ulrich, K. (2008). Modelos digitales de elevación (MDE) a partir de sistemas satelitales. Una introducción y análisis comparativo en la cordillera de Mérida-Venezuela. Revista Geográfica Venezolana, 49 (1), 11-42.
Martínez-Casasnovas, J., Ramos, M., & Ribes-Dasi, M. (2001). Soil erosion caused by extreme rainfall events: mapping and quantification in agricultural plots from very detailed digital elevation models. Geoderma, 105, 125-140.
Martínez-Casasnovas. J (2003). A spatial information technology approach for the mapping and quantification of gully erosion. Catena, 50, 293-308.
Martínez-Casasnovas, J., Ramos, M., & Poesen, J. (2004). Assessment of sidewall erosion in large gullies using multi-temporal DEMs and logistic regression analysis. Geomorphology, 58, 305-321.
Emmanouloudis, D., Filippidis, E., & Mas, F. (2004). Una técnica SIG para el cálculo del volumen de desprendimientos. Montes, 76, 22-28.
Mora, E. (2000). Algunas consideraciones sobre muestreo. Revista Geográfica Venezolana, 41 (1), 31-46.
Moreno, A. (2008). Sistemas de información geográfica. Manual de Autoaprendizaje con ArcGIS. México: Alfaomega Grupo Editor. 911 p.
Olaya, V. (2011). Sistemas de información geográfica. Recuperado de http://wiki.osgeo.org/wiki/Libro_SIG. 877 P.
Perroy, R., Bookkhagen, B., Asner, G., & Chadwick, O. (2010). Comparison of gully erosion estimates using airborne and ground-based LiDAR on Santa Cruz Island, California. Geomorphology, 118, 288-300.
Petróleos de Venezuela (2009). Código Estratigráfico de las Cuencas Petroleras de Venezuela. Recuperado de http://www.pdvsa.com/lexico/l38w.htm
Romero, A., Marín, H., Noguera, N., Maldonado, H., Infante, Y., & Valbunea, E. (1995). Análisis exploratorio de los datos de suelos de la región zuliana aprovechamiento de un SIG. Revista Geográfica Venezolana, 36 (2), 153-174.
System for Automated Geoscientific Analyses (SAGA) (2011). Versión 2.8.0. User Group Association.
Schenk, T. (2002). Fotogrametría digital. Marcombo. Vol.1 Instituto de Cataluña- España. 479 p.
Tapia, J. (2007). Introducción al análisis de datos con SPSS para Windows. Fondo Editorial Unellez, Universidad Ezequiel Zamora, Barinas - Venezuela. 184 p.
Tranarg C.A. (1971). La Machirí, Hojas D-6, D-7, E-6, E-7, Escala 1:2.500. Caracas - Venezuela.
Universidad De Castilla-La Mancha. (2008). Pruebas no paramétricas. Venezuela. Recuperado el 27 de agosto de 2013, de http://www.pdvsa.com/lexico/l38w.htm
Uzcátegui, F. (1975). Canales y diques en la micro-cuenca Los Pinos-La Machirí (San Cristóbal). Mérida: Ministerio de Agricultura y Cría. 63 p.
Vilchez, J. (2000). Introducción a los sistemas de información geoespacial. Mérida: Universidad de Los Andes, Consejo de Desarrollo Científico, Humanístico y Tecnológico. 203 p.
Vivas, l. (1992). Los Andes venezolanos. Caracas: Academia Nacional de la Historia. 255 p.
Wang, T., Fuhong He, F., Zhang, A., Gu, L., Wen, Y., Jiang, W., & Shao, H. (2014). A quantitative study of gully erosion based on object-oriented analysis techniques. The Scientific World Journal.
Wolf, P., & Brinker, R. (1997). Topografía. México D.F :Alfaomega Grupo Editor. 815 p.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
EVALUACIÓN DE MDE PARA LA ESTIMACIÓN DE VOLÚMENES POR PROCESOS DE EROSIÓN APLICANDO ANÁLISIS DE AUTOCORRELACIÓN ESPACIAL EN UNA CUENCA DE LOS ANDES VENEZOLANOS. CASO DE ESTUDIO: MICROCUENCA TORRENCIAL LA MACHIRÍ
Evaluation of digital elevation models for estimating erosion volumes by using spatial autocorrelation analysis in a catchment of the Venezuelan Andes, a case study in the torrential micro-watershed La Machirí
Título corto: Evaluación MDE aplicando autocorrelación espacial
Cristopher Edgar Camargo Roa1, Jesús Enrique Andrades Grassi2, Raúl Oswaldo Vidal García3
1Universidad Nacional Experimental del Táchira, Departamento de Carreras Técnicas Semipresenciales -CTS-UNET-, Táchira-Venezuela. Dirección postal:
San Cristóbal, UNET Sede Las Lomas: Villa Olímpica, Sede de CTS Táchira-Venezuela 5001 ccamargo@unet.edu.ve. Autor para correspondencia.
2Facultad de Ciencias Forestales y Ambientales, Centro de Estudios Forestales y Ambientales de Postgrado -CEFAP-, Universidad de Los Andes,
Mérida-Venezuela. andrades@ula.ve
3Facultad de Ciencias Forestales y Ambientales, Centro de estudios Forestales y Ambientales de Postgrado -CEFAP-, Universidad de Los Andes,
Mérida-Venezuela. rvidal@ula.ve
Recepción: 19 de octubre de 2013 / Aprobación: 20 de diciembre de 2013
RESUMEN
Los modelos digitales de elevación -MDE-, como representación visual de las formas del relieve y de los valores de altura, han sido muy útiles para estudiar los aspectos relacionados con la topografía de un área. Esta investigación se realizó en un área de 3.39 km2 de la microcuenca torrencial La Machirí (estado Táchira, Venezuela). Tuvo por objetivo evaluar un MDE obtenido por un proceso de fotogrametría digital cotejado a su vez con un MDE elaborado a partir de la edición de curvas de nivel existentes en cartas topográficas. Para ello se aplicaron métodos como el análisis exploratorio de datos espaciales -ESDA- y la geoestadística de puntos (análisis de mínima distancia, análisis de patrones espaciales, variograma y superficie variográfica). Se pudo determinar una diferencia existente entre ambos modelos, resultado de la sumatoria de los errores generados, en primer lugar, por la distribución espacial de los puntos de control señalados para el proceso fotogramétrico (número de puntos menores al valor de una distribución normal, posible sesgo espacial entre los puntos y manifestación de fenómenos de dependencia espacial), seguido del error generado a partir del método de interpolación aplicado durante el mismo y el error resultante originado por el comportamiento local de los procesos de erosión en el área. La primera valoración arrojó una diferencia en la superficie de área de 0.57 ha y en volumen de 9.41 hm3 en ambos MDE. Un análisis sectorizado permitió determinar la falta de al menos 3 puntos de control para obtener un MDE más satisfactorio.
Palabras clave: análisis exploratorio de datos espaciales -ESDA-, geoestadística de puntos, MDE, La Machirí, volumen.
ABSTRACT
Digital elevation models -DEM- as a visual representation of landforms and altitude have been very useful in the study of topography. This research took place in a 3.39 km2 area of the La Machirí torrential micro-watershed (Táchira State, Venezuela). Its purpose was to evaluate a DEM generated through a process of digital photogrammetry that was also checked against a DEM edited from existing level curves in topographic charts. Exploratory Spatial Data Analysis (ESDA) and the Multiple-Point Geostatistics (Minimal Distance Analysis, Special Pattern Analysis, Variogram, and Variographic Analysis of Surfaces) methods were used. Differences between the two models were identified generated by the sum of the errors caused by the spatial distribution of checkpoints marked for the photogrammetric process (less than the number of checkpoints of a normal distribution, possible spatial bias between checkpoints and indications of spatial dependence phenomena), the error generated from the interpolation method applied during the process, and by the error caused by local erosion processes. The first assessment indicated a difference in the surface area of 0.57 ha and of 9.41 hm3 in volume in both DEMs. A zoned analysis indicated that at least three more checkpoints are necessary in order to get a more accurate DEM.
Keywords: Exploratory spatial data analysis -ESDA, multiple- point geostatistics, digital elevation model (DEM), La Machirí, volume.
INTRODUCCIÓN
Los estudios de los procesos de erosión, al igual que otros campos dentro de las áreas del saber geográfico o ambiental han estado a la par conformes a como se han dado los avances tecnológicos. Así pues, el hacer científico ha pasado de los procedimientos manuales, laboriosos de orden analógico sobre papel, a procesamientos rápidos digitales como el que han fomentado los ordenadores modernos.
Existe una gran cantidad de enfoques cuyo objetivo es la cuantificación e inclusive la simulación de los procesos de erosión, especialmente sobre la dinámica, forma, volumen removido en tiempo y espacio, origen, entre otros. Dichos enfoques podrían clasificarse en cuatro grandes categorías esbozadas a grandes rasgos. La primera de ellas, encargada de realizar estudios de observación sobre las propias áreas donde ocurre la erosión, muestra los estudios fotogramétricos de Larsson & Strömquist (1995) en África meridional (basados en imágenes satelitales y fotografías aéreas). La segunda categoría simula lo que ocurre cuando hay presencia de procesos de erosión, mediante el uso de parcelas que controlan las variables pendiente, tipo de suelo, cobertura y pluviosidad, en laboratorios destinados exclusivamente para ello; por ejemplo: el estudio desarrollado en el municipio Uberlândia, Brasil (Junior et al., 2008). Tercera, los métodos de cuantificación directa, basada en el uso de estacas y/o levantamientos de perfiles altamente detallados de la topografía (Martínez-Casasnovas et al., 2001). Y por último, los que se hallan insertos plenamente bajo la forma de programas de computación que recogen y traducen los datos requeridos por las teorías y criterios científicos comprobados por los círculos de expertos en la materia.
Los sistemas de información geográfica (SIG) pertenecen a esta última categoría, siendo su gran capacidad de representación, análisis y ahorro de tiempo su sello distintivo. Procesos laboriosos como la preparación de datos de entrada para el desarrollo de la Ecuación Universal de Pérdida de Suelo (EUPS, conocida por sus siglas en inglés como USLE), por ejemplo, realizada de modo analógico, en la actualidad se ha visto significativamente reducida en cuanto al empleo del tiempo (Camargo, 2012).
El uso más común de los SIG ha versado principalmente en la capacidad que tienen de elaborar modelos digitales de elevación (MDE), definidos como la pieza clave en el análisis geomorfométrico, equivalente informatizado de la cartografía clásica de elevaciones tradicionales representadas mediante curvas de nivel (Olaya, 2011), presentada como variable continua sobre una superficie bidimensional a través de una red regular de valores Z referenciados a un datum común (Lobo & Ulrich, 2008).
Finalmente, los MDE han sido muy útiles para calcular la pendiente del área que contribuye a la erosión y a su inicio; la obtención de umbrales de barrancos para la iniciación y deposición de sedimentos; la localización de cárcavas incipientes en el paisaje; la estimación del retroceso de las cabezas o coronas de los barrancos y cárcavas atendiendo a la morfología y el estudio de la contribución de los sedimentos, la producción de tasas de expansión volumétrica y los procesos relacionados con erosión activa (Anton & Martínez-Casasnovas, 2001; Martínez-Casasnovas et al., 2004; Emmanouloudis et al., 2004).
La obtención del volumen de suelo erosionado se puede entender como la sustracción realizada entre dos MDE: uno que modela las características de las cárcavas en un tiempo preexistente y otro en un tiempo más reciente; así lo explican Perroy et al. (2010). Un ejemplo de alta aplicabilidad sería al momento de establecer la construcción de una carretera u otra obra ingenieril. De este modo se hace posible conocer el volumen de tierra que es necesario remover de un terreno o llevar para rellenar otro (Wolf & Brinker, 1997; Vílchez, 2000). El mismo procedimiento puede ser aplicado para conocer el volumen removido por procesos de erosión en las laderas de las montañas. Adediji et al. (2008), de manera más específica, señalan que los MDE, aparte de estimar volúmenes, pueden también ser derivados para establecer los atributos morfométricos de las cárcavas como la pendiente, el área de captación, el promedio de ancho y profundidad, así como el área y su sección transversal.
Aunque el método de estimación de volúmenes y demás aspectos de la erosión usando MDE es rápido, sencillo y fácil para realizar monitoreo periódico, su precisión de cálculo es limitada, debido a las incertidumbres de los datos de teledetección, las limitaciones en la construcción de precisión de los datos MDE y en su resolución temporal y espacial (Wang et al., 2014).
La calidad y la precisión de la información relacionada con la estimación de valores por erosión dependen de que el MDE represente el terreno de la manera más exacta posible, ya que la precisión de un MDE determina la fiabilidad del análisis morfométrico (Lobo & Ulrich, 2008). Como explica Schenk (2002), los MDE pueden presentar problemas, y más aún si son generados de modo automático a partir de fotografías aéreas o imágenes satelitales. La conclusión resulta evidente: de un MDE de buena calidad se podría generar una excelente comprensión de las amenazas que pueden representar para las poblaciones los procesos de erosión.
Los objetivos de este trabajo consistieron en: 1) detectar el sesgo estadístico existente en un MDE obtenido por medio de un proceso fotogramétrico digital aplicado sobre fotografías aéreas para un área con proceso de carcavamiento y 2) la distribución que tienen estos dentro del mismo modelo, a fin de determinar su calidad, usando como MDE de referencia un modelo generado a partir de la digitalización de curvas de nivel de unas cartas topográficas preexistentes para el área, con intervalos de curvas a 2 m.
Para ello se aplicaron herramientas de los SIG que permiten el estudio de los datos, como aseguran Romero et al. (1995), mediante análisis exploratorio de datos espaciales (ESDA, por su sigla en inglés) y el análisis geoestadístico de puntos, sobre los puntos de control utilizados para la elaboración del modelo fotogramétrico, como en otros puntos desconocidos que fueron escogidos por un método de interpolación. Estas herramientas permitieron realizar el análisis, la interpretación y la revisión del modelo de modo global y sectorizado.
Con estos análisis se reconoce a la geoestadística como un área del conocimiento para el análisis de datos espaciales y específicamente la importancia de la información georreferenciada y cuándo esta es susceptible de ser analizada por medio de dicha metodología (Giraldo, 2002).
MATERIALES Y MÉTODOS
Área de estudio
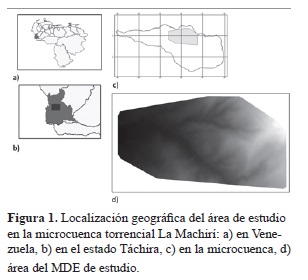
La evaluación de la calidad del MDE se realizó en un área de 3.39 km2 de la microcuenca torrencial "La Machirí" (estado Táchira, Venezuela), siendo esta el resultado de las áreas coincidentes entre un MDE obtenido por medio del proceso fotogramétrico desarrollado con el software ERDAS IMAGINE 9.2 módulo LPS 9.2, sobre las fotografías 081082-083 de la misión aérea 0102121 del año 1976 (escala 1:25.000), escaneadas a una resolución de 14 micrones, con las cuales se generó un modelo de curvas a escala 1:2.500, una ortofoto y el MDE creado a partir de la rasterización mediante un SIG de las curvas de nivel (digitalizadas previamente de forma manual sobre pantalla), presentadas en las cartas elaboradas por Tranarg C.A.( 1971) (hojas D-6, D-7, E-6, E-7, escala 1:2.500), el cual constituyó a su vez el MDE de referencia de evaluación y validación (figura 1). Cada uno de los MDE cuenta con 1382 columnas y 758 filas.
El área de estudio mencionada está ubicada en la sección central de la microcuenca torrencial "La Machirí", al norte de la ciudad de San Cristóbal (capital del estado Táchira), entre las longitudes 72º 10’ y 72º 13’ oeste y entre las latitudes 7º 47’ y 7º 49’ norte, con una extensión aproximada de 20 km2. Su altitud varía entre los 800 m en la desembocadura en el río Tórbes y los 2214 m en el pico El Oso (Hopf, 1972). Una diferencia altitudinal considerable de 1400 m, que desempeña un papel determinante en la conformación de la dinámica de los procesos de erosión que allí se desarrollan. Hopf (1972) y Uzcátegui (1975) han indicado que en la cuenca, la precipitación media anual puede ser superior a los 1300 mm, distribuida con mayor intensidad entre abril y noviembre, infiriendo a su vez que la configuración orográfica hace aumentar la precipitación a medida que se asciende en altitud dentro de esta, lo cual queda confirmado por el tipo de vegetación natural que se desarrolla en la zona (Ferrer, 1977). La temperatura promedio anual oscila entre los 21ºC en la parte inferior y los 16 ºC en la parte superior, correspondiendo al piso climático macro-mesotérmico, en la clasificación de H. Pittier (Finol, 1972).
Predominan suelos originados a partir de limolitas que poseen una coloración marrón rojiza 2.5 YR 4/4, pertenecientes a la formación La Quinta, del cretáceo (Ferrer, 1977). Según Hopf (1972), en algunas quebradas los suelos pueden variar entre 2 y 6 m de profundidad y otros se encuentran directamente sobre la roca. Sin embargo, la profundidad para el resto de la cuenca puede ser variable. En el caso de las laderas, suelen ser pocos profundos (González, 1982) y en zonas planas de mayor espesor.
La dinámica en las vertientes dentro de La Machirí ha señalado un proceso donde la geología, aunada al alto grado de pendiente y a las prácticas agropecuarias, ha ocasionado mecanismos de erosión que han configurado con el pasar de los años cárcavas espectaculares (Vivas, 1994) o farallones en zonas de grandes derrumbes (Petróleos de Venezuela S.A., 2009) y otros procesos propios activados por la erosión hídrica. En cuanto a la dinámica aluvial, ha estado presente un rellenamiento torrencial del fondo de valle (Ferrer, 1977), donde las pendientes son mucho más bajas. Los efectos de la deposición de las pérdidas de material ocurridas en las laderas se sienten, no solo en el cono de deyección inmediato, sino también a una considerable distancia del punto de cierre de la microcuenca, en las propias aguas del río Torbes y sus zonas aledañas.
La evaluación de la erosión solo se aplicó al área de las cárcavas Los Pinos y El Toro de dicha microcuenca torrencial, por ser estas la que manifestaron de modo evidente procesos de erosión, así como también otras áreas donde ocurrieron procesos y que fueron cubiertas por el proceso fotogramétrico empleado en este estudio.
DETERMINACIÓN DE ESCALA Y EMCT DE LOS MDE
La aplicación de la metodología fue desarrollada a una escala 1:2500, con base en la calidad de la información y la posibilidad de tratamiento que ofreció (no se trabajó con una escala inferior a los 2500, puesto que se usó como escala de referencia el trabajo realizado por Tragnar en 1971).
La georeferenciación de las cartas 1:2500 que fueron digitalizadas manualmente, se determinó a partir de la búsqueda del error medio cuadrático tolerable (EMCT). Este valor se calculó mediante el criterio planteado por el Laboratorio de Fotogrametría y Sensores Remotos (2007), donde el EMCT es igual a 0.25 mm (equivalente a 1-1.5 pixeles), multiplicado por la escala del mapa (ME), obteniéndose de dicha forma valores de EMCT para cada una de las cartas menores a 0.62 m. Dicho valor resultó de gran importancia, pues de estas cartas no solo se obtuvo el MDE de referencia, sino que también se definieron y extrajeron los puntos de control usados en la orientación interna del modelo MDE elaborado por medio del método fotogramétrico digital, el cual requería un valor cercano a cero (0) de EMCT.
PROCESO DE ELABORACIÓN DE LOS MDE
La elaboración del MDE fotogramétrico incluyó un proceso desarrollado en el módulo LPS de ERDAS IMAGINE 9.2, en primer lugar, de orientación interna y externa por par estéreo de las fotografías aéreas. En el caso de la primera orientación, sobre puntos de control precisos localizados en las fotografías (determinación de sus coordenadas X, Y y Z); y en la segunda, utilizando las marcas fiduciales de cada una de ellas (los valores de las marcas fiduciales no pudieron ser extraídos del certificado de calibración de la cámara pues no estaban señalados; fueron hallados propiamente en las fotos por medio de la aplicación de un SIG).
Posteriormente, se desarrolló un fase de aerotriangulación por medio del método de los haces de rayos, que permitió determinar las coordenadas terrestres midiendo los ángulos o distancias en las fotografías, aprovechando de este modo las relaciones geométricas entre fotografías como una solución espacial que usa los principios perspectivos (Hernández, 2008), y cuyo desarrollo es una etapa obligatoria en la generación de las curvas de nivel y su posterior edición (mejora y suavizado de las curvas de nivel).
EVALUACIÓN DE LOS MDE
Según Felicísimo (1994), es muy frecuente en la bibliografía la ausencia de información sobre las características de los MDE, especialmente cuando estos han sido construidos por los propios investigadores y no provienen de fuentes oficiales o de organismos cualificados. Tomando en cuenta tal aseveración se procedió a evaluarlos.
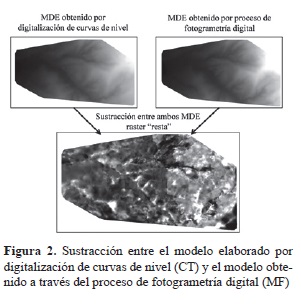
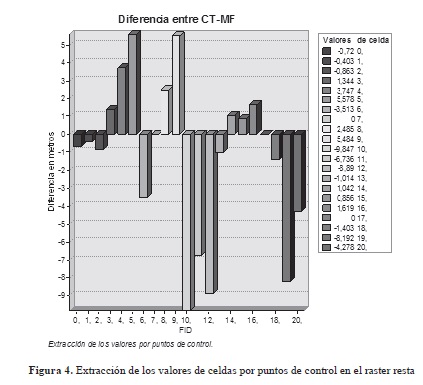
Con las curvas de nivel editadas del MDE (a intervalos de 10 m), obtenido por medio del método fotogramétrico y exportadas a un SIG en formato shape, se obtuvo un modelo TIN (red de triángulos irregulares), ameritado en la posterior interpolación de los centros de altitud de cada celda y su subsecuente conversión a formato raster (Martínez-Casasnovas et al, 2004). Dicha celda quedó definida en 2 m. Este tamaño de celda también fue fijado para el MDE elaborado por medio de la digitalización de curvas de nivel. Seguidamente, ambos modelos fueron sujetos a un remuestreo por el método bilinear cúbico para su salida en el "display" del SIG y posteriormente sometidos a una sustracción entre sí, aplicada por medio de la calculadora de algebra de mapas (herramienta de crucial importancia dentro de los SIG), a fin de evaluar las diferencias altitudinales (figura 2).
Realizada la sustracción entre ambos modelos, a fin de realizar la evaluación por medio de los valores de celda en los puntos de control establecidos con las altitudes conocidas en el área de estudio (presentados en formato vectorial), se procedió a comparar estos valores con la extracción de los valores de las celdas del raster "resta" para cada uno de los puntos, de forma automatizada.
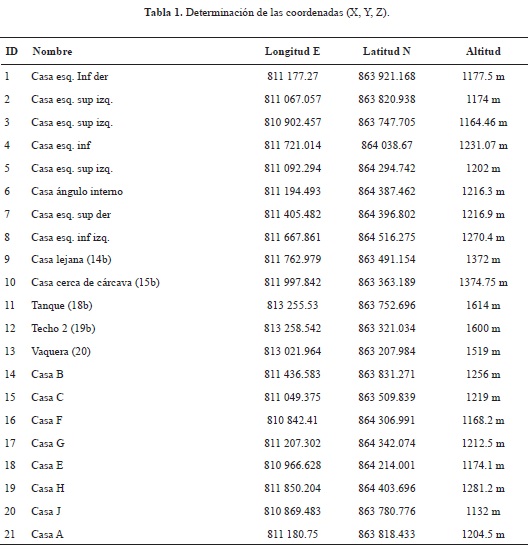
Entre las consideraciones tomadas durante el proceso fotogramétrico, las pertinentes a la vegetación en las paredes laterales de las cárcavas, así como las sombras en las fotografías aéreas, estas fueron tratadas de modo manual, con base en la interpretación visual durante el proceso de edición del MDE, pues podrían haber interferido con la restitución automatizada que desarrolló el proceso fotogramétrico, lográndose con ello evitar representaciones del terreno y estimaciones de volúmenes erróneas. Por otra parte, la determinación de los nombres de los puntos de control obedeció a criterio personal, y solo buscó servir de identificador de los puntos mostrados tanto en fotografías aéreas como en las cartas Tranarg C.A., resultando de este modo un total de 21 puntos correlacionados entre ambas fuentes de información (Cartas Tranarg C.A. correspondientes a 1971 sobre las fotografías de la misión 0102121 de 1976) (tabla 1).
La cuantificación del error sobre el MDE se realizó por comparación de un conjunto de valores conocidos de altitudes con los correspondientes de puntos homólogos del modelo, usando pruebas estadísticas convencionales (Felicísimo, 1994). Ello, aunado al procesamiento estadístico de los datos, permite que estos puedan ser manipulados y reelaborados a decisión del investigador y obtener diferentes niveles de correlaciones. Estas pueden ser presentadas en forma numérica, alfanumérica y gráfica y permiten variadas posibilidades de análisis de los resultados (Romero et al, 1995). Por estas razones se emplearon el ESDA y la geoestadística de puntos.
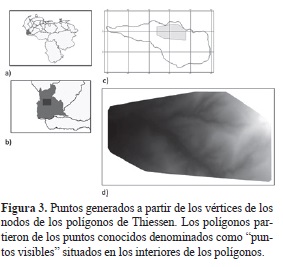
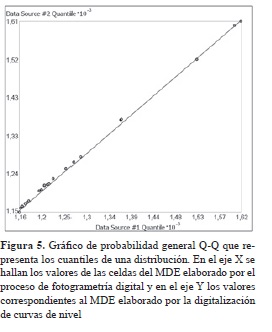
La dependencia espacial (Olaya, 2011) se estudió a partir del ESDA, módulo existente en ArcGis 9.3, el cual comprende un conjunto de herramientas, principalmente de tipo gráfico, con las que se exploran los datos antes de usar técnicas de interpolación y cuyos objetivos en el análisis exploratorio, en líneas generales, son: examinar la distribución de los datos; detectar valores extremos locales y globales; buscar tendencias globales; examinar la autocorrelación espacial y su posible influencia en el ajuste de modelos estadísticos, así como la variación direccional de los datos; entender la covariación entre múltiples variables y realizar transformaciones de los datos si estos son requeridos (Moreno, 2008). Entre las herramientas ESDA aplicadas están: el histograma, que permite una descripción univariada de los datos, al presentar una distribución de frecuencia que se representa mediante una serie de barras donde se agrupan los valores observados en un determinado número de clases o intervalos y donde la altura de cada barra representa la frecuencia absoluta (Moreno, 2008), y los polígonos de Thiessen, un método de interpolación que permite el cálculo de valores en puntos no muestreados, a partir de los valores recogidos en otra serie de puntos (Olaya, 2011). Con este se obtuvieron nuevos puntos para la valoración de sus respectivas celdas y el gráfico de probabilidad normal Q-Q, que es utilizado para comparar el grado de semejanza en la distribución de los valores de dos conjuntos de datos (Moreno, 2008).
En el caso particular, el análisis exploratorio buscó evaluar si los datos poseían una distribución normal o no, que permitiera su descripción y comprensión y, en consecuencia, el entendimiento de la calidad de los MDE generados tanto por el método fotogramétrico digital como el procedente de las cartas elaboradas por Tragnar C.A. Esto solo fue posible al analizar mediante un análisis estructural la correlación de los puntos sobre el espacio en los datos georeferenciados (Giraldo, 2002). Los tipos de análisis empleados versaron sobre medidas centrográficas que describen los datos espaciales, extendiendo las medidas de tendencia central y dispersión de la estadística clásica al ámbito espacial (Olaya, 2011).
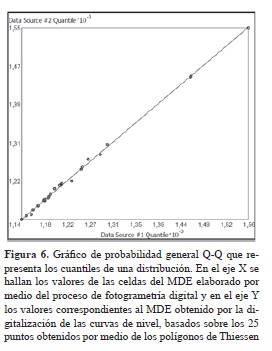
Seguidamente al análisis exploratorio sobre las celdas de ambos MDE, a partir de puntos de control conocidos, se aplicó sobre estos el método de interpolación de polígonos de Thiessen (figura 3), con el cual se extrajeron desde la intersección de los polígonos, 25 valores de celdas en puntos no conocidos, los cuales permitieron repetir el análisis de comparación del grado de semejanza en la distribución de los valores de los dos conjuntos de datos, esta vez no conocidos fehacientemente, como sí lo fue en el caso de los "puntos de control".
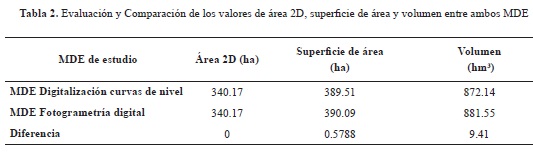
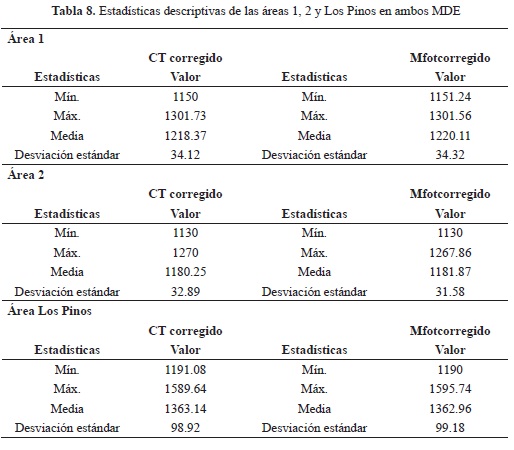
Realizadas estas primeras valoraciones de validación, se estimó el área, la superficie de las áreas y el volumen en ambos MDE, a fin de evaluar las posibles diferencias entre ellos (tabla 2). Además del proceso de comparación como medio de evaluación de los MDE, se procedió a comparar los estadísticos descriptivos (mínimo, máximo, media y desviación estándar) expresados en metros para ambos MDE. Posteriormente, se reclasificaron los valores de celdas existentes en 5 clases, que expresan la distribución que poseen las diferencias de celdas en el área de estudio y el área total que abarcan las clases. La información constituyó un dato crucial en la determinación de la existencia de una buena cantidad de celdas representando el EMCT (valores de celda comprendidos entre -0.62 y 0.62 m.).
Dado a que los datos también se presentaron como puntos, se aplicó un análisis geoestadístico sobre estos utilizando el software System for Automated Geoscientific Analyses -SAGA- versión 2.8.0, como lo fue el análisis de mínima distancia, con el cual se determina simplemente la distancia media euclidiana, el valor máximo y el valor mínimo de distancia, la desviación estándar y la presencia o no de puntos duplicados (Conrad, 2010); el análisis de patrones espaciales, que permite señalar el centro de los puntos, la distancia estándar (a través de un radio de distancia media) y un recuadro de alcance espacial de los puntos estudiados (Conrad, 2010); el variograma, una técnica estadística que permite realizar análisis de la varianza y cuyo propósito es medir los niveles de diversos factores (variable independiente) sobre una característica, medida a través de una o más variables cualitativas conocidas como dependientes (Tapia, 2007); y la superficie variográfica, que tiene por objetivo explorar y cuantificar la dependencia espacial de una variable, es decir, su "autocorrelación espacial" (Moreno, 2008). El estudio de los puntos resultó necesario, pues al ser estos concebidos como un conjunto finito de elementos, tienen una característica común que es de interés en una investigación (Mora, 2000), en este caso la altitud presentada por los las celdas del MDE elaborado por medio del proceso fotogramétrico digital.
RESULTADOS
Los MDE tienen sus propios errores y estos se propagan a los resultados que se derivan de ellos (Olaya, 2011). Por esta razón, resultó necesario evaluar los MDE a fin de estimar su calidad, para determinar la validez o no de los estudios derivados de estos. En el caso particular, los que han sido generados para estimar volúmenes removidos de suelo o roca por procesos de erosión.
La evaluación de los puntos conocidos en el resultante de la sustracción de los DEM señaló como primer resultado una diferencia entre pixeles inferior a 10 m (figura 4). Por su parte, el análisis exploratorio de los datos espaciales mediante del gráfico de probabilidad normal permitió cuantificar, en primer lugar, la calidad de los modelos superficiales midiendo sus errores estadísticos por medio de técnicas probabilísticas (métodos analíticos). A partir de ellas se obtuvo, de acuerdo con el valor obtenido de la celda en los puntos muestrales para cada uno de los MDE (valor extraído por medio del módulo extracción de valores por punto), la comparación del grado de semejanza en la distribución de los valores de estos dos conjuntos de datos. Se concluyó que estos guardan un comportamiento aparentemente similar a una distribución teórica normal gaussiana, donde no existen valores que se alejen de esta. Vale decir que no demuestran una variabilidad entre las altitudes de los dos MDE elaborados en esos puntos señalados (figura 5).
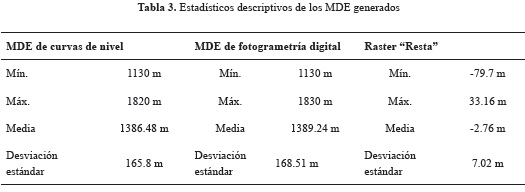
El análisis de puntos en los MDE arrojó como resultado primarios, dos modelos muy similares, salvo en el caso de los valores máximos de elevación donde el MDE obtenido por medio de la digitalización de las curvas de nivel que supera en 10 m al MDE producto del proceso fotogramétrico digital (tabla 3). En añadidura, la coherencia visual existente entre los MDE, desplegados en el display de un SIG.
La diferencia de elevación para cada celda obtenida al aplicar el álgebra de mapas sobre el raster "resta" quedó comprendida entre valores que van desde los 33.16 m como diferencia máxima, hasta los -79.7 m como la mínima. Los valores negativos generados fueron el producto de la determinación de un raster como valor de minuendo. En este caso el MDE obtenido a partir de las digitalización de las curvas de nivel representativo del relieve en 1971 y el MDE elaborado por medio del proceso fotogramétrico digital como sustraendo en las fotografías de 1976, a partir de la idea de asumir que el volumen presentado por este último año debiera ser menor en relación con el anterior por la pérdida de suelo o roca propia de los procesos de erosión.
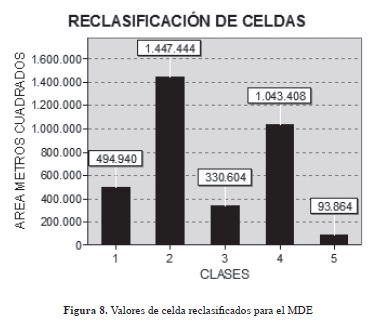
El rango -0.62 y 0.62 m expresa la efectividad de que el valor de altitud de una celda no presentó variaciones significativas entre los MDE y valores comprendidos entre estos hasta los -10 o 10 m, que pudieran ser asumidos como valores para aceptar el MDE procedente del proceso fotogramétrico digital (figuras 7 y 8).
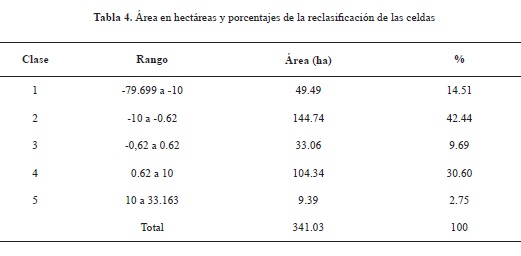
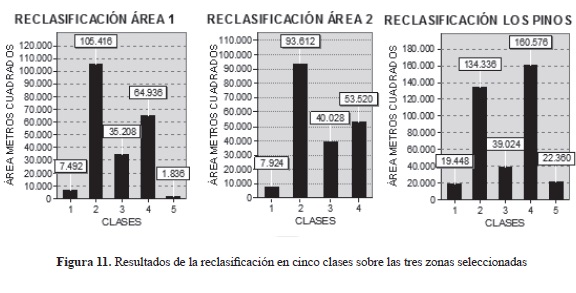
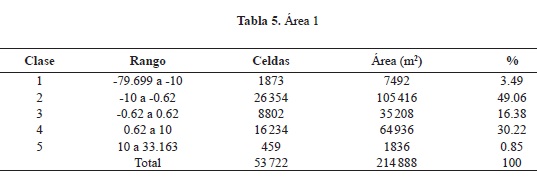
La reclasificación, considerando el EMCT de -0.62 m a 0.62 m, como una clase y clases subsiguientes en valores que van desde estos a los -10 m y a los 10 m y finalizando con clases extremas que van desde los mencionados a los 33 m o los -79 m de diferencia, permitió vislumbrar de mejor modo la relación entre ambos modelos. Se obtuvo que para la clase que responde al EMCT identificada como clase 3, el porcentaje de coincidencia entre ambos modelos fue de 9.69% (330604 m2), prosiguiendo con un 73.03% entre los límites de este rango y el límite fijado de 10 m de las clases 2 y 4 (2490852 m2), con el cual hace aceptable al modelo generado por fotogrametría digital, para finalmente arrojar como resultados extremos de diferencia un 17.26% señalado por las clases 1 y 5 (588804 m2) (tabla 4).
DISCUSIÓN
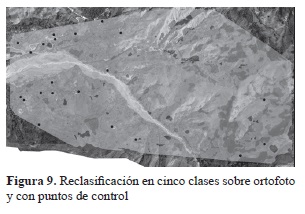
Se asume que las diferencias (todas aquellas clases excluyendo la clase correspondiente al EMCT) son el resultado de la sumatoria de los errores generados, en primer lugar, por la distribución espacial de los puntos de control señalados para el proceso fotogramétrico (número de puntos menores al valor de una distribución normal, posible sesgo espacial entre los puntos y la manifestación de fenómenos de dependencia espacial), seguida del error generado a partir del método de interpolación aplicado durante este y el error resultante originado por el comportamiento local de los procesos de erosión en el área de estudio. Estas conclusiones condujeron a observar la distribución espacial de las clases en el área. Para ello se hicieron intervenir la ortofoto y los puntos de control usados durante el proceso fotogramétrico incluidos en el MDE, y se concluyó que efectivamente buena parte del error corresponde a la desigual distribución de los puntos de control empleados en el desarrollo del proceso fotogramétrico, los cuales fueron los mismos usados en el proceso de restitución llevada a cabo por Tranarg. C.A. en 1971 sobre sus procesos de elaboración de cartas topográficas (figura 9).
En ambos casos los puntos se hallan distribuidos y concentrados en su mayoría en la zona baja del relieve del área, posibilitados a partir de la existencia de vías de comunicación. Caso contrario no ocurrió en las zonas montañosas y en las áreas que presentan cárcavas, donde la dificultad de acceso y las pendientes abruptas impidieron registrar puntos de control que pudieran mejorar el resultado del proceso de interpolación y con ello una restitución más adecuada de las curvas de nivel, necesarias para la generación de un MDE.
La falta de una mejor distribución espacial de los puntos de control obligó a realizar un análisis por zonas, excluyendo aquellas áreas de grandes diferencias señaladas por las clases, concentrando el análisis en aquellas áreas de fácil acceso para la determinación de puntos de control (definidas como áreas 1 y 2) y también en el área de la cárcava Los Pinos (definida como área Los Pinos), por ser esta de interés en el estudio, al no presentar punto de control alguno (figura 10). Se obtuvo como resultado la corroboración de la presunción hecha a partir del análisis visual para el área de estudio en conjunto, expresado en la reclasificación, de una desigual distribución de los puntos de control usados en el proceso de desarrollo fotogramétrico, los cuales generaron las diferencias significativas.
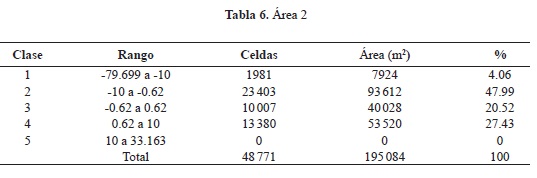
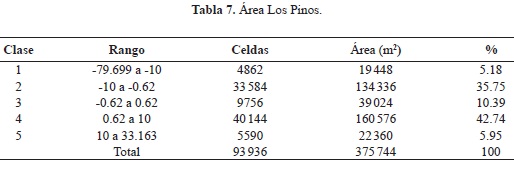
El análisis por separado permitió corroborar que, efectivamente, es la desigual distribución de los puntos de control, la que tiene un peso considerable en el error del modelo obtenido por medio del proceso fotogramétrico, pues en las áreas 1 y 2, la clase 3 comprendida entre -0.62 y 0.62 oscila entre 16 y 20%. Dicha clase es la manifestación de la muestra de celdas sin diferencias existentes entre ambos modelos. Por otro lado, la misma clase para el área Los Pinos tiene un valor menor (10.39%).
Asumiendo el criterio de las clases subsiguientes (sumatoria de las clases 2 y 4) para las áreas 1, 2 y Los Pinos, estas presentaron un valor comprendido entre el 75 y el 80%, lo que las hace símiles entre sí, impidiendo realizar una conclusión más exhaustiva sobre el modelo. Por el contrario, las clases 1 y 3, las cuales expresan las mayores diferencias existentes entre ambos modelos, en las áreas 1 y 2 no superan el 5%. En cuanto al área Los Pinos, carente de puntos de control, el resultado es mucho mayor (11%, aproximadamente) (figura 11 y tablas 5, 6 y 7).
En la tabla 3 se muestran las estructuras poblacionales para cada tipo de bosque y localidad. Se puede observar que en los bosques maduros poco intervenidos (Verdeyaco y Condagua 2), el número total de palmas adultas es mucho mayor que en las otras localidades. De igual forma, hay gran cantidad de individuos juveniles que podrán reemplazar las palmas adultas. En todos los casos se presentan estructuras poblacionales en forma de J invertida, indicando que las poblaciones tienen buena regeneración que puede reponer los individuos adultos en el futuro Se constata con estos primeros datos que las áreas que contaron con la presencia de puntos de control y una distribución homogénea de estos en las áreas 1 y 2, permitieron desarrollar áreas más satisfactorias dentro del MDE, caso inverso de los datos suministrados por el área Los Pinos donde la diferencia entre los valores máximos hace presumir la existencia de errores generados a partir del proceso de interpolación y restitución de las curvas de nivel empleado durante el proceso fotogramétrico. La diferencia de 6 m hace variar considerablemente la superficie de área y el volumen entre el modelo desarrollado por Tranarg C.A. y el modelo hecho a partir de las fotografías aéreas.
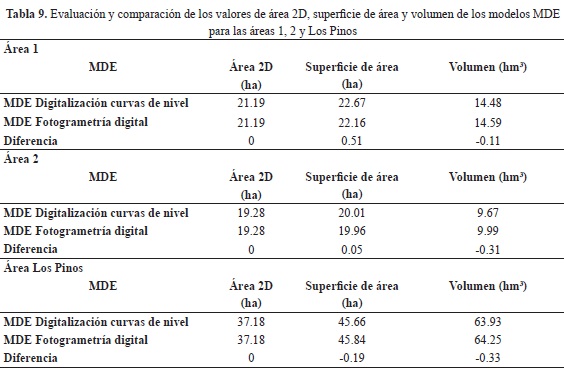
En relación con las superficies de las áreas en ambos MDE, en las tres áreas, se encontró que para el primer caso en el área 1 la diferencia entre los MDE fue de aproximadamente 5000 m2, siendo esta dimensión la mayor encontrada. En el área 2, la diferencia de superficie fue de 475 m2 y, finalmente, en el área Los Pinos hubo una diferencia de área de 1851 m2. Con respecto a los volúmenes, se halló que la diferencia entre los MDE para el área 1 (área con mayor y mejor distribución de puntos de control) resultó ser menor, con 0.11 hm3, que para el área 2, la cual contó con 0.31 hm3, y que para el área Los Pinos, con aproximadamente 0.33 hm3 (tabla 9).
Los resultados obtenidos en superficie de área impiden definir la validez de los volúmenes obtenidos, pues en zonas como el área 1, donde no se desarrollan procesos de erosión, la existencia de una diferencia de 5000 m2, en contraposición a los 1853 m2 de un área como Los Pinos, donde los procesos de erosión sí han sido concentrados, genera una gran incertidumbre. El área 2 manifestó apenas 475 m2, gracias a que el terreno representado presenta un relieve más uniforme, lo que puede explicar dicho valor en contraposición a los valores anteriormente señalados; sin embargo, persiste la duda sobre aceptar o no los resultados en cada uno de los casos.
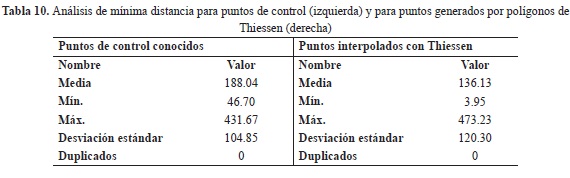
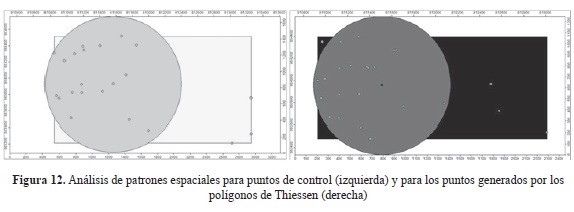
En cuanto al análisis de medidas centrográficas de puntos, el análisis de mínima distancia otorgó una descripción a través de valores como media, mínimo, máximo, desviación estándar y puntos duplicados (tabla 10). Esto permitió conocer cómo se distribuyeron los puntos de control y los puntos generados por los polígonos de Thiessen. En ambas figuras se observó claramente una distribución espacial no homogénea en ambos grupos de puntos, ubicándose estos en el sector oeste de la cuenca (círculos). También se determinó el centro y el alcance espacial de estos (rectángulos) (figura 12), generando esto un marcado sesgo espacial definido al oeste de la cuenca, teniendo el mayor sesgo los puntos generados por los polígonos de Thiessen.
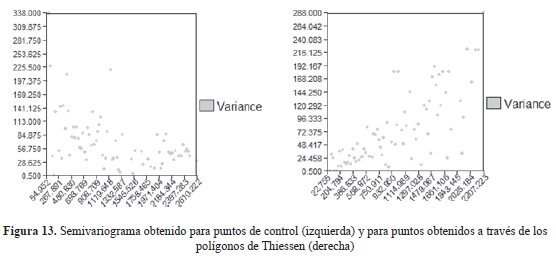
El semivariograma aplicado a los puntos de control generó como conclusión que a diferentes distancias se presentan diferentes valores de varianza y, a su vez, dentro de aquellos que tienen poca distancia se señalan altas diferencias entre sí, denotándose de este modo una autocorrelación espacial baja y desordenada.
Por el contrario, el variograma para los puntos obtenidos a través de los polígonos de Thiessen arrojó como resultado que a menor distancia, los valores de varianza tienden a ser menores, y esta aumenta a medida que se incrementa la distancia entre los pares de puntos. El variograma también permitió constatar un orden y cumplimiento del principio de autocorrelación espacial, pues puntos más próximos tienen más correlación entre sí que aquellos que se hallan más distantes (figura 13).
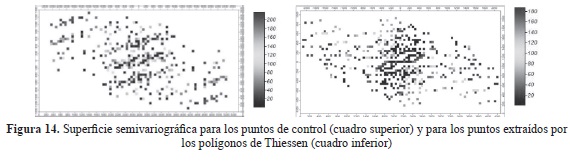
Con el estudio de la superficie variográfica se pudo constatar para los puntos de control una alta varianza en dirección oeste-este, lo que corrobora la baja correlación entre estos, conclusión ofrecida a priori por el variograma. Claramente, la varianza es mayor en el centro del MDE. Por el contrario, los puntos de control generados a partir de los nodos de los polígonos de Thiessen manifiestan un varianza cercana en los valores próximos y una varianza alta a medida que aumentan las distancias, siendo mayor en los extremos del MDE. Pareciera que los datos presentan anisotropía en los casos de los puntos de control este-oeste y de los polígonos de Thiessen norte-sur, siendo esta mucho más isotrópica que los puntos de control (figura 14).
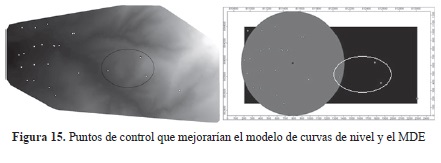
Este análisis hace retomar, efectivamente, que la presencia de puntos de control distribuidos en la forma de los puntos obtenidos a través de los nodos de los polígonos de Thiessen, hubiera permitido obtener un modelo de curvas de nivel y posterior MDE más confiable, pues incluiría mayor contenido de la variación espacial del terreno. Incluso se puede señalar que la inclusión de solo 3 puntos de control (figura 15) hubiera mejorado sustancialmente los modelos generados, dado que la desviación promedio de los puntos no estaría tan desplazada hacia la izquierda. Esta conclusión también ofrece indirectamente como resultado que es esa área en particular donde se concentra buena parte del error en la distribución de los puntos de control; es decir, los puntos de control no representan totalmente la superficie del terreno.
Un ejemplo que se asemeja al estudio de evaluación de volúmenes de suelo aquí propuesto fue realizado mediante levantamientos topográficos minuciosos por parte de Casalí et al. (1999), sobre cárcavas efímeras aparecidas en parcelas de cultivos. Dicha investigación arrojó resultados precisos de volúmenes removidos. La principal limitación para poder desarrollar dicho método estriba en contar con levantamientos topográficos previos igualmente minuciosos, aunado a que estos son muy difíciles de realizar en áreas con grados de pendiente altos, como lo es el caso de las cárcavas de la microcuenca torrencial La Machirí, siendo esta limitante lo que potencia el uso de los MDE para la obtención de los volúmenes erosionados.
El método sustentado en la sustracción de diversos MDE, aparte de estimar los volúmenes removidos, pretende reconocer las variaciones topográficas acaecidas en el tiempo. Dicha metodología también permite determinar la tasa media de retroceso de los barrancos y la producción de sedimentos por año. Ejemplos de este tipo de investigación son las realizada por Derose et al (1998), Anton & Martínez-Casasnovas (2001) y Martínez-Casasnovas (2003), en las cuales restaron dos MDE (derivados de procesos de restitución de fotografías aéreas) para la obtención de valores de volúmenes y donde señalaron además con una reclasificación, las áreas donde se presentaron los procesos de erosión y sedimentación en un lapso determinado. La precisión de los DEM para hacer estos tipos de análisis, y también los análisis de pendiente, comúnmente usados como insumos en los estudios de procesos de erosión en ladera (mapas de pendiente), depende de la exactitud y la precisión de la información topográfica y de su validación para eliminar los valores erróneos existentes, lo cual se puede obtener al aumentar la cantidad de puntos de control (James et al., 2006), a fin de contrarrestar las correspondencias imprecisas de los pixeles de la fotografías aéreas en los pares estéreos y los errores propios de los procesos de triangulación del método fotogramétrico digital empleado en la creación del MDE (Derose et al. 1998).
CONCLUSIONES Y RECOMENDACIONES
La importancia del ESDA y la geoestadística de puntos permite percibir en conjunto atributos ocultos, imposibles de evaluar en el estudio de los datos por separado, los cuales pueden ser presentados de modo numérico, alfanumérico o gráfico para su entendimiento. Dicho análisis permitiría corregir los MDE, al descubrir las tendencias, las formas de distribución, la variabilidad de los datos, las características generales, las estructuras y la existencia y posible localización de los errores.
Si bien es cierto que la obtención de MDE es un gran logro de la fotogrametría digital y de los sistemas de información geográfica, queda evidenciado en este trabajo que para lograr excelentes y precisos resultados en los MDE, hay que sortear muchos problemas de orden tecnológico que conllevan la toma de decisiones que genera resultados un tanto insatisfactorios.
En cuanto a la estimación de volumen, se encontraron diferencias significativas en los dos modelos volumétricos generados. Se asume que las diferencias (todas las clases, excluyendo aquella que representa el EMCT) son el resultado de la sumatoria de los errores: distribución espacial de los puntos de control señalados para el proceso fotogramétrico, seguida del error generado a partir del método de interpolación aplicado durante este y el error resultante originado por el mismo comportamiento local de los procesos de erosión en el área de estudio. Cabría preguntarse: ¿qué peso tienen cada uno de los errores en la generación de los modelos, tanto en los métodos desarrollados con las experiencias de Tragnar C.A. como en el llevado a cabo en este trabajo?, pues en ningún caso se conocen a ciencia cierta.
Se sugiere la definición de nuevos puntos de control en aquellas áreas que carecen de estos, a fin de generar una distribución mejor y con ello obtener mejores resultados del proceso fotogramétrico.
El análisis sectorizado realizado a través de las áreas permitió concluir que, en efecto, la ausencia de una distribución más eficiente de los puntos de control generó resultados poco adecuados para la determinación de los volúmenes (estudios 3D).
Los análisis desarrollados y basados sobre la varianza podrían ser tomados en cuenta para mejorar los MDE obtenidos mediante procesos fotogramétricos, a partir de la selección de una ecuación de ajuste de los puntos de control sobre el raster o grid.
Se puede inferir que los puntos de control poseen una distribución normal gaussiana; sin embargo, por ser estos menores a 30 puntos, no se puede concluir esto y no se puede probar la existencia de normalidad en los datos presentados. Por ello, se recomendaría en este tipo de estudios utilizar como mínimo 30 puntos o casos (Universidad Castilla-La Mancha, 2008).
Se recomienda, asimismo, considerar en los modelos de ajuste y en las inferencias estadísticas el efecto de dependencia espacial, ya que la no evaluación o inclusión puede generar sesgos espaciales e inferencias menos eficaces.
AGRADECIMIENTOS
A la Facultad del Medio Ambiente de la Universidad Distrital Francisco José de Caldas por el apoyo institucional en el marco del convenio institucional con la Universidad de los Andes (Venezuela). Al ingeniero Antonio Hernández Rojas, docente de planta de la Universidad Distrital, por su valiosa colaboración y asesoría técnica en la impartición de la metodología del proceso fotogramétrico digital sobre fotografías aéreas. Y finalmente, a los evaluadores anónimos, quienes con sus observaciones permitieron mejorar la presentación del artículo.
REFERENCIAS BIBLIOGRÁFICAS
Adediji, A., Ibitoye, M., & Ekanade, O. (2008). Generation of digital elevation models (DEMs) for gullies in Ondo-State, Nigeria. Journal of Environmental Hydrology, 16, 1-11.
Anton, C., & Martínez-Casasnovas (2001). Cartografía de la erosión por barrancos mediante restitución fotogramétrica y modelos digitales de elevación en El Penedès (Cataluña). Teledetección, medio ambiente y cambio global, 229-232.
Bosque, J. (1992). Sistemas de información geográfica. Madrid: Ediciones Rialp. 451 p.
Camargo, C. (2012). Evaluación multitemporal de procesos de erosión en laderas mediante el uso de sensores remotos. Caso de estudio: microcuenca torrencial "La Machirí" San Cristóbal, Edo. Táchira (Trabajo de Maestría, Manejo de Cuencas Hidrográficas). Mérida: Universidad de Los Andes. 146 p.
Casalí, J., López, J., & Giráldez, J. (1999). Erosión por cárcavas efímeras en el sur de Navarra (España): descripción y cuantificación. Ingeniería del Agua, 6, 251-258.
Conrad, O. (2010). Description module SAGA: Mínimun distance analysis, Spattial point pattern analysis, Variogram surface. Göttingen: Instituto de Geografía de Göttingen Revisado el 3 de junio de 2012.
Enviromental Systems Research Institute -ESRI (2008). ArcGis Versión 9.3.
Derose, R., Gómez, B., Marden, M., & Trustrum, N. (1998). Gully erosion in Mangatu forest, New Zealand, estimated from digital elevation models. Earth Surface Processes and Landforms, 23, 1045-1053.
Felicísimo, A. (1994). Modelos digitales del terreno. Introducción y aplicaciones en las ciencias ambientales. Oviedo: Pentalfa Ediciones. 118 p.
Ferrer, C. (1977). Estudio geomorfológico detallado de la cuenca media-inferior del río Torbes Estado Táchira. Mérida: Universidad de los Andes. 180 p.
Finol, U. (1972). En la micro-cuenca "La Machirí", el hombre perdió la batalla. Mérida: Universidad de Los Andes. 23 p.
Giraldo, R. (2002). Introducción a la geoestadística: Teoría y aplicación. Bogotá: Universidad Nacional de Colombia. 94 p.
González, A. (1982). Diagnóstico físico conservacionista de la cuenca del río Torbes. Mérida: Universidad de los Andes. 72 p.
Hernández, L. (2008). Proyecto fotogramétrico digital. Bogotá: Universidad Distrital Francisco José de Caldas. 179 p.
Hopf, J. (1972). Proyecto conservacionista y corrección de la cuenca La Machirí, San Cristóbal Edo. Táchira. Mérida: Corporación de los Andes. 44 p.
James, l., Watson, D., & Hansen, W. (2007). Using LiDAR data to map gullies and headwater streams under forest canopy: South Carolina, USA. Catena, 71, 132-144.
Junior, J., Cruz, L., Nogueira, T., & Rodriguez, S. (2008). Monitoramento de processos erosivos em parcelas experimentais no município de uberlândia, mg. Revista Geográfica Académica, 2 (3), 5-18.
Larsson, R., & Strömquist, L. (1995). Monitoreo del medio ambiente con análisis de imágenes satelitarias. Tryckkontakt, Uppsala. 97 p.
Laboratorio de Fotogrametría y Sensores Remotos (2007). Sistemas de información geográfica, ejercicio número 04: Escaneo y georeferenciación. Laboratorio de Fotogrametría y Sensores Remotos. Mérida: Universidad de los Andes. 9 p.
Leica Geosystems Geospatial Imaging (2008). Erdas Imagine 9.2. Leica Photogrammetry Suite 9.2.
Lobo, J., & Ulrich, K. (2008). Modelos digitales de elevación (MDE) a partir de sistemas satelitales. Una introducción y análisis comparativo en la cordillera de Mérida-Venezuela. Revista Geográfica Venezolana, 49 (1), 11-42.
Martínez-Casasnovas, J., Ramos, M., & Ribes-Dasi, M. (2001). Soil erosion caused by extreme rainfall events: mapping and quantification in agricultural plots from very detailed digital elevation models. Geoderma, 105, 125-140.
Martínez-Casasnovas. J, (2003). A spatial information technology approach for the mapping and quantification of gully erosion. Catena, 50, 293-308.
Martínez-Casasnovas, J., Ramos, M., & Poesen, J. (2004). Assessment of sidewall erosion in large gullies using multi-temporal DEMs and logistic regression analysis. Geomorphology, 58, 305-321.
Emmanouloudis, D., Filippidis, E., & Mas, F. (2004). Una técnica SIG para el cálculo del volumen de desprendimientos. Montes, 76, 22-28.
Mora, E. (2000). Algunas consideraciones sobre muestreo. Revista Geográfica Venezolana, 41 (1), 31-46.
Moreno, A. (2008). Sistemas de información geográfica. Manual de Autoaprendizaje con Arc-GIS. México: Alfaomega Grupo Editor. 911 p.
Olaya, V. (2011). Sistemas de información geográfica. Recuperado de http://wiki.osgeo.org/wiki/Libro_SIG. 877 P.
Perroy, R., Bookkhagen, B., Asner, G., & Chadwick, O. (2010). Comparison of gully erosion estimates using airborne and ground-based LiDAR on Santa Cruz Island, California. Geomorphology, 118, 288-300.
Petróleos de Venezuela (2009). Código Estratigráfico de las Cuencas Petroleras de Venezuela. Recuperado de http://www.pdvsa.com/lexico/l38w.htm.
Romero, A., Marín, H., Noguera, N., Maldonado, H., Infante, Y., & Valbunea, E. (1995). Análisis exploratorio de los datos de suelos de la región zuliana aprovechamiento de un SIG. Revista Geográfica Venezolana, 36 (2), 153-174.
System for Automated Geoscientific Analyses -SAGA-(2011). Versión 2.8.0. User Group Association.
Schenk, T. (2002). Fotogrametría digital. Marcombo. Vol.1 Instituto de Cataluña- España. 479 p.
Tapia, J. (2007). Introducción al análisis de datos con SPSS para Windows. Fondo Editorial Unellez, Universidad Ezequiel Zamora, Barinas - Venezuela. 184 p.
Tranarg C.A. (1971). La Machirí, Hojas D-6, D-7, E-6, E-7, Escala 1:2.500. Caracas - Venezuela.
Universidad De Castilla-La Mancha. (2008). Pruebas no paramétricas. Venezuela. Recuperado el 27 de agosto de 2013, de http://www.pdvsa.com/lexico/l38w.htm.
Uzcátegui, F. (1975). Canales y diques en la microcuenca Los Pinos-La Machirí (San Cristóbal). Mérida: Ministerio de Agricultura y Cría. 63 p.
Vilchez, J. (2000). Introducción a los sistemas de información geoespacial. Mérida: Universidad de Los Andes, Consejo de Desarrollo Científico, Humanístico y Tecnológico. 203 p.
Vivas, L. (1992). Los Andes venezolanos. Caracas: Academia Nacional de la Historia. 255 p.
Wang, T., Fuhong He, F., Zhang, A., Gu, L., Wen, Y., Jiang, W., & Shao, H. (2014). A quantitative study of gully erosion based on object-oriented analysis techniques. The Scientific World Journal.
Wolf, P., & Brinker, R. (1997). Topografía. México D.F: Alfaomega Grupo Editor. 815 p.
Licencia
Colombia Forestal conserva los derechos patrimoniales (copyright) de las obras publicadas, y favorece y permite la reutilización de las mismas bajo la licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional por lo cual se pueden copiar, usar, difundir, transmitir y exponer públicamente, siempre que:
Se reconozcan los créditos de la obra de la manera especificada por el autor o el licenciante (pero no de una manera que sugiera que tiene su apoyo o que apoyan el uso que hace de su obra).