Propuesta metodológica para la construcción y selección de modelos digitales de elevación de alta precisión

INTRODUCCIÓN

Los datos espaciales para variables continuas desempeñan un papel preponderante en la planificación forestal, ambiental y territorial. Estos suelen obtenerse de fuentes puntuales tomadas en campo o mediante sensores remotos (Li y Heap, 2008). Una variable continua de especial interés es la altitud, la cual puede ser representada con el modelo digital de elevación (MDE); esta es pieza clave del análisis geomorfométrico y equivalente informatizado de la cartografía clásica de elevaciones, tradicionalmente representada mediante curvas de nivel. Esto supone un enorme salto cualitativo frente a sus predecesores, pues al utilizar un modelo numérico en lugar de uno gráfico se permite una diferencia conceptual de análisis superior, en este caso, a la que tiene lugar con otras capas de información (Olaya, 2011).

Formalmente, los MDE son una estructura numérica de datos que representa la distribución espacial de la altitud de la superficie del terreno (Felicísimo, 1994). Sin embargo, estos presentan como problema fundamental la precisión que deben tener para la representación adecuada del espacio geográfico a una determinada escala cartográfica (Wang, 2005), por ello, se necesitan métodos que representen adecuadamente los datos originales (Felicísimo, 1994). La creación de MDE implica, en la mayoría de casos, la utilización de métodos de interpolación (MI), los cuales corresponden a modelos matemáticos que pronostican valores en ubicaciones donde no hay muestra disponible y que se pueden clasificar en tres categorías: no geoestadísticos, geoestadísticos e híbridos (Lloyd, 2010).

Los MI geostadísticos se basan fundamentalmente en que los datos colectados en puntos cercanos tienden a ser más similares que los colectados a mayor distancia (Mantovani y Magdalena, 2014); esto es la manifestación de la ley geográfica de Tobler (1970), la cual indica que: “Todo está relacionado con todo pero las cosas más cercanas están más relacionadas que las distantes” (p. 3). Lo que lleva a afirmar que este tipo de método considera un modelo geográfico de variación espacial, el cual contiene al menos tres componentes: 1) una estructura general llamada tendencia; 2) una estructura superimpuesta, relacionada con la correlación espacial y con una variación gradual; y 3) un componente que consiste en una variación al azar causada por errores de muestreo o variaciones espaciales a escalas menores que la red de muestras (Mantovani y Magdalena, 2014). Con ello se puede aseverar que, mediante el uso de la dependencia espacial que tienen los datos de una muestra, la geoestadística emplea un algoritmo que cuantifica una variable dada en lugares no muestreados utilizando métodos probabilísticos, lo cual da una ventaja teórica sobre los MI no geoestadísticos. En la Geoestadística se parte del concepto estocástico de que los datos son un proceso espacial aleatorio Z(x):x ∈ R donde R corresponde a una colección continua de localizaciones espaciales siendo el espacio de interés (D), un subconjunto fijo de ℝ ^d que contiene un rectángulo d-dimensional con volumen positivo (Matheron, 1970; Cressie, 1992).

Partiendo de estas ideas, cabe preguntarse si es posible mejorar la precisión de los MDE. Para ello, se definieron como objetivos de investigación proponer una metodología que permita obtener un MDE con mayor precisión a partir de métodos estadísticos y determinísticos, que conceda a su vez la estimación de la escala cartográfica de forma indirecta y la disminución del error en los MI.

MATERIALES Y MÉTODOS

Se dispuso de un levantamiento topográfico de 339 puntos, levantados con estación total Geodimeter System 500 de una zona de San Juan de Lagunillas, Estado Mérida, Venezuela (figura 1). Obtenidos los datos en campo, se realizó un análisis exploratorio de los mismos para evaluar el comportamiento de la distribución de frecuencia; lo que implicó la estimación de los cuatro momentos de una variable cuantitativa y continua (media, desviación estándar, coeficiente de asimetría y curtosis). Para ello se utilizó el lenguaje de programación con capacidad estadística R y la librería Rcmdr (Field et al., 2012; Fox, 2005; R Core Team, 2019).

Figura 1: Distribución espacial de las 339 muestras levantadas.

Dado que el interés de este estudio involucra aplicar un enfoque geoestadístico predictivo que involucra técnicas de tipo lineal, la normalidad de los datos es una condición deseable. Por el contrario, cuando esta no se alcanza los MI geoestadísticos pueden estar afectados negativamente por datos atípicos aditivos (Giraldo, 2002; Díaz, 2002; Bivand et al., 2013; Emery, 2013). En caso de no cumplir este supuesto una opción es transformar los datos y, posteriormente, invertir la transformación, mediante correcciones para el sesgo y la varianza. Sin embargo, este es un método no tan plausible si la transformación no es eficiente (Díaz, 2002), ya que la normalidad en muchas ocasiones no es una suposición sólida, y no se puede probar en práctica (Diggle y Ribeiro, 2002). En este sentido, se evaluó el comportamiento de la distribución de frecuencia de los datos y posibles transformaciones a los mismos.

Ante la posibilidad de que se manifestara la ley geográfica de Tobler (1970) se procedió a realizar un análisis exploratorio de datos espaciales. Para ello se usó el concepto sugerido por Bivand et al. (2013) de realizar diagramas de dispersión entre los pares Z(x _i ) y Z(x _j ), agrupados según su separación de distancia h _ij =‖x _i - x _j ‖, con una distancia horizontal euclidiana de 10 m, que determinó de forma exploratoria (no confirmatoria) la naturaleza de la autocorrelación espacial (lineal, no lineal e híbrida) y el aproximado de la distancia hasta donde se percibe autocorrelación espacial.

El problema de interpolación fue abordado desde dos enfoques generales. El primero corresponde al determinístico (no geoestadístico) tradicional y el segundo a un concepto estocástico de una aproximación geoestadística (Giraldo, 2002). El enfoque tradicional aplicado corresponde con la ejecución de la aproximación del MI no geoestadístico, siendo uno de los más utilizados el inverso de la distancia ponderada. Que se define como: , donde z es el valor por predecir, zi es valor observado o conocido, p _i es el peso asignado al punto i-ésimo, el cual es estimado utilizando el método de la ponderación por distancia inversa, es decir 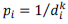, donde d corresponde a la distancia entre puntos y k el exponente que toma habitualmente el valor 2 (Felicísimo, 1994; Olaya, 2011; Li y Heap, 2008; Lloyd, 2010).

Para la correcta ejecución de un MI geoestadístico de la familia Kriging resulta necesario establecer la estacionariedad en segundo orden como regla simplificadora (medias y varianzas constantes en el espacio geográfico; Matheron, 1970; Cressie, 1992). Por ello, para demostrar si los datos poseen un proceso estacionario por media o en su defecto tienen tendencia, se procedió a realizar diversos ajustes a superficies de tendencias (polinómicas de primer a cuarto orden) y a estimar sus residuales. Lo que conduce en la práctica a la solución de dos problemas: la predicción del orden k del polinomio el cual es desconocido y la estimación a partir de los residuales (datos-deriva) del semivariograma, pues no es advertido (Díaz, 2002).

Tanto para los datos originales como los residuales (datos-deriva) se realizó el análisis estructural de dependencia espacial, el cual permite estimar el grado de dependencia espacial de un proceso (Giraldo, 2011). Esto es estimar la función de semivarianza experimental, que corresponde con una función de las diferencias entre dos lugares y la distancia que los separa (Matheron, 1970; Cressie, 1992; Moreno, 2008):

Donde γ _(h) es la función de semivarianza para todas las muestras localizadas en el espacio separado por el intervalo de distancia h, dentro de este parámetro N _(h) viene a ser el número total de pares de muestras separados por un intervalo de distancia h, siendo Z _(x) el valor de la muestra en una localización x y Z _(x+h) el valor de la muestra a la distancia de intervalo h desde x.

Según Royle (1980), Armstrong (1998), Wackernagel (1998), Diggle y Ribeiro (2007), Chilès y Delfiner (2012), Oliver y Webster (2015) y Montero et al. (2015), para el ajuste de un modelo de semivariograma los parámetros que deben estimarse para describir son: el rango (r): máxima distancia hasta donde existe dependencia espacial. La meseta (también conocida como saturación o alféizar), (s): máxima variabilidad en ausencia de dependencia espacial, y el nugget, pepita o núcleo (n): variabilidad que no puede explicarse mediante la estructura espacial, es decir, la variabilidad estimada a una distancia nula.

Resulta necesario señalar la existencia de casos en los que el semivariograma experimental solo depende de la distancia sin evidencia de cambios con la dirección, ante esto se estará en presencia de una estructura de dependencia isotrópica (Díaz, 2002). En este sentido, para evaluar si los datos poseen varianza no constante se generó una superficie variográfica que indicaría la presencia de un proceso de isotropía o anisotropía, así como el comportamiento de la función de semivarianza en ángulos azimutales.

Luego, se procedió al ajuste de diversos modelos de semivariograma. Dicho método utiliza una regresión no lineal para estimar los coeficientes de forma iterativa, lo que minimiza la suma ponderada de errores al cuadrado (Bivand et al., 2013). Para ello, se usaron los principios planteados por Olaya (2011) y Bivand et al. (2013); estos son que los modelos de semivariogramas ajustados deben cumplir con los siguientes criterios: 1) ser monótono y creciente; 2) tener un máximo constante o asintótico, es decir, un valor definido de la meseta o alféizar (funciones no acotadas superiormente, tales como las exponenciales, indicarían que la zona de estudio no es suficientemente grande, ya que no alcanza la dimensión a partir del cual el efecto de la dependencia espacial deja de existir); y 3) el nugget debe ser positivo. Con los modelos de semivariogramas ajustados se procedió a realizar diversos tipos de MI Kriging lineales y no lineales.

Según Olaya (2011), el MI conocido usualmente como Kriging es semejante a un método basado en ponderación por distancia. Esta familia de MI establece las siguientes variantes lineales de solución del Kriging: simple, ordinario, universal, residual, log normal, multigaussiano y disyuntivo (Giraldo, 2002). Los dos primeros definen que el proceso es estacionario en segundo orden, asumiendo además en el caso del simple que la media poblacional es conocida (Cressie, 1992). A diferencia de estos, el universal y residual son más flexibles, ya que no asume un proceso estacionario por media. Es decir, la variable medida posee tendencia, lo que conlleva a definir el grado de la función polinómica lineal que lo describe (Cressie, 1992; Bivand et al., 2013). En concordancia con esta idea, el Kriging residual, método empleado bajo las mismas circunstancias del universal, cuyo funcionamiento consiste en remover la tendencia y a partir de los residuales estimar una variante del Kriging estacionario (simple u ordinario), la predicción en un sitio no muestreado que es igual a la tendencia estimada más la predicción del error (Giraldo, 2002; Li y Heap, 2008).

Es importante acotar que, en los procesos lineales de los MI geoestadísticos, cuando la función aleatoria Z _(x) sigue un proceso Gaussiano el mejor predictor es un estimador lineal, de lo contrario, se puede aplicar una transformación adecuada que convierta los datos originales (no normales) en gaussianos (con posibles datos atípicos aditivos) (Giraldo, 2002). Cuando este tipo de transformación no es clara aparecen propuestas desde numerosos enfoques, tales como: el Kriging log normal y el multigaussiano, en estos dos procedimientos se hacen transformaciones de la variable regionalizada con el propósito de normalizar la distribución de frecuencia (Giraldo, 2011).

Otro enfoque que aparece es el Kriging disyuntivo, considerado cuando para la variable principal las transformaciones convencionales no pueden producir una distribución normal. En este tipo de Kriging se utilizan polinomios de Hermite (Li y Heap, 2008), siendo el resultado un tipo de estimador no lineal (Giraldo, 2002). La estimación Kriging disyuntivo se obtiene mediante un Cokriging simple de las funciones de diferente orden (Ortiz y Deustsch, 2005).

Como proceso de validación se utilizó, en primer lugar, el método de validación cruzada con exclusión (LOOCV, por sus siglas en inglés), este es un método iterativo que realiza estimaciones a partir del modelo ajustado pero utilizando k-1 observaciones. De esta manera, la observación restante omitida es estimada con el modelo y con ello se puede estimar el error, el cual difiere en su descripción de la validación cruzada tradicional porque repite otras k-1 veces con una observación diferente omitida (Lachenbruch y Mickey, 1968); aunque es más demandante computacionalmente por tener una aproximación más cercana a la máxima verosimilitud del error. El otro método de validación utilizado fue el error medio absoluto (MAE, por sus siglas en inglés) cuyo estimador es (Wilmott y Matsuura, 2005). Estos resultados fueron comparados con el error máximo tolerable (EMCT), el cual se estimó utilizando el criterio planteado por el Laboratorio de Fotogrametría y Sensores Remotos (2007). Adicionalmente, para los modelos estocásticos de interpolación debe cumplirse con los diagnósticos tradicionales de un modelo de esta naturaleza, esto es que los residuales sigan los siguientes comportamientos: normalidad, homocedasticidad e independencia (Guajarati y Porter, 2010). Para ello se realizaron diversos gráficos exploratorios, el test de Shapiro-Wilk de normalidad, el test de Breusch-Pagan de homocedasticidad y la verificación del semivariograma residual, es decir, la comprobación de que los supuestos básicos de un modelo paramétrico se cumplen.

RESULTADOS

Los datos de elevación del terreno obtenidos a través de la estación total denotaron una media de 1039.73 m de altitud, una desviación estándar de 7.99 m y un coeficiente de asimetría positivo (0.5697), configurados en una distribución no normal (figura 2a) de tipo peine, refrendado también por el diagrama Q-Q (figura 2b), el cual indica que los mismos se encuentran por fuera de los límites de los intervalos de confianza de una distribución normal (p < 0.05) (líneas punteadas), sin presencia de outliers.

Figura 2: Comportamiento de la distribución de frecuencia de la altitud.

Los resultados de los diagramas de dispersión establecidos a cada 10 m (figura 3) indicaron un proceso de autocorrelación espacial lineal hasta el rango de distancia de 70 m, con un coeficiente de correlación lineal que llega hasta un valor R de 0.71, indicativo de la existencia de un fuerte proceso de autocorrelación hasta esta distancia, en un rango de variabilidad de 0.97 a 0.31, a partir del cual el proceso se convierte aparentemente en un proceso no lineal. Del mismo modo, el semivariograma experimental indicó un proceso monótono y creciente hasta los 400 m, adquiriendo un máximo asintótico donde la meseta (o alféizar) también se alcanza, es decir, se obtiene el punto máximo y a partir de este se asume que la dependencia espacial no es significativa. Sin embargo, se evidencia que el proceso entre 300 m y 400 m tiene un comportamiento aparentemente heterocedástico. Con relación al nugget del semivariograma, este fue muy cercano a cero, resultado esperado dado que los datos fueron obtenidos con un levantamiento de alta precisión, lo que permite asumir la variabilidad no explicada por el muestreo cercano a 0.

Figura 3: Gráficos de dispersión con rezago espacial.

Con miras al semivariograma experimental se ajustó un modelo gaussiano con y sin corrección por anisotropía (figuras 4a y 4b). Ambos resultados conllevan a inferir que se está ante la presencia de un proceso isotrópico, dado que se denota una mejora en el ajuste del semivariograma cuando se asume este proceso.

Figura 4: a) Semivariograma experimental con intervalo de 0.5 m con modelo gaussiano isotrópico; b) semivariograma experimental con intervalo de 0.5 m con modelo gaussiano anisotrópico ajustado; c) predicción de Kriging Simple Residual.; d) varianza de Kriging Simple Residual.

Los resultados del modelo gaussiano isotrópico mostraron un nugget muy cercano a cero unidades de semivarianza (1.41), indicativo de que la variabilidad no explicada por el modelo es muy baja y una meseta (alféizar) que posee una semivarianza de 226.99 y un rango de 205.68 m. Con este modelo de semivariograma se logró el mejor ajuste inicial (error de ajuste de 34.61 unidades de semivarianza), alcanzado con la modificación de los parámetros del intervalo estimado.

En cuanto al análisis de los residuales obtenidos mediante los MI aplicados (tabla 1) se desprende que el Kriging Simple Residual Isotrópico fue el más acertado, pues no solo posee uno de los errores más bajos (LOOVC de 0.008 m y MAE de 0.70 m), sino que también su máximo y mínimo oscila entre 2 y 3 m, siendo menor que los resultados presentados por el Kriging Universal Isotrópico. Por ello, se podrían generar curvas de nivel a una equidistancia de 0.1 m, lo cual es indicativo que el proceso que presentan los datos es de tipo isotrópico y con tendencia. Esto va en concordancia con los resultados obtenidos en el ajuste del semivariograma en las figuras 4a y 4b, ya que es evidente que el modelo mejora sustancialmente en la medida en que se asume la isotropía de los datos. Así mismo, debe descartarse el Kriging disyuntinvo, ya que a pesar de que posee el indicador LOOVC es también es el que más rango tiene, esto es refrendado por el valor estimado del MAE que manifiesta un valor extremadamente elevado. En las figuras 4c y 4d se muestra la predicción y las varianzas respectivamente del Kriging simple residual isotrópico, siendo evidente que el proceso posee varianzas mayores dónde no hay muestras, o en su defecto donde la densidad de las observaciones es menor. Adicionalmente, el diagnóstico de este MI manifiesta un proceso homocedástico sin autocorrelación espacial residual, lo que indica que este presenta un buen rendimiento.

Tabla 1: Resultados de los métodos de interpolación.

Finalmente, tanto las versiones del Kriging disyuntivo como el inverso de la distancia fueron los que menor desempeño presentaron, siendo un indicativo de que la autocorrelación es lineal y modelable desde el punto de vista estadístico, y que el buen desempeño del Kriging simple residual isotrópico se debe a que la cantidad de muestras es tan elevada que permite que la media muestral se acerque a la media poblacional, información suficiente para ser ajustado de forma correcta.

DISCUSIÓN

Un primer elemento de discusión es la escala cartográfica del levantamiento, que se estableció en aproximadamente 1:400 por medio del semivariograma. Esta afirmación se basa en el criterio planteado por Gallardo (2006) y Kerry et al. (2010), quienes manifiestan que es posible utilizar el semivariograma y las ecuaciones del Kriging para cuantificar el grado, la escala cartográfica y de variación espacial, el intervalo de muestreo y el error tolerable específico. El método descrito es un método indirecto, ya que según Skøien y Blöschl (2006) las escalas de modelado deberían ir con los objetivos del proyecto de trabajo. Sin embargo, esto no suele ser posible, porque la verdadera estructura de covarianza de la variable de interés es desconocida a priori, así como por razones logísticas (conocimiento del relieve, accesibilidad, entre otras).

Lo expuesto está condicionado por el muestreo espacial, ya que la toma de las muestras establecerá parcialmente el comportamiento del semivariograma y, como consecuencia, la autocorrelación espacial y el módulo escalar (Skøien y Blöschl, 2006). En este orden de ideas Plant (2012) ha indicado que para comparar los métodos de muestreo espacial y la estimación del semivariograma es necesario definir estándares de comparación; una posible manera de realizarlo es considerar alguna medida de intervalos de confianza. Para alimentar estas ideas la eficiencia del muestreo se define como el inverso de la varianza muestral; por ello, el diseño más eficiente conduce a una estimación más precisa y bajo un proceso de autocorrelación espacial la densidad de los puntos de las muestras debería aumentarse en las ubicaciones que expresan una mayor variabilidad espacial (declives de altas pendientes o formas abruptas que generen heterogeneidad espacial). Los valores de las muestras con fuertes similitudes pueden evidenciar redundancia y sobre-muestreo en esas áreas, con ello debería disminuirse la varianza del estimador del Kriging (Aubry, 2000; Delmelle, 2014).

Los elementos antes descritos parten del principio de que se posee información en ciertas posiciones espaciales, que faciliten los análisis exploratorios y la caracterización de la distribución de frecuencia (Skøien y Blöschl, 2006; Plant, 2012). Una forma para sortear el problema de la covarianza espacial sin poseer datos sobre el atributo de trabajo es utilizar la aproximación de los patrones puntuales; según De la Cruz (2006), en esta aproximación las medidas de la covarianza no necesariamente involucran un atributo para la estimación de la misma, la idea principal es plantear el tipo de diseño de muestreo que se desea aplicar en el área de trabajo (aleatorio, estratificado, regular, entre otros) y, a partir de esta aproximación, simular medidas de la covarianza para el proceso de muestreo y escala(s) deseada(s).

Un método para la optimización de muestreo para datos topográficos de alta precisión es el presentado por Mao et al. (2016), quienes parten de un muestreo espacial preliminar, mediante métodos de clasificación del error y desde el supuesto de la distribución normal en los mismos, para luego aplicar diferentes filtros gaussianos con el fin de eliminar los errores en cada uno de ellos y posteriormente poder obtener la diferencia entre los datos topográficos originales y los datos topográficos libres de errores. Esto permite configurar una superficie de error en la cual se incluyen los puntos extremos, con ello el proceso es equivalente a seleccionar la menor cantidad de puntos de muestra.

Otros autores como Barrios et al. (2005), Pérez y Mas (2009), Moreno et al. (2010), Lorenzo et al. (2012), Hernández et al. (2013) y Camargo et al. (2014) han abordado el tema de la precisión en modelos digitales de elevación con enfoques determinísticos, estadísticos, fotogramétricos y Lidar, reportando errores entre 7.3 m y 10 m, con errores mínimos de 0.94 m, 0.18 m y 0.62 m; más adelante, este estudio muestra un método más efectivo para el control del error. Estos enfoques poseen diferencias sustanciales con respecto a la metodología aquí planteada, el primero es el conocimiento de la escala, con la cual pudieron establecer una medida de la precisión mínima del mismo (Congalton y Green, 2008; FAO, 2010). El segundo es la aproximación estocástica sugerida por Bivand et al. (2013) que fue aplicada en el presente trabajo, la cual indica que el valor predeterminado del intervalo da como resultado una visión general inicial de la correlación espacial, y con ello la modificación de los parámetros del intervalo resultó en más detalles y como consecuencia en la disminución del error. En tercer término, la medida del error utilizada en el presente trabajo de investigación (LOOV) tiene varias ventajas sobre estimaciones más simples de error predictivo, como es el criterio de información de Akaike (AIC) y métodos máximo verosímiles, pero que se usan menos en la práctica porque implican pasos computacionales adicionales (Vehtari et al. 2017); estos pasos fueron sorteados efectivamente en este trabajo.

CONCLUSIONES

Tras el análisis exploratorio y al comparar los distintos modelos de Kriging se hace evidente que la tendencia es significativa y correspondería a una función de al menos primer orden, que fue identificada mediante el análisis exploratorio de datos y ello implica una carga para el usuario. En concordancia, una forma automatizada de análisis no es recomendable debido a la presencia de un componente de tendencia no homogénea que hace indispensable la juiciosa aplicación del análisis exploratorio de datos, así como también la especificación de los parámetros. Por ello, se recalca que esta metodología requiere de una carga interactiva e iterativa por parte del usuario, dado que es quien toma la decisión de las características del modelo a utilizar, el método de estimación de los parámetros del semivariograma y la decisión de si se cumplen los supuestos estadísticos fundamentales de cada uno de los métodos, lo que le permite al usuario la posibilidad de disminuir el error.

Dado que una de las características de este tipo de levantamientos es que se dispone de datos altamente voluminosos en áreas de pequeña envergadura, es probable que alguna variante del Kriging simple sea el más adecuado; debido posiblemente a que la cantidad de datos sea elevada y con ello la media de los valores muestrales se aproximen sustantivamente a la media poblacional. Con los modelos que involucraban una remoción de tendencia se consiguió que los residuales se ajustaran a una distribución normal y tuvieran menor varianza del error.

Ante la alta carga que corresponde al usuario y la dificultad que implica la implementación de esta metodología en el lenguaje de programación R u otros lenguajes estadísticos, se hace necesario el desarrollo de una herramienta gráfica con documentación teórico-operativa que auxilie al usuario para la toma de decisiones, para así tener la capacidad de discernir sobre las características inherentes de sus datos.

Finalmente, el Kriging disyuntivo se considera menos adecuado para su aplicación con los datos utilizados. Esto es debido a que a pesar de que tiene menor error medio y menor varianza de los errores, presenta un rango demasiado amplio en los mismos. Adicionalmente, en obediencia al principio de parsimonia y debido a la alta dependencia de este método a la especificación por parte del usuario, no se recomienda su uso por parte de profesionales no entrenados en su aplicación.