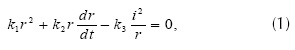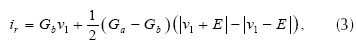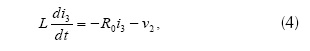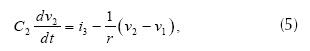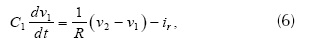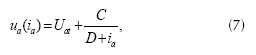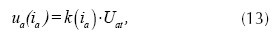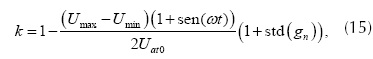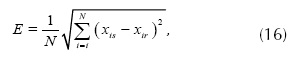DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2016.2.a01Publicado:
01-04-2016Número:
Vol. 20 Núm. 48 (2016): Abril - JunioSección:
InvestigaciónModelos de horno de arco eléctrico para estudios del efecto flicker
Electric arc furnace models for flicker study
Palabras clave:
Armónicos, horno de arco, modelo dinámico. (es).Palabras clave:
Arc furnace, dynamic models, harmonics. (en).Descargas
Referencias
Alves, M.; Assis P., Z.; Peixoto G., C. y Goncalves G., D. (2010). An integrated model for the study of flicker compensation in electrical networks. Electric Power Systems Research, 80, 1299-1305.
Alzate, A.; Marulanda, J. y Escobar, A. (2010). Electric Arc Furnace Modeling for Power Quality Analysis. Bogotá: IEEE Conference of the Andean Council ANDESCON.
Cano, E. y Tacca, H. (2005). Arc furnace modeling in ATP EMTP. Montreal Canada: Presented at the International Conference on Power Systems Transientes.
Cavallini, A.; Montanari, G.; Pitti, L. y Zaninelli, D. (mayo-junio de 1995). ATP Simulation for Arc-Furnace Flicker Investigation. European Transactions on Electrical Power Engineering, 5(3), 165-172.
Göl, M.; Özgül Salor, Bora Alboyacı, Bilge Mutluer, I¸sık Çadırcı, & Muammer Ermi¸s. (2010). A New Field-Data-Based EAF Model for Power Quality Studies. IEEE Transactions on Industry Applications, 46(3), 1230-1242.
Kennedy, M. (octubre de 1993a). Three steps to Chaos-Part I: Evolution. IEEE Transactions on Circuit and Systems-I:Fundamental, Theory and Applications, 40(10), 640-665.
Kennedy, M. (octubre de 1993b). Three steps to Chaos-Part II: A Chua's circuit primer. IEEE Transactions on Circuit and Systems-I:Fundamental, Theory and Applications, 40(10), 657-674.
Montanari, G.; Loggini, M.; Cavallini, A.; Pitti, L. y Zaninelli, D. (octubre de 1994). Arc Furnace Model for the Study of Flicker Compensation in Electrical Networks. IEEE Transactions on Power Delivery, 9(4), 2026-2036.
Mousavi Agah, S.; Hosseinian, S.; Askarian Abyaneh, H. y Moaddabi, N. (2010). Parameter Identification of Arc Furnace Based on Stochastic Nature of arc Lengh using two- step Optimization Technique. IEEE Transactions on Power Delivery, 25(4), 2859-2867.
O’Neill, E.; Heydt, G.; Kostelich, E.; Venkata, S. y Sundaram, A. (abril de 1999). Nonlinear Deterministic Modeling of Highly Varying Loads. IEEE Transactions on Power Delivery, 14(2), 537-542.
Orille F., A. (1993). Centrales eléctricas II. Introducción al sector eléctrico y al sistema de energía eléctrica. Barcelona: Universitat Politécnica de Catalunya.
Standard CEI/IEC 61000-4-15 (1997). Electromagnetic compatibility (EMC). Part 4. Testing and measurements techniques. Section 15: Flickermeter-Functional and Testing Specifications.
Trageser, J. (marzo-abril de 1980). Power Usage and Electrical Circuit Analysis for Electric Arc Furnaces. IEEE Transactions on Industry Applications, IA-16(2), 277-284.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.2.a01
Modelos de horno de arco eléctrico para estudios del efecto flicker
Electric arc furnace models for flicker study
Catalina González Castaño1, Alfonso Alzate Gómez2, Jesser James Marulanda Durango3
1 Ingeniera Electrónica, Master en Ingeniería Eléctrica. Docente de la Universidad Surcolombiana. Neiva, Colombia. Contacto: catalina.gonzalez@usco.edu.co.
2 Ingeniero Electricista, Magister en Sistemas de Generación Eléctrica. Docente de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: alalzate@utp.edu.co
3 Ingeniero Electricista, Magister en Ingeniería Eléctrica. Docente de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: jjmarulanda@utp.edu.co
Fecha de recepción: 26 de agosto de 2015 Fecha de aceptación: 15 de febrero de 2016
Cómo citar: González Castaño, C., Alzate Gómez, A., & Marulanda Durango, J. J. (2016). Modelos de horno de arco eléctrico para estudios del efecto flicker. Revista Tecnura, 20(48), 15-27. doi: 10.14483/udistrital.jour.tecnura.2016.2.a01
Resumen
Objetivo: El objetivo de este artículo es evaluar las fluctuaciones de voltaje o flicker de dos modelos de un horno de arco eléctrico a través de la comparación con datos reales.
Método: El primer modelo se fundamenta a partir del principio de conservación de la energía, de la cual se obtiene una ecuación diferencial no lineal que captura la característica voltaje - corriente del arco eléctrico. Las fluctuaciones de voltaje se generan con un circuito de caos que modula la amplitud del voltaje del arco eléctrico. El segundo modelo está basado en las relaciones empíricas entre la longitud de arco, la tensión y la corriente a través del arco. Las fluctuaciones de voltaje se obtienen agregando una señal aleatoria a la longitud del arco eléctrico. Ambos modelos son implementados en PSCADTM.
Resultados: Los resultados de ambos modelos son comparados con mediciones reales tomadas en la etapa más crítica de la operación del horno, y muestran que el modelo basado en la conservación de la potencia presenta un menor error medio cuadrático promedio en los voltajes y corrientes de 5,6 V y 1.7 kA frente a 27,2 V y 3.38 kA obtenidos con el segundo modelo.
Conclusiones: Ambos modelos consideran la no linealidad y comportamiento aleatorio que exhibe este tipo de carga, validando su inclusión en modelos computacionales de sistemas eléctricos de potencia.
Palabras clave: Armónicos, horno de arco, modelo dinámico.
Abstract
Objective: The aim of this paper is to evaluate voltage fluctuations or flicker of two electric arc furnace models through comparison with real data.
Method: The first proposed model is founded on the energy conservation principle, which generates a non-linear differential equation modelling the electric arc voltage - current characteristics. Voltage fluctuations are generated using a chaotic circuit that modulates the amplitude of arc voltage. The second model is based on the empirical relationship between the arc diameter or length as well as voltage and electrical current on the arc. Voltage fluctuations are considered adding a random signal in the arc length. Both models are implemented in PSCADTM.
Results: The results of both models are compared with real data taken at the most critical stage of the operation of the furnace, and they show that the model based on energy conservation has a lower average mean square error in the voltages and currents 5.6 V and 1.7 kA against 27,2 V y 3.38 kA obtained with the second model.
Conclusions: Both models consider the nonlinearity and random behavior present in this type of load, validating their inclusion in computer models of electric power systems.
Keywords: Arc furnace, dynamic models, harmonics.
Introducción
El término calidad de la potencia, o power quality (PQ), se refiere a una amplia variedad de fenómenos electromagnéticos que caracterizan la tensión y la corriente de un sistema de potencia en un instante y en un lugar determinados. Hoy en día, este tema es de especial atención para los entes encargados de regular el sistema eléctrico, para las empresas que prestan los servicios de energía eléctrica, para los usuarios que están conectados a los sistemas de distribución y para los fabricantes de equipos electrónicos. Por esta razón, existen normas técnicas que exigen a las empresas prestadoras del servicio unos márgenes de valores de percibility short time (PST) y de forma de onda garantizando a los usuarios una buena calidad de energía eléctrica (Standard CEI/IEC 61000-4-15, 1997). La calidad de la potencia se ve agravada en la actualidad por el incremento de cargas no lineales conectadas a la red.
Por lo general, el horno de arco eléctrico es el más utilizado por la industria metalúrgica, en donde este tipo de carga, además de ser no lineal, es caótica e inestable (Alves, Assis, Peixoto y Goncalves, 2010). Por tanto, cobra importancia implementar modelos que se aproximen al comportamiento real de los hornos, con el propósito de realizar estudios que permitan medir su impacto en un sistema eléctrico de potencia. Los modelos propuestos en la literatura son paramétricos que se basan en las características y en sus condiciones físicas de operación del horno, los cuales proporcionan sus principales aspectos de funcionamiento (Göl et al., 2010). El presente trabajo forma parte del resultado del trabajo de investigación "Análisis y atenuación de problemas de calidad de energía causados por hornos de arco en sistemas eléctricos", y de las tesis de maestría: "Modelo de horno de arco eléctrico para estudios del efecto flicker y sus métodos de compensación" y "Desarrollo de una metodología para reducir el efecto flicker generado por un horno de arco eléctrico", de la Universidad Tecnológica de Pereira. Estos trabajos presentan la forma de modelar matemáticamente un horno de arco eléctrico y el desempeño de sistemas de compensación basados en electrónica de potencia cuya función principal es atenuar los efectos nocivos sobre el sistema eléctrico de potencia que generan los hornos de arco. En este trabajo se presenta la comparación de dos modelos paramétricos propuestos en la literatura. Los resultados experimentales demuestran las características de cada modelo, adicionalmente, los modelos son comparados con mediciones reales tomadas en la etapa más crítica de la operación del horno. Se muestran las bondades y las aproximaciones de los modelos con los datos reales.
En este artículo se presenta, en principio, los métodos y modelos matemáticos aplicados que describen el horno de arco eléctrico, además de detallar el circuito de potencia que alimenta el horno. Luego, se presentan los resultados obtenidos en simulación de los dos modelos y su comparación con los voltajes y las corrientes del arco eléctrico presentadas en Cano y Tacca (2005). Por último, se plantean las conclusiones de la investigación.
Metodología
A continuación se describe los distintos elementos y componentes utilizados para el desarrollo de la simulación en el software especializado PSCADTM. Los métodos descritos están conformados por las características del circuito eléctrico de este tipo de cargas y la representación de los modelos matemáticos que describen el comportamiento eléctrico del horno de arco eléctrico, con el fin de comparar su funcionalidad en la simulación de fenómenos que pueden ser causados por la conexión de un horno de arco eléctrico.
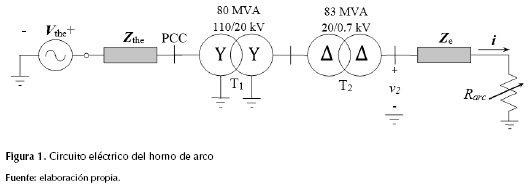
Circuito eléctrico del horno de arco
El fenómeno del arco eléctrico entre los electrodos se puede representar por una resistencia variable (Trageser, 1980). Otra característica del circuito eléctrico del horno de arco es que las impedancias de los conductores que conectan los electrodos al secundario del transformador están balanceadas. El circuito equivalente unifilar del horno para el análisis de sus características eléctricas se puede simplificar y representar como el mostrado en la figura 1.
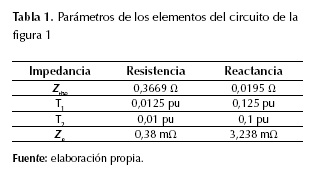
La resistencia del arco eléctrico es sustituida por la resistencia variable Rarc, mientras que la reactancia del mismo es descartada; esto es válido porque las reactancias son causadas por campos magnéticos alternos, lo que tiene una influencia insignificante para arcos eléctricos cortos (Trageser, 1980). La red de alimentación en el punto de acoplamiento común PCC se modela por un circuito equivalente de Thevenin que consta de una fuente de voltaje trifásica de secuencia positiva Vthe en serie con una impedancia serie RL (resistencia e inductancia) Zthe. Las potencias nominales de los transformadores que forman parte del circuito eléctrico del horno se indican en la figura 1. Se utiliza un transformador de horno conexión delta-delta para eliminar los armónicos de corriente múltiplos de tres veces la frecuencia fundamental. Para simplificar el circuito no se han considerado filtros ni sistemas de compensación en el secundario del transformador T2 muy utilizados en la mayoría de estas instalaciones. Los valores utilizados para las resistencias y reactancias equivalentes del circuito de la figura 1 corresponden a valores típicos reportados en la literatura y se muestran en la tabla 1.
Modelos dinámicos para un arco eléctrico alterno o de CA
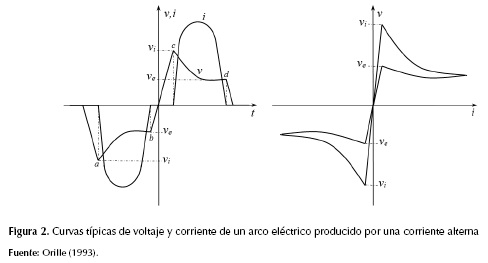
Si en un arco alimentado por una corriente alterna se miden la tensión v y la corriente i, se encuentran curvas deformadas que dependen del tipo del medio del arco, del material de los electrodos y de la frecuencia de la corriente (Orille, 1993). En la parte izquierda de la figura 2 se muestran estas curvas para un arco en aire, con electrodos de carbón.
La forma del voltaje alterno del arco es similar a una onda cuadrada y la forma de la corriente se asemeja a una señal sinusoidal pero con componentes armónicas, básicamente la tercera, quinta y séptima armónica (Alzate, Marulanda y Escobar, 2010). En los tiempos a y c se efectúan las descargas y en los puntos b y d se extingue el arco. Durante el intervalo comprendido entre los puntos b y c existen descargas inestables. El voltaje vi se conoce como el voltaje de ignición y el voltaje ve es el voltaje de extinción. Partiendo de estas curvas, puede derivarse la característica voltaje/corriente, como se muestra en la parte derecha de la figura 2.
Modelo basado en la conservación de la potencia
La característica del arco eléctrico de la figura 2 se puede obtener de forma aproximada con la ecuación diferencial no lineal (1) derivada en (O'Neill et al., 1999), que se basa en el principio de conservación de la energía (ecuación (1)),
Donde r es el radio del arco eléctrico; i es la corriente instantánea del arco, y k1, k2 y k3 son parámetros que se relacionan con la potencia eléctrica convertida en calor por el arco. En el modelo trifásico del horno de arco se debe obtener un r para cada fase. Una vez determinado r, la segunda parte del modelo determina el voltaje dinámico del arco eléctrico.
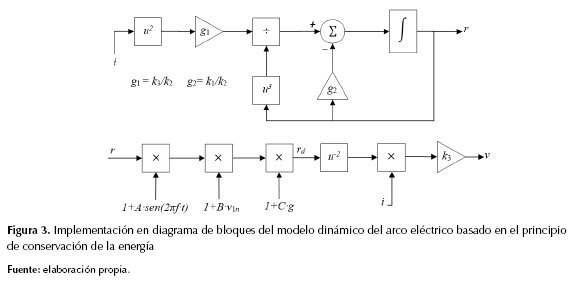
Luego, la naturaleza variable de la longitud del arco se refleja en el modelo introduciendo un comportamiento de tipo determinista, aleatorio y caótico a la variable de estado r de forma simultánea. Para esto, se realiza la modulación de amplitud de r con una señal sinusoidal, una señal de naturaleza caótica, y una señal aleatoria con distribución gaussiana. En la figura 3 se ilustra la implementación en diagrama de bloques de la segunda fase del modelo.
En la figura 3, v1n es una señal caótica de baja frecuencia normalizada (de valor máximo igual a 1), generada con el oscilador de Chua, y g es una señal aleatoria que tiene una distribución de probabilidad gaussiana con media 0 y desviación estándar C. Las constantes A, B y C representan los índices de modulación de amplitud (por fase) para las tres señales moduladoras. Una vez obtenido el radio dinámico rd, el voltaje dinámico del arco eléctrico por fase v se determina con la ecuación (2).
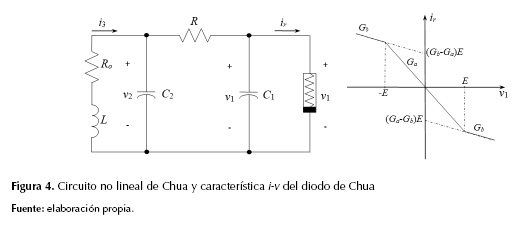
El oscilador de Chua se representa con el circuito que se muestra en la parte izquierda de la figura 4, y se implementa usando elementos lineales conectados a un dispositivo no lineal, conocido como el diodo de Chua, caracterizado por la curva ir-v1 que se muestra en la parte derecha de la figura 4.
El circuito es no lineal, autónomo y de tercer orden (tres elementos almacenadores de energía), que ha servido de prueba para áreas de investigación que involucran procesos de bifurcación y caos. La ecuación (3) describe la relación voltaje/corriente en el diodo de Chua,
Las ecuaciones (4), (5) y (6) relacionan los elementos lineales, se obtienen usando la ley de corriente de Kirchhoff.
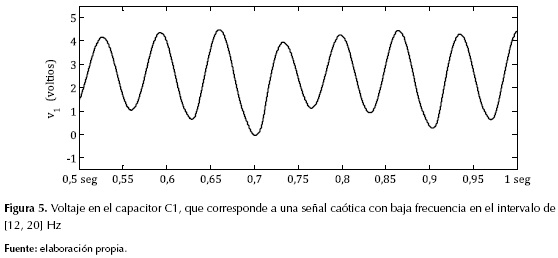
Este sistema de ecuaciones resulta de gran ayuda para implementar el oscilador de Chua con diagrama de bloques en programas en donde no es posible especificar las condiciones iniciales de las variables v1, v2 e i3. Usando los valores R0 = 12.5 Ω, L = 3.6 mH, C1 = 2 µF, C2 = 20 µF, R = 1.873 kΩ, E = 1 V, Ga = -757.576 Ʊ y Gb = -409.091 Ʊ, se obtiene en v1 una señal caótica de baja frecuencia en el rango de [12, 20] Hz, como se muestra en la figura 5.
La señal v1n que se utiliza en el modelo del horno de arco corresponde al voltaje v1 dividido entre su valor máximo. Información más detallada acerca del oscilador de Chua se encuentra en Kennedy (1993a, 1993b).
Modelo hiperbólico del arco eléctrico
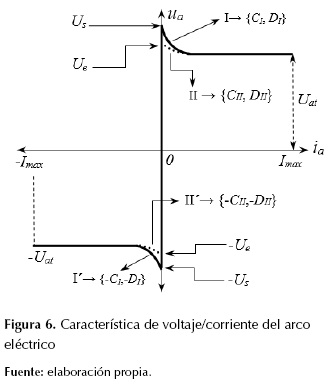
Este modelo parte de la relación entre el voltaje y la corriente del arco eléctrico presentado en Cavallini, Montanari, Pitti y Zaninelli, 1995). Se fundamenta a partir de la característica voltaje/corriente del arco eléctrico, tal como se observa en la parte izquierda de la figura 2 y se redibuja con mayor detalle en la figura 6. En esta última se distinguen cuatro regiones I, II, I' y II'. Las regiones I y I' indican la característica de encendido del arco eléctrico en el semiciclo positivo y negativo respectivamente de la corriente del arco. Las regiones II e II' muestran la parte de extinción de la corriente del arco, en el semiciclo positivo y negativo respectivamente de la corriente.
La ecuación (7) captura con precisión la característica ua-ia del arco eléctrico de la figura 6 (Montanari et al., 1994).
Donde Uat, que puede ser positivo (semiciclo positivo) o negativo (semiciclo negativo), es el voltaje umbral, el cual representa el voltaje del arco correspondiente al mayor valor de corriente (± Imáx). Los valores de C y D dependen de la evolución de la corriente del arco; por ejemplo, cuando el arco se enciende (región I o I') C = ± CI y D = ± DI (+ para el semiciclo negativo y - para el semiciclo negativo). Luego, a medida que la corriente crece, el voltaje del arco tiende al voltaje umbral ± Uat. Una vez la corriente del arco alcanza su valor máximo ± Imáx, ella empieza a decrecer y las constantes cambian ahora a C = ± CII y D = ± DII. Finalmente, el arco eléctrico se extingue en el paso por cero de la corriente. La condición ia = 0 da los valores del voltaje de arco de encendido y de extinción, para el semiciclo positivo de la corriente del arco se dan con las ecuaciones (8) y (9).
Con Us mayor que Ue. Para el semiciclo negativo, estos voltajes cambian de signo. En este trabajo se ajustan los parámetros con los valores utilizados en Mousavi, Hosseinian, Askarian y Moaddabi, 2010), que son CI = 190000 W, DI =5000 A, CII = 39000 W y DII =5000 A, y un voltaje umbral Uat0 = 240 V para cada fase. La resistencia del arco eléctrico ra se determina utilizando la ecuación (10).
En el momento de realizar la implementación del modelo, existe un problema de estabilidad debido al tiempo de paso de integración, causando que la resistencia del horno tome el valor calculado en el paso previo. Por tal razón, el valor de la corriente esperada para el tiempo de simulación ti+1, es estimada en el tiempo ti, mediante la ecuación (11).
El modelo de horno de arco debe ser viable para reproducir las condiciones que causan el efecto flicker. La variación de la tensión de horno de arco depende de la variación de la longitud de arco y se encuentran relacionados con la ecuación (12) (Cavallini, Montanari, Pitti y Zaninelli, 1995):
Donde l es la longitud de arco en cm, A es la constante que considera la suma de las caídas de tensión en los electrodos y B es la constante que representa la caída de tensión por unidad de longitud de arco. Para la implementación del modelo se consideran los valores típicos A = 40 V y B= 10 V/cm (Mousavi, Hosseinian, Askarian y Moaddabi, 2010). Para introducir fluctuaciones de tensión al voltaje se utiliza la variable k, que se relaciona con el voltaje del arco (ua) con la ecuación (13).
Con k dado como se indica en la ecuación (14).
Uat y lo son el voltaje y la longitud de arco cuando ia tiene un valor máximo. Se propone utilizar los dos comportamientos, el aleatorio y el periódico, para el modelo del horno de arco. Por tanto, el radio k no solo tendrá un movimiento cíclico sino a su vez será un movimiento aleatorio para así poder generar las fluctuaciones de tensión causadas por este tipo de comportamiento característico de los hornos de arco eléctrico (Alzate, Marulanda y Escobar, 2010). El anterior paso es descrito con la ecuación (15).
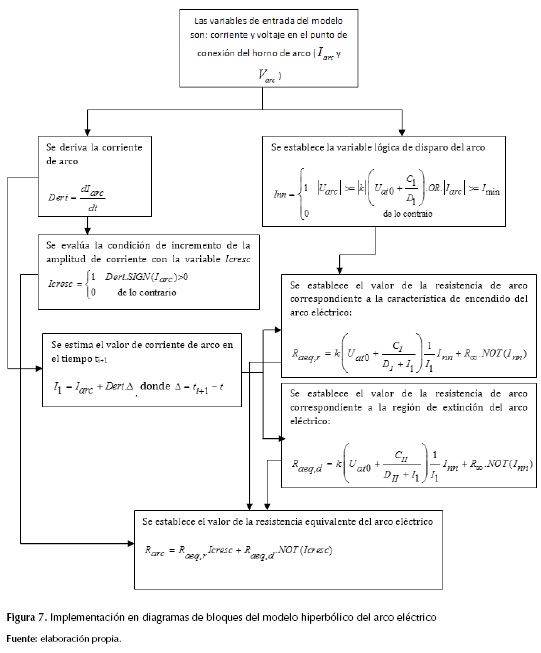
La señal gn es ruido generado, el cual tiene una distribución gaussiana con media cero y desviación estándar de gn, que se denota como std(gn), es un parámetro de entrada al modelo y es necesario establecer previamente su rango de variación. El diagrama de bloques que muestra la implementación del modelo hiperbólico del arco eléctrico se muestra en la figura 7.
En la figura 7, Imín, que es la diferencia de corriente en el cruce por 0 de la característica voltaje/corriente del arco eléctrico, se estableció en Imín =0.7 kA. La variable k es la longitud de radio de horno de arco definida en la ecuación 15, con Umáx = 600 V y Umín = -600 V.
Resultados
Base de datos
Se utilizaron las formas de onda de voltajes y corrientes reales presentadas en Cano y Tacca (2005) para comparar el funcionamiento de los dos modelos de horno de arco eléctrico. Los datos tienen una frecuencia de muestreo de 2048 mps (muestras por segundo), una frecuencia fundamental de 50 Hz y seis ciclos de voltajes y corrientes.
Software de desarrollo de los modelos
Se utilizó el programa PSCAD-EMTDC para desarrollar los dos modelos de horno de arco. Para la simulación se estableció un paso de 97.656 µS, un tiempo de simulación de cinco segundos y se usó el compilador Compaq Visual Fortran Professional Edition 6.1 para el desarrollo de algunas librerías utilizadas en la implementación de los modelos.
Resultados
Para efectos de presentación de resultados, el modelo 1 hace referencia al basado en el principio de conservación de la energía, y el modelo 2 será el modelo hiperbólico. Las mediciones para la comparación fueron tomadas en el secundario del transformador de la subestación del horno, es decir el transformador T2; y están referenciados al final de la etapa de fusión.
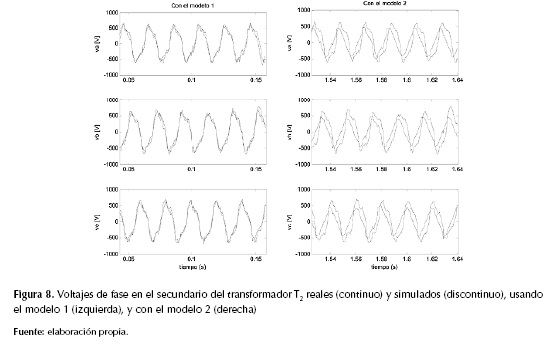
Las formas de onda de los voltajes de fase en el secundario del transformador T2, reales y simulados se muestran en la figura 8. En esta se observa que ambos modelos del horno de arco capturan la naturaleza no lineal de los voltajes reales, es decir, los voltajes se asemejan a los valores reales de los datos en cuanto a magnitud y forma. Además, se observa una mejor aproximación del modelo 1 a los voltajes reales, ya que casi ni se distinguen en el gráfico las líneas discontinuas.
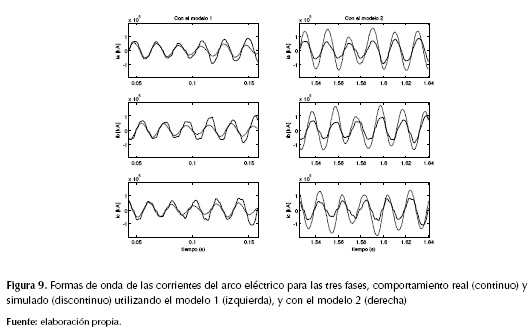
Una comparación similar se ha realizado para las formas de onda de las corrientes del arco eléctrico. En la figura 9 se muestran las corrientes del arco eléctrico real y simulado para las tres fases. Los resultados muestran que la aproximación en la dinámica del comportamiento del modelo de horno de arco, sigue la característica de operación de la carga, validando su inclusión en un sistema de potencia para efectuar análisis en calidad de la energía.
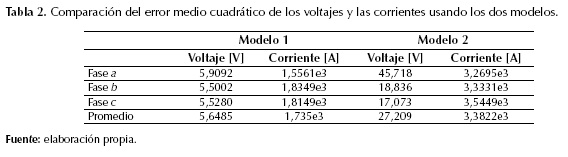
Se determinó el error medio cuadrático de las formas de onda de tensión y corriente de los datos reales y simulados, y para cada modelo se compararon los resultados. El error medio cuadrático se determinó con la ecuación (16).
Donde N es el número de datos de la señal simulada xis (que puede ser un voltaje o una corriente) y xir es la señal real (de voltaje o corriente). Los resultados se muestran en la tabla 2.
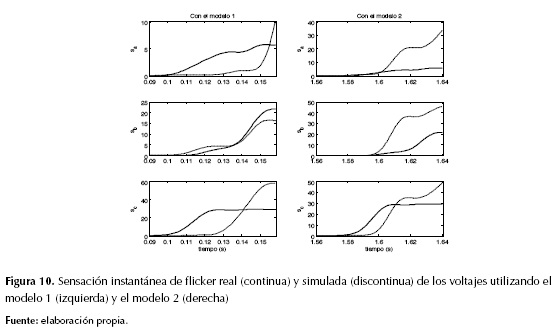
El nivel instantáneo de flicker que se denota con la letra s, es una medida de la cantidad de sensación de flicker producida por alguna fluctuación de tensión. Esta variable tiene en cuenta la sensibilidad del ojo humano respecto a la frecuencia de cambios de la luminosidad de una lámpara incandescente (Standard CEI/IEC 61000-4-15, 1997). La figura 10 muestra el comportamiento de s (para cada voltaje) producido por las fluctuaciones de tensión de los datos simulados y su comparación con los correspondientes datos reales. Se observa cómo la evolución en el tiempo de s guarda cierto nivel de similitud en el voltaje de la fase b obtenido con el modelo 1 y del voltaje de la fase c del modelo 2. Para los demás voltajes de ambos modelos la similitud con los correspondientes valores reales sus diferencias aumenta. Al final del tiempo, siempre son mayores los valores de s de los voltajes del modelo 2 comparados con los reales.
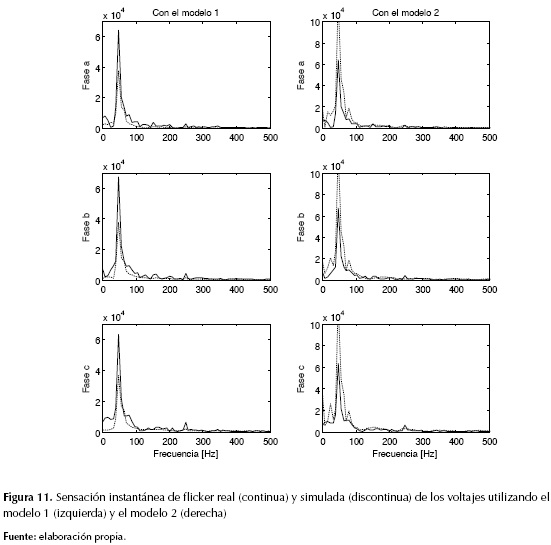
Debido a que el horno de arco es por naturaleza una fuente de armónicos, el modelo debe reproducir en forma cercana los armónicos de voltaje y corriente. La figura 11 muestra el espectro armónico de las corrientes del arco eléctrico reales y simuladas con los dos modelos.
Ambas curvas presentan un comportamiento similar, produciendo componentes interarmónicas y armónicas de orden par e impar. Sin embargo, el modelo 1 presenta una mejor aproximación a los armónicos de corriente.
Conclusiones
La comparación de los resultados obtenidos a partir de las simulaciones realizadas con los datos reales, permite observar que los modelos implementados reflejan el comportamiento caótico y aleatorio de la carga y valida su inclusión en los problemas que se van a analizar en la red de distribución.
Los resultados muestran que los modelos se aproximan a la dinámica de comportamiento del horno de arco, con mejores efectos de aproximación en forma de ondas de corriente y tensión siguiendo la característica de operación de la carga, validando su inclusión en un sistema de potencia para efectuar análisis en calidad de energía.
El modelo 1 implementado logra una mejor aproximación de la forma de onda de voltajes y corriente, pero al observar el comportamiento del fenómeno índice de severidad de flicker de corta duración, se evidencia que el modelo 2 presenta una fluctuación mayor de tensión a la luz del comportamiento de esta variable. Como un trabajo futuro se recomienda utilizar una técnica de identificación de parámetros que minimice el error entre los datos reales y los simulados en ambos modelos.
Financiamiento
Universidad Tecnológica de Pereira y Colciencias. Financiación del convenio 467/08.
Referencias
Alves, M.; Assis P., Z.; Peixoto G., C. y Goncalves G., D. (2010). An integrated model for the study of flicker compensation in electrical networks. Electric Power Systems Research, 80, 1299-1305.
Alzate, A.; Marulanda, J. y Escobar, A. (2010). Electric Arc Furnace Modeling for Power Quality Analysis. Bogotá: IEEE Conference of the Andean Council ANDESCON.
Cano, E. y Tacca, H. (2005). Arc furnace modeling in ATP EMTP. Montreal Canada: Presented at the International Conference on Power Systems Transientes.
Cavallini, A.; Montanari, G.; Pitti, L. y Zaninelli, D. (mayo-junio de 1995). ATP Simulation for Arc-Furnace Flicker Investigation. European Transactions on Electrical Power Engineering, 5(3), 165-172.
Göl, M.; Özgül Salor, Bora Alboyacı, Bilge Mutluer, I¸sık Çadırcı, & Muammer Ermi¸s. (2010). A New Field-Data-Based EAF Model for Power Quality Studies. IEEE Transactions on Industry Applications, 46(3), 1230-1242.
Kennedy, M. (octubre de 1993a). Three steps to Chaos-Part I: Evolution. IEEE Transactions on Circuit and Systems-I:Fundamental, Theory and Applications, 40(10), 640-665.
Kennedy, M. (octubre de 1993b). Three steps to Chaos-Part II: A Chua's circuit primer. IEEE Transactions on Circuit and Systems-I:Fundamental, Theory and Applications, 40(10), 657-674.
Montanari, G.; Loggini, M.; Cavallini, A.; Pitti, L. y Zaninelli, D. (octubre de 1994). Arc Furnace Model for the Study of Flicker Compensation in Electrical Networks. IEEE Transactions on Power Delivery, 9(4), 2026-2036.
Mousavi Agah, S.; Hosseinian, S.; Askarian Abyaneh, H. y Moaddabi, N. (2010). Parameter Identification of Arc Furnace Based on Stochastic Nature of arc Lengh using two- step Optimization Technique. IEEE Transactions on Power Delivery, 25(4), 2859-2867.
O'Neill, E.; Heydt, G.; Kostelich, E.; Venkata, S. y Sundaram, A. (abril de 1999). Nonlinear Deterministic Modeling of Highly Varying Loads. IEEE Transactions on Power Delivery, 14(2), 537-542.
Orille F., A. (1993). Centrales eléctricas II. Introducción al sector eléctrico y al sistema de energía eléctrica. Barcelona: Universitat Politécnica de Catalunya.
Standard CEI/IEC 61000-4-15 (1997). Electromagnetic compatibility (EMC). Part 4. Testing and measurements techniques. Section 15: Flickermeter-Functional and Testing Specifications.
Trageser, J. (marzo-abril de 1980). Power Usage and Electrical Circuit Analysis for Electric Arc Furnaces. IEEE Transactions on Industry Applications, IA-16(2), 277-284.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.