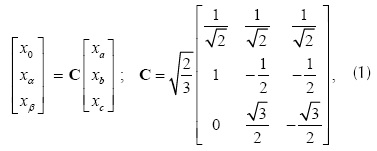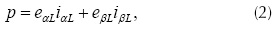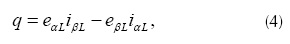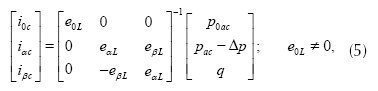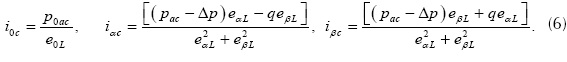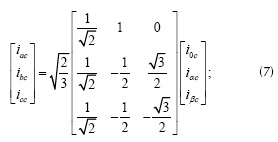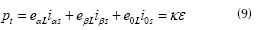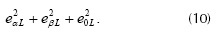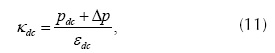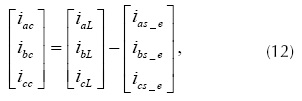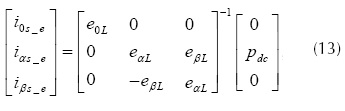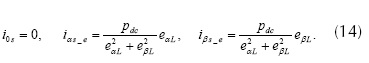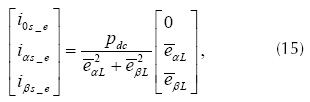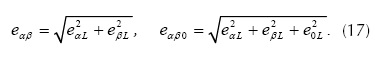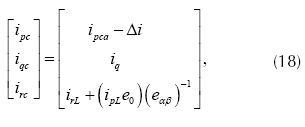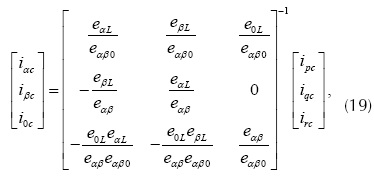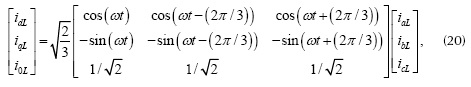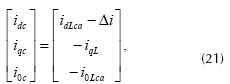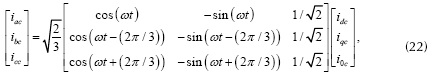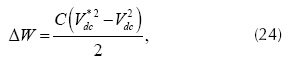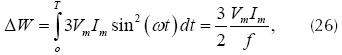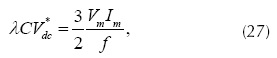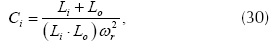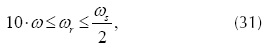Estudio comparativo de cinco estrategias de compensación de armónicos en filtros activos de potencia

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2017.2.a01

Estudio comparativo de cinco estrategias de compensación de armónicos en filtros activos de potencia

A comparative study of five methods of harmonics compensation in active power filters

Jesser James Marulanda Durango¹, Andrés Escobar Mejía², Alfonso Alzate Gómez³

¹ Ingeniero electricista, magíster en Ingeniería Eléctrica. Docente de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: jjmarulanda@utp.edu.co

² Ingeniero electricista, magíster en Ingeniería Eléctrica, doctor en Ingenierías. Docente de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: andreses1@utp.edu.co

³ Ingeniero electricista, magíster en Sistemas de Generación de Energía Eléctrica. Docente de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: alalzate@utp.edu.co

Fecha de recepción: 9 de agosto de 2016 Fecha de aceptación: 15 de febrero de 2017

Cómo citar: Marulanda D., J.J.; Escobar M., A. y Alzate G., A. (2017). Estudio comparativo de cinco estrategias de compensación de armónicos en filtros activos de potencia. Revista Tecnura, 21(52), 15-31. doi: 10.14483/udistrital.jour.tecnura.2017.2.a01

Resumen

Contexto: Una de las funciones de un filtro activo de potencia es calcular las consignas de corriente (i.e.: reducción de armónicos, corrección del factor de potencia, balancear las corrientes y voltajes) que compensen la fuente de alimentación. Existen en la literatura varios algortimos que realizan esta función. El objetivo de este artículo es presentar los resultados obtenidos sobre el funcionamiento de cinco algoritmos propuestos en la literatura, bajo condiciones de voltajes distorsionados.

Método: Consiste en la implementación de los siguientes algoritmos: potencia reactiva instantánea; factor de potencia unitario; compensación perfecta de armónicos; algoritmo pqr; y marco de referencia síncrono, en el programa de simulación Matlab - Simulink. Luego, usando un sistema eléctrico compuesto por cargas lineales y no lineales con características similares a un circuito real, se calcula la distorsión armónica total, el valor eficaz de la corriente de línea y de su componente fundamental, y el factor de potencia en la fuente trifásica. Se tomarán valores antes y después de la conexión a la red del filtro activo de potencia, considerando cada uno de los algoritmos por separado y manteniendo las mismas condiciones en el sistema para cada uno de ellos. También se calculan otras cantidades en el sistema de potencia para realizar la comparación.

Resultados: Se muestran las corrientes de la red de alimentación antes y después de la conexión del filtro activo de potencia, además de la distorsión armónica de las corrientes y el factor de potencia. También se presenta la forma de onda del voltaje de continua del inversor con cada uno de los algoritmos utilizados, para evaluar el desempeño de un controlador de tensión que requiere el filtro.

Conclusiones: En condiciones de funcionamiento con voltajes distorsionados en la red de alimentación, el algoritmo con mejor desempeño es el de compensación perfecta de armónicos, ya que este utiliza un filtro pasa bajo para mitigar los efectos de los armónicos de los voltajes sobre el cálculo de las corrientes de compensación.

Palabras clave: armónicos, calidad de la energía, compensación, factor de potencia, filtro activo de potencia.

Abstract

Context: One of the functions of an Active Power Filter (APF) is to calculate current set points (i.e. harmonic reduction, power factor correction and current and voltage balancing) that compensate the power source. There are several algorithms in the literature that perform this function, so the objective in this article is to present the results obtained from the implementation of five algorithms proposed in the literature, under conditions of distorted voltages.

Method: The methodology consists of the implementation of the following algorithms: Instantaneous reactive power; unit power factor; perfect harmonic compensation; PQR algorithm; and synchronous frame of reference in the MATLAB simulation program. Then, we calculate the total harmonic distortion (THD), the effective value of the line current and its fundamental component, and the power factor (PF) at the three-phase source, using an electrical system composed of linear and non-linear loads with similar characteristics to a real circuit. We will take values before and after the connection to the network of the active power filter, considering each of the algorithms separately and maintaining the same conditions in the system for each of them. Other quantities are also calculated in the power system to make the comparison.

Results: The main currents before and after the active power filter connection are displayed, in addition to the harmonic distortion of the currents and the power factor. We also present the waveform of the inverter continuous voltage with each of the algorithms used, in order to evaluate the performance of a voltage controller that requires filter.

Conclusions: In operating conditions with distorted voltages in the power supply network, the algorithm with the best performance is the perfect harmonic compensation algorithm, since it uses a low-pass filter to mitigate the effects of the harmonics of the voltages on the calculation of the currents of compensation.

Keywords: Active power filters, Compensation, Harmonics, Power Factor, Power Quality.

INTRODUCCIÓN

Un problema presente en las redes eléctricas de distribución de energía es el aumento progresivo de cargas no lineales que ayudan a incrementar la inyección de corrientes y tensiones armónicas. La presencia de armónicos puede originar problemas como: calentamiento en transformadores, vibraciones en motores, bajo factor de potencia, disparos indeseados en equipos de protección, excesiva corriente por el conductor neutro, entre otros (Kanjiya, Khadkikar y Zeineldin, 2015).

Convencionalmente, filtros pasivos se han utilizado para reducir la presencia de armónicos en los sistemas eléctricos. Esta alternativa presenta varias desventajas, ya que su estructura es invariable y puede ocasionar problemas de resonancia entre el filtro pasivo y la impedancia de la red (Rafiei, Toliyat, Ghazi y Gopalarathnam, 2001). Por esto, otras formas de compensación más sofisticadas como los filtros activos de potencia o active power filters (APF) han sido considerados en los últimos años. Los APF tienen entre sus principales ventajas la reducción del contenido armónico y el aumento del factor de potencia (Asiminoael, Blaabjerg y Hansen, 2007; Alzate, Murillo y Silva, 2017).

Obtener las corrientes que debe inyectar el APF para compensar el sistema es una de las principales funciones que debe realizar el sistema de control de los APF en conexión paralela. Estas corrientes, conocidas como corrientes de compensación, se obtienen a través diversos algoritmos, que emplean transformaciones matemáticas buscando desacoplar la potencia activa y la reactiva para facilitar la tarea del controlador (Akagi, Kanazawa y Nabae, 1984). Debido a los diversos algoritmos de compensación que se encuentran en la literatura, surge la siguiente pregunta: ¿Cuál algoritmo presenta un mejor desempeño en el APF para determinadas condiciones de operación? En Ranjbar, Masoum y Jalilian (2009) se realiza una comparación de cuatro algoritmos de compensación en condiciones de voltajes desbalanceados y distorsionados, para un filtro activo que utiliza un inversor de cuatro ramas. En Rafiei et al. (2001) se presenta un nuevo algoritmo y se compara su desempeño con algoritmos previamente presentados, bajo condiciones de voltajes balanceados y distorsionados.

En este artículo se pretende analizar el desempeño de cinco algoritmos de compensación bajo condiciones de voltajes distorsionados. Los algoritmos que se comparan son: teoría de la potencia instantánea o teoría pq (Akagi et al., 1984), factor de potencia unitario (Cavallini y Montanari, 1994), cancelación perfecta de armónicos (Rafiei et al., 2001), teoría pqr (Kim, Blaabjerg, Bak-Jensen y Choi, 2002) y marco de referencia síncrono (Kale y Ozdemir, 2005). En la literatura especializada la comparación del desempeño de dichos algoritmos no ha sido reportada.

El artículo está dividido de la siguiente forma: primero, se describe el sistema eléctrico de potencia bajo estudio; luego se presenta el marco teórico donde se resumen las bases de funcionamiento de los algoritmos utilizados, además se muestra el procedimiento de ajuste del controlador de tensión del voltaje dc (direct current) del inversor. Después, se muestran los resultados obtenidos en simulación, donde se realiza un análisis para cada caso. Por último, se presentan las conclusiones y se citan las referencias bibliográficas utilizadas.

METODOLOGÍA

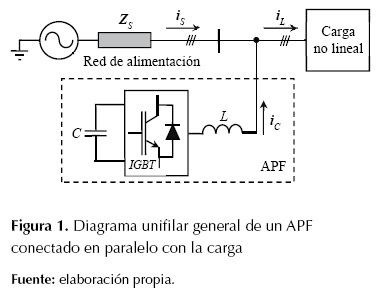
Dependiendo de cómo se conecta el APF al sistema, se puede distinguir entre filtro serie, filtro paralelo y filtro mixto. La conexión paralela es la que se utiliza en este artículo. Con dicha conexión, los APF se pueden asemejar como una fuente de corriente trifásica controlada, ya que inyectan en el punto de acoplamiento las corrientes que compensan el sistema de potencia. En la figura 1 se muestra un diagrama unifilar general de un APF en paralelo con la carga. En la figura 1, las corrientes de la carga se denotan con el subíndice L, las de la fuente con el subíndice S y las que inyecta el APF o las de compensación con el subíndice C.

El APF está conformado por un inversor trifásico de tres ramas que se conecta a la red a través de inductancias de acople (L por fase) y un capacitor C que se utiliza para mantener constante el voltaje en el lado dc del inversor. Los algoritmos de compensación se encargan de determinar las corrientes i_c en cada fase (i_ac, i_bc, i_cc) que debe inyectar el APF. Las corrientes de la carga se denotan como (i_aL, i_bL, i_cL) y las de la fuente (i_as, i_bs, i_cs).

Algoritmos de compensación

Estos algoritmos se encargan de determinar para cualquier instante de tiempo, el valor de las corrientes en cada fase que debe inyectar el APF para realizar la compensación en el sistema. La principal característica de estos algoritmos es el corto tiempo que tarda en obtener las consignas de corriente ante posibles cambios que pueda ocurrir en las condiciones de la carga. Los algoritmos utilizados se basan en el dominio del tiempo y son: teoría de la potencia reactiva instantánea, factor de potencia unitario, compensación perfecta de armónicos, teoría pqr y marco de referencia síncrono.

Potencia reactiva instantánea

Este algoritmo fue propuesto en Akagi et al. (1984). Consiste en una transformación de las tensiones y las corrientes que circulan en la carga a un marco de coordenadas estacionario y ortogonal conocido como (α, β, 0), usando la transformación dada en la ecuación

Donde x puede ser un voltaje, e, o una corriente i, y C es la matriz de transformación de Clarke. En el marco de referencia (α, β, 0), la potencia total instantánea absorbida por la carga, se expresa como la suma de dos términos, la potencia activa p asociada a las componentes de voltaje y corriente de la carga en los ejes α y β, y la potencia p₀ debida a las componentes en el eje 0 (o de secuencia cero) (Akagi et al., 1984).

Donde el subíndice L hace referencia a cantidades de la carga. La potencia reactiva instantánea q, está dada por Akagi et al. (1984).

Cada componente de potencia tiene a su vez una componente constante o dc y una componente alterna o ac. El objetivo de este algoritmo es conseguir que la red de alimentación entregue la componente dc de p y p₀, y el resto de las potencias de la carga sean suministradas por el APF. A partir de lo anterior, las corrientes de compensación que se denotan con el subíndice c en el marco de referencia (α, β, 0) están dadas por:

Al calcular la inversa de la matriz de tensiones y multiplicarla por el vector columna de potencias se obtiene que,

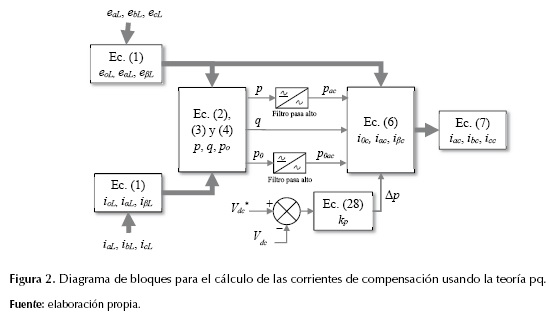
La potencia Δp se obtiene a través de un controlador proporcional y se requiere para mantener constante el voltaje dc del inversor, como se mostrará posteriormente. El signo negativo de Δp significa que esta potencia es absorbida por el filtro. En la figura 2, se resume el algoritmo del cálculo de las corrientes de compensación basado en la teoría pq.

El procedimiento para el cálculo de la constante proporcional del controlador k_p se muestra más adelante. Los voltajes V_dc y V_dc^* que aparecen en la figura 2 son el voltaje medido y el esperado en el lado dc del inversor respectivamente. Por último, usando la transformación inversa de Clark, se obtienen las corrientes de referencia en el sistema trifásico (a, b, c), como se indica en la ecuación.

Factor de potencia unitario

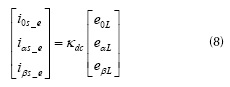
También conocida como Unity Power Factor (UPF). Esta estrategia parte de la suposición de que la carga compensada (carga más filtro) es equivalente a una carga resistiva (Cavallini y Montanari, 1994). De otra forma, lo anterior equivale a decir que las corrientes esperadas en la fuente de alimentación que se denotan con el subíndice s, sean iguales a los voltajes en terminales multiplicados por una constante de proporcionalidad (o la conductancia). En el marco de referencia (α, β, 0) el algoritmo de factor de potencia unitario busca que,

Donde el subíndice e significa componente esperada y κ_dc es un valor constante que representa la conductancia equivalente de la carga compensada. En efecto, la potencia instantánea de la carga compensada que se denota como p_t en función de los voltajes y las corrientes en las coordenadas (α, β, 0) está dada por (Rafiei et al. (2001),

Donde κ es la conductancia de la carga compensada, debe de ser constante e igual a κ_dc para tener factor de potencia unitario (Rafiei et al., 2001), y ε está dada por

El comportamiento resistivo de la carga compensada sugiere que su conductancia sea igual a (Rafiei et al., 2001),

Donde p_dc y ε_dc son los valores promedio de p_t y ε, respectivamente. La potencia Δp se requiere para mantener constante el voltaje dc del inversor y debe ser suministrada por la fuente de alimentación, por lo que se suma al valor promedio de la potencia instantánea.

Luego, usando la transformación inversa de Clark (ecuación), se transforman las corrientes esperadas en la fuente de alimentación en coordenadas (α, β, 0) al sistema (a, b, c). Finalmente, haciendo sumatoria de corrientes en el punto donde se conecta el APF (figura 1), se obtienen las corrientes de compensación cuyo resultado está dado por la ecuación.

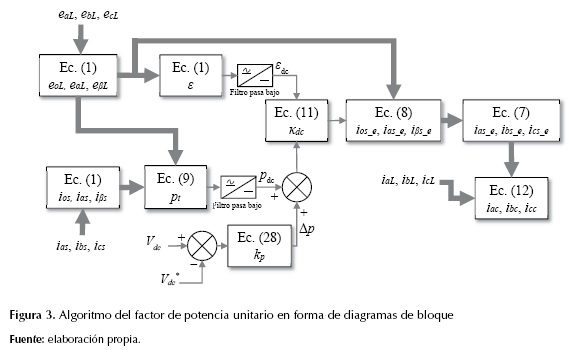
En la figura 3 se ilustra, en diagramas de bloques, el algoritmo de factor de potencia unitario.

El método UPF se conoce como un método indirecto, ya que primero se calculan las corrientes compensadas para después calcular las corrientes que debe inyectar el APF.

Compensación perfecta de armónicos

Conocido como perfect harmonic compensation (PHC) (Rafiei et al., 2001). Se trata de un método indirecto similar al UPF, que en teoría es capaz de compensar todos los armónicos presentes en la carga (Ranjbar, Masoum y Jalilian, 2009). Parte del hecho de que una vez se realiza la compensación, en la red de alimentación la potencia activa instantánea de la carga compensada es constante, y además se anula la potencia reactiva y la generada por las componentes de secuencia cero. Lo anterior se expresa en términos de las corrientes de la fuente de alimentación en el marco de referencia (α, β, 0) (ecuación) a través de la ecuación.

Donde el subíndice e hace referencia a las componentes esperadas en la red de alimentación. La ecuación se puede expresar a partir de la ecuación (14).

En el algoritmo PHC, se utilizan las componentes fundamentales de los voltajes e_αL y e_βL para obtener las corrientes de referencia (Rafiei et al., 2001), de tal manera que,

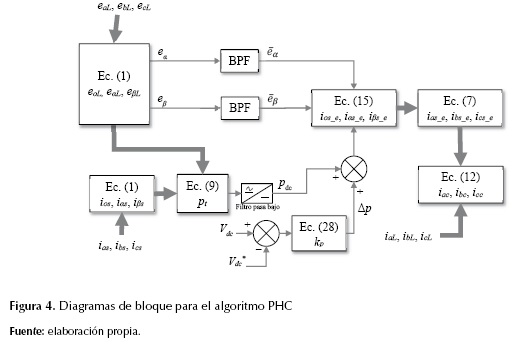
Las componentes fundamentales 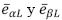se obtienen a través de filtros pasa banda (o BPF, band pass filters) para cada componente. Luego de obtener las corrientes esperadas en la fuente de alimentación en coordenadas (α, β, 0), por un procedimiento igual al algoritmo UPF, se obtienen las referencias de las corrientes en el sistema (a, b, c). En la figura 4 se muestra el procedimiento empleado en el algoritmo PHC a través de diagramas de bloque para el cálculo de las corrientes de compensación del APF.

Algoritmo pqr

Este algoritmo fue propuesto por Kim y Akagi (1999), donde se define un marco de referencia en el que la potencia activa y reactiva instantánea se expresan en términos de componentes linealmente independientes, lo cual facilita la compensación de la potencia reactiva y la mitigación de armónicos (Kim et al., 2002).

Luego de la transformación de los voltajes de fase y las corrientes de línea en la carga al marco de referencia (α, β, 0), las corrientes en el marco de referencia (p, q, r) se obtienen con la ecuación (Ucar y Oz demir, 2008),

Donde e_αβ y e_αβ0 están dados por la ecuación.

El algoritmo pqr propone calcular las corrientes de compensación en el marco (p, q, r) con la ecuación para obtener corrientes sinusoidales y balanceadas en la fuente de alimentación (Ucar y Ozdemir, 2008),

Donde i_pca es la componente alterna de i_pL y la corriente Δi se obtiene a partir de un controlador proporcional de la tensión en el lado dc del inversor, como se muestra más adelante. Luego, con la ecuación se obtienen las corrientes de compensación en el marco (α, β, 0), y con la transformación inversa de Clark dada en la ecuación se pasa al sistema trifásico convencional (a, b, c),

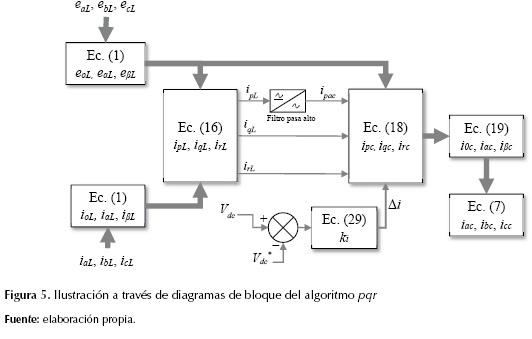
En la figura 5 se ilustra a través de diagramas de bloque la implementación del algoritmo pqr, para la obtención de las corrientes de compensación,

Marco de referencia síncrono

También conocido como dq0. Esta estrategia transforma las corrientes de la carga a un sistema de coordenadas (d,q,0) que se encuentra en movimiento, para facilitar la descomposición de las corrientes dejando solo aquellas componentes de la corriente que definen la compensación (Asiminoael, Blaabjerg y Hansen, 2007). Se utiliza la transformación de Park que está dada por la ecuación (Kale y Ozdemir, 2005), para transformar las corrientes trifásicas en la carga del sistema convencional al marco de referencia síncrono (d, q, 0),

En cargas no lineales o desbalanceadas, las corrientes en los ejes (d, q, 0) tienen componentes constantes y alternas denotada con el subíndice ac. Las componentes alternas son generadas por los armónicos y a los desbalances presentes en las corrientes de la carga. El propósito del algoritmo dq0 es obtener en la fuente de alimentación la componente constante de i_d e i₀ (generada por cargas desbalanceadas), y que las corrientes restantes sean suministradas por el filtro (Asiminoael, Blaabjerg y Hansen, 2007). Lo anterior define las consignas de corrientes en el marco de referencia síncrono (d,q,0), que se expresan a través de la ecuación.

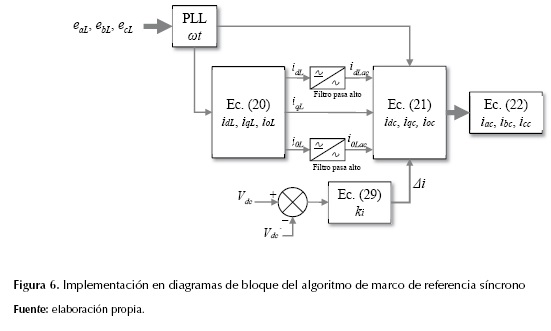
La corriente Δi se requiere para garantizar un voltaje casi constante en el enlace dc del inversor y se obtiene a través de un controlador proporcional como se muestra más adelante. En la figura 6 se detalla la implementación en diagramas de bloque del algoritmo dq0.

El ángulo ωt sincroniza los voltajes en el punto de acople del APF con el sistema de referencia en movimiento (d,q,0), y es obtenido a través de un oscilador de seguimiento de fase (o PLL, phase locked loop) que se explica detalladamente en Luna et al., 2015).

Control de la tensión continua del inversor

Como se mencionó anteriormente en cada uno de los algoritmos para obtener las corrientes de referencia o compensación, el APF requiere mantener en un valor constante el voltaje dc del inversor. Esta tarea es llevada a cabo a través de un controlador proporcional (Hsu y Wu, 1996). La diferencia entre el voltaje esperado (o de referencia) V_dc^* y el medido V_dc, se denota con la letra λ y es el error del controlador que es la entrada al controlador proporcional para establecer la potencia Δp o la corriente Δi, según el algoritmo utilizado. En efecto, la energía almacenada en el lado dc del inversor está dada por la ecuación:

Donde C es el valor del capacitor a la entrada del inversor. La variación de energía en C para un periodo de los voltajes de la red de alimentación se obtiene con la ecuación.

A través de la aproximación V_dc^*+ V_dc ≈ 2V_dc^*, se obtiene la ecuación (25).

Esta variación de energía se toma en cada ciclo de la fuente de alimentación (Hsu y Wu, 1996) y su valor está dado con la ecuación:

Donde V_m es el valor pico de las tensiones de fase en el punto de conexión del APF, I_m es el valor máximo de las corrientes de compensación (su valor se puede aproximar al valor máximo de las corrientes de la carga), T es el periodo y ω es la frecuencia fundamental de los voltajes de la red de alimentación, respectivamente. Reemplazando el resultado obtenido en la ecuación en la ecuación se obtiene la ecuación que relaciona el error de control λ con los parámetros de operación del APF.

En las estrategias de compensación donde la salida del controlador es en forma de potencia (Δp), la constante proporcional del regulador k_p se obtiene de λk_p = Δp con Δp = V_mI_m. De la ecuación resulta la ecuación para el cálculo de k_p.

Y para las estrategias de compensación que a la salida del regulador tienen una corriente (Δi), usando un planteamiento similar al caso anterior, la constante proporcional k_i se determina con la ecuación.

RESULTADOS

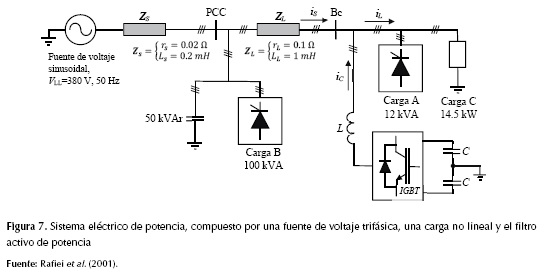
Se ha utilizado el circuito eléctrico propuesto por Rafiei et al. (2001) para evaluar el desempeño de los algoritmos de compensación. En la figura 7 se muestra el diagrama unifilar del sistema bajo estudio, que consiste en una carga de tipo industrial. La carga B es un convertidor de corriente alterna a continua de seis pulsos a base de tiristores, y su operación distorsiona los voltajes en terminales en las cargas A y C. Esta distorsión se vuelve más severa al conectar el banco de capacitores de 50 kVAr, ya que el tercer armónico pasa del 8,7 % (sin el banco) al 17 % (con el banco) respecto de la componente fundamental y el séptimo armónico pasa del 4,9 % al 24 %. Lo anterior permite evaluar el desempeño de los algoritmos de compensación en condiciones no ideales, al tratar con voltajes distorsionados como sucede en un sistema real de distribución.

El APF está compuesto por un inversor trifásico tipo puente o voltage source inverter (VSI) con condensador repartido el cual proporciona un camino de circulación de la corriente por el neutro cuando se presentan cargas desbalanceadas (Grino, Cardoner, Costa-Castello y Fossas, 2007). La conmutación de los dispositivos semiconductores tipo insulated gate bipolar transistor (IGBT) se realiza usando modulación por ancho de pulsos (o pulse width modulation (PWM)) por banda fija de histéresis, en donde la corriente de salida de cada rama del inversor se mantiene dentro de una banda de corriente de ancho fijo que tiene la misma forma de la corriente de compensación respectiva a cada fase. Cuanto más angosta sea la banda, mayor es la frecuencia de conmutación de los dispositivos del inversor (Kale y Ozdemir, 2005).

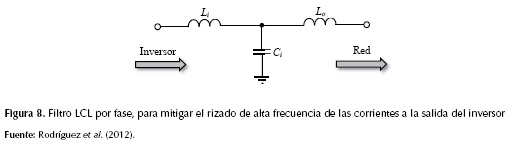
Para la simulación se ajustó el ancho de banda a 1 A, la inductancia de acople por fase del filtro con la red en 3 mH y el valor de cada capacitor en 1500 μF (Rafiei et al., 2001) con un voltaje de referencia (V_dc^*) de 800 V en el lado de continua del inversor. Adicionalmente, se instala un filtro pasivo paso-bajo (no mostrado en la figura 7 en aras de la claridad), para disminuir las componentes de alta frecuencia en las corrientes trifásicas de la red de alimentación, producidas por las conmutaciones de los IGBT. El filtro pasivo a la salida del inversor es de tipo LCL (inductancia, capacitor, inductancia) como se muestra en la figura 8, y ha sido probado en Rodríguez et al. (2012) para reducir el rizado de alta frecuencia de las corrientes generadas por un inversor.

La inductancia L_i es la del lado del inversor, que equivale a la inductancia de acople L (figura 7) cuyo valor es de 3 mH de acuerdo con los parámetros utilizados por Rafiei et al. (2001).

El valor del capacitor se ha seleccionado siguiendo el planteamiento presentado en Rodríguez et al. (2012), el cual establece la ecuación para el cálculo del capacitor.

Donde ω_r es la frecuencia de resonancia del filtro en radianes por segundo y su valor se toma en el rango dado por la ecuación.

Con ω_s igual a la frecuencia de conmutación de los IGBT. Debido a que la técnica PWM por banda fija de histéresis genera una frecuencia de conmutación variable (Kale y Ozdemir, 2005), se utiliza el valor promedio de ω_s para establecer el límite superior de la ecuación. El valor de L_o se ha establecido igual al 10 % del valor de L_i, de acuerdo con los criterios de diseño establecidos por Rodríguez et al. (2012). A partir de lo anterior, se obtienen los siguientes resultados para cuando L_o = 0,3 mH y C_i = 0,1 μF.

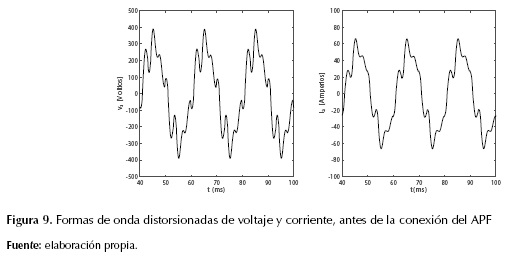
En la figura 9 se ilustran las formas de onda de el voltaje en la fase a en la barra Bc y la corriente en la fase a a través de Z_L, sin estar en operación el APF. Debido a que la carga es balanceada, se omiten las formas de onda para las otras fases.

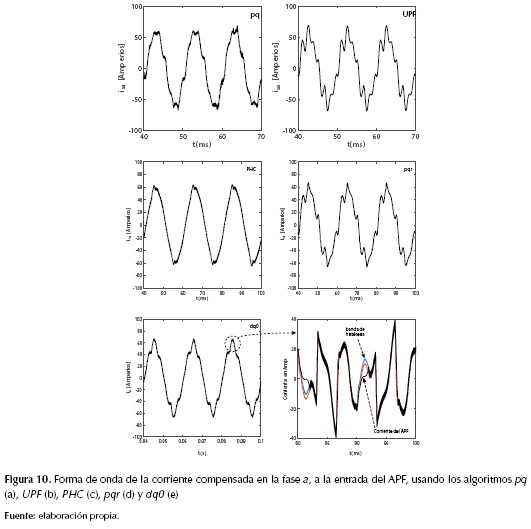
Se observa en la figura 9 la distorsión que tienen ambas formas de onda. Para cada forma de onda se ha calculado la distorsión total armónica, o total harmonic distortion (THD), que es una medida de la contribución de los armónicos y se calcula en un valor porcentual respecto al valor de la componente fundamental (Rashid, 2011). Para el voltaje se obtiene un THD de 30,46 % y 22,23 % para la corriente. En la figura 10, se muestran las formas de onda de la corriente i_s (para la fase a) a través de la impedancia Z_L, una vez realizada la compensación al sistema usando cada uno de los algoritmos presentados. Se observa que el algoritmo PHC es el que mejor reduce los armónicos en la corriente, ya que la forma de onda obtenida es muy similar a una sinusoide. Le sigue el algoritmo dq0, donde la corriente obtenida es similar a una sinusoide a excepción en los puntos cercanos a los valores pico donde ocurre una distorsión en la onda. A través de diferentes pruebas de simulación en el dominio del tiempo, se observa que dichas distorsiones se pueden reducir incrementando el voltaje en el lado dc del inversor o reduciendo el valor de la inductancia de acople del filtro con la red. Lo anterior va ligado a la dependencia que tiene la derivada de la corriente (di/dt) a la salida del inversor con el voltaje V_dc y el valor de L, que hace que está corriente, que es lineal por tramos, no siga fielmente a la corriente de referencia dentro de la banda de histéresis usada para la conmutación de los IGBT, como se muestra en la figura 10 (f). El valor mínimo que puede tener la pendiente de la corriente inyectada por el APF se aproxima con la ecuación.

Donde V_m es el valor máximo del voltaje de fase en el punto de conexión del APF y L es la inductancia de acople entre el APF y la red de alimentación. Al reemplazar los resultados obtenidos en la simulación, el valor mínimo aproximado de la pendiente es de 0,121 A/μs, y es recomendable que sea mayor a la máxima tasa de variación que presente la corriente de compensación obtenida con los algoritmos.

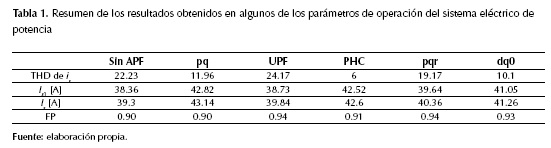
Los demás algoritmos muestran una corriente distorsionada, similares a los resultados obtenidos por Rafiei e al. (2001) y por Ranjbar, Masou y Jalilian (2009), esto debido a las formas de onda no-sinusoidales de los voltajes de fase en el punto de conexión del APF. Incluso el algoritmo UPF genera una mayor distorsión en la corriente al conectar el APF, ya que su objetivo es obtener una forma de onda de corriente semejante a la del voltaje, pero escalada. Esto se puede observar al comparar el voltaje de la figura 9 y la corriente con el algoritmo UPF en la figura 10. En la tabla 1 se muestran los resultados obtenidos para el THD, el valor eficaz de la componente fundamental (I_s1) y el valor eficaz (Is) de la corriente i_s. También se muestra el factor de potencia (FP) en el punto de conexión del APF.

Los resultados muestran que el mejor algoritmo para reducir el THD en la corriente es el PHC de 22,23 % (sin APF) a 6 % (con APF), seguido del dq0, pq, pqr y UPF. El algoritmo UPF distorsiona aún más las corrientes. El mejor FP se obtiene con los algoritmos UPF y pqr, dada la similitud que tienen estas las corrientes con el voltaje de la figura 9. Según los resultados, los valores eficaces de la corriente y su fundamental son mayores a los que presenta el sistema sin el APF en todos los casos, lo que indica que el APF además de inyectar las corrientes de compensación, inyecta un pequeño rizado de alta frecuencia en las corrientes que contribuye a aumentar los valores eficaces, incluso puede tener efectos en la forma de onda de los voltajes generando a su vez un rizado en estos y en la corriente que absorbe la carga.

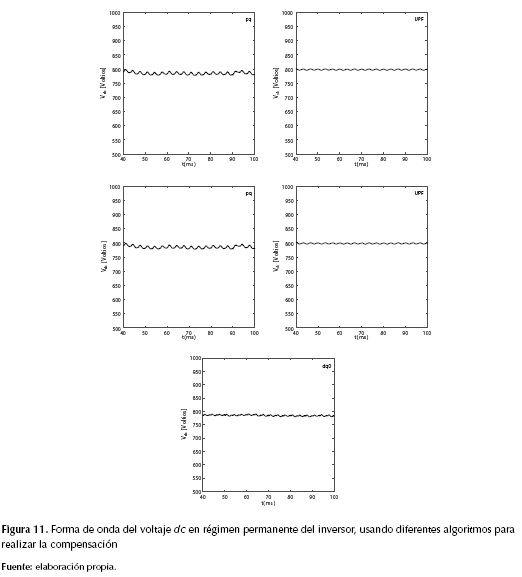
La constante k_p del controlador proporcional del voltaje dc del inversor se ajusta en 80 en el caso de que a la salida del controlador se tenga una variación en la potencia (Δp) y de 0,2 en el caso de que sea una variación en la corriente (Δi). Los resultados obtenidos en el voltaje de entrada del inversor en régimen permanente se muestran en la figura 11, para cada uno de los algoritmos implementados. De acuerdo con los resultados el voltaje dc de entrada al inversor se mantiene cercano al valor deseado, validando el procedimiento de ajuste del controlador.

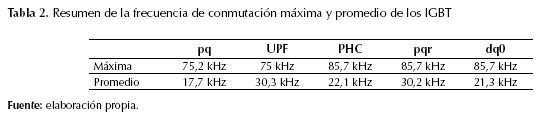
La tabla 2 lista el valor máximo y promedio de la frecuencia de conmutación de los IGBT según el algoritmo de compensación empleado. Como se puede observar, la frecuencia de conmutación promedio está entre los 20 y 30 kHz. Una forma de reducir está frecuencia sin variar la técnica PWM empleada es aumentando el ancho de la banda de histéresis, sin embargo, al realizar dicho aumento se estaría aumentando el rizado de las corrientes del inversor.

La frecuencia de conmutación y la corriente que circula por el compensador, permite seleccionar los dispositivos semiconductores en un sistema real. Según los resultados de la simulación para un ancho de banda de 1 A se deben seleccionar dispositivos semiconductores que operen a frecuencias de conmutación de hasta 85 kHz.

CONCLUSIONES

A partir de los resultados obtenidos, el algoritmo de compensación PHC es el que mejor opera para la reducción de armónicos de la corriente, ya que al utilizar filtros pasa banda atenúa el efecto que tienen los armónicos de tensión en el punto de conexión del APF sobre el cálculo de las corrientes de compensación.

El algoritmo dq0 requiere un nivel de tensión en la barra dc del inversor mayor a los otros algoritmos para llegar a resultados semejantes a los obtenidos con el PHC, ya que en algunos intervalos la rapidez de cambio de la corriente de compensación se hace mayor a la que puede entregar el inversor, lo que genera distorsiones en las corrientes que circulan por la red de alimentación como se observa en la figura 10 (f).

Los demás algoritmos, pq, UPF y pqr, no son recomendables en el caso de voltajes distorsionados, ya que la reducción de armónicos no es considerable, llegando incluso a generar más armónicos cuando se conecta el compensador como es el caso del algoritmo UPF. Lo atractivo de estos métodos es que no requieren de un PLL o de filtros pasa banda en su funcionamiento, como sucede en el dq0 y PHC. Se deja como un trabajo futuro, observar los resultados que se obtienen con estos tres métodos al modificarlos en su estructura a través de la incorporación de filtros pasa banda, para generar condiciones sinusoidales en el voltaje en el cálculo de las corrientes de compensación.

Referente a los resultados obtenidos con el controlador de tensión dc del inversor, se observó que el voltaje se mantiene cercano al esperado, con lo cual se valida el procedimiento y cálculo de la constante del controlador. Finalmente, los valores promedio y máximo de la frecuencia de conmutación de los IGBT, usando PWM por banda fija de histéresis se mostraron semejantes independiente del algoritmo empleado, por lo que ninguno de los algoritmos muestra alguna ventaja considerable en este aspecto.

REFERENCIAS BIBLIOGRÁFICAS

Akagi, H.; Kanazawa, Y. y Nabae, A. (1984). Instantaneous Reactive Power Compensators Comprising Switching Devices without Energy Storage Components. IEEE Transactions on Industry Applications, IA-20(3), 625-630. http://doi.org/10.1109/TIA.1984.4504460.

Alzate, A.; Murillo, Y. y Silva, C. (2017). Prototipo para la compensación de armónicos en sistemas trifásicos. Revista Tecnura, 20(50), 96-105. DOI: 10.14483/udistrital.jour.tecnura.2016.4.a07.

Asiminoael, L.; Blaabjerg, F. y Hansen, S. (2007). Detection is key-Harmonic detection methods for active power filter applications. IEEE Industry Applications Magazine, 13(4), 22-33. http://doi.org/10.1109/MIA.2007.4283506.

Buso, S.; Malesani, L. y Mattavelli, P. (1998). Comparison of current control techniques for active filter applications. IEEE Transactions on Industrial Electronics, 45(5), 722-729. http://doi.org/10.1109/41.720328.

Cavallini, A. y Montanari, G.C. (1994). Compensation strategies for shunt active-filter control. IEEE Transactions on Power Electronics, 9(6), 587-593. http://doi.org/10.1109/63.334773.

Grino, R.; Cardoner, R.; Costa-Castello, R. y Fossas, E. (2007). Digital Repetitive Control of a Three-Phase Four-Wire Shunt Active Filter. IEEE Transactions on Industrial Electronics, 54(3), 1495-1503. http://doi.org/10.1109/TIE.2007.894790.

Hsu, C.Y. y Wu, H.Y. (1996). A new single-phase active power filter with reduced energy-storage capacity. IEE Proceedings-Electric Power Applications, 143(1), 25-30. http://doi.org/10.1049/ip-epa:19960205.

Kale, M. y Ozdemir, E. (2005). An adaptive hysteresis band current controller for shunt active power filter. Electric Power Systems Research, 73(2), 113-119. http://doi.org/10.1016/j.epsr.2004.06.006.

Kanjiya, P.; Khadkikar, V. y Zeineldin, H.H. (2015). Optimal Control of Shunt Active Power Filter to Meet IEEE Std. 519 Current Harmonic Constraints Under Nonideal Supply Condition. IEEE Transactions on Industrial Electronics, 62(2), 724-734. http://doi.org/10.1109/TIE.2014.2341559.

Kim, H. y Akagi, H. (1999). The instantaneous power theory on the rotating p-q-r reference frames. En Proceedings of the IEEE 1999 International Conference on Power Electronics and Drive Systems, 1999. PEDS '99 (Vol. 1, pp. 422-427). http://doi.org/10.1109/PEDS.1999.794600.

Kim, H.; Blaabjerg, F.; Bak-Jensen, B. y Choi, J. (2002). Instantaneous power compensation in three-phase systems by using p-q-r theory. IEEE Transactions on Power Electronics, 17(5), 701-710. http://doi.org/10.1109/TPEL.2002.802185.

Luna, A.; Rocabert, J.; Candela, J.I.; Hermoso, J.R.; Teodorescu, R.; Blaabjerg, F. y Rodríguez, P. (2015). Grid Voltage Synchronization for Distributed Generation Systems Under Grid Fault Conditions. IEEE Transactions on Industry Applications, 51(4), 3414-3425. http://doi.org/10.1109/TIA.2015.2391436.

Rafiei, S.M.R.; Toliyat, H.A.; Ghazi, R. y Gopalarathnam, T. (2001). An optimal and flexible control strategy for active filtering and power factor correction under non-sinusoidal line voltages. IEEE Transactions on Power Delivery, 16(2), 297-305. http://doi.org/10.1109/61.915499.

Ranjbar, M.; Masoum, M.A.S. y Jalilian, A. (2009). Comparison of compensation strategies for shunt active power filter control in unbalanced tree-phase four-wire systems. En: Canadian Conference on Electrical and Computer Engineering, 2009. CCECE '09 (pp. 1061-1066). http://doi.org/10.1109/CCECE.2009.5090291.

Rashid, M. (2011). Power electronics handbook. Third Edition. ISBN: 978-0-12-382036-5 Elsevier. Printed in the USA.

Rodríguez, C.L.T.; Fuente, D.V.D.L.; Amorós, E.F.; Sanfeliú, G.G. y Moreno, J.G. (2012). Diseño, modelado e implementación de inversor conectado a la red eléctrica a partir de fuentes renovables. Revista Tecnura, 16(32), 12-28.

Ucar, M. y Ozdemir, E. (2008). Control of a 3-phase 4-leg active power filter under non-ideal mains voltage condition. Electric Power Systems Research, 78(1), 58-73. http://doi.org/10.1016/j.epsr.2006.12.008.