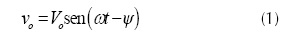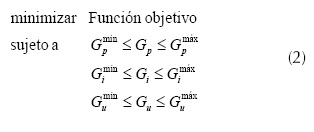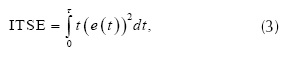DOI:
https://doi.org/10.14483/22487638.11553Publicado:
01-07-2017Número:
Vol. 21 Núm. 53 (2017): Julio - SeptiembreSección:
InvestigaciónAplicación del control inteligente en oscilaciones usando FACTS (STATCOM y SVC)
Smart control application in the oscillations using FACTS (STATCOM and SVC)
Palabras clave:
COA, controlador de oscilaciones, GA, PSO, SMIB, STATCOM, SVC (es).Palabras clave:
COA, GA, oscillations controller, PSO, SMIB, STATCOM, SVC (en).Descargas
Referencias
Alzate, A. (2000). Sistemas difusos. [Primera Edición]. Pereira: Universidad Tecnológica de Pereira.
Alzate, A., Orjuela, J. y Herrera, J. (2010). Determinación de los parámetros del motor de inducción utilizando un algoritmo de optimización por cúmulo de partículas (PSO). Revista Tecnura, 14(26), 15-26.
Cano, G. (2009). Estabilizadores de sistemas eléctricos de potencia PSSs. [Monografía,Ingeniería Electrica]. Medellín: Universidad Nacional de Colombia.
Castillo, I. (2002). Un criterio óptimo para coordinar estabilizadores en sistemas eléctricos de potencia. [Tesis, Doctorado en Ciencias]. Guadalajara, JAL: Centro de Investigación y de Estudios Avanzados del IPN Unidad Guadalajara.
Coronado, I., Ramírez, J. y Zu-iga, P. (2001). FACTS: Soluciones modernas para la industria eléctrica. Avance y Perspectiva, 20, 235-244.
Dávalos, M. y Ramírez, A. (2001). Características funcionales del STATCOM. Segundo Congreso Bienal, CIGRÉ-México. Irapuato: Gto.
Do Bomfim, A., Taranto, G. y Falcao, D. (2000). Simultaneous Tuning of Power System Damping Controllers Using Genetic Algorithms. IEEE Transactions on Power Systems, 163-169. https://doi.org/10.1109/59.852116
Farahani, S., Hemati, R., y Nikzad, M. (2009). Comparison of artificial intelligence strategies for STATCOM supplementary controller design. World Applied Sciences Journal, 7, 1428-1438.
Farahani, S., Nikzad, M., Tabar, M., Tourang, H. y Yousefpour, B. (2012). STATCOM Control Using a PSO-Based IP Controller. Research Journal of Applied Sciences, Engineering and Technology, 4(7), 768-774.
García, J. (2006). Algoritmos basados en cúmulos de partículas para la resolución de problemas complejos. [Tesis de Licenciatura]. Málaga: Universidad de Málaga.
Hassan, S., Olamaee, J. y Samadzadeh, H. (2011). Power Oscillations Damping By Static Var Compensator Using an Adaptive Neuro-Fuzzy Controller. 7th International Conference on Electrical and Electronics Engineering (ELECO).
Ixtláhuatl, C., Pável, Z., Juan, R. (2001). FACTS: soluciones modernas para la industria eléctrica. Avance y Perspectiva, 20, 235-244.
Karpagam, N., Deveraj, D. (2009). Fuzzy Logic Control of Static Var Compensator for Power System Damping. International Journal of Electrical, Computer, Energetic, Electronic and Communication Engineering, 2(2), 105 - 112.
Kumkratug, P. (2011). STATCOM Stabilizer based on fuzzy logic control for damping power oscillation. American Journal of Applied Sciences, 8(10), 1041-1044. https://doi.org/10.3844/ajassp.2011.1041.1044
Safari, A., Shayeghi, H., y Shayanfar, H. (2010). A Chaotic Optimization Algorithm to Output Feedback Damping Controller Design for a STATCOM. International Journal on Technical and Physical Problems of Engineering (IJTPE), 2(3), 44-50.
Stella, M., Dash, P., Basu, K. (2003). A fuzzy variable structure controller for STATCOM. Electric Power Systems Research, 65(1), 23-34. https://doi.org/10.1016/S0378-7796(02)00212-2
Zarringhalami, M., y Golkar, M. (2008). Coordinated Design of PSS and STATCOM Parameters for Power System Stability Improvement Using Genetic Algorithm. Third International Conference On Electric Utility Deregulation And Restructuring And Power Technologies. China: IEEE Xplore. https://doi.org/10.1109/DRPT.2008.4523634
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: https://doi.org/10.14483/22487638.11553
Aplicación del control inteligente en oscilaciones usando FACTS (STATCOM y SVC)
Smart control application in the oscillations using FACTS (STATCOM and SVC)
Alfonso Alzate Gomez,1 Andrea Bedoya Londoño,2 Jesser James Marulanda Durango3
1 Ingeniero Electricista, magister en Sistemas de Generación de Energía Eléctrica. Docente de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: alalzate@utp.edu.co
2 Ingeniera Eléctricista, magister en Ingeniería Eléctrica. Egresada de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: anbedoya@utp.edu.co
3 Ingeniero Electricista, magister en Ingeniería Eléctrica. Docente de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: jjmarulanda@utp.edu.co
Fecha de recepción: 30 de febrero de 2017 Fecha de aceptación: 28 de abril de 2017
Cómo citar: Alzate, A., Bedoya, A. y Marulanda, J. (2017). Aplicación del control inteligente en oscilaciones usando FACTS (STATCOM y SVC). Revista Tecnura, 21(53), 47-60, doi: 10.14483/22487638.11553
Resumen
Contexto: Reducir las oscilaciones de un sistema eléctrico de potencia es necesario para mantener la estabilidad del mismo. En este trabajo se presenta una metodología para la sintonización de un controlador de oscilaciones de tipo difuso, un compensador de Volts Ampere Reactive, (VAR, por sus siglas en inglés), uno estático (Static Var Compensator, SVC, por sus siglas en inglés), y un compensador estático síncrono (Static Synchronous Compensator, STATCOM, por sus siglas en inglés), por métodos inteligentes.
Método: Consiste en sintonizar un controlador de tipo difuso para amortiguar las oscilaciones de un sistema eléctrico de potencia por medio de un STATCOM o un SVC, a través de diferentes técnicas de optimización tales como: algoritmos genéticos (GA, Genetic Algorithm), optimización por enjambre de partículas (PSO, Particle Swarm Optimization) y algoritmo de optimización caótica (COA, Chaotic Optimization Algorithm).
Resultados: A través de simulación se obtienen las oscilaciones en el voltaje y la velocidad de un sistema compuesto por una máquina sincróna conectada a un barraje infinito (SMIB, Single Machine Infinite Bus) antes y después de conectar un SVC y un STATCOM, ambos instalados independientemente y en diferentes condiciones de operación. Los resultados muestran las ventajas de utilizar métodos de ajuste para el controlador difuso comparados con el ajuste a ensayo y error.
Conclusión: A partir de los resultados obtenidos, se comprueba la efectividad del controlador difuso utilizado en el control de oscilaciones con dispositivos Flexible AC Transmissions Systems (FACTS, por sus siglas en inglés) tanto en el SVC como en el STATCOM.
Palabras clave: COA, controlador de oscilaciones, GA, PSO, SMIB, STATCOM, SVC.
Abstract
Context: Reducing the oscillations of the electrical power systems is an important task in order to maintain their stability. This paper presents a methodology for adjusting the parameters of a fuzzy oscillations controller with a Static Var Compensator (SVC) and a Static Synchronous Compensator (STATCOM).
Methodology: The methodology consists of tuning a fuzzy controller to dampen oscillations in an electrical power system, with different optimization techniques such as: Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and Chaotic Optimization Algorithm (COA).
Results: The voltage and speed oscillations of a system composed of a synchronous machine connected to an infinite bus bar (SMIB) are obtained through simulations. There is data before and after connecting a SVC and a STATCOM, installed independently and in different operating conditions. The results obtained show that using a technique for adjusting parameters in the fuzzy controller is better than the adjustment of trial and error.
Conclusion: With the obtained results, it is possible to verify the effectiveness of the fuzzy controller using Flexible AC Transmissions Systems (FACTS).
Keywords: COA, GA, oscillations controller, PSO, SMIB, STATCOM, SVC.
INTRODUCCIÓN
El crecimiento de los sistemas eléctricos de potencia (SEP) ha mostrado tanto limitantes técnicos como de operación, que hacen que las líneas de transmisión se carguen cerca a sus límites de estabilidad y se produzca un aumento en la aparición de las oscilaciones de baja frecuencia, las cuales impiden abastecer la demanda bajo condiciones de seguridad, calidad, estabilidad y confiabilidad (Karpagam, Deveraj, 2009; Coronado, Ramírez, y Zuñiga, 2001). En el pasado, la amortiguación de oscilaciones del SEP estaba a cargo de los estabilizadores Power System Stabilizer (PSS, por sus siglas en inglés); sin embargo, se ha informado sobre algunos efectos oscilatorios de las condiciones de operación que el PSS no puede amortiguar (Cano, 2009; Londoño y Mora, 2006). Como consecuencia de esto, se acentúa el desarrollo de la industria electrónica, con dispositivos de transmisión flexible de corriente alterna FACTS que no solo logran una disminución de pérdidas, sino también la amortiguación de las oscilaciones (Hassan, Olamaee, y Samadzadeh, 2011).
La principal desventaja de los dispositivos FACTS, son los elevados costos comparados con la compensación reactiva tradicional; dentro de este surgimiento de los dispositivos FACTS, se han estudiado el SVC y el STATCOM, que se pueden usar para mejorar la estabilidad y la utilización de los sistemas existentes (Farahani, Hemati, y Nikzad, 2009), estos estudios abarcan el uso y control del SVC y del STATCOM en amortiguamiento de oscilaciones.
Un control auxiliar comúnmente utilizado en los dispositivos FACTS es el Proporcional Integral (PI, por sus siglas en inglés), pero solo son adecuados para una gama limitada de condiciones de funcionamiento, y por este motivo no es conveniente para el control de los dispositivos FACTS (Karpagam, Deveraj, 2009; Kumkratug, 2011). Por lo anterior, se han ido desarrollando técnicas de optimización modernas y de control inteligente para los dispositivos FACTS, tales como: redes neuronales, sistemas de lógica difusa, algoritmos genéticos, optimización por enjambre de partículas y el templado simulado. Las aplicaciones de estos métodos en algunos problemas en SEP han entregado resultados promisorios, como se evidencia en los artículos de Hassan, Olamaee, y Samadzadeh (2011); Farahani, Hemati, y Nikzad (2009); Zarringhalami y Golkar (2008); Farahani, Nikzad, Tabar, Tourang, y Yousefpour (2012).
El control basado en lógica difusa es atractivo, ya que no requiere de un modelo matemático del sistema en estudio y puede cubrir una amplia gama de condiciones de operación, además es simple de implementar (Dávalos y Ramírez, 2001). Al combinar la lógica difusa con otras técnicas de control inteligente y optimización, se logran encontrar los mejores parámetros del controlador o la mejor topología de la red.
El objetivo de este artículo es presentar el diseño de un control difuso, para aplicar en el SVC y STATCOM instalados en un sistema SMIB de manera independiente; se calculan las ganancias de cada controlador de forma heurística y por medio de AG, PSO y COA, esto con el fin de distinguir la mejor respuesta a partir de los resultados de simulación.
METODOLOGÍA
Modelado del SVC
El SVC es un dispositivo de los FACTS en derivación que regula el flujo de potencia reactiva, a través de una línea de transmisión, por medio de la utilización de tiristores que rápidamente conmutan condensadores y reactores; el SVC consiste en un arreglo de compensadores en paralelo, usualmente Thyristor Controlled Reactor (TCR, por sus siglas en inglés) o Thyristor Switched Capacitor (TSC, por sus siglas en inglés), de tal manera que se cuenta con la posibilidad de realizar compensación capacitiva o inductiva para controlar la potencia reactiva que requiere el sistema al mantener en un nivel adecuado los perfiles de tensión y, a su vez, se aprovecha su capacidad para amortiguar las oscilaciones (Ixtláhuatl, Pável, y Juan, 2001).
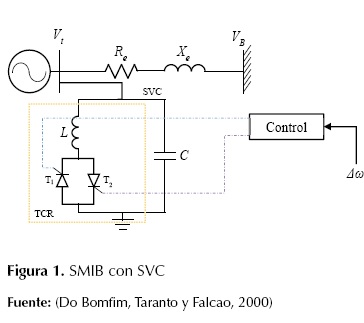
En la figura 1 se muestra la conexión en derivación del SVC al sistema SMIB; el modelo del SVC empleado está basado en un condensador fijo y una reactancia, cuya corriente es controlada en ambos semiciclos por medio de dos tiristores conectados en antiparalelo (Do Bomfim, Taranto, y Falcao, 2000).
El esquema utilizado para el SVC contiene una parte para el control de los reactivos y un compensador adicional para amortiguar las oscilaciones que aparecen cuando se presenta una perturbación; este esquema provoca una variación en el modelo del sistema SMIB. El modelo usado para el SVC es el mostrado en la figura 2 (Karpagam, Deveraj, 2009).
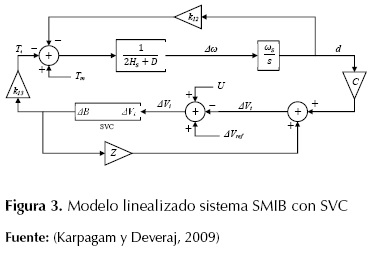
A partir del modelo linealizado en espacio de estados, se obtiene el diagrama de bloques que se muestra en la figura 3 del sistema SMIB con SVC incluido (Karpagam, Deveraj, 2009).
Modelado del STATCOM
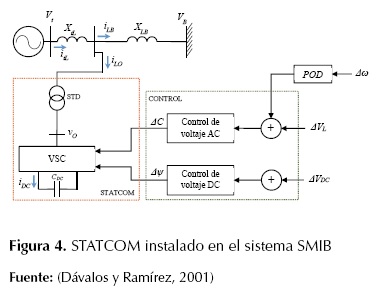
El STATCOM es un tipo de dispositivo FACTS de compensación en derivación, con fuente de voltaje y un transformador en paralelo; el STATCOM puede proporcionar compensación capacitiva o inductiva, según sea la necesidad, controlando la magnitud relativa del voltaje de línea respecto al voltaje en los terminales de salida del inversor (Farahani, Hemati, y Nikzad, 2009). El STATCOM se instala en derivación en un barraje intermedio del sistema SMIB, proporcionando una compensación en paralelo de manera muy similar al SVC, pero utilizando un convertidor de fuente de voltaje (VSC, Voltage Source Converter) en lugar de reactores y capacitores en paralelo (Dávalos y Ramírez, 2001). En la figura 4 se muestra el modelo del STATCOM conectado a un barraje intermedio del sistema SMIB (Dávalos y Ramírez, 2001).
El convertidor genera un voltaje controlable AC a través de la reactancia de salida (Dávalos y Ramírez, 2001). La ecuación presenta el voltaje de fase en la barra de conexión del STATCOM.
La diferencia de tensión entre la barra Vo y la barra Vt, produce un intercambio de potencia activa y reactiva entre el STATCOM y el sistema de potencia, cuyo flujo puede controlarse ajustando la magnitud de Vo y ψ.
Información más detallada de estos modelos se encuentra en los textos de (Karpagam, Deveraj 2009) y (Dávalos y Ramírez, 2001).
Desarrollo del control del SVC y el STATCOM
Control difuso
Los sistemas de control difuso son sistemas basados en un conjunto de reglas que representan un mecanismo de control para ajustar los efectos de determinados estímulos del sistema; en general, un controlador de tipo difuso es un algoritmo para transformar una estrategia de control dada en forma lingüística en forma de un control automático, para imitar la forma del razonamiento humano (Coronado, Ramírez y Zuñiga, 2001).
En el diseño del control difuso están involucradas las siguientes etapas (Alzate, 2000).
Entradas al controlador difuso. Se definen las entradas al controlador difuso y límites del universo de discurso.
Primera etapa: fuzificación. El difusor convierte las señales numéricas de las entradas del mundo real en variables difusas.
Segunda etapa: inferencia difusa. El protocolo de inferencia difusa seleccionado en este trabajo es de tipo Mamdani, por ser uno de los más adecuados y comunes en aplicaciones de sistemas de control con lógica difusa.
Tercera etapa: base de reglas difusas. El algoritmo de control se proporciona como una base de expresiones del tipo “si <antecedente> entonces <consecuente>”.
Cuarta etapa: defuzificación. En esta etapa la acción entregada por el sistema difuso hay que transformarla del mundo difuso al real mediante un concresor que se encarga de hacer esa transformación.
Sistema de control del SVC
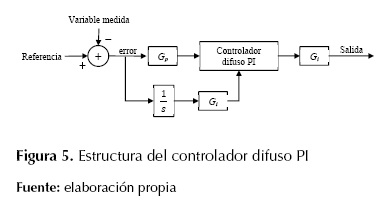
El SVC está equipado con un regulador de tensión que incrementa el torque sincronizador, pero en general la contribución de este al amortiguamiento es pequeña; si se desea amortiguamiento adicional, se requiere de una acción de control suplementaria (Do Bomfim, Taranto, y Falcao, 2000). En este caso, la acción de control suplementaria está dada por un control difuso PI, como se muestra en la figura 5.
Sistema de control del STATCOM
El controlador del STATCOM tiene como función principal la compensación de la potencia reactiva, el control primario del inversor es tal que se regula el flujo de corriente reactiva a través del STATCOM; en otras palabras, el controlador se utiliza para operar el inversor, de modo que el ángulo de fase entre el voltaje del inversor y el voltaje de línea se ajuste dinámicamente, tal que el STATCOM genere o absorba potencia reactiva en el punto de conexión (Dávalos y Ramírez, 2001). El sistema de control del STATCOM comprende dos controladores:
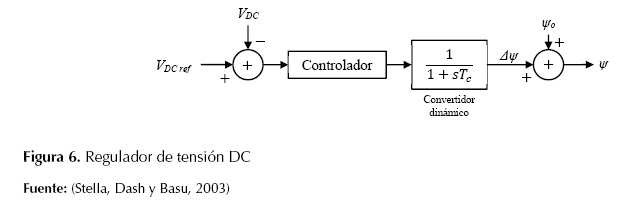
- Regulador de tensión DC: se encarga de regular la tensión del circuito intermedio. La tensión DC se regula mediante la modulación del ángulo de fase de la tensión del convertidor en derivación (Stella, Dash, y Basu, 2003); el regulador de tensión controla el voltaje DC a través del capacitor del STATCOM. La figura 6 muestra la estructura del regulador de tensión DC.
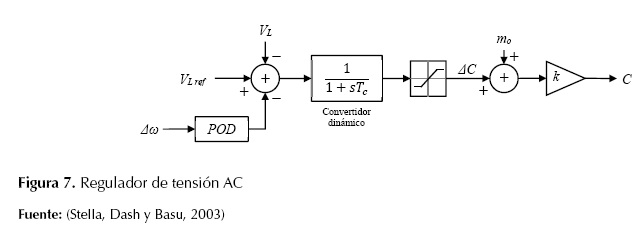
- Regulador de tensión AC: este controlador regula la tensión AC en terminales de acuerdo a la referencia que se logra a través del cambio de magnitud en la tensión de salida del convertidor, además cuenta con un amortiguador de oscilaciones AC adicional (Stella, Dash, y Basu, 2003); el amortiguador adicional puede ser considerado como un compensador de adelanto-atraso o como un bloque de control de lógica difusa, entre otros métodos. En este trabajo es considerado un controlador difuso como amortiguador de oscilaciones adicional (POD, Power Oscillation Damping). La figura 7 muestra el modelo del regulador de tensión AC con el control adicional de amortiguación de oscilaciones.
Ajuste del control de tipo difuso del SVC y el STATCOM
Para los controladores de oscilaciones de tipo difuso de los sistemas propuestos (SMIB más SVC y SMIB más STATCOM), una vez definida su estructura, se busca una sintonización aceptable de los parámetros y de las ganancias de estos, pero siempre con la incertidumbre de si esta será la mejor; por tanto, el proceso de ajuste de las ganancias de cada control difuso se convierte en un problema de optimización formulado de la siguiente forma, como se presenta en las desigualdades agrupadas en la ecuación (2).
Usando como función objetivo el índice de desempeño ITSE, definido en la ecuación (3).
Para resolver este problema, se emplean los siguientes métodos: empírico (sintonización hecha de manera heurística), algoritmo genético (AG), optimización por enjambre de partículas (PSO) y algoritmo de optimización caótica (COA).
Mediante el método empírico se requiere de experiencia, tiempo y comprensión de la dinámica del sistema para tener la seguridad de lograr una sintonización aceptable, pero siempre con la incertidumbre de si esta será la mejor. La ventaja del proceso de ajuste manual es que se hace de manera directa y se aplica de acuerdo a la forma en que el sistema responde (Zarringhalami y Golkar, 2008); la desventaja es que puede tomar bastante tiempo desarrollar la manera de captar el comportamiento del sistema de acuerdo al ajuste, y además es difícil establecer cuándo el ajuste final es óptimo. Por tanto, el control difuso se combina con otros métodos de control para la sintonización de las ganancias y obtener la mejor solución final posible.
El enfoque propuesto combina la lógica difusa con otras técnicas de optimización y de control inteligente como GA, PSO y COA, para lograr encontrar el conjunto óptimo de parámetros de los controladores, obteniendo un control más robusto.
Algoritmo genético (GA)
Los algoritmos genéticos son métodos de optimización que se pueden usar dentro de sistemas de control en conjunción con otras técnicas, por ejemplo, los controladores tradicionales PID (Proportional Integrative Derivative), ya sea para encontrar los mejores parámetros del controlador o la mejor topología de la red (Cano, 2009).
El GA implementado que se muestra en la Figura 8 consiste, a grandes rasgos, en una rutina de software que toma como entradas a los ejemplares y retorna como salidas los que deben generar descendencia para la nueva generación; a este proceso se llama ciclo de evolución, que comienza con una población de posibles soluciones, de la cual se seleccionan los mejores padres que pueden dar nuevos individuos mediante el cruce o la mutación y, de esta forma, se crea una nueva población de la que nuevamente se van a obtener padres (Do Bomfim, Taranto, y Falcao, 2000). Los pasos a seguir en la creación e implementación de un algoritmo genético se muestran en el diagrama de flujo de la figura 9 (Castillo, 2002).
Optimización por enjambre de partículas (PSO)
A través de los años se han implementado varios métodos de diseño y sintonización del controlador difuso, entre ellos el método de optimización por cúmulo de partículas (PSO), el cual fue originalmente desarrollado por James Kennedy y por Russ Eberhart (Alzate, Orjuela y Herrera, 2010). El funcionamiento básico del PSO simula el comportamiento del vuelo de las manadas de aves en busca de alimento, el razonamiento lógico consiste en seguir al ave que está más cerca del alimento; cada ave es modelada como una partícula con una solución en el espacio de búsqueda que está siempre en continuo movimiento y nunca es eliminada (Alzate, Orjuela y Herrera, 2010). En otras palabras, las partículas se consideran como agentes simples moviéndose por el espacio de búsqueda, guardan y comunican la solución óptima encontrada. El movimiento de las demás partículas es guiado por aquellas que tienen la mejor solución hasta el momento (García, 2006).
Cada partícula tiene una aptitud (fitness), una posición y un vector velocidad que dirige su movimiento. El movimiento de las partículas está guiado por las partículas óptimas en el instante actual (Alzate, Orjuela y Herrera, 2010).
En el algoritmo PSO, a cada variable de la función objetivo se le asignan valores aleatorios distribuyéndolas por todo el espacio solución, convirtiendo la función objetivo en un vector (nube) donde cada elemento se denomina partícula. Observando cuál de las respuestas se acerca más al cero o al valor deseado, al momento de evaluar todas las respuestas se escoge la mejor y se reasignan los valores de los vectores para una nueva iteración alrededor de esta; esto se realiza hasta que llegue a un punto deseado. Consecuentemente, cada partícula se ve influida por el mejor desempeño de cualquier miembro de la población debido al intercambio de información entre ellos, el rendimiento de cada partícula se mide usando una función de aptitud que varía en función del problema de optimización (Alzate, Orjuela y Herrera, 2010).
Algoritmo de optimización caótica (COA)
Los algoritmos de optimización basados en la teoría del caos (COA), son metodologías de búsqueda que difieren de cualquiera de las técnicas de optimización estocástica tradicionales existentes; no son como un algoritmo de optimización estocástica que escapa de los mínimos locales mediante la aceptación de algunas malas soluciones de acuerdo con una cierta probabilidad, COA busca con la regularidad del movimiento caótico escapar de los mínimos locales (Safari, Shayeghi, y Shayanfar, 2010). El proceso básico del algoritmo de optimización caótica incluye generalmente dos pasos principales:
Primer paso: definir un generador de secuencias caótico o un mapa del espacio caótico en el espacio de soluciones; posteriormente, generar una secuencia de puntos caóticos y asignarla a una secuencia de puntos en el espacio de diseño original. Finalmente, evaluar la función objetivo con respecto a los puntos de diseño generados y elegir el punto con el mínimo valor de la función objetivo como el óptimo actual.
Segundo paso: suponer cercano el óptimo actual al óptimo global después de ciertas iteraciones y asumirlo como el centro con un poco de perturbación caótica; al óptimo global obtenerlo a través de la búsqueda fina. Se repiten los dos pasos anteriores hasta que algún criterio de convergencia especificado se cumpla y luego se obtiene el óptimo global (Safari, Shayeghi, y Shayanfar, 2010). En la aplicación de secuencias caóticas se han adoptado, en lugar de los aleatorios, diferentes modelos entre los cuales se destacan mapa Tent, mapa de Gauss, mapa Lozi, iterador sinusoidal, oscilador de Chua, sistema de Mackey-Glass, sistema de Lorenz, mapa Hénon y mapa Ikeda (Safari, Shayeghi, y Shayanfar, 2010).
SIMULACIONES Y RESULTADOS
Con el fin de comprobar el comportamiento de cada controlador de oscilaciones de tipo difuso de los sistemas de prueba (SMIB más SVC y SMIB más STATCOM), se exponen los resultados de los sistemas de prueba bajo diferentes condiciones de operación obtenidos a partir de las simulaciones hechas en Matlab. En la tabla 1 se presentan los valores propios del STATCOM y del SVC en el sistema SMIB, para los siguientes puntos de operación: condición de operación nominal P = 0.7 (pu, por unidad) y Q = 0.3 (pu).
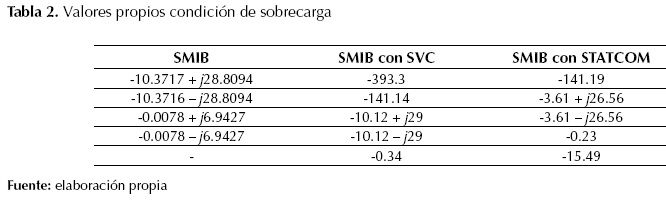
En condición de operación nominal los sistemas tienen valores propios que son pares conjugados, es decir, presentan oscilaciones amortiguadas, como se presentan en la tabla 2.
Condición de sobrecarga: P = 1.2 (pu) y Q = 0.4 (pu).
Como puede observarse, en condición de sobrecarga los valores propios del sistema SMIB son pares conjugados con parte real positiva representando oscilaciones que incrementan su amplitud, lo que implica que el sistema es inestable, mientras que los valores propios del sistema SMIB con STATCOM y con SVC son pares conjugados con parte real negativa, implicando una respuesta oscilatoria amortiguada; es decir, al incluir el STATCOM o el SVC en el sistema SMIB se logran mitigar las oscilaciones crecientes que desestabilizan al sistema en condición de sobrecarga.
Simulaciones sistema SMIB con SVC
A continuación, se muestra el comportamiento de la tensión en terminales Vt y de la potencia eléctrica Pe del sistema SMIB con SVC, bajo la acción del controlador de oscilaciones de tipo difuso y ante diferentes condiciones de operación.
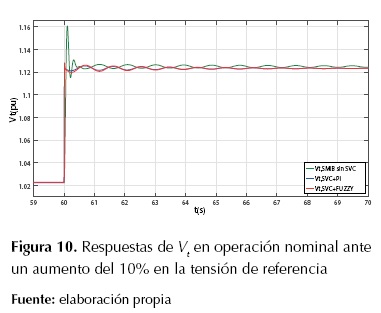
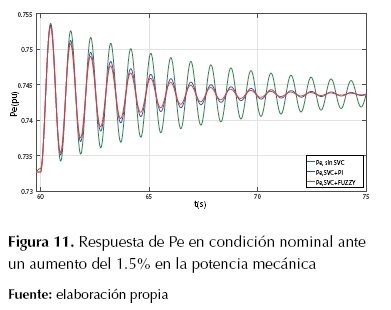
En la figuras 10 y la figura 11 se muestran las respuestas de la tensión en terminales Vt y de la potencia eléctrica Pe del sistema SMIB con SVC más el controlador de oscilaciones respectivamente, en condición de operación nominal.
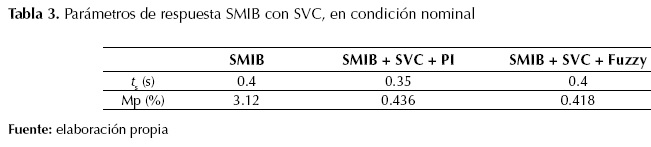
En la tabla 3 y en la figura 10 y la figura 11, se observa que las respuestas del sistema SMIB con SVC, bajo la acción de control de oscilaciones, presentan un mayor amortiguamiento y una gran disminución del máximo sobreimpulso de la tensión en terminales Vt que el sistema SMIB sin SVC. En la figura 12 y la figura 13 se muestran las respuestas de la tensión en terminales Vt y de la potencia eléctrica Pe del sistema SMIB con SVC más el controlador de oscilaciones respectivamente, en condición de sobrecarga. En la tabla 4 se reportan los valores de ts y Mp usando control PI y control difuso para el SVC.
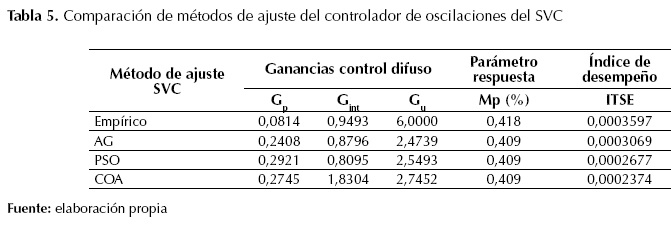
Como puede observarse en la figura 12 y la figura 13, en condición de sobrecarga, el sistema SMIB presenta oscilaciones crecientes, indicando la inestabilidad del sistema sin el SVC, mientras que con el SVC y bajo la acción de control de oscilaciones de tipo difuso, el sistema mantiene una respuesta estable y con alta amortiguación de oscilaciones. En la figura 14 y la figura 15 se muestra la comparación de respuestas de la tensión en terminales Vt y la velocidad del rotor ω, respectivamente, del sistema SMIB con SVC, bajo la acción del controlador de oscilaciones de tipo difuso sintonizado con AG, PSO y COA. En la tabla 5 se presenta una comparación cuantitativa de los métodos de ajuste empleados para el controlador del SVC.
Se observa en la figura 14 y la figura 15 que el desempeño del controlador de oscilaciones de tipo difuso es muy similar con los diferentes métodos de ajuste (empírico, GA, PSO y COA); es decir, presentan un nivel de amortiguamiento de oscilaciones muy similar.
Simulaciones sistema SMIB con STATCOM
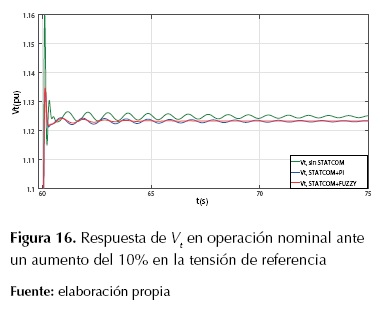
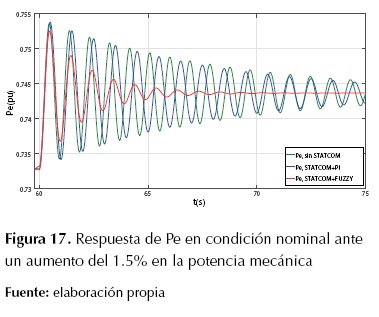
En la figura 16 se muestra las respuestas de la tensión en terminales Vt y en la figura 17 se muestra la potencia eléctrica Pe del sistema SMIB con STATCOM más el controlador de oscilaciones, en condición de operación nominal.
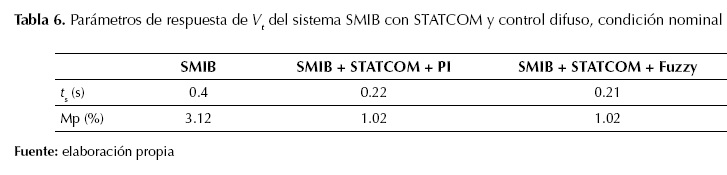
En la figura 16 se observa que la respuesta del sistema con el STATCOM es menos oscilatoria y como consecuencia se estabiliza antes. En la tabla 6 se presentan los valores de ts y Mp en valor porcentual para diversos escenarios con STATCOM.
En la tabla 6 se evidencia que el máximo sobreimpulso se minimiza con la inclusión del STATCOM.
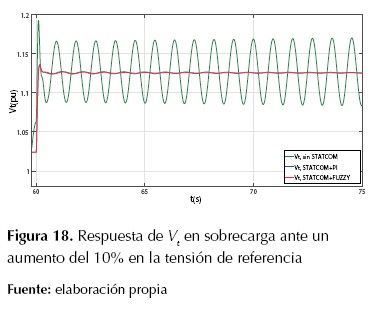
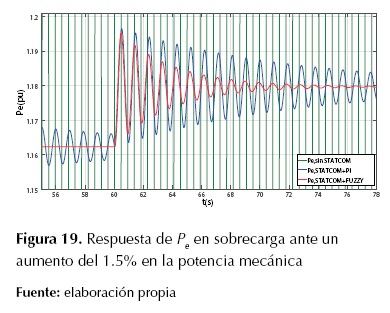
En la figura 18 se muestra la respuesta de la tensión en terminales Vt, y en la figura 19 se muestra el comportamiento de la potencia eléctrica Pe del sistema SMIB con STATCOM más el controlador de oscilaciones en condición de sobrecarga.
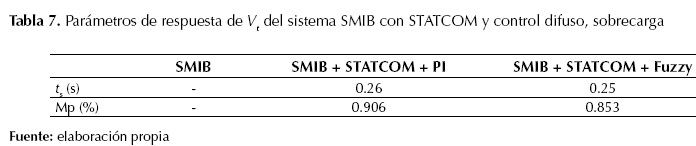
En la figura 18 se observa que la respuesta del sistema SMIB es completamente oscilatoria, mientras que con el STATCOM incluido se sigue manteniendo una respuesta estable. En la tabla 7 se muestran los valores de ts y Mp en valor porcentual para diversos escenarios con STATCOM.
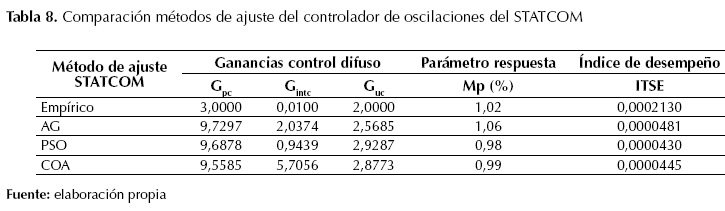
La figura 19 y en la tabla 7 se evidencia que el sistema SMIB con STATCOM y con controlador de oscilaciones de tipo difuso, presenta una mayor amortiguación de las oscilaciones que el controlador convencional PI. En la tabla 8 se resumen los valores obtenidos para Mp y ITSE con los diferentes controladores.
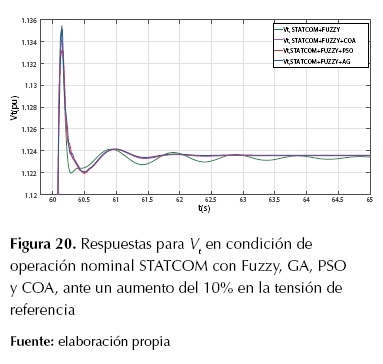
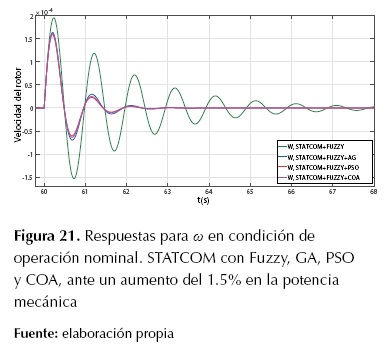
En la figura 20 aparece la respuesta de la tensión en terminales y en la figura 21 se muestra la respuesta de la velocidad del rotor del sistema en condición de operación nominal; en la tabla 8, se comparan los resultados de los métodos de sintonización del controlador de oscilaciones de tipo difuso del STATCOM.
Como se puede observar en la figura 20 y la figura 21, el rendimiento del controlador ajustado mediante el método empírico es menor que el obtenido con los métodos GA, PSO y COA; también, se muestra que el método de ajuste con PSO posee una mejor amortiguación de las oscilaciones que el GA y el COA.
CONCLUSIONES
Se comprobó la efectividad de los controladores de oscilaciones de tipo difuso del STATCOM y del SVC, ajustados con las diferentes técnicas: empírica, AG, PSO y COA, los cuales proporcionan un aumento en la amortiguación de las oscilaciones. El ajuste del control difuso con AG, COA o PSO, presenta un mejor comportamiento que el control difuso ajustado a ensayo y error (empíricamente), esto puede observarse en el sistema SMIB con STATCOM incluido.
El buen desempeño de algunos métodos de control inteligente en el amortiguamiento de oscilaciones usando FACTS, se demostró bajo diferentes condiciones de operación. En este trabajo, se observa la mejora en el sistema SMIB al incluir un dispositivo FACTS (STATCOM o SVC) bajo la acción del control de oscilaciones de tipo difuso; con la inclusión del STATCOM o del SVC se mejoran notablemente las respuestas del sistema al disminuir las oscilaciones.
Los algoritmos de optimización empleados en la sintonización del control difuso tienen como ventaja que realizan una búsqueda sobre el espacio de estado completo, encontrando la mejor solución para el sistema de control.
FINANCIACIÓN
Colciencias, jóvenes investigadores e innovadores y Universidad Tecnológica de Pereira 2012.
REFERENCIAS
Alzate, A. (2000). Sistemas difusos. [Primera Edición]. Pereira: Universidad Tecnológica de Pereira.
Alzate, A., Orjuela, J. y Herrera, J. (2010). Determinación de los parámetros del motor de inducción utilizando un algoritmo de optimización por cúmulo de partículas (PSO). Revista Tecnura, 14(26), 15-26.
Cano, G. (2009). Estabilizadores de sistemas eléctricos de potencia PSSs. [Monografía,Ingeniería Electrica]. Medellín: Universidad Nacional de Colombia.
Castillo, I. (2002). Un criterio óptimo para coordinar estabilizadores en sistemas eléctricos de potencia. [Tesis, Doctorado en Ciencias]. Guadalajara, JAL: Centro de Investigación y de Estudios Avanzados del IPN Unidad Guadalajara.
Coronado, I., Ramírez, J. y Zuñiga, P. (2001). FACTS: Soluciones modernas para la industria eléctrica. Avance y Perspectiva, 20, 235-244.
Dávalos, M. y Ramírez, A. (2001). Características funcionales del STATCOM. Segundo Congreso Bienal, CIGRÉ-México. Irapuato: Gto.
Do Bomfim, A., Taranto, G. y Falcao, D. (2000). Simultaneous Tuning of Power System Damping Controllers Using Genetic Algorithms. IEEE Transactions on Power Systems, 163-169.
Farahani, S., Hemati, R., y Nikzad, M. (2009). Comparison of artificial intelligence strategies for STATCOM supplementary controller design. World Applied Sciences Journal, 7, 1428-1438.
Farahani, S., Nikzad, M., Tabar, M., Tourang, H. y Yousefpour, B. (2012). STATCOM Control Using a PSO-Based IP Controller. Research Journal of Applied Sciences, Engineering and Technology, 4(7), 768-774.
García, J. (2006). Algoritmos basados en cúmulos de partículas para la resolución de problemas complejos. [Tesis de Licenciatura]. Málaga: Universidad de Málaga.
Hassan, S., Olamaee, J. y Samadzadeh, H. (2011). Power Oscillations Damping By Static Var Compensator Using an Adaptive Neuro-Fuzzy Controller. 7th International Conference on Electrical and Electronics Engineering (ELECO).
Ixtláhuatl, C., Pável, Z., Juan, R. (2001). FACTS: soluciones modernas para la industria eléctrica. Avance y Perspectiva, 20, 235-244.
Karpagam, N., Deveraj, D. (2009). Fuzzy Logic Control of Static Var Compensator for Power System Damping. International Journal of Electrical, Computer, Energetic, Electronic and Communication Engineering, 2(2), 105–112.
Kumkratug, P. (2011). STATCOM Stabilizer based on fuzzy logic control for damping power oscillation. American Journal of Applied Sciences, 8(10), 1041-1044.
Safari, A., Shayeghi, H., y Shayanfar, H. (2010). A Chaotic Optimization Algorithm to Output Feedback Damping Controller Design for a STATCOM. International Journal on Technical and Physical Problems of Engineering (IJTPE), 2(3), 44-50.
Stella, M., Dash, P., Basu, K. (2003). A fuzzy variable structure controller for STATCOM. Electric Power Systems Research, 65(1), 23-34.
Zarringhalami, M., y Golkar, M. (2008). Coordinated Design of PSS and STATCOM Parameters for Power System Stability Improvement Using Genetic Algorithm. Third International Conference On Electric Utility Deregulation And Restructuring And Power Technologies. China: IEEE Xplore.
Recibido: 28 de febrero de 2017; Aceptado: 28 de abril de 2017
Resumen
Contexto:
Reducir las oscilaciones de un sistema eléctrico de potencia es necesario para mantener la estabilidad del mismo. En este trabajo se presenta una metodología para la sintonización de un controlador de oscilaciones de tipo difuso, un compensador de Volts Ampere Reactive, (VAR, por sus siglas en inglés), uno estático (Static Var Compensator, SVC, por sus siglas en inglés), y un compensador estático síncrono (Static Synchronous Compensator, STATCOM, por sus siglas en inglés), por métodos inteligentes.
Método:
Consiste en sintonizar un controlador de tipo difuso para amortiguar las oscilaciones de un sistema eléctrico de potencia por medio de un STATCOM o un SVC, a través de diferentes técnicas de optimización tales como: algoritmos genéticos (GA, Genetic Algorithm), optimización por enjambre de partículas (PSO, Particle Swarm Optimization) y algoritmo de optimización caótica (COA, Chaotic Optimization Algorithm).
Resultados:
A través de simulación se obtienen las oscilaciones en el voltaje y la velocidad de un sistema compuesto por una máquina sincróna conectada a un barraje infinito (SMIB, Single Machine Infinite Bus) antes y después de conectar un SVC y un STATCOM, ambos instalados independientemente y en diferentes condiciones de operación. Los resultados muestran las ventajas de utilizar métodos de ajuste para el controlador difuso comparados con el ajuste a ensayo y error.
Conclusión:
A partir de los resultados obtenidos, se comprueba la efectividad del controlador difuso utilizado en el control de oscilaciones con dispositivos Flexible AC Transmissions Systems (FACTS, por sus siglas en inglés) tanto en el SVC como en el STATCOM.
Palabras clave:
COA, controlador de oscilaciones, GA, PSO, SMIB, STATCOM, SVC.Abstract
Context:
Reducing the oscillations of the electrical power systems is an important task in order to maintain their stability. This paper presents a methodology for adjusting the parameters of a fuzzy oscillations controller with a Static Var Compensator (SVC) and a Static Synchronous Compensator (STATCOM).
Methodology:
The methodology consists of tuning a fuzzy controller to dampen oscillations in an electrical power system, with different optimization techniques such as: Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and Chaotic Optimization Algorithm (COA).
Results:
The voltage and speed oscillations of a system composed of a synchronous machine connected to an infinite bus bar (SMIB) are obtained through simulations. There is data before and after connecting a SVC and a STATCOM, installed independently and in different operating conditions. The results obtained show that using a technique for adjusting parameters in the fuzzy controller is better than the adjustment of trial and error.
Conclusion:
With the obtained results, it is possible to verify the effectiveness of the fuzzy controller using Flexible AC Transmissions Systems (FACTS).
Keywords:
COA, GA, oscillations controller, PSO, SMIB, STATCOM, SVC.INTRODUCCIÓN
El crecimiento de los sistemas eléctricos de potencia (SEP) ha mostrado tanto limitantes técnicos como de operación, que hacen que las líneas de transmisión se carguen cerca a sus límites de estabilidad y se produzca un aumento en la aparición de las oscilaciones de baja frecuencia, las cuales impiden abastecer la demanda bajo condiciones de seguridad, calidad, estabilidad y confiabilidad (Karpagam, Deveraj, 2009; Coronado, Ramírez, y Zuñiga, 2001). En el pasado, la amortiguación de oscilaciones del SEP estaba a cargo de los estabilizadores Power System Stabilizer (PSS, por sus siglas en inglés); sin embargo, se ha informado sobre algunos efectos oscilatorios de las condiciones de operación que el PSS no puede amortiguar (Cano, 2009; Londoño y Mora, 2006). Como consecuencia de esto, se acentúa el desarrollo de la industria electrónica, con dispositivos de transmisión flexible de corriente alterna FACTS que no solo logran una disminución de pérdidas, sino también la amortiguación de las oscilaciones (Hassan, Olamaee, y Samadzadeh, 2011).
La principal desventaja de los dispositivos FACTS, son los elevados costos comparados con la compensación reactiva tradicional; dentro de este surgimiento de los dispositivos FACTS, se han estudiado el SVC y el STATCOM, que se pueden usar para mejorar la estabilidad y la utilización de los sistemas existentes (Farahani, Hemati, y Nikzad, 2009), estos estudios abarcan el uso y control del SVC y del STATCOM en amortiguamiento de oscilaciones.
Un control auxiliar comúnmente utilizado en los dispositivos FACTS es el Proporcional Integral (PI, por sus siglas en inglés), pero solo son adecuados para una gama limitada de condiciones de funcionamiento, y por este motivo no es conveniente para el control de los dispositivos FACTS (Karpagam, Deveraj, 2009; Kumkratug, 2011). Por lo anterior, se han ido desarrollando técnicas de optimización modernas y de control inteligente para los dispositivos FACTS, tales como: redes neuronales, sistemas de lógica difusa, algoritmos genéticos, optimización por enjambre de partículas y el templado simulado. Las aplicaciones de estos métodos en algunos problemas en SEP han entregado resultados promisorios, como se evidencia en los artículos de Hassan, Olamaee, y Samadzadeh (2011); Farahani, Hemati, y Nikzad (2009); Zarringhalami y Golkar (2008); Farahani, Nikzad, Tabar, Tourang, y Yousefpour (2012).
El control basado en lógica difusa es atractivo, ya que no requiere de un modelo matemático del sistema en estudio y puede cubrir una amplia gama de condiciones de operación, además es simple de implementar (Dávalos y Ramírez, 2001). Al combinar la lógica difusa con otras técnicas de control inteligente y optimización, se logran encontrar los mejores parámetros del controlador o la mejor topología de la red.
El objetivo de este artículo es presentar el diseño de un control difuso, para aplicar en el SVC y STATCOM instalados en un sistema SMIB de manera independiente; se calculan las ganancias de cada controlador de forma heurística y por medio de AG, PSO y COA, esto con el fin de distinguir la mejor respuesta a partir de los resultados de simulación.
METODOLOGÍA
Modelado del SVC
El SVC es un dispositivo de los FACTS en derivación que regula el flujo de potencia reactiva, a través de una línea de transmisión, por medio de la utilización de tiristores que rápidamente conmutan condensadores y reactores; el SVC consiste en un arreglo de compensadores en paralelo, usualmente Thyristor Controlled Reactor (TCR, por sus siglas en inglés) o Thyristor Switched Capacitor (TSC, por sus siglas en inglés), de tal manera que se cuenta con la posibilidad de realizar compensación capacitiva o inductiva para controlar la potencia reactiva que requiere el sistema al mantener en un nivel adecuado los perfiles de tensión y, a su vez, se aprovecha su capacidad para amortiguar las oscilaciones (Ixtláhuatl, Pável, y Juan, 2001).
En la Figura 1 se muestra la conexión en derivación del SVC al sistema SMIB; el modelo del SVC empleado está basado en un condensador fijo y una reactancia, cuya corriente es controlada en ambos semiciclos por medio de dos tiristores conectados en antiparalelo (Do Bomfim, Taranto, y Falcao, 2000).
Figura 1: SMIB con SVC
El esquema utilizado para el SVC contiene una parte para el control de los reactivos y un compensador adicional para amortiguar las oscilaciones que aparecen cuando se presenta una perturbación; este esquema provoca una variación en el modelo del sistema SMIB. El modelo usado para el SVC es el mostrado en la Figura 2 (Karpagam, Deveraj, 2009).
Figura 2: Modelo del SVC planteado
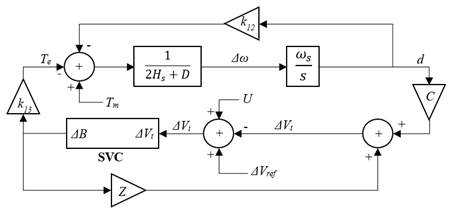
A partir del modelo linealizado en espacio de estados, se obtiene el diagrama de bloques que se muestra en la Figura 3 del sistema SMIB con SVC incluido (Karpagam, Deveraj, 2009).
Figura 3: Modelo linealizado sistema SMIB con SVC
Modelado del STATCOM
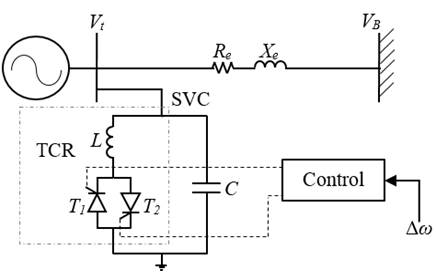
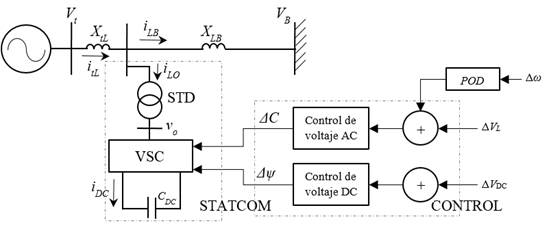
El STATCOM es un tipo de dispositivo FACTS de compensación en derivación, con fuente de voltaje y un transformador en paralelo; el STATCOM puede proporcionar compensación capacitiva o inductiva, según sea la necesidad, controlando la magnitud relativa del voltaje de línea respecto al voltaje en los terminales de salida del inversor (Farahani, Hemati, y Nikzad, 2009). El STATCOM se instala en derivación en un barraje intermedio del sistema SMIB, proporcionando una compensación en paralelo de manera muy similar al SVC, pero utilizando un convertidor de fuente de voltaje (VSC, Voltage Source Converter) en lugar de reactores y capacitores en paralelo (Dávalos y Ramírez, 2001). En la Figura 4 se muestra el modelo del STATCOM conectado a un barraje intermedio del sistema SMIB (Dávalos y Ramírez, 2001).
Figura 4: STATCOM instalado en el sistema SMIB
El convertidor genera un voltaje controlable AC a través de la reactancia de salida (Dávalos y Ramírez, 2001). La ecuación presenta el voltaje de fase en la barra de conexión del STATCOM.
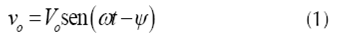
La diferencia de tensión entre la barra Vo y la barra Vt , produce un intercambio de potencia activa y reactiva entre el STATCOM y el sistema de potencia, cuyo flujo puede controlarse ajustando la magnitud de Vo y ψ.
Información más detallada de estos modelos se encuentra en los textos de (Karpagam, Deveraj 2009) y (Dávalos y Ramírez, 2001).
Desarrollo del control del SVC y el STATCOM
Control difuso
Los sistemas de control difuso son sistemas basados en un conjunto de reglas que representan un mecanismo de control para ajustar los efectos de determinados estímulos del sistema; en general, un controlador de tipo difuso es un algoritmo para transformar una estrategia de control dada en forma lingüística en forma de un control automático, para imitar la forma del razonamiento humano (Coronado, Ramírez y Zuñiga, 2001).
En el diseño del control difuso están involucradas las siguientes etapas (Alzate, 2000).
Entradas al controlador difuso. Se definen las entradas al controlador difuso y límites del universo de discurso.
Primera etapa: fuzificación. El difusor convierte las señales numéricas de las entradas del mundo real en variables difusas.
Segunda etapa: inferencia difusa. El protocolo de inferencia difusa seleccionado en este trabajo es de tipo Mamdani, por ser uno de los más adecuados y comunes en aplicaciones de sistemas de control con lógica difusa.
Tercera etapa: base de reglas difusas. El algoritmo de control se proporciona como una base de expresiones del tipo “si <antecedente> entonces <consecuente>”.
Cuarta etapa: defuzificación. En esta etapa la acción entregada por el sistema difuso hay que transformarla del mundo difuso al real mediante un concresor que se encarga de hacer esa transformación.
Sistema de control del SVC
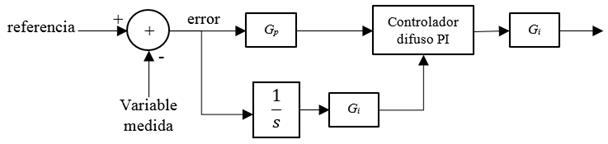
El SVC está equipado con un regulador de tensión que incrementa el torque sincronizador, pero en general la contribución de este al amortiguamiento es pequeña; si se desea amortiguamiento adicional, se requiere de una acción de control suplementaria (Do Bomfim, Taranto, y Falcao, 2000). En este caso, la acción de control suplementaria está dada por un control difuso PI, como se muestra en la Figura 5.
Figura 5: Estructura del controlador difuso PI
Sistema de control del STATCOM
El controlador del STATCOM tiene como función principal la compensación de la potencia reactiva, el control primario del inversor es tal que se regula el flujo de corriente reactiva a través del STATCOM; en otras palabras, el controlador se utiliza para operar el inversor, de modo que el ángulo de fase entre el voltaje del inversor y el voltaje de línea se ajuste dinámicamente, tal que el STATCOM genere o absorba potencia reactiva en el punto de conexión (Dávalos y Ramírez, 2001). El sistema de control del STATCOM comprende dos controladores:
-
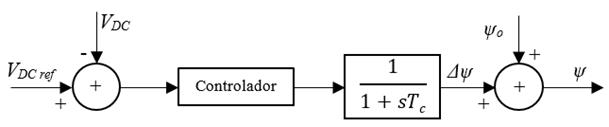
Regulador de tensión DC: se encarga de regular la tensión del circuito intermedio. La tensión DC se regula mediante la modulación del ángulo de fase de la tensión del convertidor en derivación (Stella, Dash, y Basu, 2003); el regulador de tensión controla el voltaje DC a través del capacitor del STATCOM. La Figura 6 muestra la estructura del regulador de tensión DC.
Figura 6: Regulador de tensión DC
-
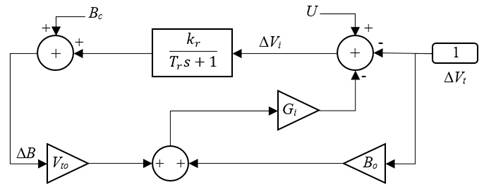
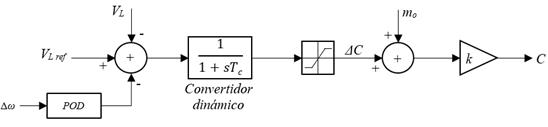
Regulador de tensión AC: este controlador regula la tensión AC en terminales de acuerdo a la referencia que se logra a través del cambio de magnitud en la tensión de salida del convertidor, además cuenta con un amortiguador de oscilaciones AC adicional (Stella, Dash, y Basu, 2003); el amortiguador adicional puede ser considerado como un compensador de adelanto-atraso o como un bloque de control de lógica difusa, entre otros métodos. En este trabajo es considerado un controlador difuso como amortiguador de oscilaciones adicional (POD, Power Oscillation Damping). La Figura 7 muestra el modelo del regulador de tensión AC con el control adicional de amortiguación de oscilaciones.
Figura 7: Regulador de tensión AC
Ajuste del control de tipo difuso del SVC y el STATCOM
Para los controladores de oscilaciones de tipo difuso de los sistemas propuestos (SMIB más SVC y SMIB más STATCOM), una vez definida su estructura, se busca una sintonización aceptable de los parámetros y de las ganancias de estos, pero siempre con la incertidumbre de si esta será la mejor; por tanto, el proceso de ajuste de las ganancias de cada control difuso se convierte en un problema de optimización formulado de la siguiente forma, como se presenta en las desigualdades agrupadas en la ecuación .
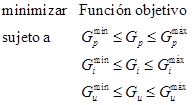
Usando como función objetivo el índice de desempeño ITSE, definido en la ecuación .
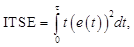
Para resolver este problema, se emplean los siguientes métodos: empírico (sintonización hecha de manera heurística), algoritmo genético (AG), optimización por enjambre de partículas (PSO) y algoritmo de optimización caótica (COA).
Mediante el método empírico se requiere de experiencia, tiempo y comprensión de la dinámica del sistema para tener la seguridad de lograr una sintonización aceptable, pero siempre con la incertidumbre de si esta será la mejor. La ventaja del proceso de ajuste manual es que se hace de manera directa y se aplica de acuerdo a la forma en que el sistema responde (Zarringhalami y Golkar, 2008); la desventaja es que puede tomar bastante tiempo desarrollar la manera de captar el comportamiento del sistema de acuerdo al ajuste, y además es difícil establecer cuándo el ajuste final es óptimo. Por tanto, el control difuso se combina con otros métodos de control para la sintonización de las ganancias y obtener la mejor solución final posible.
El enfoque propuesto combina la lógica difusa con otras técnicas de optimización y de control inteligente como GA, PSO y COA, para lograr encontrar el conjunto óptimo de parámetros de los controladores, obteniendo un control más robusto.
Algoritmo genético (GA)
Los algoritmos genéticos son métodos de optimización que se pueden usar dentro de sistemas de control en conjunción con otras técnicas, por ejemplo, los controladores tradicionales PID (Proportional Integrative Derivative), ya sea para encontrar los mejores parámetros del controlador o la mejor topología de la red (Cano, 2009).
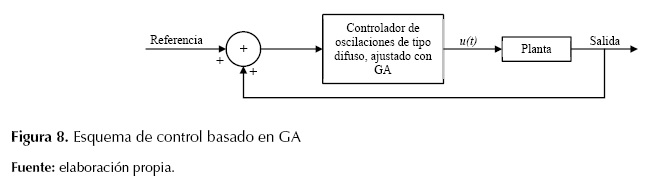
Figura 8: Esquema de control basado en GA
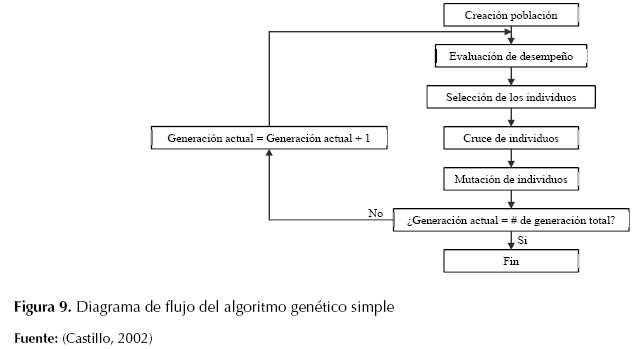
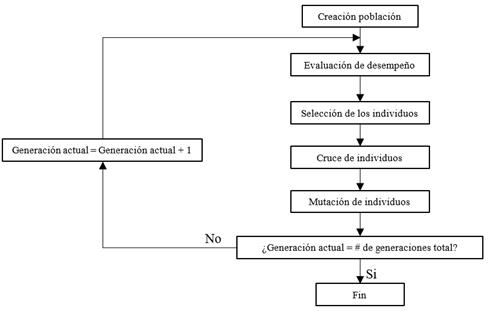
El GA implementado que se muestra en la Figura 8 consiste, a grandes rasgos, en una rutina de software que toma como entradas a los ejemplares y retorna como salidas los que deben generar descendencia para la nueva generación; a este proceso se llama ciclo de evolución, que comienza con una po blación de posibles soluciones, de la cual se seleccionan los mejores padres que pueden dar nuevos individuos mediante el cruce o la mutación y, de esta forma, se crea una nue va población de la que nuevamente se van a obtener padres (Do Bomfim, Taranto, y Falcao, 2000). Los pasos a seguir en la creación e implementación de un algoritmo genético se muestran en el diagrama de flujo de la Figura 9 (Castillo, 2002).
Figura 9: Diagrama de flujo del algoritmo genético simple
Optimización por enjambre de partículas (PSO)
A través de los años se han implementado varios métodos de diseño y sintonización del controlador difuso, entre ellos el método de optimización por cúmulo de partículas (PSO), el cual fue originalmente desarrollado por James Kennedy y por Russ Eberhart (Alzate, Orjuela y Herrera, 2010). El funcionamiento básico del PSO simula el comportamiento del vuelo de las manadas de aves en busca de alimento, el razonamiento lógico consiste en seguir al ave que está más cerca del alimento; cada ave es modelada como una partícula con una solución en el espacio de búsqueda que está siempre en continuo movimiento y nunca es eliminada (Alzate, Orjuela y Herrera, 2010). En otras palabras, las partículas se consideran como agentes simples moviéndose por el espacio de búsqueda, guardan y comunican la solución óptima encontrada. El movimiento de las demás partículas es guiado por aquellas que tienen la mejor solución hasta el momento (García, 2006).
Cada partícula tiene una aptitud (fitness), una posición y un vector velocidad que dirige su movimiento. El movimiento de las partículas está guiado por las partículas óptimas en el instante actual (Alzate, Orjuela y Herrera, 2010).
En el algoritmo PSO, a cada variable de la función objetivo se le asignan valores aleatorios distribuyéndolas por todo el espacio solución, convirtiendo la función objetivo en un vector (nube) donde cada elemento se denomina partícula. Observando cuál de las respuestas se acerca más al cero o al valor deseado, al momento de evaluar todas las respuestas se escoge la mejor y se reasignan los valores de los vectores para una nueva iteración alrededor de esta; esto se realiza hasta que llegue a un punto deseado. Consecuentemente, cada partícula se ve influida por el mejor desempeño de cualquier miembro de la población debido al intercambio de información entre ellos, el rendimiento de cada partícula se mide usando una función de aptitud que varía en función del problema de optimización (Alzate, Orjuela y Herrera, 2010).
Algoritmo de optimización caótica (COA)
Los algoritmos de optimización basados en la teoría del caos (COA), son metodologías de búsqueda que difieren de cualquiera de las técnicas de optimización estocástica tradicionales existentes; no son como un algoritmo de optimización estocástica que escapa de los mínimos locales mediante la aceptación de algunas malas soluciones de acuerdo con una cierta probabilidad, COA busca con la regularidad del movimiento caótico escapar de los mínimos locales (Safari, Shayeghi, y Shayanfar, 2010). El proceso básico del algoritmo de optimización caótica incluye generalmente dos pasos principales:
Primer paso: definir un generador de secuencias caótico o un mapa del espacio caótico en el espacio de soluciones; posteriormente, generar una secuencia de puntos caóticos y asignarla a una secuencia de puntos en el espacio de diseño original. Finalmente, evaluar la función objetivo con respecto a los puntos de diseño generados y elegir el punto con el mínimo valor de la función objetivo como el óptimo actual.
Segundo paso: suponer cercano el óptimo actual al óptimo global después de ciertas iteraciones y asumirlo como el centro con un poco de perturbación caótica; al óptimo global obtenerlo a través de la búsqueda fina. Se repiten los dos pasos anteriores hasta que algún criterio de convergencia especificado se cumpla y luego se obtiene el óptimo global (Safari, Shayeghi, y Shayanfar, 2010). En la aplicación de secuencias caóticas se han adoptado, en lugar de los aleatorios, diferentes modelos entre los cuales se destacan mapa Tent, mapa de Gauss, mapa Lozi, iterador sinusoidal, oscilador de Chua, sistema de Mackey-Glass, sistema de Lorenz, mapa Hénon y mapa Ikeda (Safari, Shayeghi, y Shayanfar, 2010).
SIMULACIONES Y RESULTADOS
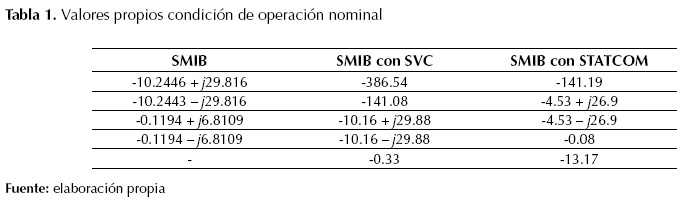
Con el fin de comprobar el comportamiento de cada controlador de oscilaciones de tipo difuso de los sistemas de prueba (SMIB más SVC y SMIB más STATCOM), se exponen los resultados de los sistemas de prueba bajo diferentes condiciones de operación obtenidos a partir de las simulaciones hechas en Matlab. En la Tabla 1 se presentan los valores propios del STATCOM y del SVC en el sistema SMIB, para los siguientes puntos de operación:
condición de operación nominal P = 0.7 (pu, por unidad) y Q = 0.3 (pu).
Fuente: elaboración propia
Tabla 1: Valores propios condición de operación nominal
SMIB
SMIB con SVC
SMIB con STATCOM
-10.2446 + j29.816
-386.54
-141.19
-10.2443 - j29.816
-141.08
-4.53 + j26.9
-0.1194 + j6.8109
-10.16 + j29.88
-4.53 - j26.9
-0.1194 - j6.8109
-10.16 - j29.88
-0.08
-
-0.33
-13.17
En condición de operación nominal los sistemas tienen valores propios que son pares conjugados, es decir, presentan oscilaciones amortiguadas, como se presentan en la Tabla 2.
Condición de sobrecarga: P = 1.2 (pu) y Q = 0.4 (pu).
Fuente: elaboración propia
Tabla 2: Valores propios condición de sobrecarga
SMIB
SMIB con SVC
SMIB con STATCOM
-10.3717 + j28.8094
-393.3
-141.19
-10.3716 - j28.8094
-141.14
-3.61 + j26.56
-0.0078 + j6.9427
-10.12 + j29
-3.61 - j26.56
-0.0078 - j6.9427
-10.12 - j29
-0.23
-
-0.34
-15.49
Como puede observarse, en condición de sobrecarga los valores propios del sistema SMIB son pares conjugados con parte real positiva representando oscilaciones que incrementan su amplitud, lo que implica que el sistema es inestable, mientras que los valores propios del sistema SMIB con STATCOM y con SVC son pares conjugados con parte real negativa, implicando una respuesta oscilatoria amortiguada; es decir, al incluir el STATCOM o el SVC en el sistema SMIB se logran mitigar las oscilaciones crecientes que desestabilizan al sistema en condición de sobrecarga.
Simulaciones sistema SMIB con SVC
A continuación, se muestra el comportamiento de la tensión en terminales Vt y de la potencia eléctrica Pe del sistema SMIB con SVC, bajo la acción del controlador de oscilaciones de tipo difuso y ante diferentes condiciones de operación.
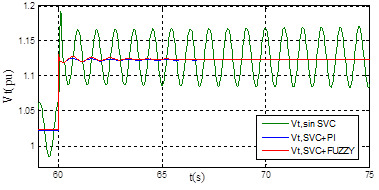
En la Figuras 10 y la Figura 11 se muestran las respuestas de la tensión en terminales Vt y de la potencia eléctrica Pe del sistema SMIB con SVC más el controlador de oscilaciones respectivamente, en condición de operación nominal.
Figura 10: Respuestas de
Vt
en operación nominal ante un aumento del 10% en la tensión de referencia
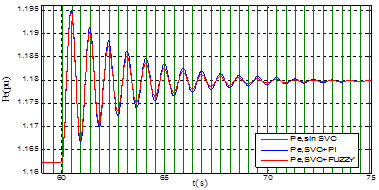
Figura 11: Respuesta de Pe en condición nominal ante un aumento del 1.5% en la potencia mecánica
Fuente: elaboración propia
Tabla 3: Parámetros de respuesta SMIB con SVC, en condición nominal
SMIB
SMIB + SVC + PI
SMIB + SVC + Fuzzy
t
s (s)
0.4
0.35
0.4
Mp (%)
3.12
0.436
0.418
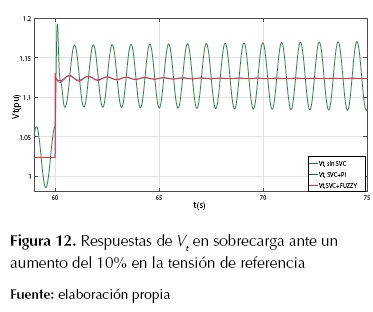
En la Tabla 3 y en la Figura 10 y la Figura 11, se observa que las respuestas del sistema SMIB con SVC, bajo la acción de control de oscilaciones, presentan un mayor amortiguamiento y una gran disminución del máximo sobreimpulso de la tensión en terminales Vt que el sistema SMIB sin SVC. En la Figura 12 y la Figura 13 se muestran las respuestas de la tensión en terminales Vt y de la potencia eléctrica Pe del sistema SMIB con SVC más el controlador de oscilaciones respectivamente, en condición de sobrecarga. En la Tabla 4 se reportan los valores de ts y Mp usando control PI y control difuso para el SVC.
Figura 12: Respuestas de
Vt
en sobrecarga ante un aumento del 10% en la tensión de referencia
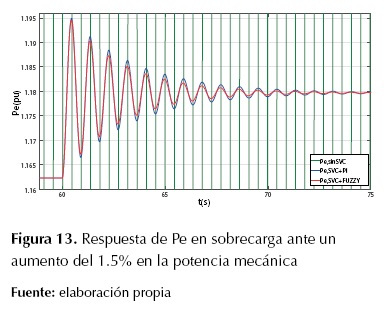
Figura 13: Respuesta de Pe en sobrecarga ante un aumento del 1.5% en la potencia mecánica
Fuente: elaboración propia
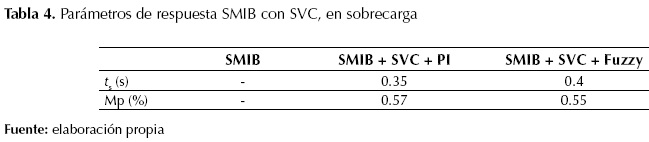
Tabla 4: Parámetros de respuesta SMIB con SVC, en sobrecarga
SMIB
SMIB + SVC + PI
SMIB + SVC + Fuzzy
t
s (s)
-
0.35
0.4
Mp (%)
-
0.57
0.55
Como puede observarse en la Figura 12 y la Figura 13, en condición de sobrecarga, el sistema SMIB presenta oscilaciones crecientes, indicando la inestabilidad del sistema sin el SVC, mientras que con el SVC y bajo la acción de control de oscilaciones de tipo difuso, el sistema mantiene una respuesta estable y con alta amortiguación de oscilaciones. En la Figura 14 y la Figura 15 se muestra la comparación de respuestas de la tensión en terminales Vt y la velocidad del rotor ω, respectivamente, del sistema SMIB con SVC, bajo la acción del controlador de oscilaciones de tipo difuso sintonizado con AG, PSO y COA. En la Tabla 5 se presenta una comparación cuantitativa de los métodos de ajuste empleados para el controlador del SVC.
Fuente: elaboración propia
Tabla 5: Comparación de métodos de ajuste del controlador de oscilaciones del SVC
Método de ajuste
SVC
Ganancias control difuso
Parámetro respuesta
Índice de desempeño
Gp
Gint
Gu
Mp (%)
ITSE
Empírico
0,0814
0,9493
6,0000
0,418
0,0003597
AG
0,2408
0,8796
2,4739
0,409
0,0003069
PSO
0,2921
0,8095
2,5493
0,409
0,0002677
COA
0,2745
1,8304
2,7452
0,409
0,0002374
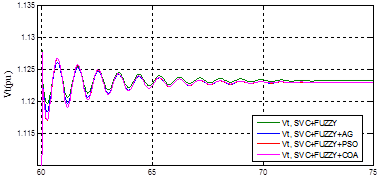
Figura 14: Respuestas para
Vt
en condición de operación nominal SVC con Fuzzy, GA, PSO y COA, ante un aumento del 10% en la tensión de referencia
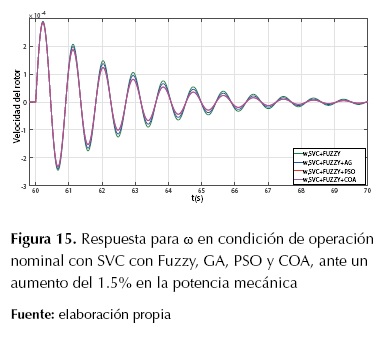
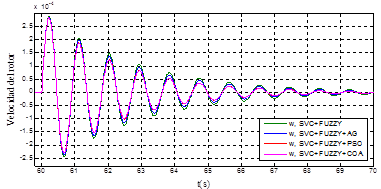
Figura 15: Respuesta para ω en condición de operación nominal con SVC con Fuzzy, GA, PSO y COA, ante un aumento del 1.5% en la potencia mecánica
Se observa en la Figura 14 y la Figura15 que el desempeño del controlador de oscilaciones de tipo difuso es muy similar con los diferentes métodos de ajuste (empírico, GA, PSO y COA); es decir, presentan un nivel de amortiguamiento de oscilaciones muy similar.
Simulaciones sistema SMIB con STATCOM
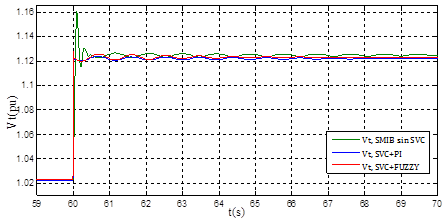
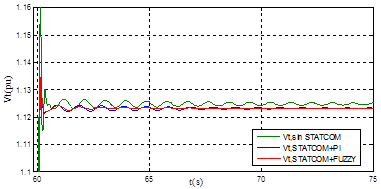
En las Figura 16 se muestra las respuestas de la tensión en terminales Vt y en la Figura 17 se muestra la potencia eléctrica Pe del sistema SMIB con STATCOM más el controlador de oscilaciones, en condición de operación nominal.
Figura 16: Respuesta de
Vt
en operación nominal ante un aumento del 10% en la tensión de referencia
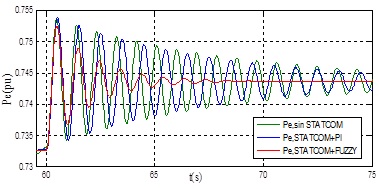
Figura 17: Respuesta de Pe en condición nominal ante un aumento del 1.5% en la potencia mecánica
En la Figura 16 se observa que la respuesta del sistema con el STATCOM es menos oscilatoria y como consecuencia se estabiliza antes. En la Tabla 6 se presentan los valores de ts y Mp en valor porcentual para diversos escenarios con STATCOM.
Fuente: elaboración propia
Tabla 6: Parámetros de respuesta de V
t
del sistema SMIB con STATCOM y control difuso, condición nominal
SMIB
SMIB + STATCOM + PI
SMIB + STATCOM + Fuzzy
t
s (s)
0.4
0.22
0.21
Mp (%)
3.12
1.02
1.02
En la Tabla 6 se evidencia que el máximo sobreimpulso se minimiza con la inclusión del STATCOM.
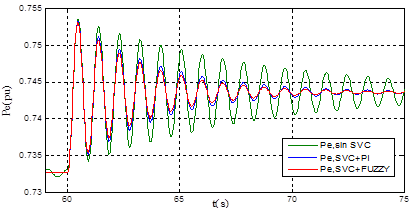
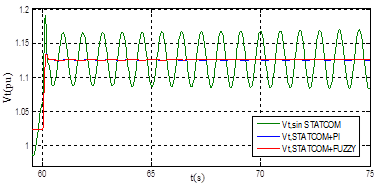
En la Figura 18 se muestra la respuesta de la tensión en terminales Vt , y en la Figura 19 se muestra el comportamiento de la potencia eléctrica Pe del sistema SMIB con STATCOM más el controlador de oscilaciones en condición de sobrecarga.
Figura 18: Respuesta de
Vt
en sobrecarga ante un aumento del 10% en la tensión de referencia
En la Figura 18 se observa que la respuesta del sistema SMIB es completamente oscilatoria, mientras que con el STATCOM incluido se sigue manteniendo una respuesta estable. En la Tabla 7 se muestran los valores de ts y Mp en valor porcentual para diversos escenarios con STATCOM.
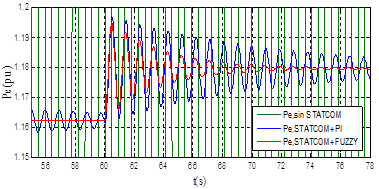
Figura 19: Respuesta de
Pe
en sobrecarga ante un aumento del 1.5% en la potencia mecánica
Fuente: elaboración propia
Tabla 7: Parámetros de respuesta de V
t
del sistema SMIB con STATCOM y control difuso, sobrecarga
SMIB
SMIB + STATCOM + PI
SMIB + STATCOM + Fuzzy
t
s (s)
-
0.26
0.25
Mp (%)
-
0.906
0.853
La Figura 19 y en la Tabla 7 se evidencia que el sistema SMIB con STATCOM y con controlador de oscilaciones de tipo difuso, presenta una mayor amortiguación de las oscilaciones que el controlador convencional PI. En la Tabla 8 se resumen los valores obtenidos para Mp y ITSE con los diferentes controladores.
Fuente: elaboración propia
Tabla 8: Comparación métodos de ajuste del controlador de oscilaciones del STATCOM
Método de ajuste
STATCOM
Ganancias control difuso
Parámetro respuesta
Índice de desempeño
Gpc
Gintc
Guc
Mp (%)
ITSE
Empírico
3,0000
0,0100
2,0000
1,02
0,0002130
AG
9,7297
2,0374
2,5685
1,06
0,0000481
PSO
9,6878
0,9439
2,9287
0,98
0,0000430
COA
9,5585
5,7056
2,8773
0,99
0,0000445
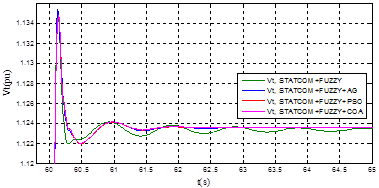
En la Figura 20 aparece la respuesta de la tensión en terminales y en la Figura 21 se muestra la respuesta de la velocidad del rotor del sistema en condición de operación nominal; en la Tabla 8, se comparan los resultados de los métodos de sintonización del controlador de oscilaciones de tipo difuso del STATCOM.
Figura 20: Respuestas para
Vt
en condición de operación nominal STATCOM con Fuzzy, GA, PSO y COA, ante un aumento del 10% en la tensión de referencia
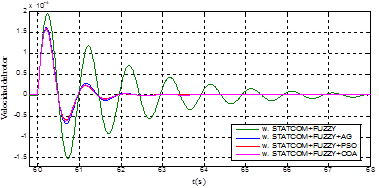
Figura 21: Respuestas para ω en condición de operación nominal. STATCOM con Fuzzy, GA, PSO y COA, ante un aumento del 1.5% en la potencia mecánica
Como se puede observar en la Figura 20 y la Figura 21, el rendimiento del controlador ajustado mediante el método empírico es menor que el obtenido con los métodos GA, PSO y COA; también, se muestra que el método de ajuste con PSO posee una mejor amortiguación de las oscilaciones que el GA y el COA.
CONCLUSIONES
Se comprobó la efectividad de los controladores de oscilaciones de tipo difuso del STATCOM y del SVC, ajustados con las diferentes técnicas: empírica, AG, PSO y COA, los cuales proporcionan un aumento en la amortiguación de las oscilaciones. El ajuste del control difuso con AG, COA o PSO, presenta un mejor comportamiento que el control difuso ajustado a ensayo y error (empíricamente), esto puede observarse en el sistema SMIB con STATCOM incluido.
El buen desempeño de algunos métodos de control inteligente en el amortiguamiento de oscilaciones usando FACTS, se demostró bajo diferentes condiciones de operación. En este trabajo, se observa la mejora en el sistema SMIB al incluir un dispositivo FACTS (STATCOM o SVC) bajo la acción del control de oscilaciones de tipo difuso; con la inclusión del STATCOM o del SVC se mejoran notablemente las respuestas del sistema al disminuir las oscilaciones.
Los algoritmos de optimización empleados en la sintonización del control difuso tienen como ventaja que realizan una búsqueda sobre el espacio de estado completo, encontrando la mejor solución para el sistema de control.
REFERENCIAS
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.