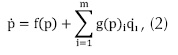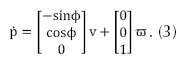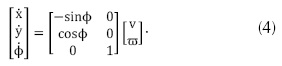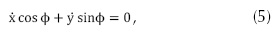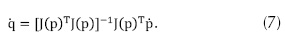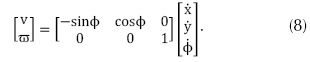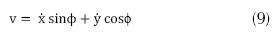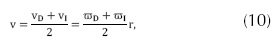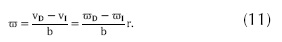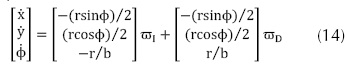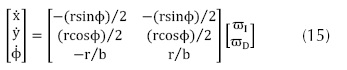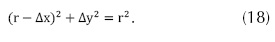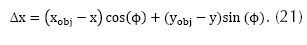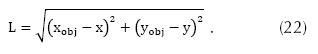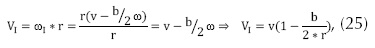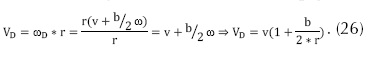Implementación de un controlador de posición y movimiento de un robot móvil diferencial

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.2.a09

Implementación de un controlador de posición y movimiento de un robot móvil diferencial

Implementation of a position and movement controller for a differential mobile robot

Germán Hernández Millán¹, Luís Hernando Ríos Gonzales², Maximiliano Bueno López³

¹ Ingeniero Electricista, Magister en Ingeniería Eléctrica, Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: germanhernadez08@gmail.com
² Ingeniero Electrónico, Especialista en Computadores y Sistemas Digitales, Master of Science in engineering, Diploma de Estudios Avanzados (DEA), Magister en Ingeniería Eléctrica. Docente de la Universidad Tecnológica de Pereira- UTP. Pereira, Colombia. Contacto:  lhgonza@utp.edu.co
³ Ingeniero Electricista, Magister en Ingeniería Eléctrica, Doctor en Ingeniería, Director Programa de Ingeniería en Automatización Universidad de La Salle. Bogotá D.C., Colombia. mbueno@lasalle.edu.co

Fecha de recepción: 10 de junio de 2014 Fecha de aceptación: 15 de febrero de 2016

Cómo citar: Hernández Millán, G., Ríos Gonzales, L. H., & Bueno López, M. (2016). Implementación de un controlador de posición y movimiento de un robot móvil diferencial. Revista Tecnura, 20(48), 123-136. doi: 10.14483/udistrital.jour.tecnura.2016.2.a09

Resumen

Contexto: La robótica móvil continúa siendo un área de constante actualización, donde se busca tener aplicaciones que permitan mejorar la calidad de vida de los seres humanos. Con base en lo anterior, en este artículo se presenta un novedoso diseño de un controlador de posición y movimiento para un robot móvil diferencial, utilizando redes neuronales artificiales y cuyo fin es llevarlo a aplicaciones reales en diferentes campos de acción.

Método: La propuesta presentada está basada en un controlador PID, el cual ha sido sintonizado con una red neuronal y requiere conocer el modelo cinemático del robot.

Resultados: Las simulaciones muestran la eficiencia del control de posición para el seguimiento de caminos explícitos, en este caso para el seguimiento de trayectorias rectilíneas y curvilíneas. La interfaz gráfica presentada permite ajustar las ganancias con facilidad y verificar el seguimiento de la trayectoria en línea.

Conclusiones: De los resultados obtenidos se puede concluir que la estrategia propuesta es de fácil implementación ya que se requiere información que de manera general entregan los sensores de un robot móvil. Finalmente la sintonización realizada del controlador PID con la red neuronal permite obtener un correcto desempeño para seguimiento de trayectorias.

Palabras clave: Control Automático, Modelo Dinámico, Robot Móvil Diferencial.

Abstract

Context: Mobile robotics remains being an area of constant updating, which seeks to have applications to improve the life quality of human beings. Therefore, the paper presented a novel design of a position and move controller to a differential mobile robot using artificial neural networks, which aims is to bring a real applications in different fields.

Method: The proposal is based on a PID controller, which has been tuned using a neural network and requires knowledge of the kinematic model of the robot.

Results: The simulations show the efficiency of the control position for following paths, in this case for tracking straight and curved paths. The graphical interface allows adjusting the gains easily and verifies the trajectory tracking online.

Conclusions: From the results we can conclude that the proposed strategy is easy to implement since the required information is generally deliver by mobile robot sensors. Finally, tuning PID controller with the neural network allows obtaining a correct performance for trajectory tracking.

Keywords: Automatic Control, Differential mobile robot, Dynamic model.

Introducción

Los robots móviles son dispositivos electromecánicos capaces de desplazarse en un espacio de trabajo con cierto grado de autonomía. De acuerdo con su forma de locomoción se clasifican en: robots móviles de locomoción mediante orugas, mediante patas y mediante ruedas.

Los robots móviles propulsados por ruedas, a su vez, se clasifican según el número y el tipo de grados de libertad (Blazic, 2014).

Cuando se trata de generar trayectorias o caminos en sistemas no holónomos, hay características relevantes directamente relacionadas con el tipo de trayectorias que pueden seguir estos sistemas; en efecto, una configuración inicial y una final no pueden unirse mediante cualquier trayectoria. Las restricciones cinemáticas del sistema imponen unas condiciones que solo algunos caminos cumplirán, entendiendo por camino la discretización de una función continua que interpola las configuraciones definidas en una ruta. Por último, cuando se habla de trayectoria, se hace referencia a un camino que tiene asociado un perfil cinemático; es decir, a cada configuración perteneciente al camino se le asocia una velocidad (Campion, Bastin y d'Andréa Novel, 1993).

Para poder llevar el robot móvil hasta una posición deseada siguiendo una trayectoria se han propuesto diferentes estrategias de control (Kwon, y Dongkyoung, 2012; Jingkui, Wenxin y Liangliang, 2010; Rezaee y Abdollahi, 2014; Yandong, Zongyi y Ling, 2010), algunas no requieren la utilización del modelo matemático, por el contrario otras requieren obtener el modelo cinemático y dinámico. En este artículo se obtuvo un modelo cinemático del robot asumiendo que el punto de referencia se encuentra en medio de las dos ruedas de tracción de la plataforma, optando así por un método basado en el centro de masa con restricciones no holonómicas. Este control utiliza un modelo geométrico, el cual emplea el cálculo del radio de curvatura para realizar el seguimiento de una trayectoria deseada. Con las primeras simulaciones se pudo comprobar que este método funciona muy bien tanto para seguimiento de trayectorias rectilíneas como curvilíneas.

CONTROL DE POSICIÓN DEL ROBOT MÓVIL DIFERENCIAL

El objetivo de este control es que el robot diferencial ejecute de forma autónoma movimientos previamente planificados (Saidonr, Desa y Rudzuan, 2011). Se pretende que el robot móvil siga un camino específico de forma autónoma. Este problema puede formularse como la obtención de las leyes de control que permitan estabilizar al robot sobre un punto de trabajo. En un problema de seguimiento de caminos explícitos se pretende que el error entre la posición deseada y la posición actual q_d(t)-q(t) tienda a cero (0), manteniéndose acotadas las señales de control (Toda y Kubota, 2013).

El camino explicito que se pretende seguir puede especificarse de varias formas, de las cuales cabe mencionar las siguientes (Vachhani, Mahindrakar y Sridharan, 2011):

• Especificación previa en coordenadas absolutas a partir de planos o mapas.
• Especificación iterativa desde un terminal empleando técnicas de teleoperación.

En una arquitectura de control inteligente se emplean por lo general métodos de planificación de caminos mediante la utilización de sistemas de percepción, tal como ocurre en el seguimiento de líneas obtenidas mediante un sistema de visión (Velrajkumar, Manohar y Raju, 2010).

Para el control de posición de robots móviles se distinguen varias técnicas, entre las que se pueden mencionar:

• Técnica basada en teorías de control, la cual utiliza los modelos matemáticos del robot para encontrar un controlador que lo estabilice y a la vez consiga la tarea deseada.
• Técnica basada en métodos geométricos para seguir trayectorias o planificar caminos matemáticamente.
• Técnica basada en sistemas inteligentes, como redes neuronales, algoritmos genéticos o lógica difusa, para el control de movimiento y la coordinación de comportamientos.

CONTROL DE MOVIMIENTO DEL ROBOT MÓVIL DIFERENCIAL

Para diseñar el controlador se hace uso del conocimiento del modelo dinámico del robot y de las herramientas de análisis y diseño aportadas por la teoría del control (Jung-Hoon, Arkin y Dong-Soo, 2003).

Dada una estructura particular (robot móvil diferencial), será necesario determinar los movimientos requeridos por cada rueda del robot (dichas ruedas son controladas por los motores), para que pueda ser llevado a una posición y orientación requeridas en el espacio de trabajo. Este tipo de control tiene como objetivo procurar que las trayectorias seguidas por el robot q(t) sean lo más parecidas a las que el control de movimiento propone como trayectoria deseada q_d(t) (Yang et al., 2010).

La cinemática del robot diferencial estudia el movimiento del mismo con respecto a un sistema de referencia (Spyros, 2014; Cook, 2011). La cinemática se interesa por la descripción analítica del movimiento espacial del robot como una función del tiempo, y en particular por las relaciones entre la posición y la orientación final del robot con los valores que toman sus coordenadas.

En el tipo de tracción diferencial, el robot se mueve por la acción de dos ruedas motrices independientes; para plantear el modelo cinemático de este tipo de robots se utilizan las siguientes hipótesis que ayudan a simplificar el modelo:

• El robot se mueve en una superficie plana.
• El eje guía es perpendicular al plano.
• Las ruedas se mueven sin restricciones.
• El robot no tiene partes flexibles.
• Durante los pequeños intervalos de tiempo en que la dirección se mantiene constante, el vehículo se moverá de un punto a otro siguiendo un arco de circunferencia.
• El robot es considerado como un cuerpo rígido y cualquier parte movible de las ruedas de dirección, se desplazará siguiendo un comando del control de posición.

Todas estas suposiciones se cumplen razonablemente bien en la mayoría de los robots móviles actuales. El deslizamiento es de hecho el mayor problema con que se encuentra cualquier robot móvil a la hora de establecer una autolocalización precisa.

Modelo jacobiano

Asumiendo que p representa un lugar en el espacio con n coordenadas generalizadas y q un vector de m variables de actuadores (para n > m), y asumiendo que 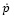y 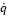son las respectivas derivadas de tales vectores, entonces el modelo directo es obtenido por la matriz jacobiana, J (p) dado por la ecuación (1).

Esta expresión del jacobiano puede escribirse en la forma mostrada en la ecuación 2:

La ecuación 2 se presenta en forma matricial por la ecuación 3, donde v es la velocidad lineal del vehículo y ω es la velocidad angular, estas ecuaciones pueden ser también escritas en la forma de (1) como

Para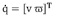

De la ecuación 4 se puede obtener la ecuación 5:

Esto es debido a que el vehículo solamente puede moverse a lo largo de su eje longitudinal. ϕ viene dado por la ecuación 6:

Las anteriores expresiones permiten asegurar que la posición del vehiculó (x, y) y la orientación ϕ no son independientes.

Cinemática directa e inversa

Existen dos problemas fundamentales para resolver la cinemática del robot. El primero de ellos se conoce como el problema cinemático directo, y consiste en determinar cuál es la posición y orientación final del robot con respecto a un sistema de coordenadas que se toma como referencia. Los valores de las velocidades angulares de las ruedas del robot son conocidos. El segundo, denominado problema cinemático inverso, resuelve el proceso de la determinación de los parámetros de control para llevar al robot a un lugar deseado, proporcionando las velocidades angulares que deben tomar las ruedas del robot para una posición y orientación conocidas.

La cinemática inversa del sistema implica la inversa del jacobiano. Cuando este último no es una matriz cuadrada, es necesario calcular su seudoinversa, multiplicando ambos lados por J^T, y resolviendo para 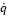, con lo cual se obtiene la ecuación 7:

Entonces, para el modelo se obtiene la expresión dada por la ecuación 8:

Donde v está dada por la ecuación 9:

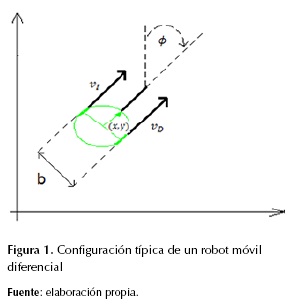
Configuración del robot móvil diferencial

La figura 1 muestra el clásico vehículo de tracción diferencial, el cual usa en ambas ruedas, velocidades independientes (V_I y V_D, respectivamente), que se mueven en el plano 2D hacia un punto específico (x, y) y una orientación ϕ específica.

Asumiendo para el modelo de tracción diferencial, que ω_I y ω_D son las velocidades correspondientes de las ruedas izquierda y derecha, dado el radio de las ruedas como r, las correspondientes velocidades lineal y angular están dadas por las ecuaciones 10 y 11 respectivamente

Donde b es la separacion entre las dos ruedas del vehículo. También si las velocidades lineal y angular son dadas, entonces la velocidad angular puede ser obtenida por las ecuaciones 12 y 13:

Sustituyendo las ecuaciones 10 y 11 en el modelo de robot móvil (3) se obtienen las ecuaciones 14 y 15:

IMPLEMENTACIÓN DEL CONTROLADOR DE POSICIÓN Y MOVIMIENTO DEL ROBOT MÓVIL DIFERENCIAL

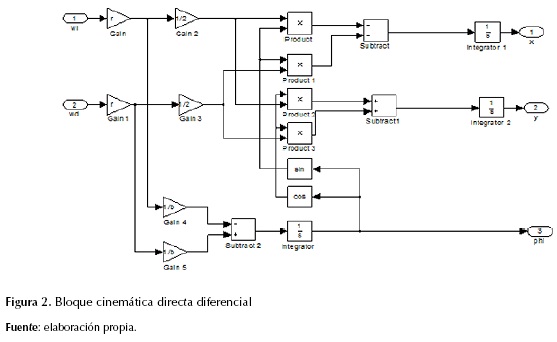
El siguiente paso es representar las ecuaciones del modelo cinemático (15) en un diagrama de bloques del SimuLink, el cual permite calcular la posición del robot móvil en cada instante de tiempo. Este bloque se llama cinemática directa diferencial y servirá para probar el control de posición, el cual será diseñado posteriormente. El bloque cinemática directa diferencial se muestra en la figura 2.

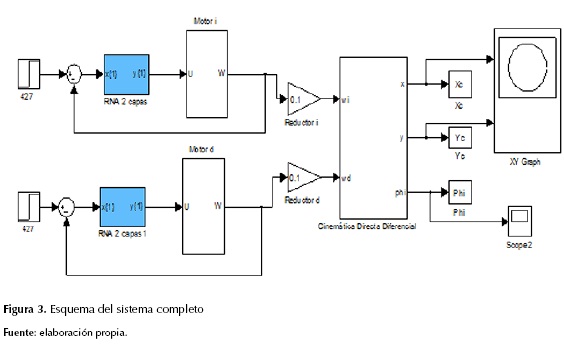
Para probar el funcionamiento del esquema de la figura 2 se integraron en un bloque de SimuLink los siguientes elementos: dos modelos de los motores con sus respectivos controles de velocidad manejados por redes neuronales artificiales (RNA), dos bloques reductores de velocidad y el bloque cinemática directa diferencial; a dicho esquema se le aplicaron diferentes señales de control en las entradas de referencia, tal como se muestra en la figura 3.

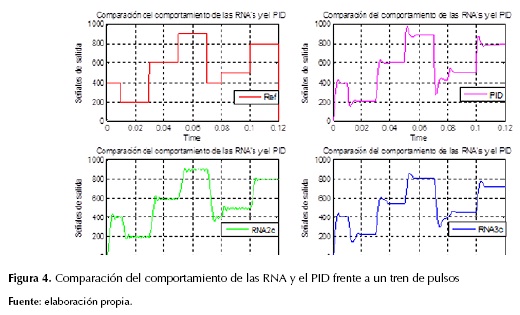
En este artículo se ha comprobado que las redes neuronales pueden emular el comportamiento de un controlador PID para controlar los perfiles de velocidad de los motores de tracción un robot móvil tipo diferencial. La configuración de la red neuronal es un punto fundamental para que una aplicación produzca buenos resultados. Si los datos de entrenamiento son correctos, pero la arquitectura de la red no es la adecuada para la aplicación, la red neuronal no se comportará como se espera. Inicialmente se obtuvo un modelo en forma de función de transferencia de todas las partes eléctricas y mecánicas del modelo físico que eran necesarias para la construcción del robot móvil de tracción diferencial. En este modelo no se tuvieron en cuenta las no linealidades del modelo y se consideró el motor libre de carga. Para el diseño del controlador de velocidad se estudiaron diferentes técnicas de control, pero al final se optó por reemplazar un PID sintonizado con la herramienta sisotool por una RNA. Después de tener sintonizado el controlador de velocidad PID se desarrollaron varias arquitecturas de RNA con un tipo de redes de retropropagación (back-propagation), entrenadas con los datos obtenidos del controlador PID. En la figura 4 se muestra la comparación entre estas dos estrategias de control.

Para verificar el correcto funcionamiento del esquema mostrado en la figura 3 se partió de una posición inicial de coordenadas x_in = 0 y_in = 0, φ_in = 0 que son las coordenadas del origen. Las simulaciones que se realizaron fueron las siguientes:

Velocidades angulares iguales ωi = ωd.
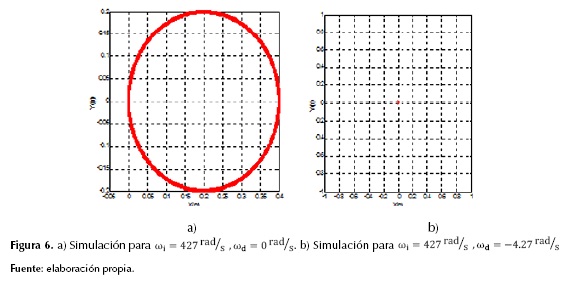
Velocidad angular ωi = 247 rad/s y ωd = 0 rad/s.
Velocidad angular ωi = 247 rad/s y ωd = -247 rad/s.

Para estas simulaciones se asumieron los siguientes valores:

r = 0,05 m radio de las rueda del robot diferencial.
b = 0,4 m distancia de separación entre las ruedas del robot diferencial.

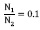índice de reducción.

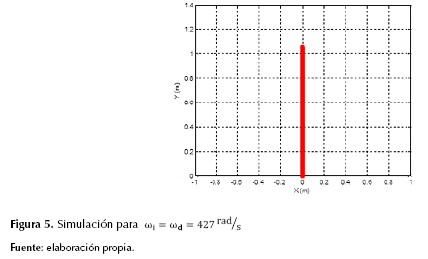
Con estos valores y un tiempo de simulación de 500 ms, la primera simulación hizo un recorrido en línea recta de aproximadamente de 1.07 m. Para la segunda prueba se describió una circunferencia perfecta de radio 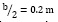y para la tercera se mostró un punto fijo. Los resultados de las simulaciones son presentados en las figuras 5 y 6.

MÉTODO DE PERSECUCIÓN PURA PARA EL SEGUIMIENTO DE CAMINOS EXPLÍCITOS

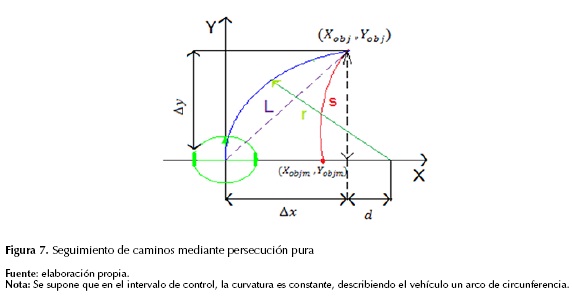
Considérese un sistema de referencia local asociado al movimiento del vehículo, tal como se muestra en la figura 7.

Del análisis de la figura 7 se deducen las ecuaciones 16 y 17:

Siendo r el radio de curvatura del vehículo.

Despejando d en 16 y sustituyendo en 17, se obtiene la ecuación 18:

De donde el radio de curvatura necesario para que el vehículo se desplace Δx, Δy es dado por la ecuación 19:

Por tanto, la curvatura que es necesario suministrar al vehículo se expresa por la ecuación 20:

Donde el signo viene dado por el sentido de giro necesario para alcanzar el punto objetivo en la figura 7, L es la distancia a la que se encuentra el punto objetivo y Δx es el desplazamiento lateral.

La expresión anterior constituye la ley de control de persecución pura (pure pursuit), lo que permite identificar con claridad la forma de una ley de control proporcional al error lateral (Δx) con respecto al punto objetivo. La constante de proporcionalidad varía con la inversa del cuadrado de L.

En la figura 7 puede verse también que la curvatura de la persecución pura es la inversa del radio de una de las circunferencias que pasa por la posición actual del vehículo y por el punto objetivo.

El algoritmo para la aplicación de esta ley de control solo necesita determinar el punto del camino que se encuentra a una distancia previamente definida L, y calcular el error lateral (Δx) con respecto a la posición actual del centro de guiado del vehículo. Si las coordenadas están en un sistema global, es necesario tener en cuenta la orientación del vehículo para obtener Δx, es decir, si el vehículo está en las coordenadas globales (x, y) con orientación ϕ. El punto objetivo sobre el camino está en las coordenadas globales (x_obj, y_obj) y se expresa mediante la ecuación 21:

Un método práctico para aplicar la ley de control consiste en obtener a la tasa de muestreo, el punto (x_obm, y_om) del camino objetivo que está más próximo al vehículo (x, y) y elegir el punto (x_ob, y_ob) a una distancia fija s sobre el camino tomado en el sentido de avance a partir de (x_obm, y_obm) tal como se muestra en la figura 6; posteriormente se calcula L y se aplica la ley de control 20 y 21. El cálculo de L se realiza con el teorema de Pitágoras mediante la ecuación 22:

La ley de control es dependiente de la velocidad, obteniéndose las ecuaciones 23 y 24:

Aislando las velocidades lineales de cada rueda, y sabiendo que v = r*ω estas ecuaciones se pueden reescribir mediante las ecuaciones 25 y 26:

Donde r es el radio de giro, b la distancia entre las ruedas y v la velocidad lineal del móvil.

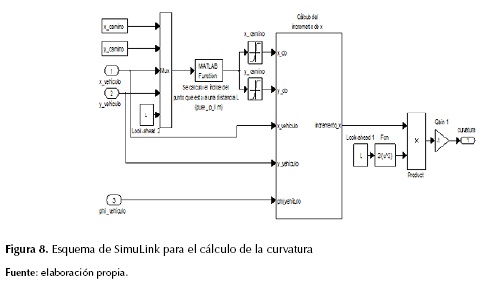
El algoritmo de persecución pura se puede implementar en SimuLink mediante el bloque de la figura 8.

Este bloque es llamado persecución pura I y consta de una MATLAB Function con nombre pure_p_I que es la encargada de calcular el índice de los valores x_camino y y_camino más próximos a la posición del robot y un sub-bloque denominado cálculo de incremento de x que es la representación de la función 21. Este bloque fue tomado del toolbox Hemero y entrega a su salida el valor de la función 20 que es la curvatura entregada al robot móvil (Vachhani, Mahindrakar y Sridharan, 2011).

Con este bloque se pueden realizar las siguientes simulaciones:

• Se comprobara cómo evoluciona el robot diferencial al momento de seguir una trayectoria rectilínea de la forma y = x.
• Se comprobara cómo se comporta el robot diferencial ante el requerimiento de seguir una parábola de la forma y = x².
• Se comprobara cómo se comporta el robot diferencial ante el requerimiento de seguir una trayectoria en forma de circunferencia de la forma y = sen (t) y y = cos(t).

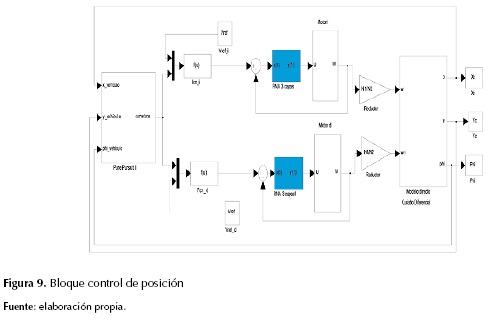
Por último, en la figura 9 se muestra el bloque implementado para el control de posición.

RESULTADOS OBTENIDOS. SIMULACIÓN DEL CONTROL DE POSICIÓN

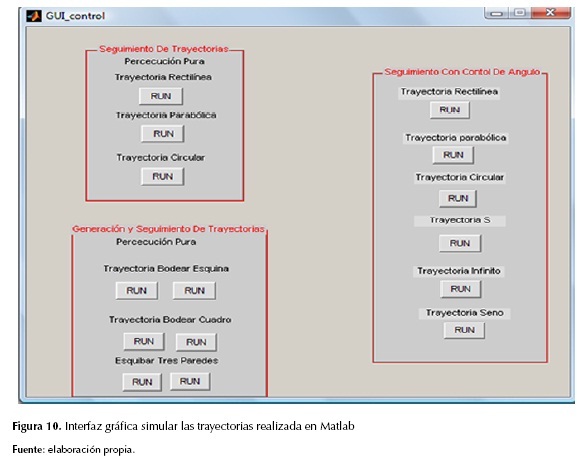
Se implementó una interfaz gráfica GUI para la presentación de las diferentes trayectorias seguidas por el robot móvil. En la figura 10 se muestra la GUI implementada.

Se simularon trayectorias realizadas controlando solamente el ángulo de giro y utilizando el control de posición mediante el método geométrico de persecución pura implementado. Las simulaciones que se implementaron utilizando el control de posición mediante el método geométrico de persecución pura fueron las siguientes:

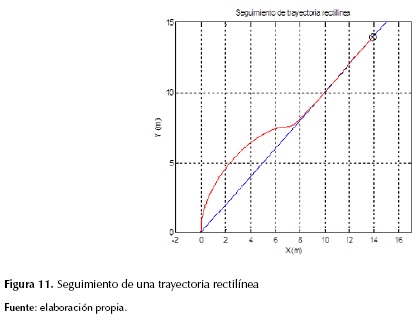
• Seguir una trayectoria rectilínea de la forma y = x (figura 11).



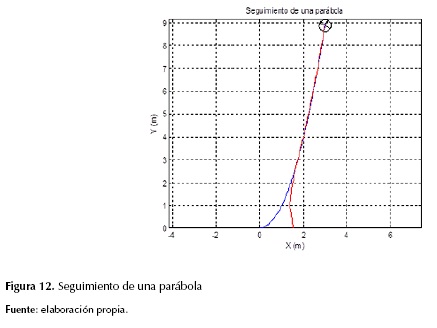
• Seguir una trayectoria con forma de parábola de la forma y = x² (figura 12).



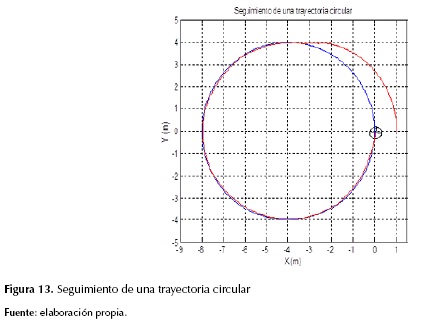
• Seguir una trayectoria en forma de circunferencia de la forma y = sen (t) y y = cos(t) (figura 13).

Conclusiones

De las simulaciones se puede observar la eficiencia del control de posición para el seguimiento de caminos explícitos, en este caso para el seguimiento de trayectorias rectilíneas y curvilíneas. Como se puede apreciar en estas simulaciones se observa que el control de posición se comporta muy bien al momento de seguir cualquier curva, en especial frente a curvas suaves.

En algunas simulaciones donde se trató de seguir trayectorias rectilíneas muy inclinadas y Δx se hace muy pequeño este controlador presenta fallas, debido a que la función del radio de curvatura para una trayectoria vertical es 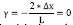, y en ese momento los perfiles de velocidad serán cero (0) y por este motivo se pierde el control de seguimiento.

El trabajo realizado permite la implementación práctica de las técnicas estudiadas en una plataforma real, garantizando el éxito de dichas técnicas.

Referencias

Blazic, S. (2014). On Periodic Control Laws for Mobile Robots. IEEE Transactions on Industrial Electronics, 61(7), 3660-3670.

Campion, G.; Bastin, G. y d'Andréa Novel, B. (1993). Structural Properties and Classification of Kinematic and Dynamics Models of Wheeled Mobile Robots. IEEE Transaction on Robotics and Automation, 12(1), 47-61.

Cook, G. (2011). Mobile Robots: Navigation, Control and Remote Sensing. Nueva Jersey: Wiley-IEEE Press.

Jingkui , S.;Wenxin , H. y Liangliang, Y. (2010). A New Sensor-Follow Control Strategy for Tracking Control Mobile Robot. International Conference on Electrical and Control Engineering (ICECE) (pp. 163-167). Wuhan.

Jung-Hoon , H.; Arkin, R. y Dong-Soo, K. (2003). Mobile Robots at Your Fingertip: Bezier Curve On-Line Trajectory Generation for Supervisory Control. International Conference on Intelligent Robots and Systems (pp. 1444-1449).

Kwon, J.W. y Dongkyoung , C. (2012). Hierarchical Formation Control Based on a Vector Field Method for Wheeled Mobile Robots. IEEE Transactions on Robotics, 28(6), 1335-1345.

Rezaee, H. y Abdollahi, F. (2014). A Decentralized Cooperative Control Scheme with Obstacle Avoidance for a Team of Mobile Robots. IEEE Transactions on Industrial Electronics, 61(1), 347-354.

Saidonr, M.; Desa, H. y Rudzuan, M. (2011). A Differential Steering Control with Proportional Controller for an Autonomous Mobile Robot. IEEE 7th International Colloquium on Signal Processing and its Applications (pp. 90-94). Penang.

Spyros, G. (2014). Introduction To Mobile Robot Control. Londres: Elsevier.

Toda, Y. y Kubota, N. (2013). Self-Localization Based on Multiresolution Map for Remote Control of Multiple Mobile Robots. IEEE Transactions on Industrial Informatics, 9(3), 1772-1781.

Vachhani, L.; Mahindrakar, A. y Sridharan, K. (2011). Mobile Robot Navigation Through a Hardware-Efficient Implementation for Control-Law-Based Construction of Generalized Voronoi Diagram. IEEE/ASME Transactions on Mechatronics, 16(6), 1083-1095.

Velrajkumar, P.; Manohar, S. y Raju, A. (2010). Development of Real-Time Tracking and Control Mobile Robot Using Video Capturing Feature for Unmanned Applications. Communication Control and Computing Technologies (ICCCCT) (pp. 90-92). Ramanathapuram.

Yandong, L.; Zongyi, W. y Ling , Z. (2010). Adaptive Neural Network PID Sliding Mode Dynamic Control of Nonholonomic Mobile Robot. IEEE International Conference on Information and Automation (pp. 735-757). Harbin.

Yang , Y.; Fu, M.; Zhu , H.; Xiong , G. y Sun, C. (2010). Control Methods of Mobile Robot Rough-Terrain Trajectory Tracking. 8th IEEE International Conference on Control and Automation (pp. 731-738). Xiamen.