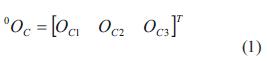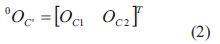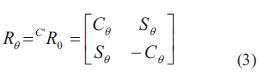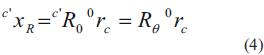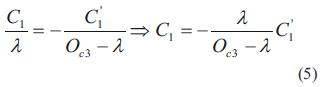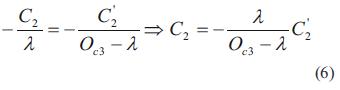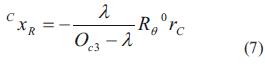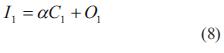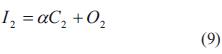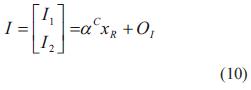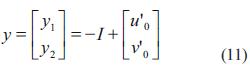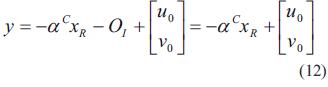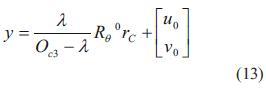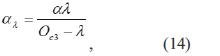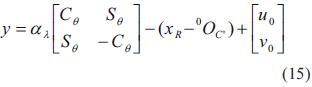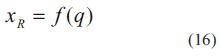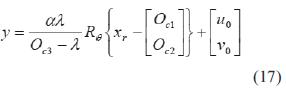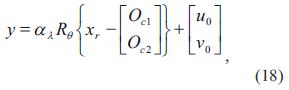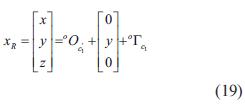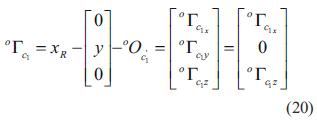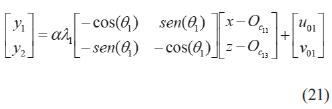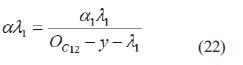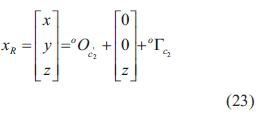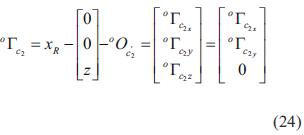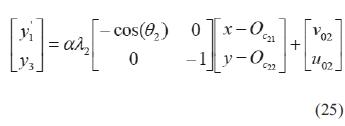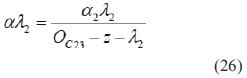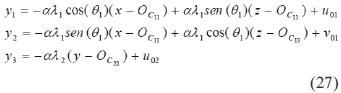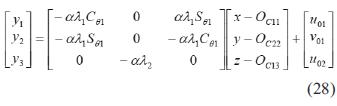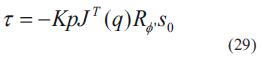Modelado de sistemas de visión en 2D y 3D: un enfoque hacia el control de robots manipuladores

Modelado de sistemas de visión en 2D y 3D: un enfoque hacia el control de robots manipuladores

Vision systems modelling in 2D and 3D: An approach to the control of manipulator robots

Maximiliano Bueno López¹, Marco Arteaga Pérez², Antonio Candea Leite³

¹Ingeniero Electricista, Doctor en Ingeniería. Docente de la Universidad de La Salle. Bogotá, Colombia. Contacto: maxbueno@unisalle.edu.co
²Ingeniero en Computación, Doctor en Ingeniería. Docente de la Universidad Nacional Autónoma de México. México D.F., México. Contacto: marteagp@unam.mx
³Ingeniero Electrónico, Doctor en Ingeniería. Investigador de la Universidad Federal de Rio de Janeiro. Rio de Janeiro, Brasil. Contacto: toni@coep.ufrj.br

Fecha de recepción: 31 de agosto de 2012 Fecha de aceptación: 21 de mayo de 2013

Resumen

El control servovisual de robots manipuladores ha sido un tema en evolución en los últimos años, especialmente en aplicaciones donde el ambiente es no estructurado o el acceso para un operador es difícil. Para diseñar este tipo de controladores se hace importante realizar simulaciones previas para ajustar los parámetros o tener una aproximación del comportamiento. En este trabajo se presentan dos diferentes modelos de sistemas de visión, enfocados a aplicaciones en el control de robots manipuladores. El modelado de las cámaras de video se obtendrá con la ya conocida proyección de perspectiva. Para validar los modelos se presentaran simulaciones de dos controladores servovisuales en 2D y 3D.

Palabras clave: control servovisual, modelado, robótica, visión 2D y 3D.

Abstract

Visual servoing of robot manipulators has been an evolving issue in recent years, especially in applications where the environment is not structured or where access is difficult for operators. To design these controllers, previous simulations are important to adjust parameters or implement a behavioral approach. In this paper we present two different models of vision systems. The models focus on applications in the field of manipulator-robot control. The modeling of video cameras is obtained by using perspective projections. To validate the models, two servo visual controllers in 2D and 3D are simulated.

Key words: visual servoing, modelling, robotic, vision 2D and 3D.

1. Introducción

La visión es, por analogía con la mayoría de los seres vivos, la manera más precisa de conseguir información en cualquier entorno [1]. Desde un principio se ha tratado de aplicar a la robótica, pero exige grandes cantidades de datos a procesar, lo que en algunos casos hace poco útil su uso [2]. A pesar de esto, la evolución que han seguido los procesadores en los últimos años ha permitido introducir la visión en el bucle de control [3].

La realización de tareas por parte de robots manipuladores en entornos estructurados con presencia de objetos cuya posición y orientación son conocidas, es un problema suficientemente estudiado [4]; sin embargo, la realización de tareas en entornos donde la configuración del sistema puede variar, presenta numerosas dificultades aún no resueltas [5], [6].Los entornos no estructurados se caracterizan porque la tarea se define en función de la información sensorial presente en el sistema, que puede ser obtenida a través de diferentes tipos de sensores como posición, velocidad, fuerza, tacto o visión [7]. De todos ellos, son los sensores visuales los que presentan mejor desempeño, pues aparte de aportar lfexibilidad al sistema, suministran información geométrica y dinámica del entorno en el cual se mueve el robot, permitiendo conocer tanto los objetos presentes en la escena como su posición, orientación y velocidad con elevada precisión. La utilización de un sistema de visión en la realización de una tarea por parte de un robot, tiene la denominación genérica de Control Visual (Visual Servoing) [3]. El sistema de visión obtiene información de la escena en forma de características de imagen, que son realimentadas al lazo de control del sistema. Los sistemas de visión se han combinado con algunas técnicas de control bastante reconocidas tales como PID, Control Adaptable, Control Robusto y técnicas de inteligencia artificial [6], [8], [9], lo que demuestra la importancia que esta estrategia ha adquirido. La robótica y la visión requieren actualmente de una aproximación científica formal con experimentación en tiempo real además de un enfoque teórico [8], [10], [11]. En el área de control, las simulaciones son una parte importante para el ajuste de los algoritmos, por lo que es interesante tener un modelo confiable de la cámara que se pueda utilizar en cualquier aplicación de control de robots manipuladores, lo que hace valioso el aporte realizado en este articulo, ya que permite llevar a cabo simulaciones de controladores que involucren cámaras. El sistema empleado en este trabajo está constituido por un brazo robótico de seis grados de libertad (CRS Robotics) y dos cámaras que, dependiendo de la aplicación (2D o 3D), es posible que sea necesario utilizar solo una de estas.

2. Modelo del sistema de Visión en 2d

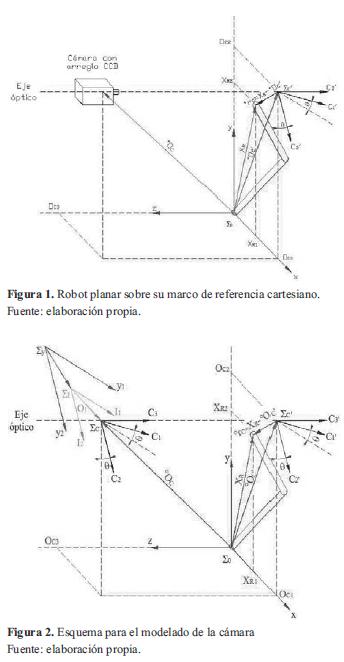
Para este modelo se asume que la cámara esta fija, de tal manera que el eje óptico se encuentra perpendicular al plano de trabajo del robot. Se utiliza una cámara que cuenta con un arreglo CCD y se ubica de la forma mostrada en la figura 1. Para la obtención de la ecuación que relaciona los puntos de la escena observada por la cámara con los correspondientes en la imagen, se considera el sistema que se presenta en la figura 2, que tiene el marco de referencia Σ₀ fijo a la base del robot de dos grados de libertad, moviéndose en el plano x -y . El vector x_R =[x_R1  x_R2   x_R3 ]^T representa las coordenadas de un punto x con respecto al marco de referencia cartesiano Σ₀.

Con referencia al lente de la cámara se tiene el marco de referencia Σ_C= {C₁, C₂, C₃}. El origen del marco de referencia de la cámara está sobre el eje óptico y en el centro de la lente. Los planos (C₁,C₂) y (x, y) definen un plano perpendicular para el eje óptico. Por tanto, el eje C₃ se alinea con el eje óptico. Un punto x con respecto al marco de referencia de la cámara se denota por x_C =[x_C1  x_C2   x_C3 ]^T . Con referencia a la ubicación relativa entre los marcos de referencia Σ₀ y Σ_C se asume que los ejes C₃ y z son paralelos; además, los planos C₁ -C₂ y x -y son también paralelos. El origen del marco de referencia de la cámara Σ_C con respecto al marco de referencia cartesiano Σ₀ se denota por ⁰O_C y está dado por la ecuación (1).

El plano C₁ -C₂ está localizado a una distancia O_C3 del plano x -y , si se traslada el centro de la cámara al mismo plano donde se mueve el robot, desaparecen las coordenadas C₃ y z y se obtiene la ecuación (2).

Se asume que hay una rotación θ del marco coordenado Σ_C con respecto a Σ₀ alrededor del eje z. Por convención, el sentido positivo para el ángulo θ es dado por la regla de lamano derecha, por tanto se obtiene una matriz de rotación

Por simplicidad se utiliza la notación C_θ= Coseno θ y S_θ= Seno θ.

La matriz R_θ será constante, ya que el usuario situará el marco coordenado de la cámara rotado por un ángulo de valor θ con respecto al marco coordenado del robot, y una vez situados en una posición determinada ya no se cambiara la posición. La posición del efector final con respecto al marco de referencia de la cámara sin desplazar Σ_C' está dada por la ecuación (4).

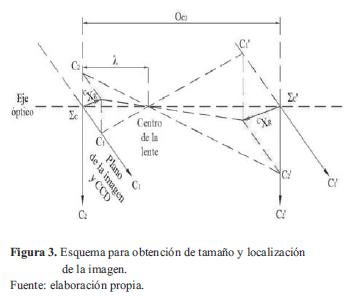
La figura 3 se utiliza para determinar el tamaño y la localización de la imagen y permite deducir las ecuaciones (5) y (6).

A partir de las ecuaciones (1) - (6) se obtiene la posición del efector final con respecto al marco de referencia de la cámara Σ_C que está dada por la ecuación (7).

Siendo λ la distancia focal de la cámara.

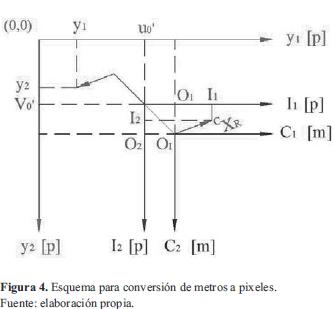
La figura 4, ayuda a visualizar cómo se realiza la conversión de metros a pixeles, para lo cual se requiere obtener el factor de escalamiento α, calculado a partir del tamaño de la superficie del arreglo CCD.

El plano de imagen (imagen frontal) es el arreglo discreto CCD de elementos foto sensoriales. Esto es asociado con el marco de referencia de la imagen 2D, Σ_I={I₁ I₂} cuyo origen está en el centro geométrico del arreglo y cuyos ejes son paralelos a las direcciones de los elementos del sensor CCD. La posición de la intersección del eje óptico con respecto del marco de referencia Σ_I , es denotada por O_I . El vector O_I puede no ser cero debido a posibles desajustes internos entre la lente y el arreglo CCD, se denota a α como el factor de conversión de metros a pixeles. Debido a que la imagen se proyecta invertida, es necesario multiplicar por un signo negativo, además considerando que el origen del sistema de coordenadas de imagen no se ubica al centro, sino en la esquina superior izquierda de la pantalla (figura 4), resultan las ecuaciones (8) - (11):

La imagen de la escena en el CCD es digitalizada y transferida a la memoria de la computadora y se mostrará en la pantalla de esta. El marco de referencia de la pantalla de la computadora está dado por Σ_y ={y₁, y₂}. El origen de Σ_y se sitúa en la esquina izquierda superior de la pantalla de la computadora. Los ejes y₁ y y₂ son paralelos a la pantalla.

El vector [u₀ v₀ ]^T es el corrimiento en la imagen del centro óptico de la cámara. Entonces la posición del efector final en el marco de referencia de imagen Σ_y (coordenadas de imagen) está dado en la ecuación (12):

Al sustituir ^C x_R en (12), se obtiene la ecuación (13),

Al definir ,

y sustituir todos los valores de la ecuación (13) se tiene

Que es la función que realiza el mapeo entre el espacio cartesiano y el de la imagen.

Para un controlador servovisual de seguimiento se debe tener en cuenta la posición del efector final del robot con respecto al marco de referencia cartesiano Σ₀.

X_R se obtiene como función de las coordenadas articulares (q) al aplicar la cinemática directa de un robot manipulador; además, también se requiere de la posición del efector final en el marco de referencia de imagen Σ_y dado, en las ecuaciones (17) y (18):

donde y es la función que realiza el mapeo entre el espacio cartesiano y el de la imagen.

3. Modelo Del Sistema De Visión En 3D

En esta sección se considera un punto tridimensional con coordenadas (x, y, z) y se proyecta sobre una pantalla, o bien, un plano de imagen. Dicha proyección se compone solo de dos coordenadas, llamadas ( y₁, y₂ ) . Si de manera inversa se quisiera partir de estas coordenadas de pantalla para obtener las coordenadas tridimensionales del punto en cuestión, no sería posible, ya que no se puede aplicar el mapeo de dos coordenadas a tres, puesto que se ha perdido la información de profundidad. Para controlar movimientos en 3D es necesario resolver el problema de la profundidad. Varias son las soluciones que se han empleado con éxito, una de las cuales consiste en mover la cámara de video y tomar imágenes desde distintos puntos de visión para realizar posteriormente un cómputo que entregue la información requerida.

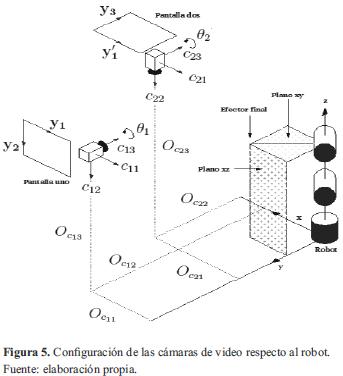
Es posible estimar la profundidad sin mover la cámara siempre y cuando se tenga un amplio conocimiento a priori sobre la geometría del sistema, que ayude a realizar una serie de cálculos. Sin embargo, una manera más directa de atacar el problema es utilizar una segunda cámara de video. En este trabajo se propone el uso de dos cámaras de video, una colocada al frente del robot denominada cámara 1 y otra por arriba de él denominada cámara 2, tal como se aprecia en la figura 5.

Inicialmente se supone que las cámaras pueden tener cualquier posición, además de una rotación, para la cámara 1, respecto a su eje óptico C_B, y para la cámara 2, respecto a su eje C_B. Las restricciones referentes a la orientación de las cámaras son:

• El plano de imagen de la cámara 1 debe ser paralelo al plano x del marco de referencia.
• El eje de la cámara 1 debe ser paralelo al eje C_B de la cámara 2, esto es, que los ejes ópticos de ambas cámaras sean perpendiculares.
• Los ejes de pantalla y₁, y₂ y y₃ deben formar un sistema dextrógiro.

De esta manera, con la cámara 1 se obtienen las coordenadas (y₁, y₂ ) correspondientes al plano x, mientras que con la cámara 2, la coordenada y₃ que es paralela al eje y. Nótese que la información de y₁^' no es relevante. Es decir, basta con despreciar y₁^' para aplicar el control de posición en 3D mediante las coordenadas ( y₁, y₂, y₃). El objetivo de modelar las cámaras de video es conocer la expresión matemática que asigna las coordenadas de pantalla ( y₁, y₂ ) a un punto tridimensional con coordenadas (x, y, z) expresadas respecto a un sistema de referencia. Aunque en la realidad las coordenadas de pantalla se obtienen mediante el empleo de técnicas para el procesamiento de imágenes y herramientas computacionales, el modelo es necesario para realizar el diseño y el análisis del sistema de control, así como la simulación por computadora.

La geometría de las cámaras, es decir, la manera en que se forma una imagen, es el punto inicial para obtener la aproximación matemática mencionada. A la distancia que existe entre la lente de la cámara y el foco o punto focal se le conoce como longitud focal, mientras que a la intersección del eje óptico, que pasa por el centro de la lente, con el plano de imagen, se le conoce como centro óptico. El modelo de proyección perspectiva constituye un mapeo no lineal a partir del cual se generan algunos modelos lineales que pueden resultar útiles dependiendo de la naturaleza de la aplicación que se tenga en mente. A continuación se muestran los pasos para obtener el modelo de ambas cámaras; para ello, se toma como punto de partida la figura 5, en donde se ilustran los vectores, marcos de referencia y relaciones necesarios para la obtención del modelo.

4. Metodología

4.1 Modelo cámara 1

De la figura 5 se puede observar que el vector de posición del efector final del robot viene dado en la ecuación (19):

despejando da la ecuación (20),

que representa la posición del efector final del robot con respecto a un sistema de referencia auxiliar Σ_c1' de la cámara 1, el cual es una proyección sobre el plano x en el que se encuentra el punto de interés. Considerando trabajar únicamente en el plano x y con un proceso similar al realizado para el caso de 2D se obtiene la ecuación (21) para la cámara 1.

donde

4.2 Modelo cámara 2

De la figura 5 se obtiene la ecuación (23)

despejando da la ecuación (24),

La expresión obtenida para la cámara 2 es la ecuación (25),

donde

4.3 Modelo usando ambas cámaras

Para obtener un modelo que considere la información de ambas cámaras, basta combinar las ecuaciones (21) y (25). Como ya se mencionó, se necesita la tercia de coordenadas ( y₁, y₂, y₃)

Finalmente se escribe de manera matricial el modelo que relaciona las coordenadas (x, y, z) que representan la posición del efector final del robot, con las coordenadas de imagen (y₁, y₂, y₃)

5. Resultados

Para validar los modelos se han simulado inicialmente dos controladores, los cuales son explicados ampliamente en [5] y [12]. El primero de ellos es básicamente un controlador PID en 2D que posee un observador de velocidad y tiene un término deslizante que suaviza el seguimiento de la trayectoria. El segundo es un controlador difuso del tipo Mamdani en 3D que utiliza información solo de la cámara para generar la ley de control. La ecuación (29) muestra la ley de control implementada para el controlador en 2D.

donde

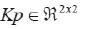
J^T (q) es la matriz jacobiana transpuesta.

El término y^•_o depende del valor estimado de velocidad y del error de observación.

El término y^•_r depende de la velocidad deseada y de la diferencia entre la posición deseada y la posición estimada. Todos los parámetros se encuentran en coordenadas de imagen.

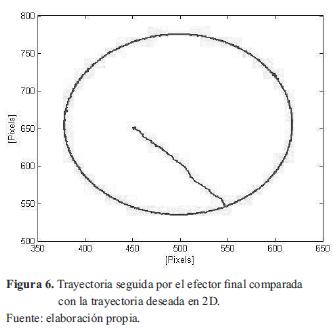
Este resultado fue obtenido con el robot LAW3 de SCHUNK ubicado en la Universidad Federal de Rio de Janeiro (figura 7), gracias al cual el seguimiento de trayectoria es satisfactorio y permite obtener errores de 0 pixeles.

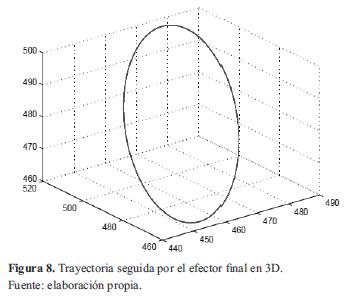
La ley de control implementada para validar el modelo en 3D está basada en la estructura básica del sistema Mamdani. Se establecieron como entradas los errores en la trayectoria en cada una de las coordenadas de imagen y las salidas son los valores de voltaje que se deben aplicar en cada una de las articulaciones del robot. En la figura 8 se muestra la forma de onda obtenida con el robot CRS-A465 de Robotics ubicado en la Universidad Nacional Autónoma de México (figura 9).

6. Conclusiones

En este trabajo se ha presentado el modelo de un sistema de visión en 2D y 3D con el fin de ser utilizado en el control servovisual de robots manipuladores. Los modelos han sido probados mediante simulaciones y plataformas reales con dos controladores previamente diseñados por los autores. Estos modelos pueden ser utilizados en diferentes aplicaciones y permiten realizar ajustes desde antes de implementar los controladores.

De acuerdo con los resultados de simulación, se confirmó lo expuesto en la teoría. Las tres coordenadas de imagen utilizadas convergen a su valor deseado en un tiempo bueno, considerando que se trata de un controlador servovisual en el que además se incluyen efectos de fricción.

7. Financiamiento

Este trabajo está basado en una investigación soportada por Conacyt con referencia 58112 y por la DGAPA UNAM (Dirección General del Personal Académico de la Universidad Nacional Autónoma de México) con referencia IN109611.

Referencias

[1] R. Kelly and F. Reyes, "On vision systems identification with application to fixed camera robotic systems", International Journal of Imaging Systems and Technology, vol. 11, no. 3, pp. 170-180, 2000.

[2] M. Arteaga-Pérez, A. Castillo and V. Parra-Vega, "Cartesian control of robots without dynamic model and observer design", Automatica, vol. 42, no. 3, pp. 473-480, 2006.

[3] F. Chaumette and S. Hutchinson, "Visual servo control, Part I: Basic approaches", IEEE Robotics and Automation Magazine, vol. 13, no. 4, pp. 82-90, 2006.

[4] M. Arteaga- Pérez and R. Kelly, "Robot control without velocity measurements: New theory and experimental results", IEEE Transactions on Robotics and Automation, vol. 20, no. 2, pp. 297-308, 2004.

[5] M. Arteaga-Perez, M. Bueno-Lopez and A. Espinosa-Romero, "A simple approach for 2D visual servoing", in Control Applications, (CCA) & Intelligent Control, (ISIC), Saint Petersburg, Russia, 2009, pp. 1557-1562.

[6] J. Hwang and E. Kim, "Robust tracking control of an electrically driven robot: Adaptive fuzzy logic approach", IEEE Transactions On Fuzzy Systems, vol. 14, no. 2, pp. 232-247, 2006.

[7] W. Tang and G. Chen, "A modified fuzzy PI controller for a flexible joint robot arm with uncertainties", Fuzzy sets and systems, vol. 118, no. 1, pp. 109-111, 2001.

[8] S. Alavandar and M. Nigam, "Adaptive neuro-fuzzy inference system based control of six dof robot manipulator", Engineering Science and Technology Review, vol. 1,106-111, 2008.

[9] T.M. Guerra, A. Kruszewski, and M. Bernal, "Control law proposition for the stabilization of discrete Takagi Sugeno models", IEEE Transactions on Fuzzy Systems, vol. 17, no. 3, pp. 724-731, 2009.

[10] K. Passino K. And S. Yurkovich, "Fuzzy Control", 1^sted., pp. 23-110, Sand Hill Road, Menlo Park, California: Addison Wesley Longman, 1993.

[11] M.A. Moreno, "Visión artificial estero con aplicación al control de un brazo de robot", Tesis Doctoral, Instituto Politécnico Nacional, Facultad de Ingeniería, México, D.F. México, 2003.

[12] M. Bueno and M. Arteaga, "Fuzzy Logic Control of a robot manipulator in 3D based on visual servoing", in 18^th IFAC World Congress, Mila.