DOI:
https://doi.org/10.14483/22487638.19676Publicado:
12-10-2023Número:
Vol. 27 Núm. 77 (2023): Julio - SeptiembreSección:
InvestigaciónIntegración de la incertidumbre natural temporal y espacial asociada al coeficiente de rugosidad Manning en modelos bidimensionales de inundaciones rápidas
Time and spatial natural uncertainty integration associated with the Manning’s roughness coefficient in two-dimensional flash flood models
Palabras clave:
propagación de la incertidumbre, coeficiente de rugosidad, inundación rápida, amenaza por inundación (es).Palabras clave:
uncertainty propagation, roughness coefficient, flash flood, flood hazard (en).Descargas
Referencias
Altarejos-García, L., Martínez-Chenoll, M. L., Escuder-Bueno, I. y Serrano-Lombillo, A. (2012). Assessing the impact of uncertainty on flood risk estimates with reliability analysis using 1-D and 2-D hydraulic models. Hydrology and Earth System Sciences, 16(7), 1895-1914. https://doi.org/10.5194/hess-16-1895-2012. DOI: https://doi.org/10.5194/hess-16-1895-2012
Arévalo-Algarra, H. M., Perico-Granados, N. R., Reyes-Rodríguez, C. A., Vera, M. C., Monroy, J. y Perico-Martínez, C. A. (2021). Sitios de inundaciones causadas por los ríos La Vega y Jordán, Tunja (Boyacá). Tecnura, 25(67), 86–101. https://doi.org/10.14483/22487638.15248. DOI: https://doi.org/10.14483/22487638.15248
Arévalo-Mendoza, G., Ramos-Cañón, A. M. y Prada-Sarmiento, L. F. (2014). Análisis de confiabilidad en un modelo de descarga de silos de almacenamiento mediante el método de elementos discretos DEM. Obras y Proyectos, 15, 19-28. DOI: https://doi.org/10.4067/S0718-28132014000100002
Baecher, G. y Christian, J. (2003). Reliability analysis and error propagation. En Reliability and Statistics in Geotechnical Engineering (pp. 301-319). Wiley.
Brunner, G. (2016). HEC-RAS, River analysis system. Hydraulic reference manual. Version 5.0. U. S. Army Corps of Engineers.
Castro-Maldonado, J. J., Gómez-Camacho, L. K. y Camargo-Casallas, E. (2023). La investigación aplicada y el desarrollo experimental en el fortalecimiento de las competencias de la sociedad del siglo XXI. Tecnura, 27(75), 140-174. https://doi.org/10.14483/22487638.19171. DOI: https://doi.org/10.14483/22487638.19171
Chang, C., Yang, J. y Tung, Y. (1993). Sensitivity and uncertainty analysis of a sediment transport model: A global approach. Stochastic Hydrology and Hydraulics, 7(4), 299- 314. https://doi.org/10.1007/BF01581617 DOI: https://doi.org/10.1007/BF01581617
Cortés-Zambrano, M., Lara-Pérez, M. Y. y Acosta-Sabogal, I. D. (2022). Urban drainage water quality modeling on the SWMM software, northeastern sector, Santa Inés District, Tunja. Tecnura, 26(72), 167-184. https://doi.org/10.14483/22487638.17575 DOI: https://doi.org/10.14483/22487638.17575
Da Costa, E., Lara, M., de Andrade, E., Guimaraes, J. y Maia, A. (2018). Manning’s roughness coefficient for the Doce River. Revista Brasileira de Recursos Hídricos, 23(52), 1-12.
Dingman, S. L. y Sharma, K. P. (1997). Statistical development and validation of discharge equations for natural channels. Journal of Hydrology, 199, 13-35. https://doi.org/10.1016/S0022-1694(96)03313-6. DOI: https://doi.org/10.1016/S0022-1694(96)03313-6
Horritt, M. S. y Bates, P. D. (2001). Effects of spatial resolution on a raster based model of flood flow. Journal of Hydrology, 253(1-4), 239–249. https://doi.org/10.1016/S0022-1694(01)00490-5. DOI: https://doi.org/10.1016/S0022-1694(01)00490-5
Jakob, M., Stein, D. y Ulmi, M. (2012). Vulnerability of buildings to debris flow impact. Natural Hazards, 60(2), 241-261. https://doi.org/10.1007/s11069-011-0007-2. DOI: https://doi.org/10.1007/s11069-011-0007-2
Kim, J. S., Lee, C. J., Kim, W. y Kim, Y. J. (2010). Roughness coefficient and its uncertainty in gravel-bed river. Water Science and Engineering, 3(2), 217-232. https://doi.org/10.3882/j. issn.1674-2370.2010.02.010.
Lumbroso, D. y Gaume, E. (2012). Reducing the uncertainty in indirect estimates of extreme flash flood discharges. Journal of Hydrology, 414-415, 16-30. https://doi.org/10.1016/j.jhydrol.2011.08.048. DOI: https://doi.org/10.1016/j.jhydrol.2011.08.048
Maskey, S. y Guinot, V. (2003). Improved first-order second moment method for uncertainty estimation in flood forecasting. Hydrological Sciences Journal, 48(2), 183-196. https://doi.org/10.1623/hysj.48.2.183.44692. DOI: https://doi.org/10.1623/hysj.48.2.183.44692
Pappenberger, F., Beven, K., Horritt, M. y Blazkova, S. (2005). Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. Journal of Hydrology, 302(1-4), 46-69. https://doi.org/10.1016/j.jhydrol.2004.06.036. DOI: https://doi.org/10.1016/j.jhydrol.2004.06.036
Prada-Sarmiento, L. F., Cabrera, M. A., Camacho, R., Estrada, N. y Ramos-Cañón, A. M. (2019). The Mocoa Event on March 31 (2017): Analysis of a series of mass movements in a tropical environment of the Andean-Amazonian Piedmont. Landslides, 16(12), 2459-2468. https://doi.org/10.1007/s10346-019-01263-y. DOI: https://doi.org/10.1007/s10346-019-01263-y
Ramos, A., Ruiz, G., Munévar, M., Reyes, A., Prada, L., Rangel, M., Machuca, S., Ramírez, K., Cabrera, M., Quintero, C., Capachero, C., López, C., Escobar, J., Navarro, S., Giraldo, J., Pérez, M., Rodríguez, C., León, D., Escobar, N. ... Castro, C. (2021). Guía metodológica para zonificación de amenaza por avenidas torrenciales. Servicio Geológico Colombiano. https://libros.sgc.gov.co/index.php/editorial/catalog/book/75
Romanowicz, R. y Beven, K. (2003). Estimation of flood inundation probabilities as conditioned on event inundation maps. Water Resources Research, 39(3), 1-12. https://doi.org/10.1029/2001WR001056. DOI: https://doi.org/10.1029/2001WR001056
Teng, J., Jakeman, A. J., Vaze, J., Croke, B. F. W., Dutta, D. y Kim, S. (2017). Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environmental Modelling and Software, 90, 201-216. https://doi.org/10.1016/j.envsoft.2017.01.006. DOI: https://doi.org/10.1016/j.envsoft.2017.01.006
Trieste, D. y Jarrett, R. (1987). Roughness coefficients of large floods. En L. James y M. English (eds.), Proceedings of a Conference sponsored by the Irrigation and Drainage Division of the American Society of Civil Engineers and the Oregon Section (pp. 32-40). ASCE.
Unidad Nacional para la Gestión del Riesgo de Desastres (UNGRD) y Pontificia Universidad Javeriana (PUJ). (2018). Consultoría de los estudios de diseño del sistema de alerta temprana para avenidas torrenciales y crecientes súbitas generadas por precipitaciones de la microcuenca de los ríos Multao, Sangoyaco, quebradas Taruca y Taruquita del municipio de Mocoa - Putumayo. http://repositorio.gestiondelriesgo.gov.co/handle/20.500.11762/27207?show=full&locale-attribute=es
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 16 de julio de 2022; Aceptado: 29 de septiembre de 2022
Resumen
Contexto:
La variabilidad natural (incertidumbre) espacial y la temporal de los insumos que intervienen en la modelación hidrodinámica, para la evaluación de la amenaza y la delimitación de las zonas potencialmente inundables, se propagan en las variables de salida de los modelos. En la práctica, suele considerarse la variabilidad natural temporal en términos de periodo de retorno, pero poco se ha analizado la propagación de la incertidumbre espacial del coeficiente de rugosidad.
Metodología:
En este trabajo se presenta el análisis de la propagación de la incertidumbre a través del método primer orden segundo momento del coeficiente de rugosidad de Manning, en las variables de salida de profundidad, velocidad e intensidad de flujo del modelo numérico de aguas someras, implementado en HEC RAS 2D. Se analizó una inundación súbita simulada en el municipio de Mocoa (Putumayo) y la correspondiente probabilidad de alcanzar un nivel de daño para diferentes periodos de retorno, a propósito de los eventos ocurridos en marzo de 2017.
Resultados:
Se obtiene un procedimiento aplicable a la evaluación de la amenaza de inundación, en el que se integra la variabilidad natural temporal asociada a las hidrógrafas con diferentes periodos de retorno, y la variabilidad natural espacial relacionada con el coeficiente de rugosidad de Manning.
Conclusiones:
La propagación de la incertidumbre establece una relación directa entre el aumento del caudal (periodos de retorno) y el aumento de la incertidumbre en la evaluación del indicador de amenaza por inundación.
Palabras clave:
propagación de la incertidumbre, coeficiente de rugosidad, inundación rápida, amenaza por inundación.Abstract
Context:
The natural spatial and temporal variability (uncertainty) of the inputs involved in hydrodynamic modeling for hazard assessment and delineation of potentially flood-prone areas is propagated in the output variables of the models. In normal practice, only natural temporal variability in terms of return period is usually considered, but the propagation of spatial uncertainty is unknown.
Methodoly:
This paper presents the analysis of uncertainty propagation using the first order second moment method of Manning’s roughness coefficient in the depth, velocity and flow intensity output variables of the numerical shallow water model implemented in HEC RAS 2D. A simulated flash flood in the municipality of Mocoa (Putumayo) and the corresponding probability of reaching a damage level for different return periods were analyzed, regarding the events occurred in March 2017.
Results:
A procedure applicable to flood hazard assessment is obtained where the temporal natural variability associated to hydrographs with different return periods and the spatial natural variability associated to the Manning’s roughness coefficient are integrated.
Conclusions:
The propagation of uncertainty was able to establish a direct relationship between the increase of flow (return periods) and the increase of uncertainty in the evaluation of the flood hazard indicator.
Keywords:
Uncertainty propagation, roughness coefficient, flash flood, flood hazard.INTRODUCCIÓN
La delimitación de las zonas susceptibles a inundaciones súbitas forma parte del conocimiento de la amenaza que permite tomar decisiones en cuanto a la gestión del riesgo (ArévaloAlgarra et al., 2021; Castro-Maldonado et al., 2023). Estas zonas se pueden delimitar a través de simulaciones hidrodinámicas en las que intervienen insumos hidrológicos y topográficos. Cada uno de estos insumos tiene asociada una incertidumbre natural que se propaga a través de los modelos y repercute en los resultados de simulaciones (Teng et al., 2017). La cuantificación y análisis de la propagación de la incertidumbre cobra importancia en los mapas de amenaza por inundaciones, en los que se basa el ordenamiento territorial. Por lo general, estos mapas están en función de las variables de salida de la simulación (alturas de inundación, velocidades del flujo); por tanto, su elaboración debería tener en cuenta, además de la variabilidad natural temporal (en términos de periodos de retorno), la influencia de la variabilidad inherente de parámetros físicos incluidos en los modelos (p. ej.: el coeficiente de rugosidad en las ecuaciones de aguas someras).
Con el propósito de cuantificar la propagación de la incertidumbre natural de una variable dentro de un modelo numérico de aguas someras, se propone implementar una evaluación de confiabilidad a través del método primer orden segundo momento (first order second moment [FOSM]) evaluado a través de diferencias finitas para funciones matemáticas implícitas (Baecher y Christian, 2003). La variable que se analiza es el coeficiente de rugosidad de Manning, que se usa para calibrar las manchas de inundación. En la evaluación de la amenaza es necesario cuantificar la incertidumbre a través de la función de densidad de probabilidad y de los momentos estadísticos para la variable aleatoria de entrada analizada. Para el caso de estudio, la disponibilidad de información relacionada con la incertidumbre es limitada porque, usualmente, no se considera su variabilidad natural (Horritt y Bates, 2001; Romanowicz y Beven, 2003); por consiguiente, se hace un análisis para asignar un valor representativo de la zona con base en estudios previos que permiten estimar órdenes de magnitud de la incertidumbre natural del coeficiente de rugosidad de Manning (Kim et al., 2010).
La propagación de incertidumbre y evaluación de amenaza se ejecuta sobre las variables de salida de profundidad, velocidad y de intensidad de flujo (Jakob et al., 2012; Ramos et al., 2021) para escenarios hipotéticos de inundación súbita en el municipio de Mocoa (Putumayo), a propósito de los eventos ocurridos en marzo de 2017 (Prada-Sarmiento et al., 2019). Las simulaciones se efectúan en HEC RAS 2D para la aproximación de onda difusiva de las ecuaciones de aguas someras bidimensionales (Brunner, 2016). Los resultados permitieron concluir un rango de incertidumbre en términos del coeficiente de variación (COV) para las variables de salida del 0 % al 25 % con mayor incertidumbre para el índice de intensidad de flujo y menor para la velocidad. Se pudo establecer que, a mayor incertidumbre natural del coeficiente de rugosidad de Manning, aumenta la incertidumbre de manera proporcional en las variables de análisis para amenaza por inundación (altura, velocidad e índice de intensidad de flujo).
Método FOSM
La cuantificación de la incertidumbre se puede expresar a través del coeficiente de variación (ecuación (1)), que relaciona la desviación estándar y el valor esperado de la función de desempeño. En este estudio, la función de desempeño corresponde a la profundidad, velocidad e intensidad del flujo (variables de las ecuaciones de aguas someras), y la variable de entrada para la que se hace el análisis de propagación de incertidumbre es el coeficiente de rugosidad de Manning. Existen diferentes métodos para calcular los momentos estadísticos de la función de desempeño; por ejemplo: estimación puntual, primer orden segundo momento, segundo orden segundo momento, método de Hasofer-Lind, simulaciones de Montercarlo (Baecher y Christian, 2003).
El método empleado en este trabajo es primer orden segundo momento (first order second moment [FOSM]). Para la estimación del primer y segundo momento estadístico (el valor esperado E[g] y la varianza Var[g]) se usan los dos primeros términos de la expansión de la serie de Taylor de una función de desempeño g con n variables aleatorias X n (ecuación (3)). En FOSM se supone una diferencia pequeña entre la variable X i y el valor promedio de la misma µX i , por lo que el cuadrado o las potencias de orden mayor son más pequeñas y pueden ser ignoradas (Arévalo-Mendoza et al., 2014; Baecher y Christian, 2003).
Para encontrar los momentos estadísticos de la función de desempeño, es necesario conocer información de la función de densidad de probabilidad de las variables analizadas. FOSM permite calcular la esperanza matemática y la varianza de la función de desempeño, sin conocer la función de densidad de probabilidad de las variables de entrada. Estos momentos estadísticos se calculan alrededor del valor medio y la desviación estándar de las variables analizadas. Las ecuaciones (3) y (4) se obtienen de la definición general de E [g] y Var[g], suponiendo que las variables de entrada son independientes entre sí (no hay correlación) y aplicando la expansión de la serie de Taylor para la función de desempeño (Baecher y Christian, 2003; Maskey y Guinot, 2003).

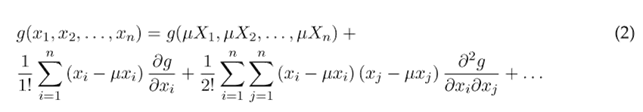
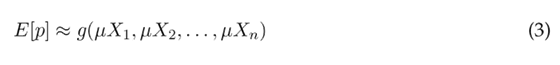
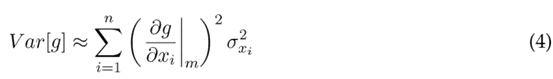
En la ecuación (4), las derivadas parciales de la función de desempeño son evaluadas en los valores medios de las correspondientes variables de entrada (m = µX
1
, µX
2
, . . . , µX
n
) y σ
2 es 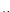 la varianza de cada una de estas variables. Si hay n variables de entrada, es necesario evaluar n derivadas parciales de la función de desempeño.
la varianza de cada una de estas variables. Si hay n variables de entrada, es necesario evaluar n derivadas parciales de la función de desempeño.
Modelo numérico de inundación
La función de desempeño corresponde a las variables de salida del modelo numérico de aguas someras implementado en HEC-RAS 2D, solucionadas con el método de volúmenes finitos (Brunner, 2016). Estas ecuaciones son una simplificación de las ecuaciones de Navier-Stokes que describen el movimiento de un fluido en el espacio (x, y, z). Las ecuaciones (5) y (6) corresponden a la ecuación de conservación de masa y las ecuaciones de conservación de momentum, respectivamente, que conforman las ecuaciones de aguas someras bidimensionales.

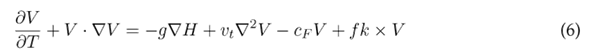
Donde t es el tiempo; H es la elevación de la superficie de agua; ∇ es el vector de derivadas parciales (∂/∂x, ∂/∂y); h es la profundidad del flujo; V = (u, v) es la velocidad vectorial; a la vez, u es el componente horizontal y v el componente vertical; q son fuentes o sumideros de masa; g corresponde a la aceleración de la gravedad; v t es el coeficiente horizontal de la viscosidad turbulenta; c f es el coeficiente de fricción de fondo; f es el parámetro de Coriolis, y k es un vector unitario en la dirección vertical.
HEC-RAS 2D implementa la aproximación de Gauckler-Manning-Strickler (Cortés-Zambrano et al., 2022) para calcular el coeficiente de fricción de fondo c f (ecuación (7)). Al reemplazarlo en la ecuación de momentum (6), y a partir de las consideraciones para onda difusiva se obtiene una expresión en función del coeficiente empírico de rugosidad de Manning (n) y del radio hidráulico (R) (ecuación (8)).


El índice de intensidad de flujo (I DF ) no es una variable del modelo numérico de aguas someras, sin embargo, su cálculo depende de la profundidad y la velocidad producto de las simulaciones hidrodinámicas. El I DF y la magnitud de la velocidad al cuadrado (ecuación (9)); los valores para I DF se toman como estimaciones de la severidad del flujo (véaseAltarejos-García et al., 2012).

Recientemente, Ramos et al. (2021) plantearon el I DF para la evaluación de amenaza por avenidas torrenciales en Colombia así: si el I DF ≥ 50, la probabilidad de colapso es alta y corresponde a amenaza alta. Si 1 ≤ I DF < 50, la probabilidad de colapso es baja pero la probabilidad de algún daño estructural es considerable, por lo que se asigna una categoría media de amenaza. Por último, si 0 ≤ I DF < 1, la probabilidad de daño estructural es baja; por tanto, corresponde a amenaza baja.
Incertidumbre del coeficiente de rugosidad de Manning
Para determinar la variabilidad natural del coeficiente de rugosidad de Manning se debe contar con información espacial y temporal detallada de la zona de estudio (Lumbroso y Gaume, 2012; Pappenberger et al., 2005; Trieste y Jarrett, 1987). En las simulaciones hidrodinámicas para inundaciones es común que el valor de este coeficiente sea usado para calibrar las manchas de inundación y que el valor supuesto corresponda a un valor representativo de toda la zona de estudio. En la tabla 1 se presenta el valor medio y el coeficiente de variación (COV) para los coeficientes de rugosidad de Manning reportados por Chang et al. (1993); Da Costa et al. (2018); Dingman y Sharma (1997), y Kim et al. (2010).
Los valores presentados en la tabla 1 reportados por Dingman y Sharma (1997) fueron calculados a partir de una muestra total de 621 datos obtenidos de múltiples estaciones en Nueva Zelanda y Estados Unidos. Por consiguiente, los COV de Dingman y Sharma (1997) corresponden a la variación de la muestra total (sin consideración de su ubicación espacial), lo que justifica la diferencia en el orden de magnitud con los otros COV resumidos en la tabla 1. Para los otros autores, el COV de Manning varía entre 1 % y el 10 % aproximadamente.
1Las unidades del coeficiente de rugosidad están dadas por la constante de conversión; para SI k
n
= 1 s/m
1/3
Tabla 1: Valores reportados en la literatura del valor medio y COV para el Manning

METODOLOGÍA
Caso de estudio
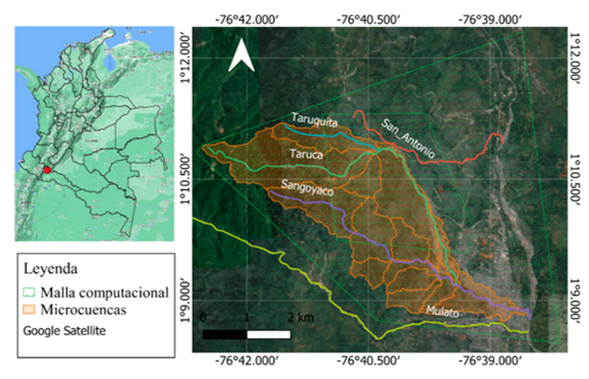
Prada-Sarmiento et al. (2019) reportaron que los principales flujos de detritos, flujos de lodos y flujos hiperconcentrados del evento ocurrido el 31 marzo de 2017 se transportaron por el río Sangoyaco y por las quebradas Taruca y Taruquita, afectando la zona nororiental del casco urbano de Mocoa (Putumayo). Luego de estas observaciones y de la delimitación hidrológica para estos cauces, se identificaron catorce subcuencas (microcuencas) que formaron parte de la iniciación y el transporte del flujo. La delimitación del dominio computacional para la simulación hidrodinámica incluyó la zona de depósito, la quebrada San Antonio y parte del río Mocoa (desembocadura de los cauces ya mencionados) (figura 1).
Figura 1: Localización de Mocoa (Colombia) y generalidades de la zona de estudio: microcuencas, dominio computacional y cauces de interés
Simulación hidrodinámica
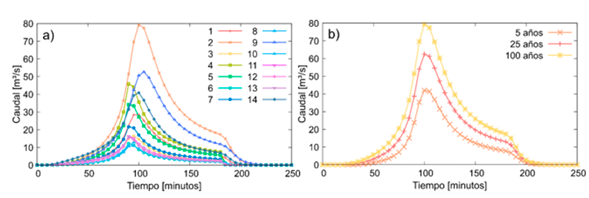
Para la simulación en HEC-RAS 2D se usó un modelo digital de elevación DEM. Se generó una malla de 5 m de tamaño de celda para el dominio computacional de la figura 1. En cada punto de cierre de las microcuencas se cargó una hidrógrafa de caudal líquido como condición de borde interna dentro del dominio computacional (fuente de masa). Las hidrógrafas de caudal fueron tomadas del cálculo realizado por Ramos et al. (2021). En la figura 2A se muestran las catorce hidrógrafas que se cargaron para un periodo de retorno de cien años. En la figura 2b se ilustra la hidrógrafa con el caudal pico para cada periodo de retorno. Se evidencia la diferencia entre los tres periodos de retorno usados; para el de cien años el caudal de entrada en la microcuenca 2 (79,39 m3/s) es aproximadamente el doble que el del periodo de retorno de 5 años (42,05 m3/s).
Figura 2: Hidrógrafas de entrada del modelo fluidodinámico para una duración de tormenta de tres horas a) Hidrógrafas para las catorce microcuencas de la zona de estudio para un Tr = 100 años. b) Comparación de las hidrógrafas de la microcuenca 2 para los tres periodos de retorno simulados (5, 25 y 100 años).
Cálculo de la propagación de la incertidumbre
El cálculo de los COV para cada variable de salida de las simulaciones hidrodinámicas requiere del primer y segundo momento estadístico. En el segundo se debe evaluar las derivadas parciales de la función de desempeño para cada variable de entrada (ecuación (4)). Cuando la función de desempeño no tiene forma matemática explícita, es necesario implementar un método numérico para evaluar las derivadas parciales (Arévalo-Mendoza et al., 2014). En este estudio se implementó el método de diferencias finitas centrales para calcular la derivada parcial de la profundidad, la velocidad y la intensidad del flujo respecto al coeficiente de rugosidad de Manning. Teniendo en cuenta que las ecuaciones de aguas someras no tienen una forma matemática explícita, la derivada parcial de la ecuación de la varianza (ecuación (4)) en función del coeficiente de Manning se calcula como se muestra en la ecuación (10); donde g(µn ± ∆ n ) es cualquiera de las variables de salida evaluadas en µn + ∆ n . La magnitud de ∆ n deber ser lo suficientemente pequeña para encontrar la variación en dicho intervalo. Para este estudio se determinó ∆ n = σ n (desviación estándar del coeficiente de rugosidad).
Los valores que se suponen en este estudio para µn y σ n se relacionan con los valores medios y los COV presentados en la tabla 1. Se propone un valor medio del coeficiente de Manning µn representativo (µn = 0.12) para toda la zona de estudio teniendo en cuenta las similitudes del lecho del río analizado por Kim et al. (2010) y el lecho del río Sangoyaco y las quebradas Taruca y Taruquita. Para considerar el impacto de la variabilidad natural del coeficiente de Manning, se analiza la incertidumbre para varios COV que están en el rango de la tabla 1: COV = 2 %, 5 %, 10 %, 15 % y 20 %.
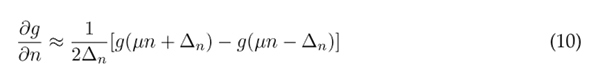
Las ecuaciones (11), (12) y (14) resumen los cálculos que se realizaron para cada variable de salida del modelo. Estas ecuaciones se aplicaron en cada pixel, resultado de las simulaciones hidrodinámicas mediante una calculadora ráster.
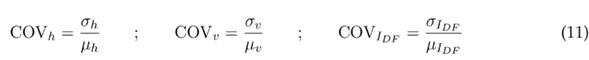
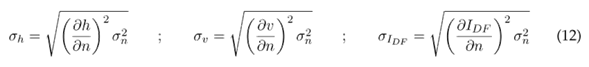
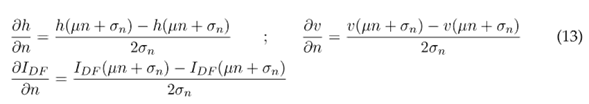
RESULTADOS
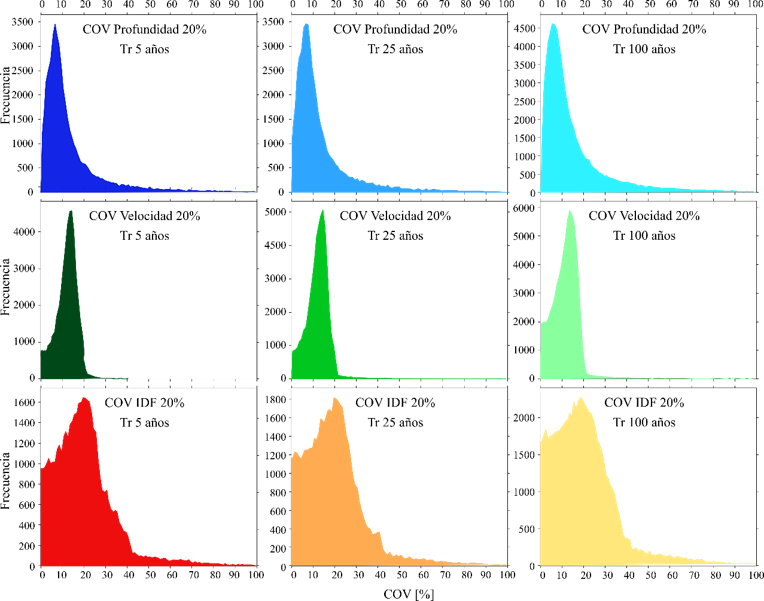
La figura 3muestra la frecuencia de los valores de los coeficientes de variación de la altura (COV h ), de la velocidad (COV v ) y del índice de intensidad de flujo (COV I DF ) correspondientes a un coeficiente de variación de Manning COV n = 20 % para los tres periodos de retorno (5, 25 y 100 años) en todo el dominio de cálculo del proceso de inundación. En la misma figura se reportan valores de COV h , v, I DF de hasta 100 %; por consiguiente, los valores máximos de COV h , v, I DF no se presentan. Se evidencia que la frecuencia de los COV h , v, I DF no es uniforme y que tanto la dispersión de los datos como la frecuencia máxima se alteran de acuerdo con las variables analizadas y no con el periodo de retorno; por ejemplo, para la profundidad se observa una disminución gradual de la frecuencia después de COV h = 8 % que es aproximadamente la frecuencia máxima en los tres periodos de retorno, para la velocidad se observa una disminución más abrupta después de COV v = 13 % (frecuencia máxima) para los tres periodos de retorno, y para el COV I DF
La figura 4 ilustra el valor más frecuente de COV h , COV v y COV I DF . Se observa que a mayor incertidumbre de la variable de entrada (n de manning), consecuentemente se incrementa la incertidumbre en la función de desempeño (altura, velocidad e índice de intensidad de flujo). La línea roja punteada indica una relación 1:1 entre los COV h,v,I DF y el COV n . Los valores sobre la línea muestran un incremento en la incertidumbre debido al modelo que basa su variabilidad en el coeficiente de Manning.
En la figura 4los resultados de incertidumbre para el I DF son los únicos ubicados sobre la línea de referencia, sus COV indican que, a mayor incertidumbre en el Manning n y mayor periodo de retorno, mayor incertidumbre habrá para la moda de los resultados.
En las figuras 3y 4 se observa que la propagación de la incertidumbre del coeficiente de variación a través de un modelo matemático como el de aguas someras para simulación de inundaciones no presenta un resultado trivial y que en algunos sitios del dominio computacional se incrementa la incertidumbre en las variables de salida, y en otros puntos se disminuye. Al aumentar la incertidumbre, necesariamente se incrementa la incertidumbre del nivel de amenaza en cada sitio, de allí la importancia de incluir en el análisis de amenaza tanto la variabilidad natural temporal (periodos de retorno), como la natural espacial de los parámetros de los modelos.
Propagación de la incertidumbre y evaluación de la amenaza en puntos específicos
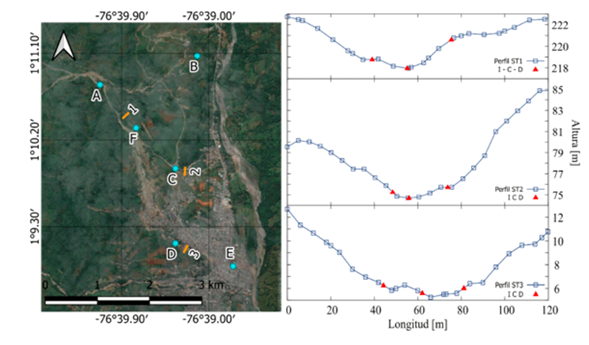
Se realizó un análisis de la propagación de la incertidumbre en puntos de la mancha de inundación, seleccionados de tal forma que existiera información para todos los periodos de retorno analizados. Los seleccionados fueron: el punto A, en la confluencia de las quebradas Taruca y Taruquita, después del ingreso de la hidrógrafa. El punto B, en la parte baja de la quebrada San Antonio, antes de su desembocadura en el río Mocoa. El punto C, en la intersección con la vía y la quebrada Taruca que se desvía hacia el sector de Pueblo viejo. El punto D, en la parte alta del río Sangoyaco, después de la entrada de la penúltima hidrógrafa de esta quebrada. El punto E, en la quebrada Sangoyaco antes de desembocar en el río Mocoa y de la última hidrógrafa. El punto F, entre los puntos A y C, en la zona de mayor dispersión de la mancha de inundación (figura 5).
Figura 5: Izquierda: ubicación de los puntos específicos en los que se analiza la propagación de la incertidumbre. Derecha: puntos sobre secciones transversales del dominio ST1, ST2 y ST3
La propagación de la incertidumbre también se analizó a través de tres puntos ubicados perpendicularmente a la dirección del flujo (análogos a secciones transversales [ST]), así: (1) en la zona de mayor dispersión sobre la quebrada Taruquita entre los puntos A y F; (2) en la zona de menor dispersión del flujo sobre la quebrada Taruca y después de la intersección de esta quebrada con la vía, unos metros abajo del punto C; por último (3) unos metros después del punto D en la quebrada Sangoyaco. Las ST se asumieron de acuerdo con tres puntos: margen izquierda (I), centro (C) y margen derecha (D). La imagen de la derecha de la figura 5 muestra los perfiles de cada una de las ST y la ubicación de los puntos I, C, D dentro de cada ST.
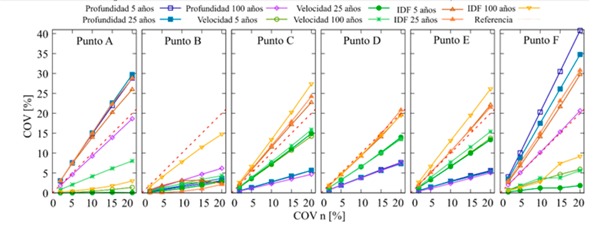
La figura 6 muestra la relación entre el COV h , COV v , COV I DF con el COV n para cada uno de los puntos escogidos (A, B, C, D, E y F), donde se evidencia que a mayor COV n hay mayor incertidumbre en la profundidad, la velocidad y el I DF . Sin embargo, esta relación no es proporcional y los aumentos reales de incertidumbre se deben observar a través de la línea de referencia (línea punteada): para todos los puntos hay al menos un resultado que supera dicha línea, excepto el punto B. En la figura 6 también se puede identificar que la velocidad es la única variable que no tiene aumento real de la incertidumbre en ninguno de los puntos analizados, mientras que el comportamiento de la profundidad y del I DF varían. Tampoco se identifica un comportamiento de la incertidumbre relacionado con los periodos de retorno para cada variable.
Figura 6: Valor del COV
h
, COV
v
, COV
I
DF en función del COV
n
para cada uno de los puntos seleccionados de la mancha de inundación (A, B, C, D, E y F)
Los resultados mostrados en la figura 6 para los puntos C y E son muy similares, mientras que los resultados de cada variable en el punto D son muy parecidos entre periodos de retorno; en todo caso, estos tres puntos son los que muestran menor dispersión comparados con los puntos A, B y F. Según las figuras 1 y 5, los puntos B y C coinciden con puntos de confluencia en zonas de previa dispersión de la mancha de inundación, pero de diferentes quebradas; mientras que los puntos D y E corresponden a una misma quebrada en una zona uniforme de la mancha de inundación. Por otro lado, los puntos A y F están ubicados en una zona de alta dispersión de la mancha de inundación, la dispersión de los resultados en estos puntos coincide: tanto la profundidad como el I DF para Tr = 5 y 25 años tienen incertidumbres ubicadas por encima de la línea de referencia.
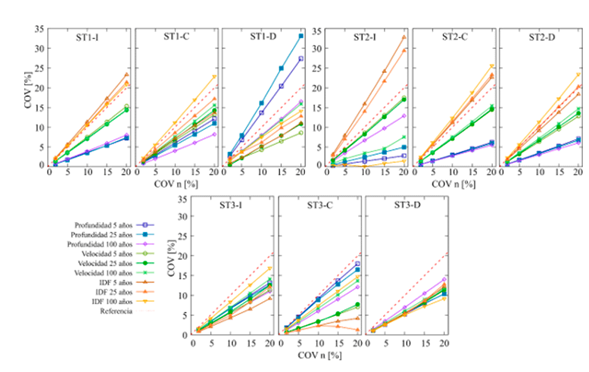
En cuanto a los resultados para las ST, la ubicación de los puntos se condicionó de tal forma que existiera información en todos los escenarios, i.e. para los tres periodos de retorno y las tres variables analizadas. La figura 7 muestra los valores de los COV h , COV v , COV I DF en función del COV n para los tres periodos de retorno graficados por cada punto dentro de las ST. De las tres ST de la figura 7, la ST N. º3 es la de menor incertidumbre (p. ej.: no se sobrepasa la línea de referencia); sin embargo, en esta ST no es sencillo identificar un comportamiento particular para cada variable como sí es posible identificar en las otras ST; en la ST 1, por ejemplo, para el margen izquierdo la profundidad tiene una incertidumbre entre 0-8 % con una relación directa para los periodos de retorno (a mayor Tr, mayor COV ), la velocidad entre 0-16 % con una relación inversa para los periodos de retorno y el I DF entre 1-25 %, también con una relación inversa para los periodos de retorno. La ST 2, margen derecho y centro, coincide con la ST 1 en cuanto a los rangos, pero no para la relación de los periodos de retorno: para la profundidad la relación es inversa, mientras que, para la velocidad y el I DF la relación es directa. De acuerdo con la ST 1 y ST 2 de la figura 7, la variable con mayor incertidumbre es el I DF , solo el margen derecho de la ST 1 indica que la profundidad tiene mayor incertidumbre.
Figura 7: Resultados del COV
h
, COV
v
, COV
I
DF en función del COV
n
para cada uno de los puntos de las secciones transversales analizadas
Altarejos-García et al. (2012) exponen mapas de desviación estándar y del valor esperado para la profundidad y la velocidad que son resultados de una simulación bidimensional en el software GUAD-2-D (ecuaciones de aguas someras-volumen finito) para un tramo de corriente con tres caudales picos. En un cálculo del COV al relacionar los valores máximos de cada uno de los mapas presentados, se obtiene un 0 ≤ COV h ≤ 18 % y 0 ≤ COV v ≤ 16 %; el rango de la velocidad coincide con los resultados generalizados para la figura 6.
La incertidumbre en la evaluación de la amenaza es menor en las partes altas de las cuencas, mientras que en las zonas donde las pendientes son menores, la incertidumbre en la altura, velocidad e intensidad de flujo es mayor. Lo anterior tiene implicaciones serias en el ordenamiento del territorio, dado que típicamente las comunidades habitan en las partes bajas de las cuencas donde, a pesar de que las velocidades y alturas de flujo pueden ser menores, su comportamiento es menos predecible y por ende su incertidumbre aumenta.
Los resultados evidencian que al evaluar la amenaza por inundación, teniendo en cuenta únicamente la incertidumbre o variabilidad natural temporal asociada a los periodos de retorno, se subestima la cuantificación de la amenaza debida a la variabilidad natural espacial de aspectos relacionadas con las propiedades físicas del flujo.
No se observa un incremento significativo de la incertidumbre de las alturas, velocidades o índice de intensidad de flujo cuando aumenta el caudal representado por escenarios de diferentes periodos de retorno; sin embargo, la evaluación de la magnitud del peligro es mayor debido a que los valores esperados de las alturas, velocidades e índice de intensidad de flujo sí se incrementan con los escenarios de periodos de retorno.
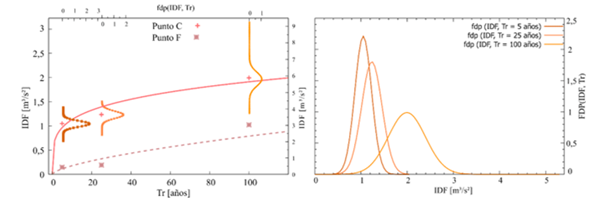
Para la evaluación de la amenaza por cualquier peligro natural (inundaciones, avenidas torrenciales), se usa la curva de amenaza que relaciona en las abscisas los valores de periodo de retorno y en las ordenadas se representa la variable que caracteriza la amenaza (altura, velocidades o índices de intensidad de flujo). En la figura 8A se presenta la curva de amenaza para el I DF de los puntos F y C de la figura 5. Es claro que la curva del punto C tiene un nivel de amenaza mayor que la curva F y que la incertidumbre natural está dada únicamente por el periodo de retorno, es decir, variabilidad natural temporal. Con el procedimiento acá presentado, se obtiene además la posibilidad de calcular la probabilidad que el I DF sea mayor a un valor determinado (asociado a un nivel de amenaza alta, media o baja I DF −Amenaza ) dado un periodo de retorno (Tr) P (I DF ≤ I DF −Amenaza )/Tr, debido a que la relación periodo de retorno e I DF no es determinística, sino que existe variabilidad natural espacial debido a los parámetros físicos que se encuentran en el modelo de inundación. La incertidumbre asignada a cada valor del I DF dado un Tr se obtiene de lo reportado en la figura 6. En la figura 8b se presenta la función de distribución de probabilidad del I DF para Tr 5, 25 y 100 años del punto C. Se observa claramente que la incertidumbre es mayor en la determinación del I DF a medida que aumenta el periodo de retorno de las hidrógrafas. Para el punto C, se tiene lo siguiente:
Figura 8: a. Curva de amenaza contra inundación de los puntos C y F en términos del IDF. b. Función de distribución de probabilidad del IDF para tres periodos de retorno (5, 25 y 100 años) en el punto C de la figura 5
P [(I DF ≤ I DF = 1 m3/s2)/Tr = 5 años] = 0, 39; P [ (I DF ≤ I DF = 1m3/s2)/Tr = 25 años] = 0, 14; P [ (I DF ≤ I DF = 1 m3/s2)/Tr = 100 años ] = 0, 0069. Según Ramos et al. (2021), un I DF ≤ 1 m3/s2 se encuentra asociado a un nivel de amenaza baja. Por lo tanto, en el punto C de análisis y a manera de ejemplo, se encuentra que a medida que el periodo de retorno aumenta, la probabilidad de estar en un nivel de amenaza baja disminuye. Consistentemente, la probabilidad de estar en un nivel de amenaza medio o alto es superior con el aumento del periodo de retorno de las hidrógrafas.
En resumen, la figura 8A ilustra la evaluación de la amenaza por inundación en términos del IDF, considerando únicamente la incertidumbre natural temporal dada por la variación de la magnitud de la amenaza en función del periodo de retorno, mientras que la figura 8B muestra la influencia de la incertidumbre natural espacial en los resultados de la evaluación de la magnitud de la amenaza.
La integración de las dos incertidumbres naturales (espacial y temporal) y la evaluación de la amenaza integrada se efectuarían a través de la ecuación (14):
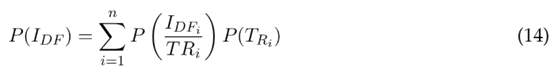
Donde las probabilidades P (I DF i/TR i ) se obtienen con el procedimiento presentado en este artículo para los n periodos de retorno y P (TR i ) están asociados a la probabilidad de excedencia de las hidrógrafas reportadas en la figura 2 .
CONCLUSIONES
El estudio general que se realizó a través de los valores medios de los resultados permitió establecer un rango de incertidumbre entre 0 % ≤ COV ≤ 25 %, con mayores incertidumbres para el I DF y menores para la velocidad, resultado que concuerda con el análisis puntual y por secciones transversales. También fue posible establecer una relación directa con los periodos de retorno: a mayor periodo de retorno, asociado a mayor caudal, se incrementa la incertidumbre en la determinación de alturas y velocidad. Esto se evidencia en los mapas de amenaza donde zonas altas y medias tienen mayor incertidumbre que aquellas delimitadas con amenaza baja.
El análisis de la propagación de la incertidumbre mediante el método FOSM es una manera de obtener la incertidumbre en términos del COV de la función objetivo o de las variables de salida con un costo computacional aceptable, pues no requiere grandes cantidades de simulaciones. Esto se vuelve útil cuando los dominios de computación son grandes y por tanto las simulaciones toman un tiempo considerable (p. ej.: más de cuatro horas).
Se presenta un procedimiento para integrar la incertidumbre natural espacial y temporal en la evaluación de la amenaza por inundaciones. Dicho procedimiento tiene la potencialidad de ser aplicado a peligros que tienen procesos similares como las avenidas torrenciales. A medida que aumenta el periodo de retorno de las hidrógrafas en la zona de estudio, se incrementa la incertidumbre en el parámetro representativo de la amenaza al tener en cuenta la variabilidad natural espacial del coeficiente de rugosidad de Manning.
Acknowledgements
Agradecimientos
Los autores agradecen a Jorge Escobar, Andrés Vargas, David Trujillo, Paula Solarte y Leandro Durán por su colaboración en la conceptualización y el levantamiento de información para el establecimiento de las simulaciones de prueba iniciales.
REFERENCIAS
Licencia
Derechos de autor 2023 Alfonso Mariano Ramos-Cañón, Lady Carolina Castro Malaver, Nicolás Escobar-Castaneda

Esta obra está bajo una licencia internacional Creative Commons Atribución-CompartirIgual 4.0.
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.