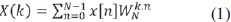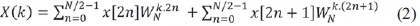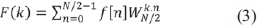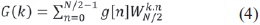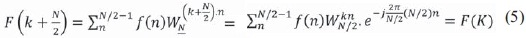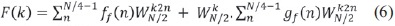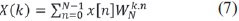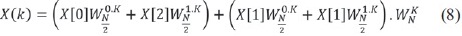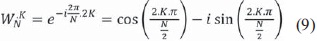Diseño y construcción de un prototipo para la medición de distorsión armónica en redes eléctricas

Diseño y construcción de un prototipo para la medición de distorsión armónica en redes eléctricas

Designing and building a harmonic-distorsion measurement prototype for electrical networks

Duvan Cardona¹, Danilo López², Cesar A. Hernández³

¹ Tecnólogo en electricidad. Tecnólogo de Condensa S.A. Esp. Bogotá. Colombia. Contacto: dfcardonaa@correo.udistrital.edu.co
² Ingeniero Electrónico. Docente e investigador de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: dalopezs@udistrital.edu.co
³ Ingeniero Electrónico. Docente e investigador de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: cahernandezs@udistrital.edu.co

Fecha de recepción: 27 de marzo de 2012 Fecha de aceptación: 27 de noviembre de 2012

Resumen

El presente artículo ilustra la forma de implementar la transformada rápida de Fourier usando el algoritmo de Cooley-Tukey, aplicado al análisis y el cálculo de la distorsión armónica en hogares y pequeñas empresas donde no se tiene la certeza de la calidad de energía que les es entregada a diario. La investigación está basada en una arquitectura de Microcontrolador para obtener un buen rendimiento con un lenguaje de alto nivel, además, se desarrollan las diferentes partes del hardware necesarias para el cálculo de la FFT de 1024 puntos y el cálculo del nivel de THD.

Palabras clave: algoritmo, diezmado, factor de giro, FFT, THD.

Abstract

This investigation work shows the way to implement the rapidly transformed of Fourier using the algorithms of Cooley-Tukey, applied to the analysis and calculation of the harmonic distortion in homes and small businesses that it's don't knows the energy's quality that is delivered daily. The investigation is based on a diferent parts of hardware necesary for the recmicrocontroller architecture for good perfoman-koning of the FFT of 1024 points and the reckoce whit a high level language, olso develop the ning of THD level.

Key words: algorithm, decimated, twist factor, FFT, THD.

1. Introducción

La calidad de servicio es un tema que preocupa tanto a empresas eléctricas como a consumidores, ya que las perturbaciones en una red pueden alterar el correcto funcionamiento de los equipos instalados. Durante la última década, se han desarrollado muchas aplicaciones informáticas para simular y analizar problemas de calidad de servicio, el aumento de equipos sensibles a variaciones de tensiones y corrientes, como computadoras, o equipos de alta precisión, ha incrementado la preocupación de empresas eléctricas y consumidores por la calidad del servicio.

El mal funcionamiento de los equipos en redes de potencia puede ser originado por un amplio espectro de perturbaciones que pueden ser originadas tanto en redes de potencia como en las instalaciones de los usuarios.

El avance tecnológico, en cuanto a plataformas robustas, ha permitido la implementación de diferentes algoritmos que permiten técnicas de simulaciones digitales, las cuales han sido métodos muy eficaces en el estudio de la calidad del servicio, estas técnicas están basadas en el empleo de transformadas [1]. Una de las técnicas utilizadas para este análisis es la transformada rápida de Fourier (FFT), para la cual se han implementado diversos algoritmos, la FFT transforma una señal discreta en el dominio del tiempo a su representación en el dominio de la frecuencia, de una manera rápida y eficiente, y se convierte en un método muy sencillo en el análisis de las perturbaciones que presenta la red [2], [3].

El algoritmo aquí utilizado es el de Cooley-Tukey, ya que es el algoritmo base para el cálculo de la FFT por ser el primer algoritmo realizado, y permite realizar modificaciones que optimizan el cálculo este algoritmo, este algoritmo consiste básicamente en dividir por dos la cantidad de datos discretos que se tienen de una señal e ir separándolos hasta obtener n cantidad de parejas de datos [4].

2. Metodología

Para realizar este proyecto se utilizó un micro-controlador 18f2550, también el conversor ADC (convertidor analógico digital) del microcontrolador para discretizar la señal, para el cálculo de la FFT se implementó el método de Cooley-Tukey con una modificación, partiendo del hecho que se tiene una señal dada polinomialmente [1] como la ecuación (1):

Siendo:

N el número de datos.

n la posición del dato.

W el factor de giro.

k constante multiplicativa

Sabiendo que la cantidad de datos N es par potencia de 2, se empieza a descomponer la sumatoria, dividiéndola en 2 de la siguiente manera, ecuación (2):

Reorganizando la ecuación se reemplaza x[2n] por f[n] y x[2n+1] por g[n] y se obtienen las ecuaciones (3) y (4).

Siendo F(k) y G(k) funciones periódicas, se puede ir reduciendo en N/2 la longitud de cada sumatoria hasta obtener n sumatorias de longitud 2, siendo ésta la unidad básica de la FFT conocida como mariposa, ecuación (5), ecuación (6) y que se explica más adelante.

Donde y son lo mismo para f[n] que para x[n]. Analógicamente, se hace los mismo con G(k). Es decir, que ahora sobre f[n] y g[n] se realizan 4 DFT de longitud N/4. Entonces, se pueden hacer múltiples divisiones del intervalo [0, N-1] mientras se pueda dividir N entre 2.

Finalmente, se se utilizó una display LCD de 16x2 para la visualización de los resultados.

2.1 Conversor analógico digital

Una vez se tiene la señal de tensión, se inicia la función del ADC del microcontrolador y se procede a tomar lectura de la señal, por cada fanco de subida de una señal de reloj, cuyo periodo es 31,14 micro segundos, se toma una lectura para asi tomar los 1024 datos en un periodo de la señal que corresponde a 16,66 mili segundos, a su vez, estos datos se van almacenando en un arreglo previamente declarado en la memoria ROM (memoria de solo lectura no volátil) del microcontrolador [5], [6].

2.2 Algoritmo para obtener la FFT

En primera instancia se verifcó la efectividad de la FFT por medio de un software avanzado (Matlab) para el cálculo de la transformada discreta de Fourier, que es implementada para representar una señal en el dominio de la frecuencia [7].

El algoritmo que ha sido utilizado para la obtención de la FFT (cooley tukey modificado) se describe a continuación: primero, se realizó una réplica del algoritmo de cooley tukey (modificado) mencionado anteriormente, y se le aplicó a una cadena de datos, con una precisión de tan solo 4 bits como prueba piloto, para realizar este algoritmo la cadena de datos tiene que tener una cantidad de datos igual a N, siendo N una potencia de 2.

La implementación de la réplica de este algoritmo se realizó de la siguiente manera: en primer lugar, se hizo un diezmado en el dominio del tiempo de los datos a analizar, el diezmado consiste en tomar la cadena de datos que se tiene y separar los datos que se encuentran ubicados en las posiciones pares de la cadena con los de las posiciones impares de la misma, obteniendo así dos cadenas de datos con una longitud igual a la mitad de la longitud inicial de la cadena principal, este proceso se repite hasta obtener n cadenas de datos con una longitud igual a 2, siendo esta, la unidad básica de la FFT conocida como la mariposa, en donde sólo se necesita una multiplicación y dos sumas complejas.

El cálculo de la FFT se realiza en un número de etapas equivalente al logaritmo en base 2 del número de puntos N, donde, en cada etapa, la salida es la entrada de la siguiente, es decir; en el ejemplo piloto se tienen 4 bits (16 datos); en la primera etapa, los datos se almacenan en un primer arreglo de datos en la memoria ROM del microcontrolador, estos datos son la entrada de la segunda etapa donde se hace el primer diezmado, en la salida de esta etapa se tienen dos cadenas de datos cada una de ocho datos, que se almacenan en un segundo arreglo en la memoria ROM del microcontrolador; a su vez, esta salida se convierte en la entrada de la tercera etapa donde se hace nuevamente un diezmado de datos y, en la salida de esta etapa, se obtienen cuatro cadenas de cuatro datos, que se almacenan en el primer arreglo anteriormente utilizado; por último, la salida de esta etapa, se convierte en la entrada de la cuarta etapa donde se realiza el último diezmado, donde se obtiene en la salida de esta etapa ocho cadenas de dos datos, almacenándose en el segundo arreglo que se utilizó anteriormente, en la figura 1 se observan las etapas realizadas para la obtención de la FFT de 16 puntas [8], [9].

En la Figura 1 es el factor de giro, N es el número de datos, a es las veces que se ha diezmado y n es la posición del dato en el arreglo.

Posteriormente, se procedió a multiplicar por un factor de giro o constante multiplicativa, ecuación (7), correspondiente a cada dato en cada etapa, según la cantidad de diezmados que se le hayan aplicado a cada dato. Para explicar un poco mejor esto, se tienen las siguientes ecuaciones:

Diezmado de los datos, separando los que están ubicados en las posiciones pares de las impares, siendo X[n] el dato en la posición n se tiene la ecuación (8).

Reemplazando W (Factor de giro) por la constante de Euler correspondiente para cada dato la ecuación (9).

Posteriormente, se compararon los datos obtenidos con la aplicación de este algoritmo, con los datos que arroja el software Matlab (software de alto nivel), una vez realizadas las principales pruebas se inicia la extensión del código realizado a una capacidad de 10 bits (1024 puntos). Para proceder con la FFT de 10 bits (1024 puntos), se escogió un micro de la familia 18fxx, para almacenar los datos discretizados se reservó un arreglo de 1024 posiciones de 32 bits, posteriormente, para diezmar los datos, se reservaron dos arreglos más de 32 bits utilizando punteros para un mejor aprovechamiento de la memoria ROM del micro.

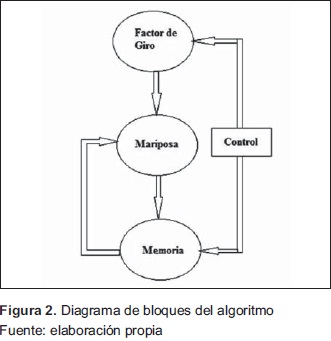
El diseño del algoritmo se divide en cuatro bloques funcionales distribuidos como se indica en la Figrua 2, que realizan el proceso del cálculo sucesivo de la FFT de 2 puntos para las muestras almacenadas en el arreglo principal, los datos procesados ocupan un tamaño de 32 bits para la componente real y 32 bits para la componente imaginaria, la parte de la mariposa procesa los datos de entrada procedentes de la memoria, con los factores de giro, determinantes por el exponente calculado en el bloque de control, y entrega el resultado de nuevo para ser procesado en la siguiente etapa. Ver Figura 2.

Una vez los datos ingresados, provenientes del conversor analógico digital, se almacenaron en un rango de memoria de 1024x32, se procedió con el almacenamiento de los datos procesados por medio de dos rangos de memoria más de 1024x32; una vez se tienen estos datos totalmente procesados, se les aplicó el factor de giro y se almacenaron en dos nuevos rangos de memoria de 1024x34, uno para la parte real y otro para la parte imaginaria. La necesidad de usar dos rangos de memoria para el procesamiento de datos se da ya que es necesario una vez guardados los datos leerlos nuevamente para así procesarlos nuevamente, esto se ilustra mejor en la Tabla 1.

Los factores de giro se almacenaron cada uno en un espacio de memoria de 32 bits, estos factores se obtuvieron multiplicando unos valores preestablecidos por una constante k, que varía de acuerdo al índice de cada etapa, estos factores de giro están representados por 128 configuraciones de bits.

3. Resultados

A continuación se describen los resultados obtenidos en la presente investigación en términos de los tiempos de procesamiento, la precisión y eficacia del algoritmo modificado e implementado y la eficiencia del mismo.

3.1 Tiempos de procesamiento

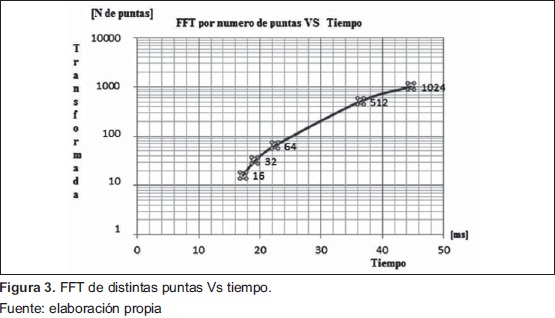
Luego de realizar simulaciones, resulta prometedor el desempeño del procesador FFT que se ha diseñado. Inicialmente se cuenta con un oscilador de 40MHz, lo que lleva al sistema a hacer un cálculo completo de la FFT de 1024 puntas en 44,69ms, para un total de 45826,81 transformadas por segundo.

Se utilizaron pruebas en Matlab que confrman la efectividad del algoritmo y los procesos usados en el microcontrolador.

En la Figura 3 se puede observar la velocidad de procesamiento de la FFT con distintas transformadas (16 puntas, 32 puntas, 64 puntas y 1024 puntas).

3.2 Precisión del algoritmo

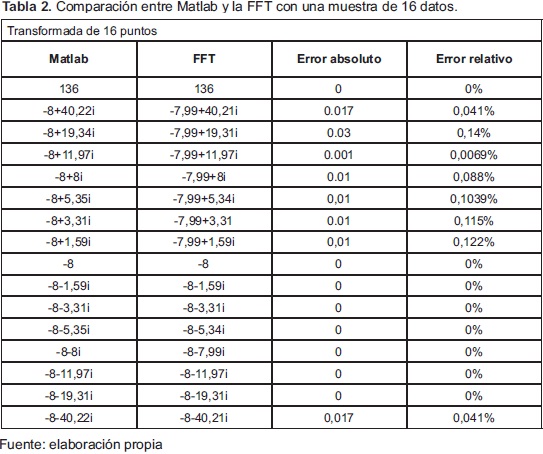
Los resultados que se obtuvieron en cuanto a precisión al comparar el proceso realizado por el microcontrolador frente al proceso que realiza Matlab se muestran a continuación en la Tabla 2.

Sin embargo, tomando todos los datos de la tabla anterior, se obtiene un error relativo total de 0,41%.

3.3 Eficiencia del algoritmo

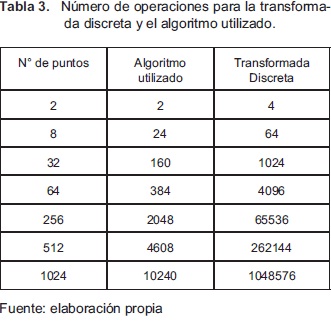
Al hacer el cálculo de la cantidad de operaciones complejas que se requieren para el obtener de la transformada, se confrma la eficiencia del algoritmo utilizado ver Tabla 3.

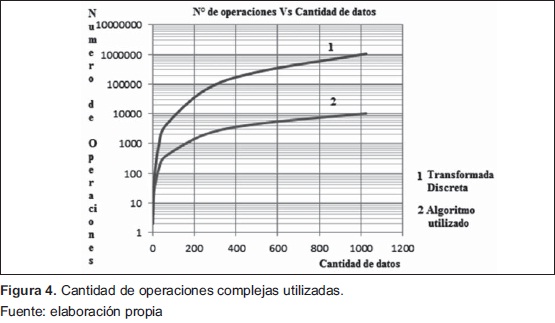
Con la Figura 4 se observó el crecimiento en cuanto a la cantidad de operaciones complejas tanto en el algoritmo utilizado como en la transformada de Fourier Discreta.

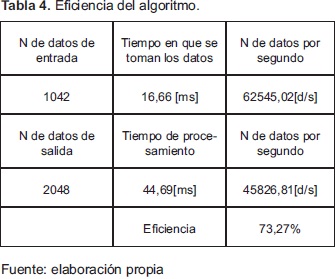
Analizando el tiempo en que el microcontrolador lee los datos entregados por el ADC, se comparó con el tiempo en que el microcontrolador tarda en entregar los datos transformados, y así se obtuvo un promedio de datos leídos por segundo y datos entregados por segundo para posteriormente calcular la eficiencia del algoritmo en porcentaje. Ver Tabla 4.

4. Conclusiones

La arquitectura de esta FFT cooley tukey modificado brinda varios beneficios, como: bajo número de funciones combinacionales, registros y memoria en comparación con otros trabajos realizados.

La metodología aplicada en el diseño del código para el presente artículo permite una fácil configuración del sistema para N= datos de entrada (n2 2), de cualquier número de bits. Esto se logra debido a la creación de bloques funcionales que permiten una fácil manipulación de los datos. Por lo tanto, se ha obtenido una arquitectura base que puede utilizarse en varias situaciones para diferentes requerimientos.

Para el uso de esta herramienta FFT cooley tukey modificado en cualquier aplicación, no es necesario tener en cuenta las condiciones preliminares, como el formato de los datos de entrada, ya que el algoritmo está diseñando para recibir cualquier tipo de dato (decimal o entero) y, asi mismo, entregar resultado sin hacer truncaciones.

Referencias

[1] M. Jamali, J. Downey, N. Wilikins, C. Rehm and J. Tipping, "Development of a fpga-based high speed fft processor for wideband direction of arrival applications", Radar Conference, 2009 IEEE, pp. 1-4, May 2009.

[2] J. Proakis, Digital Signal Processing: Principles, Algorithms, and Applications. Englewood Cliffs, NJ: Prentice-Hall, 1996.

[3] Oppenheim, R. Schaefer and J. Buck, Discrete-Time Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1998.

[4] J. Cooley and J. Tukey, "An algorithm for the machine calculation of complex fourier series", Math. Comput., Vol. 19, pp. 297-301, Apr 1965.

[5] H. Sorensen, M. Heideman and C. Burrus, "On computing the split-radix fft", Acoustics, Speech and Signal Processing, IEEE Transactions on, Vol. 34, No. 1, pp. 152-156, Feb 1986.

[6] J. Kuo, C. Wen, C. Lin and A. Wu, "VLSI design of a variable length FFT/IFFT processor for OFDM based communication systems", J. Appl. Signal Process., Vol. 13, pp. 1306-1316, Jan 2003.

[7] X. Guan, Y. Fei and H. Lin, "A hierarchical design of an application specifc instruction set processor for high-throughput FFT", Proc. Int. Symp. Circuits Syst., May 2009, pp. 2513-2516.

[8] H. Ishebabi, G. Ascheid, H. Meyr, O. Atak, A. Atalar and E. Arikan, "An efficient parallelization technique for high throughput FFT-ASIPs" in Proc. Int. Symp. Circuits Syst., pp. 5664-5667, May 2006.

[9] G. Liu and Q. Feng, "ASIC design of lowpower reconfigurable FFT processor", in Proc. Int. Conf. ASIC, pp. 44-47, Oct. 2007.