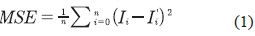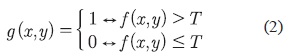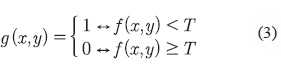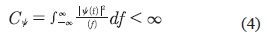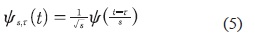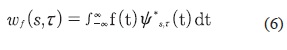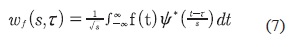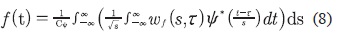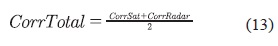Calibración de imágenes de radares meteorológicos

Calibración de imágenes de radares meteorológicos

Calibration of weather radar images

Virgilio Santander Socorras Quintero¹, Ernesto Gómez Vargas², Nelson Obregón Neira³

¹Ingeniero Electrónico y de Telecomunicaciones. Estudiante de Maestría en Teleinformática, Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: vssocarrasq@correo.udistrital.edu.co
²Ingeniero Electrónico, Magíster en Teleinformática. Facultad de Ingeniería, Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: egomezvargas@udistrital.edu.co
³Ingeniero Civil, Doctorado en Hidráulica. Facultad de Ingeniería, Pontificia Universidad Javeriana. Bogotá, Colombia. Contacto: nobregon@javeriana.edu.co

Fecha de recepción: 14 de marzo de 2013 Fecha de aceptación: 23 de noviembre de 2013

Clasificación del artículo: investigación
Financiamiento: Universidad Distrital Francisco José de Caldas

Resumen

En este documento se ilustran las técnicas de fusión de imágenes para complementar y calibrar la información meteorológica presente en imágenes de radares terrestres con el uso de imágenes satelitales meteorológicas. Para realizar la calibración de las imágenes de radares terrestres se implementó un método de fusión de imágenes basado en la herramienta matemática transformada wavelet discreta. Ya que existe una familia de wavelets, es necesario determinar cuál wavelet ofrece el mejor resultado; para esto se determina la correlación existente entre los resultados de fusión de diferentes wavelets y las imágenes utilizadas en cada fusión. Se define una metodología para selección de umbral global de segmentación y una metodología para realizar la calibración de las imágenes de radares terrestres. Siguiendo la metodología de calibración de imágenes, se generan algunos resultados y se muestran sus ventajas.

Palabras clave: fusión de imágenes, histograma, segmentación de imágenes, transformada wavelet discreta.

Abstract

This paper shows the image fusion techniques to complement and calibrate weather radar images present in terrestrial using meteorological satellite images. To calibrate the images weather radar images implemented a fusion method was used discrete wavelet transform (DWT) mathematics tool. As there is a family of wavelets, wavelets is necessary to determine which offers the best results, and it was determined, with the correlation between the results of different wavelet and fusion of the images used in each fusion. We defined a methodology for selecting global threshold segmentation and a methodology for calibration of terrestrial radar images. Following the methodology of calibration images, some results are generated and displayed its advantages. The methodology of calibration images, some results are generated and displayed its advantages.

Key words: Discrete wavelet transform, histogram, image fusion, image segmentation.

Introducción

El funcionamiento de un radar meteorológico está basado en radiaciones de ondas electromagnéticas que luego son reflejadas por los cuerpos (blancos) en el espacio. La energía reflejada por los blancos es recibida por el radar y convertida en datos digitales para ser procesados por un software especializado que interpreta y genera productos como: imágenes de reflectividad Z, topes de ecos, acumulaciones, indicador de plan de posición, etc.

En el cielo hay más que lluvia, nieve y viento; otros objetos (migración de aves, insectos a bajas altitudes, montañas, edificaciones, aeronaves, etc.) pueden ser mal interpretados como lluvia por el radar meteorológico. Es posible eliminar algunos falsos ecos con equipos más complejos en el postratamiento de datos, los cuales usan re-flectividad de radares Dopplero mapas de ecos falsos (Zhiying et al., 2010); pero en última instancia el ojo humano entrenado es el que puede distinguir estos objetos, utilizando para ello las características especiales que los diferencian de un fenómeno meteorológico. No obstante, en ocasiones el ojo humano falla y se generan falsas alertas metrologías (tornados, huracanes, tormentas, etc.), que generan retrasos en el transporte aéreo, impacto económico y pánico en la población supuestamente afectada por el fenómeno meteorológico.

Existen nubes precipitantes y no precipitantes; una nube no precipitante puede estar formada por pequeñas gotas de agua o por pequeños cristales de hielo, que se mantienen suspendidos en el aire (Rinehart, 2004). Cuando hay cambios de temperatura o fuertes corrientes de aire, las pequeñas gotas de agua en las nubes pueden crecer y la nube puede convertirse en precipitante rápidamente. Se podría decir que las nubes no precipitantes son de gran importancia para una buena predicción del clima. Pero los radares meteorológicos están limitados para detectar este tipo de nubes, ya que solo detectan nubes precipitantes. Con la fusión de imágenes de radares meteorológicos y las imágenes de satélites geoestaciona-rios de operación ambiental (GOES) se podrían obtener imágenes con nubes precipitantes y no precipitantes de una región y, además, calibrar la imagen de los radares meteorológicos terrestres para que se muestre la menor cantidad de ecos falsos en la imagen y así poder mejorar la representación del estado del clima.

En la primera parte del artículo se muestra el esquema metodológico para realizar la calibración de imágenes; en la segunda parte se muestra una explicación del método de segmentación empleado y el método de calibración de imágenes y, finalmente, se muestran los resultados obtenidos con la transformada wavelet discreta seleccionada.

Metodología

Método de calibración de imágenes

El método de calibración planteado para integrar la información de las imágenes satelitales meteorológicas con las imágenes de radares meteorológicos terrestres está basado en la segmentación por umbralización, en la transformada wavelet discreta y la familia de wavelets. Para realizar la calibración de las imágenes de radar se crearon los siguientes pasos:

• Filtrar imágenes satelitales: ya que las imágenes satelitales contienen objetos no meteorológicos, estos interfieren con la segmentación de las imágenes satelitales. Para mejorar de alguna manera la imagen digitales necesario hacer un pre-procesamiento de la imagen, y así prepararla para una posterior segmentación. Este primer paso se realiza con un filtro digital píxel a píxel, que retira cualquier objeto que interfiera con la segmentación de las nubes presentes en las imágenes. En este caso en particular el procedimiento solo se hace en las imágenes satelitales, ya que son las únicas que cuentan con objetos (desiertos, montañas, ríos, etc.) que interfieren con la extracción de las nubes.
• Segmentar imágenes satelitales: en este procedimiento se realiza la extracción de las nubes presentes en las imágenes satelitales. La extracción se hace con el método de umbralización de niveles de grises; se define un umbral único y se realiza una comparación píxel a píxel para dejar solo nubes en la imagen.
• Ajustar dimensiones de imágenes: para poder fusionar las imágenes es necesario que estas tengan la misma dimensión. A simple vista pareciera que son iguales, pero las imágenes de radar obtenidas son ligeramente más pequeñas, y es necesario ajustarlas a las dimensiones de las imágenes satelitales.
• Seleccionar wavelet: se selecciona una wavelet diferente de la familia de wavelets (Haar, Daubechies, Symlet, Biortogonal, Coiflet, Discrete Meyer y Reverse Biortogonal) en cada iteración, hasta implementar las todas.
• Obtención de los coeficientes wavelet de las imágenes: en este procedimiento se utilizan las wavelets seleccionadas en el paso anterior, para descomponer las imágenes en los coeficientes de aproximación, detalle horizontal, detalle vertical y detalle diagonal.
• Combinar los coeficientes wavelet de las imágenes: en este procedimiento se implementa un criterio de calibración y un criterio de fusión (máximos, mínimos, media aritmética, etc.) para combinar los coeficientes de las imágenes de radar con los de las imágenes satelitales.
• Aplicar la transformada inversa wavelet: en este último procedimiento se reconstruye una imagen de los coeficientes wavelet combinados, para poder obtener y visualizar la imagen de radar calibrada.

Método de selección de umbral de segmentación

Para realizar la segmentación de las nubes es necesario escoger el umbral global óptimo. Para realizar esta elección se diseñó una metodología, que sigue los siguientes pasos:

• Filtrar imagen satelital: este primer paso se realiza con un filtro digital pixel a pixel, que retira cualquier objeto que interfiera con la segmentación de las nubes de las imágenes. En este caso en particular, el procedimiento solo se hace en la imagen satelital, ya que es la única que cuenta con objetos (desiertos, montañas, ríos, etc.) que interfieren con la extracción de las nubes las imágenes.
• Segmentar imagen con umbral de prueba: en este procedimiento se realiza la extracción de las nubes presentes en las imágenes satelitales con varios umbrales.
• Segmentación con el software Sistema de Información Geográfico (SIG) Integrated Land and Water Information System (ILWIS): se realiza la segmentación de las nubes con el método de clustering, que consiste básicamente en agrupar pixeles similares (Kim et al., 2013; Saraswathi y Allirani, 2013; Isa et al., 2009). La imagen resultado de este paso va a ser usada como referencia (valor esperado) para medir la efectividad de la segmentación con diferentes umbrales.
• Calcular el error cuadrático medio: como criterio de evaluación de la segmentación conseguida con cada umbral de prueba, se mide el promedio de los cuadrados de las diferencias entre los valores pronosticados y observados. Ver ecuación (1).

En este paso se calcula el error cuadrático medio entre los valores de la imagen segmentada con un umbral de prueba (valores obtenidos) y los valores de la imagen segmentada con el software ILWIS (valores esperados). Y se obtiene una medida que permite medir la similitud entre las dos imágenes segmentadas (Arathi y Soman, 2009).

• Por último se compara cada uno de los errores obtenidos hasta encontrar el mejor umbral.

Procesamiento Digital De Imágenes

El procesamiento digital de imágenes es un conjunto de técnicas que busca mejorar la calidad de las imágenes para la interpretación humana, y facilitar la búsqueda de información en las imágenes. Esto surgió desde que se cuenta con tecnología necesaria para captar y manipular grandes cantidades de información espacial en forma de matrices de valores (Esqueda y Palafox, 2005). Para el análisis de imágenes existen dos dominios, el espacial y el de la frecuencia, en el dominio espacial se opera directamente sobre los píxeles con técnicas como: filtros pasa bajos espacial (suaviza la imagen), filtro pasa altos (aumenta el contraste), filtros detección de bordes, filtro de dirección. En el dominio de la frecuencia contamos con herramientas como: transformada de Fourier, transformada discreta coseno y transformada wavelet.

En el dominio de la frecuencia las imágenes son representadas por la suma de señales periódicas con diferentes frecuencias (Esqueda y Palafox, 2005). Con el procesamiento en el dominio de la frecuencia es posible realizar eficiente y eficazmente la eliminación de ruido en imágenes (Biswas y Om, 2013; Parmar y Patil, 2013), búsqueda de información en las imágenes, fusión de imágenes (Sruthy et al., 2013; Pradnyay Sachin, 2013; Kaplan y Erer, 2013), compresión de imágenes (Xie et al., 2013), amplificación de imágenes, etc.

Segmentación por umbralización de niveles de grises

La segmentación permite identificar secciones comunes en la imagen, sin descartar las características relevantes en esta (Díaz y de Haro, 2004). De una buena segmentación se pueden obtener mejores resultados en el análisis o el procesamiento de las imágenes. El nivel de segmentación se realiza hasta obtener los objetos deseados. Para poder realizar la segmentación debe existir una similitud entre los píxeles del objeto y una diferencia con el resto (Alam et al., 2013). Los algoritmos de segmentación de imagen que utilizan los niveles de gris de la imagen se concentran en dos propiedades básicas: discontinuidad y similitud entre los niveles de gris de los píxeles vecinos (Zafra. 2008). En esta investigación se desea separar las nubes del resto de objetos (ríos, lagos, mar, continente, montanas) presentes en la imagen, y el método de segmentación por umbralización niveles de grises permite realizar esta tarea (Gómez et al., 2013; Wenlong etal, 2009).

La segmentación por umbralización de niveles de grises tiene como objetivo resaltar las regiones de características similares en una imagen. Este método trabaja bien cuando los objetos de la imagen tienen una intensidad de grises que los distinguen del fondo de la imagen (Zafira, 2008; Xiang et al., 2004). El histograma se construye calculando para cada nivel de grises el número de píxeles en la imagen que tienen ese nivel de grises (Angulo y Serra, 2005). Al analizar el histograma se puede definir el umbral. Este umbral podría ser el punto medio entre los dos máximos principales del histograma, o podría obtenerse de manera óptima maximizando la varianza entre clases (método de Otsu), mediante una búsqueda exhaustiva (Pepsi y Mala, 2013). Con el umbral (T) se toma la imagen en escala de grises, f(x,y) y se convierte todo lo que pertenece al objeto en 1 y lo que pertenece al fondo en 0, consiguiendo con esto una imagen binarizada. Cuando el objeto es más claro que el fondo se aplica la ecuación (2).

Pero si el objeto es más oscuro que el fondo de la imagen se aplica la ecuación (3).

Ya que en esta investigación el objeto de interés son las nubes presentes en las imágenes y estas son menos oscuras que el fondo, se podría utilizar la primera regla. Con la imagen binarizada g(x,y) se puede separar el objeto del resto de la imagen y conseguir el objetivo final de la segmentación. Este método de segmentación es el ideal para esta investigación, ya que existe una similitud en los niveles de grises de las nubes y una considerable diferencia entre los niveles de grises de las nubes y el fondo de las imágenes meteorológicas que se va a usar.

Transformada wavelet

La transformada de wavelet es una herramienta matemática que cuenta con la capacidad de analizar señales no estacionarias y de rápida tran-sitoriedad; para lograr esto el análisis espectral de la señal se realiza dependiendo del tiempo (Dragotti y Vetterli, 2003). Su funcionamiento es similar al de la transformada de Fourier con ventana, donde la señal es dividida en segmentos de tiempo (ventana) y se puede aplicar la transformada de Fourier localmente. La diferencia entre estas dos herramientas es que en la transformada de wavelet la ventana no es fija y se adapta a las frecuencias de la señal. Con dicha diferencia la transformada de wavelet obtiene un mejor comportamiento con este tipo de señales. Además del análisis local de señales no estacionarias, esta herramienta es comúnmente usada en el procesamiento de imágenes, fusión, compresión y reconocimiento de patrones.

Una ventaja de esta transformada frente a otras técnicas matemáticas es que dispone de una amplia familia de transformadas que permiten tratar imágenes de diferentes índoles (Hernández, 2010).

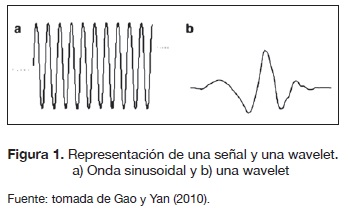
La wavelet es una pequeña onda que tiene una característica de oscilación ondulatoria y una energía concentrada en el tiempo. En la figura 1 se muestra una ilustración de una onda sinusoidal y una wavelet.

La principal diferencia entre una onda y una wavelet es que una onda usualmente es de forma regular y suave, y puede ser eterna, mientras que una wavelet puede ser de forma irregular y normalmente dura un periodo límite. Una wavelet puede servir como una plantilla determinista y no determinista para analizar variables en el tiempo o señales no estacionarias por descomposición de la señal en el dominio del tiempo y la frecuencia (Gao y Yan, 2010; Fernández, 2007).

Matemáticamente una wavelet es una función de cuadrado integrable ψ(ί), que satisface la condición de admisibilidad. Ver ecuación (4).

La transformada wavelet está compuesta por unas funciones base llamadas wavelets. Esta familia de wavelets es generada a partir de la wavelet madre ψ(t), con la ecuación (5) por medio de translación y dilatación.

S es el factor de dilatación y τ es el factor de traslación.

La transformada wavelet de una función f(t) es la descomposición de f(t) en un conjunto de funciones ψ_ST(t) llamadas wavelets. La transformada wavelet se define mediante la ecuación (6).

Reemplazando la ecuación (5) en la ecuación (6) se obtiene la ecuación (7).

En general con la transformada wavelet de la ecuación (7) se pueden extraer características de una señal, que no serían reveladas en su forma original. Por último, para recuperar la señal original f(t) existe la transformada wavelet inversa, que corresponde a una integral de los parámetros a y b. Ver ecuación (8).

Resultados Calibración De Imágenes

En esta investigación se utilizan imágenes satelitales del continente australiano, que se encuentra ubicado en el hemisferio sur entre los océanos índico y Pacífico, entre las latitudes 9°S y 44 °S y entre las longitudes 112°E y 154°. Se usarán imágenes GOES infrarrojas combinadas con imágenes estáticas de la superficie de la tierra y el océano del continente australiano. Las imágenes infrarrojas son derivadas de la radiación emitida por la tierra y su atmósfera en longitudes de onda del infrarrojo térmico (10-12 micras). Son imágenes de onda corta (IRCH2) que permiten tener una percepción de la nubosidad existente sin importar la luz solar (operativa de noche) y proporcionan información sobre la temperatura las nubes. Estas imágenes se combinarán con imágenes de radares meteorológicos terrestres de la misma zona geográfica. Las imágenes de los radares contienen información de reflectividad Z en decibelio (dBZ), que muestran la intensidad de lluvia que se encuentra en el radio de alcance de cada radar. Para la implementación de esta técnica de segmentación se desarrolló un software en Matlab, que permite cargar la imagen de radar y de satélite correspondientes al mismo espacio de tiempo.

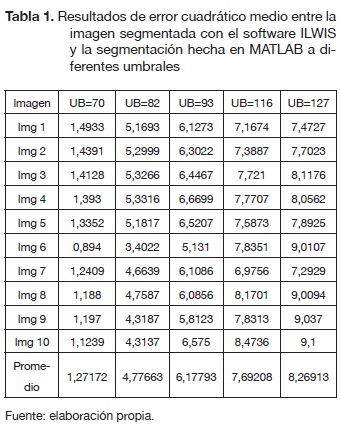
El primer objetivo en la investigación es segmentar las nubes de la imagen satelital. Ya que la segmentación es por umbralización y es necesario escoger un umbral global óptimo. Siguiendo la metodología de selección de umbral, se realizó la segmentación de 10 imágenes con 5 umbrales diferentes; cada segmentación se comparó con la segmentación hecha en la herramienta ILWIS, y se obtuvo los resultados de la tabla 1.

Si se observan los resultados de los promedios de errores cuadráticos medios de la tabla 1, se puede determinar que el 12,71 %, que se obtuvo con un umbral de 70 y con 10 imágenes, es determinante para escogerlo como el umbral global óptimo de segmentación.

En la investigación se encontró un problema al segmentar las nubes de la imagen de la figura 2. Estas imágenes satelitales meteorológicas cuentan con un suelo que se confunde con las nubes durante el proceso de segmentación. A pesar de que en Gómez et al., 2013 se comprobó que la técnica de segmentación por umbralización es la óptima para segmentar las nubes de una imagen satelital GOES, esto no aplica para algunas imágenes de ciertas partes de mundo. Para las imágenes de esta investigación es necesario realizar un prefiltrado.

Se diseñó un filtro que trabaja pixel a pixel sobre la imagen satelital original en color, sobre los tres planos (RGB) de la imagen, con el objetivo de no dejar pasar los objetos con un patrón de colores diferentes al de las nubes.

En la figura 3 vemos el resultado de aplicar el filtro digital a la imagen de la figura 2, y podemos observar que todo el continente australiano es retirado de la imagen y así evitamos que los tonos del suelo interfieran con la segmentación de las nubes.

Con la imagen satelital filtrada podemos realizar la segmentación (ver figura 4) y conseguir que el umbral para la segmentación sea un poco más bajo y se pueda extraer la mayor cantidad de nubes.

En la figura 4 se nota cómo después de filtrada la imagen de la figura 2 se pueden obtener mejores resultados en la segmentación de las nubes. Ya es posible extraer únicamente la información de nubosidad presente en la imagen, de esta manera se logra el primer objetivo.

Con la imagen satelital segmentada podemos hacer la fusión con la imagen de radar. Para realizar la fusión por medio de wavelet es necesario utilizar una función madre. Existe una familia de wavelets de las que seleccionamos las que son comúnmente utilizadas para fusionar imágenes: Discrete Meyer, Haar, Daubechies, Biorthogonal, Reverse Biorthogonal y Coiflets.

De igual manera, existen varios criterios de fusión de píxeles que define la forma en que inte-ractúan los píxeles de las imágenes por fusionar. Entre estos métodos tenemos los siguientes:

• Linear: C = A*paramMETH + B*(1-param- METH), donde 0>=paramMETH<=1.
• Max : D = abs(A)abs(B) ; C = A(D) + B(∼D)
• Min D = abs(A)abs(B) ; C = A(D) + B(∼D)
• Mean : C = (A+B) / 2 ; D = ones(size(A))
• Rand : C = A(D) + B(∼D); D is a Boolean random matrix
• Img1 : C = A
• Img2 : C = B

Después de realizar varias pruebas con cada uno de estos criterios de fusión se pudo determinar, por medio de la correlación entre las dos imágenes origen y la fusionada, que el mejor método es "Max" para aproximaciones y detalles.

La correlación entre dos imágenes consiste en la identificación automática de puntos homólogos entre una o varias imágenes digitales. Esta correlación se calcula con la ecuación (8).

Para encontrar la correlación entre la imagen de satélite y la imagen fusionada se tuvo en cuenta que estas imágenes están formadas por tres planos RGB (Red, Green, Blue), y es necesario encontrar la correlación de cada plano (ecuaciones (9), (10), (11) y (12)) para encontrar la correlación total entre las dos imágenes. Para encontrar la correlación de cada plano se utilizó una función de Matlab (corr2) que recibe como parámetro dos matrices y retorna la correlación entre estas dos matrices.

Además las ecuaciones (9), (10), (11) y (12) se utilizan para encontrar la correlación de la imagen fusionada con la imagen de radar. Como último paso se encuentra el promedio entre la correlación de la imagen fusionada y la imagen satelital y la correlación de la imagen fusionada y la imagen de radar, denominada correlación total como se muestra en la ecuación (13).

La ecuación (13) permite determinar qué tan parecida es la imagen fusionada con las imágenes (imagen de radar y la imagen satelital) que la generaron. Esta medida es un buen indicador de la calidad del método de fusión, ya que indica qué tanta información se logró pasar a la imagen fusionada de las dos originales.

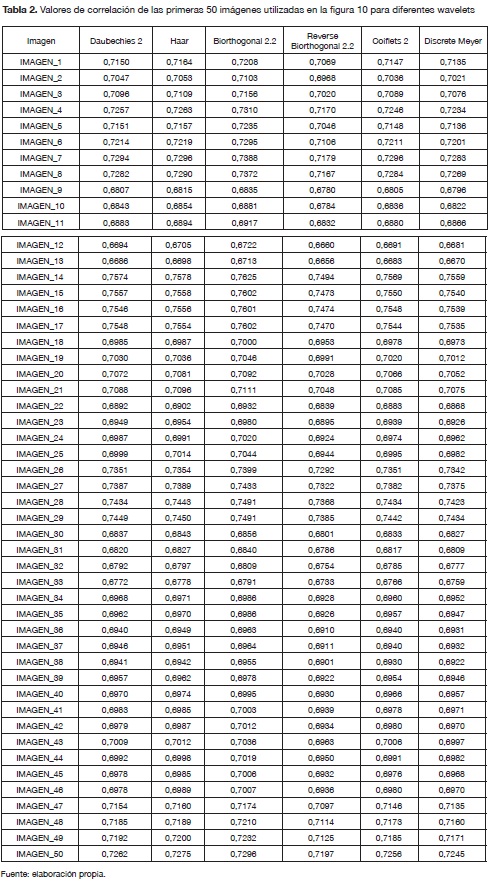
Se realizaron pruebas con cada una de wavelets mencionadas con 100 imágenes de radar y satélites; se evaluó la efectividad de la fusión con cada una de la familia de wavelets por medio del promedio de la correlación existente entre la imagen fusionada y la imagen de radar y la imagen satelital. Aunque la diferencia no es mucha, en la tabla 2 se ve claramente que la wavelet que conserva mejor la información de las imágenes de radares y de satélites en el proceso de fusión es Biorthogonal 2.2.

A continuación vamos a ver una serie de resultados de calibración de imágenes de radar generados con el software implementado. Se mostrará una imagen de radar, una imagen de satélite y el resultado, respectivamente.

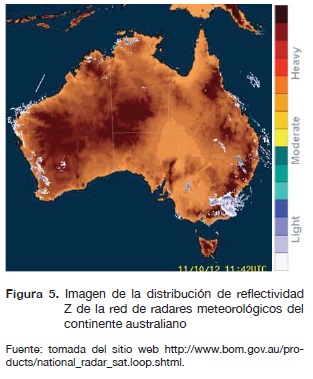
En la figura 5 se encuentra una imagen de radar con información anómala que se ve como líneas rectas saliendo de la base del radar; están en la parte superior izquierda de la imagen.

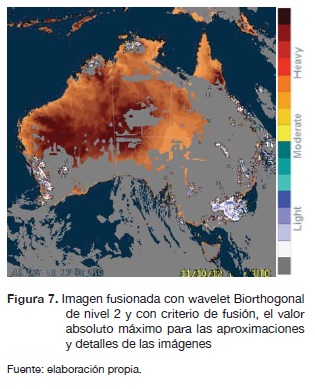
Al pasar las imágenes de la figuras 5 y 6 por el proceso de calibración, se genera el resultado mostrado en la figura 7.

En este caso el algoritmo de calibración detecta que el radar muestra una información que no corresponde con la del satélite y realiza los ajustes donde es necesario. En este caso se realizó en la parte superior izquierda del continente australiano.

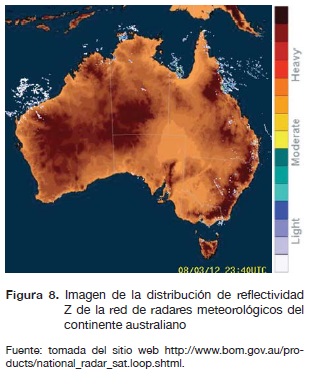
La imagen de radar de la figura 8 también contiene información anómala e información certera del estado del clima.

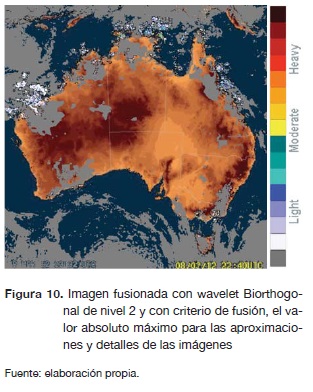
Al pasar las imágenes de la figuras 8 y 9 por el proceso de calibración se genera el resultado mostrado en la figura 10. En esta se ve cómo el algoritmo de calibración detecta las anomalías en la imagen de radar y realiza la calibración correspondiente; en este caso se ve en la parte inferior derecha del continente.

En los resultados se aprecia visualmente que todas las imágenes obtenidas contienen mayor información que la imagen de radar original. La información de la red de radares es complementada y calibrada con la información de nubosidad presente en la imagen satelital meteorológica. La información de la imagen satelital en ningún momento se sobrepone a la información de los radares y no altera la información de color de los radares donde es considerada como correcta.

Conclusiones

Si bien el método de segmentación por umbra-lización es óptimo para extraer las nubes de una imagen satelital meteorológica, existen zonas con objetos que tienen niveles de grises muy parecidos o iguales a los niveles de gris de las nubes; esto hace imposible realizar una segmentación con buenos resultados. Por esta razón, antes de realizar la segmentación de nubes en una imagen GOES se debe analizar la zona de estudio y realizar primero el preprocesamiento necesario.

Al realizar la fusión de imágenes con diferentes wavelets, se obtuvieron valores de correlación muy similares, con los que se pudo establecer que la wavelet que conserva la mayor cantidad de información en la imagen fusionada es la Biortho-gonal 2.2. El hecho de que se obtuvieran valores de correlación muy parecidos indica que todas las wavelet utilizadas (Haar, Biorthogonal, Coiflets, Daubechies, Discrete Meyer y Reverse Biortho-gonal) son muy buenas integrando información procedente de dos imágenes.

Así como es importante elegir la mejor wavelet para fusionar las imágenes, también se debe escoger un buen criterio de combinación de píxeles para lograr una buena fusión. En esta investigación se escogió el método de máximos para los coeficientes de aproximaciones y los de detalles, y se logró mantener la información de reflectividad Z y nubosidad en la imagen fusionada de manera eficiente.

Las imágenes de radares que fueron calibradas con el método propuesto tienen información meteorológica más acorde al verdadero estado del tiempo. Con estas imágenes los meteorólogos no tendrán que evaluar qué información del radar es verdadera o falsa, ya que estas imágenes están libres de ecos falsos y de reflexiones anómalas, y permiten hacer mejores pronósticos del tiempo.

Referencias

Alam, F.I., Chowdhury, M.I.H., Rabbani, M.R. y Bappee, F.K. (2013). An Optimized Image Segmentation Algorithm. Informatics, Electronics & Vision (ICIEV), International Conference, pp. 1-6. DOI: 10.1109/ ICIEV.2013.6572644.

Arathi, T. y Soman, K.P. (2009). Performance Evaluation of Information Theoretic Image Fusion Metrics over Quantitative Metrics. Advances in Recent Technologies in Communication and Computing. ARTCom '09, International Conference, pp. 225-227. DOI: 10.1109/ARTCom.2009.192.

Angulo, J. y Serra, J. (2005). Segmentación de imágenes en color utilizando histogramas bi-variables en espacios color polares luminancia/ saturación/ matiz. Computación y Sistemas, 8(4), 303-316.

Biswas, M. y Om, H. (2013). An Adaptive Wavelet Thresholding Image Denoising Method. Communications (NCC), National Conference, pp. 1-5. DOI: 10.1109/ NCC.2013.6488014.

Díaz, C. y de Haro, F. (2004).Técnicas de exploración en medicina nuclear. España: Elsevier Masson.

Dragotti, P. y Vetterli, M. (2003).Wavelet Footprints: Theory, Algorithms, and Applications.

Esqueda,J., y Palafox, L. (2005). Fundamento de procesamiento de imágenes. México: Departamento Editorial de la Universidad Autónoma de Baja California.

Fernández, A. (2007). Estudio de técnicas basadas en la transformada wavelet y optimización de sus parámetros para la clasificación por textura de imágenes digitales. (Tesis doctoral). Universidad Politécnica de Valencias, España. Recuperado el 10 de octubre de 2012, de http://riunet.upv.es/bitstream/handle/10251/1955/tesisUPV2573.pdf.

Gómez, E., Obregón, N., y Rocha, D. (2013). Métodos de segmentación de nubes en imágenes satelitales. Tecnura, 77(36), 95-110.

Gao, R., y Yan, R. (2010). Wavelets Theory and Applications for Manufacturing. New York: Springer.

Hernández, R. (2010). Procesamiento digital de imágenes de ultrasonido. (Tesis de pregrado). Instituto Politécnico Nacional, México. Recuperado el 15 de diciembre de 2012, de http://itzamna.bnct.ipn.mx/dspace/bits-tream/123456789/8591/l/582.pdf.

Isa, N.A.M., Salamah, S.A., y Ngah, U.K. (2009). Adaptive Fuzzy Moving K-means Clustering Algorithm for Image Segmentation. Consumer Electronics IEEE Transactions, 55, 2145-2153. DOI: 10.1109/ TCE.2009.5373781

Kim, K., Zhang, D., Kang, M., y Ko, S. (2013). Improved Simple Linear Iterative Clustering Superpixels. Consumer Electronics (ISCE), IEEE 17th International Symposium, pp. 259-260. DOI: 10.1109/ ISCE.2013.6570216.

Kaplan, N.H., y Erer, I. (2013) An Additive Empirical Mode Decomposition Based Method for The Fusion of Remote Sensing Images. Recent Advances in Space Technologies (RAST), 6th International Conference, pp. 165-169. DOI: 10.1109/ RAST.2013.6581193.

Pepsi, M., y Mala, K. (2013).Similarity Search On Metric Data Of Outsourced Lung Images. Green High Performance Computing (IC-GHPC), IEEE International Conference, pp. 1-6.DOI: 10.1109/ICGHPC.2013.6533912.

Pradnya, P.M., y Sachin, D R. {20U).Wavelet Based Image Fusion Techniques. Intelligent Systems and Signal Processing (ISSP), International Conference, pp. 77-81.DOI: 10.1109/ISSP.2013.6526878.

Parmar, I.M., y Patil, S.A. (2013). Performance Evaluation and Comparison of Modified Denoising Method and the Local Adaptive Wavelet Image Denoising Method. Intelligent Systems and Signal Processing (ISSP), International Conference, pp. 101-105. DOI: 10.1109/ISSP.2013.6526883.

Rinehart, R. (2004). Radar for Meteorologists (Fifth Edition). Rinehart Publishing.

Sruthy, S., Parameswaran, L., y Sasi, A.P. (2013). Image Fusion Technique Using DT-CWT. Automation, Computing, Communication, Control and Compressed Sensing (iMac4s), International Multi-Conference, pp. 160-164.DOI: 10.1109/iMac4s.2013.6526400.

Saraswathi, S., y Allirani, A. (20\3).Survey on Image Segmentation Via Clustering. Information, Communication and Embedded Systems (ICICES), International Conference, pp. 331-335. DOI: 10.1109/ ICICES.2013.6508376.

Wenlong, F., Hong, L., y Zhihui, W. (2009). Satellite Cloud Image Segmentation Based on the Improved Normalized Cuts Model. Information Science and Engineering (ICISE), 1st International Conference, pp. 1418-1421. DOI: 10.1109/ICISE.2009.1044.

Xiang, L., Ramachandran, R., He, M., Mowa, S., Rushing, J., Graves, S., Lyatsky, W., Arjun, T. y Germany, G. (2004). Comparing Different Thresholding Algorithms for Segmenting Auroraslnformation Technology: Coding and Computing. Proceedings. ITCC. International Conference, 2, 594 -601. DOI: 10.1109/ITCC.2004.1286718.

Xie S., Wang, C. y Yang, Z. (2013). Image Compression Using Wavelet Transform with Lifting Scheme and SPIHT in Digital Cameras for Bayer CFA. Wavelet Analysis and Pattern Recognition (ICWAPR), International Conference, pp. 163-167. DOI: 10.1109/ ICWAPR.2013.6599310.

Zhiying, L., Huan, Z., Hongmin M. y Huizhen, J., (2010). Hailstone Detection Based on Time Series Association Rules. Fuzzy Systems and Knowledge Discovery (FSKD), Seventh International Conference, 5, 2143-2146. DOI: 10.1109/FSKD.2010.5569742.

Zafra, C. (2008). Análisis de métodos de procesamiento de imágenes estereoscópicas forestales. (Tesis de maestría) .Universidad Complutense de Madrid, España. Recuperado el 10 de octubre de 2012, de http://eprints.ucm.es/10046/l/Carlos_Zafra_Fer-nandez_de_Tejada_Curso_2007-08.pdf.