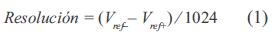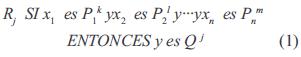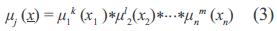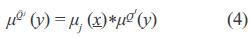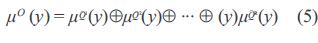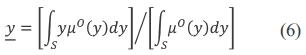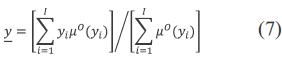Generación automática de sistemas lógicos difusos (SLD) tipo Mamdani sobre microcontrolador de 8 bits

Generación automática de Sistemas Lógicos Difusos tipo Mamdani sobre microcontrolador de 8 bits

Automatic generation of Mamdani fuzzy logic systems on 8-Bit microcontroller

Sebastián Fernando Puente Reyes¹, César Andrey Perdomo Charry², Elvis Eduardo Gaona García³

¹Ingeniero Electrónico, estudiante de la Maestría en Ciencias de la Información y las Comunicaciones de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: sfpuenter@correo.udistrital.edu.co
²Ingeniero Electrónico, magíster en Ciencias de la Información y las Comunicaciones. Docente de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: cperdomo@udistrital.edu.co
³Ingeniero Electrónico, magíster en Ciencias de la Información y las Comunicaciones. Docente de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: egaona@udistrital.edu.co

Fecha de recepción: 15 de octubre de 2012 Fecha de aceptación: 12 de febrero de 2013

Resumen

En los últimos años, en diferentes sectores como el científico e industrial, ha aumentado considerablemente el uso de los Sistemas Lógicos Difusos (SLD), obteniéndose un considerable número de aplicaciones. Existen varias herramientas que permiten el desarrollo de estos sistemas que en su mayoría son paquetes de software costosos para PC o hardware costoso difícil de obtener. En este documento se presenta el desarrollo y resultados de la herramienta creada, la cual brinda la posibilidad de interactuar con los sistemas lógicos difusos tipo Mamdani permitiendo su implementación como sistema embebido y con características limitadas sobre un microcontrolador PIC (Peripheral Interface Controller o Controlador de Interfaz Periférico) de 8 bits de Microchip Inc. El objetivo principal es la generación automática del código en lenguaje C para el SLD deseado por el usuario, el cual será establecido a través de la herramienta desarrollada en Matlab integrando las diferentes funciones que ofrece el Fuzzy Logic Toolbox.

Palabras clave: lógica difusa, microcontrolador, sistemas lógicos difusos tipo Mamdani.

Abstract

In the last years in different sectors such as science and industry has greatly increased the use of fuzzy logic systems, obtaining a considerable number of applications. There are several tools that allow the development of these systems, which are costly software packages for PC or expensive hardware that is difficult to obtain. This paper presents the development and results of the tool that was created, which provides the possibility to interact with Mamdani Fuzzy Logic Systems, allowing its implementation as embedded system and with limited features on a 8 bits microcontroller PIC from Microchip Inc. The main objective is the automatic generation of the C code for fuzzy logic system wanted by the user, which will be established through the tool developed in Matlab integrating the different features offered by the Fuzzy Logic Toolbox.

Key words: fuzzy logic, microcontroller, Mamdani fuzzy logic systems.

1. Introducción

El concepto de lógica difusa fue introducido por Lotf Zadeh en 1965 con su famoso artículo "Fuzzy Sets" [1]. Zadeh presentó los conjuntos difusos para procesar y manipular información y datos afectados de incertidumbre e imprecisión no probabilística. Fueron diseñados para representar matemáticamente incertidumbre y vaguedad, y proporcionar herramientas formalizadas para trabajar con la imprecisión intrínseca en muchos problemas. La lógica difusa debe su éxito a que puede procesar información lingüística y numérica sin la necesidad de un modelo matemático preciso, ya que actúa de acuerdo a información empírica establecida mediante reglas difusas dictadas por un experto [2], [3]. De ahí su creciente intervención en la ingeniería como solución a problemas y un sinnúmero de aplicaciones en diferentes sectores de la industria, situación en la cual se hace casi imposible la obtención de modelos exactos que involucren todas las excepciones posibles en un sistema [4], [5]. Ha sido tanta la aceptación de la lógica difusa que desde hace varios años es ampliamente utilizada para aplicaciones en el hogar [6].

Los sistemas de control automático han sido el campo más explotado de la lógica difusa con sus inicios en 1972, cuando Mamdani aplicó un algoritmo difuso para el control de una planta donde la inferencia es realizada a través de una base de reglas [7]. En 1984, Sugeno presentó un control difuso para el parqueo automático de un automóvil, donde el esquema de control difuso tiene un consecuente basado en ecuaciones lineales de primer orden, proporcionando así más versatilidad a los sistemas difusos [8], [9].

La implementación de SLD ha sido diversa de acuerdo a los requisitos de las diferentes aplicaciones. Se tienen las implementaciones software, las cuales se caracterizan por el uso de un lenguaje de programación de alto nivel, presentando la desventaja de la ejecución de un código secuencial, lo que hace que este tipo de implementaciones deba aplicarse a procesos que no demanden un alto tiempo de respuesta en la salida del SLD.

Las implementaciones software tienen la gran ventaja del bajo costo, mayor versatilidad y la posibilidad de ser llevadas a sistemas embebidos como un microcontrolador (MCU), obteniéndose así, en adición, las ventajas de este tipo de sistemas [10] - [13].

Desde mediados de 1980 se ha presentado una buena cantidad de implementaciones de SLD en hardware, cuya ventaja principal es la alta velocidad de procesamiento y el uso del paralelismo. La desventaja de las implementaciones en hardware es el alto costo de la tecnología utilizada (Very Large Scale Integration [VLSI], Application – Specific Integrated Circuit [ASIC], y Field Programmable Gate Arrays [FPGA]) [14], y la necesidad de hardware periférico. Sin embargo, son la opción a elegir cuando de acuerdo a la aplicación se requieran SLD de alta velocidad de respuesta.

En resumen, existe gran variedad de implementaciones de SLD tanto en software como en hardware, dependiendo de las diferentes aplicaciones. Las implementaciones software para sistemas embebidos prácticamente son realizadas manual y específicamente para cada caso, requiriendo que la persona que las lleve a cabo sea especialista tanto en los SLD como en el perfecto manejo de la plataforma seleccionada, lo que resulta en una gran limitación que hace este proceso lento, costoso y de difícil acceso especialmente para entornos educativos. De esta manera, se hace deseable contar con una herramienta o entorno que de forma automática haga transparente para el usuario el proceso de trasladar el SLD como sistema embebido a la plataforma seleccionada, y en adición, se reduzca el tiempo de desarrollo para un SLD.

La herramienta desarrollada permite a un bajo precio la implementación en MCU (PIC18F452) [15] de un SLD tipo Mamdani con características limitadas. El objetivo principal es la generación automática del código en lenguaje C para el SLD deseado por el Usuario, el cual será establecido a través de la herramienta desarrollada en Matlab, integrando las diferentes funciones que ofrece el Fuzzy Logic Toolbox [16]. En el presente artículo se muestra a manera global la metodología utilizada y los resultados obtenidos durante el desarrollo del proyecto.

Como primera parte, se realizó una revisión teórica de los SLD tipo Mamdani y metodologías usadas para su implementación software en sistemas embebidos. Luego, se hizo una revisión a la arquitectura del MCU utilizado y herramientas para su programación en C. Posteriormente, se crea en C un SLD tipo Mamdani general, de tal forma que sea lo suficientemente f exible para poder ajustarse a las características que establezca el usuario. Una vez logrado lo anterior, se presenta la herramienta en Matlab que hace posible la generación automática del código en lenguaje C para el SLD, para que así pueda ser llevado al MCU. Por último, se presenta la validación con diferentes pruebas realizadas obteniendo de esta manera los diferentes resultados y las conclusiones respectivas.

2. Implementación de sistemas Lógicos difusos en sistemas Embebidos

La implementación dentro de sistemas embebidos resulta ser una de las opciones más apropiada para muchas de las aplicaciones de la lógica difusa como el control difuso. En la literatura se encuentra un gran número de implementaciones hardware cuya ventaja principal es la alta velocidad de procesamiento y el uso del paralelismo [14]. Como desventajas de las implementaciones hardware de SLD encontramos el alto costo de la tecnología utilizada (Very Large Scale Integration [VLSI], Application Specific Integrated Circuit [ASIC], y Field Programmable Gate Arrays [FPGA]), mayor consumo de potencia y poca fexibilidad. Por otra parte, periféricos externos como una memoria y hardware extra para el acondicionamiento de la entrada y la salida del SLD son requeridos, añadiendo costo, espacio y complejidad al sistema global. Las implementaciones hardware son la opción a elegir cuando de acuerdo a la aplicación se requiera una alta velocidad de respuesta del SLD.

Una opción más fexible, amplia y fácil es la implementación en MCU, donde, dependiendo de los requerimientos del sistema, pueden elegirse arquitecturas de MCU de 8, 16 o 32 bits de acuerdo a la velocidad y resolución requerida [10] - [13]. Es importante aclarar que este tipo de implementación es solo aplicable para casos donde el tiempo de respuesta sea apropiado para el sistema global. A manera de costo-rendimiento, resulta más eficiente el uso de un sistema de procesamiento estándar (MCU) a un 90 % de su capacidad que un sistema de procesamiento dedicado (ASIC) a un 10 % de su capacidad [12].

Por lo general, los sistemas embebidos como un MCU pueden ser programados directamente en lenguaje ensamblador, o por medio de un lenguaje de programación de alto nivel como el lenguaje C utilizando el compilador específico. La desventaja de este tipo de implementaciones es la ejecución de un código secuencial, pero esto es compensado por la alta integración, bajo costo y fácil uso.

El proceso de inferencia difusa consta de tres pasos, los cuales pueden realizarse eficientemente usando las operaciones matemáticas de un MCU estándar. Aprovechando todo lo anterior, actualmente existen varios trabajos que abordan la implementación de un SLD en MCU de propósito general para una determinada aplicación, entre las cuales tenemos: navegación de robots [17], [18], control de motores [19], convertidores DC-DC [20], control de velocidad en vehículos eléctricos [21], ahorro de energía en motores de inducción [22], aprovechamiento máximo de la energía en un panel solar [23], [24], optimización de acelerómetros [25], entre otros.

Por otro lado, las implementaciones software para sistemas embebidos como el MCU, prácticamente son realizadas manual y específicamente para cada caso, requiriendo que la persona que las lleve a cabo sea especialista tanto en los SLD como en el perfecto manejo del MCU y lenguaje de programación seleccionado. Lo que resulta en una gran limitación que hace este proceso lento, costoso y de difícil acceso especialmente para entornos educativos. De esta manera, es deseable contar con una herramienta o entorno que haga transparente para el usuario y de forma automática el proceso de trasladar el SLD al MCU, y en adición, se reduzca el tiempo de desarrollo para el SLD requerido para determinada aplicación.

3. Sistemas lógicos difusos tipo Mamdani

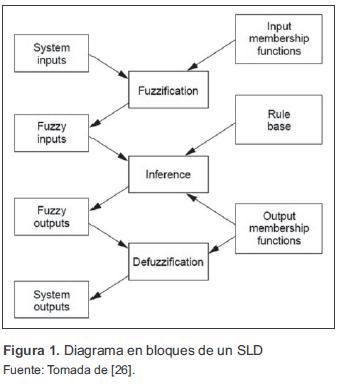
Un SLD utiliza procesos de razonamiento difuso para convertir entradas concretas (crisp) en salidas crisp. Los tres principales componentes de un SLD son: una sección de fuzificación, el mecanismo de inferencia, y una sección de desfuzificación. Un conjunto de reglas, generalmente en la forma modus ponens (si-entonces) llamada base de reglas, especifica cómo son tomadas las decisiones con base en las entradas medidas. La figura 1 muestra un diagrama en bloques de un SLD.

El SLD tipo Mamdani es el más comúnmente tratado en la metodología difusa y fue uno de los primeros sistemas de control construidos usando la teoría de conjuntos difusos. Fue propuesto en 1975 por Ebrahim Mamdani como un intento para controlar una máquina de vapor por medio de la sintetización de un conjunto de reglas de control lingüísticas obtenidas a través de la experiencia humana de los operadores [7]. En estos sistemas, el consecuente de cada regla es un conjunto difuso. Por el contrario, en el SLD tipo Takagi-Sugeno [27], los consecuentes son expresiones matemáticas.

En el bloque de fuzificación se asigna a las entradas del sistema un grado de pertenencia a cada uno de los conjuntos difusos que se han definido mediante las funciones de pertenencia de entrada. Las entradas a este bloque son valores crisp de las entradas y las salidas son grados de pertenencia a los conjuntos difusos. En el bloque de inferencia, el mecanismo de inferencia determina el grado en que cada regla de la base de reglas se aplica a la situación actual del sistema y forma un correspondiente conjunto difuso de implicación-de cada regla. Si la regla presenta una conjunción de varias entradas como antecedente, el grado de activación de cada regla es determinado por la aplicación de un operador t-norma de cada una de las entradas de la conjunción. La función de pertenencia del conjunto difuso de implicación de cada regla es calculada por la aplicación de un operador t-norma entre el grado de activación de la regla y la función de pertenencia del conjunto difuso de salida para la regla. Después de evaluar todas las reglas y obtener los conjuntos difusos de implicación correspondientes, estos son combinados por medio del mecanismo de agregación que se lleva a cabo mediante la aplicación de un operador t-conorma, de esta manera se forma un único conjunto difuso de salida. En el bloque de desfuzificación, el conjunto difuso de salida es llevado a un valor crisp a través de un método de desfuzificación. Para una mayor profundización ver [4], [5], [27], [28], [29].

4. Metodología

Como se mencionó anteriormente, el objetivo principal es la generación automática del código en lenguaje C para el SLD deseado por el usuario, el cual será establecido a través de la herramienta desarrollada en Matlab integrando las diferentes funciones que ofrece el Fuzzy LogicToolbox. Para ello, se dividió en dos partes o subsistemas la elaboración de dicha herramienta. La primera parte consiste en la creación en C de un SLD tipo Mamdani en su forma más general. La segunda parte aborda la creación del software en Matlab para la herramienta.

Es importante aclarar que, en cuanto al tiempo de respuesta para un SLD, el presente trabajo no abordó como objetivo principal la optimización de dicho tiempo. Lo anterior podrá ser abordado por trabajos futuros que busquen la reducción en el tiempo de respuesta mediante diferentes técnicas.

4.1 Desarrollo del SLD tipo Mamdani general

A continuación se presentan los aspectos generales y desarrollo del código en lenguaje C para un SLD tipo Mamdani en forma general.

4.1.1 Especii caciones generales

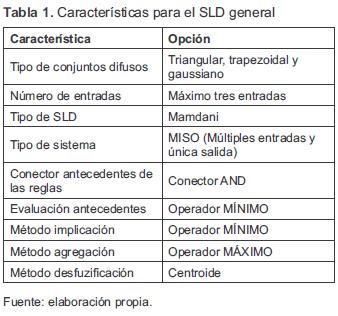
Algunas partes del código (definición de los conjuntos difusos, obtención de las entradas, base de reglas, entre otros) son modificadas automáticamente por medio del software de la herramienta de acuerdo a las características establecidas por el usuario. El código general en C del SLD puede manejar y está limitado a las características que se describen a continuación y que se resumen en la tabla 1. Lo anterior, de acuerdo con los recursos hardware y software que brinda el MCU escogido (PIC18F452). Se eligió trabajar con este MCU de 8 bits, ya que posee buena cantidad de memoria de programa y de datos, facilitando su programación en C a través del compilador MPLAB C18 de Microchip. En adición, este MCU puede ser conseguido fácilmente en el mercado nacional a un bajo precio [15].

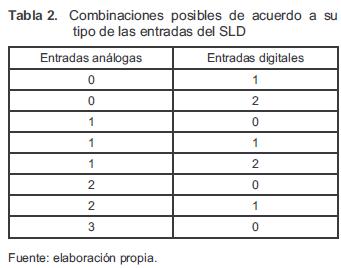
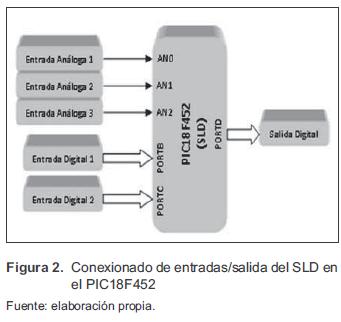
1. Entradas/Salidas. El SLD puede tener como máximo 3 entradas y una única salida, las entradas pueden ser digitales o análogas de acuerdo a la tabla 2. El rango para las entradas análogas es de 0-5 Voltios. La resolución para las entradas digitales y para la salida es de 8 bits. En la figura 2 puede verse la configuración de los puertos del MCU para el conexionado de las entradas y salidas del SLD. Las entradas análogas son convertidas a digitales por medio del conversor A/D del MCU, el cual tiene una resolución de 10 bits y 8 canales de entrada. La resolución que tiene cada bit procedente de la conversión tiene un valor que es función de la tensión de referencia Vref como se ve en la ecuación (1). Luego, la resolución será de 4,8 mV/bit.

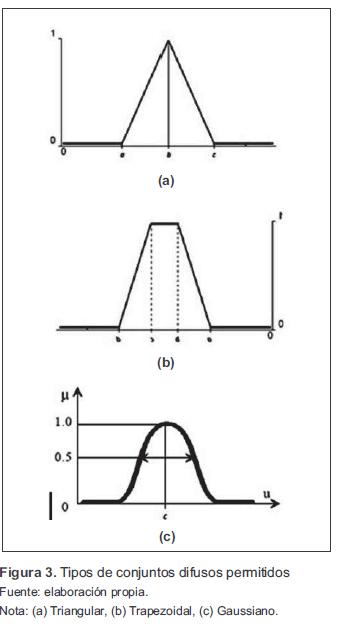
2. Tipos de conjunto. Los conjuntos que pueden ser usados son: tipo triangular, trapezoidal y gaussiano (figura 3). El número máximo de conjuntos por variable es de 9, lo que implica que en total se pueden tener máximo 36 conjuntos en el SLD.

3. Reglas difusas. El tipo de reglas que pueden ser establecidas en el módulo son de la forma que se presenta en la sentencia (1), la cual obedece a la forma modus ponens y representa la regla R_j para un SLD con entradas, x₁, x₂,^..., x_n, y una salida y.

Donde, x_n es una variable lingüística de entrada definida en el universo X_n, P_n^m es un valor m lingüístico descrito por el conjunto difuso P_n definido en el universo X_n, es la variable lingüística de salida definida en el universo Y, y Q ^j es un valor lingüístico descrito por el conjunto difuso Q ^j definido en el universo Y. La primera parte de la sentencia (1), "x₁ es P₁ ^k ", es llamado el antecedente de la regla. En este caso para la sentencia (1), el antecedente es una conjunción de condiciones. Y la segunda parte de la sentencia (1), "y es Q ^j", es llamado el consecuente de la regla. El consecuente de la regla es afrmado por la afirmación del antecedente, es decir, si el antecedente es verdadero, el consecuente es también verdadero.

4. Inferencia difusa. Como se mencionó anteriormente, la primera función de la etapa de inferencia es determinar el grado de activación de cada regla de la base de reglas, considerando la regla R_j en la sentencia (1), la cual tiene n entradas x₁, x₂,... x_n. El producto cartesiano P^k×P^l×...×P es el conjunto difuso que indica la combinación de los conjuntos difusos del antecedente de la regla. El conjunto P_n está caracterizado por la función de pertenencia µ_n^m. Luego, el conjunto difuso denotado por µP^k×P^l×...×P^m, es caracterizado por la función de pertenencia P^k×P^l×...×P^m. Para una entrada particular conjuntos por variable es de 9, lo que implica real µ(P₁ ^k×P₁ ^l×...×P_n^m) x = (x₁, x₂,...x_n) ε X₁×que en total se pueden tener máximo 36 con-X₂×^...×X , se dice entonces que la regla R_j es activada con un grado de (ver ecuación (2)):

Donde el operador^* es un operador t-norma (mínimo, producto, etc.). La ecuación (2) es un número real en el intervalo [0,1]. En forma general, el conjunto difuso P^k×P^l×^...×P^m es llamado el conjunto difuso del antecedente para la Regla 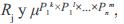, que se puede denotar por µ_j, es llamado la función de pertenencia del antecedente para la regla . Entonces, para una entrada particular real x, la regla R_j es activada con un grado expresado por la ecuación (3).

Para el presente trabajo, el operador t-norma empleado para la ecuación (3) es el operador mínimo.

La segunda función de la etapa de inferencia es determinar el grado en que la recomendación de cada regla será ponderada para llegar a la decisión final y determinar un conjunto difuso implicado para cada regla. Considerando la regla R_j en la sentencia (1) con una entrada x = x₁, x₂, ...x_n, la cual es activada con un grado µ_j (x). Se tiene que la recomendación de la regla R_j, representada por el conjunto difuso Q ^j caracterizado por (µQ^s (y), es atenuada o ponderada por el factor _j (x). Lo anterior produce un conjunto difuso implicado Q^{^ j} de-finido en Y ^j y caracterizado por la función de pertenencia en la ecuación (4).

Donde el operador es un operador t-norma (por ejemplo, mínimo, producto, etc.). Para el presente trabajo, el operador t-norma empleado para la ecuación (4) es el operador mínimo.

Si hay reglas de la forma (2), cada regla tiene su propio grado de activación µ_j (x), j =1, 2,..., R. Las R reglas producen los conjuntos difusos implicados Q^{^ j}, j =1, 2,..., R, cada uno caracterizado por la función de pertenencia calculada con la ecuación (4).

Después de evaluar todas las reglas y obtener cada uno de los conjuntos difusos implicados correspondientes Q^{^ j} con sus funciones de pertenencia µ^{Q^ j} (y), estos son combinados a través del mecanismo de agregación, formando así un único conjunto difuso de salida O definido en Y y caracterizado por la función de pertenencia expresada por la ecuación (5)

Donde el operador es un operador t-conorma (por ejemplo, máximo, suma algebraica, entre otros). Para el presente trabajo, el operador t-conorma empleado para la ecuación (5) es el operador máximo.

5. Desfuzificación. Existen varios métodos para el proceso de desfuzificación, de los cuales los más conocidos son: valor máximo, media de los máximos, método de la altura y centro de gravedad. El método que se escogió para convertir el conjunto de salida total a un valor concreto (valor crisp) fue el del centro de gravedad o centroide [4], [27], [29], el cual se calcula de acuerdo a la ecuación (6).

Donde S denota el soporte de µ^O (y). Frecuentemente y para este caso, S es discretizado, de modo que la salida crisp y del SLD puede ser aproximada por la ecuación (7).

Donde I es el número de muestras en que µ^O (y) es discretizado. Para este caso, se escogió un valor de I=80. Lo que quiere decir que el conjunto de salida del SLD O es discretizado usando 80 muestras.

4.1.2 Programación en C del SLD

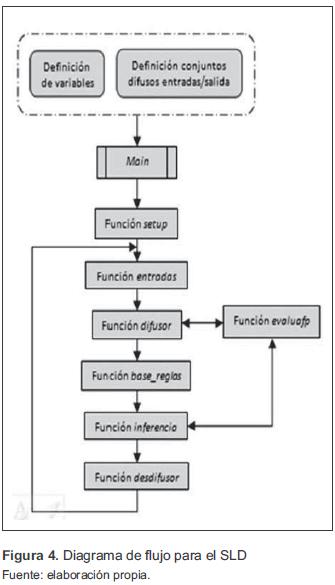
El código general para un SLD tipo Mamdani se realizó en lenguaje C para ser implementado en el PIC18F452. Se eligió la programación en lenguaje C por su facilidad en el manejo de las funciones y módulos del PIC. Para lograr esto, se usó el software MPLAB C18 (compilador de C para la familia de los MCUs PIC18xxxx), que puede ser integrado al software de desarrollo MPLAB IDE v8.83. Tanto el compilador C, como el entorno de desarrollo MPLAB, pueden ser obtenidos a través de la página web de Microchip (http://www.microchip.com).El diagrama de flujo del software para el SLD está dividido en varias subrutinas (figura 4). Las subrutinas o funciones se describen a continuación:

1. Función setup: se configuran los respectivos puertos del MCU para las variables de entrada y la variable de salida del SLD.
2. Función entradas: se obtienen las entradas análogas del SLD para ser digitalizadas en un código de 10 bits a través del módulo A/D del MCU, y se obtienen las entradas digitales a través de los puertos B y C.
3. Función difusor: se evalúan los grados de pertenencia a los conjuntos difusos definidos para un valor concreto de cada una de las entradas del SLD. El cálculo de los grados de pertenencia se realiza de acuerdo al tipo de conjunto difuso por medio de la función característica respectiva.
4. Función evaluafp: se aplica la función característica para un valor (), dependiendo del tipo de conjunto y sus respectivos parámetros.
5. Función base_reglas: se almacenan todas las reglas para el SLD y se llama a la función inferencia en cada una de las reglas para aplicar el proceso de inferencia de acuerdo a los grados de pertenencia de la entrada a los conjuntos difusos involucrados en la regla.
6. Función inferencia: se realizan para cada una de las reglas que se encuentran en la función base_reglas las siguientes tareas: aplicación del operador mínimo en los antecedentes de cada regla, aplicación del método de implicación por medio del operador mínimo y agregación de todas las salidas por medio del operador máximo.
7. Función desdifusor: se aplica el método de desdifusión del centroide al conjunto difuso de salida total del SLD, y así, se obtiene un valor concreto (crisp) como salida para el SLD. El valor crisp de la salida tiene una resolución de 8 bits y es fijado en la salida física del SLD, puerto D del MCU. El conjunto difuso de salida total es un conjunto discretizado usando 80 muestras, ya que el centro de gravedad es calculado por medio de la ecuación (7).

4.2 Desarrollo del software de la herramienta en Matlab

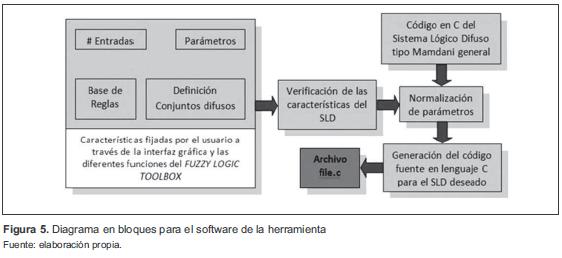
El software de la herramienta es el encargado de recibir todas las características específicas: definición de las variables de entrada y la variable de salida, definición de los conjuntos difusos que conforman cada variable, reglas difusas o base de conocimiento, tipos de conjuntos difusos a usar, entre otras, requeridas por el usuario para el diseño del SLD deseado.

El diseño del SLD se realiza mediante la integración de las diferentes funciones que ofrece el Fuzzy Logic Toolbox de Matlab [16]. Después de especificar el SLD deseado, el software procede a verificar todas las características vistas en la tabla 1, para así proceder a crear el código en lenguaje C del SLD. En la figura 5 puede verse el diagrama en bloques del software desarrollado en Matlab.

El software en su totalidad permite realizar las siguientes tareas:

1. Crear un SLD tipo Mamdani usando las funciones del Fuzzy Logic Toolbox.
2. Abrir un SLD tipo Mamdani usando las funciones del Fuzzy Logic Toolbox.
3. Editar las diferentes propiedades o características para el SLD usando el Fuzzy Logic Toolbox.
4. Verificar las propiedades para establecer si el SLD puede ser implementado en el MCU PIC18F452.
5. Generar el código en lenguaje C para el SLD deseado.

5. Resultados

En esta sección se presentan los resultados y el análisis de resultados obtenidos para el SLD difuso sobre el MCU PIC18F452, teniendo en cuenta diferentes aspectos como el número de entradas, cantidad de conjuntos, tipos de conjuntos, cantidad de reglas, número de reglas activadas, etc. Las pruebas que se hicieron para obtener estos resultados se basaron en observar el uso de la memoria de programa y datos del PIC18F452, los tiempos de respuesta y la fiabilidad en la salida del SLD.

5.1 Análisis del uso de memoria de programa y datos del PIC18F452

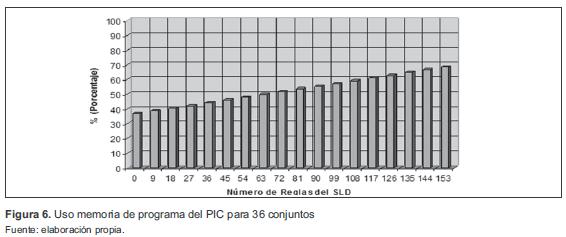
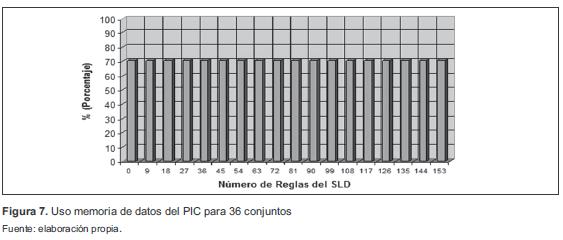
El código en C diseñado para una SLD tipo Mamdani resulta ser muy efectivo, ya que no usa en totalidad las prestaciones del MCU. Para la memoria de programa, el número máximo de instrucciones que se pueden tener es de 16 384 (100 %), y el número máximo de bytes en la memoria de datos que posee el mismo es de 1536 (100 %). Las figuras 6 y 7 presentan los resultados obtenidos teniendo en cuenta el máximo número de conjuntos difusos posibles (36 conjuntos). Se puede observar que para las características máximas que pueden configurarse en la herramienta, el uso de la memoria de programa no supera el 80 % y solo se emplea el 70,8 % de la memoria de datos, brindando así la posibilidad de hacer adiciones o ajustes al software, o la inclusión de otros subprogramas o rutinas por parte del usuario.

Cuando se tienen menos conjuntos en las variables de entrada, la memoria de programa es menos utilizada, ya que los conjuntos difusos de las entradas son almacenados en la memoria de programa. Y cuando se tienen menos conjuntos para la variable de salida, se usa menos la memoria de datos, ya que los conjuntos difusos para la salida son almacenados en la memoria de datos.

El aumento del número de reglas difusas hace que se ocupe más espacio en la memoria de programa. Como se ve en la figura 6, para un sistema con las características máximas en el número de conjuntos y de variables de entrada, si se tienen 153 reglas el SLD ocupa solamente el 68,44 % en memoria de programa y el 70,77 % en memoria de datos, lo que es muy bueno, ya que podrían agregarse un poco más de reglas al SLD. Sin embargo, un SLD con un número elevado de reglas difusas no es muy común, ya que no es la intención en sí de los SLD.

En cuanto al uso de memoria de programa y de datos por parte de los conjuntos difusos, resulta indiferente el tipo de conjunto usado en cada una de las variables, ya que los tres tipos de conjuntos (triangular, trapezoidal o gaussiano) que pueden usarse en el módulo son definidos en una forma estándar bajo el mismo número de parámetros y ocupan el mismo espacio en memoria.

5.2 Análisis de los tiempos de respuesta para un SLD

Se estableció como frecuencia de operación 40 MHz, usando un cristal externo de 10 MHz. Esta frecuencia se logra a través de un circuito PLL interno en el PIC que da la opción de multiplicar por 4 la frecuencia del cristal, consiguiendo los 40 MHz a partir de una frecuencia de entrada de 10 MHz. Luego, el ciclo de instrucción es de 100 ns y los periféricos funcionarán a 40 MHz.

Los tiempos de respuesta de cada una de las partes del SLD son variantes, ya que dependen del número de entradas, número de conjuntos de cada una de las variables, tipo de conjunto, número de reglas y número de reglas que se activen de acuerdo a los valores en las variables de entrada. Luego, nunca existirá un tiempo constante para cada ciclo del SLD ni para todos los SLD.

A continuación se presentan los tiempos de respuesta para un SLD que controla la temperatura en una incubadora [30].

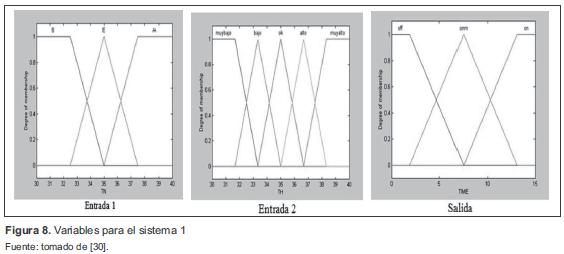
5.2.1 Sistema 1

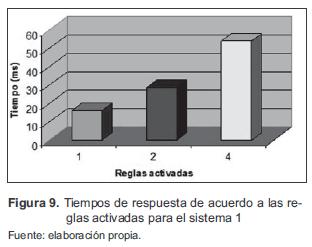
El primer sistema es un SLD con 15 reglas difusas, dos entradas y la salida, usando conjuntos triangulares y trapezoidales (figura 8). La figura 9 visualiza los resultados para el sistema 1.

5.2.2 Sistema 2

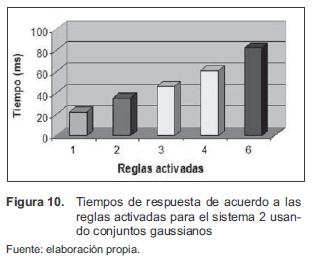
Es el mismo sistema 1, pero usando conjuntos tipo gaussiano en sus dos entradas, mientras que la salida tiene los mismos conjuntos de la figura 8. La figura 10 visualiza los resultados para el sistema 2.

En cuanto a los tiempos de respuesta de acuerdo con los diferentes bloques del SLD, se tiene lo siguiente.

El tiempo para el bloque Setup es constante para el SLD ya que en este se realiza la inicialización de las diferentes variables del sistema. El tiempo necesario para la obtención de las entradas del SLD es constante y depende del tipo de la variable, es decir, si son entradas análogas o digitales. El tiempo de adquisición para una variable análoga es de 37,2 us, y el tiempo de adquisición para una variable digital es de 0,4 us.

El tiempo del bloque difusor es variable y depende de:

1. El valor de las entradas del sistema: ya que un valor determinado en una entrada del sistema, puede pertenecer a un solo conjunto o a dos conjuntos difusos.
2. Tipo de conjunto: de acuerdo con el tipo de conjunto al que se le evalúa la pertenencia de un valor para una entrada los tiempos varían, ya que si el conjunto difuso es de tipo gaussiano, los tiempos para el cálculo del grado de pertenencia son mucho mayores que los tiempos necesarios para los conjuntos tipo triangular o trapezoidal, debido a que los conjuntos tipo gaussiano tienen un soporte mayor que los trapezoidales y triangulares.
3. Número de conjuntos: el tiempo aumentará si hay más conjuntos difusos por evaluar.

El tiempo de respuesta para un SLD depende del número de reglas que se activan para determinados valores de las variables de entrada, debido a que cada una de las reglas tiene un determinado conjunto de salida después de realizar el proceso de inferencia.

La evaluación de las reglas es el proceso que requiere más tiempo dentro del SLD. Este tiempo depende del número de reglas difusas que tenga el SLD, ya que habrá que evaluar cada una de ellas y esto aumentará el tiempo. La evaluación de una regla difusa que no es activada tiene un tiempo de 11,6 us aproximadamente usando conjuntos triangulares o trapezoidales y 14,8 us usando conjuntos gaussianos. Luego, el tiempo de respuesta del SLD dependerá del diseño de la base de reglas y de la determinación de los conjuntos para cada variable.

El tiempo que gasta el desdifusor en hallar un valor concreto (crisp) a través del centro de masa no supera los 8 ns para cualquier tipo de conjunto usado. Este tiempo no varía mucho, ya que el conjunto total de salida se encuentra discretizado en un total de 80 muestras y dependerá del número de muestras diferentes de cero.

Cuando se usan conjuntos gaussianos se obtienen mayores tiempos de respuesta para el SLD, ya que se activan más reglas. Lo anterior es debido a que los conjuntos gaussianos poseen una base más ancha que los triangulares o trapezoidales y un valor correspondiente en una variable de entrada puede pertenecer hasta en 3 conjuntos al mismo tiempo. Para que no se tuvieran tiempos de respuesta mucho mayores cuando se usan conjuntos gaussianos, se estableció que si el grado de pertenencia a un conjunto no es superior al 1 %, se tomará como una no pertenencia, es decir 0 %.

5.3 Fiabilidad en la salida del SLD

De acuerdo con los resultados obtenidos para los sistemas 1 y 2 vistos anteriormente, a través de la simulación (simulación realizada mediante el MPLAB IDE 8.83 y el MPLAB C18) del código en C generado por la herramienta creada para el PIC del SLD, y los resultados obtenidos para el mismo sistema por medio del Fuzzy Logic Toolbox de Matlab 6.0, se pudo observar que los resultados obtenidos por medio de la herramienta se diferencian por menos del 0,7 % a los resultados obtenidos por medio del Fuzzy Logic Toolbox de Matlab. Lo anterior hace que el código generado para un determinado SLD a través del software del módulo sea muy fable, obteniendo así resultados verídicos y seguros.

6. Conclusiones

La herramienta elaborada facilita la implementación de SLD tipo Mamdani de una manera sencilla usando para ello recursos hardware económicos, haciendo así más accesible el manejo de este tipo de sistemas usados actualmente en muchas aplicaciones con gran éxito.

La utilización del PIC18F452 de Microchip Inc. ofreció grandes ventajas, ya que tiene una memoria de programa y de datos superiores a la de los PIC clásicos, trabaja hasta 40 MHz y es eficaz para la programación en C, facilitando considerablemente el desarrollo del SLD tipo Mamdani general, ya que permite hacer más manejable la programación, el manejo de números en coma fotante, el uso de librerías matemáticas y de datos indispensables para el correcto desarrollo.

El código en C desarrollado resulta ser muy eficiente en cuanto al uso de recursos del PIC18F452, ya que no usa más del 80 % de cada una de las memorias del PIC, aún teniendo las características máximas configuradas para el SLD.

El tiempo de respuesta para un determinado SLD será variable y dependerá de cada una de las características fijadas para el mismo (la base de reglas, tipos de conjuntos difusos y número de entradas).Para obtener mejores tiempos de respuesta para un determinado SLD es conveniente no usar conjuntos difusos tipo gaussianos, ya que estos aumentan un poco el tiempo de respuesta del sistema. Pueden ser usados siempre y cuando el tiempo para la aplicación específica no sea crítico.

La respuesta para un determinado SLD e implementado en el PIC tendrá como máximo un margen de error del 0,7 %, lo que hace que sea muy fable y se tengan resultados fables y verídicos.

Por último, el presente trabajo abre las puertas a dos, como por ejemplo buscar optimizar, median-futuros trabajos que hagan uso o que se encarguen te diferentes técnicas, el tiempo de respuesta para de buscar mejorar los resultados aquí presenta-el SLD.

Referencias

[1] L. A. Zadeh, "Fuzzy Sets," Inf. Control, vol.8, no.3, pp.338-353, 1965.

[2] L. A. Zadeh, "Fuzzy logic," Computer, vol.21, no.4, pp.83-93, April 1988.

[3] E. Cox, "Fuzzy fundamentals," Spectrum IEEE, vol.29, no.10, pp.58-61, Oct. 1992.

[4] J. M. Mendel, "Fuzzy logic systems for engineering: a tutorial", Proceedings of the IEEE, vol.83, no.3, pp.345-377, Mar 1995.

[5] T.J. Ross, Fuzzy Logic With Engineering Applications, USA: John Wiley & Sons Inc. - University of New Mexico, 2004.

[6] N. Wakami, S. Araki, and H. Nomura, "Recent applications of fuzzy logic to home appliances", Industrial Electronics, Control, and Instrumentation, 1993. Proceedings of the IECON ‘93, International Conference on, vol.1, pp. 155-160, 15-19 Nov 1993.

[7] E. H. Mamdani, "Application of fuzzy algorithms for control of simple dynamic plant", Electrical Engineers, Proceedings of the Institution of, vol.121, no.12, pp.1585-1588, December 1974.

[8] M. Sugeno, and K. Murakami, "Fuzzy parking control of model car", Decision and Control, 1984. The 23rd IEEE Conference on, vol. 23, pp.902-903, Dec. 1984.

[9] E. H. Mamdani, H. J. Efstathiou, and K. Sugiyama, "Developments in fuzzy logic control", Decision and Control, 1984. The 23rd IEEE Conference on, vol. 23, pp.888893, Dec. 1984.

[10] N. Govind, "Fuzzy logic control with the intel 8XC196 embedded microcontroller", Chandler, Arizona: Intel Corp., 12/01/2012.

[11] J. Schwarz, "Motorola microcontroller as the platform for fuzzy applications," Proc. Sci. Int. Conf. Commun., Signal Syst.,pp. 239-242, Sep. 1996.

[12] R. Bannatyne, "Microcontrollers and fuzzy logic for embedded control applications", Industrial Automation and Control: Emerging Technologies, 1995, International IEEE/IAS Conference on, pp.500-504, 2227 May 1995.

[13] J. M. Sibigtroth, "Fuzzy logic for small microcontrollers", WESCON/'93. Conference Record, pp.532-535, 28-30 Sep. 1993.

[14] A. H. Zavala, O.C. Nieto, "Fuzzy Hardware: A Retrospective and Analysis", Fuzzy Systems, IEEE Transactions on, vol. 20, no. 4, pp. 623-635, Aug. 2012.

[15] Microchip Technology Inc. "PIC18FXX2 Data Sheet",2002. [online]. Available: http://ww1.microchip.com/downloads/en/devicedoc/39564c.pdf

[16] The MathWorks, Inc."Fuzzy Logic Toolbox User's Guide". 2002. [online]. Available: http://faculty.petra.ac.id/resmana/private/matlabhelp/pdf_doc/fuzzy/fuzzy_ tb.pdf

[17] U. Farooq, K. M. Hasan, G. Abbas, M. U. Asad, and S. O. Saleh, "Design, low cost implementation and comparison of MIMO Mamdani Fuzzy Logic Controllers for wall tracking behavior of mobile robot", Information and Communication Technologies (ICICT), 2011 International Conference on, pp.1-9, 23-24 July 2011.

[18] M. Thompson, "Microcontrollers' fuzzy logic and 16-bit MCUs: a matter of intuition", Wescon/97. Conference Proceedings, pp. 219-221, 4-6 Nov 1997.

[19] P. Guillemin, "Fuzzy logic applied to motor control", Industry Applications, IEEE Transactions on, vol.32, no.1, pp. 51-56, Jan/Feb 1996.

[20] T. Gupta, R. R. Boudreaux, R. M. Nelms and J.Y. Hung, "Implementation of a fuzzy controller for DC-DC converters using an inexpensive 8-b microcontroller", Industrial Electronics, IEEE Transactions on, vol. 44, no. 5, pp. 661-669, Oct 1997.

[21] S. S. M. Verma, S. P. Verma, "Implementation of a fuzzy logic speed controller for electric vehicles on a 32-bit microcontroller", Power Electronics and Drive Systems, 2003. PEDS 2003. The Fifth International Conference on, vol. 2, pp. 1004-1009, 1720 Nov. 2003.

[22] B. Sutopo, and S. F. D. Widjaya, "Energy saving algorithm on induction motors controlled by a 68HC11 microcontroller system using fuzzy logic approaching", Power Electronics and Drive Systems, 2001. Proceedings, 2001 4th IEEE International Conference on, vol. 1, pp. 59- 61, 22-25 Oct. 2001.

[23] Yueh-Ru Yang, "A fuzzy logic controller for maximum power point tracking with 8-bit microcontroller", IECON 2010 - 36th Annual Conference on IEEE Industrial Electronics Society, pp.2895-2900, 7-10 Nov., 2010.

[24] Z. Yan, and Z. Jiaxing, "Application of Fuzzy Logic Control Approach in a Microcontroller-Based Sun Tracking System", Information Engineering (ICIE), 2010 WASE International Conference on, vol.2, pp.161-164, 14-15 Aug., 2010.

[25] J. Gaysse, "Using fuzzy logic in low cost microcontroller to increase accelerometer performances", Soft Computing in Industrial Applications, 2005. SMCia/05. Proceedings of the 2005 IEEE Mid-Summer Workshop on, pp. 6-11, 28-30 June 2005.

[26] A. Costa, A. De Gloria, F. Giudici, and M. Olivieri, "Fuzzy logic microcontroller", Micro, IEEE, vol. 17, no. 1, pp. 66-74, Jan/ Feb 1997.

[27] J. Lilly, Fuzzy Control and Identification, Hoboken, New Jersey: Wiley-IEEE Press, 2010.

[28] C. C. Lee, "Fuzzy logic in control systems: fuzzy logic controller. I," Systems, Man and Cybernetics, IEEE Transactions on, vol. 20, no. 2, pp. 404-418, Mar/Apr 1990.

[29] C. C. Lee, "Fuzzy logic in control systems: fuzzy logic controller. II," Systems, Man and Cybernetics, IEEE Transactions on, vol. 20, no. 2, pp. 419-435, Mar/Apr 1990.

[30] O. Rozo, Diseño e implementación de un control de temperatura por medio de lógica difusa y monitoreo de variables físicas y biomédicas en una incubadora para neonatos, Tesis Pregrado, Universidad de los Llanos,Villavicencio, Colombia, 2005.