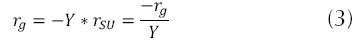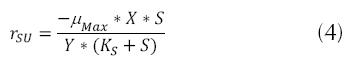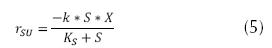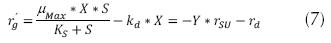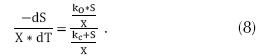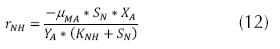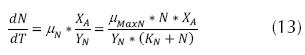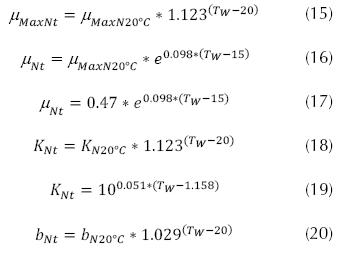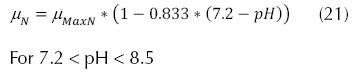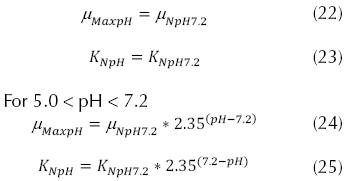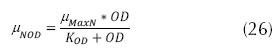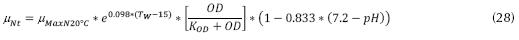DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2015.2.a11Publicado:
01-04-2015Número:
Vol. 19 Núm. 44 (2015): Abril - JunioSección:
RevisiónTheoretic similitude of the aerobic biological growth kinetics for the stabilization of organic matter in wastewaters treatment
Similitud teórica de la cinética de crecimiento biológico aeróbico para la estabilización de materia orgánica en el tratamiento de aguas residuales
Descargas
Referencias
APHA (1989). Standard methods for the examination of water and wastewater. AWWA-WEF Washington
Chiavola A.; Farabegoli, G. and Antonetti F. (2014). Biological treatment of olive mill wastewater in a sequencing batch reactor. Biochemical Engineering Journal, 85, 71-78.
Cosenza, A.; Mannina, G.; Vanrolleghem, P., and Neumann, M. (2014). Variance-based sensitivity analysis for wastewater treatment plant modelling. Science of the Total Environment, 470-471, 1068-077
Crites, R. (2000). Small and decentralized wastewater management systems. New York: McGraw-Hill.
Crittenden, J. (2005). Water treatment: principles and design. Second ed. Wiley & Sons INC.
Droste, R. (1997). Theory and practice of water and wastewater treatment. New York: John Wiley & Sons Inc.
Eckenfelder, W. (2000). Industrial water pollution control. New York: McGraw- Hill.
Eldyasti, A.; Nakhia, G., and Zhu, J. (2012). Development of a calibration protocol and identification of the most sensitive parameters for the particulate biofilm models used in biological wastewater treatment. Bioresource Technology, 111, 111-121.
EPA (1975). Process design manual for nitrogen control. Chapter 3.
Escaler, M.I.; Mujeriego, R. (2001). Eliminación biológica de nutrientes (Nitrógeno y Fósforo) mediante un proceso discontinuo de fangos activados. Ingeniería del agua, 8, No. 1, 67-77.
Eweis, J.B.; Ergas, S.J.; Chang, D.P.Y. and Schroeder, E.D. (1998). Bioremediation principles. New York: McGraw-Hill.
Ferrer, J. y Torrecillas, A. (2008). Tratamientos biológicos de aguas residuales. Valencia: Universidad Politécnica de Valencia.
Gil, M. (2005). Procesos de descontaminación de aguas: Cálculos informatizados avanzados. Madrid: Thompson.
Gil, M. (1998). Modelo dinámico del proceso secundario de depuración de aguas residuales urbanas. Revista Internacional de Métodos Numéricos para Cálculo y Diseño de Ingeniería, 14, No. 4, 525-538.
Günay, A. and Çetin, M. (2013). Determination of aerobic biodegradation kinetics of olive oil mill wastewater. International Biodeterioration & Biodegradation, 85, 237-242.
Hatzikonstantinou, G. and Andreadakis A. (2002). Differences in nitrification potential between fully aerobic and nitrogen removal activated sludge systems. Water Science and Technology, 46, No. 1-2, 297-304.
Henze, M.; Aspergen, H.; Jansen, J.; Nielsen, P.H.; Lee, N.N. (2002). Effect of solid retention time and wastewater characteristics on biological phosphorus removal. Water Science and Technology, 45, No. 6, 137-144.
Holakoo, L. (2005). Simultaneous nitrogen and phosphorus removal in a continuously fed and aerated membrane bioreactor. Journal of Environmental Engineering, 131, No. 10, 1469-1472.
Horan, N.J. (1990). Biological Wastewater Treatment Systems. Systems Wiley, Chichester.
Jenicek, P.; Svehia, P.; Zabranska, J., and Dohanyos, M. (2004). Factors affecting nitrogen removal by nitritation/desnitritation. Water Science & Technology, 49, No. 5-6, 73-79.
Keller, J.; Watts, S.; Battye-Smith, W., and Chong, R. (2001). Full scale demonstration of biological nutrient removal in a single tank SBR process. Water Science & Technology, 43, No. 3, 355-362.
Krzeminski, P.; Iglesias-Obelleiro, A.; Madebo, G.; Garrido, J.M.; van der Graaf, J.H., and vam Lier, J.B. (2012). Impact of temperature on raw wastewater composition and activated sludge filterability in full-scale MBR systems for municipal sewage treatment. Journal of Membrane Science, 423-424, 348-361.
Lawrence, A.W., and McCarty, P. (1970). Unified basis for biological treatment design and operation. Journal of the Sanitary Engineering Division, 96, No. 3, 757-778.
Lee, N.; la Cour Jansen, J.; Aspegren, H.; Henze, M.; Nielsen, P.H., and Wagner, M. (2002). Population dynamics in wastewater treatment plants with enhanced biological phosphorous removal operated with and without nitrogen removal. Water Science & Technology, 46, No. 1, 163-170.
Liu, D. (2000). Wastewater treatment. Lewis publishers.
Mandt, M.G. (1982). Oxidation ditches in Wagewater Treatment. Ann Arbor Science.
Manser, R.; Gujer, W., and Siegrist, H. (2006). Decay processes of nitrifying bacteria in biological wastewater treatment systems. Water Research, 40, No. 12, 2416-2426.
Mara, D. (1997). Design manual for waste stabilization ponds in India. Leeds: University of Leeds.
Metcalf & Eddy (2003). Wastewater Engineering: Treatment, Disposal, Reuse. 4th Edition. New York: McGraw-Hill.
Nodal, E. (2001). Procesos biológicos aplicados al tratamiento de agua residual. Ingeniería Hidráulica y Ambiental, 22, No. 4, 52-56.
Orhan, U. (1994). Wastewater management for Istanbul: Basis for treatment and disposal. USA: Environmental Pollution
Orozco, A. (2005). Bioingeniería de aguas residuales: teoría y diseño. Bogotá: ACODAL.
Park, J. (2008). Biological nutrient removal. Theories and design. Madisson, Winconsin.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a11
Theoretic similitude of the aerobic biological growth kinetics for the stabilization of organic matter in wastewaters treatment
Similitud teórica de la cinética de crecimiento biológico aeróbico para la estabilización de materia orgánica en el tratamiento de aguas residuales
Juan Pablo Rodríguez Miranda*,
Cesar Augusto García Ubaque**,
María Camila García Vaca*
* Sanitary and Environmental Engineering. Master in Environmental Engineering. PhD (C) Engineering. Faculty of Environment, Universidad Distrital Francisco José de Caldas. Bogota, Colombia. Contact: jprodriguezm@udistrital.edu.co.
** Civil Engineer. PhD in Engineering. Faculty of Technology, Universidad Distrital Francisco José de Caldas. Bogota, Colombia. Contact: cagarciau@udistrital.edu.co.
*** Chemical engineer. Department of Chemical Engineering, Universidad de Los Andes. Bogota, Colombia. Contact: mcgarcia149@uniandes.edu.co.
Fecha de recepción: 7 de mayo de 2014 Fecha de aceptación: 19 de enero de 2015
Citation / Para citar este artículo: Rodríguez Miranda, J. P., García Ubaque, C. A., & García Vaca, M. C. (2015). Theoretic similitude of the aerobic biological growth kinetics for the stabilization of organic matter in wastewaters treatment. Revista Tecnura, 19(44), 145-156. doi: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a11
Abstract
To achieve the stabilization of organic matter in wastewaters treatment, it is not only significant to establish the microbial growth kinetics, but also the interrelation of the removal of nutrients such as nitrogen, given the similitude of coefficients, specific growth rate and the adjustments for water temperature, which represents it for both the removal of organic matter as well as for the nitrification and denitrification processes present in the biological wastewaters treatment. Therefore, this theoretic similitude between microbial growth kinetics and nitrogen removal processes constitutes concise considerations for the dimensioning process of wastewater biological treatment systems, which contribute in the understanding of the simultaneous process of removing organic matter and nutrients from raw wastewater.
Keywords: organic matter, nitrogen, wastewater, wastewater treatment.
Resumen
Para la estabilización de la materia orgánica en el tratamiento de las aguas residuales no solo es significativo establecer la cinética de crecimiento microbiano sino la interrelación de la remoción de nutrientes como el nitrógeno, dada la similitud de coeficientes, tasa de crecimiento específica y los ajustes por temperatura del agua, que lo representa tanto para la remoción de la materia orgánica como para los procesos de nitrificación y denitrificación presentes en el tratamiento biológico de las aguas residuales. Por ello, esta similitud teórica de las cinéticas de crecimiento microbiano y de los procesos de remoción de nitrógeno constituye consideraciones concisas para el proceso de dimensionamiento de sistemas de tratamiento biológicos de tratamiento de aguas residuales, que ayudan a entender el proceso simultáneo de remover materia orgánica y nutrientes del agua residual cruda.
Palabras clave: agua residual, materia orgánica, nitrógeno, tratamiento de aguas residuals.
Introduction
The composition of raw or untreated wastewater may vary depending on the eating habits, the economic and industrial activity and the socioeconomic environment of the populations and generally the composition may have organic matter compounds (BOD, COD, TOC). However, organic matter in wastewaters is highly heterogeneous, containing substances with different molecular weights, ranging from simple to very complex polymers (Krzeminski, 2012) and the rate of degradation or the rate of reduction of organic matter and specific substances may vary according to factors that proportionally affect the stabilization of organic matter. Within the context of wastewater treatment engineering, the decomposition of organic matter may be adequately described as the loss of biomass or the loss of activity through the activation of microorganisms degraders of the same (Manser, 2006). In contrast to the above, the biomass activities, and the concentration of microbial products can be analyzed through aerobic growth kinetics for the stabilization of organic matter in aerobic biological reactors (Sabia, 2013), and through them, the activated sludge models have the purpose of modeling the concentrations of nutrients and not the number and conditions of the microorganisms (Chiavola, 2014). The application of aerobic microbian growth kinetics in the design of reactors for the stabilization of organic matter, requires a balance between the steady state approach and the unidimensional approach, which are widely used and implemented in the design of the aerobic biological treatment of municipal wastewaters (Eldyasti, 2012). The Monod type equations have been widely used to describe the kinetics of aerobic degradation. Up to now, very few studies have been conducted to determine the optimum kinetic values in aerobic treatment (Günay, 2013, Chiavola, 2014, Pomiès, 2013 and Cosenza, 2014); as well as the similitude of the kinetics for the stabilization of organic matter and the stabilization of the nitrogen present in wastewaters.
Due to the above, the treatment of wastewater using biological technologies presents a large variety of reactors and special configurations for the stabilization of biodegradable organic compounds as a fraction of total organic matter, suspended solids, nitrogen and phosphorus among others (Rodríguez, 2012). Special care shall be given to having an adequate nutritional balance among the input substrate (affluent), the microbian consortium and the nutritional and energy requirements inside the reactor tank; hence, the importance of establishing kinetic coefficients in order to know the velocity of the biological reaction of the microbian consortium and its rapid or slow stabilization of the organic compounds present in the raw wastewater. Accordingly, this study presents the considerations of comparison and similitude of the aerobic biological growth kinetics for the stabilization of organic matter and the removal of nitrogen in the treatment of wastewater, in terms of the criteria germane to the coefficients and equations that represent the biological event within the reactors applied in the management of wastewaters.
BIOLOGICAL KINETICS FOR THE STABILIZATION OF ORGANIC MATTER
The composition of wastewater comprises substrates of multicomponents (Crittenden, 2005) (in many cases, the carbon source is the substrate, but an inorganic nutrient, an aminoacid, vitamin or any other compound necessary for cellular synthesis may be referred to as a substrate in particular cases), namely, a mix of compounds that can be reported as BOD o COD o TOC (APHA, 1989) and each of these components are present in the water in different concentrations and are removed in accordance with an order of kinetics, at different velocities though, it could happen that to the extent that a substrate (growth limiting nutrient) de-creases, the velocity of removal decreases in the same proportion, originating an inflexion point in a removal curve. The kinetic phenomena and the stoichiometry of the removal of the substrate, the growth of the biomass and the consumption of oxygen are a fundamental and explicative base of the processes involved in the treatment of wastewaters (Nodal, 2001 and Rodríguez, 2013). Meaning that the study of the kinetics determines the velocity at which the microorganism degrades a specific residue, which provides the necessary basic information to determine the adequate size of the aerobic biological, anaerobic or hybrid reactors (Romero, 2004). In all treatment systems, it is indispensable to control the environmental conditions to ensure an optimum environment for the development of the microorganisms, but additionally, sufficient time of permanence is required for these to reproduce, such time of permanence is directly related to the growth rate and the velocity at which they degrade the substrate, which leads to the calculation of the kinetic coefficients.
The knowledge of the stabilization of organic matter in the treatment of wastewaters is represented through the description of microbian growth, and the most widely used method is the Monod method (Eckenfelder, 2000, Droste 1997 and Gil, 2005) which relates microbian growth with the limiting substrate, that is, describes the growth dynamics of a bacterial culture, limited solely by the concentration of substrate (Eweis, 1999) which is highly dependable on the temperature of water, pH, nutrients and the type of microbian consortium present, which can be expressed as follows (Crites, 2000, Metcalf & Eddy, 2003, Eweis, 1999 and Ferrer, 2008).
Where µ is the growth rate (h-1); Max is the maximum
growth rate (h-1); KS is the saturation coefficient
(mg/L) and S is the concentration of the
substrate (mg/L). The above indicates that if S >>
KS, the growth rate shall be approximately equal
to µMax. The values of KS in the stabilization of organic
matter indicate a high affinity of the microbian
consortium with the affluent substrate, which
shows that the growth rate is generally present for a slightly lower concentration of affluent substrate,
but if the concentration of the affluent substrate is
diluted, the growth rate takes a tendency towards
zero. In addition to the above, if there is an effect
of the concentration of the substrate over the specific
growth rate, the following equation is obtained,
taking into account that the biological growth corresponds
to a first order reaction with a concentration
of active biomass 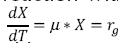 , as follows
(Crites, 2000, Metcalf & Eddy, 2003, Eweis, 1999
and Ferrer, 2008).
, as follows
(Crites, 2000, Metcalf & Eddy, 2003, Eweis, 1999
and Ferrer, 2008).
Where rg is the bacterial growth rate or velocity of growth of the microorganisms (mg/L * h), X is the concentration of biomass (mg/L). When a substantial growth of microorganisms is present, their extinction can be considered negligible, during the exponential growth stage; thereby, a part of the substrate transforms into new cells and the other is oxidized (Crites, 2000 y Metcalf & Eddy, 2003) and the relationship between the degree of utilization of the substrate and the rate of growth is as follows.
Where Y is the coefficient of maximum production (mass of cells produced mg and the mass of the substrate consumed mg); rSU is the rate of utilization of the substrate (mg/L * h) or the quantity of contaminant eliminated. The above may be considered through the expression of Lawrence and Mc Carty (Orozco A., 2005).
The expression above can be applied to low concentrations of substrate, presenting a zero order model, in some cases, having the opportunity of changing the model to first order, if there is a high concentration of substrate in the affluent. But if 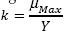 , then the following is established (Crites, 2000, Metcalf & Eddy, 2003, Eweis, 1999 and Ferrer, 2008).
, then the following is established (Crites, 2000, Metcalf & Eddy, 2003, Eweis, 1999 and Ferrer, 2008).
Where k is the maximum rate of utilization of the substrate (h-1). Another special consideration is endogenous metabolism, which represents that not all the cells of the microbian consortium are in exponential growth, reason why there should be a correction of the energy required for the expense of stabilization of the organic matter and can be expressed as follows: (Eweis, 1999 and Ferrer, 2008).
Where rd is the endogenous decay rate (mg/L * h); kd is the coefficient of endogenous decay (h-1). Consequently, the net growth rate (rg).
It should be clarified that these biological reaction velocity rates shall be corrected to the temperature of water to be treated (Crites, 2000 and Metcalf & Eddy, 2003), given that this is an influencing factor in the stabilization of the organic matter, which can be expressed as follows: 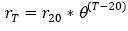 , where rT is the rate of reaction at the indicated temperature, r20 is the rate of reaction at 20 °C, θ is the coefficient of activity of the temperature (if the temperature of the water is between 5 and 15 °C then θ is 1.11, but if the temperature of the water is between 15 and 30 °C then θ is 1.047 (Gil, 1998) and T is the temperature of water (°C).
, where rT is the rate of reaction at the indicated temperature, r20 is the rate of reaction at 20 °C, θ is the coefficient of activity of the temperature (if the temperature of the water is between 5 and 15 °C then θ is 1.11, but if the temperature of the water is between 15 and 30 °C then θ is 1.047 (Gil, 1998) and T is the temperature of water (°C).
Other expressions of the biological growth kinetics may be: Orozco’s (2005) equation for the net rate of soluble substrate removal, with limitation of substrate, as follows:
In addition of the equations of Eckenfelder and McKinney (Eckenfelder W., 2000) for starvation, as follows: 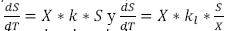 respectively. On the other hand, there are equations such as that of Contonis, which is applied to growth with limited substrate and high concentrations of biomass, that is, sufficient enzymes are present for the reaction to continue without limitation and the equation is:
respectively. On the other hand, there are equations such as that of Contonis, which is applied to growth with limited substrate and high concentrations of biomass, that is, sufficient enzymes are present for the reaction to continue without limitation and the equation is:
where Kc is Contonis’ constant (Orozco, 2005). In addition to the above, there are also other expressions that were developed to describe the growth of the microorganisms and the stabilization of the substrate, as follows:
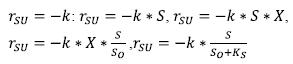
(Crites, 2000, Metcalf & Eddy, 2003 and Eckenfelder, 2000).
The equations above present kinetic coefficients, which can vary in accordance with the type of wastewater or liquid waste, reason why table 1 presents the optimum values and ranges for each of the kinetic coefficients shown in the aforementioned equations, according to different authors, which are applicable to the aerobic biological treatment at a water temperature of 20 °C (Orham, 1994; Mandt, 1982; Pearson, 1999; Lawrence, 1970; Mara, 1997; San, 1992; Horan, 1990; Ferrer, 2008; Droste, 1997; Rich, 1973 and Gil, 1998).
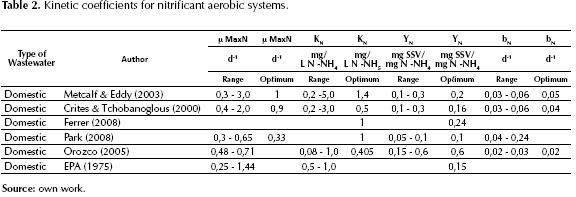
BIOLOGICAL KINETICS FOR THE REMOVAL OF NITROGEN
A large percentage of the nitrogen present in raw wastewaters is found as ammoniacal nitrogen or organic nitrogen (Metcalf & Eddy, 2003; Zalakain, 2010), which can be soluble or particulate. The biological transformation and elimination are expressed in two stages, one of Nitrification and the other known as Denitrification (Escaler, 2001).
The first stage known as Nitrification, where ammoniacal nitrogen is oxidized into nitrites, and these in turn into nitrates, requiring 4.57 grams of oxygen per each gram of ammoniacal nitrogen (Hatzicontantinou, 2002) and this stage generally occurs after the carbonaceous demand for oxygen is satisfied, although the oxidation of carbonaceous and nitrogenous matters may occur simultaneously. (Liu, 2000). The efficiency of the nitrification process depends on the specific velocity of nitrification (Henze, 2002), which in turn is established by the following factors: a) dissolved oxygen, b) temperature, c) pH (adequate between 7.2 and 8.5), d) the ratio DBO5/NTK, and e) the presence of inhibitor and toxic substances (Droste, 1997; Metcalf & Eddy, 2003; Lee, 2002; Randall, 1992; Holakoo, 2005; Jenicek, 2004 and Keller, 2001). The kinetic expressions involved in this stage are given by the equation that interrelates cell growth and the elimination of ammonium, in function of the growth of autotroph organisms through the Monod equation (Gil, 1998; Ferrer, 2008; Metcalf & Eddy, 2003; Crites, 2000; Orozco, 2005 and EPA, 1975), both in the nitrosomonas phase and in the nitrobacter, as follows.
Where µ is the growth rate of the microorganisms
(h-1), µMax is the maximum growth rate (h-1),
KN is the coefficient of semi-saturation for nitrogen
(mg/L) and N is the concentration of substrate
(mg/L N). On the other hand, the oxidation rate
of ammonium can be: 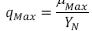 Although the kinetics of the nitrosomonas presents the following
Although the kinetics of the nitrosomonas presents the following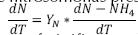 (Park, 2008): , where YN is the yield coefficient of nitrificant substances (mg VSS/ mg N – NH4). The nitrification process, according to the stoichiometric equations, indicates that the reaction of NH4 to NO2 is too slow due to the reduced velocity of the nitrosomonas to convert the NO2 (Orozco, 2005) in comparison with the velocity of the nitrobacter, reason why the expression for the nitrification rate can be
(Park, 2008): , where YN is the yield coefficient of nitrificant substances (mg VSS/ mg N – NH4). The nitrification process, according to the stoichiometric equations, indicates that the reaction of NH4 to NO2 is too slow due to the reduced velocity of the nitrosomonas to convert the NO2 (Orozco, 2005) in comparison with the velocity of the nitrobacter, reason why the expression for the nitrification rate can be
Where µN is the growth rate of the nitrosomonas (h-1), µMaxis the maximum growth rate (h-1), KN is the semi-saturation coefficient for nitrogen (mg/L) and N is the concentration of the substrate (mg/L N – NH4). At the same time, the velocity of ammonium utilization can be expressed as follows: (Ferrer, 2008).
Where rNH is the velocity of ammonium utilization (g N – NH4/ m3 day), µMA is the specific velocity of growth of autotroph bacteria (d-1), YA is the maximum production coefficient (g VSS/g N – NH4), XA is the concentration of autotroph microorganisms (g COD/m3). The above can be expressed through the rate of growth as follows (Park J., 2008).
On the other hand, endogenous respiration during nitrification can be expressed as follows (Park, 2008), very similar to endogenous respiration of the organic matter.
Where bN is the coefficient of endogenous de cay by nitrosomonas (d-1), in some cases may be at 20 °C and take a value between 0.04 a 0.24 d-1 Also the specific rate of nitrification can be (Park, 2008): 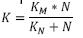 , where K is the specific rate of nitrification (mg N/mg VSS day), N is the concentration
of nitrogen (mg N – NH4/L) which can be
between 0 and 70 mg/L; KM is the ratio µMaxN/YN,
where YN can be 0.05 and 0.10 mg VSS/mg N and
µMaxN can be between 0.30 and 0.65 d-1. Within the
factors influencing nitrification there can be corrections
for water temperature, pH, DBO5/TKN, oxygen
dissolved at the job site, as follows (Park, 2008;
Metcalf & Eddy, 2003; Crites, 2000 and EPA, 1975).
Adjustments for water temperature:
, where K is the specific rate of nitrification (mg N/mg VSS day), N is the concentration
of nitrogen (mg N – NH4/L) which can be
between 0 and 70 mg/L; KM is the ratio µMaxN/YN,
where YN can be 0.05 and 0.10 mg VSS/mg N and
µMaxN can be between 0.30 and 0.65 d-1. Within the
factors influencing nitrification there can be corrections
for water temperature, pH, DBO5/TKN, oxygen
dissolved at the job site, as follows (Park, 2008;
Metcalf & Eddy, 2003; Crites, 2000 and EPA, 1975).
Adjustments for water temperature:
Adjustments for the pH of water, where it was observed that the maximum nitrification rate occurs at pH values ranging from 7.2 to 9.0, and the general application can be:
EPA Method:
Where µNpH7.2 can be 0.33 d-1, KNpH7.2 can be 1.0 d-1. The adjustments for the concentration of dissolved oxygen, which affects the specific velocity of growth of the nitrificant organisms, and the expression can be:
Where TW is the temperature of water (°C), DO is the concentration of oxygen dissolved in the water (mg/L) and whose minimum concentration should be 2 mg/L, KOD is the constant of medium saturation (mg/L) which can be between 0.3 and 2 mg/L. And the adjustments for the ratio DBO5/ TKN, is due to the presence of a fraction of nitrificant organisms present in the liquor mixed and that can be expressed as follows:
Even though there are equations that interrelate the aforementioned factors, such as:
If pH < 7.2 for nitrosomonas is valid temperatures between 8 and 30 °C:
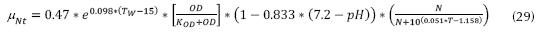
South African Method: If the pH < 7.2
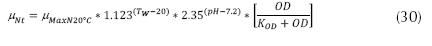
If the pH is between 7.2 and 8.5
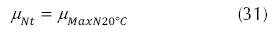
On the other hand, the growth rate for heterotrophic organisms in the nitrification can be (EPA, 1975).
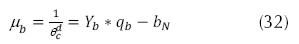
Where µb is the growth rate of heterotrophic organisms (h-1), qb is the removed substrate rate (mg BOD/ mg VSS day), Yb is the coefficient of heterotrophic organisms (mg VSS/mg BOD), θ cd is the time of retention of solids (days), which can be :

The above expresses that µN>µb if the condition is that the pH and the DO do not have a limiting growth rate in the nitrification.
Just as there are biological kinetic coefficients for the stabilization of organic matter, there are also kinetic coefficients for nitrification; these are presented in table 2, which shows the optimum values and recommended ranges according to different authors, which are applicable to the aerobic biological treatment at a water temperature of 20 °C (Metcalf & Eddy, 2003; Crites, 2000; Ferrer, 2008; Orozco, 2005 and EPA, 1975).
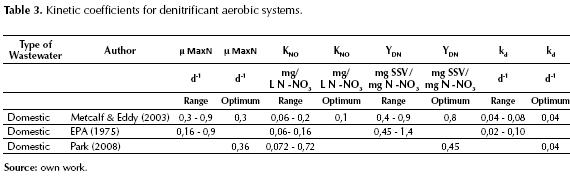
The second stage is Denitrification, during which, nitrates are reduced to gaseous nitrogen, which is released into the atmosphere. To carry out this process, the organisms need a source of organic carbon, which can be the organic matter contained in the wastewater (organic compounds contained in raw wastewater) or applied externally such as methanol (easily biodegradable and that is the reason for a higher denitrification velocity) or as endogenous carbon source (it is a much slower process). The efficiency of the denitrification process depends on several factors: a) the dissolved oxygen, b) the carbon source used, c) the concentration of nitrites, d) the temperature, e) the pH and f) the presence of inhibitor and toxic substances (Droste, 1997; Metcalf & Eddy, 2003 and Randall, 1992).
It is important to establish that this process contains a high presence of carbon, on that basis, an expression can be related as follows (Pérez, 2007):
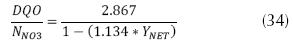
where N – NO3 is the concentration of nitrate available (mg/L), YNET is the yield of the biomass according to COD (mg VSS/mg COD), COD in mg/L, and these variables assumes that the COD and the VSS produced are 1.42 g COD/g VSS and that the biomass contains approximately 10% nitrogen. In the denitrification reactions, the elimination of NO3 is much slower (Pérez J., 2007), therefore the equation is expressed as follows (Park, 2008): 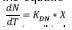 , where N is the concentration of nitrates
(mg/L), KDN is the specific denitrification constant
(mg N/mg VSS day); but is also expressed as
follows, since it is an expression of Monod (Pérez
J., 2007; Metcalf & Eddy, 2003; Crites, 200 and
EPA, 1975), in which the velocity of growth of the
denitrificant microorganisms is related to the concentration
of nitrate, as follows:
, where N is the concentration of nitrates
(mg/L), KDN is the specific denitrification constant
(mg N/mg VSS day); but is also expressed as
follows, since it is an expression of Monod (Pérez
J., 2007; Metcalf & Eddy, 2003; Crites, 200 and
EPA, 1975), in which the velocity of growth of the
denitrificant microorganisms is related to the concentration
of nitrate, as follows:
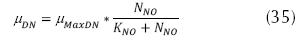
Where μDN is the specific velocity of growth of the denitrificant microorganisms (d-1), µMaxDN the maximum velocity of specific growth of the denitrificant microorganisms, (d-1).NNO is the concentration of N-NO3 (mg/L) and KNO: constant of semi-saturation for denitrification (mg/L), the usual values are between 0.1 and 0.2 mg/L. The aforementioned expression can be transformed in order zero, if KNO is much smaller than NNO. The velocity of growth of the denitrificant microorganisms is very similar to that of aerobe heterotroph organisms; therefore, greater than the nitrificants. Additionally, it can be expressed (EPA, 1975):

where qDN is the nitrate removal rate (mg N –NO3/ mg VSS day), YDN is the gross yield of the denitrification (mg VSS/ mg N – NO3). Consequently, the velocity of nitrate decrease present in the system can be related to the specific growth velocity of the microorganisms, and its expression can be (Ferrer, 2008):
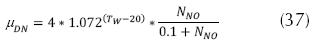
It is also important to mention that the expression for the gross yield of denitrification can be (EPA, 1975):
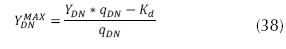
where YDN MAX is the maximum rate of denitrification (mg VSS/ mg N – NO3), kd is the coefficient of decay (d-1). In addition, there is an effect on the concentration of carbon according to the Monod type, which affects the velocity of nitrate removal, given the source of carbon, accordingly, the concentration of nitrate as well as the concentration of organic substrate (carbon), limit the velocity of nitrification, and on this basis it is expressed as follows (Metcalf & Eddy, 2003 and Crites, 2000):
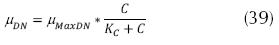
Where µDN is the specific velocity of growth of the denitrificant microorganisms (d-1), µMaxDN the maximum velocity of the specific growth of the denitrificant microorganisms, (d-1). C is the concentration of carbon or organic substrate (mg/L) and KC: the constant of semi-saturation for the carbon source (mg/L), it presents very low values in comparison with the organic matter represented as BOD or COD, therefore, the usual value is 0.1 mg/L. Then, for the denitrification process to take place, a combination of reactions can be made, of both, nitrate as well as organic substrate (methanol in some cases as carbon source), as follows:
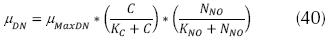
In some cases, KNO can be low, indicating that concentrations between 1 and 2 mg/L N – NO3 present very little effect on the velocity of denitrification. This constant can have corrections for water temperature as follows (Park J., 2008): 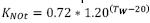 , but if the temperature of water is below 13 °C, then the equation is:
, but if the temperature of water is below 13 °C, then the equation is: 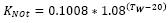
Just as there are biological kinetic coefficients for nitrification, there are also kinetic coefficients for denitrification, which are presented in table 3, which shows the optimum values and recommen at a water temperature of 20 °C (EPA, 1975; Metcalf & Eddy, 2003 and Park, 2008).
Elements of theoretic similitude in the kinetics of biological growth
One of the elements of similitude in the kinetics of biological growth, for the stabilization of organic matter, the nitrification and the denitrification is the consideration of utilizing growth rates for conditions of limiting substrate, in this way this growth is present according to the concentration which can be expressed mathematically through the Monod equation, as a common denominator, but it is worth highlighting that when these equations are used with high concentrations or concentrations above normal for the substrate, the progress of the expression may have growth limitations, creating barriers to the biodegradability reactions in nitrification and denitrification conditions, but in a different condition for organic substrates, carbonaceous organic matter and even dissolved oxygen. Table 4 shows the similitude in the equations using the Monod expression, additionally, the same tendency is observed in the temperature correction for each biological kinetic.
Another element of similitude is the high dependency of water temperature, pH, nutrients and the type of microbian consortium present, on each of the biological kinetics equations for organic matter, nitrification and denitrification, as well as a correction given for the energy required for the stabilization expense of organic matter, nitrification and denitrification, which is known as endogenous decay. In terms of kinetic coefficients for organic matter, nitrification and denitrification, great concordance is observed in the values among themselves, in spite of the variation of liquid waste in some cases, and in others the testing conditions.
Conclusions
In general, it can be expressed that the theoretical elements of similitude between the biological kinetics for organic matter, nitrification and denitrification, build fundamental and concise considerations for the dimensioning process of wastewater treatment systems, in which they are a solid and explanatory base of the processes involved in the conversion of the substrate into another element or byproduct as a result of the biological activity. That is, the study of kinetics determines the velocity, at which the microorganisms degrade a specific residue to the special conditions of the treatment, which provides the basic information necessary to determine the adequate size of the aerobic, anaerobic or hybrids biological reactors, namely, the design of the wastewater treatment systems.
Acknowledgements
The authors wish to thank the Universidad Distrital Francisco José de Caldas and in particular the Engineering PHD Program for their support in the preparation of this document. Likewise, the authors express their gratitude to tenured professor Vidal Fernando Peñaranda Galvis of the Environmental and Natural Resources Faculty of the Universidad Distrital Francisco José de Caldas, for his review of this document.
References
APHA. (1989). Standard methods for the examination of water and wastewater. Washington: AWWA - WEF.
Chiavola A. (2014). Biological treatment of olive mill wastewater in a sequencing batch reactor. Biochemical Engineering Journal, 71 - 78.
Cosenza A. (2014). Variance-based sensitivity analysis for wastewater treatment plant modelling. Science of the Total Environment, 1068-1077.
Crites R. (2000). Small and descentralized wastewater management systems. New York: McGraw Hill.
Crittenden J. (2005). Water treatment: principles and design. Second edition. USA: Wiley & sons INC.
Droste R. (1997). Theory and practice of water and wastewater treatment. New york: John Wiley & Sons Inc.
Eckenfelder W. (2000). Industrial water pollution control. New york: McGraw Hill.
Eldyasti A. (2012). Development of a calibration protocol and identification of the most sensitive parameters for the particulate biofilm models used in biological wastewater treatment. Bioresource Technology, 111 - 121.
EPA. (1975). Process design manual for nitrogen control. Chapter 3.USA: EPA.
Escaler M.I. (2001). Eliminación bioógica de nutrientes (nitrógeno y fósforo) mediante un proceso discontinuo de fangos activados. Tecnología del agua., 67 - 77.
Eweis J. (1999). Bioremediation principles. New York: Mc Graw Hill.
Ferrer J. (2008). Tratamiento biológicos de aguas residuales. Valencia: Universidad politécnica de valencia.
Gil M. (2005). Procesos de descontaminación de aguas. Cálculos avanzados informáticos. Madrid: Thompson.
Gil Rodríguez M. (1998). Modelo dinámico del proceso secundario de depuración de aguas residuales urbanas. Revista internacional de métodos númericos para cálculo y diseño de ingeniería., 525 - 538.
Günay A. (2013). Determination of aerobic biodegradation kinetics of olive oil mill wastewater. International Biodeterioration & Biodegradation, 237 - 242.
Hatzicontantinou G. (2002). Differences in nitrification potential between fully aerobic and nitrogen remo-val activated sludge systems. Water science and technology, 297 - 304.
Henze M. (2002). Effect of solid retention time and wastewater characteristics on biological phosphorus removal. Water science and technology, 137 - 144.
Holakoo L. (2005). Simultaneous nitrogen and phosphorus removal in a continuosly fed and aerated membrana bioreactor. Journal of environmental engineering ASCE, 1469 - 1472.
Horan N.J. (1990). Biological Wastewater Treatment Systems. Chichester UK: Systems Wiley.
Jenicek P. (2004). Factors affecting nitrogen removal by nitritation/desnitritation. Water science and technology, 73 - 79.
Keller J. (2001). Full scale demostration of biological nutrient removal in a single tank SBR process. Water science and technology, 355 - 362.
Krzeminski P. (2012). Impact of temperature on raw wastewater composition and activated sludge filterability in full-scale MBR systems for municipal sewage treatment. Journal of Membrane Science, 348 - 361.
Lawrence A.W. (1970). Unifield basis for biological treatment. Design and operation. USA: ASCE.
Lee N. (2002). Population dynamic in wastewater treatment plants with enhanced biological phosphorous removal operated with and without nitrogen remo-val. Water science and technology, 163 - 170.
Liu D. (2000).Wastewater treatment. USA: Lewis publishers.
Mandt M.G. (1982). Oxidation ditches in wastewater treatment. USA: Ann arborscience.
Manser R. (2006). Decay processes of nitrifying bacteria in biological wastewater treatment systems. WATER RESEARCH, 2416 - 2426.
Mara D. (1997). Design manua for waste stabilization ponds in india. Leeds: University of Leeds.
Metcalf & Eddy. (2003). Wastewater engineering: treatment, disposal and reuse. 4 edition. New york: Mc Graw Hill.
Nodal E. (2001). Procesos biológicos aplicados al tratamiento de aguas residuales. Ingeniería hidráulica y ambiental, 52 - 56.
Orhan U. (1994). Wastewater management for Istanbul: Basis for treatment and disposal. USA: Environmental Pollution.
Orozo A. (2005). Bioingeniería de aguas residuales. Teoría y diseño. Bogotá: ACODAL.
Park J. (2008). Biological nutrient removal. Theories and design. Winconsin: Madisson.
Pearson H.W. (1999). A hybrid waste stabilization pond and wastewater storage and treatment reservoir system for wastewater reuse for both restricted and unrestricted crop irrigation. Water Research, 591 - 594.
Pérez J. (2007). Variantes de procesos de nitrificación denitrificación para un sistema de biomasa en suspensión para el tratamiento de aguas residuales. Ingeniería hidráulica y ambiental, 57 - 64.
Pomiès M. (2013). Modelling of micropollutant remo-val in biological wastewater treatments: A review. Science of the Total Environment, 733-748.
Randall C. (1992). Design and retrofit of wastewater treatment plants for biological nutrient removal. USA: Technomic publishing CO inc.
Rich L.G. (1973).Environmental systems engineering. USA: Mc Graw Hill.
Rodríguez J.P. (2012). Assessment of an aerobic treatment system for. Int. J. Environmental Engineering, 307 - 314.
Rodríguez J.P. (2013). Diseño y evaluación de un sedimentador SEDHELCON y reactor biológico aeróbico FLORICARRFP en planta piloto para tratamiento de aguas residuales. Bogotá: Universidad Distrital Francisco José de caldas.
Romero J. (2004). Tratamiento de aguas residuales. Teoría y principios de diseño. Bogotá: Escuela Colombiana de Ingeniería.
Sabia G. (2013). Effect of solid retention time on sludge filterability and biomass activity: Long-term experiment on a pilot-scale membrane bioreactor treating municipal wastewater. Chemical Engineering Journal, 176 - 184.
San A. H. (1992). Mechanism of Biological Treatment in Plug-Flow or Batch Systems. Journal of Environmental Engineering, 614 - 628.
Zalakain G. (2010). Ampliación de la capacidad de los tratamientos biológicos de fangos activos empleando soporte móviles para la eliminación de nutrientes. RETEMA, 20 - 27.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.