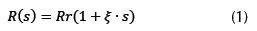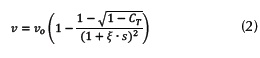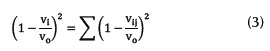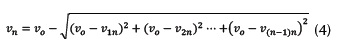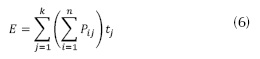Distribución óptima de turbinas en parques eólicos mediante PSO considerando el efecto sombra

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.1.a04

Distribución óptima de turbinas en parques eólicos mediante PSO considerando el efecto sombra

Optimal Distribution of Wind Farm Turbines Using PSO Considering the Wake Effect

Juan David Ramírez Ramírez¹, Alejandro Garcés Ruiz², Jose Santiago Arrieta Giraldo³

¹ Ingeniero Electricista, estudiante de maestría en Ingeniería Eléctrica. Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: daviramirez@utp.edu.co
² Ingeniero Electricista, magister en Ingeniería Eléctrica, doctor en Ingeniería Electrónica. Profesor asociado programa de Ingeniería Eléctrica Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: alejandro.garces@utp.edu.co
³ Ingeniero Electricista, estudiante de Maestría en Ingeniería Eléctrica Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: jsarrieta@utp.edu.co

Fecha de recepción: 24 de septiembre de 2014 Fecha de aceptación: 18 de septiembre de 2015

Cómo citar: Ramírez Ramírez, J. D., Arrieta Giraldo, J. S., & Garcés Ruiz, A. (2016). Distribución óptima de turbinas en parques eólicos mediante PSO considerando el efecto sombra. Revista Tecnura, 20(47), 49-55. doi: 10.14483/udistrital.jour.tecnura.2016.1.a04

Resumen

En este artículo se presenta una propuesta novedosa para ubicar de manera óptima las turbinas de un parque eólico, considerando el efecto sombra y cualquier disposición de vientos, usando la técnica metaheurística de optimización por enjambre de partículas (PSO). De igual manera se muestra la disposición que genera mayor energía para un caso propuesto, teniendo en cuenta las restricciones de distancias entre las turbinas, el área del parque eólico y el efecto sombra. La optimización de la energía generada por el parque se realiza para una rosa de los vientos en un periodo de tiempo determinado.

Palabras clave: efecto sombra, metaheurística, optimización, parque eólico, rosa de los vientos, sistemas eléctricos de potencia.

Abstract

This paper proposes a novel algorithm based on particle swarm optimization (PSO) for optimal placement of the turbines in a wind farm. Wake effect is considered for different directions and magnitudes of wind speeds according to a given compass rose. Likewise, energy optimization for a proposed case is shown which takes into account constraints related to distances between the turbines, the wind farm area and the wake effect. Simulation results demonstrate the efficiency of the proposed algorithm.

Keywords: Compass rose, Metaheuristic, Optimization, Power systems, Wake effect, Wind farm.

Introducción

La velocidad del viento dentro de un parque eólico se ve afectada por la ubicación de las turbinas, ya que estas toman parte de la energía cinética del viento, disminuyendo la velocidad del mismo en la parte posterior de la turbina. Este efecto es denominado efecto sombra.

Un gran número de modelos numéricos, de diversa complejidad, se han desarrollado para describir el efecto sombra. En general, pueden ser clasificados explícita o implícitamente. La manera explícita o cinemática consiste en modelos que utilizan los perfiles de velocidad propios, describiendo el efecto de manera semiempírica. Los modelos implícitos del efecto sombra fueron desarrollados como alternativas a partir de los modelos explícitos, los cuales se basan en aproximaciones de Naviere-Stokes o de ecuaciones de transporte de vorticidad. El modelado exacto de la distribución de la velocidad del viento en un parque eólico es una tarea bastante complicada y muchos de los parámetros necesarios no están disponibles fácilmente (Gresch et al., 2005). La elección de un adecuado modelo depende de tres factores: el tiempo de cálculo deseado, la precisión necesaria de predicción, y la información del viento disponible como parámetro de entrada. En este trabajo se realiza un enfoque simplificado para el modelado del efecto sombra y se observa cómo este puede afectar la energía producida por un parque eólico según la disposición de las turbinas.

Se pretende optimizar la energía generada por el parque eólico mediante la distribución de las turbinas, aprovechando la información suministrada por la rosa de los vientos para el caso experimental propuesto, y teniendo en cuenta todas las restricciones espaciales a las que se ve sometida cada turbina, como el tamaño del parque eólico, el no traslape entre turbinas y disminuyendo en la mayor medida el efecto sombra.

La técnica metaheurística, adelantada en este proceso de optimización, fue particle swarm optimization (PSO) la cual consiste en la naturaleza (algoritmo bioinspirado), en concreto, en el comportamiento social del vuelo de las bandadas de aves y el movimiento de los bancos de peces. El algoritmo PSO es un sistema multiagente, en el que las partículas son agentes simples que se mueven por el espacio de búsqueda, guardan y posiblemente comunican la mejor solución que han encontrado. Además, el movimiento de las partículas por el espacio está guiado por las partículas que tienen la mejor solución del momento (Del Valle et al., 2008).

Aspectos te�ricos

En la actualidad no existen muchos reportes en la literatura especializada acerca de este tema, el cual toma fuerza debido a la importancia de la energías renovables y el correcto aprovechamiento de la mimas. Una de las principales dificultades que enfrenta esta temática es que los datos de viento no cuentan con muchos registros de las condiciones reales; desafortunadamente, la mayoría de los datos históricos de viento no fueron recogidos con fines de evaluación de energía eólica. Así, los resultados a menudo representan las condiciones medias cerca de centros de población en terrenos relativamente llanos o áreas de poca elevación y no de los lugares en donde van a ser ubicados los parques eólicos, lo que se convierte en un gran problema debido a la aleatoriedad del viento y un fenómeno difícil de modelar con la rosa de los vientos.

Por otra parte, es importante la selección del sitio para la ubicación del parque eólico que depende, entre otros elementos, del potencial eólico (velocidad media del viento), de la cantidad de aerogeneradores o turbinas a instalar (área a utilizar), de las características circundantes de actividad humana y de producción, de la distancia a las líneas del sistema eléctrico al que se va a conectar y de la facilidad de acceso al predio.

Expresiones para considerar el efecto sombra

Considerar el efecto sombra para la ubicación óptima de las turbinas de un parque eólico constituye una tarea importante ya que puede afectar directamente la capacidad de generación de energía del parque.

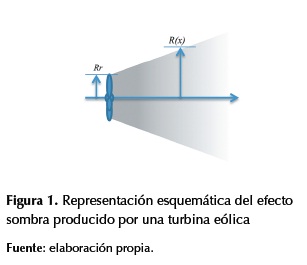
El efecto sombra producido por una turbina eólica es representado por un cono con centro en el eje de la turbina como se muestra en la figura 1. El radio del cono crece linealmente de acuerdo con la ecuación (1).

En donde ξ es una constate que depende del tipo de terreno (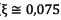 para terrenos llanos) y s es la distancia relativa respecto al radio 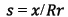(González, 2011).

La velocidad nominal del viento se ve afectada después de ser aprovechada por una turbina de acuerdo con la ecuación (2).

En donde v₀' es la velocidad nominal del viento y C_T es un coeficiente adimensional el cual depende del tipo de turbina. En la mayoría de los casos C_T puede ser aproximado como C_T =7/v₀

El efecto sombra debe considerar la superposición de múltiples turbinas. En tal caso, la velocidad está dada por la suma cuadrática de los efectos como se muestra en la ecuación (3).

En donde v_ijv_ij es la velocidad en la turbina i por efecto de la turbina j. Utilizando el mismo procedimiento se puede determinar la velocidad del viento en turbinas ubicadas detrás de varias turbinas. Sin embargo, en este caso la velocidad de la turbina debe considerar el efecto sombra de todas las turbinas que estén ubicadas delante de ella. Por tanto, se calculan tantas velocidades como turbinas se encuentren delante de ella (Zhang y Wang, 2009).

La velocidad resultante en la turbina deseada se calcula finalmente usando una relación cuadrática que se muestra en la ecuación (4).

El efecto sombra puede cambiar según la disposición de las turbinas respecto a la dirección del viento, de allí la importancia de una adecuada disposición de las turbinas en el parque eólico.

Técnica metaheurística de optimización por enjambre de partículas

La técnica metaheurística de optimización implementada es PSO, en la cual los agentes de búsqueda (partículas) intercambian información. Las partículas modifican su dirección en función de las direcciones de las partículas de su vecindario. Esta técnica almacena la experiencia propia o historia de cada agente. La partícula decide su nueva dirección en función de la mejor posición por la que pasó anteriormente (Del Valle et al., 2008).

La población del algoritmo se inicia de forma aleatoria y evoluciona, iteración tras iteración, buscando siempre la solución más óptima posible, y fundamenta la búsqueda exclusivamente en los valores de la función objetivo.

Es importante tener una buena codificación del problema para el buen funcionamiento del algoritmo PSO, siendo una técnica estocástica referida en fases (inicialización y transformación). PSO tiene operadores de movimiento, pero no de evolución como la mutación o el cruzamiento, que están presentes en otras técnicas. La técnica no crea nuevas partículas durante su ejecución, sino que siempre son las mismas partículas iniciales modificadas a lo largo del proceso, las cuales suelen tener una convergencia rápida a buenas soluciones (Shi, 2004).

Rosa de los vientos

La información de la rosa de los vientos es de suma importancia para modelar el futuro comportamiento de un parque eólico, esta contiene la información de los posibles vientos que ocurrirán en determinados periodos de esta manera es posible realizar los estimados de la producción de energía del parque eólico.

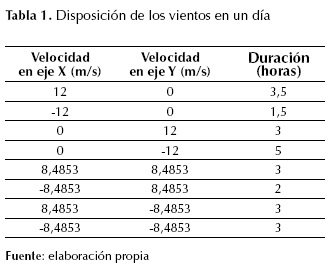
Teniendo en cuenta que el viento tiene una dirección y una velocidad diferente dependiendo de la hora del día, este se modelara como una matriz en la cual se tiene un estimado de la dirección, la magnitud de la velocidad y la duración de este comportamiento hasta cumplir las 24 horas del día. En la tabla 1, se tiene la información correspondiente a la variación de la velocidad, dirección y duración de los vientos para la realización de las pruebas.

Cálculo de la energía total producida por el parque eólico

Para el problema en cuestión es importante el cálculo de la energía producida por el parque eólico debido a que esta es la variable que se quiere optimizar, de manera que se obtenga una distribución favorable de turbinas. La potencia que proveerá cada turbina y la energía total producida por el parque eólico fueron calculadas como se expresa en las ecuaciones (5) y (6) respectivamente (Barthelmie, Hansen, Frandsen y Rathman, 2009).

En donde P_nom es la potencia nominal de la turbina. Pi y vi son la potencia producida por la turbina i y la velocidad que llega a la turbina i respectivamente.

En la ecuación (6), P_ij es la potencia generada por la turbina i para la disposición de viento j; n es la cantidad de turbinas; t_j es la duración de la disposición de viento; j y k representan la cantidad de disposiciones de viento obtenidas durante 24 horas.

Restricciones espaciales de la ubicación de turbinas en un parque eólico

Es importante tener una estrategia adecuada para la ubicación de las turbinas en un parque eólico teniendo en cuenta las restricciones de extensión del terreno que delimitan el área del parque eólico y el área que ocupa cada turbina más un factor de seguridad. Cabe resaltar que el área que ocupa una turbina corresponde a un área circular de radio igual al alabe de la misma, esto debido al joke angle, que le permite realizar giros de 360° sobre el eje del poste con el fin de ubicarse perpendicularmente a la dirección de entrada del viento.

Estas serán restricciones que se deben tener en cuenta en el momento de modelar y codificar el problema de optimización.

Metodología

Un componente fundamental para dar solución óptima al problema es su codificación, mostrar cómo se ajustaron las variables, las restricciones y la función objetivo a la técnica metaheurística PSO. En principio, se muestran todos los componentes del problema y se describe cómo es su codificación.

La función objetivo del problema que para la técnica PSO toma el nombre de función de adaptación y tiene como objetivo evaluar la energía generada por cada configuración específica de turbinas. Es muy importante destacar que esta función de adaptación tiene en cuenta las infactibilidades que pueda presentar una configuración de turbinas en específico; esto se realiza penalizando la función de adaptación mediante la resta de un valor importante a la energía generada por la configuración del parque eólico para cada infactibilidad que este presente, ya que el problema es de maximización.

Las infactibilidades para este problema son interpretadas como traslape en el movimiento de las turbinas y salir del área permitida para la construcción del parque como se mencionó anteriormente.

La técnica PSO necesita definir las partículas, las cuales se encargan de explorar el espacio de soluciones y encontrar el óptimo del problema. Para este caso cada partícula corresponde a una matriz que contiene la información de la ubicación geográfica de cada una de las turbinas que componen el parque eólico.

El desplazamiento o velocidad de cada partícula en busca del óptimo se compone de tres componentes que se exponen a continuación:

1. El vector velocidad o desplazamiento de la anterior iteración, lo que indica que el algoritmo PSO tiene memoria.
2. Un componente cognitivo que indica la decisión que tomará la partícula. Este componente depende de su propia experiencia, dicho de otra manera, representa la distancia entre la posición actual y la mejor conocida por esa partícula.
3. El componente social que apunta la decisión que tomará la partícula en base a la influencia del resto de partículas que componen la nube, es decir, representa la distancia entre la posición actual y la mejor posición encontrada por vecindario.

El modelo matemático resultante es el que representa el fundamento del algoritmo PSO.

Todas las partículas se van moviendo hasta llegar a una solución de buena calidad, basadas en la propuesta descrita anteriormente y el proceso iterativo hasta donde se define el criterio de parada (Zhang, Liu y Clerc, 2003).

En el desarrollo del algoritmo fue necesario crear una función que, cabe resaltar, permite calcular el efecto sombra entre turbinas sin importar la dirección del viento; esto es posible gracias a la rotación de ejes, que hace que las coordenadas cartesianas en las cuales se encuentran ubicadas las turbinas, se alineen con el vector de dirección del viento, simplificando los cálculos enormemente, permitiendo calcular la energía producida por la configuración de turbinas que se esté analizando.

Resultados

Como sistema se prueba se consideró un área de 3 km², del cual se tuvieron consideraciones como que el terreno es llano y además cuadrado. La cantidad de turbinas eólicas disponibles para ser ubicadas es de 50, las cuales tienen un diámetro de 75 metros cada una. Se consideró también una distancia de seguridad entre las turbinas del 5 % de su diámetro. La potencia nominal de cada una de estas turbinas es de 2MW y la velocidad nominal del viento es de 12 m/s.

Para el algoritmo de PSO se consideró una población de 500 individuos aleatorios en donde cada individuo corresponde a una posible ubicación de las 50 turbinas en el parque eólico. Esta población aleatoria fue controlada de manera que todas las soluciones iniciales fueran factibles. El algoritmo fue ejecutado durante 100 iteraciones de la cual se escogió la mejor solución (la ubicación de las turbinas que hará que se produzca mayor cantidad de energía en el parque) obtenida durante todo el proceso.

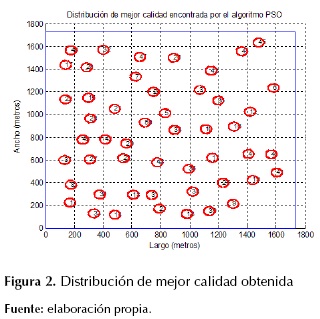
El resultado obtenido después de 100 iteraciones se muestra en la figura 2, la cual corresponde a la ubicación de las turbinas en el parque eólico de mejor calidad encontrada por el algoritmo de PSO.

La figura 2 también ilustra el área delimitada para la ubicación del parque eólico y la disposición geográfica de cada turbina en el cual es representado por un círculo formado por el movimiento circular de cada turbina teniendo en cuenta su diámetro de modo que no haya traslape entre dos o más turbinas.

Cabe señalar que la disposición encontrada se considera de buena calidad más no óptima, debido a que esta distribución fue obtenida mediante la técnica metaheurística PSO la cual no es exacta.

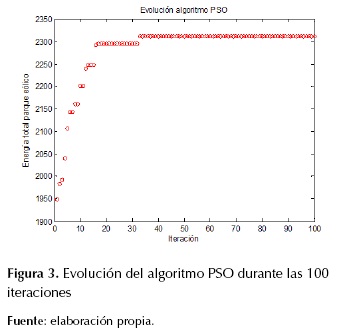
Por otro lado, en la figura 3 se detalla la evolución que se tuvo durante las 100 iteraciones en la función objetivo la cual es maximizar la energía producida.

Se puede observar cómo el algoritmo PSO fue mejorando paulatinamente durante las primeras 33 iteraciones hasta llegar a un valor de energía producida de 2312,65 Mw/día, el cual no siguió mejorando durante las iteraciones restantes por lo cual se considera que no era necesario ejecutar el algoritmo durante mas iteraciones, debido a que no es probable una mejora considerable en la función objetivo en iteraciones posteriores.

Financiamiento

Universidad Tecnológica de Pereira

Conclusiones

La metodología implementada permite obtener respuestas de buena calidad para dar solución al problema de la ubicación óptima de turbinas en un parque eólico considerando el efecto sombra.

El trabajo propuesto en este artículo realiza un aporte novedoso ya que no existen muchos planteamientos para dar solución al tema tratado, siendo este el más útil y permitiendo encontrar resultados de buena calidad.

Es importante destacar que el uso eficiente de los recursos, en este caso el viento, para generar energía se convierte en un factor decisivo y determinante a la hora de encontrar buenas relaciones costo/beneficio en una planta de generación eólica, como lo muestran los resultados.

Es posible profundizar este trabajo codificando el problema con otras técnicas de solución, que permitan mejorar los resultados.

Referencias

Barthelmie, R. J.; Hansen, K.; Frandsen, S. T. & Rathmann, O. (2009). Modeling and measuring flow and wind turbine wakes in large wind farms offshore. Wind Energy 12(5), 431-444.

Del Valle, Y.; Kumar Venayagamoorthy, G.; Mohagheghi, S.; Hernandez, J. & Harley, R.G. (2008). Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power Systems. IEEE Transaction on Evolutionary Computation 12(2), 171-195.

González Longatt, F. (2011). Wake effect in wind farm performance: Steady-state and dynamic behavior. Renewable Energy 39(1), 329-338.

Gresch, M.; Shewarega, F.; Erlich, I.; Bachmann, U. & Koch, F. (2005). Consideration of wind farm wake effect in power system dynamic simulation. Power Tech, 1-7.

Shi, Y. (2004). Feature article on particle swarm optimization. IEEE Neural Network Society, 8-13.

Zhang, W.; Liu, Y. & Clerc, M. (2003). An adaptive PSO algorithm for reactive power optimization. Proc. 6th Int. Conf. Advances in Power System Control, Operation and Management 1(497), 302-307.

Zhang, X.Y. & Wang, W.Q. (2009). Wind farm and wake effect modeling for simulation of a studied power system. IEEE/PES power systems conference and exposition, 1-6.