DOI:
https://doi.org/10.14483/22487638.16606Publicado:
01-10-2020Número:
Vol. 24 Núm. 66 (2020): Octubre - DiciembreSección:
InvestigaciónHybrid Optimization Strategy for Optimal Location and Sizing of DG in Distribution Networks
Estrategia de optimización híbrida para ubicación y dimensionamiento óptimo de GD en redes de distribución
Palabras clave:
Algoritmo genético Chu-Beasley, generación distribuida, optimización híbrida, algoritmo maestro-esclavo, flujo de potencia óptimo, redes de distribución radial (es).Palabras clave:
Chu-Beasley genetic algorithm, distributed generation, hybrid optimization, master–slave algorithm, optimal power flow, radial distribution networks (en).Descargas
Referencias
Balamurugan, K., Srinivasan, D., & Reindl, T. (2012). Impact of Distributed Generation on Power Distribution Systems. Energy Procedia, 25, 93–100. https://doi.org/10.1016/j.egypro.2012.07.013
Chu, P. C., & Beasley, J. E. (1997). A genetic algorithm for the generalised assignment problem. Computers & Operations Research, 24(1), 17–23. Research, 24(1), 17-23.
https://doi.org/10.1016/S0305-0548(96)00032-9
Ellabban, O., Abu-Rub, H., & Blaabjerg, F. (2014). Renewable energy resources: Current status, future prospects and their enabling technology. Renewable and Sustainable Energy Reviews, 39, 748–764. https://doi.org/10.1016/j.rser.2014.07.113
Gil-González, W., Montoya, O. D., Holguín, E., Garces, A., & Grisales-Noreña, L. F. (2019). Economic dispatch of energy storage systems in dc microgrids employing a semidefinite programming model. Journal of Energy Storage, 21, 1–8. https://doi.org/10.1016/j.est.2018.10.025
Gómez-Expósito, A., Conejo, A. J., & Cañizares, C. (2017). Electric energy systems: analysis and operation. CRC press. https://doi.org/10.1201/9781420007275
Grisales-Noreña, L. F., Gonzalez Montoya, D., & Ramos-Paja, C. A. (2018). Optimal sizing and location of distributed generators based on PBIL and PSO techniques. Energies, 11(4), 1018. https://doi.org/10.3390/en11041018
Hernandez, J. A., Velasco, D., & Trujillo, C. L. (2011). Analysis of the effect of the implementation of photovoltaic systems like option of distributed generation in Colombia. Renewable and Sustainable Energy Reviews, 15(5), 2290–2298. https://doi.org/10.1016/j.rser.2011.02.003
Jain, N., Singh, S. N., & Srivastava, S. C. (2014). PSO based placement of multiple wind DGs and capacitors utilizing probabilistic load flow model. Swarm and Evolutionary Computation, 19, 15–24. https://doi.org/10.1016/j.swevo.2014.08.001
Kansal, S., Kumar, V., & Tyagi, B. (2013). Optimal placement of different type of DG sources in distribution networks. International Journal of Electrical Power & Energy Systems, 53, 752–760. https://doi.org/10.1016/j.ijepes.2013.05.040
Kansal, S., Kumar, V., & Tyagi, B. (2016). Hybrid approach for optimal placement of multiple DGs of multiple types in distribution networks. International Journal of Electrical Power & Energy Systems, 75, 226–235. https://doi.org/10.1016/j.ijepes.2015.09.002
Kaur, S., Kumbhar, G., & Sharma, J. (2014). A MINLP technique for optimal placement of multiple DG units in distribution systems. International Journal of Electrical Power & Energy Systems, 63, 609–617. https://doi.org/10.1016/j.ijepes.2014.06.023
Keane, A., & O’Malley, M. (2005). Optimal allocation of embedded generation on distribution networks. IEEE Transactions on Power Systems, 20(3), 1640–1646. https://doi.org/10.1109/TPWRS.2005.852115
Kefayat, M., Ara, A. L., & Niaki, S. A. N. (2015). A hybrid of ant colony optimization and artificial bee colony algorithm for probabilistic optimal placement and sizing of distributed energy resources. Energy Conversion and Management, 92, 149–161. https://doi.org/10.1016/j.enconman.2014.12.037
Mahmoud, K., Yorino, N., & Ahmed, A. (2016). Optimal Distributed Generation Allocation in Distribution Systems for Loss Minimization. IEEE Transactions on Power Systems, 31(2), 960–969. https://doi.org/10.1109/TPWRS.2015.2418333
MATLAB. (n.d.). fmincom (2019). https://doi.org/10.1109/TPWRS.2015.2418333
Montoya, O. D., Grajales, A., Garces, A., & Castro, C. A. (2017). Distribution systems operation considering energy storage devices and distributed generation. IEEE Latin America Transactions, 15(5), 890–900. https://doi.org/10.1109/TLA.2017.7910203
Sahoo, N. C., & Prasad, K. (2006). A fuzzy genetic approach for network reconfiguration to enhance voltage stability in radial distribution systems. Energy Conversion and Management, 47(18–19), 3288–3306. https://doi.org/10.1016/j.enconman.2006.01.004
Su, X. (2017). Master–slave control for active suspension systems with hydraulic actuator dynamics. IEEE Access, 5, 3612–3621. https://doi.org/10.1109/ACCESS.2017.2672598
Sultana, S., & Roy, P. K. (2016). Krill herd algorithm for optimal location of distributed generator in radial distribution system. Applied Soft Computing, 40, 391–404. https://doi.org/https://doi.org/10.1016/j.asoc.2015.11.036 https://doi.org/10.1016/j.asoc.2015.11.036
Sun, H., Guo, Q., Zhang, B., Guo, Y., Li, Z., & Wang, J. (2015). Master–Slave-Splitting Based Distributed Global Power Flow Method for Integrated Transmission and Distribution Analysis. IEEE Transactions on Smart Grid, 6(3), 1484–1492. https://doi.org/10.1109/TSG.2014.2336810 https://doi.org/10.1109/TSG.2014.2336810
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 2 de marzo de 2019; Aceptado: 13 de agosto de 2020
Abstract
Objective:
This paper presents a hybrid optimization methodology for the optimal location and sizing of distributed generators (DG) in electrical distribution networks. We propose a mixed-integer nonlinear problem (MINLP) model for the mathematical formulation, whose objective function is the minimizing of power losses due to the Joule effect in conductors. The constraints we considered include active and reactive power balance, voltage regulation, percentage of penetration of DG into the distribution network, and the total amount of DG allowed in such network.
Methodology:
To solve the MINLP model, we employed a master-slave strategy that uses the Chu-Beasley genetic algorithm (CBGA) and the optimal power flow (OPF) model as the master and slave algorithms, respectively. This hybrid technique helps reduce the complexity of the MINLP model by eliminating binary variables through the master algorithm and then solving the resulting nonlinear problem (NLP), which corresponds to the OPF model, and uses a classical interior-point method available in MATLAB's fmincon toolbox.
Results:
We tested the efficiency and robustness of the proposed methodology in 33- and 69-node radial distribution networks. The results show its high performance in terms of power loss reduction and final sizing of DG.
Conclusions:
The results obtained in the test systems under analysis reveal that there is a direct and proportional relationship between technical losses, the percentage of distributed generation penetration, and the number of generators available.
Keywords:
Chu-Beasley genetic algorithm, distributed generation, hybrid optimization, master-slave algorithm, optimal power flow, radial distribution networks.Resumen
Objetivo:
En este documento se presenta una metodología de optimización híbrida para la ubicación y el tamaño óptimos de generadores distribuidos (DG) en redes de distribución eléctrica. Se propone un modelo de problema no lineal de enteros mixtos (MINLP) para la formulación matemática, cuya función objetivo es la minimización de las pérdidas de potencia debido al efecto Joule en los conductores. Las restricciones incluyen el equilibrio de potencia activa y reactiva, regulación del voltaje, porcentaje de penetración de las DG en la red de distribución y las DG totales permitidas en dicha red.
Metodología:
Para resolver el modelo MINLP, se emplea una estrategia maestro-esclavo que utiliza el algoritmo genético Chu-Beasley (CBGA) y el modelo de flujo de potencia óptimo (OPF) como algoritmos maestro y esclavo, respectivamente. Esta técnica híbrida ayuda a reducir la complejidad del modelo MINLP al eliminar las variables binarias a través del algoritmo maestro y luego resolver el problema no lineal resultante (PNL) que corresponde al modelo OPF, utilizando un método clásico de punto interior disponible en la caja de herramientas fmincon de MATLAB
Resultados:
Se prueba la eficiencia y la solidez de la metodología propuesta en redes de distribución radial de 33 y 69 nodos. Los resultados muestran un alto rendimiento en términos de reducción de pérdida de potencia y dimensionamiento final de DG.
Conclusiones:
Existe una relación directa y proporcional entre las pérdidas técnicas, el porcentaje de penetración de generación distribuida y el número de generadores disponible.
Palabras clave:
Algoritmo genético Chu-Beasley, generación distribuida, optimización híbrida, algoritmo maestro-esclavo, flujo de potencia óptimo, redes de distribución radial.
INTRODUCTION
Electrical systems have evolved from conventional electrical networks that used traditional power generation technologies including hydraulic and thermal plants (coal, diesel, natural gas, etc.) (Gómez-Expósito, Conejo, & Cañizares, 2017) to systems that take advantage of high penetration of distributed energy resources-mainly wind and solar photovoltaic power generation (Hernandez, Velasco, & Trujillo, 2011; Jain, Singh, & Srivastava, 2014).
This paradigm shift in the structure of power systems has been driven mainly by the growing global concern over the harmful consequences of the greenhouse effect, as evidenced in the agreement to combat climate change signed in Paris in 2015 (Montoya, Grajales, Garces, & Castro, 2017). In this regard, a great number of governments worldwide have made a commitment to gradually replace the use of fossil fuels with renewable resources for power generation because power systems along with transportation systems are the largest producers of greenhouse gases into the atmosphere (Ellabban, Abu-Rub, & Blaabjerg, 2014). Therefore, to combat the harmful effects of fossil fuel-based power generation, various alternative technologies have been developed-mainly, distributed solar and wind energy resources along with battery-based long-term energy storage systems (Gil-González, Montoya, Holguín, Garces, & Grisales-Noreña, 2019; Montoya et al., 2017).
Several studies have proposed solutions to incorporate renewable energies into power systems, improve the technical aspects of the network, and reduce the environmental impact caused by conventional power generation processes (Balamurugan, Srinivasan, & Reindl, 2012). In particular, the authors in (Kaur, Kumbhar, & Sharma, 2014) used the sequential quadratic programming technique and the branch and bound algorithm for the location and sizing of DG; also, they proposed the minimization of system power losses during peak hours as the objective function.
In (Keane & O'Malley, 2005), an analytical method was implemented for the optimal location of multiple DG and an optimal power flow (OPF) model for their sizing. In that case, the objective was to reduce active power losses during a peak demand scenario. The authors in (Keane & O'Malley, 2005) developed a linear programming-based methodology to determine the optimal location and sizing of DG. The objective function in such study was the maximization of the power supplied by such generators, considering the classical operating limitations of DS. In (Kansal, Kumar, & Tyagi, 2013), a methodology that integrated three different types of DG into a DS was presented; its objective function was power loss reduction. To solve the problem, the authors proposed the use of a metaheuristic algorithm known as particle swarm optimization (PSO).
In (Kefayat, Ara, & Niaki, 2015), a hybrid optimization strategy combined two algorithms: ant colony optimization and artificial bee colony optimization. The first algorithm was responsible for the location of the DG, and the second for their sizing. The objective function was a linear combination that reduced active and reactive power losses, CO2 emissions, investment costs in DG, and an index associated with voltage stability. The authors in (Kansal, Kumar, & Tyagi, 2016) presented a hybrid approach for locating multiple DG. To solve the problem, they combined the PSO technique with an analytical method for sizing said generators, using the reduction of power losses in the DS as the objective function. Moreover, in (Grisales-Noreña, Gonzalez Montoya, & Ramos-Paja, 2018), the authors proposed a hybrid metaheuristic algorithm to locate and size DG in radial distribution networks with a master-slave strategy. In the master stage, a population-based incremental learning (PBIL) method was responsible for the optimal location of DG, while a PSO algorithm was used for their sizing in the slave stage. In said work, the objective function was the minimization of active power losses and the improvement of the voltage profile.
In this state-of-the-art review, we found that the problem of optimal integration and sizing of DG in electrical networks using metaheuristic optimization techniques is divided into two stages. The first stage is in charge of their location, and the second one of their sizing. Also, we determined that one of the best alternatives to solve this problem is to combine different optimization strategies that exploit the nature of both subproblems (the discrete nature of the location problem and the continuous nature of the sizing problem).
Therefore, this paper presents a master-slave hybrid optimization technique, where the master problem defines the location nodes of DG by means of a combinatorial optimization metaheuristic method known as the Chu-Beasley genetic algorithm (CBGA) (Chu & Beasley, 1997), whereas the slave problem is responsible for sizing such generators for each configuration provided by the master stage. This is achieved by solving an OPF problem using the interior-point method available in MAT-LAB's fmincon optimization package. We propose the reduction of active power losses as the objective function, while the constraints evaluate typical characteristics in the operation of DS, such as active and reactive power balance, voltage regulation limits, and generation capacities, among others.
The main contribution of this hybrid method, which combines the CBGA with the fmincon optimization package, lies in the ability of the CBGA to solve discrete problems together with the OPF that ensures the efficient sizing of DG. Additionally, unlike in studies in the specialized literature, our proposed master-slave technique can be used to analyze different percentages of active power in the penetration of DG, as well as to modify the number of DG to be located. As a result, this strategy is a flexible tool that may be used in problems regarding the planning and expansion of electrical networks.
An important new aspect of this study is the possibility of analyzing multiple distributed generation scenarios, which allow us to identify sensitivities between the number and capacity of DG with respect to the reduction of active power losses. This proves that solving the problem is still a work in progress, and multiple studies should be conducted to find better solutions in reasonable computational times.
The rest of this paper is structured as follows. Section 2 introduces the mathematical formulation of the problem. Section 3 describes the proposed master-slave optimization methodology. Section 4 presents the 33- and 69-node test systems employed here. Section 5 details the parameterization of the CBGA and the OPF model, as well as the simulation scenarios. Section 6 reports the results. Section 7 draws some conclusions. Finally, a list of references is provided at the end of this paper.
MATHEMATICAL FORMULATION
To mathematically describe the problem of optimal location and sizing of DG in DS, we used a MINLP model, whose objective function was the reduction of the DS' active power losses during peak hours [6, 19]. The constraints included the traditional operating characteristics of power flow in DS, the allowed DG penetration percentage in the DS, and the number of DG available. The complete mathematical model is presented in equations (1) to (8).
Objective function:

Constraints:
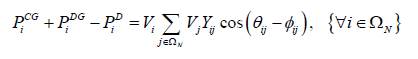
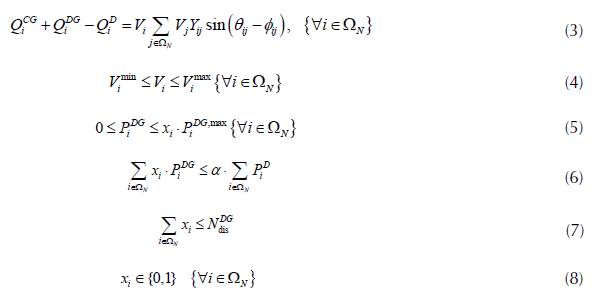
The objective function in equation (1) corresponds to the active power losses in the distribution lines as a function of the magnitudes and angles of the voltages across all the system busbars and the parameters of the conductors. Constraints equations (2) and (3) determine the balance of active and reactive power at each node in the system, respectively. Equation (4) presents the maximum and minimum voltage regulation conditions at each node; equation (5), the maximum and minimum active power values that can be supplied by each DG located at node i; equation (6), the percentage of penetration in terms of active power generated by the DG; and equations (7) and (8) present the maximum number of DG allowed in the system and the binary nature of the decision variables associated to the location of the DG, respectively.
The mathematical formulation presented from equations (1) to (8) reveals that the binary nature of the decision variables associated with the location of the DG makes this a non-differentiable model; therefore, traditional derivative-based optimization techniques are not applicable (Grisales-Norena et al., 2018). This proves that hybrid models should be used to separate the binary location problem from the continuous OPF problem associated with the sizing of DG. The next section details our CBGA-fmincon method used to address this problem using a master-slave strategy.
PROPOSED SOLUTION METHODOLOGY
To solve the problem of optimal location and sizing of DG in DS, we propose a master-slave strategy (referred to as hybrid optimization technique in literature) (Grisales-Norena et al., 2018). This strategy involves dividing the MINLP model into two optimization sub problems: the first one corresponds to the master algorithm; the second one, to the slave problem (Su, 2017; Sun et al., 2015).
Master problem
In the master problem, we define the location of the DG nodes by means of the combinatorial optimization metaheuristic technique known as the Chu-Beasley genetic algorithm (CBGA). Said technique is very efficient in solving binary optimization problems (Mahmoud, Yorino, & Ahmed, 2016), such as placing a DG at node i. However, to define the adaptation function of the CBGA, we first need to find the optimal solution to the slave problem.
Mathematically speaking, the CBGA is responsible for determining the location of the DG. In other words, regarding the mathematical formulation presented from equations (1) to (8), the CBGA solves equations (5) to (8).
To calculate the decision vector x = [x 1 x 2 ,x n ] by means of the CBGA, we consider the following basic aspects:
a. The initial population is randomly generated when there are more than two DG. Its size should not exceed ten individuals who must be different.
Define the set of variables x. to be enabled so that the binary nature required byequation (8)is maintained, validate that the maximum number of distributed generators to be installed is not exceeded (equation (7)), and enable constraintsequation (5)andequation (6)in the nodes where distributed generation will be installed.
b. When one or two distributed generators are to be located, all possible combinations are created in the initial population. In other words, an exhaustive search is performed, and all the individuals are evaluated in the slave algorithm; then, the optimal solution would be the individual with the lowest losses. In this case, the optimization process ends at this point.
c. Every individual in the population generated in step a is evaluated using the slave algorithm.
d. To select the descendant, four randomly selected individuals in the population participate in a tournament that produces two winners. We use a single-point crossover and a mutation rate with a probability above 90%.
e. If the individuals created in the previous stage have a number of generators different from that assigned for location, a reconstructive algorithm is applied to remove extra nodes from individuals and to add generators to those that need them.
f. The individual with the best adaptation function from the previous step is selected. Furthermore, if its adaptation function is better than that of the worst individual in the population and is different from all the others,
g. The individual with the best adaptation function in the population is selected as the incumbent.
h. The process goes back to step d, and the procedure is repeated until all the generational cycles are completed or the adaptation function of the best individual does not change for at least ten continuous generations.
It should be noted that the adaptation function corresponds to the technical losses stated by equation (1) and obtained through the solution proposed by the slave algorithm.
Slave problem
After obtaining the locations of the DG in the DS during the master stage, the MINLP mathematical model presented on equations (1) to (8) is reduced to a nonlinear problem (NLP)-referred to as optimal power flow (OPF) problem in literature- for distribution networks, where the expressions on equations (7) and (8) have already been guaranteed during the generation of individuals in the master stage. The mathematical model that must be solved in the slave stage is presented is as follows
Minimizing equation (1) corresponds to the value of the adaptation function that is subject to the set of constraints defined from equations (1) to (6).
The previous description presents the generic mathematical model of an OPF problem, solved using MATLAB's optimization package for nonlinear programming problems known as fmincon. This tool uses the interior-point optimization method to retrieve an optimal feasible solution to said problem.
The DG considered in this study do not have the sufficient capacity to control the voltage in the busbars to which they are connected; therefore, they are modeled as PQ nodes, where the generation of active and reactive power varies and depends on the capacity of the distributed energy resource and the electronic power converter.
To clarify the type of problems that the fmincon package solves, equation (9) provides an overview of all the mathematical models that this tool can address.
Where y is the set of variables of the problem, i.e.
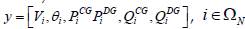 being f(y) the objective function (1); c(y), the set of nonlinear inequalities (null for the OPF problem under study); c(y), the set of nonlinear equations that represent the balance of active and reactive power (equations (2) and (3)); Ay ≤ b, the set of linear inequalities (equation (6)); A
eq
y ≤ b
eq
, the set of linear equations of the optimization problem that generates an empty set for the OPF problem; and y
min
. ≤ y ≤ y
max
, the upper and lower limits of the decision variables as presented in equations (4) and (5).
being f(y) the objective function (1); c(y), the set of nonlinear inequalities (null for the OPF problem under study); c(y), the set of nonlinear equations that represent the balance of active and reactive power (equations (2) and (3)); Ay ≤ b, the set of linear inequalities (equation (6)); A
eq
y ≤ b
eq
, the set of linear equations of the optimization problem that generates an empty set for the OPF problem; and y
min
. ≤ y ≤ y
max
, the upper and lower limits of the decision variables as presented in equations (4) and (5).
Finally, the syntax for the fmincon package in MATLAB is
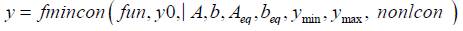
where y 0 is a feasible point in the solution space, and nonlcon is the set of nonlinear constraints. For more details about the implementation of NLP problems in MATLAB, see (MATLAB, n.d.).
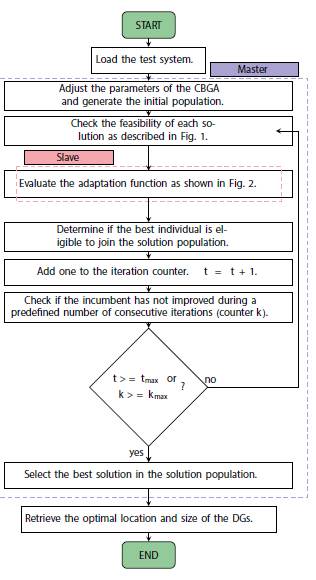
Flow diagram
The flow diagram in Figure 1 summarizes the master-slave methodology we propose to solve the problem of optimal location and sizing of DG in DS using a hybrid optimization strategy, referred to here as CBGA-fmincon.
Figure 1: Proposed master-slave methodology combining the CBGA and MATLAB's fmincon package.
In this type of hybrid optimization strategies, the master algorithm is completely dependent on the slave algorithm because the latter guides the former in the search for the best solution (Grisales-Norena et al., 2018). Hence, the same master stage with different slave strategies might find potentially different solutions (mainly in nonconvex NLP problems). This demonstrates that hybrid optimization is still an open field of study with great research potential.
TEST SYSTEMS
In order to evaluate the proposed methodology to solve the problem of optimal location and sizing of DG in DS, we employed two test systems implemented in the specialized literature (Sahoo & Prasad, 2006): a 33-node test system and the classical Baran & Wu 69-node test system.
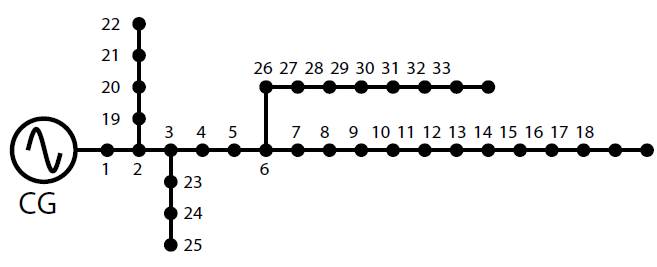
Test system 1
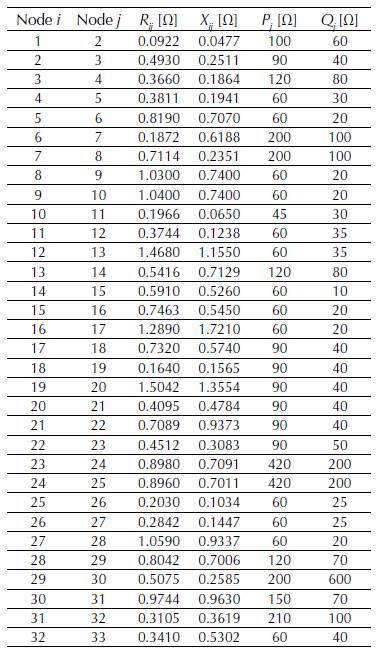
This feeder-whose topology is shown in Figure 2, has a single conventional generator (slack node in busbar 1), 33 nodes, and a radial nature. It operates at 12.66 kV and has an active and reactive power demand of 3715 kW and 2300 kVAr, respectively. Table 1 details the line parameters and the demand at each node (Grisales-Noreha et al., 2018).
Figure 2: Topology of test system 1.
Source: Authors.
Table 1: Information about network segments and demand of Test system 1.
Test system 2
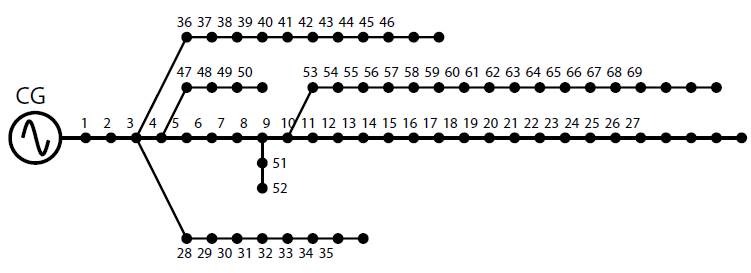
This test system-whose topology is shown in Figure 3, has a single conventional generator (slack node in busbar 1), 69 nodes, and 68 feeders. It operates at 12.66 kV (Sultana & Roy, 2016) and has an active and reactive power demand of 3890.67 kW and 2693.6 kVAr, respectively. Information about its parameters can be consulted in (Grisales-Noreha et al., 2018).
Figure 3: Topology of Test system 2.
PARAMETERIZATION OF THE CBGA-OPF METHODOLOGY AND SIMULATION SCENARIOS
This section presents the parameters employed to solve the problem of optimal location and sizing of DG in DS using the master-slave strategy described in Section 3, as well as the simulation scenarios.
Parameterization of the CBGA-OPF methodology
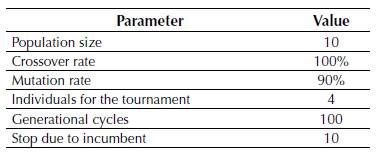
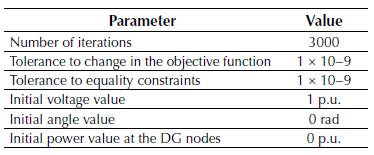
Parameterizing the CBGA is an essentially heuristic process that adjusts the parameters of the optimization process by trial and error (Chu & Beasley, 1997). In this paper, we selected the parameters presented in Table 2.
Source: Authors.
Table 2: Parameters of the CBGA.
The CBGA considers a single-point crossover, and the dimension of each individual in the population is equivalent to the number of nodes in the system under study except for the slack node. Moreover, the tournament to select the parents is held with the information from the objective function of each individual; the two winning individuals (selected as parents) will be entitled to produce offspring through crossover and mutation. At this point, note that the two resulting offspring are compared in terms of the objective function, and only the one with the best performance will be able to join the population provided that it meets the diversity criteria and outperforms the worst solution contained in the population.
For the OPF model, we used the parameters shown in Table 3, which served to implement the interior-point method used by the fmincon package, as well as its stopping criteria.
Source: Authors.
Table 3: Parameters of the CBCA.
We used the fmincon package, available in MAT-LAB (2017a version)(MATLAB, n.d.), to solve the OPF problem.
Simulated scenarios and considerations
To evaluate the proposed methodology for the optimal selection of DG in DS with the CBGA-fmincon master-slave algorithm, we applied the following criteria:
-
Three scenarios were simulated. The first scenario (S1) considers a DG penetration rate at 20% of the active power demand; the second scenario (S2) at 40%; and the third scenario (S3) at 60%.
-
The maximum active power generation capacity of each DG is below or equal to the total distributed generation penetration allowed in each scenario.
-
In every simulation scenario, all the DG operate with a unity power factor, i.e. they can only generate active power Q DG = 0, i Є Ω N .
-
Regarding permissible voltage regulation, the voltage at each node after locating the DG is 5%. If the problem is not feasible due to voltage, this limit is extended to 10%.
-
The maximum number of DG considered is equal to three.
-
The voltage and power base values used for both test systems are 12.66 kV and 1 MVA, respectively.
APPLICATION AND RESULTS
For the implementation of the CBGA-OPF master-slave strategy, we used MATLAB (2017a version) on a computer with an AMD A10-8700p Radeon R6 processor, 8 GB of RAM, and Windows 10 (Single Language).
Results in test system 1
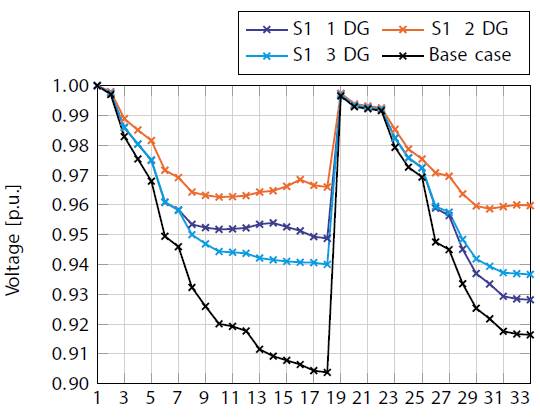
The base case of this test system presents active power losses of 210.98 kW, and its lowest voltage is 0.908 p.u. at node 18. Table 4 presents the active power losses obtained after the proposed methodology was applied to Test system 1 in each simulation case described in the previous section. Figure 4 illustrates the voltage regulation of this system in S1, and Table 5 lists the location and size of each DG.
Source: Authors.
Table 4: Active power losses in Test system 1.

Source: Authors.
Table 5: Distributed generation in Test system 1.
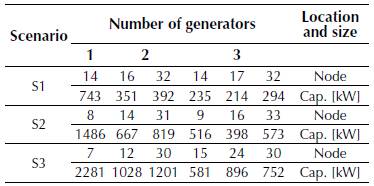
Figure 4: Voltage regulation behavior in Test system 1 in S1.
The results in Table 5 indicate that the percentage of DG penetration and the number of generators allowed have a direct impact on the minimization of the active power losses in the DS.
Therefore, if we consider the active power losses of the system without DG (i.e., 210.98 kW) to be the base case, S1 shows a reduction in losses equivalent to 34.05% with a single generator, while S3 produces a reduction of 61.45% with three generators. These percentages suggest that there is a direct and proportional relationship in Test system 1 between the percentage of DG penetration, the number of generators allowed, and the reduction in technical losses in the system.
Furthermore, Figure 4 presents the behavior of the voltage profiles of all the system nodes in S1. Note that the voltage regulation of several nodes in the base case is above 5%. However, when a 20% DG penetration is allowed, the system's voltage profiles can be improved.
It should be noted that the number of generators allowed in the system has a significant impact on voltage profiles. For instance, when one or three DG are employed, voltage regulation is not achieved. This occurs because a 20% of active power injection at a single node of the system cannot affect the behavior of the voltages across the entire network in the case of a single generator. This also happens with three generators because the average injection falls below 8%, which does not help modify substantially the local voltage profiles. However, when two generators are used, their average injection at each node is around 10%; that and their location (nodes 16 and 32) allow them to modify all the network voltage profiles until the whole system presents a regulation below 5%.
Finally, the sizes of the DG in Table 5 suggest that the capacities of the DG are evenly distributed depending on the scenario under analysis and the number of generators allowed. In particular, note that in S2 a single generator is assigned a net power generation capacity of 1486 kW; two generators, 667 kW and 819 kW, respectively; and three generators, 516 kW, 398 kW, and 573 kW, respectively. Nevertheless, when the combined capacities of the two and three generators add up, we obtain a net installed capacity of 1486 kW, which clearly shows that the net installed capacity corresponds to 40% of the total power demand regardless of the number of generators available.
Results in test system 2
The base case of this test system presents active power losses of 242.14 kW, and its lowest voltage is 0.9029 p.u. at node 69.
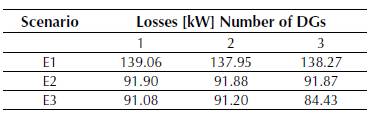
Table 6 presents the active power losses obtained after applying the proposed methodology to Test system 2 in each simulation case described in the previous section. Figure 5 details the voltage profile of this system in S2, and Table 7 shows the location and size of each DG.
Source: Authors.
Table 6: Active power losses in Test system 2.
Source: Authors.
Table 7: Active power losses in Test system 2.
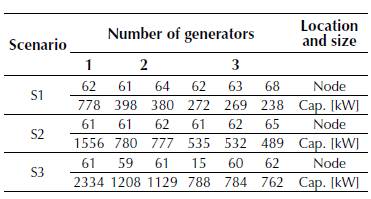
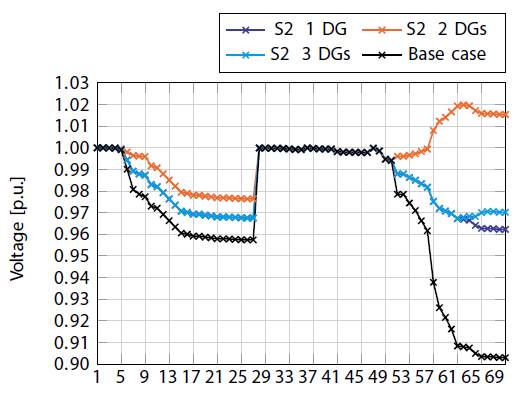
Figure 5: Voltage regulation behavior in Test system 2 in S2.
We conclude from Table 6 that taking as a reference the base case mentioned above, S1 with a single generator shows the lowest reduction in active power losses (42.57%), while S3 with three generators exhibits the highest reduction (65.13%).
However, Table 6 also suggests that the best solutions are found in S2 because they lead to an average reduction in technical losses of 62.05% with a DG penetration of 40% regardless of the number of generators that are installed; nodes 61 and 62 (see Table 7) are the most preferred nodes for DG location.
Figure 5 presents the voltage profiles of S2 considering one to three available DG. Note that the base case violates the voltage regulation constraints from node 57 onward. Nonetheless, the rest of the cases ensure that voltage regulation remains within the allowed limits. Additionally, the voltage profiles are above 1 p.u. from node 57 onward in the case of two generators, which does not occur in the two other cases. Finally, the cases with one and three generators have very similar voltage profiles and only differ from node 61 onward. This is evidence that the positive effect of DG integration on voltage profiles, as it keeps them within the allowed ranges in all scenarios.
Comparative results
To validate the performance of the proposed master-slave methodology, which integrates the CBGA and the nonlinear optimization package (fmincon), this section compares it with the methodology proposed in (Grisales-Noreha et al., 2018), where the population-based incremental learning (PBIL) algorithm is combined with the particle swarm optimization (PSO) algorithm to solve the problem of optimal location and sizing of DG in radial networks. The authors of that study recommend for the base case a distributed generation penetration equivalent to 40% of the power injected by the slack node and a maximum capacity of 1200 kW for each DG that is installed.
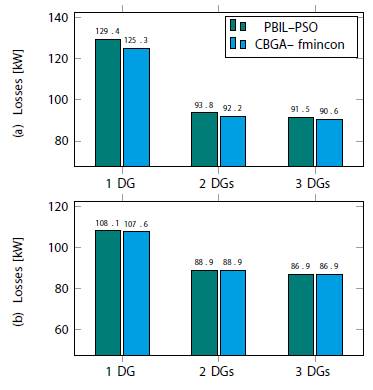
Figure 6 shows the results of the comparison between the PBIL-PSO method and the methodology proposed here in Test system 1. Note that our proposed hybrid algorithm exhibits superior performance regarding the minimization of power losses in each scenario under analysis. In particular, Figure 6(a) reveals that there was a reduction in power losses of 4.1 kW with one DG, while such reductions were 1.6 kW and 0.9 kW, respectively for two and three DG. Therefore, these results prove that the CBGA-fmincon method is numerically superior to the PBIL-PSO reported in (Grisales-Noreha et al., 2018) for the IEEE 33-node system.
Figure 6: Comparison between our proposed method and its PBIL-PSO counterpart: (a) Test system 1. (b) Test system 2.
Regarding Test system 2, Figure 6(b) indicates that the CBGA-fmincon method is numerically equivalent to the PBIL-PSOin the case of two and three DG because both methods produced the same objective function. However, in the case of one DG, our proposed method exhibited a slight improvement of 0.5 kW in the objective function. This can be considered a positive result because the CB-GA-fmincon method usually exceeds or matches the results reported by the specialized literature. The locations of the DG were not included in this section because they correspond to those previously reported in (Grisales-Noreha et al., 2018).
CONCLUSIONS AND FUTURE WORK
We proposed a hybrid optimization technique that combines the Chu-Beasley generic algorithm (CBGA) and the optimal power flow (OPF) model to solve the problem of optimal location and sizing of distributed generators (DG) in distribution systems (DS). This technique divides the original mixed-integer nonlinear programming problem into two sub-problems that are then sequentially solved using a master-slave methodology.
The results obtained in the test systems under analysis reveal that there is a direct and proportional relationship between technical losses, the percentage of distributed generation penetration, and the number of generators available. Therefore, our proposed integration methodology may be very useful for companies in the electricity sector that are interested in maximizing the economic benefit of using distributed energy resources to improve the quality, reliability, and continuity of the service they provide to end-users. This happens because our methodology is flexible and can be easily adapted to the specific conditions and requirements of each distribution company.
Future work can explore economic analyses to establish the minimum temporal relationship between the profits obtained from technical loss reduction and the costs associated with the installation, operation, and maintenance of distributed generation units considering different demand scenarios.
The integration of distributed generators using electronic power converters that control the flow of active and reactive power between the electrical network and the generator may also be considered. This could lead to greater reductions in technical losses and a significant improvement in the voltage profiles at each busbar.
REFERENCES
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.