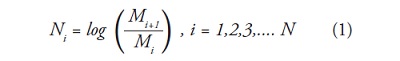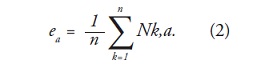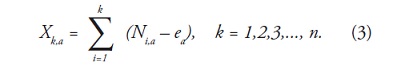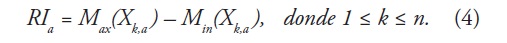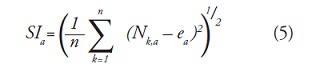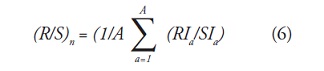Estimación del exponente de Hurst y la dimensión fractal de una superficie topográfica a través de la extracción de perfiles

ESTIMACIÓN DEL EXPONENTE DE HURST Y LA DIMENSIÓN FRACTAL DE UNA SUPERFICIE TOPOGRÁFICA A TRAVÉS DE LA EXTRACCIÓN DE PERFILES

HURST EXPONENT AND FRACTAL DIMENSION ESTIMATION OF A TOPOGRAPHIC SURFACE THROUGH A PROFILES EXTRACTION

Oscar Yesid Quintero Delgado¹, Jonathan Ruiz Delgado²

¹Universidad Distrital “Francisco Jose de Caldas”oskr.kintero@gmail.com

²Universidad Distrital “Francisco Jose de Caldas”jonathan.darkside@gmail.com

Recibido: 01/05/2011 - Aceptado: 01/07/2011

RESUMEN

La geometria fractal nace como una alternativa para interpretar y representar de manera mas precisa las diferentes formas presentes en la naturaleza. Es asi como en este articulo, el cual nace del trabajo de investigacion del proyecto de grado titulado “Simulaciones de campos aleatorios tipo movimiento browniano fraccionado aplicadas al estudio de observables espaciales en geociencias” se presenta una alternativa para estimar el exponente de Hurst y la dimension fractalde de una superficie a traves de la evaluacion de algunos perfiles topograficos extraidos de la misma, los cuales se presentan como parametros importantes dentro de dicha geometria.

Para lograr el objetivo se extrajo, en primera instancia, un mosaico del Modelo Digital de Elevacion generado de las planchas oficiales de Colombia a escala 1:100.000, obteniendo para la superficie de trabajo valores representativos entre 0,53 y 0,79 en el exponente de Hurst, mientras que por otro lado se obtuvo un valor caracteristico para la dimension fractal de dicha superficie de 2,42; permitiendo asi catalogar las superficies topograficas como objetos de naturaleza fractal.

Palabras clave: dimension fractal, exponente de Hurst, geometria fractal, perfiles, superficies topograficas.

ABSTRACT

Fractal Geometry was created as an alternative to interpret and represent more accurately the different forms present in nature. Thus, in this article, which is born of the research Project grade entitled “Simulation of random fields type fractional brownian motion applied to the geosciences space observations study” presents an alternative to estimate of a surface the Hurst Exponent and its Fractal Dimension through the evaluation of some topographic profiles drawn from the same, the surface, which are presented as important parameters in this geometry.

To achieve the goal was extracted in the first instance a mosaic of Digital Elevation Model generated from Colombia official plates at 1:100.000 scale, getting to the work surface representative values in the Hurst Exponent between 0.53 and 0.79, while on other side scored to the surface a characteristic value for the Fractal Dimension of 2.42, catalog allowing topographic surfaces as objects of fractal nature.

Key words: Fractal dimension, Hurst exponent, fractal geometry, profiles, topographic surfaces.

INTRODUCCIÓN

Dadas las complejas formas de la geografia terrestre se hace necesario encontrar modelos que vayan mas alla de la clasica geometria euclidea. A principios del siglo XX, con el surgimiento de la geometria fractal o geometria moderna, la cual estudia los aspectos geometricos que son invariantes con el cambio de escala, se origina una nueva herramienta para la representacion de las diversas formas presentes en la naturaleza.

Para encontrar una respuesta solida, que solucione el problema de representar elementos de la superficie de forma mas precisa, se presenta la forma de evaluar dos atributos de gran relevancia en el estudio de la geometria fractal, como son el exponente de Hurst y la dimension fractal, los cuales se relacionan con el grado de rugosidad que pueden llegar a adquirir las superficies topograficas.

De esta manera, para el caso de la variable de interes (topografica), el procedimiento consistio en extraer del modelo digital del terreno (MDT) original las coordenadas especificas de la zona de estudio, de donde se obtuvo la grafica de la superficie real, luego se trazaron varios perfiles sobre el mapa de contornos y, por medio de un algoritmo, se estimaron los exponentes de Hurst (H) para cada perfil, obteniendose de esta forma un valor representativo para dicho exponente (H).

EXPONENTE DE HURST

El coeficiente o exponente de Hurst es una medida de independencia de las series de tiempo que fue estudiada inicialmente por el cientifico britanico Harold Edwin Hurst (1880-1978), como elemento para distinguir series fractales. Hurst descubrio que muchos fenomenos naturales exhiben un comportamiento que puede ser caracterizado por un proceso aleatorio sesgado, en el cual existe “memoria de largo plazo” entre las observaciones, es decir, que los eventos de un periodo influyen en todos los siguientes.

Posteriormente, las ideas de Hurst fueron retomadas por Benoit B. Mandelbrot quien generalizo su trabajo y lo llamo analisis de rango reescalado (R/S), definido como un metodo estadistico utilizado para evaluar la ocurrencia de eventos poco comunes, dando origen a una herramienta ideal para procesos fisicos y financieros, aunque no se limita solamente a este tipo de eventos, por lo que puede ser usado en cualquier serie de tiempo (Gutierrez, 2008).

Análisis de Rango Reescalado (R/S)

El permite encontrar el parametro o exponente de Hurst, el cual es un valor numerico que hace posible determinar la auto-correlacion en una serie de datos.

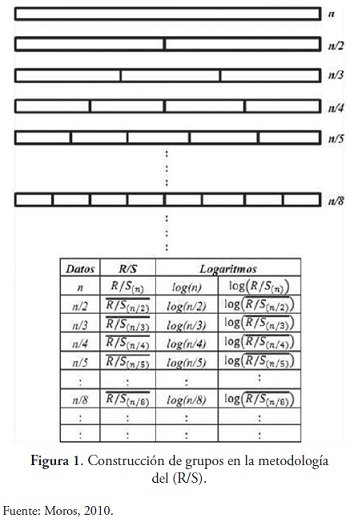
A continuacion se describe la metodologia desarrollada por Hurst: [2]

1. Se inicia con una serie de tiempo de tamano M, pero como interesa los rendimientos logaritmicos entonces la serie original se reduce a una nueva serie de tiempo de tamano N=M donde cada rendimiento esta definido por:

   

2. Este periodo de tiempo N se divide en A subperiodos contiguos de longitud n, tal que A * n = N. Se nombra cada uno de los subperiodos o subgrupos I_a, con a = 1,2,3,..., A. Cada elemento en I_a,, es etiquetado N_k,a, tal que k = 1,2,3,..., n. Para cada subperiodo I_a, de longitud n, el valor promedio esta definido por la siguiente expresion:

   

3. Las diferencias de cada elemento N_k,a, con respecto a la media e_a, para cada subperiodo I_a, se van sumando para obtener la serie de tiempo acumulada (Xk,a ), definida como:

   

4. El rango R I_a, se define como la diferencia entre el valor maximo y el valor minimo de X_k,a, para cada subperiodo I_a,:

   

5. Se calcula la desviacion estandar muestral SIa de la forma tradicional para cada periodo I_a,:

   

6. Para cada periodo I_a,, su rango R I_a, se normaliza dividiendo por su desviacion estandar muestral S I_a, correspondiente. Por lo tanto el rango reescalado para cada subperiodo I_a, es igual a R I_a, /S I_a,. Como tenemos periodos continuos de longitud , entonces tomamos el valor promedio R/S para periodos de longitud y que esta definido como:

   

7. La longitud n o el tamano del subperiodo se incrementa al siguiente valor posible de tal forma que sea un valor entero. Iniciamos con el valor mas pequeno de acuerdo a la condicion anterior y se repiten los pasos del 1 al 6 hasta utilizando siempre la serie completa (figura 1). Posteriormente aplicamos una regresion de minimos cuadrados de log(R/S)n contra log(n). La ordenada al origen es el log(c) y la pendiente de la ecuacion es la estimacion del exponente Hurst H.

VALORES DEL COEFICIENTE DE HURST

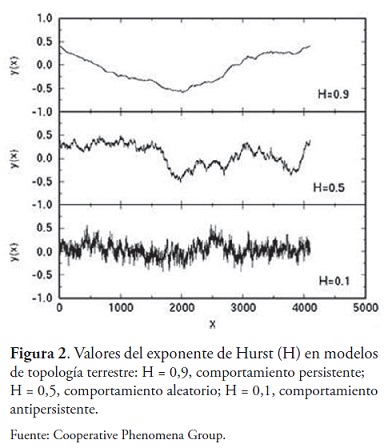
Si H=0.5 (ruido blanco) implica un proceso completamente aleatorio e independiente, con ausencia de correlacion entre los incrementos de la senal. Correlacion = 0.

Si 0.5 < H ≤ 1 implica series de tiempo que muestran procesos persistentes o correlacionados (un periodo de crecimiento es seguido de otro analogo) y presentan un aspecto suave. Una serie persistente esta caracterizada por efectos de memoria de largo plazo. Teoricamente lo que suceda hoy impactara en el futuro por siempre, todos los cambios diarios estan correlacionados con todos los cambios futuros. Se ha encontrado que las series persistentes son las mas comunes en la naturaleza. Un H=1 indicaria un comportamiento deterministico. A este comportamiento tambien se le atribuye el nombre de Ruido Negro, ya que se relaciona con procesos ciclicos de largo plazo, como niveles de rios, cambios de precios en la bolsa de valores, entre otros.

Si 0 ≤ H < 0.5 corresponde a un comportamiento de anti-persistencia o anti-correlacional en la serie de tiempo (un periodo de crecimiento es seguido de otro de decrecimiento) que se caracteriza por un mayor contenido de alta frecuencia. Un incremento en los sucesos del pasado, supone un descenso en los sucesos futuros y viceversa. Un sistema anti-persistente tiende a regresar constantemente al lugar de procedencia y tienen la particularidad de ser senales muy irregulares. A este tipo de comportamientos se le conoce tambien como Ruido Rosa y se caracterizan por que abundan en la naturaleza y se encuentran relacionados con procesos de turbulencia. [3]

En 1975 Mandelbrot demostro que el valor del exponente de Hurst (H) se encuentra acotado entre 0 y 1, explicando que este fenomeno ocurria debido a un sintoma de invariancia al cambio de escala, que es la caracteristica clave de las series de tiempo fractales. (figura 2)

Dimensión fractal

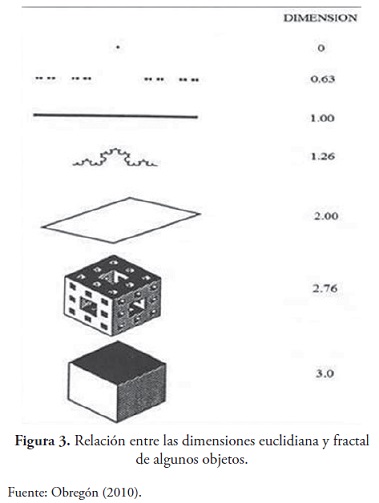
El concepto de dimension fractal se introduce dado el hecho de que los objetos de la naturaleza en su gran mayoria no cuentan con dimension entera, es decir, se encuentran en una dimension fraccionada (claro esta que algunos objetos pueden contar con dimension entera); asimismo, esta dimension debe ser mayor que su dimension topologica.

De una manera mas general, la dimension fractal se puede definir como el numero que sirve para cuantificar el grado de irregularidad y fragmentacion de un conjunto geometrico o de un objeto natural (Strecker, 2004).

Existen varios tipos de dimension fractal, entre las mas utilizadas se encuentran la dimension de similaridad, la dimension de Box Counting y la dimension de Hausdorff- Besicovitch, cada una de estas se enfoca en medir la dimension de acuerdo con las propiedades de cada objeto fractal y de esta manera obtener diferentes resultados. Todas estas dimensiones concuerdan con el objetivo de encontrar que tanto espacio ocupa el objeto y su relacion con la invariancia de la escala (Gutierrez, 2008).

En la Figura 3 se presenta la relacion entre la dimension euclidiana y la dimension fractal de algunos objetos.

El exponente de Hurst y la dimensión fractal

El exponente de Hurst puede ser determinado a partir de la dimension fractal o viceversa, utilizando la formula:

Dado lo anterior, si H = 0,5, entonces D = 1,5, lo que significa que los dos valores coinciden con un proceso aleatorio e independiente. Para valores que se encuentren entre 0.5 > H > 1, es decir, series de tiempo persistentes, la dimension fractal se acercara a una linea con un aspecto de suavidad y menos picos que un proceso aleatorio; para una serie que tome valores entre 0 < H < 0.5, es decir, una serie antipersistente, la dimension fractal arrojara un valor mayor que la anterior y tomara un aspecto mas puntiagudo e irregular que un proceso aleatorio, con tendencia a acercarse cada vez mas a una superficie.

METODOLOGÍA

Descripción general de la zona de trabajo

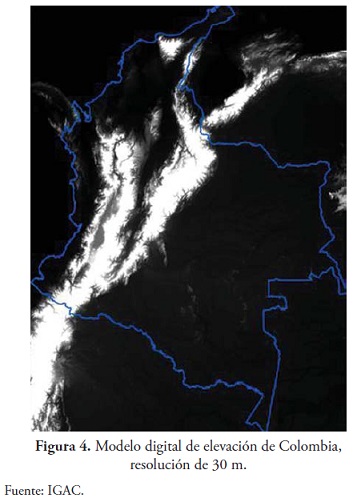
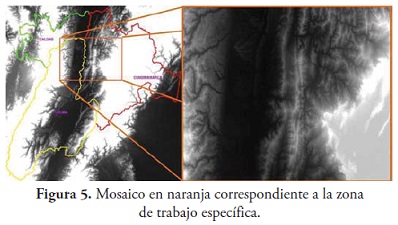
Para la estimacion de la rugosidad de una superficie se trabaja con el modelo digital de elevaciones de Colombia a 30 m de resolucion (figura 4) , modelo para el cual se utilizaron las planchas a escala 1:100.000. Como zona de trabajo especifica se genero un mosaico compuesto por cuatro de estas planchas correspondientes a una zona limitrofe entre los departamentos de Tolima, Caldas y Cundinamarca, teniendo como coordenadas planas de referencia del marco de dicha zona los siguientes valores: 1079753,270576, 1000084,538439 m en el norte, 999875,295327, 879903,557521 m en el este, cubriendo un area total de 9557,996118 km2 de extension; el departamento de Cundinamarca es el de mayor aporte de informacion en el mosaico tal como se muestra en la figura 5 , en la cual el rectangulo de color naranja corresponde al mosaico extraido para la generacion de la superficie.

En la zona elegida se identifico que el mosaico preparado abarca alrededor de 5 municipios en el departamento de Caldas, 18 municipios del departamento de Tolima y 53 municipios en el area del departamento de Cundinamarca, cubriendolos en parte de su area o en su totalidad; adicional a estos municipios tambien se encuentra la zona noroccidental de la ciudad de Bogota D.C.; para todos los municipios anteriormente descritos se encontro un rango de alturas que oscila entre los 150 y los 3720 m sobre el nivel del mar, donde los puntos de menor altitud (3) se encuentran en los municipio de Guaduas en Cundinamarca y La Dorada en Caldas, en inmediaciones o zonas aledanas al rio Magdalena en lo que se refiere a su presencia a lo largo del limite entre los departamentos mencionados; por otra parte, los puntos con la mayor altura (4) se encuentran en los municipios de Pacho y Subachoque, ambos del departamento de Cundinamarca.

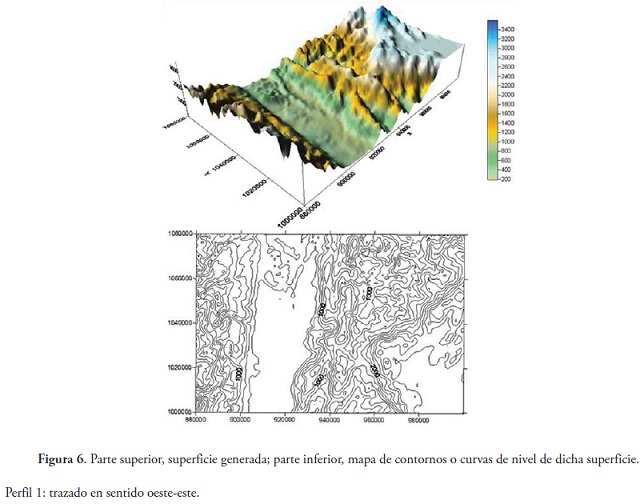
El siguiente proceso que se llevo a cabo fue la extraccion de los puntos con coordenadas X, Y y Z a partir del mosaico descrito con anterioridad, mediante la generacion de los contornos para dicho modelo raster, a los cuales posteriormente se les crearon los puntos respectivos en el centroide de cada una de las respectivas curvas de nivel generadas, obteniendo asi un total de 22.643 puntos, los cuales representan la superficie que se muestra en la figura 6, al igual que sus respectivos contornos.

La representacion que se muestra en la figura 6 fue realizada a traves del software Surfer 8, a partir de los datos descritos anteriormente, los cuales van a ser la base para la estimacion y posterior evaluacion de los exponentes de Hurst de cada perfil.

Evaluación del exponente de Hurst para los diferentes perfiles

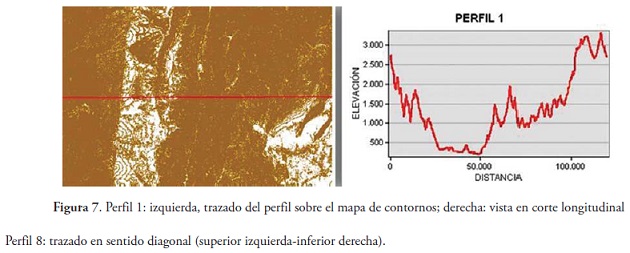
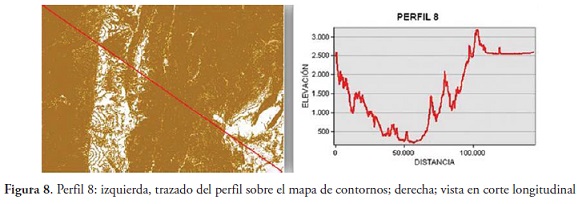
Una vez obtenida la superficie topografica y los contornos (curvas de nivel) del area de estudio, se procedio a evaluar el exponente de Hurst para ocho perfiles trazados sobre el mapa de contornos y en diferentes direcciones. En las Figura 7 y Figura 8 se observa el trazado que se realizo en dos de los ocho perfiles y su vista en corte longitudinal, la cual relaciona la distancia (eje X) con la elevacion (eje Y) de cada uno de los puntos por donde pasa el corte o perfil.

Perfil 1: trazado en sentido oeste-este.

Perfil 8: trazado en sentido diagonal (superior izquierda-inferior derecha).

Para cada uno de los perfiles se obtuvo su respectiva serie de datos, la cual representa la variable de interes (elevacion) de los puntos por donde se hizo el trazado de cada perfil, de esta manera se procedio a estimar el exponente de Hurst de cada una de las series por el metodo del Rango Reescalado.

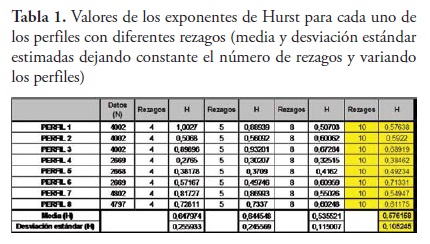
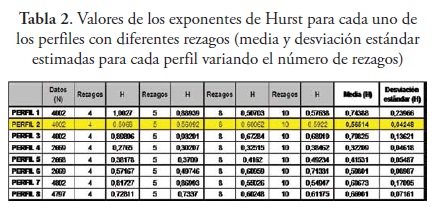
En las tabla 1 y tabla 2 se observan los diferentes valores estimados del exponente de Hurst de cada perfil al igual que su media y su desviacion estandar, realizando variaciones en el numero de rezagos de la serie. El valor del campo N hace referencia al numero total de datos de la serie, es decir, el numero de datos de elevacion obtenidos en cada perfil.

Como se menciono, se realizaron pruebas para diferentes rezagos, esto se hizo debido a que los valores del exponente de Hurst siempre tienden a variar en su resultado. De esta forma, y a partir de los valores de la media y la desviacion estandar obtenidos en cada perfil y rezago, se determinaron los valores mas representativos para el exponente de Hurst y que tuvieran un mejor ajuste con las graficas de los perfiles.

Para encontrar el valor del exponente de Hurst mas representativo se decidio evaluar los valores a traves de dos posibles alternativas, la primera consistio en hacer el analisis en cada rezago a lo largo de los ocho perfiles (tabla 1). La segunda alternativa se baso en tomar los resultados obtenidos para cada uno de los perfiles, pero ahora variando el numero de rezagos (tabla 2).

En las dos alternativas el criterio que se utilizo para elegir los exponentes de Hurst mas representativos se enfoco en elegir aquellos valores que tuvieran las desviaciones estandar mas pequenas. De esta forma, para la primera alternativa el mejor comportamiento se encuentra en los valores estimados con 10 rezagos, ya que el valor de la desviacion estandar para este caso fue de 0,105245. En la segunda alternativa el perfil que arrojo la desviacion estandar mas pequena fue el 2, con un valor de 0,04248.

Los valores representativos para el exponente de Hurst fueron de 0,576158, para la primera alternativa, y de 0,56514, para la segunda; estos valores hacen referencia a la media y se consideran representativos dado que se asocian con un comportamiento de persistencia del proceso (H > 0,5), y se validan en la medida en que la superficie real posee cambios significativos en sus alturas, los cuales se pueden asociar a su grado de rugosidad.

Se observa tambien que para las dos alternativas los valores obtenidos se encuentran muy cercanos, corroborandose aun mas como valores significativos de la superficie.

AGRADECIMIENTOS

Al Ph.D. Nelson Obregon Neira, por convertirse en el principal motivador en la elaboracion del proyecto, por sus conocimientos en el area de trabajo y por ser la guia y luz en nuestro arduo camino durante el desarrollo de la investigacion. A la Pontificia Universidad Javeriana, y en particular al Instituto Geofisico, por brindarnos desinteresadamente sus espacios academicos e instalaciones. A la Universidad Distrital “Francisco Jose de Caldas”, por ser la institucion que durante todo este tiempo nos concedio las bases y el conocimiento para lograr enfrentar este proyecto, por convertirse en el pilar de nuestra formacion integral como ingenieros.

Referencias bibliográficas

1. Addison, P. (1997). Fractals and Chaos: An Illustrated Course. Bristol: Institute of Physics Publishing.
2. Amaro, I. R., Demey, J. R. y Macchiavelli, R. (ANO). Aplicacion del analisis R/S de Hurst para estudiar las propiedades fractales de la precipitacion en Venezuela. CIUDAD: EDITORIAL.
3. Arguello, V. y Gustavo, H. (2005). Diseno e implementacion de un algoritmo con base fractal para realizar analisis de rango re-escalado en registros de pozo. Sartenejas: Universidad Simon Bolivar-Ingenieria Geofisica.
4. Barbulescu, A., Serba, C. y Maftei, C. (ANO). Evaluation of Hurst Exponent for Precipitation Time Series. Constantza: Ovidius University of Constantza.
5. Bras, R. L. y Rodriguez-Iturbe, I. (1985). Random Functions and Hidrology. Toronto-Ontario: Courier Dover Publications.
6. Carbone, A. (2007). Algorithm to Estimate the Hurst Exponent of High-Dimensional Fractals. Torino: Physics Department. Politecnico di Torino.
7. Cimino, G., Del Duce, G., Kadonaga, L. K., Rotundo, G., Sisani, A., Stabile, G. et al. (1999). Time Series Analysis of Geological Data. Chemical Geology, 161 (1-3), 253-270.
8. Devynck, P., Wang, G., Antar, G. y Bonhomme, G. (2000). The Hurst Exponent and Long-Time Correlation. ECA, 24B, 632-635.
9. Falconer, K. (2003). Fractal Geometry, Mathematical Foundations and Applications. 2nd ed. United Kingdom: University of St. Andrews.
10. Feder, J. (1988). Fractals. Oslo: University of Oslo-Department of Physics.
11. Gutierrez, H. E. (2008). Estudio de geometria fractal en roca fracturada y series de tiempo. Santiago de Chile: Departamento de Ingenieria Civil, Universidad de Chile.
12. Mandelbrot, B. B. (1977). The Fractal Geometry of Nature. Oxford: International Business Machines Thomas J. Watson Research Center.
13. Mandelbrot, B B. y van Ness, J. W. (1968). Fractional Brownian Motions, Fractional Noises and Applications. SIAM Review, 10 (4), 422-437.
14. Ortiz-Romero, A. I. (2008). Construccion y programacion de un algoritmo paralelo para determinar el exponente de Hurst. Mexico D.F.: Centro de Innovacion y Desarrollo Tecnologico en Computo-Instituto Politecnico Nacional.
15. Paredes, C. (1995). Aplicacion de la geometria fractal en las ciencias de la tierra. Oviedo: Escuela Tecnica Superior de Ingenieros de Minas, Departamento de Matematica Aplicada y Metodos Informaticos.
16. Peters, E. (1994). Fractal Market Analysis (Applying Chaos Theory to Investment an Economic). New York: John Wiley and Sons.
17. Quezada-Len, A. (2006). Fractales y opinion publica: una aplicacion del exponente de Hurst al estudio de la dinamica de la identificacion ideologica. Barcelona: Universidad de Barcelona, Departamento de Psicologia Social.
18. Racine, R. (2011). Estimating the Hurst Exponent. Zurich: Mosaic Group.
19. Salvador, A. A. (1996). Fractales y caos: estructura fractal de las series temporales. Coeficiente de Hurst. Aplicaciones. Madrid: Universidad Politecnica de Madrid.
20. Sierra-Juarez, G. (2007). Procesos Hurst y movimiento browniano fraccional en mercados fractales: valuacion y aplicaciones a los derivados y finanzas. Mexico D.F.: Instituto Tecnologico de Estudios Superiores de Monterrey.
21. Soria, B. K. y Zuniga, J. S. (s. f.). Algunas estimaciones del coeficiente de Hurst para el IGPA chileno. Coquimbo: Universidad Catolica, Escuela de Ingenieria del Norte.
22. Strecker, J. (2004). Fractional Brownian Motion Simulation: Observing Fractal Statistics in the Wild and Raising Them in Captivity. Wooster: The College of Wooster, Department of Mathematics and Computer Science.
23. Toro-Salas, K. J., Murcia-Duran, L. F. y Dominguez-Cajeli, D. (2007). Calculo de la dimension fractal de la falla geologica del sur occidente de Colombia. Ciencia e Ingenieria Neogranadina, 17, 35-45.