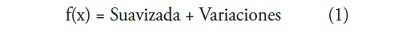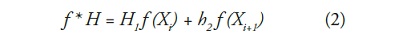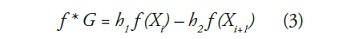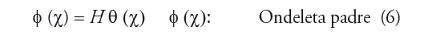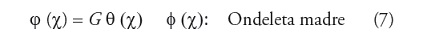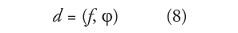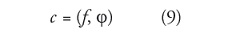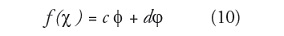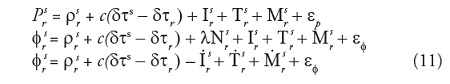Aplicación de ondeletas en datos de posicionamiento continuo para la región colombiana con fines geodinámicos

APLICACIÓN DE ONDELETAS EN DATOS DE POSICIONAMIENTO CONTINUO PARA LA REGIÓN COLOMBIANA CON FINES GEODINÁMICOS

APPLICATION OF WAVELETS IN DATA OF CONTINUOUSLY POSITIONING STATIONS FOR THE COLOMBIAN REGION WITH GEODYNAMIC PURPOSES

Oscar Daniel Beltrán Rodríguez¹, Claudia Liliana Colmenares Rojas²

¹Universidad Distrital “Francisco Jose de Caldas” danbelt@gmail.com

² Universidad Distrital “Francisco Jose de Caldas”ing.colmenares@gmail.com

Recibido: 08/09/2011 - Aceptado: 26/10/2011

RESUMEN

En el trabajo realizado en el proyecto de grado Aplicacion de Wavelets en datos de “Estaciones continuas de posicionamiento en Colombia con fines geodinamicos” (Beltran y Colmenares, 2011) se utilizaron, por un lado, las soluciones semanales fijas ofrecidas por el Sistema de Referencia Geocentrico para las Americas (Sirgas) ¹ que es una densificación regional del Marco Internacional de Referencia Terrestre (ITRF) ², y por otro lado, la informacion meteorologica de la zona de las estaciones de posicionamiento global continuo suministrada por el Instituto de Hidrologia, Meteorologia y Estudios Ambientales de Colombia (Ideam) ³. Se presentan los resultados de aplicar el algoritmo de las ondeletas para detectar, medir y analizar las variaciones de la posicion dadas por un conjunto de estaciones de posicionamiento global continuas a fin de evaluar su aplicabilidad como herramienta para llevar a cabo estudios con fines geodinamicos, encontrandose que el desempeno de la tecnica es muy similar a las tecnicas utilizadas tradicionalmente, con el valor agregado de permitir asociar temporalmente otro tipo de mediciones en la localizacion de las estaciones; es indispensable realizar la medicion de diversos fenomenos en un mismo punto para llevar a cabo las asociaciones que permitan disminuir la incertidumbre en la asociacion del fenomeno que perturba la posicion.

¹ http://www.sirgas.org

²http://www.igs.com

³ http://www.ideam.gov.co

Palabras clave: estaciones continuas, geodesia satelital, geodinamica, ondeletas, series temporales, sistema global de posicionamiento satelital.

ABSTRACT

In the work carried out in the project wavelets application over continuously positioning stations data in Colombia with geodynamics purposes, used for a side the fixed weekly solutions offered for the geocentric reference system for the Americas (Sirgas) that it is a regional densification of the international terrestrial reference frame (ITRF), and for other side the meteorological information of the area of the continuously positioning stations supplied for the institute of environmental hydrology, meteorology and studies of Colombia (Ideam), present the results to apply the algorism of the wavelets to detect, measure and analyze the variations of the position considered a whole of stations of global continuously positioning, to evaluate it applicability as tool to carry out studies die geodynamics, finding that the acting of the technique is very similar to the techniques used traditionally, with the aggregate value of permitting temporarily associate other type of measurements in the localization of the stations, is indispensable to carry out the measurement of diverse phenomenon in a same point, in order that to the carries out the associations that permit decrease the uncertainty in the association of the phenomenon that disturbs the position.

Key words: Continuously positioning stations, geodynamic, global navigation satellite system, satellite geodesy, time series, wavelets.

INTRODUCCIÓN

Una de las tematicas de estudio de la geodinamica es la medicion, la cuantificacion y el monitoreo de los desplazamientos de la corteza terrestre en el transcurso del tiempo (Lutgens y Tarbuck, 2005). Para la realizacion de este monitoreo se deben hacer una serie de mediciones de posicion obtenidas en estaciones continuas GNSS que interactuan y establecen coordenadas geodesicas de la superficie sobre la que se encuentran respecto a un sistema fijo terrestre.

Con el analisis de la informacion recibida es posible evidenciar los movimientos de la corteza en magnitud y direccion en un determinado intervalo de tiempo (Hofmann, 2006), cuyos resultados permiten realizar estudios especificos como:

Analisis de esfuerzos (tension-compresion) que pudiesen sufrir las redes de servicios electricos, hidraulicos, de transporte y telecomunicaciones.

Determinacion de la direccion y magnitud del movimiento en procesos de expansion de volcanes (Keller, 2004).

Analisis de estabilidad de terrenos para la construccion de asentamientos residenciales e industriales.

La ejecucion de estos estudios lleva a un mejor desarrollo y planificacion de zonas urbanas y rurales.

Actualmente, para la region de las Americas se ha planteado un modelo para analizar y relacionar la informacion GNSS recepcionada con la deriva continental. El modelo continental denominado VEMOS2009 (Velocity Model Sirgas-2009) es el resultado de la aplicacion de minimos cuadrados y metodos estadisticos.

El metodo de las ondeletas ha sido desarrollado para analizar la variacion de senales y datos en el tiempo (Walnut, 2002).

Su principal aplicacion en las geociencias es en el campo de la geofisica, especificamente en el area de la sismica, cuya funcion principal es la de servir como herramienta para el analisis y la interpretacion de las senales sismicas recepcionadas por una serie de geofonos. Sin embargo, esta herramienta ha sido utilizada en otros campos de las ciencias en los cuales se analizan, tratan e interpretan senales electricas, imagenes, datos economicos y senales de audio-video (Freeden y Thorsten, 2002).

En este articulo se presentan los resultados alcanzados de aplicar la metodologia Wavelets a series de tiempo obtenidas a partir de datos recibidos en las estaciones TUNA, BOGA y BOGT de la red de Sirgas, y las diferencias entre los valores de las velocidades del modelo VEMOS2009 y los obtenidos a traves de wavelets.

ECUACIONES MATEMÁTICAS DEL MÉTODO DE LAS ONDELETAS

Las wavelets u ondeletas son funciones que permiten realizar transformaciones y analisis de una serie de datos en el espacio-tiempo al dominio espectral (frecuencia-energia) o en el temporal; asimismo, son utilizadas como herramientas de tratamiento de senales, filtrado, prediccion, estimacion y compresion de datos (Nguyen y Strang, 1996). Aunque se considera que las ondeletas aplican el mismo principio de Fourier donde se busca representar una funcion X(t) en terminos de tiempo-espacio, como una funcion X(w) cuyas caracteristicas sean del dominio espectral, es decir, sean dadas por la amplitud y la longitud de onda por medio de operaciones como la convolucion, las caracteristicas de las ondeletas ofrecen ciertas ventajas para el tratamiento de la informacion, a continuacion enunciaremos algunas de ellas:

• Las ondeletas deben presentar oscilaciones que permitan identificar cambios a diversas escalas.
• Deben poseer un soporte compacto, es decir, que la cantidad de informacion o energia de entrada debe ser la misma de la transformada sin modificar a alguno de sus componentes.
• Las ondeletas permiten la transformación de informacion no estacionaria.
• El algoritmo de cálculo es igual o más eficiente que la transformada rapida de Fourier.
• El tratamiento de los datos a diversas escalas es más eficiente que la transformada rapida de Fourier la cual debe aplicarse cada vez que se ajusta el ancho de la ventana de transformacion.
• Las ondeletas permiten reconstruir la información transformada sin modificar su contenido.
• Es posible obtener versiones reducidas por niveles de la informacion transformada.
• Con las ondeletas se pueden identificar cambios en la informacion dando la posibilidad de ubicarlos en el dominio temporal.
• Las ondeletas permiten realizar procesos de suavizado de informacion a diversas escalas, sin ocasionar perdidas de la informacion inicial.
• Las ondeletas permiten trabajar sobre información continua y discreta, de caracter real o complejo, en n-esimas dimensiones.

Informalmente se puede decir que los coeficientes wavelet obtenidos son el ’monto’ de la onda contenido en la funcion f(x).

Suponga que se posee una funcion f(x) sobre la que se desea obtener una version suavizada y una version compuesta por las variaciones o diferencias en su comportamiento a traves del traslado en el tiempo, que al unirlas pueda reconstruir la funcion original.

La version suavizada sera obtenida mediante la tecnica conocida en la teoria de Fourier como filtrado, donde a partir de la operacion de convolucion es posible obtener una funcion libre de ruido o suavizada. Siguiendo el mismo procedimiento, debe ser posible obtener la funcion de ruido o de las diferencias. Esto ha sido abordado desde la tecnica conocida como filtrado, donde ha sido posible obtener basicamente dos tipos de filtros: de paso bajo H (suavizado), y de paso alto G (diferencias).

Filtro de suavizado de la funcion f(x):

Filtro de detalle o diferencias de la funcion f(x):

Donde h₁ y h₂ son los coeficientes de la funcion filtro.

Cabe aclarar que el numero y los valores de los coeficientes por utilizar en el filtro esta dado por la cantidad y el tipo de informacion que se desea tratar y obtener. Generalmente, los valores de los coeficientes son asignados de manera tal que obedezcan a un indicador estadistico.

A partir del desarrollo de la tecnica del filtrado ha sido posible plantear clasificaciones de filtros y tecnicas derivadas para analizar el comportamiento de una serie o secuencia de datos de caracter discreto y continuo. Entre las tecnicas vale la pena mencionar los bancos de filtros que como definicion general e informal se pueden asumir como el conjunto de filtros aplicados a la informacion para realizar analisis y operaciones a diversas escalas, diversas epocas (polifase), desarrollando de esta manera la base para el metodo de compresion de informacion.

Relación entre los filtros y las ondeletas

Como se senalo, una funcion puede ser expresada en versiones suavizadas y versiones de diferencias o detalle, generadas de la aplicacion de filtros sobre los datos originales. Ahora piensese en una funcion en forma de onda base a la que al aplicar la tecnica de filtrado se le modifican sus caracteristicas de forma tal que se generan dos funciones, una de paso alto y otra de paso bajo.

Entonces, en notacion wavelet los coeficientes de los filtros se pueden asumir como:

Generando las ondeletas

Donde la funcion θ(χ) es la funcion u onda base que se va a modificar por medio de la tecnica de filtrado.

Ahora supongase que los filtros que se desea o se deben aplicar son funciones que representan ondas con diversa longitud, frecuencia y amplitud. La diferencia de este tipo de filtros radica en su capacidad de mantener la cantidad de energia o informacion de entrada u origen aun despues de realizar su trasformacion. Es decir, que para obtener los valores de detalle y suavizado usted debe realizar la convolucion de la senal con las funciones en forma de onda:

Donde:

d: coeficientes de detalle (wavelet) que representan el monto de la onda j contenido en la funcion f.

c: coeficientes de suavizado (filtrado) que representan el monto de la onda f contenido en la funcion f.

A partir de lo anterior, la reconstruccion f(x) o senal original se expresaria en terminos de ondeletas:

Los coeficientes d o wavelet son la herramienta adecuada para determinar discontinuidades en la informacion, ademas son la representacion aproximada del tiempo en el dominio de las frecuencias, es decir, altos coeficientes representan altas frecuencias, mientras que si estos coeficientes se acercan a cero o son muy pequenos estos se relacionan con las frecuencias bajas.

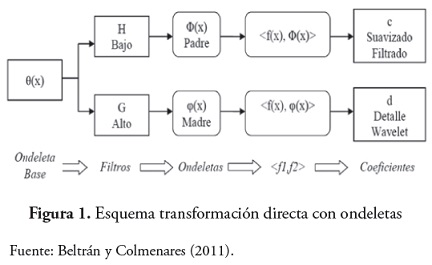
Transformación directa Wavelet (análisis Wavelet)

Permite obtener informacion adicional a partir de la descomposicion de la senal en terminos de coeficientes que representan versiones suavizadas y de diferencias de la senal original a diversas escalas. La transformacion directa wavelet (figura 1) permite llevar a cabo procesos de analisis multitemporal de la informacion, deteccion y filtrado de ruido (Mallat, 1999).

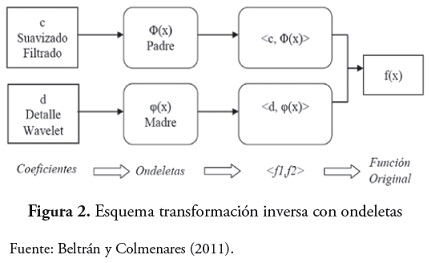
Transformación inversa Wavelet (síntesis Wavelet)

Permite obtener la senal original a partir de la composicion de la misma en terminos de coeficientes que representan versiones suavizadas y de diferencias de la senal original, a diversas escalas. Esta transformacion (figura 2) permite llevar a cabo procesos de mejoramiento y realce de la informacion original o de alguna de sus versiones simplificadas (Mallat, 1999).

OBSERVABLES GNSS Y PROCESAMIENTO DE DATOS

El principio funcional del Global Navigation Satellite System (GNSS) se basa en medir el tiempo empleado por la senal transmitida por los satelites en llegar al receptor del usuario, este intervalo de tiempo es multiplicado por la velocidad de la luz para obtener la distancia satelite receptor (Huerta, Mangiaterra y Noguera, 2005). Para ello se puede utilizar cualquiera de los tres tipos de observables GNSS: pseudodistancia, fase de portadora (diferencias de fases portadoras), Doppler.

En el primero, el tiempo de propagacion de la senal se mide correlacionando la secuencia PRN generada localmente en el receptor con la recibida del satelite. Se denomina pseudodistancia por los errores presentes en la medida. La fase de portadora es un metodo mas preciso de obtener la pseudodistancia, con errores mas pequenos que el metodo anterior. Este observable es la diferencia de la fase de portadora que le llega al receptor con la generada internamente, existiendo un numero ambiguo de ciclos que hay que resolver para poder utilizar este metodo.

Las medidas Doppler representan la velocidad de cambio de la frecuencia observada de la senal de los satelites, producto del movimiento relativo satelite-receptor. Las medidas Doppler se utilizan generalmente para derivar la velocidad del receptor.

Matematicamente, los tres observables se representan como:

Donde:

ρ: pseudodistancia entre satelite y receptor.

φ: fase.

c: velocidad de la luz.

I: componente por ionosfera.

T: componente por troposfera.

M: componente de mareas.

N: ambiguedad.

ε: error asociado.

(δts- δtr): diferencia de relojes.

Errores presupuestados y correcciones

Existen diversas fuentes de errores que alteran la precision de los receptores GNSS, las cuales es posible compensar de diversas maneras. Los principales errores que pueden degradar el rendimiento de los datos GNSS son aquellos atribuidos a los errores atmosfericos, la geometria de los satelites, multiple direccionamiento de la senal, el calendario y los errores de orbita de los satelites (Seeber, 2003).

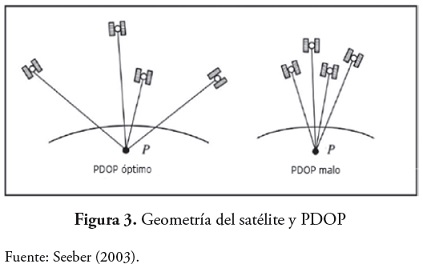
GEOMETRÍA DEL SATÉLITE

El efecto de la geometria de los satelites en el error de posicion (figura 3) se denomina dilucion de la precision, comunmente conocida como DOP. Un receptor GNSS calcula un valor constante DOP basado en los satelites que se utilizan para el calculo de la posicion. La mejor geometria (disposicion adecuada de los satelites) sera la que arroje menor DOP. Con todos los satelites confinados en una parte del cielo o bloqueados por los edificios, montanas, etc., la geometria sera pobre y el valor calculado DOP sera alto.

Sabiendo que el valor de DOP ideal es de 1, diversas aplicaciones requieren diferentes precisiones y correcciones de DOP. Por lo general, de 1 a 2 es excelente, de 3 a 4 es bueno, de 5 a 7 es justo y 8 o por encima es pobre.

EFEMÉRIDES Y RELOJES

Las discrepancias entre la orbita real y la estimada del satelite pueden corromper la determinacion de la distancia y con ello la posicion del usuario, por ello es indispensable corregir la orbita estimada, asi como el arco orbital observado. Respecto a las diferencias en los relojes de los satelites y los receptores, estos pueden perturbar las cantidades temporales de viaje y con ello la determinacion de la distancia, por ello es necesario hacer la calibracion de los relojes mediante relojes atomicos ubicados en las estaciones de control que estabilicen la escala temporal de aquellos de los satelites.

REFRACCIÓN IONOSFÉRICA

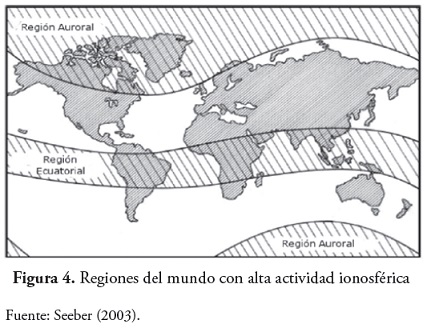
La ionosfera es aquella region de la atmosfera comprendida entre 100 y 1000 km de altitud, donde las radiaciones solares y otras radiaciones ionizan una porcion de las moleculas gaseosas liberando electrones que interfieren en la propagacion de ondas de radio (figura 4). La ionosfera es un medio disperso para ondas de radio, por tanto su indice de refraccion es funcion de la frecuencia de la onda. Tambien es funcion de la densidad de electrones y, en menor grado, de la intensidad del campo magnetico de la tierra.

Si solo se registran medidas en una sola frecuencia, tanto en pseudodistancias como en medida de fase, entonces se tiene que emplear un procedimiento alternativo para eliminar el efecto ionosferico. Normalmente se usan modelos empiricos para corregir el efecto, en los que se modela el TEC en funcion del tiempo, lugar de observacion y direccion de la senal. En el mensaje de navegacion se incluyen unos parametros para tal modelo; usandolo se pueden llegar a reducir en un 50% los efectos de la ionosfera.

Actualmente estamos saliendo de un minimo en la actividad de las manchas solares (once anos de ciclo), por lo que las condiciones ionosfericas son ahora mas idoneas. Pero dentro de unos cuatro anos estaremos cerca del maximo, y entonces los efectos de la ionosfera en las senales seran mucho peores. El retardo ionosferico depende del angulo de elevacion del satelite, siendo menor en el cenit, y mayor cuando disminuye el angulo de elevacion. En observaciones nocturnas los niveles de TEC son menores que durante el dia, lo que implica un menor error en la pseudodistancia. Pero despues de la aplicacion del modelo empirico transmitido puede quedar algun error ionosferico residual que afectara principalmente al componente altimetrico del punto y a la estimacion del error del reloj del receptor. Este error contribuye poco a la posicion planimetrica cuando la concentracion de electrones encima del receptor es uniforme.

REFRACCIÓN TROPOSFÉRICA

La troposfera es la ultima zona o capa de la atmosfera (hasta unos 80 km, pero solo en los ultimos 40 se producen retardos significativos) donde se produce retardo y donde las temperaturas decrecen con el incremento de altura. El espesor de la troposfera no es el mismo en todas las zonas. La presencia de atomos y moleculas neutras en la troposfera afecta a las senales de propagacion electromagnetica. El indice de refraccion para un area parcial es funcion de su temperatura, de la presion de los gases secos y del vapor de agua. Esta atmosfera neutra es un medio no disperso con respecto a las ondas de radio de frecuencias superiores a 15 GHz, por tanto, la propagacion es independiente de la frecuencia. Consecuentemente, no es necesario distinguir entre medidas de codigo y fase sobre las portadoras L1 y L2. La desventaja esta en que no es posible eliminar la refraccion troposferica con medidas en las dos frecuencias.

Se puede mejorar el calculo del retardo troposferico tomando datos meteorologicos en el lugar de observacion. A diferencia de la componente seca, la componente humeda varia espacialme y temporalmente. La componente seca es la causante de un 90% del total del retardo y puede ser obtenida con precision de algunos milimetros a partir de medidas de presion en superficie. La componente humeda es funcion del vapor de agua a lo largo del camino de la senal. El gradiente termico admite modelacion con precision aceptable, pero el principal problema esta en la forma de modelar el vapor de agua, que tiene una distribucion irregular. El uso de mediciones meteorologicas en superficie no puede dar la precision alcanzable con los radiometros de vapor de agua. Estos instrumentos miden la radiacion basal que se recibe desde el espacio en la direccion de la observacion, y son capaces de calcular el contenido de vapor de agua en la atmosfera.

El retardo se puede evaluar en 1,9-2,5 m en la direccion cenital y se incrementa aproximadamente con la cosecante del angulo de elevacion, llegando a ser de 20-28 m a unos 5.. El efecto del retardo ionosferico y troposferico debido al vapor de agua sobre las emisiones de la banda radioelectrica es menor cuanto mayor sea la frecuencia, o cuanto menor sea la longitud de la onda. Las refracciones ionosferica y troposferica pueden ser eliminadas trabajando en modo diferencial, pero esto es solo cierto para lineas base pequenas, donde las medidas de distancia satelite-receptor se ven afectadas de igual forma por la refraccion. De otro modo, ya vimos que la refraccion ionosferica puede ser eliminada utilizando una adecuada combinacion de datos en doble frecuencia.

EFECTO MULTICAMINO

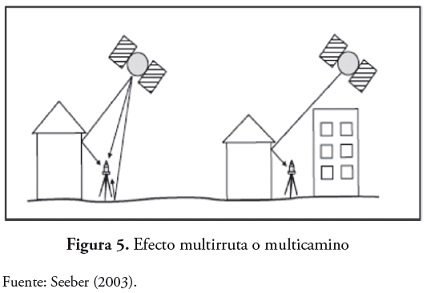
El efecto multirruta o multicamino es causado principalmente por multiples reflexiones de la senal emitida por el satelite en superficies cercanas al receptor (figura 5). Estas senales reflejadas que se superponen a la senal directa son siempre mas largas, ya que tienen un tiempo de propagacion mas largo y pueden distorsionar significativamente la amplitud y forma de la onda. Este efecto puede ser considerablemente reducido eligiendo puntos de estacion protegidos de reflexiones (edificios, vehiculos, arboles, etc.), es decir, evitando las superficies reflectantes en las proximidades del receptor, y por un apropiado diseno de la antena, como es la utilizacion de planos de tierra que reducen las interferencias de senales con baja elevacion o incluso con elevacion negativa, que son las que provocan el multipath, en otras palabras, se intenta reducir la intensidad de las senales secundarias y aislar a la senal directa. El efecto multipath depende de la frecuencia de la portadora. Por tanto, las medidas de fase se veran menos afectadas que las medidas de codigo, donde el efecto multipath puede alcanzar hasta el nivel de metro.

ERROR EN EL ESTACIONAMIENTO DE LA ANTENA

Los errores en el estacionamiento de la antena tienen menos influencia y las exigencias de estacionamiento son muy inferiores a las de los instrumentos de observacion clasica. No necesitan una altisima estabilidad, ya que pequenos desplazamientos, vibraciones o torsiones en nada afectan a la observacion de las senales de los satelites.

ERRORES EN LA MANIPULACIÓN DE LOS EQUIPOS

Los errores de manipulacion se producen cuando no se siguen las instrucciones del fabricante del instrumento o cuando estas suelen descuidarse cuando se trabaja rutinariamente. Por ejemplo, es importante no comenzar una observacion hasta que no se hayan sincronizado perfectamente todos los satelites, ya que lo unico que estaremos haciendo es introducir ruido a la observacion.

VARIACIÓN DEL CENTRO RADIOELÉCTRICO DE LA ANTENA

La variacion y el desfase del centro de la antena se debe a la falta de coincidencia entre el centro radioelectrico o punto que realmente se posiciona —ya que es al que llega la senal—, y el centro mecanico o fisico, generando un error residual por excentricidad que puede ser de unos milimetros. Para evitar este error en posicionamiento relativo se recomienda una orientacion aproximada comun para todas las antenas, ya que el fabricante monta en el interior de todas las carcasas el elemento fisico receptor en la misma posicion respecto a alguna referencia exterior del conjunto; trabajando en modo diferencial este error se eliminara en ambas estaciones.

MATERIALES Y MÉTODOS

Sistema de Referencia Geocentrico para las Americas (Sirgas) Sirgas es el Sistema de Referencia Geocentrico para las Americas. Su definicion corresponde con el Sistema Internacional de Referencia Terrestre (ITRS: International Terrestrial Reference System) y su realizacion es una densificacion regional del Marco Internacional de Referencia Terrestre (ITRF: International Terrestrial Reference Frame). Ademas del sistema de referencia geometrico, Sirgas se ocupa de la definicion y realizacion de un sistema vertical de referencia basado en alturas elipsoidales como componente geometrico y en numeros geopotenciales (referidos a un valor W0 global convencional) como componente fisico.

Características de Sirgas

Las coordenadas Sirgas estan asociadas a una epoca especifica de referencia y su variacion con el tiempo es tomada en cuenta ya sea por las velocidades individuales de las estaciones Sirgas o mediante un modelo continuo de velocidades que cubre todo el continente. Las realizaciones o densificaciones de Sirgas asociadas a diferentes epocas y referidas a distintas soluciones del ITRF materializan el mismo sistema de referencia y sus coordenadas, reducidas a la misma epoca y al mismo marco de referencia (ITRF), son compatibles en el nivel milimetrico.

El datum geodesico Sirgas esta definido por el origen, la orientacion y la escala del sistema Sirgas (ITRS). La conversion de coordenadas geocentricas a coordenadas geograficas se adelanta utilizando los parametros del elipsoide GRS80. La extension del marco de referencia Sirgas esta dada a traves de densificaciones nacionales, las cuales a su vez sirven de marcos de referencia local.

Características generales de procesamiento

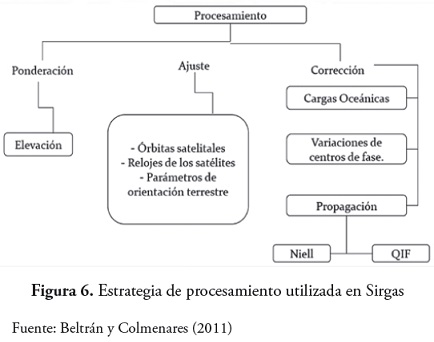
Los productos ofrecidos por Sirgas son procesados mediante el aplicativo Bernese v. 5¹ siguiendo una estrategia aprobada a nivel internacional (figura 6).

Aplicativos empleados

Para la aplicacion de la propuesta metodologica se utilizaron programas libres y se crearon rutinas que permitieran descargar, calcular y generar archivos, de manera tal que el desarrollo de la metodologia fuese llevado a cabo rapidamente. Entre los aplicativos se utilizaron ejecutables generados durante el desarrollo de esta propuesta metodologica disenados para la descarga de los datos desde el servidor de Sirgas, la depuracion de las estaciones y la generacion de archivos de comandos interpretables por el programa de calculo empleado. Los ejecutables fueron desarrollados en el lenguaje python, la aplicacion para realizar los calculos y el analisis wavelet es R (Nason, 2008).

METODOLOGÍA

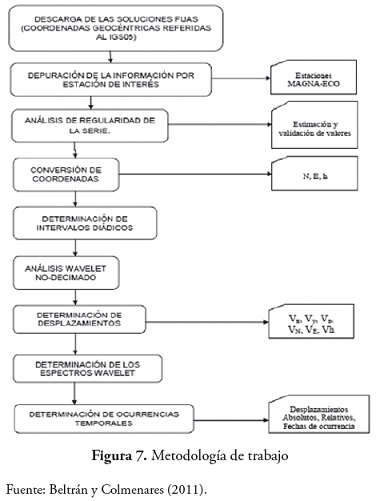
Para desarrollar del trabajo es necesario definir una secuencia de procedimientos (figura 7) que permitan replicar los resultados obtenidos, o bien obtener resultados en otras regiones de estudio a partir del modelo propuesto.

ÁREA DE INVESTIGACIÓN

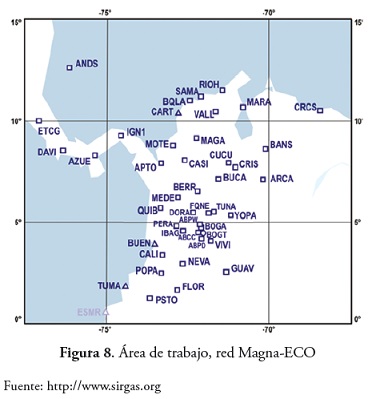
El area de investigacion del proyecto estuvo localizada en la zona noroccidental suramericana, correspondiente a Colombia, comprendida entre las coordenadas de latitud 4°00’00” S y 12°0’0” N y entre 78°00’00” W 67°00’00” W de longitud (figura 8).

RESULTADOS Y CONCLUSIONES

Durante el desarrollo del trabajo fue necesario depurar la informacion obtenida del servidor de Sirgas, solo incluyendo como informacion relevante aquellas estaciones que pertenecieran a la red de estaciones geodesicas continuas de Colombia (Magna-ECO), cuyas series temporales fuesen lo mas robustas, es decir, que sus periodos de captura fuesen superiores a dos anos y que en caso de tener que realizar estimaciones estas no superasen un umbral del 13% de la totalidad de la serie. Ademas, las estaciones deberian poseer un modelo de velocidades asociado y validado como el VEMOS09, para llevar a cabo una comparacion de los desplazamientos obtenidos mediante la utilizacion de las ondeletas. Otra condicion que deberia cumplir la region donde se ubica la estacion de posicionamiento es la de poseer informacion meteorologica en por lo menos el mismo intervalo de tiempo de recepcion de datos GNSS, para llevar a cabo los procesos de asociaciones temporales obtenidas mediante la tecnica de las ondeletas.

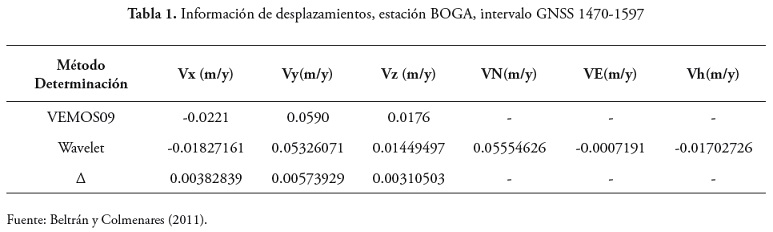
Una vez hecha esta depuracion se procede a realizar el procedimiento de analisis wavelet o transformacion directa para luego reescalar los desplazamientos obtenidos mediante los coeficientes de detalle, y poderlos expresar en las mismas unidades para llevar a cabo la comparacion (tabla 1) con la determinacion de desplazamientos mediante la tecnica convencional.

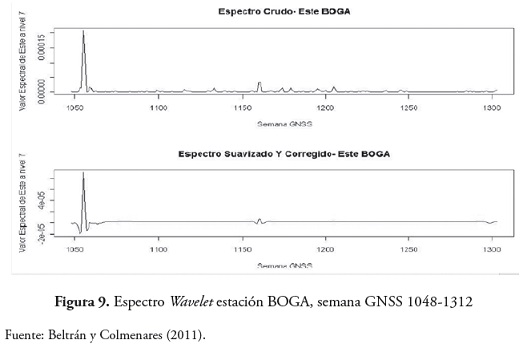
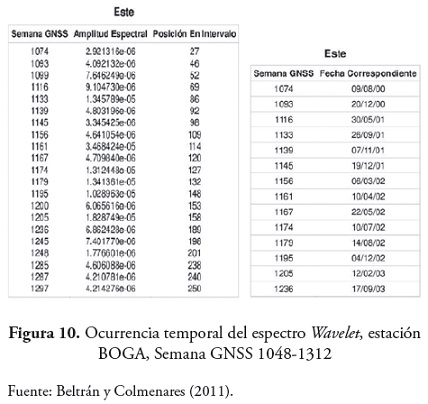
Luego se determinaron los espectros wavelet para magnificar las diferencias representativas y de esta manera detectar las correspondencias temporales a las magnitudes significativas (figura 9) y (figura 10) .

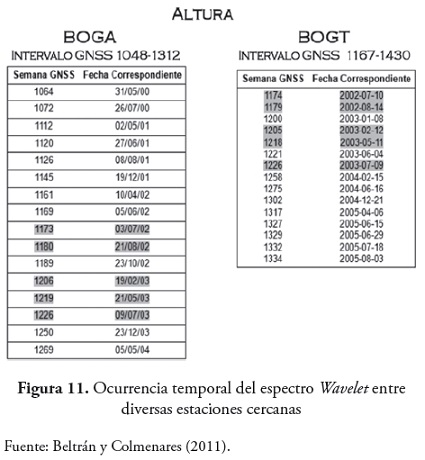
Con estos resultados es posible realizar analisis de fenomenos entre estaciones cuya linea base es muy corta (figura 11), o de desplazamientos en la componente vertical a partir de informacion de precipitacion.

CONCLUSIONES

El valor de desplazamiento obtenido mediante la transformacion wavelet depende de las caracteristicas de la ondeleta utilizada como momentos de desvanecimiento y grado de asimetria.

La transformacion Wavelet permite obtener desplazamientos escalados a diversas resoluciones temporales. El espectro Wavelet permite resaltar las diferencias mas relevantes en la serie de tiempo sobre el nivel mas fino o sobre otros niveles.

La aplicacion de ondeletas a series temporales de posicionamiento GNSS permite obtener productos relacionados con el desplazamiento de la estacion y su correspondencia en un intervalo de tiempo. Estos productos obtenidos, asociados a otro tipo de mediciones temporales, pueden ser de utilidad para otras disciplinas relacionadas con temas geoespaciales y ambientales, como la geodinamica, la geofisica, la meteorologia, etc.

AGRADECIMIENTOS

Al Instituto Geografico Agustin Codazzi y a la colaboracion del ingeniero William Martinez; al ingeniero Luis Gomez, docente de la Universidad Distrital por su aporte en la actividad academica en ramas relacionadas con las geociencias. Al grupo Geored del Instituto Colombiano de Geologia y Mineria (Ingeominas) en cabeza del ingeniero Hector Mora por su apoyo en las diversas tematicas relacionadas con la geodinamica. Al Instituto Colombiano de Hidrologia, Meteorologia y Estudios Ambientales (Ideam) y Sirgas por su aporte de informacion de uso libre, asi como a la formacion academica proporcionada por la Universidad Distrital “Francisco Jose de Caldas”.

REFERENCIAS BIBLIOGRÁFICAS

1. Beltran, O. y Colmenares, C. (2011). Aplicacion de wavelets en datos de estaciones continuas de posicionamiento en Colombia con fines geodinamicos (Tesis Ingenieria Catastral y Geodesia). Bogota: Universidad Distrital “Francisco Jose de Caldas”.
2. Freeden, W. y Thorsten, M. (2002). A survey on wavelets methods for geo applications. Alemania: University of Kaiserslautern.
3. Hofmann, B. (2006). Physical Geodesy. 2 ed. Voslau: Institut Fur Navigation Und Satellitengeodasie.
4. Huerta, E., Mangiaterra, A. y Noguera, G. (2005). GPS: Posicionamiento Satelital. Rosario: UNR Editora, Universidad Nacional de Rosario.
5. Keller, W. (2004). Wavelets in Geodesy And Geodynamics. Berlin: Geodatisches Institut, Universitat Stuttgart.
6. Lutgens, F. K. y Tarbuck, E. J. (2005). Ciencias de la Tierra. Una introducción a la geología física. Madrid: Prentice Hall.
7. Mallat, S. (1999). A wavelet tour of signal processing. 2 ed. Paris: Ecole Polytechnique.
8. Nason, G. (2008). Wavelet methods with R. Bristol: University of Bristol.
9. Nguyen, T. y Strang, G. (1996). Wavelets and Filter Banks. Wisconsin: University of Wisconsin.
10. Seeber, G. (2003). Satellite Geodesy. 2 ed. Berlin: Institut fur Erdmessung, Universitat Hannover.
11. Walnut, D. F. (2002). An Introduction to Wavelet Analysis. Boston: University of Maryland.