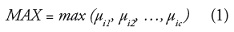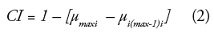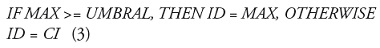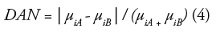DOI:
https://doi.org/10.14483/23448407.4415Publicado:
2012-12-20Número:
Núm. 6 (2012)Sección:
Artículo de investigación científica y tecnológicaClasificación de la cobertura del suelo urbano usando objetos de imagen difusos
Descargas
Referencias
Anderson, J.; Hardy, E. y Roach, J. (1976). A Land Use And Land Cover Classification System For Use With Remote Sensor Data. Geological Survey Professional Paper 964.Bezdek (primavera de 1999).
Fuzzy models and algorithms for pattern recognition and image processing. Nueva York.Burrough, P. A.; van Gaans, P. y Hoostmans (1997).
Con-tinuous classification in soil survey: spatial correlation, confusion and boundaries. Geoderma, 77(2-4), 115-135.Cohn, A., y Gotts, N. (1996).
The Egg-Yolk representation of regions with indeterminate boundaries. Geographical Objects with Undetermined Boundaries, 171-187.Chanussot, J.; Nyström, I. y Sladoje, N. (2005).
Shape signatures of fuzzy star-shaped sets based on distance from the centroid, Pattern Recognition Letters, 26(6), 735-746. Cheng, T.; Molenaar, M. y Lin, H. (enero de 2001).
For-malizing fuzzy objects from uncertain classification results. International Journal of Geographical Information Science, 15, (1), 27-42.De Jong, S. M. y Freek, D. van der M. (eds.), (primavera de 2006). Remote Sensing Image Analysis: including the spatial domain. Dordrecht.Dilo, A.; Bos, P.; Kraipeerapun, P. y de By, R. A., (prima-vera de 2006).
Storage and manipulation of vague spatial objects using existing GIS functionality. En G. Bordogna y G. Psaila (Edics.) Flexible databases supporting imprecision and uncertainty (pp. 293-321) (pp. 293-321).Hastie, T.; Tibshirani, R. y Friedman, J. (2001).
The El-ements of Statistical Learning: Data Mining, Inference and Prediction. Nueva York, NY: Verlag.Hay y Castilla (s.f.) Geographic Object-Based Image Analysis (GEOBIA): Paradigm shift or new methods?. En: T. Blaschke, S. Lang y G. J. (Edits.) Object-Based Image Analysis – Spatial Concepts for Knowledge-Driven Remote Sensing Applications. (pp. 20) Hay. Springer-Verlag.Herold, M.; Gardner, M., Roberts, D., (2003).
Spectral resolution requirements for mapping urban areas, IEEE Transactions on Geoscience and Remote Sensing, 41, 1907-1919.Jensen J. R. (2006).
Introductory Digital Image Processing - A Remote Sensing Perspective. Upper Saddle River, Nueva Jersey: Prentice Hall.Lang, S.; Albrecht, F. Blaschke, T. (2006).
OBIA Tutorial: Introduction to Object-Base Image Analysis. Centre for Geoinformatics (Z_GIS), 96.Lizarazo y Elsner (2008). Fuzzy Regions for Handling Uncertainty in Remote Sensing Image Segmentation.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
CLASIFICACIÓN DE LA COBERTURA DEL SUELO URBANO USANDO OBJETOS DE IMAGEN DIFUSOS
URBAN LAND COVER CLASSIfiCATION USING FUZZY IMAGE OBJECTS
Iván Lizarazo
Universidad Distrital Francisco José de Caldas Universidad Distrital Francisco José de Caldas.
Recibido: 20/02/2012 - Aceptado: 15/07/2012
RESUMEN
La clasificación de la cobertura del suelo urbano a partir de imágenes multiespectrales de alta resolución espacial es un asunto problemático debido a la similitud de la respuesta espectral que presentan diferentes categorías. Una posible solución a este problema consiste en la agrupación de pixeles en objetos discretos y su utilización como elementos básicos de análisis. Aunque exitosa en muchas ocasiones, esta técnica no siempre produce exactitudes temáticas altas. Este artículo investiga el potencial de utilizar objetos de imagen con fronteras difusas, con el propósito de superar el problema de confusión espectral entre clases. Para el efecto, se propone un método de análisis de imágenes que consta de cuatro fases: (a) asignación difusa de clases, (b) segmentación difusa, (c) análisis de atributos y (d) asignación discreta de clases. El método se utiliza para realizar la clasificación de la cobertura del suelo en una zona urbana de Bogotá. Los resultados demuestran que el método permite alcanzar mejor exactitud temática que otros métodos basados en pixeles y en objetos de imagen discretos. Se concluye que los objetos de imagen con fronteras difusas constituyen una alternativa útil para resolver problemas complejos de clasificación.
Palabras clave: análisis de imágenes orientado a objetos, cobertura del suelo urbano, objetos con fronteras difusas.
ABSTRACT
Urban land cover classification from high spatial resolution multispectral images is problematic due to similarity of spectral response from different categories. One possible solution to this problem relies on grouping pixels into discrete objects and using such image objects as building blocks for analysis. Although successful in many instances, this technique does not always produce high thematic accuracies. This paper investigates the potential of using image objects with fuzzy boundaries in order to overcome spectral confusion between classes. To this end, we propose an image analysis method that consists of four phases: (a) fuzzy grouping, (b) fuzzy segmentation, (c) attribute analysis, and (d) categorical class assignment. fie method is used for the classification of urban land cover in an urban area of Bogotá. Results demonstrate that the proposed method achieves better accuracy than pixel and discrete object based methods. We conclude that fuzzy image objects provide a useful framework to solve complex problems of classification.
Key words: image objects based image analysis, urban land cover, objects with fuzzy boundaries.
INTRODUCCIÓN
Una apropiada clasificación de la cobertura del suelo urbano es útil en diversas aplicaciones que incluyen modelamiento hidrológico y climático, gestión ambiental y zonificación de usos del suelo. En las décadas pasadas la mayoría de aplicaciones de percepción remota no se enfocaron en ambientes urbanos debido a la limitada resolución espacial de las imágenes multiespectrales disponibles. Ello se explica porque las técnicas tradicionales, basadas en el análisis de pixeles individuales, no permiten obtener clasificaciones confiables a partir de imágenes cuyos tamaños de pixel son más grandes que el tamaño de los objetos de interés. Aunque la disponibilidad de imágenes de resolución espacial más fina desde principios del siglo XXI no resolvió el problema, sí sugirió la conveniencia de incluir el dominio espacial y no solo el dominio espectral en el proceso de análisis de imágenes (Jensen, 2006; De Jong y Freek, 2006; fiomas et al., 2003).
El nuevo paradigma para analizar imágenes de alta resolución espacial es el denominado “análisis de imágenes basado en objetos geográficos” (Geobia, por sus siglas en inglés). Geobia utiliza técnicas de segmentación para agrupar pixeles en objetos de imágenes con fronteras discretas, como un primer paso para extraer clases u objetos existentes en el mundo real (Hay y Castilla, 2008). Diversos trabajos han demostrado que usando objetos de imágenes discretos en lugar de pixeles, es posible incluir propiedades espaciales que mejoran los resultados del proceso de clasificación (Blaschke et al., 2006; Lang et al., 2006).
Aunque el paradigma Geobia ha probado ser útil en diversos estudios urbanos (por ejemplo, Wei et al., 2005; Zhou et al., 2007), no puede considerarse como una panacea: cuando las clases de interés se superponen en el dominio espectral, es difícil obtener exactitudes de clasificación muy altas (Platt y Rapoza, 2008). En particular, la creación de objetos de imagen discretos requiere el uso de métodos de prueba y error para obtener los parámetros de segmentación óptimos para cada imagen y aplicación específica. En muchas ocasiones, la segmentación de imágenes se convierte en una tarea dispendiosa que no siempre tiene éxito (Lang et al., 2006). Dependiendo de la complejidad del paisaje, la calidad de la imagen y las habilidades del usuario, la segmentación de una imagen puede producir objetos de imagen que representan objetos geográficos, partes de dichos objetos, agrupaciones de dichos objetos o simplemente ruido (Schiewe et al., 2001).
Una segmentación exitosa produce objetos de imagen que representan de una manera apropiada los objetos geográficos de interés. Sin embargo, una segmentación es afectada por anomalías del sensor, sombras, diferencias en iluminación (Bezdek et al., 1999). Este problema se agrava en zonas urbanas en las cuales existen objetos geográficos de diferentes tamaños que exhiben alta heterogeneidad espectral (Herold et al., 2003). Más aún, diferentes categorías de coberturas del suelo pueden estar compuestas de materiales similares y no tienen fronteras discretas entre ellas (por ejemplo, las vías con pavimento asfáltico y las cubiertas de construcciones hechas en tela asfáltica) (Mesev, 2003). La segmentación discreta no tiene en cuenta esa ambigüedad espectral toda vez que los objetos de imagen son regiones discretas en las cuales la membresía de un pixel sólo puede tomar uno de dos valores posibles, 1 si el pixel es miembro de la región y 0 si el pixel no es miembro de ella. <(p>
Lizarazo y Elsner (2008) propusieron la segmentación difusa de imágenes como una alternativa para realizar análisis Geobia. La segmentación difusa es un proceso supervisado que reconoce que los pixeles de una imagen pueden tener membresía parcial y múltiples a diferentes clases. A diferencia de la segmentación discreta que produce una sola imagen con regiones cuyos límites están bien definidos y cuya asignación temática es desconocida, la segmentación difusa produce un conjunto de imágenes que representan regiones con límites indeterminados y con asignación temática indefinida o ambigua. Estas regiones pueden ser posteriormente transformadas en diferentes tipos de objetos de imagen, cada uno representando características espaciales o temáticas diferentes (Cheng et al., 2001). Existen algunos trabajos previos que muestran el potencial de la segmentación difusa de imágenes para realizar clasificación categórica y clasificación continua de cobertura del suelo usando imágenes multiespectrales e hiperespectrales. El lector interesado puede consultar, por ejemplo, Lizarazo y Elsner (2009), Lizarazo y Barros (2010) y Lizarazo (2012).
El objetivo de este artículo es evaluar el potencial predictivo de los objetos de imagen difusos y comparar su desempeño con el que ofrecen otros métodos de clasificación basados en pixeles y en objetos de imagen discretos. Para el efecto se realiza un experimento de clasificación de la cobertura del suelo en el contexto de la complejidad y ambigüedad espectral que caracteriza la capital colombiana.
METODOLOGÍA
Área de estudio
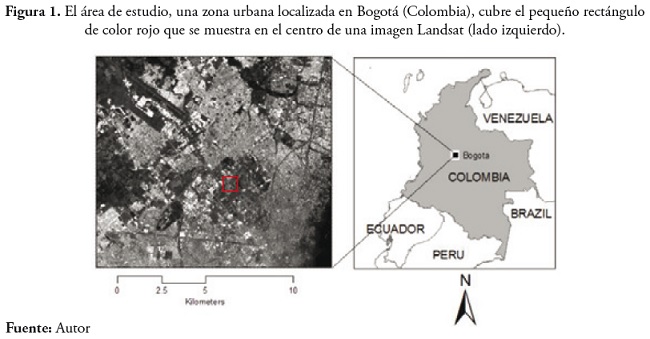
El área de estudio es una pequeña zona urbana localizada en Bogotá (Colombia), de dimensiones 842 m x 825 m, en la cual existen siete categorías de cobertura del suelo: vías, construcciones de media refiectancia, construcciones de alta refiectancia, pastos, árboles, agua y suelo descubierto. El terreno es plano con elevación de 2.600 m sobre el nivel medio del mar. Los usos del suelo son residencial y recreacional. La figura 1 muestra la localización y delimitación del área de estudio.
Datos
La imagen utilizada es una imagen multiespectral QuickBird adquirida en 2004 por DigitalGlobe en cuatro bandas: azul (centrada en 479.5 nm), verde (546.5 nm), roja (654 nm) e infrarroja-cercana (814.5 nm). Dicha imagen tiene 352 columnas y 344 filas. La resolución espacial es 2.44 m y la resolución radiométrica es 11 bits. La figura 2 muestra las cuatro bandas que componen la imagen.
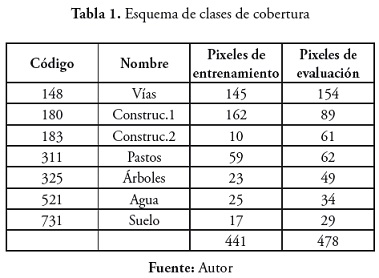
Las clases de cobertura del suelo se representan usando el esquema de clasificación mostrado en la tabla 1,, cuyos códigos han sido definidos de acuerdo con el sistema de clasificación USGS (Anderson et al., 1976).
Descripción conceptual del método de análisis
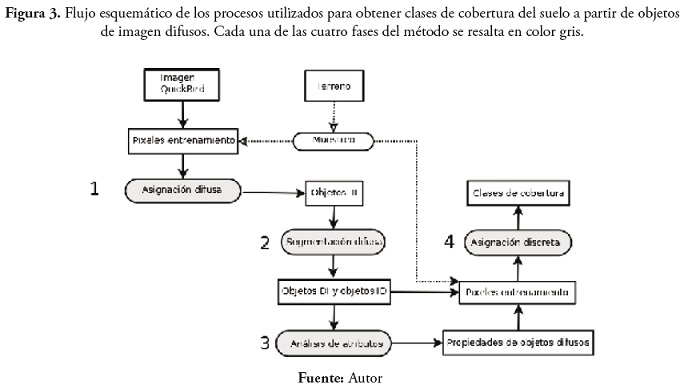
La figura 3 muestra el diagrama de fiujo de procesos que conforman el método utilizado para realizar la clasificación de cobertura, el cual pertenece a la categoría de métodos supervisados de clasificación y comprende cuatro fases: (a) asignación difusa de clases, (b) segmentación difusa, (c) análisis de atributos y (d) asignación discreta de clases.
La fase de asignación difusa de clases permite obtener, a partir de la imagen multiespectral y de unas muestras de entrenamiento, siete bandas nuevas que se conceptualizan como regiones difusas. Cada región difusa almacena el grado de membresía de cada pixel a una categoría de cobertura del suelo específica. Cada región difusa se entiende como una agrupación de objetos de imagen II, es decir, objetos que tienen límites indeterminados (denotados por la primera I) y categorías temáticas inciertas (denotados por la segunda I).
La fase de segmentación difusa permite obtener, a partir de las siete regiones difusas obtenidas previamente, dos bandas nuevas. La primera de esas bandas es una imagen que agrupa objetos de imagen que tienen límites definidos y categorías temáticas inciertas. Esta banda es una agrupación de objetos DI, en los cuales la letra D representa los límites discretos o definidos y la letra I representa las categorías inciertas. La segunda de esas bandas es una imagen que agrupa objetos de imagen con límites indeterminados y asignación temática discreta o cierta. Esta banda es por tanto una agrupación de objetos ID.
La fase de análisis de atributos permite extraer un conjunto relevante de propiedades espectrales y espaciales de los objetos de imagen difusos creados en la etapa anterior con la intención de resolver la ambigüedad espectral de las diferentes clases de cobertura.
La fase de asignación discreta de clases permite obtener, a partir de las imágenes que representan objetos de imagen difusos o atributos espectrales y espaciales de dichos objetos, y del conjunto original de muestras de entrenamiento, una imagen que representa las categorías de cobertura del suelo que existen en la zona de estudio.
IMPLEMENTACIÓN DEL MÉTODO DE ANÁLISIS
En la fase de asignación difusa de clases se utilizó la técnica conocida como máquinas de soporte vectorial (SVM, por sus siglas en inglés) (Hastie et al., 2001) para realizar una regresión supervisada y obtener objetos de imagen difusos II. En estos objetos cada pixel tiene almacenado un valor de membresía a cada clase de interés en el rango entre 0 y 1. La suma total de membresías de un pixel no puede ser mayor que 1.
Las muestras de entrenamiento utilizadas se muestran en la figura 2c. Hay que anotar que dichas muestras representan menos del 0.5% de los pixeles de la imagen.
En la fase de segmentación difusa, las siete regiones difusas se transformaron en una imagen de objetos DI. Los límites discretos de esos objetos se obtuvieron utilizando el operador difuso de t-conorma MAX que realiza una unión lógica de acuerdo con la ecuación (1) (Ross, 2004):
donde max() indica el valor de membresía máximo del pixel iTh a la clase c. Luego de aplicar ese operador, los pixeles contiguos pertenecientes a una misma clase fueron agrupados para crear objetos con límites discretos y con categorías discretas o ciertas (es decir objetos DD). Finalmente, a los pixeles de cada objeto DD se les asignó nuevamente el valor de membresía máximo, lo cual permitió obtener objetos DI.
Por otra parte, los límites indeterminados de los objetos ID se obtuvieron mediante la definición de un límite condicional expresado por el índice de confusión (CI) de acuerdo con la ecuación (2) (Burrough et al., 1997):
donde y
son, respectivamente, el más alto y
el segundo más alto valor de membresía del pixel iTh . Los
valores de CI están en el rango [0,1], donde los valores
cercanos a 1 representan zonas de mayor incertidumbre
temática. Una región difusa ID sigue la representación eggyolk
propuesta por Cohn y Gotts (1996). En este estudio se
obtuvieron tres regiones difusas ID mediante la unión de
núcleos discretos (usando como umbrales las membresías
0.80, 0.70 y 0.60) y la frontera condicional representada
por CI. Para el efecto se utilizó la ecuación (3) (Lizarazo
y Barros, 2010):
En la fase de análisis de atributos se midieron los siguientes atributos espectrales y espaciales: (a) mediana de cada una de las bandas en cada objeto DD, y (b) índices DAN entre objetos de imagen II correspondientes a vías y cada tipo de construcción.
El índice DAN (diferencia absoluta normalizada) expresa el traslapo existente entre objetos difusos II y está definido por la ecuación 4 (Lizarazo y Barros, 2010):
donde iA y
iB representan los valores de membresía del
pixel iTh a las clases A y B, respectivamente. Dichos valores
de membresía se evalúan usando el valor promedio en una
ventana de 3 x 3 pixeles. El valor DAN es un indicador del
traslapo existente entre dos regiones difusas II específicas.
Los valores ANDI están en el rango [0,1]. Los valores DAN
cercanos a 0 representan zonas de indefinición temática.
En la fase de asignación discreta de clases se utilizó una máquina de soporte vectorial para realizar la clasificación categórica de la cobertura del suelo. Las variables predictoras usadas para ajustar el modelo SVM fueron las siguientes:
• Objetos difusos DI
• Objetos difusos ID con umbral = 0.8
• Objetos difusos ID con umbral = 0.7
• Objetos difusos ID con umbral = 0.6
• Índice DAN entre regiones II correspondientes a vías y construcciones de media refiectancia
• Índice DAN entre regiones II correspondientes a vías y construcciones de alta refiectancia
• Valor de la mediana de la banda 1 dentro de objetos DD
• Valor de la mediana de la banda 2 dentro de objetos DD
• Valor de la mediana de la banda 3 dentro de objetos DD
• Valor de la mediana de la banda 4 dentro de objetos DD
La muestra de entrenamiento de esta máquina vectorial fue la misma utilizada para realizar la fase de agrupación difusa. El modelo SVM se construyó utilizando el procedimiento automatizado descrito en Lizarazo y Elsner (2008), el cual permite encontrar parámetros funcionales óptimos. Dicho modelo utilizó una función de base radial (RBF) para transformar el espacio original espectral en un nuevo espacio que permitiera encontrar un hiperplano óptimo de separación (Hastie et al., 2001).
El paso final del proceso consistió en la evaluación de la exactitud temática de la clasificación. Para el efecto se utilizó la muestra de evaluación, mostrada en la figura 2d, que representa el 0.5% del tamaño de la imagen.
El método descrito anteriormente se implementó utilizando el software estadístico R versión 2.15.2 (R Development Core Team, 2012). Además de la librería base se utilizaron los siguientes paquetes: rgdal, sp, raster, maptools, RSAGA y e1071.
RESULTADOS
La figura 4 muestra siete regiones difusas II obtenidas en la fase de asignación difusa: (a) vías, (b) construcciones de refiectancia media, (c) construcciones de refiectancia alta, (d) pastos, (e) árboles, (f ) agua, y (g) suelo descubierto.
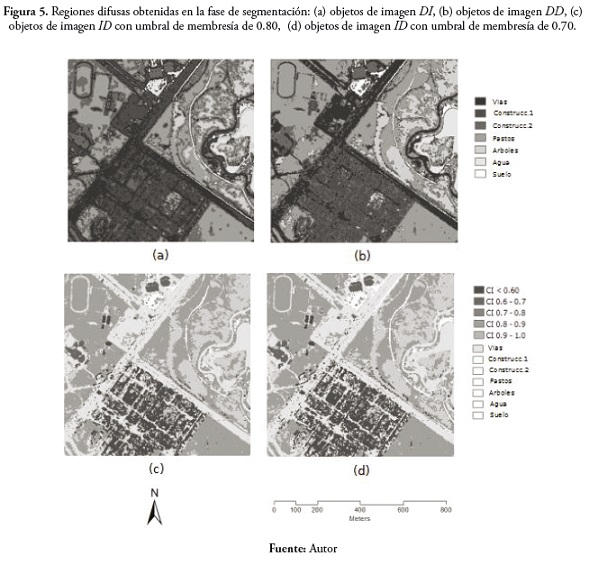
La figura 5 muestra cuatro regiones difusas obtenidas en la fase de segmentación difusa: (a) objetos de imagen DI, (b) objetos de imagen DD, (c) objetos de imagen ID con umbral de membresía igual a 0.8, y (d) objetos de imagen ID con umbral de membresía igual a 0.7.
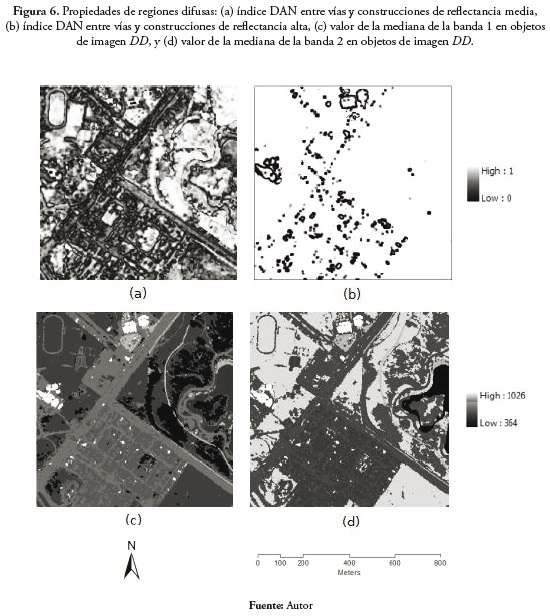
La figura 6 muestra propiedades de regiones difusas obtenidas en la fase de análisis de atributos: (a) índice DAN entre vías y construcciones de refiectancia media, (b) índice DAN entre vías y construcciones de refiectancia alta, (c) valor de la mediana de la banda 1 en objetos de imagen DD, y (d) valor de la mediana de la banda 2 en objetos de imagen DD.
DISCUSIÓN DE RESULTADOS
La figura 7a muestra la clasificación de cobertura del suelo obtenida mediante el método basado en objetos de imagen difusos. Como referencia, la mejor clasificación obtenida mediante el método basado en objetos de imagen discretos, usando las técnicas Geobia convencionales se muestra en la figura 7b. Adicionalmente, el resultado de realizar la clasi ficación basada en pixeles usando lógica difusa se muestra en la figura 7c. Finalmente, el resultado de realizar la clasi ficación basada en pixeles usando el método de máxima probabilidad se muestra en la figura 7d. La clasificación basada en objetos discretos se realizó utilizando el software Erdas Imagine. Las dos clasificaciones basadas en pixeles se realizaron usando el software Idrisi.
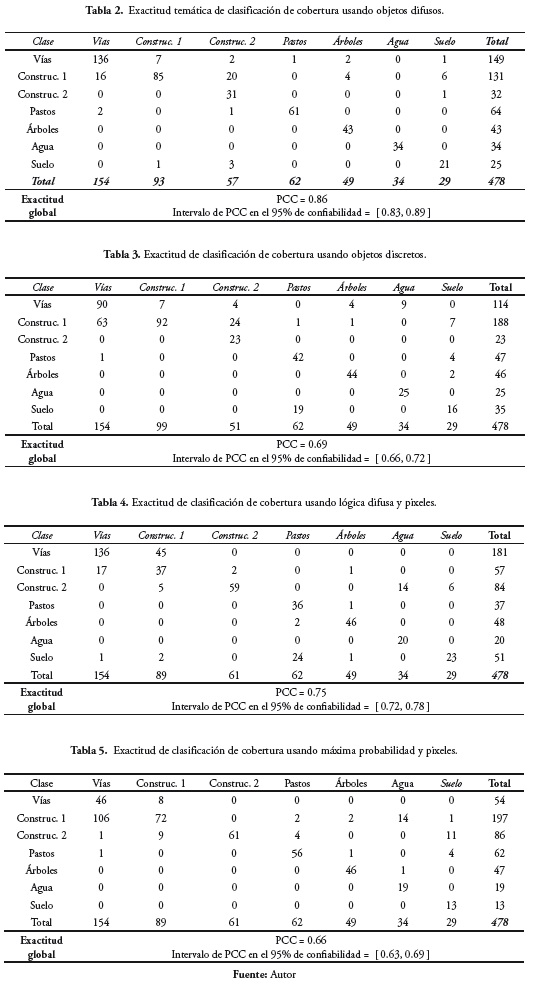
Es evidente que el método de análisis de imágenes basado en objetos difusos permitió obtener clases de cobertura más “limpias” que las obtenidas mediante los otros métodos. La exactitud temática global, medida como porcentaje de clasificación correcta (PCC), alcanzó un valor de 86%. Las matrices de error y los valores de PCC correspondientes a cada uno de los métodos indicados se muestran en las tablas 2,3,4 y 5.
Aunque el método basado en objetos difusos alcanzó los mejores resultados, es claro que la confusión entre vías y construcciones de refiectancia media (indicadas como Construc. 1 en las tablas) no se resolvió completamente. Esta confusión puede ser explicada por el hecho de que muchos objetos geográficos pertenecientes a esas clases de cobertura contienen asfalto y concreto en proporciones similares.
De manera inesperada, la confusión entre los dos tipos de construcción, aquellas cuya refiectancia es alta (por ejemplo, cubiertas metálicas o en fibra de vidrio) y aquella cuya refiectancia es media (por ejemplo, cubiertas de concreto, asbesto-cemento o ladrillo) también fue alta. Este problema puede ser causado debido a la mezcla de diferentes materiales en una sola cubierta, lo mismo que por el tamaño pequeño de la muestra de entrenamiento de la clase de construcciones cuya refiectancia es alta (denotada en las tablas como Construc. 2).
Los resultados muestran que el método de clasificación basado en objetos difusos permite obtener una exactitud temática aceptable en ambientes urbanos complejos. Ello sugiere que la aplicación de conjuntos difusos (Zadeh, 1965; Mendel, 2001) proporciona información útil para el análisis de imágenes que los objetos discretos, basados en lógica booleana o clásica, no pueden suministrar.
Aunque la exactitud temática obtenida mediante objetos difusos se puede considerar aceptable para muchos propósitos prácticos, una evaluación visual de la imagen clasificada muestra que los límites de las diferentes clases de cobertura no están definidos completamente. Esto significa, por una parte, que la integración posterior entre los resultados de una clasificación temática y datos geográficos existentes en formato vectorial puede causar eventuales problemas. Por otra parte, esa situación es inherente a cualquier proceso de clasificación digital y es una muestra evidente de las limitaciones de exactitud posicional que tienen las clasificaciones que utilizan únicamente información derivada de sensores pasivos. Al respecto, es pertinente realizar investigaciones sobre métodos de posclasificación que permitan eliminar ruido y suavizar las imágenes sin comprometer la exactitud final (Rencai et al., 2006).
Teniendo en cuenta que en este estudio no se analizó sino un pequeño conjunto de atributos espectrales y espaciales de los objetos difusos II, ID, y DI es procedente examinar la utilidad de propiedades adicionales que han sido propuestas para objetos “espacialmente vagos” (Chanussot et al., 2005; Dilo et al., 2006; Verstraete et al., 2007; Zinn et al., 2007).
CONCLUSIONES
La principal contribución de este artículo es que demuestra que el método de clasificación basado en objetos difusos permite resolver, hasta cierto punto, la ambigüedad espectral que caracteriza ambientes urbanos. Su aplicación permite obtener exactitudes temáticas superiores a las obtenidas mediante técnicas de análisis basadas en objetos de imagen discretos o en pixeles individuales.
El método propuesto tiene las siguientes ventajas respecto a la clasificación basada en objetos de imagen discretos: (a) simplicidad: el usuario debe suministrar únicamente muestras de entrenamiento confiables y puede olvidarse de realizar pruebas de ensayo y error para obtener parámetros óptimos de segmentación; (b) fiexibilidad: el usuario puede utilizar diferentes métodos de aprendizaje de máquina para ejecutar cada una de las fases del método; y (c) bajo costo: el usuario puede usar herramientas de software libre y gratuito para realizar clasificación de la cobertura del suelo urbano.
AGRADECIMIENTOS
El autor agradece a la Universidad Distrital Francisco José de Caldas por suministrar la imagen multiespectral utilizada en estos experimentos. Igualmente, agradece a los ingenieros catastrales y geodestas Ricardo Cuítiva y Samuel Mesa por su apoyo en la recolección de las muestras de entrenamiento y de validación utilizadas en este estudio.
Referencias
- Anderson, J.; Hardy, E. y Roach, J. (1976). A Land Use And Land Cover Classification System For Use With Remote Sensor Data. Geological Survey Professional Paper 964.
- Bezdek (primavera de 1999). Fuzzy models and algorithms for pattern recognition and image processing. Nueva York.
- Burrough, P. A.; van Gaans, P. y Hoostmans (1997). Continuous classification in soil survey: spatial correlation, confusion and boundaries. Geoderma, 77(2-4), 115-135.
- Cohn, A., y Gotts, N. (1996). The Egg-Yolk representation of regions with indeterminate boundaries. Geographical Objects with Undetermined Boundaries, 171-187.
- Chanussot, J.; Nyström, I. y Sladoje, N. (2005). Shape signatures of fuzzy star-shaped sets based on distance from the centroid, Pattern Recognition Letters, 26(6), 735-746.
- Cheng, T.; Molenaar, M. y Lin, H. (enero de 2001). Formalizing fuzzy objects from uncertain classification results. International Journal of Geographical Information Science, 15,_(1), 27-42.
- De Jong, S. M. y Freek, D. van der M. (eds.), (primavera de 2006). Remote Sensing Image Analysis: including the spatial domain. Dordrecht.
- Dilo, A.; Bos, P.; Kraipeerapun, P. y de By, R. A., (primavera de 2006).fiStorage and manipulation of vague spatial objects using existing GIS functionality. En G. Bordogna y G. Psaila (Edics.) Flexible databases supporting imprecision and uncertainty (pp. 293-321) (pp. 293-321).
- Hastie, T.; Tibshirani, R. y Friedman, J. (2001). The Elements of Statistical Learning: Data Mining, Inference and Prediction. Nueva York, NY: Verlag.
- Hay y Castilla (s.f.) Geographic Object-Based Image Analysis (GEOBIA): Paradigm shift or new methods?. En: T. Blaschke, S. Lang y G. J. (Edits.) Object-Based Image Analysis – Spatial Concepts for Knowledge-Driven Remote Sensing Applications. (pp. 20) Hay. Springer-Verlag.
- Herold, M.; Gardner, M., Roberts, D., (2003). Spectral resolution requirements for mapping urban areas, IEEE Transactions on Geoscience and Remote Sensing, 41, 1907-1919.
- Jensen J. R. (2006). Introductory Digital Image Processing - A Remote Sensing Perspective. Upper Saddle River, Nueva Jersey: Prentice Hall.
- Lang, S.; Albrecht, F. Blaschke, T. (2006). OBIA Tutorial: Introduction to Object-Base Image Analysis. Centre for Geoinformatics (Z_GIS), 96.
- Lizarazo y Elsner (2008). Fuzzy Regions for Handling Uncertainty in Remote Sensing Image Segmentation. Lecture Notes in Computer Science, Volume 5072/2008, 724-739.
- Lizarazo, I. y Elsner, P. (2009). Fuzzy segmentation for object-based image classification. International Journal of Remote Sensing, 30 (6), 1643-1649.
- Lizarazo, I. y Barros, J. (2010). Fuzzy Image Segmentation for Urban Land Cover Classification. Photogrammetric Engineering and Remote Sensing, 76(2), 151-162.
- Lizarazo, I. (2012). Quantitative land cover change analysis using fuzzy segmentation. International Journal of Applied Earth Observation and Geoinformation, 15 16-27.
- Mendel, J. M. (2001). Uncertain Rule-Based Fuzzy Logic Systems: Introduction and new directions. Nueva Jersey, N.J.: Prentice-Hall.
- Mesev, V, (2003). Remotely Sensed Cities. Londres, R.U. Taylor & Francis.
- Platt, R.V. y Rapoza, L., (2008). An evaluation of an object-oriented paradigm for land use/land cover classification. The Professional Geographer, 60(1), 87-100.
- R. Development Core Team (2012). R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Viena, Austria. URL http:// www.R-project.org (fecha de último acceso: 14 de enero de 2013).
- Rencai, D.; Jiajia, D.; Gand, W. y Hongbing, D. (2006). Optimization of post-classification processing of high-resolution satellite image: A case study. Science en China Series E: Technological Sciences, 49(1), pp. 98-107.
- Ross, T. J. (2004). Fuzzy Logic with Engineering Applications. Wiley, Chichester.
- Schiewe, J.; Tufte, L. y Ehlers, M. (2001). Potentials and problems of multiscale segmentation methods in remote sensing. GeoBIT/GIS, 6, 34-39.
- Thomas, N.; Hendrix, C., y Congalton, R.G., (2003). A comparison of urban mapping methods using high-resolution digital imagery. Photogrammetric Engineering and Remote Sensing, 69 (9) 963-972.
- Verstraete, J.; Hallez, A. y De Tre, G. (2007). Fuzzy Regions: Theory and Applications. En A. Morris y S. Kokhan. (Edits.), Geographic Uncertainty in Environmental Security. 1-17.
- Wei, W.; Chen, X. y Ma, A. (2005). Object-oriented information extraction and application in high resolution remote sensing images. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), 6, 3803-3806.
- Zadeh, L. (1965). Fuzzy sets. Information and Control, (8), 338–353.
- Zhou, C.; Wang, P.; Zhang, Z.; Qi, C. y Wang, Y. (2007). Object-oriented information extraction technology from QuickBird pan-sharpened images. Proceedings of SPIE, 6279(2), 62793L.
- Zinn, D.; Bosch, J. y Gertz, M. (septiembre 23-28 de 2007). Modeling and Querying Vague Spatial Objects Using Shapelets. 33rd International Conference on Very Large Data Bases, University of Vienna, Austria, 567-578.
Licencia
La revista UD y la Geomática se encuentra bajo una licencia Creative Commons - 2.5 Colombia License.
Atribución - No Comercial - Sin Derivadas