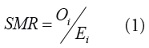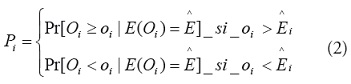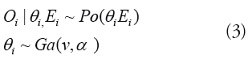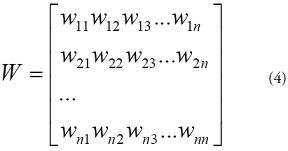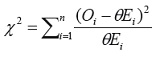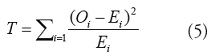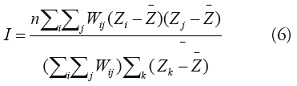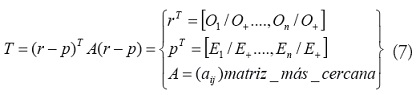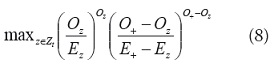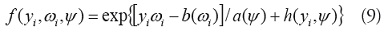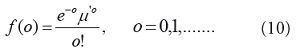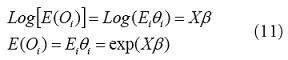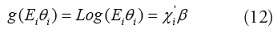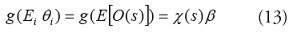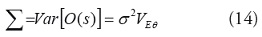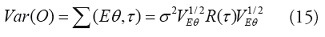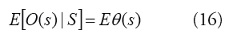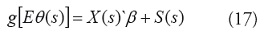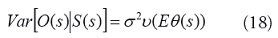Publicado:
2012-12-20Número:
Núm. 6 (2012)Sección:
Artículo de investigación científica y tecnológicaModelos de regresión espacial para el comportamiento de las enfermedades infecciosas dengue y malaria en Colombia para los años 2000, 2005 y 2010
Palabras clave:
modelos Lineales Generalizados, Epidemiologia Espacial, malaria, dengue, riesgo, tasa de morbilidad estandarizada (es).Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Visitas
Descargas
MODELOS DE REGRESIÓN ESPACIAL PARA EL COMPORTAMIENTO DE LAS ENFERMEDADES INFECCIOSAS DENGUE Y MALARIA EN COLOMBIA PARA LOS AÑOS 2000, 2005 Y 2010
SPATIAL REGRESSION MODELS FOR THE BEHAVIOR OF INFECTIOUS DISEASES DENGUE AND MALARIA IN COLOMBIA FOR THE YEARS 2000, 2005 AND 2010
Dania Lorena Sánchez Pérez1, Fernando Santa2, Héctor Javier Fuentes López3
1Dirección General Marítima del Ministerio de la Defensa (Dimar) Colombia dlorena01@gmail.com
2 Universidad Distrital Francisco José de Caldas, Bogotá–Colombia fernando.santa@gmail.com
3 Universidad Distrital Francisco José de Caldas, Bogotá–Colombia hjfuentesl@udistrital.edu.co
Recibido: 20/11/2012 - Aceptado: 15/12/2012
RESUMEN
El artículo consintió en estimar modelos de regresión espacial lineales generalizados con respuesta tipo Poisson para explicar el comportamiento de las enfermedades infecciosas malaria y dengue en varios años, identificando factores sanitarios determinantes en la aparición de los casos de estas enfermedades y finalmente obtener mapas de riesgo de las enfermedades. Los resultados obtenidos muestran que la necesidad de vincular de los efectos espaciales en los modelos y las variables explicativas consideradas aportan en la explicación del número de casos reportados de la enfermedad en los años analizados.
Palabras clave:modelos lineales generalizados, epidemiología espacial, malaria, dengue, riesgo, tasa de morbilidad estandarizada.
ABSTRACT
Article consented to estimate spatial regression models with generalized linear Poisson response to explain the behavior of infectious diseases malaria and dengue for different years, identifying health determinants in the occurrence of cases of these diseases and eventually obtain risk maps diseases. The results show that the need for linking spatial effects in models and provide the explanatory variables in explaining the number of reported cases of the disease in the years analyzed.
Key words: generalized linear models, spatial epidemiology, malaria, dengue, risk, standardized morbidity ratio.
INTRODUCCIÓN
La malaria y el dengue son enfermedades infecciosas que requieren de un vector para transmitirse a los seres humanos. Estas enfermedades afectan de forma desproporcionada a los pobres que no tienen acceso a la atención sanitaria. La Organización Mundial de la Salud (OMS) calcula que la incidencia del dengue ha aumentado extraordinariamente en todo el mundo en los últimos decenios. Unos 2.500 mil millones de personas (dos quintos de la población mundial) corren el riesgo de contraer la enfermedad, y el 40% de la población mundial, de contraer malaria. En el contexto nacional se reportaron en 2009, 79.909 casos de malaria, de los que, 51.721 (64,7%) de los afectados fueron hombres y 28.188 (35,3%) mujeres. En cuanto a los casos de dengue, fueron notificados 64.729, de los cuales el 86% (55.592) casos corresponden a dengue y 14% restante (9.137 casos) a dengue grave.
Con relación a las investigaciones que adelantan los países en materia de salud pública, aparece el análisis espacial dentro de los métodos estadísticos, como principio básico al tratar de examinar la dependencia entre las observaciones de casos de ocurrencia de una enfermedad y el contexto geográfico, esto debido a que la transmisión de enfermedades infecciosas está estrechamente ligada con el concepto espacio–temporal. En este sentido, el riesgo de contraer una enfermedad es mucho más alto cuando existen personas o regiones vecinas infectadas. Por consiguiente y distinguiendo el rasgo espacial en la propagación de enfermedades, se busca con la ejecución del presente proyecto de grado, analizar y modelar la ocurrencia de la malaria y el dengue teniendo en cuenta el componente espacial; elaborar mapas de las enfermedades que sirvan para estratificar las zonas de acuerdo con el número de ocurrencia y el riesgo que presentan y analizar las posibles relaciones entre variables que permitan decidir sobre las necesidades y las prioridades en la lucha contra estas enfermedades de forma que orienten a las autoridades competentes (a nivel nacional el Instituto Nacional de Salud y el Ministerio de la Protección Social) en la definición de políticas de salud pública.
MARCO TEÓRICO
La estadística espacial ha sido extensamente aplicada en la epidemiología para el estudio de la distribución de las enfermedades. La variación espacial de la incidencia de una enfermedad puede ayudar a descubrir áreas donde la enfermedad es particularmente prevaleciente, por lo que se pueden encontrar factores de riesgo desconocidos [8]. A continuación se muestra una revisión de los conceptos fundamentales de epidemiologia y de estadística espacial, los cuales serán necesarios para la comprensión del fenómeno estudiado, su análisis y presentación de resultados.
Epidemiologia espacial
El término epidemiología espacial [9] se ha empleado para describir estudios sobre las causas y la prevención de las enfermedades utilizando diferentes perspectivas de análisis en las cuales la ubicación de los eventos es un componente fundamental.
La epidemiología espacial goza de una larga tradición, remontándose a principios del siglo XIX, en el que se realizaron mapas de la ocurrencia de enfermedades en di- ferentes países con el objetivo de caracterizar la extensión y las posibles causas de brotes de enfermedades infecciosas tales como la fiebre amarilla y el cólera. Con posterioridad, la epidemiología espacial creció en complejidad, sofisticación y utilidad. Recientes avances en la disponibilidad de datos y en los métodos analíticos para tratarlos, proporcionaron nuevas oportunidades para extender las investigaciones epidemiológicas tradicionales a escala nacional o regional, hasta el estudio de las variaciones en las enfermedades a nivel local. Las investigaciones que se realizan actualmente contemplan no solo factores etiológicos, sino factores de riesgo para la salud con relevancia a nivel local, tales como exposiciones ambientales, la distribución local de condiciones socioeconómicas y los hábitos y estilos de vida.
Uno de los principales objetivos [10] de la epidemiología espacial es el de mostrar qué parte de la variación espacial de la distribución de la ocurrencia de una enfermedad no está explicada ni por la distribución espacial de factores explicativos conocidos ni por una variación aleatoria. De hecho, a menudo el interés es encontrar pistas sobre algún factor de riesgo desconocido de la enfermedad. El estudio de una enfermedad desde la epidemiología espacial es abordado a través de tres grandes perspectivas: mapas de probabilidad de las enfermedades, pruebas de autocorrelación espacial y agregaciones de casos y modelos de regresión espacial.
Modelos estadísticos
Una hipótesis estadística común [11] para modelar el
número de casos observados en una región i es que estos
se extraen de una distribución de Poisson con media
donde
es el riesgo relativo y
es el número de casos
esperados; así se supone que no hay interacción entre el
riesgo y la población, es decir, el riesgo relativo depende
solo de la región. Para este caso, se denota por
y
la
población en riesgo y el número de casos observados en la
región i. La población en riesgo para todo el área de estudio
se denota como P + y el número total de casos como
O +. Un aspecto importante es que el número de casos
observados
proporciona información del riesgo, pero
no es conveniente trabajar con estos datos crudos, debido
a que el riesgo se distribuye de acuerdo con la población,
por lo que un número elevado de casos podría ser o no
relevante de acuerdo con tamaño de la población expuesta,
por lo que es necesario emplear algún tipo de tasa que sea
una buena estimación del riesgo y que a la vez supere este
inconveniente. Para obtener una estimación del riesgo
, el número de casos observados debe ser comparado con el
número esperado de casos. Si
y
son conocidos, el
número esperado de casos en la región i se puede calcular
como
, donde r +es el tasa de incidencia total (O+/P+) Una estimación básica del riesgo en una regióndada se puede calcular como
donde se conoce como la tasa de morbilidad estandarizada.
Para el mapeo de una enfermedad y la aplicación de los
estadísticos, se emplea la tasa de morbilidad y no el número
de casos
[12], ya que si se encuentra autocorrelación
espacial, esta se debería a la distribución espacial de la
población subyacente (es bien sabido que a mayor población,
mayor
es
el
número
de
casos)
y
no
a
la
distribución
de
la enfermedad.
Mapas de probabilidad
El objetivo es proporcionar una representación de la
distribución espacial del riesgo de una enfermedad en la
zona de estudio [13]. Los mapas de probabilidad permiten
establecer si las unidades espaciales están caracterizadas por
un mayor o menor conteo de casos de alguna enfermedad
respecto de los casos esperados. Asumiendo que los casos
siguen una distribución de Poisson, el primer paso en
la representación de la variación espacial de la enfermedad
es mapearla a un nivel de significancia. El riesgo puede
refiejar el número de personas que sufren una enfermedad
(morbilidad) en un período de tiempo determinado, para
una población expuesta. Por lo tanto, un riesgo relativo de
1 significa que el riesgo en la región es el promedio y será de
interés la ubicación de las regiones donde el riesgo relativo
es significativamente mayor que 1. Los riesgos que resulten
altamente significativos (cuyos intervalos de confianza son
mayores a uno) son de mayor interés, y permiten identificar
regiones con casos mayores a lo que se esperaría.
Por otro lado, los mapas de probabilidad (Choynowski, 1959) son una manera conveniente de representar la significancia de los valores observados [14]. Estos muestran la probabilidad de que un valor sea mayor o menor al valor esperado, de acuerdo con la suposición que se hace sobre el modelo. Se deben probar distintos modelos y comparar los mapas obtenidos, de forma que se pueda apreciar cómo varía la significancia de los valores de acuerdo con el modelo escogido. Se exponen dos modelos por ser los más usados:
• Distribución de Poisson: el procedimiento consiste en
calcular la probabilidad de los casos observados para cada
región i. Si se tiene el valor esperado
, la estimación de la media
global del riesgo se puede calcular como
A continuación se calcula la probabilidad de que el número observado de casos para cada región i, sea el valor más extremo de acuerdo con el número casos esperados [15]:
Los valores de
se basan en la probabilidad acumulada
de una distribución de Poisson y ofrecen un índice de
desviación de la hipótesis de que los riesgos son iguales.
• Distribución Poisson gamma: la distribución de Poisson implica supuestos, una cuestión clave es que para esta distribución
el valor
de la media y la varianza
de se supone que son los mismos. En el caso en que los datos tengan sobre dispersión, de modo que la variación de los datos es mayor que su media, el modelo estadístico debe ser ampliado, en este caso una forma de permitir una mayor varianza, es el uso de una distribución binomial negativa, que puede ser considerada como un modelo mixto en el que se considera un efecto aleatorio siguiendo una distribución gamma paracada región. Esta formulación se conoce como la de Poisson gamma
(PG),
y puede ser estructurada
a dos niveles
[16]:
El riesgo relativo es una variable aleatoria, que se extrae de
una distribución gamma con media
y la varianza
. Ahora, la distribución de
está condicionada al valor de
.
La distribución condicionada de cada
es fácil de obtener y es una binomial negativa con tamaño
v y probabilidad
.
Agregaciones espaciales de enfermedades
Los mapas de SMR proporcionan la base para plantearse la pregunta de si hay agregaciones de casos de la enfermedad. La estructura típica de datos para la evaluación de los patrones espaciales de salud consiste en una colección de datos que corresponden al conteo de casos de alguna enfermedad asociados a una región durante un periodo de tiempo determinado. Las preguntas más comunes [17] relacionadas con la agregación de casos están relacionadas a si estos tienden a ocurrir cerca de otros (lo cual podría sugerir un agente infeccioso), (o.k.) si existe algún área en particular dentro de la región de estudio que parezca contener un exceso significativo de casos observados (lo cual sugiere un factor de riesgo ambiental) o dónde podrían estar las agrupaciones más inusuales de casos. Para responder a esto, se debe evaluar la existencia de algún patrón de distribución espacial.
Existen muchas pruebas basadas en la hipótesis nula
H0No hay agregación de casos
Las cuales se caracterizan por tener como principio la matriz de pesos espaciales W[18]:
donde Wij es la interdependencia entre las regiones i y j.
Entre las pruebas de autocorrelación espacial más usadas en datos de salud, se encuentran:
• Prueba de homogeneidad en los riesgos relativos:
antes de realizar cualquier análisis de la presencia de
agregaciones, se debe evaluar la heterogeneidad en los
riesgos relativos. Esto se debe a que la sobre dispersión
en los datos puede afectar el valor p de las pruebas,
además se debe comprobar si existen diferencias reales
entre los diferentes riesgos relativos. La razón de esta
heterogeneidad puede estar relacionada con diferentes
factores,
tales como la presencia
de una fuente de
contaminación
en la zona,
lo que puede conducir a un
aumento
en el riesgo alrededor
de una región.
Teniendo
en
cuenta que para cada área
se ha calculado el número
esperado
de casos
y observado de casos
, una prueba
de chi-cuadrado puede llevarse a cabo para probar de
forma global si existen diferencias significativas entre
estas dos cantidades. La prueba se define como [19]:
donde
es la SMR que sigue una distribución chicuadrado
con n
grados de libertad.
La prueba
Considera como
hipótesis nula que los riesgos relativos
entre
las
regiones
es una constante
, mientras que la hipótesis
alternativa supone que no todos los riesgos relativos son iguales. Como se planteó al inicio, el riesgo relativo se
calcula a partir de la SMR, lo cual es una estandarización
interna, por lo que la hipótesis nula plantea que
todos
los
riesgos
relativos
son
iguales
a
1
(esto
se
debe
al
hecho de que
O+=E+). En este caso el estadístico
queda como [20]
Con n-1 grados de libertad
La I de Moran: el estadístico de Moran está dado por [21]:
donde
corresponde a los residuales
de la
tasa de morbilidad estandarizada SMR y Wij es el peso
espacial entre la regiones i y j.
Las desventajas que presenta esta prueba consisten en que se asume que la población en riesgo se distribuye uniformemente dentro del área de estudio y además que la correlación o covarianza es isotrópica, es decir, igual en todas las direcciones, aspecto que puede ser superado si se manipula la matriz de pesos espaciales para reflejar las desigualdades en las direcciones [22].
• Prueba de Tango para agregaciones globales: esta prueba compara el número observado y esperado de casos en cada región. Los diferentes tipos de interacciones entre regiones vecinas pueden ser considerados. La prueba propone una medida de fuerza de interacción entre las regiones, sobre la base de una función de descomposición de la distancia entre las dos regiones. El estadístico propuesto por Tango es [23]:
dónde
es la distancia entre las
regiones i y j medida desde sus coordenadas representativas
y
es una constante positiva que refleja
el grado de dependencia entre las áreas y la escala en
la que la interacción se produce. Es recomendable probar diferentes valores de
, porque esto puede tener un impacto importante en los resultados y en
la significancia de la prueba. La desventaja de esta prueba está relacionada con la definición de
, pues
este no se conoce a priori, lo que produce problemas de comprobación múltiple
Hasta ahora se consideraron métodos que evalúan solamente la presencia de heterogeneidad de los riesgos en el área de estudio y la presencia de agregaciones a nivel general. Para detectar la ubicación real de los grupos presentes en la zona se debe seguir un enfoque distinto que consiste en una ventana móvil que cubre áreas pequeñas, en las cuales se lleva a cabo una prueba de agregación. Al repetir este procedimiento para toda el área de estudio, será posible detectar la ubicación de los grupos de enfermedades.
• Estadístico de Kulldorff: este trabaja con las regiones dentro de una ventana circular y compara el riesgo relativo de las regiones de la ventana con el de las regiones que están fuera de esta. La hipótesis nula, de no agregación, es que los dos riesgos relativos son iguales, mientras que la hipótesis alternativa (agregación espacial) consiste en que el riesgo relativo dentro de la ventana es mayor. Para un modelo de Poisson, la prueba es [24]:
donde z es un elemento de z1 , el conjunto de todos los círculos centrados en la región i. El inconveniente que presenta esta prueba consiste en que se puede tener más de un grupo importante a la vez, por lo que algunos grupos pueden superponerse. En el caso en que los datos sean muy dispersos, se pueden producir falsos positivos en el nivel de significancia.Modelos lineales generalizados: regresión de Poisson
El primer aspecto para modelar algún fenómeno es considerar el tipo de variable que está bajo estudio. En el caso de la epidemiologia, como se trata de comprender enfermedades que afectan a una población, lo más usual es encontrar el conteo de eventos de una enfermedad para determinadas áreas o simplemente una variable binaria que represente la ausencia o no de una enfermedad en un área determinada [25]. El conocimiento de este tipo de variables señala la importancia de determinar una técnica de regresión que se ajuste a las características de estos datos y que pueda tener en cuenta la dependencia espacial.
La familia de modelos lineales generalizados (GLM) proporciona una colección de modelos de regresión lineal que se extiende a una amplia variedad de distribuciones, incluyendo las familias de los datos de conteo como la Binomial y Poisson [26]. Los GLM constan de un componente aleatorio que determina la distribución de los términos de error, un componente sistemático que define la combinación lineal de las variables explicativas y la función de enlace que permite definir la relación entre los componentes sistemáticos y aleatorios. En general, las distribuciones que son miembro de la familia exponencial tienen la forma [27],
dondeREGRESIÓN DE POISSON
Una distribución adecuada para los datos de conteo de salud es la distribución de Poisson, que es un miembro de la familia exponencial [28]:
Donde el parámetro y
y representa el número de eventos promedio o la
media del número de casos por unidad de area. Para conteos regionales de
independientes e idénticamente distribuidos como variables aleatorias de una Poisson, con
media y varianza igual a
, el valor esperado es una función de las covariables
regionales
La función de enlace usada es la cadena logarítmica [29], la cual tiene como interesante para la distribución Poisson el asegurar que todos los valores predichos de la variable respuesta no serán negativos:
Para datos espaciales, el conteo de casos de puede ser expresado en función de una ubicación si, por lo que
En este caso,
En las aplicaciones tradicionales de modelos lineales generalizados [30], la matriz de varianza-covarianza de los datos O(s) es:
Dado que no siempre se puede asumir que los datos son independientes, es necesario adaptar los GLM para permitir la autocorrelación espacial. Para incorporar a los modelos lineales generalizados el efecto espacial, es necesario modificar la matriz de varianza-covarianza de los datos. Se presentan dos alternativas, los efectos fijos y la especificación marginal y los modelos mixtos y la especificación condicional [31].
Para un modelo de efectos fijos y especificación marginal [32], se asume que es un vector de parámetros fijos desconocido y el modelo de la media marginal esta en función de parámetros fijos no aleatorios (pero desconocidos). De acuerdo con las ideas de Wolfinger y O’Connell (1993) [33] y Gotway y Stroup (1997) [34], se define el modelo de varianza-covarianza de los datos como:
donde τ
es un vector de parámetros desconocidos,
R(τ
) es una matriz de correlación con los elementos . La diagonal de la matriz
, contiene elementos iguales a la raíz cuadrada de la función de varianza
Una especificación alternatica, como son los modelos mixtos y la especificación condicional, incorpora el proceso espacial no observado a través de la utilización de efectos aleatorios dentro de la función de la media; y los modelos de la media y la varianza condicional de O(s) como una función de los efectos fijos de las covariables y los efectos aleatorios derivados del proceso espacial no observado [35]. La formulación condicional conduce a un modelo lineal generalizado mixto (GLMM). Se asume que los datos son condicionalmente dependientes de un proceso espacial .
Si se obtiene S(s), O(s) tiene una distribución de la familia exponencial. En lugar de partir de la media marginal
Para las covariables, ahora consideramos la media condicional [36]:
La función de enlace relaciona esta media condicional con las covariables explicativas:
y S (s) es un efecto aleatorio en el lugar s, y entra en el componente lineal de un GLM como una adición a la intersección. En cualquier lugar, se puede considerar S (s) para representar una intersección aleatoria que varía con la ubicación espacial (o más exactamente, una adición aleatoria a la intersección). En este caso la varianza condicional depende de la media a través de:
donde la función v(.) es la función de varianza descrita
anteriormente y es un parámetro de sobre dispersión. Las hipótesis de independencia condicional implica que cualquier correlación espacial entre O se debe únicamente a los patrones espaciales en el campo aleatorio S . Para completar la especificación del modelo, es necesario especificar la estructura de dependencia espacial en los datos, se asume que estos son condicionalmente independientes
(independientes obtenidos de S ), y que
es un campo
aleatorio gaussiano con media 0 y función de covarianza
En cuanto a la estimación de los modelos [37], se debe mencionar que los GLM tradicionales (no espaciales) permiten alejarse de la distribución de Gauss y utilizar otras distribuciones que admiten relaciones entre la media y la varianza. Sin embargo, la inferencia basada en la verosimilitud, que por lo general se utiliza con estos modelos, requiere de una distribución multivariante, y cuando los datos son espacialmente autocorrelacionados no se puede construir esta distribución multivariante como producto de las probabilidades marginales (como se hace cuando los datos son independientes). Para hacer frente a la situación en la que se pueden definir medias y varianzas, pero no necesariamente una verosimilitud completa, Wedderburn (1974) [38] introdujo la noción de cuasiverosimilitud basada en los dos primeros momentos de una distribución. Esto lleva a una estimación iterativa, basada solo en los dos primeros momentos de una distribución que puede ser usada con datos espaciales. Otra solución se basa en una expansión de la serie inicial de Taylor, que permite métodos de pseudoverosimilitud para inferencia espacial. Un tercer enfoque, llamado cuasiverosimilitud penalizada, descrita por Breslow y Clayton (1993) [39], utiliza una aproximación de Laplace para el logaritmo de la verosimilitud.
MATERIALES Y MÉTODOS
Para la construcción del modelo se tomó como información el número de casos ocurridos de los eventos dengue y malaria en los años 2000, 2005 y 2010 para cada uno de los municipios del país (en MS Excel). Con esta información se elaboró una base de datos (BD), a la cual se adicionó información referente a otro tipo de variables con las que se formularon los modelos. Una vez lista la BD y con un archivo shapefile de los municipios de Colombia, se realizo un join tomando como atributo identificador el código DANE del municipio, el cual estaba tanta en la BD como en el shapefile. De esta forma se obtuvo un shapefile de los municipios del país con información referente al número de casos ocurridos de los dos eventos para los referidos años. Este shape se cargó en R y se procedió a escribir y ejecutar la rutina para formular y escoger las matrices de pesos espaciales, los mapas de significancia, los contrates de autocorrelación espacial y los modelos espaciales.
Elaboración de la base de datos
La información proporcionada en las hojas de datos contenía desagregado el número de casos para los eventos dengue y malaria en: eventos 210 (dengue), 220 (dengue hemorrágico), 490 (malaria vivax), 480 (Malarie), 470 (malaria Falciparum) y 460 (malaria asociada), para los tres años. De cada año, cada evento tenía el reporte de casos por semana (para un total de 52 semanas) y por municipio (para 1.103 municipios). Cada reporte de caso tenía asociado el municipio de procedencia (municipio donde reside la persona que sufre el evento), el municipio de notificación (aquel donde se atiende la persona que padece el evento), el código DANE del municipio, el departamento y el código DANE de este.
Para cada hoja de datos se tenía por cada municipio un total de casos reportados. Una vez listas las 18 hojas de datos, se relacionaron los eventos dengue por año (210 y 220) y malaria (490, 480, 470 y 460), obteniendo 6 hojas de datos. Nuevamente se aplicaron consultas para sumar de un mismo municipio los casos reportados en distintos eventos.
Luego se montó un servidor en IIS (Internet Information Server) con PHP y se hizo la conexión con las tablas almacenadas en la base de datos de MYSQL. Una vez conectadas, se aplicaron consultas para llevar a una nueva y única hoja de datos la información del número de casos ocurridos por evento y por año para cada uno de los municipios del país.
Una vez lista la BD, se cargó a ArcGIS el shapefile de municipios, el cual contenía 1.103 objetos con información de su geometría (polígono), perímetro y área. Cada objeto tenía asociado el código DANE del municipio. Se cargó la BD como una tabla a ArcGIS y se procedió a relacionar a través de un join cada municipio del shape con cada municipio de la BD. De esta forma se llevó a cada municipio del shape el número de casos ocurridos de dengue y malaria para los tres años de estudio.
Mapeo de la enfermedad
Se obtuvo el mapa de las tasas de morbilidad estandarizada en cada una de las seis variables de interés: SMR para malaria en 2000, SMR para malaria en 2005, SMR para malaria en 2010, SMR para dengue en 2000, SMR para dengue en 2005 y SMR para dengue en 2010. De esta forma se pudo identificar la distribución de cada una de las enfermedades y aquellos municipios con conteo de casos mayor a lo esperado, así como los que presentaron un número menor de casos a lo que se podría esperar teniendo en cuenta la población expuesta.
Asumiendo una distribución de Poisson del conteo de casos, se empleó la función de Choynowski, la cual pliega dos colas de probabilidad, una para los valores pequeños y otra para valores extraordinariamente altos. De esta forma se grafican por separado los municipios con bajas y altas tasas.
Otra función empleada fue la probmap, que tiene la ventaja frente a la anterior, de retornar un Data Frame con los datos en crudo, los casos esperados, el riesgo relativo y la probabilidad de encontrar un valor extremo o uno más bajo a lo que se esperaría.
Un enfoque que evalúa el posible impacto de una falla en el supuesto de que los datos siguen una distribución de Poisson, consiste en estimar la dispersión por el ajuste de un modelo lineal generalizado del conteo de casos observados, incluyendo solo el intercepto y la población en riesgo.
En el caso de que los datos presenten sobredispersión, no se puede mantener el supuesto de una distribución de Poisson, por lo que una forma fácil de permitir gran varianza es asumir una distribución binomial negativa. Este enfoque se utilizó a través de la función empbaysmooth. Los parámetros con los que se suavizaron el número observado y esperado de casos fueron estimados vía estimadores empíricos bayesianos.
Por último, se probó la función EBest. El enfoque de esta función permite dar niveles de significancia a la SMR sin asumir alguna distribución de probabilidad, pues asume que la media y la varianza de los riesgos relativos se conoce.
RESULTADOS
Para la selección de la mejor matriz de pesos, el análisis de los mapas, las pruebas de autocorrelación y agregaciones, las variables usadas fueron la SMR para el evento malaria en 2000, SMR para malaria en 2005, SMR para malaria en 2010, SMR para dengue en 2000, SMR para dengue en 2005 y SMR para dengue en 2010. Para los modelos, las variable respuesta fue el número de casos observados en el evento dengue y malaria en cada uno de los tres años. Los resultados fueron:
Selección de la mejor matriz de pesos espaciales
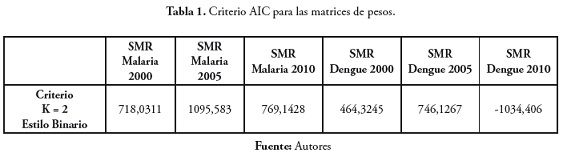
Las matrices de pesos seleccionadas corresponden a las que tenían menor valor para el criterio de AIC. En la tabla 1 se presenta el valor de AIC de las matrices de pesos seleccionadas.
Mapas de probabilidad
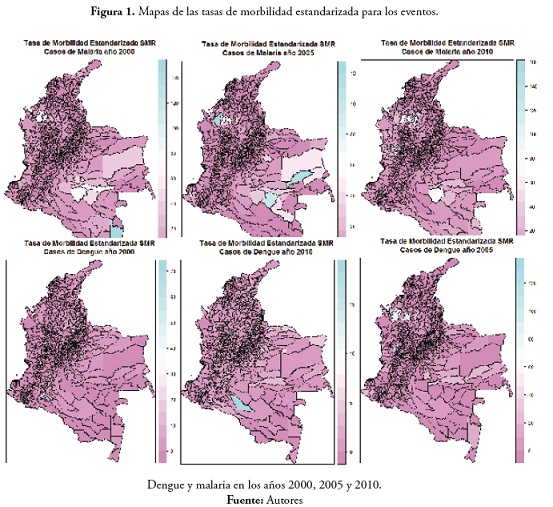
Los mapas de las tasas de morbilidad estandarizada para las seis variables de interés se presentan en la figura 1.
De acuerdo con el mapa de SMR para el evento malaria en 2000, se pudo apreciar que los municipios que presentaron un número de casos observados mayor al esperado fueron los de Tierralta, Puerto Libertador y Valencia, en el departamento de Córdoba. En el Amazonas los municipios de Tarapacá y La Pedrera, y en el Guaviare los municipios de Calamar y El Retorno. Se observaron en casi todos los municipios del país valores bajos de SMR (esto sucede porque el número de casos observados fue de cero o porque los casos observados fueron menores a lo esperado).
En el evento malaria en 2005, los municipios que presentaron un valor alto para la tasa de morbilidad fueron El Morichal, en el departamento de Guainía; Calamar en Guaviare y Tierralta en Córdoba. En cuanto a municipios con valores medios de la tasa encontramos Pacoa, en Vaupés, Cumaribo en Vichada, Inírida en Guainía, Maní en Casanare, Puerto Libertador en Córdoba y Cáceres en Antioquia. Se observa en general un valor bajo de la tasa en casi todo el país. En el evento malaria en 2010 los municipios con valores altos para la SMR fueron Bagadó en Chocó y El Bagre en Antioquia. Con valores medios, Puerto Libertador y Cáceres en Antioquia, San José del Palmar en Chocó y Calamar en el departamento del Guaviare.
En el evento dengue en 2000, Valparaíso y Currillo en Caquetá presentaron valores altos para la SMR. En el evento dengue en 2005, los municipios San José del Palmar en Chocó, Cáceres en Antioquia y Tierralta en Córdoba, y en el evento dengue en 2010 tan solo el municipio de Cartagena del Chairá en Caquetá presentó un valor alto.
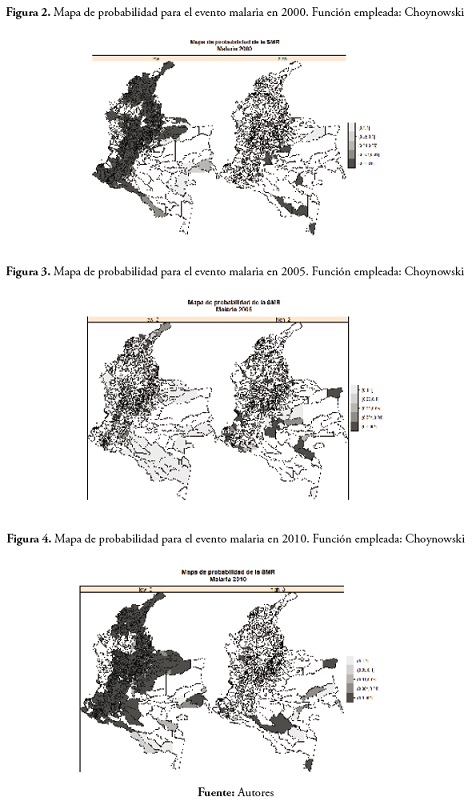
En cuanto a los mapas de probabilidad bajo el enfoque de Choynowski, nos centramos en el rango de probabilidad 0-0.001. En el evento malaria en 2000, los municipios observados con la probabilidad de presentar valores muy bajos para la tasa de morbilidad pertenecen a la región Andina, Arauca, Nariño, la región Caribe y La Guajira. En cuanto a los municipios que presentaron la probabilidad de obtener valores altos de la SMR fueron los localizados en el Amazonas, parte del Meta, Córdoba, Antioquia y Chocó. Estos resultados se aprecian en la figura 2
En el evento malaria en 2005 no fueron muchos los municipios con probabilidad de presentar valores bajos de la tasa de morbilidad. En cuanto a los municipios con valores altos para la SMR tenemos que estos se ubican principalmente en los departamentos de Meta, Vichada y Vaupés. Esto se puede apreciar en la figura 3
En el evento malaria en 2010, el comportamiento de la SMR se asemeja más al del año 2000; se apreciaron valores bajos de la SMR en la región Andina y valores altos en el Amazonas, Vichada, Antioquia, Chocó y Córdoba. Estos resultados pueden verse en la figura 1
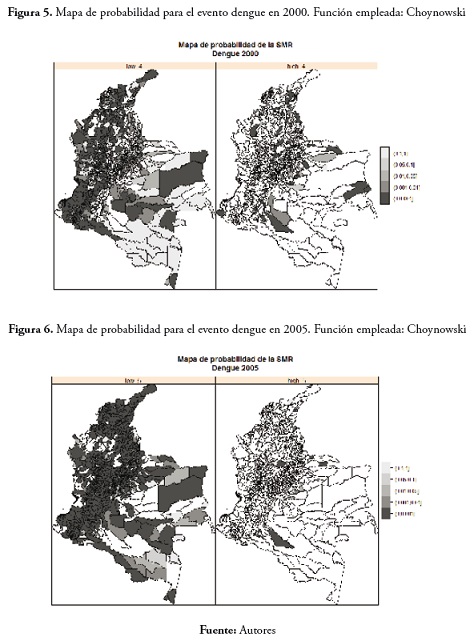
Del evento dengue en 2000 se observaron valores bajos en los municipios de la región Andina, pero también valores altos figura 5.
Del evento dengue en 2005, se observaron muchos municipios con valores bajos para la SMR 001 y muy pocos municipios con valores altos de la tasa. Estos resultados se pueden ver en la figura 6.
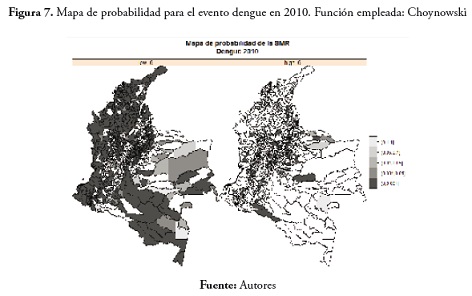
En 2010 se observó un comportamiento similar al del año anterior, pocos municipios con probabilidad de presentar valores altos para la SMR y muchos municipios del país con la misma probabilidad de presentar valores bajos de la SMR. Estos resultados se pueden apreciar en la figura 7.
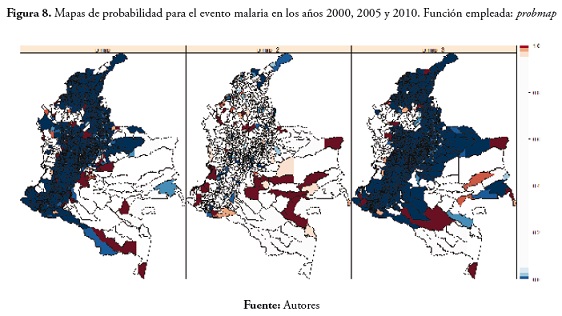
Los mapas de probabilidad obtenidos a partir de la función probmap dieron resultados muy similares a los obtenidos por la función de Choynowski. En el evento malaria se observa un comportamiento similar entre 2000 y 2010. Valores bajos de la SMR en la región Andina, el Caribe y los Santanderes (Estos municipios se ven de color azul oscuro en el mapa) y municipios con valores altos en la amazonia, Caquetá, Vaupés y Guainía (estos municipios se rojizos en el mapa). En el año 2005 se observan muchos menos municipios con probabilidad de presentar valores bajos de la SMR y nuevamente, los municipios con la mayor probabilidad de obtener valores altos se ubican en la Orinoquia, el choco, Antioquia y Córdoba.
Estos resultados se presentan a continuación en la figura 8.
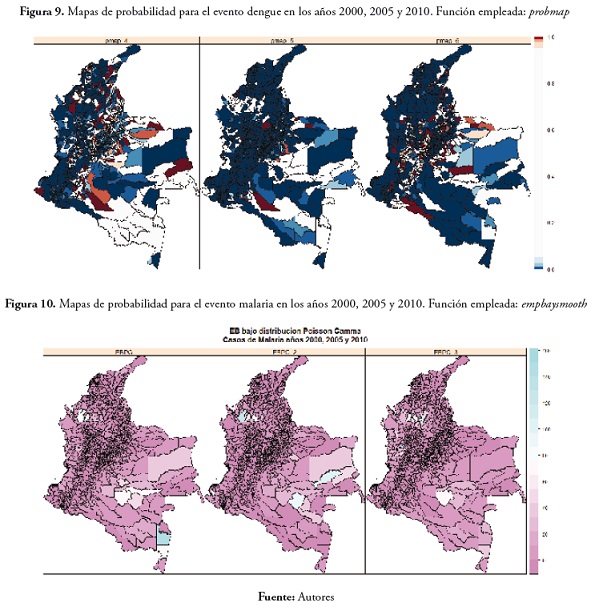
En el evento dengue se observó un aumento en el transcurso del tiempo en los municipios con probabilidad de obtener valores bajos de la tasas de morbilidad; en cuanto a los municipios con probabilidad de presentar valores altos de la SMR, se observó que no son siempre los mismos, caso contrario al que se había presentado para el evento malaria, en el que los municipios con probabilidad de presentar valores altos fueron casi siempre los mismos (figura 9).
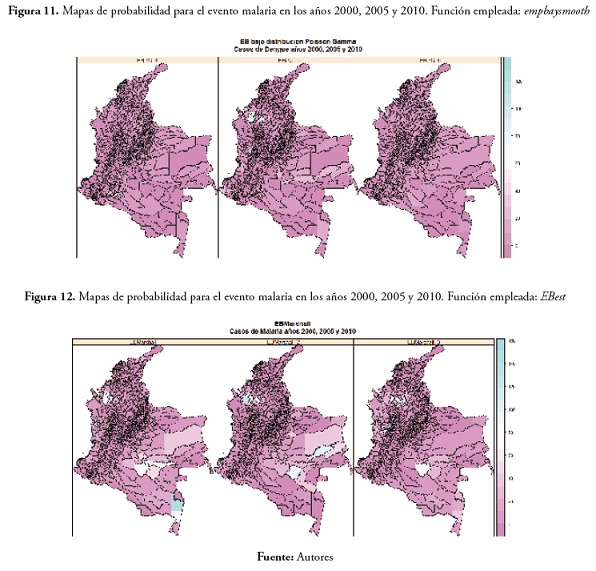
Los mapas de probabilidad, asumiendo una distribución Poisson gamma, dejaron ver para el evento malaria en los tres años una disminución en la cantidad de municipios con probabilidad de presentar valor alto en la SMR, aunque los municipios que sí la presentan se ubican (como ha sido una constante, sin importar la función empleada) en la regiones de la Orinoquia, el Amazonas, Córdoba y Chocó. A continuación se presentan estos resultados en la figura 10. (municipios en color verde con probabilidad de obtener valores altos de SMR).
En el evento dengue, todos los municipios presentaron valores bajos.
Por último, los mapas obtenidos a partir del enfoque propuesto por Marschall (recordemos que este asume que se conocen a priori la media y la varianza de los riesgos relativos), el cual no asume distribución alguna, mostró resultados similares a los presentados inmediatamente anterior; muy pocos municipios con probabilidad de presentar valores altos para la SMR en cualquiera de los dos eventos (los municipios con probabilidad de presentar valores altos de SMR se muestran en verde) ( figura 11 ).
En el evento malaria, los municipios que presentaron probabilidad alta de valores altos para la SMR fueron: Tierralta y Puerto Libertador en Córdoba, Cáceres en Antioquia, Tarapacá en el Amazonas, Calamar y Mirafiores en el Guaviare, Cumaribo en Vichada, Inírida y Barranco Mina en el Guainía y Tadó en el Chocó. Los resultados se pueden ver en la figura 12
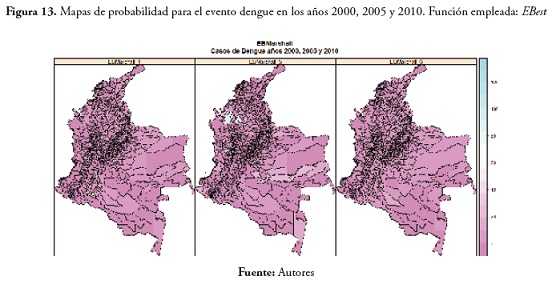
En cuanto al evento dengue, no hubo casos significativamente altos, excepto en 2005, en los municipios de Tierralta, en el departamento de Córdoba, Cáceres en Antioquia y San José del Palmar en el Chocó. Los resultados se pueden ver en la figura 13 .
Autocorrelación espacial y agregaciones de casos
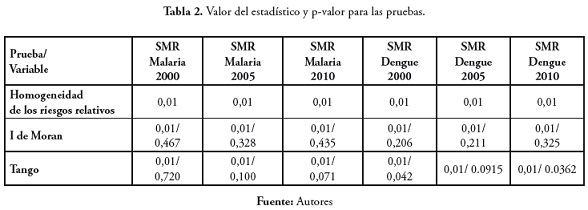
La prueba de homogeneidad de los riesgos relativos fue significativa para las seis variables, por lo que se rechazó la hipótesis nula de riesgos iguales. La prueba I de Moran fue significativa para las variables, por lo que se comprobó la existencia de una estructura espacial en la distribución espacial de las enfermedades dengue y malaria. El valor del estadístico fue positivo en los seis casos, lo cual sugiere que en la distribución espacial se casos los municipios con valores altos de SMR están rodeados de municipios que presentan este mismo comportamiento y municipios con tasas muy bajas de SMR tienen como vecinos municipios con valores bajos para la SMR. En cuanto a la prueba de Tango para agregaciones globales de casos, en las seis variables fue significativa, lo cual es una confirmación a la hipótesis de presencia de autocorrelación espacial en los casos de enfermedades, lo que ya había sido mostrado por el estadístico de Moran.
A continuación se presenta la tabla 2 con los resultados arrojados por las pruebas. Para cada prueba y variable se muestra el p-valor y en los casos del estadístico de Moran y Tango se presentan tanto el p-valor como el valor del estadístico.
Las pruebas se corrieron asumiendo una distribución de Poisson para el muestreo con 99 simulaciones y método de remuestreo paramétrico.
En cuanto a la prueba para agregaciones de casos bajo el enfoque de Besag y Newell´s, los resultados fueron:
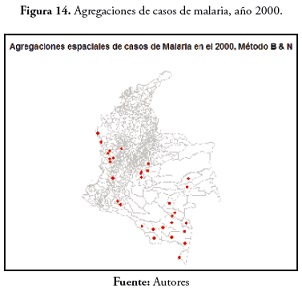
Para el evento de malaria en 2000, los municipios con agregaciones de casos fueron: Puerto Nariño, Tarapacá, La Pedrera, Puerto Arica, el Encanto, Puerto Alegría, La Chorrera, Puerto Santander, La Victoria y Miriti Paraná, todos en el departamento de Amazonas. El único municipio que no tuvo agregación de casos fue Leticia. En Antioquia encontramos el municipio de La Pintada; en el Caquetá, Albania y Solita; Padilla en el Cauca; Paratebueno en Cundinamarca; Atrato, Bahía Solano, El Cantón de San Pablo, Juradó, Nóvita, San José del Palmar y Sipi en el Chocó; El Castillo, El Dorado, San Carlos de Guaroa y San Juan de Arama en el Meta; Barranco Mina y Morichal Nuevo en Guainía; Carurú, Pacoa y Tataraira en el Vaupés (31 municipios). Estos resultados se pueden observar en la figura 14.
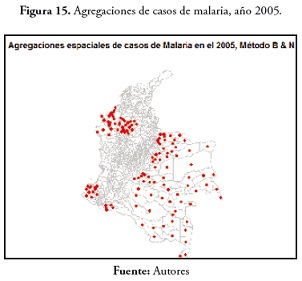
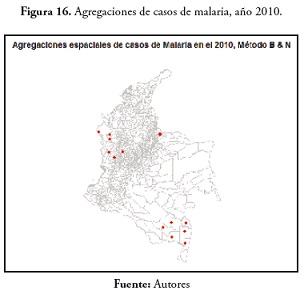
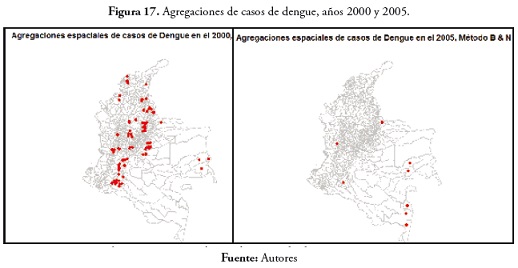
En el evento de malaria en 2005, 129 municipios mostraron agregaciones de casos, todos concentrados en la región Orinoquia, Amazonas, Chocó, Antioquia, Caquetá y Nariño (figura 15 ). En la variable malaria, en 2010 ( figura 16 ) hubo pocos municipios con agregaciones de casos (13), Miriti Parana, Puerto Santander, La Pedrera, Puerto Arica y Tarapacá en el Amazonas; Murindó y Vigía del Fuerte en Antioquia; Cubará en Boyacá; La Merced en Caldas; el cantón de San Pablo, Juradó y San José del Palmar en el Chocó.En el evento de dengue, en 2000, se registran 84 municipios en regiones más como la región Andina y los departamentos de Guainía, Antioquia y Choco. En 2005, solo 8 municipios presentaron agregaciones de casos: Tarapacá y la Pedrera en el Amazonas; Barranco Mina y Morichal Nuevo en el Guainía; Taraira en el Vaupés; Cubará en Boyacá, Solita en Caquetá y Nóvita en Chocó. Estos resultados están disponibles en la figura 17 .
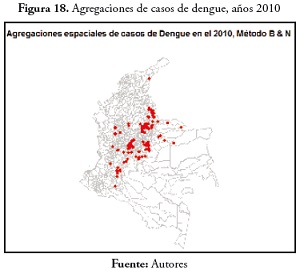
En el evento de dengue en 2010, cien municipios presentaron agregaciones de casos. Esta enfermedad presentó, al igual que en 2000, un comportamiento predominante en la región Andina. (Ver estos resultados en la figura 18)
CONCLUSIONES
Los estudios realizados para entender el comportamiento de una enfermedad pueden emprenderse de distintas formas, dependiendo de la información con la que se cuente y del enfoque que se quiera dar, que en muchos países como el nuestro no pasan de ser exclusivamente descriptivos. La metodología propuesta aquí no es nueva, por el contra- rio, en los países desarrollados ha sido implementada con buenos resultados. En el proyecto se intentó hacer una aproximación a estos métodos propuestos y desarrollados, obteniendo resultados satisfactorios, por lo menos, desde el enfoque de probar una metodología diferente a la que se emplea en el contexto nacional.
Los resultados proporcionados por los mapas de la tasa de morbilidad estandarizada y los mapas de significancia estadística, reflejaron un número importante de personas que aún en la actualidad (después de haber sido descubiertas las vacunas contra estas enfermedades) sufren de estas enfermedades. Estos mapas permitieron identificar aquellas regiones donde el riesgo relativo es significativamente mayor que 1 y cuyos casos observados de eventos dengue y malaria son mayores a lo esperado, teniendo en cuenta la población expuesta. Los departamentos que resultaron tener alta tasa de morbilidad fueron Chocó y Amazonas, aunque también se observaron municipios en Antioquia, Córdoba, Guainía, Vaupés y el Meta con reporte de casos significativos.
En conjunto los mapas de SMR y los mapas de agregaciones de casos mostraron que para el evento malaria los municipios con más altas tasas de morbilidad fueron Tarapacá, La Pedrera, Puerto Arica, Puerto Santander y Miriti Paraná en el Amazonas, así como El Cantón de San Pablo, Juradó y San José del Palmar en el Chocó. Estos resultados nos permiten discutir acerca de la eficiencia de las políticas en salud pública emprendidas por el Gobierno, que parecen no ser suficientes para mejorar las condiciones sanitarias en estas regiones, que son las más olvidadas, pobres y menos desarrolladas del país. En el caso del evento dengue las regiones con tasas altas fueron la Andina, Chocó y Guainía. Los municipios que resultaron ser los más afectados fueron Barranco Mina y El Morichal en el Guainía.
En cuanto a la distribución geográfica de las dos enfermedades, esta fue similar, aunque es común encontrar casos de dengue en regiones con mayor altura, con respecto a las regiones donde es frecuente encontrar casos importantes de malaria.
Las pruebas de autocorrelación espacial fueron significativas y positivas para ambos enfermedades en los tres años, lo que apoyó la idea de pensar en modelos de regresión que tuvieran en cuenta la distribución espacial del riesgo de estas enfermedades. El hecho de que estas pruebas fueran significativas y positivas es lógico en la medida en que corresponden con la etiología conocida de estas enfermedades. La distribución espacial de estos dos eventos y las pruebas mostraron que no es común encontrar regiones afectadas aisladas unas de otras, sino por el contrario, el comportamiento de estas muestran agregaciones espaciales en municipios vecinos, lo que corresponde con la propagación de estas enfermedades, la cuales son transmitidas solo por los vectores (mosquitos) y estos no se desplazan más de 3 km, pues tienen una vida no mayor de catorce días. Esto significa que cuando aparece un gran número de casos de dengue y malaria, esto se debe a una epidemia del mosquito, el cual se desarrolla en condiciones climatológicas especiales (regiones tropicales y subtropicales) y condiciones sanitarias deficientes (estos mosquitos se desarrollan en aguas empozadas). De esta forma, las preguntas más comunes relacionadas con la agregación de casos de una enfermedad fueron resueltas: estos tienden a ocurrir cerca de otros casos, lo cual sugiere un agente infeccioso, y los municipios con mayores números de casos en el transcurso del tiempo fueron los mismos, lo cual sugiere factores de riesgo ambiental (pues no se presentaron agrupaciones de casos en regiones inusuales).
En cuanto a los modelos de regresión, fueron probados uno sin estructura de correlación y otro con estructura (gaussiana, esférica, exponencial y lineal). Los modelos sin estructura espacial presentaron todas las variables significativas y valores muy altos para el AIC. La prueba de autocorrelación a los residuales de estos modelos fue significativa, mostrando la necesidad de incorporar efectos espaciales en ellos. En cuanto a los modelos con efectos espaciales (estructura de correlación gaussiana), ninguna variable fue significativa; los valores para la desviación estándar de los residuales del desvío fueron muy altos y los valores para el AIC y BIC no se obtuvieron por la forma de estimación de los parámetros (cuasiverosimilitud penalizada). El criterio de comparación entre los modelos fue el de la desviación estándar de los residuales del desvío, presentando los menores valores los modelos de regresión sin estructura espacial.
El hecho de que las covariables resultaran ser no significativas en los modelos con efectos espaciales, indica que el efecto que tienen estas sobre el fenómeno no es importante cuando la estructura de correlación presente en el fenómeno es muy fuerte, por lo cual se sugiere probar con otro tipo de variables. En cuanto a los altos valores para la desviación estándar de los residuales, se sugiere probar con modelos no tan globales, de tal manera que las variables representen mejor el fenómeno en estudio.
Por último, en el proceso de desarrollar el presente trabajo de grado los inconvenientes vinieron del acceso y la calidad de la información adquirida. En cuanto al acceso, los organismos públicos como es el Instituto Nacional de Salud, INS (que es la entidad encargada de manejar la información referente a la incidencia de una enfermedad por medio del Sistema Nacional de Vigilancia en Salud Pública, SIVIGILA), ponen demasiadas trabas, condiciones y papeleo para proporcionar información, aun cuando su uso tiene fines académicos. En cuanto a la calidad, el sistema por el que se recoge la información aún no asegura este atributo, por lo que el registro de casos presenta duplicidad o pérdida de información.
Referencias
- Bivand, R. (2011). Introduction to the North Carolina SIDS data set (revised). [Versión electrónica]. Disponible en: http://cran.r-project.org/web/packages/spdep/ vignettes/sids.pdf
- Bivand, R. y Pebesma, E. (2008). Applied Spatial data Analysis with R. UseR! Series, Springer.
- Breslow, N. y Clayton, D. (1993). Approximate inference in generalized linear mixed models. Journal of the American Statistical Association.
- Dobson, A. y Barnett, A. (2008). Introduction Generalized Linear Models. Texts in Statistical Science.
- Gotway, C. y Stroup, W. (1997). A generalized linear model approach to spatial data analysis and prediction. Journal of Agricultural, Biological and Environmental Statistics.
- Maldonado, D. y Bohórquez, M. (2011). Modelos de regresión espacial: una aplicación para datos de pobreza según necesidades básicas insatisfechas. (Tesis especialista), Universidad Nacional de Colombia, Departamento Estadística, Bogotá, Colombia.
- Manterola, A. (2006). Métodos de estadística espacial para evaluar la influencia de factores medioambientales sobre la incidencia y mortalidad por cáncer. (Tesis de doctorado), Universidad de Girona, Departamento de Economía, España.
- Organización Mundial de la Salud (2011). Declaración del Milenio. [En línea]. Disponible en: http:// www.undp. org/spanish/mdg/basics.shtml
- Organización Mundial de la Salud (2011). Closing the gap in a generation health equity through action on the social determinants of health. [En línea]. Disponible en: http:// www.who.int/hq/2008/WHOIERCSDH08.1eng.pdf
- Organización Mundial de la Salud (2011). Colombia, Health Profile. [En línea]. Disponible en: http:// www.paho. org/spanish/sha/prflcol.htm
- Instituto Nacional de Salud (2011). Informe Epidemiológico Nacional 2009. Enfermedades transmitidas por vectores. [En línea]. Disponible en: http:// www.ins.gov.co
- Organización Mundial de la Salud (2011). Paludismo [En línea]. Disponible en: http://www.who.int/topics/ malaria/es/
- Pfeiffer, D. y Robinson, T. (2008). Spatial Analysis in Epidemiology. Oxford, RU: Oxford University Press.
- Poh-chin, L. y Fun-Mun, S. (2009). Spatial Epidemiological approaches in disease mapping and analysis. Hardcover.
- Schabenberger, O. y Gotway, C. (2004). Statistical Methods for Spatial Data Analysis. Texts in Statistical Science.
- Waller, L. y Gotway C. (2004). Applied Spatial Statistics for Public Health Data. Wiley.
- Wedderburn, R. (1974). Quasi-likelihood functions, generalized linear models and the Gauss-Newton method. Biometrika.
- Wolfinger, R. D. y O’Connell, M. (1993). Generalized linear mixed models: a pseudo-likelihood approach. Journal of Statistical Computing and Simulation.
Licencia
La revista UD y la Geomática se encuentra bajo una licencia Creative Commons - 2.5 Colombia License.
Atribución - No Comercial - Sin Derivadas