Publicado:
2008-12-31Número:
Vol. 2 (2008)Sección:
ArtículosCalidad de datos en levantamientos topográficos
Palabras clave:
densidad de puntos, precisión, Teorema de Pappus, procesamiento, datos, relieve, modelo digital de terreno (es).Descargas
Referencias
Boada, A. Conceptos Básicos de Geoestadistica, Bogotá D.C., Instituto Geográfico Agustín Codazzi, CIAF, 2002.
López, S. y Estévez, C., Topografía, 2ª ed., Madrid (España), Ediciones Mundi-Prensa, 1996
Memorias Sexto Congreso Nacional de Topografía, Tercero Internacional, Sociedad Colombiana de Topógrafos, Medellín (Colombia), 1998.
Norma técnica colombiana TC-ISO 9001 (segunda actualización), Bogotá, ICONTEC, 2000.
Soberats, M., “Levantamientos Topográficos sin Croquis”, en: Topografía y Cartografía,Madrid (España), vol XV, núm 84., 1998.
Spiegel, M., Estadística – Serie Schaum, México, McGraw-Hill de México, 1970.
Swokowski, E. Cálculo con geometría analítica, México D.F., Grupo Editorial Ibero América, 1982.
Torres, A. y Villate, E. Topografía, 4ª ed., Bogotá (Colombia), Escuela Colombiana de Ingeniería, 2001.
Wonnacott, T., y Wonnacott, R., Introducción a la Estadística, 5ª ed., México, D. F., Editorial Limusa, S. A. de C.V., 1997.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Visitas
Descargas
Calidad de datos en levantamientos topográficos
Quality of Data in Topographic Raisings
Wilmar Darío Fernández Gómez
Tecnólogo en Topografía, ingeniero civil, magíster en Ingeniería – Infraestructura Vial
Docente tiempo completo, Facultad del Medio Ambiente y Recursos Naturales
Grupo de Investigación GEOTOPO
Enviar correspondencia a Wilmar Darío Fernández Gómez, Avenida Circunvalar Venado de oro, tel. 0571-3376981, wfernandez@udistrital.edu.co
Resumen
La motivación que conduce a este estudio radica en la necesidadde lograr un buen nivel de certidumbre en los resultadosque se obtienen cuando se efectúa un levantamiento topográfico conducente básicamente a la obtención de áreas yvolúmenes, variables muy comunes en la determinación decantidades en un proyecto de infraestructura. Volúmenes, yase traten estos de excavaciones, terraplenes o acopios en superficies que se pueden considerar irregulares, es decir, que noexiste una uniformidad en las pendientes que resultan entrepuntos que se obtienen aleatoriamente sobre la superficie deun terreno, mediante diversos procedimientos topográficos.
Palabras claves: densidad de puntos, precisión, Teoremade Pappus, procesamiento, datos, relieve, modelo digitalde terreno.
Summary
The motivation that leads to this study bases in the need ofachieving a good certainty level in the results that are obtainedwhen is effected a conducive topographic raising basically tothe areas and volumes obtainment, variable very common inthe determination of quantities in an infrastructure project.Volumes, already are tried these to quarries, terraces orcollections in surfaces that they can be considered irregularthat is to say that it does not exist a uniformity in the slopesthat result between points that are obtained ramdomlyon the surface from an area, through various topographicprocedures.
Key words: points density, precision, Theorem ofPappus, processing, data, relief, Digital Area Model.
Introducción
El objetivo principal de la topografía es conocerla forma y dimensiones de un terreno, estudiandoel relieve que lo conforma. En tal sentidoen la determinación de estos modelos deterreno, toman relevancia la metodología y losinstrumentos utilizados. Si se utilizan equiposconfiables de última tecnología, debidamentecalibrados, suponemos que las diferencias se encuentran en la metodología. Estas diferenciasredundaran al final en los resultados de los movimientos de tierra que allí se realicen.Para confirmar o desmentir este supuesto,se ha realizado una prueba de campo en donde, para la determinación del modelo delterreno se han utilizado densidades de puntosdiferentes y sobre estos dos modelos, se ha diseñado una vía, de la cual se ha determinadoel movimiento de tierra utilizando seccionestransversales cada 10, 5 y 2 metros, para luego comparar los volúmenes resultantes.Es claroque en las curvas horizontales de carreteras,canales, terraplenes longitudinales, etc., lassecciones transversales son verticales comoen las tangentes, pero ya no paralelas, pues toman una dirección radial. En este caso la cubicación, por el sistema del área media entresecciones multiplicado por la distancia entreellas, o incluso el sistema prismoidal ocasionaun error mayor debido a la posición relativadel eje del proyecto respecto al centro decurvatura, por lo que es másconveniente multiplicarla sección promedio por una longitudmedia entre secciones, que resulta ser la longitudde arco, producto de considerar las distanciasradiales (horizontales) de los centroides decada sección involucrada.
Metodología
El trabajo corresponde a parte experimental que, partiendo de la ejecución de levantamientos topográficos clásicos en prediosde la Universidad Distrital-Sede Vivero,se desarrollaron mediante procedimientos topográficos de poligonales y radiación desdelos vértices de la poligonal, teniendo encuenta la densidad de puntos por cada 100 metros cuadrados de área.Con base en ellos se realizó el procesamientode los datos hasta encontrar los modelosdigitales del terreno TIN (Triangulateregular Network) que definen el relieve encada caso.
Los terrenos levantados corresponden ala caracterización de tipos de terreno montañoso y escarpado, según la clasificación propuestapor el Instituto Nacional de Vías INVIAS, y sobre ellos se realizó un diseñogeométrico de una carretera. Con esta información se generó el diseño con ayuda de diferente software de ingeniería apropiados para el diseño de carreteras y se analizaron los resultados de área y volúmenes arrojados por los diferentes algoritmosde cálculo. Posteriormente se compararon resultadosy se hizo una correlaciónestadísticade tal manera que condujeran a generar conceptos, parámetros, formulaciones y criteriostécnicos que agilizaran la asimilación de las nuevas tecnologías en materia de levantamientos no solo topográficos, también de cartografía, arquitectura, etc. Dependiendo de su propósito o finalidad,los modelos y proyectos pueden ser generadosen tiempos relativamente breves con los métodos clásicos y apoyados en las modernas tecnologías. En particular, el trabajo genera resultadospartiendo de las aplicaciones en la ingeniería civil, pues el mayor desempeño de un profesionalde la topografía en la República de Colombia secentra en esta rama de la ingeniería.
Modelo digital del terreno
Un modelo digital del terreno se puede definir como una adecuada aproximación matemática del terreno, expresada mediante una base de datos topográfica (x, y, z), con lacual se puedan obtener por interpolación lascoordenadas de cualquier otro punto. Las mediciones topográficas precisas para definir las coordenadas de los puntosdel modelo se capturan con tal densidad ydistribución como para que las formas topográficas, obtenidas directamente o por interpolacióntengan la precisión impuesta allevantamiento. En cuanto a sus detalles planímetros,está en función de la precisión inherentey a la escala requerida, y en los altimétricossegún el estándar de precisión quese imponga a los puntos de altitud, desde loscuales, y por los criterios usuales de interpolación,se podrán derivar curvas de nivel o cualquierotro procedimiento de representación del relieve.Los métodos topográficos son los mismos
que los usados en topografía convencional, únicamente se modifica la forma deltratamiento de los datos y su captura se realiza pensando en tal consideración. El método más operativo para crear esta base de datoses el que se conoce bajo la denominación de TIN (Triangulate Irregular Network), el cualestá constituido por triángulos irregulares cuyos vértices definen todos los cambios significativos que es preciso medir para lograr unacorrecta definición topográficadel terreno.Planimetricamente es fácil la captura de los puntos necesarios para definir sus formas
topográficas (naturales o artificiales), lo mismoque plantear sus relaciones topológicas
mediante la asignación de estructura de información.La altimetría implica mayor complejidad, tanto por la dificultad que entrañaa elección de los puntos notables del terrenopara la correcta definición de la superficie poliédrica que se ajuste a la superficie del terreno,como por la definición de aquellos elementosque introducen cambios bruscos en su representación. Estas formas topográficassingulares constituidas por la red de drenaje,senderos, pie y corona de taludes, vaguadas,etc. se conocen con el nombre de líneas derotura o líneas de quiebre y constituyen unaparte fundamental para la definición del relievey comprenden todos aquellos elementoslineales que presentan cambios de pendiente ydirección en su desarrollo.Las líneas de rotura son elementos geométricos y, como tal, tienen que definirse mediante la asignación de códigos de identificación y además imponer una estructura secuencialque permita identificar su estructura geométrica.Todas estas líneas se introducen en el proceso de cálculo de forma independiente, es decir,definiendo su punto inicial y final, así como todoslos puntos intermedios de forma correlativa. Con base en estas estructuras se ajusta el relieve de los puntos altimétricos que definen las
superficies poliédricas inscritas. Los puntos definidos planimetría y altimétricamentede forma aleatoria sirven paragenerar los triángulos que unen los vérticescontiguos mediante líneas de pendiente constante. La definición de estos triánguloscompleta la estructura topológica que es precisoimponer al conjunto de puntos que definen el relieve de la zona. De la multitud detriángulos que se pueden construir los másadecuados son los máspróximos a los equiláteros,puesto que estos son los que se han seleccionado de forma secuencial en la tomade datos como los más correctos para la definicióndel relieve, tanto por sus valores altimétricoscomo por su ubicación en la zona.Por tanto, la definicióntopológica de la basede puntos aleatorios deberá responder a talconsiderando.Una de las muchas estructuras topológicasque cumplen este requisito son los triángulosde Delaunay. El método Delaunay constituye una definicióntopológica y un métodode interpolación, que a partir de una red depolígonos convexos (poligonos de Thiessen)cumplen la condición de que todos los puntosde su interior sean los máspróximos alpunto de control. Estos polígonos se construyenobteniendo la mediatriz entre cada dospuntos de control próximos. Con la intersección de cada tres se hallan los circunveniros, puntos que constituyen los vértices de estasfiguras. A partir de estos polígonos y medianteun ajuste en tres dimensiones se obtiene latriangulación de Delaunay, la cual impone lacondición de que el circum-circulo de cualquierade los triángulos no contenga ningúnotro punto en su interior. La base de datos topográficosasí definidaconstituye una de las unidades fundamentalesde los sistemas de ingenieríay su composición debe responder en cuanto a precisióny densidad a los requerimientos del proyectopara la cual se ha generado. El paso de lasformas discretas que definen dichas estructurasde puntos a formas continuas se realizamediante algoritmos de interpolación. Ahorabien, estas funciones serán tanto más complejasen cuanto mayores sean las zonas a rellenar,caso que no debe presentarse en los modelos de cierta precisión, al ser contradictorio
tal procedimiento con la tolerancia exigida.La precisión del MDT (Modelo Digital del Terreno) depende principalmente de la geometríay del intervalo del muestreo. La mejor geometría se obtiene a partir de triángulosirregulares, al ser esta la forma más simple yque mejor se puede ajustar a la topografíadelterreno, mientras que el intervalo de muestreo depende fundamentalmente de la precisión del modelo, y esta se fija con el criterio de quelas superficies definidas por los triángulos formadosse ajusten de tal forma al terreno que la separación entre el modelo analítico definidopor el MDT y las formas topográficas sea inferiora la precisión impuesta. En los modelos digitalesdel terreno de aplicación en Ingeniería su densidad y distribución deben asegurar lastolerancias impuestas para la determinaciónde sus coordenadas.
En general, la experiencia ha demostradoque los algoritmos de interpolaciónno tienen
una incidencia positiva en cuanto a la mejora de precisiónde un modelo, sino en cuanto a ladensidad de puntos y la correcta elección de las línea de rotura lo que más condiciona a esta, yque las funciones sencillas son las más adecuadas para los modelos topográficos. Es importante resaltar que este tipo demodelos obtenidos por topografía digital sonlos mas indicados para la fase del proyecto,donde pueden competir en calidad y costocon otras técnicas de levantamientos. No obstante, si la superficie de la zona se hace inabordableeconómicamente por tales métodos,será preciso recurrir a los procedimientos fotogramétricos,hasta llegar a una reducción de lazona de actuación del proyecto que permitaeste tipo de procedimiento.Hoy en día, se está aceptando que, pormétodosfotogramétricos, difícilmente se puedanalcanzar precisiones altimétricas superioresa los 15-20 cm, frente a los 1-2 cm, factiblesde conseguir por métodosgeométricos, y queestos rangos de precisión tienen una notableincidencia en la ejecución del proyecto aplicandosistemas de Ingeniería. Con estos procedimientos,la definición de rasantes, secciones,etc., se realiza por métodos grafico-numéricoscon toda precisión. A ello debe tender el levantamiento topográfico, además de las ventajasque se puedan derivar en las fases del replanteo,al actuar directamente sobre el terreno.
Calidad de datos
“Calidad es el grado en el que un conjuntode características inherentes de un servicio oproducto, cumplen con los requistos”3 (inherente:existe en algo, como una característica permanente). El termino calidad se refiere al conjuntode características inherentes a un producto oservicio que lo hacen apto para su uso (Andrade,2006).La calidad es una característica cualitativade algo que supone su excelencia y su certeza,cumpliendo una serie de requerimientoso normas, pero el hecho de que sean los requisitos mínimos y que el producto los cumpla no significa que este tenga calidad
cuando las expectativas del usuario son otras,cumpla con los requisitos mínimos para serusado, dependiendo del usuario y de las expectativascon que este lo use, lo puede calificar como de baja, media o alta calidad. La calidad de un dato topográfico suponela intervención de procesos y recursos,que deben ser óptimos para que “el dato” seafiel a la realidad, dependiendo del uso que sequiere dar.Es necesario en topografía reconocerque la calidad se refiere no solo a la precisión,entendida como el grado de acercamiento ala realidad, en este caso a la determinación delas coordenadas de cada punto, también involucratodos los procesos y procedimientosque intervienen en su obtención.
El dato para que sea necesario debe ser:
• Preciso
• Confiable
• Determinante
• Suficiente
Para su determinación debe haber:
• Personal calificado
• Tecnología apropiada para ladeterminación
• Tecnología apropiada para elprocesamiento
El control de cada uno de los procesospuede estar inmerso en un sistema de gestiónde calidad, siguiendo lineamientos, porejemplo, de las normas ISO 9000.
Área de estudio
Para el presente proyecto, en particular, paraefectuar las pruebas de los programas informáticosa los que ya se ha hecho referenciase hizo la selección de los terrenos,buscandoreunir unas característicasmínimas con elobjetivo de poder realizar en ellos los levantamientos topográficos planteados; estos terrenosson:
El terreno montañoso que se ha denominadoTerreno 1, seleccionado para el presenteproyecto se encuentra ubicado en lacolindancia de las vias circunvalar y Av. Venadode oro, el cual hace parte de la UniversidadDistrital sede “El Vivero”. Presenta unapendiente en el sentido oriente-occidente superior al 10%, con un área aproximada de una ha (figura 1).El terreno ondulado seleccionado que seha denominado Terreno 2 se encuentra ubicadoen la colindancia de la Universidad Distrital,sede “El Vivero”, costado sur, y en el sentidooriente –occidente con la vía Venado deoro y la parte alta de la montaña. Dicho prediopresenta una pendiente promedio de entreel 3 y 7%. Con un área aproximada de unaha (fi gura 1). Con el fin de que los levantamientosqueden georeferenciados al sistema de coordenadas del Instituto GeográficoAgustínCodazzi (IGAC) se tomó como punto de amarreel CD 554 ubicado en la parte superior delTeatro al aire libre “la Media Torta”, en el andéninmediato a la avenida Circunvalar y cuyascoordenadas planas son: 1001302.403E,1000346.927N, y cota 2674.561. Para orientarcorrectamente el levantamiento a partirdel CD 554 se tomó azimut hacia el cerro deMonserrate y específicamente al centro de lacruz situada en la cúpula de la iglesia ubicadaallí, y cuyo valor es de 59o01’58”
Procesamiento
Para llevar a efecto el objetivo planteado seprocedió a elaborar los modelos digitales delos terrenos en estudio, de acuerdo con losesquemas que se presentan a continuación. A fin de obtener la información planteada,además de los modelos digitales, se handiseñado dos tramos de vía: el primero en elTerreno 1, paralelo a la vía existente en el tramoaledaño a la media torta en una longitudde 90 metros, el cual incluye dos tramos linealesy uno en curva; el segundo en un tramototalmente en curva, también en unalongitud de 90 metros, lo que permite trabajarlos modelos en un caso típico de víasen planta. En lo respectivo al nivel de diseñopara efectos de la experiencia se ha supuestoque las vías planteadas presentan una pendientede 0% longitudinalmente, y lo mismose ha considerado transversalmente, a fin defacilitar el objetivo final: las áreas transversalesy los volúmenes. La sección típica que resulta se esquematiza en la figura 2.
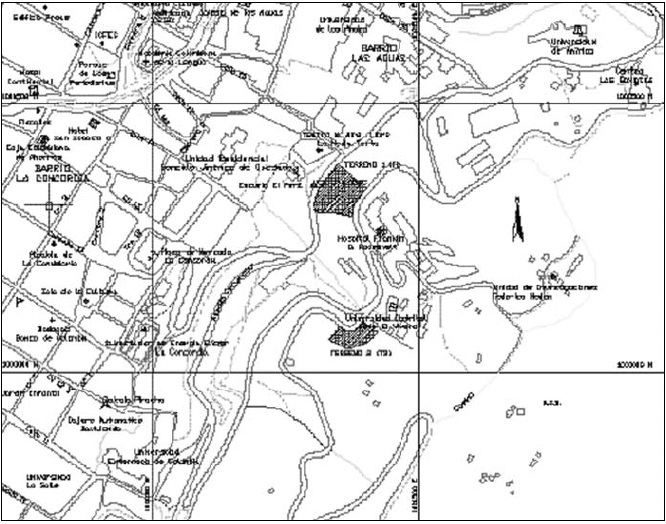
Figura 1. Localización de área de estudio
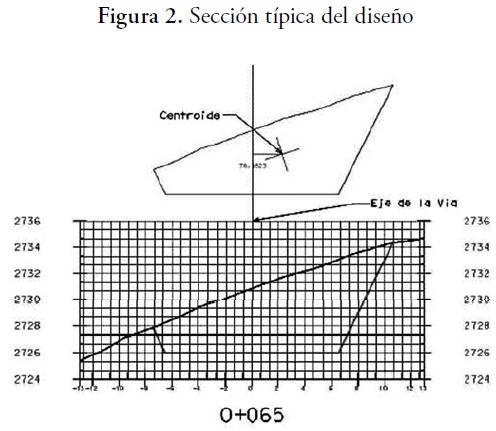
Figura 2. Sección típica del diseño
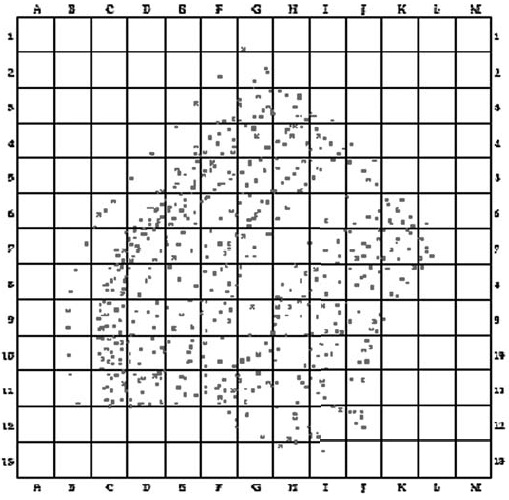
Figura 3. Nube de puntos T1

Figura 4. Modelo TIN T1
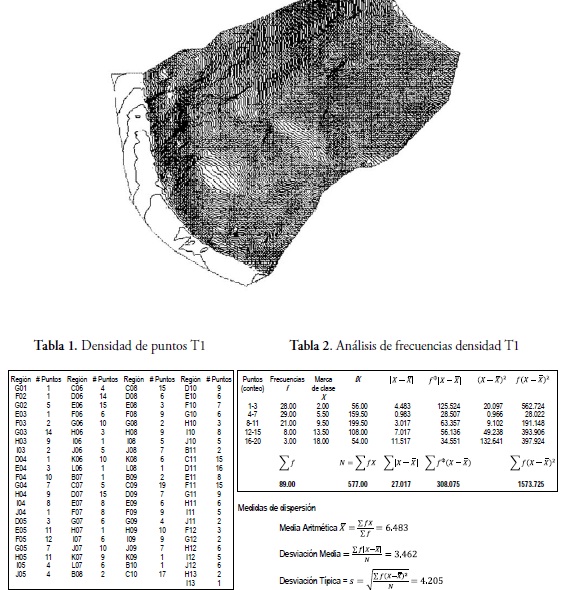
Figura 5. Perspectiva T1
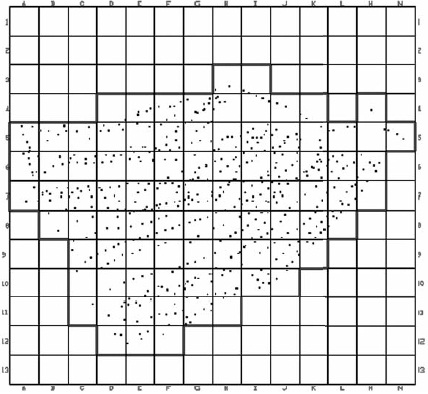
Figura 6. Nube de puntos T2
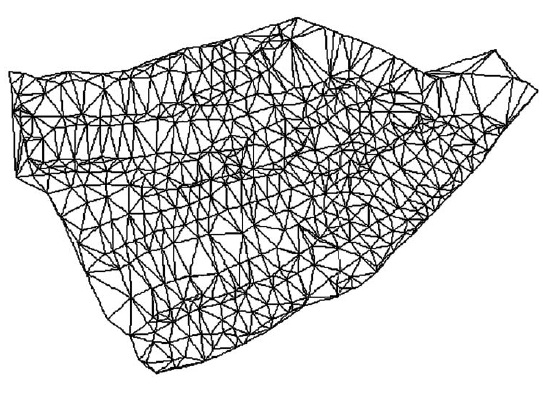
Figura 7. Modelo TIN T2
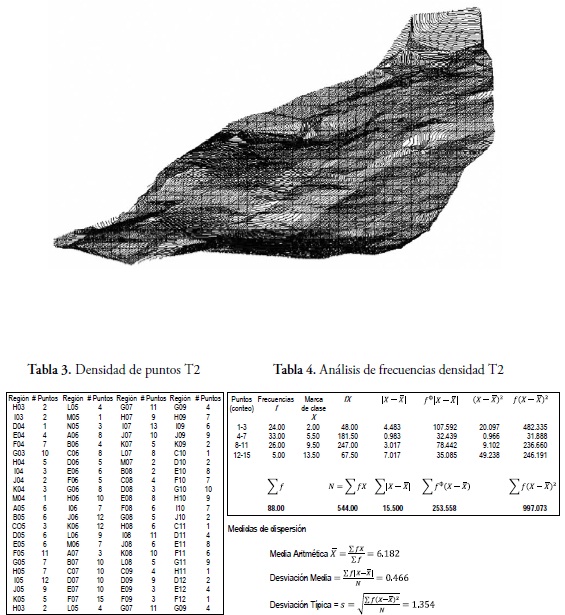
Figura 8. Perspectiva T2
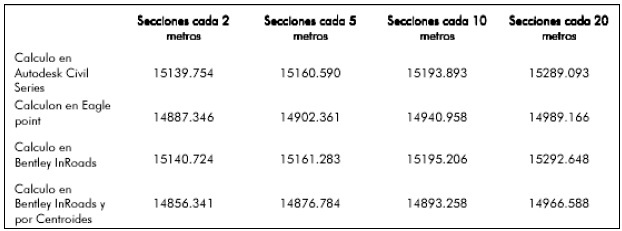
Comparación de resultados
Como puede observarse en las tablas de resultados,la diferencia entre cada uno de losvolúmenes calculados en el mismo softwarecon diferente espaciamiento entre seccionesson muy similares y no hay una desviaciónmayor a 100 metros cúbicos. Si se analiza la figura 9, para el terreno1, clasificado como montañoso, existeun comportamiento similar de las líneas detendencia, el rango de separación no superaen 300 metros cúbicos de desviación, lo queequivale al 2% del volumen calculado, estoindica que los algoritmos son muy parecidos,pero si se muestra una marcada diferencia alcalcularlos con secciones paralelas a lo largodel eje (secciones transversales) y seccionestransversales en recta y radiales en curva ycalculo por centroides. En el caso de la líneade tendencia por centroides, arroja el menorvalor de los volúmenes calculados.
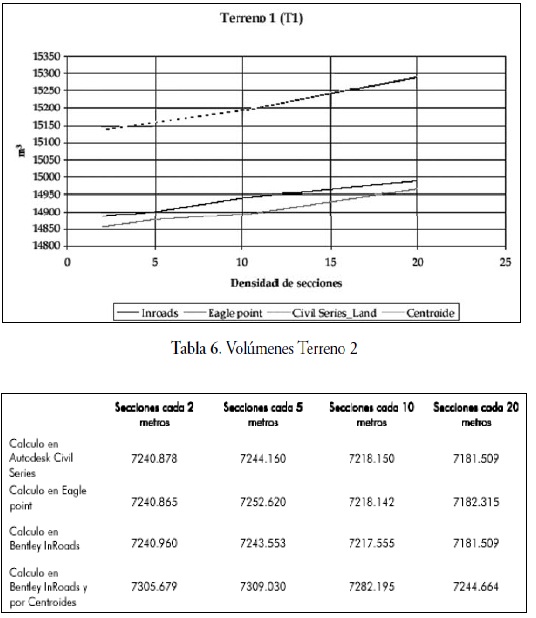
Figura 9. Volúmenes Terreno 1
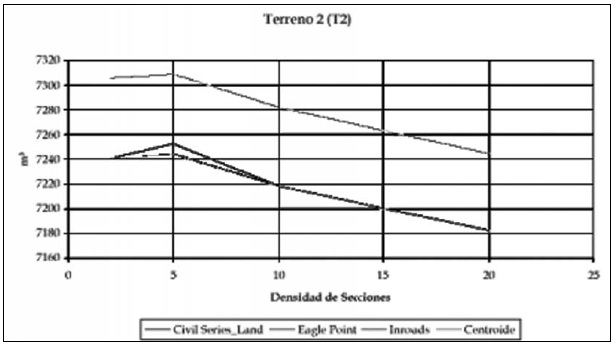
Figura 10. Volúmenes Terreno 2. Sin embargo, comparando los valores de volumenarrojado por todos los algoritmos de cálculo son muy similares, no exceden susdiferencias igualmente en un 2% en volumen, pero hay que considerar que es unejercicio en una longitud de carreteras no mayor a 100 m, en proyectos reales ese 2% envolúmenes totales supriores a 20.000 metros cúbicos, son costos considerables.
En el terreno 2, clasificado como ondulado,observa un comportamiento muy similaral caso anterior, es decir que la tendenciade las curvas se mantiene paralela. Llama laatención que el cálculo por centroides queconsideramos el más cercano a la realidad,seencuentra ahora como la curva de máximovalor de volumen.
Reflexiones
El ingeniero debe tener la capacidad deaprender y desaprender conocimientos,métodosy aplicaciones revaluadas.La calidad de un dato no se obtiene conel argumento “Es que siempre lo he hecho asíy así debe ser”.Aunque la tecnología permite optimizaren tiempo y precisión no es la que prima enla concepción de los proyectos.
Conclusiones
En general, la experiencia ha demostradoque los algoritmos de interpolación en unmodelo digital no tienen una incidencia positivaen cuanto a la mejora de precisión deun modelo, sino más bien que es la densidadde puntos y la correcta elección de las líneasde rotura lo que más condiciona a esta, y quelas funciones sencillas son las más adecuadas para los modelos topográficos. La certidumbre en la calidad del dato esdirectamente dependiente del conocimientoexperto y de los recursos tecnológicos, elementoque aun aquí no hemos evaluado. El procesamiento influye en los resultados,los paquetes de software aplican algoritmosmuy similares, pero en realidad y en proyectosreales, largos y complejos, la aproximación de cantidades si difiere ostensiblemente.
Bibliografía
Boada, A. Conceptos Básicos de Geoestadística, Bogotá D.C., Instituto GeográficoAgustínCodazzi, CIAF, 2002.
López, S. y Estévez, C., Topografía, 2a ed., Madrid (España), Ediciones Mundiprensa,
1996
Memorias Sexto Congreso Nacional de Topografía,Tercero Internacional, SociedadColombiana de Topógrafos, Medellín (Colombia),1998.
Norma técnica colombiana TC-ISO 9001 (segundaactualización), Bogotá, ICONTEC,
2000.
Soberats, M., “Levantamientos Topográficossin Croquis”, en: Topografía y Cartografía,Madrid (España), vol XV, num 84., 1998.
Spiegel, M., Estadística– Serie Schaum, México,McGraw-Hill de México, 1970.
Swokowski, E. Calculo con geometríaanalítica,México D.F., Grupo Editorial Ibero América,1982.
Torres, A. y Villate, E. Topografía, 4a ed., Bogotá(Colombia), Escuela Colombiana de Ingeniería,2001.
Wonnacott, T., y Wonnacott, R., Introducción ala Estadística, 5a ed., México, D. F., EditorialLimusa, S. A. de C.V., 1997.
Licencia

Revista de Topografía AZIMUT is licensed under a Creative Commons Reconocimiento-NoComercial-SinObraDerivada 2.5 Colombia License.

