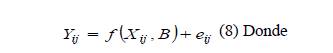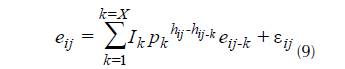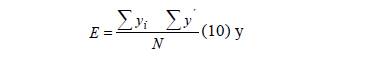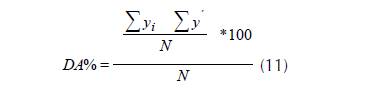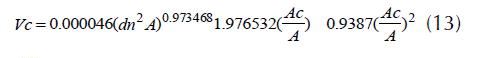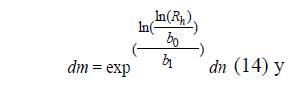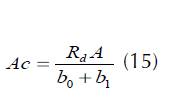DOI:
https://doi.org/10.14483/2256201X.11965Publicado:
01-01-2018Número:
Vol. 21 Núm. 1 (2018): Enero-JunioSección:
Artículos de investigación científica y tecnológicaEcuaciones de volumen total y de razón para estimar el volumen comercial de Swietenia macrophylla King
Total volume and ratio equations to estimate the commercial volume of Swietenia macrophylla King
Palabras clave:
forest harvesting, cubication, timber products, volume table (en).Palabras clave:
aprovechamiento forestal, cubicación, productos maderables, tabla de volumen (es).Descargas
Referencias
Albrecht, H., Belisle, M., Caballero, C., Forster, R., Galletti, H., Lacayo, O., Robinson, D., & Ortiz, S. (2002). Comunidades forestales y el mercado de maderas tropicales poco comerciales de Mesoamérica. México, D. F.: Ed. Durece S. A. 158 p
Alder, D. (1980). Estimación del volumen forestal y predicción del rendimiento con referencia especial a los trópicos. vol. II – Predicción del rendimiento. Estudio FAO: Montes 22/2. Roma, Italia: FAO. 80 p.
Apodaca-Martínez, M., Curiel-Alcaraz, G.M., Mendoza-Briseño, M.A., Vargas-Mendoza, M., Valdez, H.I.J., & Platas, R.D.E. (2014). El plan costa como una mejor opción de manejo para especies tropicales de Jalisco. Revista Mexicana de Ciencias Forestales, 5(22), 10-25.
Bailey, R.L. (1995). Upper-stem volumes from stem-analysis data: An overlapping bolt method. Canadian Journal of Forest Research, 25, 170-173. DOI: https://doi.org/10.1139/x95-020
Balzarini, M.G., González, M.L., Tablada, F., Casanoves, J., Di Rienzo, A., & Robledo, C.W. (2008). Infostat, manual del usuario. Córdoba, Argentina: Editorial Brujas. 336 p.
Barrena, B., Dancé, C., & Sáenz, T.D. (1986). Metodología para la selección de ecuaciones de volumen. Revista Forestal del Perú, 13(2), 1-10.
Barrio, A.M., Álvarez, G.J.G., & Díaz-Maroto, H.I.J. (2004). Elaboración de una tarifa con clasificación de productos para Quercur robus L. en Galicia basada en un modelo de volumen porcentual. Investigación agraria. Sistemas y recursos forestales, 13(3), 506-517.
Barrios, A., López, A.M., & Nieto, V. (2014). Predicción de volúmenes comerciales de Eucalyptus grandis a través de modelos de volumen total y de razón. Colombia Forestal, 17, 137-149. DOI: https://doi.org/10.14483/udistrital.jour.colomb.for.2014.2.a01
Barrio, M., Sixto, H., Cañellas, I., & González, F. (2007). Sistema de cubicación con clasificación de productos para plantaciones de Populus x euramericana (Dode) Guinier cv. ‘I-214’ en la meseta norte y centro de España. Investigación Agraria: Sistemas y Recursos Forestales, 16, 65-75.
Casnati, C. R., Mason, E.M., Woollons, R., & Resquin, F. (2014). Volume and taper equations for P. taeda (L.) and E. grandis (Hill ex. Maiden). Agrociencia Uruguay, 18(2), 47-60.
Cao, Q., Burkhart, H., & Max, T. (1980). Evaluation of two methods for cubic volume prediction of loblolly pine to any merchantable limit. Forest Scices, 26, 71-80.
Chapela, F. (2012). Estado de los bosques de México. México, D.F.: Consejo civil mexicano para la silvicultura sostenible A.C. 217 p.
Chauchard, L., & Sbrancia, R. (2005). Funciones de razón para la estimación de los volúmenes maderables de Pino radiata en el País Vasco. Investigación Agraria: Sistemas y Recursos Forestales, 14,185-194. DOI: https://doi.org/10.5424/srf/2005142-00883
Convención sobre el Comercio Internacional de Especies Amenazadas de Fauna y Flora Silvestres (Cites). (2016). Apéndices I, II y III: En vigor a partir del 4 de abril de 2017. Recuperado de: https://cites.org/esp/app/appendices.php
Concari, S.B. (2001). Las teorías y modelos en la explicación científica: implicaciones para la enseñanza de las ciencias. Ciencia y educación, 7(1), 85-94.
Cruz, C.F., Mendía S.R., Jiménez F.A.A., Nájera L.J.A., & Cruz G.F. (2016). Ecuaciones de volumen para Arbutus spp. (madroño) en la región de Pueblo Nuevo, Durango. Investigación y Ciencia, 24(68), 41-47.
Da Cunha, T.A., & Guimaraes, F.C.A. (2009a). Modelo de regresión para estimar el volumen total con corteza de árboles de Pinus taeda L. en el sur de Brasil. Nota Técnica. Kurú: Revista Forestal (Costa Rica), 6(16), 1-15.
Da Cunha, T.A., Vargas, M.J.O., & Escalier, H.M. (2009b). Ajuste y selección de modelos de regresión para estimar el volumen total de árboles. Documento técnico n.° 5-2009/ Proyecto de Manejo de Bosques en Bolivia (Fomabo). Cochabamba, Bolivia: Escuela de Ciencias Forestales de la Universidad Mayor de San Simón. 28 p.
Escuela Nacional de Ciencias Forestales-Organización Internacional de las Maderas Tropicales (Esnacifor-OIMT). (2003). Guías silviculturales de 23 especies forestales del bosque húmedo de Honduras. Proyecto PD 022/99 Rev.2 (F) Estudio de comportamiento de especies maderables Nativas con Importancia Comercial del Bosque Húmedo tropical en Honduras. Siguatepeque, Comayagua, Honduras: Esnacifor-OIMT. 261 p.
Organización de las Naciones Unidas para la Alimentación y la Agricultura (FAO). (2017). Conjunto de Herramientas para la Gestión Forestal Sostenible (GFS). Recuperado de: http://www.fao.org/sustainable-forest-management/toolbox/modules/silviculture-in-natural-forests/basic-knowledge/es/
García, E. (2004). Modificaciones al Sistema de clasificación climática de Köppen. Serie 6. México, D.F.: Instituto Nacional de Geografía-Unam. 98 p.
García, M.J.J., Velarde, R.J.C., Hernández, R.J., García, C.X., Muñoz, F.H.J., & García, E.G.G. (2013). Ecuaciones para determinar el volumen en pie para árboles de Pinus michoacana Mtz. y Pinus michoacana var. Cornuta Martínez, en dos municipios de Michoacán. Ciencia Nicolaita, 58, 67-89.
Gilabert, H., & Paci, C. (2010). An assessment of volumen-ratio funtions for Eucalyptus globulus and E. nites in Chile. Ciencia e Investigación Agraria, 37(1), 5-15. DOI: https://doi.org/10.4067/S0718-16202010000100001
Hernández-Ramos, J., De los Santos-Posadas, H.M., Valdéz-Lazalde, J.R., Tamarit-Urias, J.C., Ángeles-Pérez, G., Hernández-Ramos, A., Méndez-Lopez, B., & Pedizzi, A. (2017). Estimación del volumen comercial en plantaciones de Eucalyptus urophylla con modelos de volumen total y de razón. Agrociencia, 51, 561-580.
Hernández-Ramos, J., Hernández-Ramos, A., García-Cuevas, X., Martínez-Salvador, M., & García-Espinoza, G.G. (2016). Funciones de perfil para árboles de Swietenia macrophylla King en Quintana Roo, México. Revista Mitigación del Daño Ambiental Agropecuario y Forestal de México, 2(2), 151-157.
Hernández-Ramos, J., Hernández-Ramos, A., García-Magaña, J.J., García-Cuevas, X., García-Espinoza, G.G., Muñoz-Flores, H.J., & Olvera-Delgadillo, E.H. (2017). Sistema compatible de ahusamiento-volumen comercial para plantaciones de Pinus greggii Engelm. en Hidalgo, México. Revista Mexicana de Ciencias Forestales, 9(39), 59-70.
Honner, T.G. (1967). Standard volume tables and merchantable conversion factors for the comercial tree species of central and eastern Canada. Information Report FMR-X-5. Forest Management Research and Service Institute. 162 p.
International Business Machines (IBM). (2011). IBM SPSS Statistics Base 22. Armonk, N.Y. EE. UU.: IBM Corporation. 211p.
Magaña, T.O.S., Torres, R.J.M., Rodríguez, F.C.A., Aguirre, D.H., & Fierros, G.A.M. (2008). Predicción de la producción y rendimiento de Pinus rudis Endl. en Aloapan, Oaxaca. Madera y Bosques, 14(1), 5-19.
Martínez-González, M.A., Sánchez-Villegas, A., & Faulin-Fajardo, J. (2006). Bioestadística amigable. 2da edición. Barcelona: Editorial Díaz de Santos. 919 p.
Montes de Oca, C.E., Rojas, M.J.C., & Corral, R.S. (2011). Modelos de ahusamiento para Pinus leillophylla en la localidad de Chavarría Nuevo, Durango, México. InterSedes, 12(24), 129-135.
Mora, F., & Hernández, W. (2007). Estimación del volumen comercial por producto para rodales de teca en el pacífico de Costa Rica. Nota Técnica. Agronomía Costarricense, 31(1),101-112.
Moras, G., & Vallejos-Barra, O.S. (2013). Tabla de volumen para árboles individuales de Eucalyptus globulus ssp. Globulus cultivados en la región sur de Uruguay. Agrociencia Uruguay, 17(2), 11-24.
Muñoz, F.H.J., Velarde, R.J.C., García, M.J.J., Sáenz, R.J.T., Olvera, D.E.H., & Hernández, R.J. (2012). Predicción de volúmenes de fuste total para plantaciones de Pinus greggii Engelm. Revista Mexicana de Ciencias Forestales, 3(14), 11-22.
Murray, R.S. (1985). Estadística: teoría y 875 problemas resueltos. Serie Schaum. México, D.F.: Editorial McGraw-Hill. 357 p.
Negreros-Castillo, P., & Martínez Salazar, I. (2011). Crecimiento y regeneración avanzada de Lysiloma latisiliquum (L.) Benth. en una selva de Quintana Roo. Revista Mexicana de Ciencias Forestales, 2(5), 15-27.
Negreros-Castillo, P., & Mize, C. (2012). Soil-site preferences for mahogany (Swietenia macrophylla King) in the Yucatan Peninsula. New Forests. 44(1), 85-99. DOI: https://doi.org/10.1007/s11056-011-9303-7
Negreros-Castillo, P., Cámara-Cabrales L., Devall M.S., Fajvan M.A., Mendoza Briseño M.A., Mize C. W., & Navarro-Martínez A. (2014). Silvicultura de las selvas de caoba en Quintana Roo, México: Criterios y recomendaciones. Jalisco, México: Semarnat. 186 p.
Patiño, V.F., López T.J.L., & Gómez A.D. (1994). Selva (versión 4). Paquete de cómputo para procesar datos de inventarios forestales para especies de la península de Yucatán. Folleto técnico. Mérida, Yucatán, México: Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (Inifap). 46 p.
Prodan, M., Peters, R., Cox, F., & Real, P. (1997). Mensura forestal. Serie investigación y educación en desarrollo sostenible. San José, Costa Rica: Deutsche Gesellschaft füt Technische Zusammenarbeit GmbH-Instituto Internacional de cooperación para la Agricultura (GTZ-IICA). 586 p.
Ramos-Uvilla, J.A., García-Magaña, J.J., Hernández-Ramos, J., García-Cuevas, X., Velarde-Ramírez, J.C., Muñoz-Flores, H.J., & García-Espinoza, G.G. (2014). Ecuaciones y tablas de volumen para dos especies de Pinus de la Sierra Purhépecha, Michoacán. Revista Mexicana de Ciencias Forestales, 5(23), 92-108.
Rodríguez-Toro, A., Rubilar-Pons, R., Muñoz-Sáez, F., Cártes-Rodríguez, E., Acuña-Carmona, E., & Cancino-Cancino, J. (2016a). Taper model by type of soil for Pinus radiata in the regions of Biobío and the Araucanía, Chile. Revista Chapingo Serie Ciencias Forestales y del Ambiente, 22(2), 203-220. DOI: https://doi.org/10.5154/r.rchscfa.2015.05.021
Rodríguez-Toro, A., Rubilar-Pons, R., Muñoz-Sáez, F., Cártes-Rodríguez, E., Acuña-Carmona, E., & Cancino-Cancino, J. (2016b). Modelo de ahusamiento para Eucalyptus nitens, en suelos de cenizas volcánicas de la región de La Araucanía (Chile). Revista de la Facultad de Ciencias Agrarias – UNCuyo, 48(1), 101-114.
Sánchez, G.M., & Montero, G.G. (2004). Modelo de incremento en diámetro para Quercus suber L. en el parque natural de Los Alcornocales. Cuadernos de la Sociedad Española de Ciencias Forestales, 18, 2005-2009.
SAS Institute Inc. (2008). SAS/STAT® 9.2 User’s Guide Second Edition. Raleigh, NC, EE. UU.: SAS Institute Inc. s/p. Recuperado de: https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/viewer.htm
Secretaria de Desarrollo Económico de Quintana Roo (Sedeqroo). (2005). Plan Gran Visión 2000-2025-Quintana Roo: Avances al 2005. Quintana Roo, México: Editorial Sedeqroo. 202 p.
Secretaria de Medio Ambiente y Recursos Naturales (Semarnat). (2016). Anuario estadístico de la producción forestal 2015. México, D.F.: Semarnat. 228 p.
Secretaria de Medio Ambiente y Recursos Naturales-Comisión Nacional Forestal (Semarnat-Conafor). (2014). Inventario estatal forestal y de suelos–Quintana Roo 2013. Colección de inventarios estatales forestales y de suelos 2013-2014. Jalisco, México: Editorial Prometeo. 125 p.
Sol-Sánchez, A., Sánchez-Gutiérrez, F., Hernández-Melchor, G.I., Zamora, C.L.F., Sardiña, G.O., Rivera, C., & Toruño, P.J. (2015). Volumen maderable de mangle negro (Avicennia germinans L.) impactado por herbivoria de Anacamtodes sp. en Cárdenas, Tabasco. Revista Iberoamericana de Bioeconomia y Cambio Climático, 1(1), 115-133. DOI: https://doi.org/10.5377/ribcc.v1i1.2145
Spurr, S.H. (1952). Forest Inventory. Nueva York: Ronald Press. 476 p.
Synnott, T.J. (2007). La caoba en la península de Yucatán. Reporte final: diagnóstico de los sistemas de silvicultura de caoba en los corredores de la península de Yucatán (CBM-M/UTRP/2C/011/2006). Coahuila, México: Comisión Nacional para la Biodiversidad (Conabio). 22 p.
Tlaxcala-Méndez, R.M., De los Santos-Posadas, H.M., Hernández-De la Rosa, P., & López-Ayala, J.L. (2016). Variación del factor de forma y el ahusamiento en procedencias de cedro rojo (Cedrela odorata L.). Agrociencia, 50(1), 89-15.
Quiñonez-Barraza, G., De los Santos-Posadas H.M., Álvarez-González J.G., & Velázquez-Martínez A. (2014). Sistema compatible de ahusamiento y volumen comercial para las principales especies de Pinus en Durango, México. Agrociencia, 48(5), 553-567.
Tamarit, U.J.C., De los Santos P.H.M., Aldrete A., Valdez-Lazalde J.R., Ramírez M.H., & Guerra C.V. (2014). Sistema de cubicación para árboles individuales de Tectona grandis L. f. mediante funciones compatibles de ahusamiento–volumen. Revista Mexicana de Ciencias Forestales, 5(21), 58-74.
Torres, R.J.M., & Magaña, T.O.S. (2001). Evaluación de plantaciones forestales. México, D.F.: Editorial Limusa. 472 p.
Torres, R.J.M. (2004). Estudio de tendencias y perspectivas del sector forestal en. América Latina al año 2020. Roma, Italia: Organización de las Naciones Unidas para la Alimentación y la Agricultura (FAO). 145 p.
Trincado, V.G., & Vidal, B.J. (1999). Aplicación de interpolación “Spline” cúbica en la estimación de volumen. Bosque, 20(2), 3-8. DOI: https://doi.org/10.4206/bosque.1999.v20n2-01
Trincado, V.G., Von Gadow, K., & Sandoval, V. (1997). Estimación de volumen comercial en latifoliadas. Bosque, 18, 39-44. DOI: https://doi.org/10.4206/bosque.1997.v18n1-05
Tschieder, E.F., Fassola, H.E., & García, C.M. (2011). Ecuaciones de volumen total para Populus deltoides de plantaciones del bajo delta del Paraná. Revista de Investigaciones Agropecuaria, 37, 172-179.
Uranga-Valencia, L.P., De los Santos-Posadas, H.M., Valdéz-Lazalde, J.R., López-Upton, J., & Navarro-Garza, H. (2015). Volumen total y ahusamiento para Pinus patula Schiede ex Schltdl. et Cham. en tres condiciones de bosque. Agrociencia, 49(7), 787-801.
Van Deusen, P., Sullivan, A., & Matney, T. (1981). A prediction system for cubic foot volume of loblolly pine applicable through much of its range. Southern J. Appl. For, 5, 186-189.
Velasco, B.E., Madrigal, H.S., Vázquez, C.I., González, H.A., & Moreno, S.F. (2006). Manual para la elaboración de tablas de volumen fustal en pino. Libro técnico n.° 1. México, D.F.: INIFAP-Conacyt-Conafor. 34 p.
Verbeek, M. (2004). A guide to modern econometrics. 2 ed. West Sussex: John Wiley & Sons. Rotterdam, Países Bajos: Erasmus University Rotterdam. 429 p.
Zimmerman, D.L., & Núñez-Antón, V. (2001). Parametric modelling of growth curve data: An overview (with discussion). Test, 10,1-73. DOI: https://doi.org/10.1007/BF02595823
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
ARTÍCULOS/INVESTIGACIÓN CIENTÍFICA Y TECNOLÓGICA
ECUACIONES DE VOLUMEN TOTAL Y DE RAZÓN PARA ESTIMAR EL VOLUMEN COMERCIAL DE Swietenia macrophylla King
Total volume and ratio equations to estimate the commercial volume of Swietenia macrophylla King
Jonathan Hernández-Ramos1, Adrián Hernández-Ramos2, Xavier García-Cuevas3, Juan Carlos Tamarit-Urias4, Luis Martínez-Ángel5, Jesús García-Magaña6
1Instituto Nacional de Investigaciones Agrícolas y Pecuarias (Inifap).Chetumal, Quintana Roo, México. forestjonathanhdez@gmail.com Autor para correspondencia
2 Instituto Nacional de Investigaciones Agrícolas y Pecuarias (Inifap). Saltillo, Coahuila, México. adrian.hernandezr90@gmail.com
3 Instituto Nacional de Investigaciones Agrícolas y Pecuarias (Inifap). Chetumal, Quintana Roo, México. xavier_garciacuevas@yahoo.com.mx
4 Instituto Nacional de Investigaciones Agrícolas y Pecuarias (Inifap). San Martinito, Puebla, México. tamarit.juan@inifap.gob.mx
5 Instituto Tecnológico Superior de Venustiano Carranza (ITSVC). Puebla, México. luis_90chi@hotmail.com
6 Universidad Michoacana de San Nicolás de Hidalgo. Michoacán, México. garma@umich.mx
Recibido: 15 de Mayo de 2017; Aprobado: 28 de Agosto de 2017
RESUMEN
La estimación del volumen es indispensable para el manejo forestal sustentable. En el trópico de México, la especie arbórea de mayor interés comercial es caoba (Swietenia macrophylla King). Por tanto, la actualización constante y uso de herramientas cuantitativas es fundamental en su óptimo aprovechamiento. El objetivo fue ajustar modelos de volumen total y generar un sistema de volumen comercial para S. macrophylla a partir de modelos de razón de volumen. Se utilizó información dasométrica de 116 árboles para ajustar dos modelos de volumen total y cinco de razón de volumen. Por los valores en los estadísticos y la significancia de parámetros, el modelo de volumen total de Spurr y los modelos de razón de volumen de Van Deusen y Zepeda fueron los mejores. Los sesgos y la diferencia agregada muestran que las estimaciones son precisas, por lo que los sistemas se pueden usar para estimar el volumen de manera confiable.
Palabras clave: aprovechamiento forestal; cubicación; productos maderables; tabla de volumen.
ABSTRACT
Reliable estimates of volume are indispensable for sustainable forest management. In tropical Mexico, a tree species of major commercial interest is mahogany (Swietenia macrophylla King). Therefore, the use of up to date quantitative tools is fundamental in forest harvesting. The objective was to adjust a total volume model and to generate a commercial volume system for S. macrophylla from volume ratio models. Dasometric information from 116 trees was used to adjust two models of total volume and five of volume ratio. Considering statistics fitness and significance of their parameters, the Spurr total volume model and the volume ratio models of Van Deusen and Zepeda were selected as the best. Bias and aggregate difference show that estimates are accurate, so systems can be used reliably.
Key words: forest harvesting; cubication; timber products; volume table.
INTRODUCCIÓN
En el año 2015, el estado de Quintana Roo ocupó el segundo lugar a nivel nacional (México) en aprovechamiento de especies tropicales de maderas preciosas con 4.689 m3rta (metros cúbicos rollo total árbol) y una de las especies de mayor importancia comercial maderable fue S. macrophylla (Semarnat-Conafor, 2014; Semarnat, 2015). Sin embargo, el conocimiento en décadas pasadas para el manejo de esta especie fue deficiente (Torres, 2004; Sedeqroo, 2005; Synnott, 2007), aun cuando está incluida en el listado Cites, en el apéndice II, como especie de aprovechamiento controlado (Cites, 2016) y es la especie guía en los aprovechamiento forestales de la región (Synnott, 2007). Esto ocasionó que no se cubriera la variabilidad de crecimiento en las prácticas silvícolas aplicadas (Chapela, 2012; Apodaca-Martínez et al., 2014) y que las existencias volumétricas por hectárea en el estado hayan disminuido (Albrecht et al., 2002; Negreros-Castillo & Martínez, 2011). Esta situación ha estado en proceso de cambio en años recientes al realizar esfuerzos que nos permiten conocer más a fondo la ecología de la especie (Negreros-Castillo & Mize, 2012; Negreros-Castillo et al., 2014) y disponer de técnicas cuantitativas, actualizadas y confiables que contribuyan a mejorar el manejo forestal de esta especie. Por ejemplo, la ejecución en el estado del Sistema Biométrico para la Planeación del Manejo Forestal Sustentable de los Ecosistemas con Potencial Maderable en México.
La estimación de las existencias volumétricas de rodales y bosques es esencial para planear, ejecutar y evaluar actividades propuestas en los programas de manejo forestal (Alder, 1980; Barrena et al., 1986; Prodan et al., 1997; Magaña et al., 2008). Sin embargo, este cálculo realizado a través de información de inventario forestal siempre ha causado la incertidumbre de su precisión (Ramos-Uvilla et al., 2014) por las diversas condiciones de crecimiento y el sin número de interacciones que tienen con otros individuos. Ambos generan factores de forma en los individuos distintos y que dos árboles tengan el mismo volumen con dimensiones de diámetro normal y altura total diferentes (Velasco et al., 2006).
Los factores de forma y la descripción del perfil fustal de los árboles permiten cuantificar el volumen total, el volumen comercial (Vc) y la distribución de productos maderables por tipo de producto o por individuo, situación que contribuye a mejorar la planeación y ejecución de las actividades propuestas en un programa de manejo forestal y a valorar económicamente los aprovechamientos maderables de acuerdo a sus condiciones (Mora & Hernández, 2007), ya sea de un bosque natural (Uranga-Valencia et al., 2015; Rodríguez-Toro et al., 2016a; Rodríguez-Toro et al., 2016b) o de plantaciones forestales comerciales (PFC) (Tamarit et al., 2014; Hernández-Ramos et al., 2017).
El Vc se define como la proporción del volumen total en función del diámetro mínimo comercial (dm) (Torres & Magaña, 2001). Según Prodan et al. (1997), se puede estimar de tres formas: 1) funciones parciales de Vt con un diámetro o altura límite sin considerar el resto del árbol (volumen de fuste limpio ) como lo refieren Sol-Sánchez et al. (2015) para Avicennia germinans; 2) funciones de perfil o ahusamiento estableciendo una altura o diámetro comercial mínimo para estimar el Vc, tal como lo realizaron Rodríguez-Toro et al. (2016b) para Eucalyptus nitens; y 3) modelos de razón volumétrica (r) correspondientes a la proporción entre el Vc y el Vt de acuerdo a un límite de altura dada como el caso que abordan Barrios et al. (2014) para Eucalyptus grandis.
Los modelos de razón volumétrica (r) utilizan el cociente del Vc y el Vt y han sido utilizadas con éxito por la precisión y simplicidad con que se generan (Trincado et al., 1997;Chauchard & Sbrancia, 2005; Gilabert & Paci, 2010; Barrioset al., 2014), debido a que al ajustar este tipo de modelos se minimizan los errores de estimación del volumen de forma directa y no del diámetro, o diámetro cuadrático de diferentes alturas, como lo hacen las funciones ahusamiento Vc (Prodan et al., 1997) que posteriormente son empleadas para estimar el Vc a cualquier límite de utilización dado, haciendo que la estimación se realice de forma indirecta y se tenga el error de haber descrito el perfil fustal y no del Vc.
Debido a que la caoba es una especie guía en el manejo de los bosques tropicales en el estado (Synnott, 2007) y que es una especie incluida en el apéndice II del Cites, donde no se hace restrictivo su aprovechamiento y comercialización en México, se debe de asegurar su supervivencia y propiciar la regeneración (Cites, 2016). Además de la importancia que tiene contar con técnicas confiables para el manejo sostenible de los recursos en los bosques (FAO, 2017). Se planteó el objetivo de evaluar el ajuste estadístico de dos modelos de volumen total y cinco modelos de razón de volumen para generar un sistema de funciones que estimen el volumen comercial para S. macrophylla que crece en bosques naturales de la zona centro y sur del estado de Quintana Roo, México.
MATERIALES Y MÉTODOS
El área de estudio se ubica en el centro y sur del estado de Quintana Roo, México, en los ejidos Felipe Carrillo Puerto, Chan Santa Cruz, Naranjal Poniente, X-Hazil Sur y Anexos, San Felipe Bacalar y Caobas, además del sitio experimental San Felipe Bacalar del Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (Inifap). Las topoformas son de tipo lomeríos bajos (LBJ) y llanura rocosa (LRO). El clima es de tipo cálido subhúmedo (Aw) con una temperatura media anual mayor a 22°C y un régimen de lluvias en la estación de verano con una precipitación media anual de alrededor de 1300 mm (García, 2004). Los suelos son de tipo Litosol y Rendzina y la altitud del área de estudio va de los 50 a los 200 m (Semarnat-Conafor, 2014).
La base de datos utilizada se conformó de una muestra representativa de 116 árboles que se distribuyeron en la zona de estudio para cubrir la variabilidad de formas, tamaños y crecimientos de la especie. En los árboles se midieron de forma directa los diámetros a 0.3, 0.6, 0.9, 1.3 y 2.5 m de altura sobre el fuste; posteriormente, con un telerelascopio de Biterlich, se registraron las dimensiones de diámetros y altura de secciones ( dmi y Aci ) a diferentes alturas de acuerdo con la forma del árbol y la visibilidad para medir el fuste, hasta llegar a la altura total (A) y diámetro cero ( d0 ). El cálculo del volumen por troza se realizó con la fórmula de Smalian y la punta del árbol con la fórmula del cono, el volumen total (Vt) por árbol se obtuvo con el método de trozas traslapadas (Bailey, 1995). La razón de volumen (r) en cada árbol se obtuvo al dividir el volumen comercial (Vc) entre el Vt.
La estadística descriptiva de la muestra integrada por 116 árboles, posterior a ser auditada y eliminar datos atípicos (tabla 1) señala que el rango de aplicabilidad del estudio va de las categorías diamétricas de 5 a 65 cm, con alturas entre los 6 a 26 m. El índice de Curtosis (IC) de la distribución normal indica que es de tipo Mesocúrtica en las dos variables (dn y A), mientras que el coeficiente de asimetría (CA) señala que la información de la variable dn tiene una ligera carga hacia la derecha (asimetría positiva) y la A hacia la izquierda (asimetría negativa).
Para el volumen total se evaluaron dos modelos reportados en literatura especializada (Da Cunha & Guimaraes, 2009; Muñoz et al., 2012; Ramos-Uvilla et al., 2014). Por su parte, de los modelos de razón de volumen evaluados, tres fueron basados en la razón porcentual del diámetro ( Rd ) y dos en la altura ( Rh ); estos fueron estudiados para las especies de Fagus sylvatica, Eucalyptus grandis, E. nites y Pinus radiata (Trincado et al., 1997;Chauchard & Sbrancia, 2005; Gilabert & Paci, 2010; Barrios et al., 2014; Hernández-Ramos et al., 2017; tabla 2).
El ajuste de todos los modelos propuestos se realizó en el programa estadístico SAS 9.2 mediante el procedimiento de Proc Model que ajusta de igual forma modelos lineales y no lineales, y la técnica de máxima verosimilitud (Fiml, por sus siglas en inglés) (SAS Institute Inc., 2008). La selección de los mejores modelos se realizó de acuerdo a los menores valores en la suma de cuadrados del error (SCE) y en la raíz del cuadrado medio del error (RCME), el mayor valor en el coeficiente de determinación ajustado (R2aj.) y la significancia de los parámetros (Da Cunha & Guimaraes, 2009).
La normalidad de los datos se verificó con la prueba de Shapiro-Wilk (SW) a un nivel de significancia del 5 % (Balzarini et al., 2008). Al mejor modelo de Vt se le aplicó una regresión ponderada empleando el diámetro ( d, d2, 1/dy 1/d2 ) y la variable combinada ( dn2A y 1/ dn2A ) como base sobre los residuales para corregir la heterocedasticidad evaluada de forma gráfica (Tschieder et al., 2011). Por otra parte, a los dos mejores modelos de razón de volumen, tanto al emplear el diámetro ( Rd ) y la altura ( Rh ) a distintas secciones en el fuste, se les aplicó una estructura autorregresiva continua de primer orden (CAR) utilizando la altura sobre el fuste a la cual se encuentra el diámetro evaluado (d) para corregir la autocorrelación, evaluada a través de la prueba de Durbin-Watson (DW) y la estructura utilizada por Zimmerman & Nuñez-Antón (2001) (8 y 9).
donde Yij es el vector de la variable dependiente, Xij la matriz de las variables independientes, B es el vector de los parámetros a estimar, eij es el j-ésimo residuo del árbol i, Ik = 1 para j>k y es 0 para j≤k, pk es el parámetro autoregresivo de orden k a estimar, hij-hij-k es la distancia que separa la altura de medición j-ésima de la altura de medición j-ésimo-k en cada árbol ( hij>hij-k ) y ε ij es el error aleatorio (Barrios et al., 2014).
La evaluación de la capacidad predictiva de los modelos se realizó mediante el sesgo promedio (E) individual por estimación (10) y la diferencia agregada en porciento (DA %) para toda la muestra empleada (11) (Gilabert & Paci, 2010).
Donde son los datos observados, los valores predichos y N el número de observaciones.
La estimación del volumen comercial (Vc) a cualquier medida específica del fuste del árbol (diámetro o altura mínima comercial) se obtuvo a través de la construcción de un sistema de cubicación compuesto por los mejores modelos de razón y de Vt como lo recomienda Chauchard & Sbrancia (2005).
RESULTADOS
Modelo de volumen total (Vt)
El ajuste estadístico de los modelos de Vt, de acuerdo con R2aj. , indica que las variables independientes explican más del 96 % de la variabilidad de la variable dependiente, las valores en la SCE y la RCME son semejantes para ambos modelos y sus parámetros son significativos al 5 % de significancia (tabla 3).
La prueba de SW mostró normalidad en ambos modelos al presentar un valor de 0.96 a un nivel de significancia de a=0.05, mientras que la variable de ponderación que mejores resultados mostró en ambos modelos para corregir la heterocedasticidad fue el inverso de la variable combinada ( 1/dn2A ). La prueba de DW mostró que los modelos de Spurr y Meyer no presentaron problemas de auto correlación en Vt (tabla 3).
Modelos de razón de volumen (r)
Los modelos de razón de volumen tuvieron parámetros significativos y valores bajos en la SCE y en la RCME, además de una R2aj con valores entre 0.82 y 0.98 (tabla 4). En todos los modelos se corrigió la autocorrelación de los errores aplicando un retardo de primer orden (p1r) para así obtener valores en la prueba de DW superiores a 1.5 y cercanos a 2.
Los modelos basados en el dm explican la variabilidad presente entre el 82 % y 96 %, mientras que los modelos que utilizan la Ac fueron de entre 93 % y 98 %. Al evaluar los modelos a través de los valores de SCE, RCME y R2aj. , los mejores fueron el de Van Deusen et al. (1981) cuando se usa el dm como variable independiente y el de Zepeda et al. (1990) que utiliza el Ac.
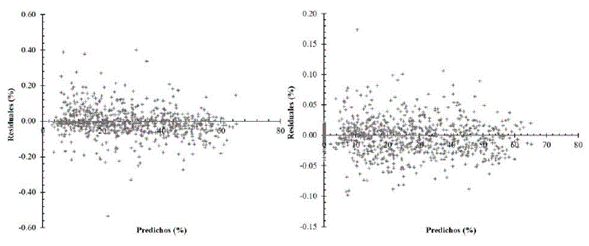
La prueba de SW en los modelos señala que la frecuencia de los residuales estudentizados es normal (SW > 0.93, α= 0.05). Para el caso de la distribución de residuales fue homocedástica en los dos modelos (figura 1).
El sesgo individual es de -0.0121 y 0.0053 para los mejores modelos de razón volumétrica 3 y 7, respectivamente; mientras que la DA es menor a 1 % (-0.0175 y -0.0017). Al graficar la razón volumétrica de los datos observados frente a los valores predichos, la tendencia se asemeja a una línea recta que indica la adecuada estimación de las ecuaciones obtenidas (figura 2).
Sistema de cubicación de Vc
Los sistemas de volumen comercial (Vc) al utilizar componentes de un modelo de Vt y uno de razón de volumen (r) para S. macrophylla al considerar dm (3) y Ac (7), adoptan las siguientes formas:
La evaluación de la capacidad predictiva de los sistemas revela que la DA % es de 4.5 % con el modelo de Van Deusen et al. (1981) que utiliza dm como variable explicativa, mientras que tal diferencia es de 1.6 % al usar el modelo de Zepeda et al. (1990) que utiliza a Ac.
Con la finalidad de ampliar la aplicabilidad de los sistemas generados y poder estimar cualquier diámetro o altura comercial para S. macrophylla, solo se despeja dm de la ecuación 3 y se remplaza por Rh , (14), o de forma opuesta, se despeja Ac de 7 y se remplaza por Rd , (15).
DISCUSIÓN
Los valores tanto en el IC como el CA indican que la forma y simetría de la distribución de los datos utilizados es normal, debido a que IC tiene un valor inferior a dos, tal como lo describen Murray (1985) y Martínez-González et al.(2006), mientras que para el CA el valor es cercano a cero (IBM, 2011).
Para los dos modelos de Vt la prueba de SW mostró normalidad deseable como lo indican Martínez-González et al.(2006) al explicar los supuestos que se deberán de cumplir en una regresión y Da Cunha et al. (2009) al mencionar la forma de seleccionar estadísticamente el mejor modelo de Vt. Por otro lado, al realizar la corrección por heterocedasticidad con base a lo descrito por Tschieder et al. (2011) y utilizado por Cruz et al. (2016) al ajustar modelos de volumen para Arbutus spp. De estos se obtuvieron resultados adecuados, situación que cumple con lo mencionado por Torres & Magaña (2001) donde los modelos de Vt presentan con frecuencia problemas de heterocedasticidad debido a que, a mayor diámetro y altura, los errores en los volúmenes son mayores, por lo cual se deberá evitar que esto suceda y ocasionar que los residuales se distribuyan homocedasticamente. La prueba de DW no reportó problemas de auto correlación en los modelos de Vt, ya que el valor fue superior a 1.5 como lo describen Barrios et al. (2014) al emplear un procedimiento similar al predecir los volúmenes comerciales de E. grandis a través de modelos de volumen total y de razón.
De acuerdo con el principio de parsimonia descrito por Concari (2001) y aplicado por Sánchez & Montero (2004) y a que le modelo de Meyer presentó parámetros no significativos, se seleccionó el modelo de Spurr para ser incluido en el sistema de cubicación de árboles individuales de S. macrophylla. Este modelo mostró resultados satisfactorios al ser utilizado en otros estudios para estimar el Vt, por ejemplo, para Pinus michoacana Mtz. y Pinus michoacanaMartínez en Michoacán, México (García et al. 2013) y Eucalyptus globulus ssp. globulus en la región sur de Uruguay (Moras & Vallejo-Barra, 2013).
El modelo de Spurr describe la forma geométrica del árbol (Spurr, 1952; Tlaxcala-Méndez et al., 2016). Por lo tanto, con el valor del parámetro b0 se puede observar un factor de forma del fuste de ff=0.49 calculado con la expresión (ff = β0×40000/π), por lo que de acuerdo al valor del parámetro b0 en el modelo de Spurr, se puede afirmar que la forma promedio del fuste para esta especie es de tipo paraboloide casi perfecto (ff=0.5 corresponde a un paraboloide). El valor de ff aquí obtenido es similar al promedio de 0.46 reportado por Esnacifor-OIMT (2003) para esta misma especie en Honduras y al reportado por Hernández-Ramos et al. (2016) para esta especie en Quintana Roo, México de 0.48; sin embargo, es inferior a la reportada por Patiño et al. (1994) de 0.57 en la península de Yucatán.
En los modelos de razón de volumen la corrección por autocorrelación de los errores concuerda con lo propuesto por Verbeek (2004), de tal forma que al aplicar solamente un retardo (p1r) dentro del modelo CAR(X) se corrigió este problema, tal y como lo realizan Barrio et al. (2007) al construir un sistema de cubicación y clasificación de productos para plantaciones de Populus x euramericana en España; Barrios et al. (2014) al predecir y clasificar el Vcde E. grandis en Colombia; Quiñonez-Barraza et al. (2014) y Tamarit et al. (2014) ambos al construir un sistema compatible de ahusamiento y volumen comercial para Pinus spp. y Tectona grandis, respectivamente; y Hernández-Ramos et al. (2017) al estimar el volumen comercial en plantaciones de E. urophylla mediante modelos de volumen fustal y de razón de volumen.
La prueba de SW en los modelos de razón de volumen señala que la frecuencia de los residuales es normal, tal como lo señalan Martínez-González et al. (2006) y es aplicado por Montes et al. (2011) al emplear modelos que describen el ahusamiento en Pinus leiophylla para un bosque de coníferas en Durango, México; así como Hernández-Ramos et al. (2017) al emplear sistemas compatibles de volumen comercial y ahusamiento (Vc-dm) en plantaciones forestales de P. greggii en Hidalgo, México. Mientras que la distribución de residuales fue homocedástica en los dos modelos de acuerdo al análisis gráfico de su distribución, semejante a lo reportado por Barrio et al. (2004) en Quercus robus y Barrios et al. (2014) en E. grandis en la estimación de volumen comercial a través de funciones de razón.
El sesgo individual y la DA obtenidos son superiores a los reportados por Trincado & Vidal (1999) al aplicar una función de interpolación para modelar el ahusamiento en Nothofagus pumilio y Barrios et al. (2014) al construir un sistema de cubicación para E. grandis, además fueron semejantes a los reportados por Chauchard & Sbrancia (2005) al aplicar funciones de razón volumétrica en Pinus radiata. De igual manera, fueron semejantes a los reportados por Rodríguez-Toro et al. (2016) al ajustar modelos de ahusamiento para E. nitens en Chile. Las tendencias de los datos observados versus los valores estimados cumplen con lo descrito por Casnati et al. (2014) al ajustar sistemas compatibles de Vc-dm para Pinus taeda (L.) y E. grandis en Uruguay, donde al graficar ambos valores la tendencia será hacia la línea recta.
Con los sistemas de volumen comercial (Vc) propuestos, se puede encontrar la razón acumulativa del volumen a medida que aumenta la altura en el fuste (Ac), además del volumen correspondiente a cualquier diámetro o altura límite establecido (dm) para S. macrophylla en Quintana Roo, México, al igual que lo hicieron Trincado et al.(1997) para Fagus sylvatica en Alemania; Chauchard & Sbrancia (2005) en Pino radiata en España; y Barrios et al. (2014) en Eucalyptus grandis en Colombia.
El resultado de la evaluación de la capacidad predictiva de los sistemas revela que son precisos en las estimaciones de Vt y Vc; además, son semejantes a lo encontrado por Chauchard & Sbrancia (2005) y Barrio et al.(2007) ambos en P. radiata; Barrios et al. (2014) en E. grandis y Hernández-Ramos et al. (2017) en E. urophylla, sin presentar estimaciones entrecruzadas con respecto al Vt como lo menciona Prodan et al. (1997) al emplear este tipo de modelos en la estimación del Vc.
Los modelos de Vc analizados en este estudio presenta una ventaja comparativa respecto a los modelos de ahusamiento, que también estiman el volumen comercial variable de árboles individuales. Sin duda, el Vcpresenta una parsimonia por la estructura matemática ya que permite una aplicación rápida y directa en las estimaciones de volumen comercial, además de que estos sistemas de Vc son de fácil implementación operativa, sin que se tenga la necesidad de realizar procesos complejos. Mientras que las expresiones 10 y 11 arrojan como resultado la razón de proporción del Ac con respecto al dn y del dm en función con la A, respectivamente.
CONCLUSIONES
Con los modelos de razón de volumen evaluados se determinó la proporción en los árboles de S. macrophyllaentre el volumen total con respecto al volumen comercial a medida que la altura en el fuste se acerca a la altura total.
El conjunto de ecuaciones desarrolladas es confiable para construir un sistema de cubicación y con este poder realizar estimaciones de volumen comercial o de distribución de productos para un mercado diferenciado donde se establece un diámetro o altura límite de utilización.
Con el despeje matemático de los modelos de razón seleccionados y la apropiada combinación entre las expresiones de volumen que emplean el diámetro y/o la altura a diferentes secciones del árbol, se puede calcular de forma confiable cualquier altura o diámetro comercial de interés.
AGRADECIMIENTOS
Esta investigación fue financiada por el gobierno del estado de Quintana Roo a través del Instituto Forestal (INFOQROO) por medio del proyecto "Estudio para realizar acciones de tablas de volúmenes de 8 especies forestales maderables". SINCOP-INIFAP 232179Y.
REFERENCIAS BIBLIOGRÁFICAS
Albrecht, H., Belisle, M., Caballero, C., Forster, R., Galletti, H., Lacayo, O., Robinson, D., & Ortiz, S. (2002). Comunidades forestales y el mercado de maderas tropicales poco comerciales de Mesoamérica. México, D. F.: Ed. Durece S. A. 158 p
Alder, D. (1980). Estimación del volumen forestal y predicción del rendimiento con referencia especial a los trópicos. vol. II Predicción del rendimiento. Estudio FAO: Montes 22/2. Roma, Italia: FAO. 80 p.
Apodaca-Martínez, M., Curiel-Alcaraz, G.M., Mendoza-Briseño, M.A., Vargas-Mendoza, M., Valdez, H.I.J., & Platas, R.D.E. (2014). El plan costa como una mejor opción de manejo para especies tropicales de Jalisco. Revista Mexicana de Ciencias Forestales, 5(22), 10-25.
Bailey, R.L. (1995). Upper-stem volumes from stem-analysis data: An overlapping bolt method. Canadian Journal of Forest Research, 25, 170-173. DOI: https://doi.org/10.1139/x95-020 [ Links ]
Balzarini, M.G., González, M.L., Tablada, F., Casanoves, J., Di Rienzo, A., & Robledo, C.W. (2008). Infostat, manual del usuario. Córdoba, Argentina: Editorial Brujas. 336 p.
Barrena, B., Dancé, C., & Sáenz, T.D. (1986). Metodología para la selección de ecuaciones de volumen. Revista Forestal del Perú, 13(2), 1-10.
Barrio, A.M., Álvarez, G.J.G., & Díaz-Maroto, H.I.J. (2004). Elaboración de una tarifa con clasificación de productos para Quercur robus L. en Galicia basada en un modelo de volumen porcentual. Investigación agraria. Sistemas y recursos forestales, 13(3), 506-517.
Barrios, A., López, A.M., & Nieto, V. (2014). Predicción de volúmenes comerciales de Eucalyptus grandis a través de modelos de volumen total y de razón. Colombia Forestal, 17, 137-149. DOI: https://doi.org/10.14483/udistrital.jour.colomb.for.2014.2.a01 [ Links ]
Barrio, M., Sixto, H., Cañellas, I., & González, F. (2007). Sistema de cubicación con clasificación de productos para plantaciones de Populus x euramericana (Dode) Guinier cv. 'I-214' en la meseta norte y centro de España. Investigación Agraria: Sistemas y Recursos Forestales, 16, 65-75.
Casnati, C. R., Mason, E.M., Woollons, R., & Resquin, F. (2014). Volume and taper equations for P taeda (L.) and E. grandis (Hill ex. Maiden). Agrociencia Uruguay, 18(2), 47-60.
Cao, Q., Burkhart, H., & Max, T. (1980). Evaluation of two methods for cubic volume prediction of loblolly pine to any merchantable limit. Forest Scices, 26, 71-80.
Chapela, F. (2012). Estado de los bosques de México. México, D.F.: Consejo civil mexicano para la silvicultura sostenible A.C. 217 p.
Chauchard, L., & Sbrancia, R. (2005). Funciones de razón para la estimación de los volúmenes maderables de Pino radiata en el País Vasco. Investigación Agraria: Sistemas y Recursos Forestales, 14,185-194. DOI:https://doi.org/10.5424/srf/2005142-00883 [ Links ]
Convención sobre el Comercio Internacional de Especies Amenazadas de Fauna y Flora Silvestres (Cites). (2016). Apéndices I, II y III: En vigor a partir del 4 de abril de 2017. Recuperado de:https://cites.org/esp/app/appendices.php [ Links ]
Concari, S.B. (2001). Las teorías y modelos en la explicación científica: implicaciones para la enseñanza de las ciencias. Ciencia y educación, 7(1), 85-94.
Cruz, C.F., Mendía S.R., Jiménez F.A.A., Nájera L.J.A., & Cruz G.F. (2016). Ecuaciones de volumen para Arbutus spp. (madroño) en la región de Pueblo Nuevo, Durango. Investigación y Ciencia, 24(68), 41-47.
Da Cunha, T.A., & Guimaraes, F.C.A. (2009a). Modelo de regresión para estimar el volumen total con corteza de árboles de Pinustaeda L. en el sur de Brasil. Nota Técnica. Kurú: Revista Forestal (Costa Rica), 6(16), 1-15.
Da Cunha, T.A., Vargas, M.J.O., & Escalier, H.M. (2009b). Ajuste y selección de modelos de regresión para estimar el volumen total de árboles. Documento técnico n.° 5-2009/ Proyecto de Manejo de Bosques en Bolivia (Fomabo). Cochabamba, Bolivia: Escuela de Ciencias Forestales de la Universidad Mayor de San Simón. 28 p.
Escuela Nacional de Ciencias Forestales-Organización Internacional de las Maderas Tropicales (Esnacifor-OIMT). (2003). Guías silviculturales de 23 especies forestales del bosque húmedo de Honduras. Proyecto PD 022/99 Rev.2 (F) Estudio de comportamiento de especies maderables Nativas con Importancia Comercial del Bosque Húmedo tropical en Honduras. Siguatepeque, Comayagua, Honduras: Esnacifor-OIMT. 261 p.
Organización de las Naciones Unidas para la Alimentación y la Agricultura (FAO). (2017). Conjunto de Herramientas para la Gestión Forestal Sostenible (GFS). Recuperado de: http://www.fao.org/sus-tainable-forest-management/toolbox/modules/ silviculture-in-natural-forests/basic-knowledge/es/ [ Links ]
García, E. (2004). Modificaciones al Sistema de clasificación climática de Koppen. Serie 6. México, D.F.: Instituto Nacional de Geografía-Unam. 98 p.
García, M.J.J., Velarde, R.J.C., Hernández, R.J., García, C.X., Muñoz, F.H.J., & García, E.G.G. (2013). Ecuaciones para determinar el volumen en pie para árboles de Pinus michoacana Mtz. y Pinus michoacana var. CornutaMartínez, en dos municipios de Michoacán. Ciencia Nicolaita, 58, 67-89.
Gilabert, H., & Paci, C. (2010). An assessment of volumen-ratio funtions for Eucalyptus globulus and E. nites in Chile. Ciencia e Investigación Agraria, 37(1), 5-15. DOI: https://doi.org/10.4067/S0718-16202010000100001[ Links ]
Hernández-Ramos, J., De los Santos-Posadas, H.M., Valdéz-Lazalde, J.R., Tamarit-Urias, J.C., Ángeles-Pérez, G., Hernández-Ramos, A., Méndez-Lopez, B., & Pedizzi, A. (2017). Estimación del volumen comercial en plantaciones de Eucalyptus urophylla con modelos de volumen total y de razón. Agrociencia, 51, 561-580.
Hernández-Ramos, J., Hernández-Ramos, A., García-Cuevas, X., Martínez-Salvador, M., & García-Espinoza, G.G. (2016). Funciones de perfil para árboles de Swietenia macrophylla King en Quintana Roo, México. Revista Mitigación del Daño Ambiental Agropecuario y Forestal de México, 2(2), 151-157.
Hernández-Ramos, J., Hernández-Ramos, A., García-Magaña, J.J., García-Cuevas, X., García-Espinoza, G.G., Muñoz-Flores, H.J., & Olvera-Delgadillo, E.H. (2017). Sistema compatible de ahusamiento-volumen comercial para plantaciones de Pinus greggii Engelm. en Hidalgo, México. Revista Mexicana de Ciencias Forestales, 9(39), 59-70.
Honner, T.G. (1967). Standard volume tables and merchantable conversion factors for the comercial tree species of central and eastern Canada. Information Report FMR-X-5. Forest Management Research and Service Institute. 162 p.
International Business Machines (IBM). (2011). IBM SPSS Statistics Base 22. Armonk, N.Y. EE. UU.: IBM Corporation. 211p.
Magaña, T.O.S., Torres, R.J.M., Rodríguez, F.C.A., Aguirre, D.H., & Fierros, G.A.M. (2008). Predicción de la producción y rendimiento de Pinus rudis Endl. en Aloapan, Oaxaca. Madera y Bosques, 14(1), 5-19.
Martínez-González, M.A., Sánchez-Villegas, A., & Faulin-Fajardo, J. (2006). Bioestadística amigable. 2da edición. Barcelona: Editorial Díaz de Santos. 919 p.
Montes de Oca, C.E., Rojas, M.J.C., & Corral, R.S. (2011). Modelos de ahusamiento para Pinus leillophylla en la localidad de Chavarría Nuevo, Durango, México. InterSedes, 12(24), 129-135.
Mora, F., & Hernández, W. (2007). Estimación del volumen comercial por producto para rodales de teca en el pacífico de Costa Rica. Nota Técnica. Agronomía Costarricense, 31(1),101-112.
Moras, G., & Vallejos-Barra, O.S. (2013). Tabla de volumen para árboles individuales de Eucalyptus globulus ssp. Globulus cultivados en la región sur de Uruguay. Agrociencia Uruguay, 17(2), 11-24.
Muñoz, F.H.J., Velarde, R.J.C., García, M.J.J., Sáenz, R.J.T., Olvera, D.E.H., & Hernández, R.J. (2012). Predicción de volúmenes de fuste total para plantaciones de Pinus greggii Engelm. Revista Mexicana de Ciencias Forestales, 3(14), 11-22.
Murray, R.S. (1985). Estadística: teoría y 875 problemas resueltos. Serie Schaum. México, D.F.: Editorial McGraw-Hill. 357 p.
Negreros-Castillo, P., & Martínez Salazar, I. (2011). Crecimiento y regeneración avanzada de Lysiloma latisiliquum (L.) Benth. en una selva de Quintana Roo. Revista Mexicana de Ciencias Forestales, 2(5), 15-27.
Negreros-Castillo, P., & Mize, C. (2012). Soil-site preferences for mahogany (Swietenia macrophylla King) in the Yucatan Peninsula. NewForests, 44(1), 85-99. DOI: https://doi.org/10.1007/s11056-011-9303-7 [ Links ]
Negreros-Castillo, P., Cámara-Cabrales L., Devall M.S., Fajvan M.A., Mendoza Briseño M.A., Mize C. W., & Navarro-Martínez A. (2014). Silvicultura de las selvas de caoba en Quintana Roo, México: Criterios y recomendaciones. Jalisco, México: Semarnat. 186 p.
Patiño, V.F., López T.J.L., & Gómez A.D. (1994). Selva (versión 4). Paquete de cómputo para procesar datos de inventarios forestales para especies de la península de Yucatán. Folleto técnico. Mérida, Yucatán, México: Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (Inifap). 46 p.
Prodan, M., Peters, R., Cox, F., & Real, P. (1997). Mensura forestal. Serie investigación y educación en desarrollo sostenible. San José, Costa Rica: Deutsche Gesellschaft füt Technische Zusammenarbeit GmbH-Instituto Internacional de cooperación para la Agricultura (GTZ-IICA). 586 p.
Ramos-Uvilla, J.A., García-Magaña, J.J., Hernández-Ramos, J., García-Cuevas, X., Velarde-Ramírez, J.C., Muñoz-Flores, H.J., & García-Espinoza, G.G. (2014). Ecuaciones y tablas de volumen para dos especies de Pinus de la Sierra Purhépecha, Michoacán. Revista Mexicana de Ciencias Forestales, 5(23), 92-108.
Rodríguez-Toro, A., Rubilar-Pons, R., Muñoz-Sáez, F., Cártes-Rodríguez, E., Acuña-Carmona, E., & Cancino-Cancino, J. (2016a). Taper model by type of soil for Pinus radiata in the regions of Biobío and the Araucanía, Chile. Revista Chapingo Serie Ciencias Forestales y del Ambiente, 22(2), 203-220. DOI:ht- tps://doi.org/10.5154/r.rchscfa.2015.05.021 [ Links ]
Rodríguez-Toro, A., Rubilar-Pons, R., Muñoz-Sáez, F., Cártes-Rodríguez, E., Acuña-Carmona, E., & Cancino-Cancino, J. (2016b). Modelo de ahusamiento para Eucalyptus nitens, en suelos de cenizas volcánicas de la región de La Araucanía (Chile). Revista de la Facultad de Ciencias Agrarias UNCuyo, 48(1), 101-114.
Sánchez, G.M., & Montero, G.G. (2004). Modelo de incremento en diámetro para Quercus suber L. en el parque natural de Los Alcornocales. Cuadernos de la Sociedad Española de Ciencias Forestales, 18, 2005-2009.
SAS Institute Inc. (2008). SAS/STAT® 9.2 User's Guide Second Edition. Raleigh, NC, EE. UU.: SAS Institute Inc. s/p. Recuperado de: https://support.sas.com/ documentation/cdl/en/statug/63033/HTML/default/ viewer.htm[ Links ]
Secretaria de Desarrollo Económico de Quintana Roo (Sedeqroo). (2005). Plan Gran Visión 2000-2025-Quintana Roo: Avances al 2005. Quintana Roo, México: Editorial Sedeqroo. 202 p.
Secretaria de Medio Ambiente y Recursos Naturales (Semarnat). (2016). Anuario estadístico de la producción forestal 2015. México, D.F.: Semarnat. 228 p.
Secretaria de Medio Ambiente y Recursos Naturales-Comisión Nacional Forestal (Semarnat-Conafor). (2014). Inventario estatal forestal y de suelos-Quintana Roo 2013. Colección de inventarios estatales forestales y de suelos 2013-2014. Jalisco, México: Editorial Prometeo. 125 p.
Sol-Sánchez, A., Sánchez-Gutiérrez, F., Hernández-Melchor, G.I., Zamora, C.L.F., Sardiña, G.O., Rivera, C., & Toruño, P.J. (2015). Volumen maderable de mangle negro (Avicennia germinans L.) impactado por herbivoria de Anacamtodes sp. en Cárdenas, Tabasco. Revista Iberoamericana de Bioeconomia y Cambio Climático, 1(1), 115-133. DOI: https://doi.org/10.5377/ribcc.v1i1.2145 [ Links ]
Spurr, S.H. (1952). Forest Inventory. Nueva York: Ronald Press. 476 p.
Synnott, T.J. (2007). La caoba en la península de Yucatán. Reporte final: diagnóstico de los sistemas de silvicultura de caoba en los corredores de la península de Yucatán (CBM-M/UTRP/2C/011/2006). Coahuila, México: Comisión Nacional para la Biodiversidad (Conabio). 22 p.
Tlaxcala-Méndez, R.M., De los Santos-Posadas, H.M., Hernández-De la Rosa, P., & López-Ayala, J.L. (2016). Variación del factor de forma y el ahusamiento en procedencias de cedro rojo (Cedrela odorata L.). Agrociencia, 50(1), 89-15.
Quiñonez-Barraza, G., De los Santos-Posadas H.M., Álvarez-González J.G., & Velázquez-Martínez A. (2014). Sistema compatible de ahusamiento y volumen comercial para las principales especies de Pinus en Durango, México. Agrociencia, 48(5), 553-567.
Tamarit, U.J.C., De los Santos, P.H.M., Aldrete, A., Valdez-Lazalde, J.R., Ramírez, M.H., & Guerra, C.V. (2014). Sistema de cubicación para árboles individuales de Tectona grandis L. f. mediante funciones compatibles de ahusamiento-volumen. Revista Mexicana de Ciencias Forestales, 5(21), 58-74.
Torres, R.J.M., & Magaña, T.O.S. (2001). Evaluación de plantaciones forestales. México, D.F.: Editorial Limusa. 472 p.
Torres, R.J.M. (2004). Estudio de tendencias y perspectivas del sector forestal en. América Latina al año 2020. Roma, Italia: Organización de las Naciones Unidas para la Alimentación y la Agricultura (FAO). 145 p.
Trincado, V.G., & Vidal, B.J. (1999). Aplicación de interpolación "Spline" cúbica en la estimación de volumen. Bosque, 20(2), 3-8. DOI:https://doi. org/10.4206/bosque.1999.v20n2-01 [ Links ]
Trincado, V.G., Von Gadow, K., & Sandoval, V. (1997). Estimación de volumen comercial en latifoliadas. Bosque, 18, 39-44. DOI: https://doi.org/10.4206/bosque.1997.v18n1-05 [ Links ]
Tschieder, E.F., Fassola, H.E., & García, C.M. (2011). Ecuaciones de volumen total para Populus deltoides de plantaciones del bajo delta del Paraná. Revista de Investigaciones Agropecuaria, 37, 172-179.
Uranga-Valencia, L.P., De los Santos-Posadas, H.M., Valdéz-Lazalde, J.R., López-Upton, J., & Navarro-Garza, H. (2015). Volumen total y ahusamiento para Pinus patula Schiede ex Schltdl. et Cham. en tres condiciones de bosque. Agrociencia, 49(7), 787-801.
Van Deusen, P., Sullivan, A., & Matney, T. (1981). A prediction system for cubic foot volume of loblolly pine applicable through much of its range. Southern Journal of Applied Forestry, 5, 186-189.
Velasco, B.E., Madrigal, H.S., Vázquez, C.I., González, H.A., & Moreno, S.F. (2006). Manual para la elaboración de tablas de volumen fustal en pino. Libro técnico n.° 1. México, D.F.: INIFAP-Conacyt-Conafor. 34 p.
Verbeek, M. (2004). A guide to modern econometrics. 2 ed. West Sussex: John Wiley & Sons. Rotterdam, Países Bajos: Erasmus University Rotterdam. 429 p.
Zimmerman, D.L., & Núñez-Antón, V. (2001). Parametric modelling of growth curve data: An overview (with discussion). Test, 10,1-73. DOI:https://doi. org/10.1007/BF02595823
CONTRIBUCIÓN POR AUTOR El autor único es responsable de la obra en todos los aspectos que condujeron a la elaboración de su publicación.
CONFLICTO DE INTERESES Los autores declaran no tener conflicto de intereses.
Recibido: 15 de mayo de 2017; Aceptado: 28 de agosto de 2017
Resumen
La estimación del volumen es indispensable para el manejo forestal sustentable. En el trópico de México, la especie arbórea de mayor interés comercial es caoba (Swietenia macrophylla King). Por tanto, la actualización constante y uso de herramientas cuantitativas es fundamental en su óptimo aprovechamiento. El objetivo fue ajustar modelos de volumen total y generar un sistema de volumen comercial para S. macrophylla a partir de modelos de razón de volumen. Se utilizó información dasométrica de 116 árboles para ajustar dos modelos de volumen total y cinco de razón de volumen. Por los valores en los estadísticos y la significancia de parámetros, el modelo de volumen total de Spurr y los modelos de razón de volumen de Van Deusen y Zepeda fueron los mejores. Los sesgos y la diferencia agregada muestran que las estimaciones son precisas, por lo que los sistemas se pueden usar para estimar el volumen de manera confiable.
Palabras clave:
aprovechamiento forestal, cubicación, productos maderables, tabla de volumen..Abstract
Reliable estimates of volume are indispensable for sustainable forest management. In tropical Mexico, a tree species of major commercial interest is mahogany (Swietenia macrophylla King). Therefore, the use of up to date quantitative tools is fundamental in forest harvesting. The objective was to adjust a total volume model and to generate a commercial volume system for S. macrophylla from volume ratio models. Dasometric information from 116 trees was used to adjust two models of total volume and five of volume ratio. Considering statistics fitness and significance of their parameters, the Spurr total volume model and the volume ratio models of Van Deusen and Zepeda were selected as the best. Bias and aggregate difference show that estimates are accurate, so systems can be used reliably.
Key words:
forest harvesting, cubication, timber products, volume table..INTRODUCCIÓN
En el año 2015, el estado de Quintana Roo ocupó el segundo lugar a nivel nacional (México) en aprovechamiento de especies tropicales de maderas preciosas con 4.689 m3rta (metros cúbicos rollo total árbol) y una de las especies de mayor importancia comercial maderable fue S. macrophylla (Semarnat-Conafor, 2014; Semarnat, 2015). Sin embargo, el conocimiento en décadas pasadas para el manejo de esta especie fue deficiente (Torres, 2004; Sedeqroo, 2005; Synnott, 2007), aun cuando está incluida en el listado Cites, en el apéndice II, como especie de aprovechamiento controlado (Cites, 2016) y es la especie guía en los aprovechamiento forestales de la región (Synnott, 2007). Esto ocasionó que no se cubriera la variabilidad de crecimiento en las prácticas silvícolas aplicadas (Chapela, 2012; Apodaca-Martínez et al., 2014) y que las existencias volumétricas por hectárea en el estado hayan disminuido (Albrecht et al., 2002; Negreros-Castillo & Martínez, 2011). Esta situación ha estado en proceso de cambio en años recientes al realizar esfuerzos que nos permiten conocer más a fondo la ecología de la especie (Negreros-Castillo & Mize, 2012; Negreros-Castillo et al., 2014) y disponer de técnicas cuantitativas, actualizadas y confiables que contribuyan a mejorar el manejo forestal de esta especie. Por ejemplo, la ejecución en el estado del Sistema Biométrico para la Planeación del Manejo Forestal Sustentable de los Ecosistemas con Potencial Maderable en México.
La estimación de las existencias volumétricas de rodales y bosques es esencial para planear, ejecutar y evaluar actividades propuestas en los programas de manejo forestal (Alder, 1980; Barrena et al., 1986; Prodan et al., 1997; Magaña et al., 2008). Sin embargo, este cálculo realizado a través de información de inventario forestal siempre ha causado la incertidumbre de su precisión (Ramos-Uvilla et al., 2014) por las diversas condiciones de crecimiento y el sin número de interacciones que tienen con otros individuos. Ambos generan factores de forma en los individuos distintos y que dos árboles tengan el mismo volumen con dimensiones de diámetro normal y altura total diferentes (Velasco et al., 2006).
Los factores de forma y la descripción del perfil fustal de los árboles permiten cuantificar el volumen total, el volumen comercial (Vc) y la distribución de productos maderables por tipo de producto o por individuo, situación que contribuye a mejorar la planeación y ejecución de las actividades propuestas en un programa de manejo forestal y a valorar económicamente los aprovechamientos maderables de acuerdo a sus condiciones (Mora & Hernández, 2007), ya sea de un bosque natural (Uranga-Valencia et al., 2015; Rodríguez-Toro et al., 2016a; Rodríguez-Toro et al., 2016b) o de plantaciones forestales comerciales (PFC) (Tamarit et al., 2014; Hernández-Ramos et al., 2017).
El Vc se define como la proporción del volumen total en función del diámetro mínimo comercial (dm) (Torres & Magaña, 2001). Según Prodan et al. (1997), se puede estimar de tres formas: 1) funciones parciales de Vt con un diámetro o altura límite sin considerar el resto del árbol (volumen de fuste limpio ) como lo refieren Sol-Sánchez et al. (2015) para Avicennia germinans; 2) funciones de perfil o ahusamiento estableciendo una altura o diámetro comercial mínimo para estimar el Vc, tal como lo realizaron Rodríguez-Toro et al. (2016b) para Eucalyptus nitens; y 3) modelos de razón volumétrica (r) correspondientes a la proporción entre el Vc y el Vt de acuerdo a un límite de altura dada como el caso que abordan Barrios et al. (2014) para Eucalyptus grandis.
Los modelos de razón volumétrica (r) utilizan el cociente del Vc y el Vt y han sido utilizadas con éxito por la precisión y simplicidad con que se generan (Trincado et al., 1997; Chauchard & Sbrancia, 2005; Gilabert & Paci, 2010; Barrios et al., 2014), debido a que al ajustar este tipo de modelos se minimizan los errores de estimación del volumen de forma directa y no del diámetro, o diámetro cuadrático de diferentes alturas, como lo hacen las funciones ahusamiento Vc (Prodan et al., 1997) que posteriormente son empleadas para estimar el Vc a cualquier límite de utilización dado, haciendo que la estimación se realice de forma indirecta y se tenga el error de haber descrito el perfil fustal y no del Vc.
Debido a que la caoba es una especie guía en el manejo de los bosques tropicales en el estado (Synnott, 2007) y que es una especie incluida en el apéndice II del Cites, donde no se hace restrictivo su aprovechamiento y comercialización en México, se debe de asegurar su supervivencia y propiciar la regeneración (Cites, 2016). Además de la importancia que tiene contar con técnicas confiables para el manejo sostenible de los recursos en los bosques (FAO, 2017). Se planteó el objetivo de evaluar el ajuste estadístico de dos modelos de volumen total y cinco modelos de razón de volumen para generar un sistema de funciones que estimen el volumen comercial para S. macrophylla que crece en bosques naturales de la zona centro y sur del estado de Quintana Roo, México.
MATERIALES Y MÉTODOS
El área de estudio se ubica en el centro y sur del estado de Quintana Roo, México, en los ejidos Felipe Carrillo Puerto, Chan Santa Cruz, Naranjal Poniente, X-Hazil Sur y Anexos, San Felipe Bacalar y Caobas, además del sitio experimental San Felipe Bacalar del Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (Inifap). Las topoformas son de tipo lomeríos bajos (LBJ) y llanura rocosa (LRO). El clima es de tipo cálido subhúmedo (Aw) con una temperatura media anual mayor a 22°C y un régimen de lluvias en la estación de verano con una precipitación media anual de alrededor de 1300 mm (García, 2004). Los suelos son de tipo Litosol y Rendzina y la altitud del área de estudio va de los 50 a los 200 m (Semarnat-Conafor, 2014).
La base de datos utilizada se conformó de una muestra representativa de 116 árboles que se distribuyeron en la zona de estudio para cubrir la variabilidad de formas, tamaños y crecimientos de la especie. En los árboles se midieron de forma directa los diámetros a 0.3, 0.6, 0.9, 1.3 y 2.5 m de altura sobre el fuste; posteriormente, con un telerelascopio de Biterlich, se registraron las dimensiones de diámetros y altura de secciones ( dmi y Aci ) a diferentes alturas de acuerdo con la forma del árbol y la visibilidad para medir el fuste, hasta llegar a la altura total (A) y diámetro cero ( d0 ). El cálculo del volumen por troza se realizó con la fórmula de Smalian y la punta del árbol con la fórmula del cono, el volumen total (Vt) por árbol se obtuvo con el método de trozas traslapadas (Bailey, 1995). La razón de volumen (r) en cada árbol se obtuvo al dividir el volumen comercial (Vc) entre el Vt.
La estadística descriptiva de la muestra integrada por 116 árboles, posterior a ser auditada y eliminar datos atípicos (tabla 1) señala que el rango de aplicabilidad del estudio va de las categorías diamétricas de 5 a 65 cm, con alturas entre los 6 a 26 m. El índice de Curtosis (IC) de la distribución normal indica que es de tipo Mesocúrtica en las dos variables (dn y A), mientras que el coeficiente de asimetría (CA) señala que la información de la variable dn tiene una ligera carga hacia la derecha (asimetría positiva) y la A hacia la izquierda (asimetría negativa).
Tabla 1: Estadística descriptiva de la muestra de árboles de S. macrophylla analizada

Para el volumen total se evaluaron dos modelos reportados en literatura especializada (Da Cunha & Guimaraes, 2009; Muñoz et al., 2012; Ramos-Uvilla et al., 2014). Por su parte, de los modelos de razón de volumen evaluados, tres fueron basados en la razón porcentual del diámetro ( Rd ) y dos en la altura ( Rh ); estos fueron estudiados para las especies de Fagus sylvatica, Eucalyptus grandis, E. nites y Pinus radiata (Trincado et al., 1997; Chauchard & Sbrancia, 2005; Gilabert & Paci, 2010; Barrios et al., 2014; Hernández-Ramos et al., 2017; tabla 2).
Tabla 2: Modelos de volumen total (Vt) y modelos de razón de volumen con diámetros (Rd) y de alturas (Rh) evaluados para S. macrophylla en el centro y sur de Quintana Roo.

El ajuste de todos los modelos propuestos se realizó en el programa estadístico SAS 9.2 mediante el procedimiento de Proc Model que ajusta de igual forma modelos lineales y no lineales, y la técnica de máxima verosimilitud (Fiml, por sus siglas en inglés) (SAS Institute Inc., 2008). La selección de los mejores modelos se realizó de acuerdo a los menores valores en la suma de cuadrados del error (SCE) y en la raíz del cuadrado medio del error (RCME), el mayor valor en el coeficiente de determinación ajustado ( R2aj. ) y la significancia de los parámetros (Da Cunha & Guimaraes, 2009).
La normalidad de los datos se verificó con la prueba de Shapiro-Wilk (SW) a un nivel de significancia del 5 % (Balzarini et al., 2008). Al mejor modelo de Vt se le aplicó una regresión ponderada empleando el diámetro ( d, d2, 1/d y 1/d2 ) y la variable combinada ( dn2A y 1/ dn2A ) como base sobre los residuales para corregir la heterocedasticidad evaluada de forma gráfica (Tschieder et al., 2011). Por otra parte, a los dos mejores modelos de razón de volumen, tanto al emplear el diámetro ( Rd ) y la altura ( Rh ) a distintas secciones en el fuste, se les aplicó una estructura autorregresiva continua de primer orden (CAR) utilizando la altura sobre el fuste a la cual se encuentra el diámetro evaluado (d) para corregir la autocorrelación, evaluada a través de la prueba de Durbin-Watson (DW) y la estructura utilizada por Zimmerman & Nuñez-Antón (2001) (8 y 9).
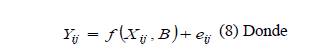
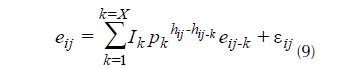
donde Yij es el vector de la variable dependiente, Xij la matriz de las variables independientes, B es el vector de los parámetros a estimar, eij es el j-ésimo residuo del árbol i, Ik = 1 para j>k y es 0 para j≤k, pk es el parámetro autoregresivo de orden k a estimar, hij-hij-k es la distancia que separa la altura de medición j-ésima de la altura de medición j-ésimo-k en cada árbol ( hij>hij-k ) y ε ij es el error aleatorio (Barrios et al., 2014).
La evaluación de la capacidad predictiva de los modelos se realizó mediante el sesgo promedio (E) individual por estimación (10) y la diferencia agregada en porciento (DA %) para toda la muestra empleada (11) (Gilabert & Paci, 2010).
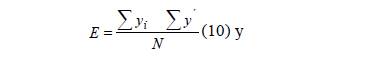
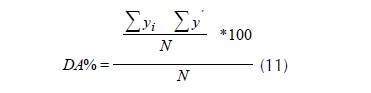
Donde son los datos observados, los valores predichos y N el número de observaciones.
La estimación del volumen comercial (Vc) a cualquier medida específica del fuste del árbol (diámetro o altura mínima comercial) se obtuvo a través de la construcción de un sistema de cubicación compuesto por los mejores modelos de razón y de Vt como lo recomienda Chauchard & Sbrancia (2005).
RESULTADOS
Modelo de volumen total (Vt)
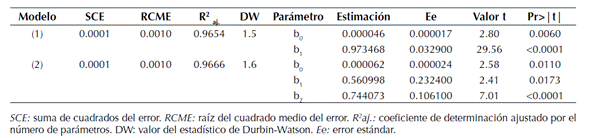
El ajuste estadístico de los modelos de Vt, de acuerdo con R2aj. , indica que las variables independientes explican más del 96 % de la variabilidad de la variable dependiente, las valores en la SCE y la RCME son semejantes para ambos modelos y sus parámetros son significativos al 5 % de significancia (tabla 3).
La prueba de SW mostró normalidad en ambos modelos al presentar un valor de 0.96 a un nivel de significancia de a=0.05, mientras que la variable de ponderación que mejores resultados mostró en ambos modelos para corregir la heterocedasticidad fue el inverso de la variable combinada ( 1/dn2A ). La prueba de DW mostró que los modelos de Spurr y Meyer no presentaron problemas de auto correlación en Vt (tabla 3).
Tabla 3: Ajuste estadístico, valores de los parámetros de los modelos de Vt evaluados para para S. macrophylla y prueba de autocorrelación de Durbin-Watson (DW).
Modelos de razón de volumen (r)
Los modelos de razón de volumen tuvieron parámetros significativos y valores bajos en la SCE y en la RCME, además de una R2aj con valores entre 0.82 y 0.98 (tabla 4). En todos los modelos se corrigió la autocorrelación de los errores aplicando un retardo de primer orden (p1r) para así obtener valores en la prueba de DW superiores a 1.5 y cercanos a 2.
Tabla 4: Ajuste estadístico y valores de los parámetros de los modelos de razón de volumen (Rd y Rh) para S. macrophylla.
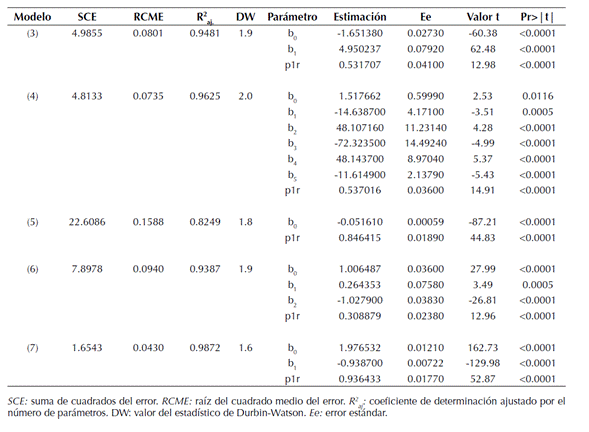
Los modelos basados en el dm explican la variabilidad presente entre el 82 % y 96 %, mientras que los modelos que utilizan la Ac fueron de entre 93 % y 98 %. Al evaluar los modelos a través de los valores de SCE, RCME y R2aj. , los mejores fueron el de Van Deusen et al. (1981) cuando se usa el dm como variable independiente y el de Zepeda et al. (1990) que utiliza el Ac.
La prueba de SW en los modelos señala que la frecuencia de los residuales estudentizados es normal (SW > 0.93, α= 0.05). Para el caso de la distribución de residuales fue homocedástica en los dos modelos (figura 1).
Figura 1: Distribución de residuales vs. valores predichos de los modelos de razón de Rd (izquierda) y Rh (derecha) para S. macrophylla.
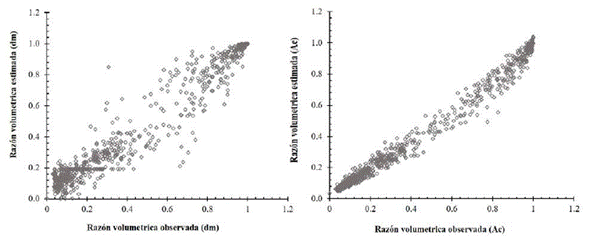
El sesgo individual es de -0.0121 y 0.0053 para los mejores modelos de razón volumétrica 3 y 7, respectivamente; mientras que la DA es menor a 1 % (-0.0175 y -0.0017). Al graficar la razón volumétrica de los datos observados frente a los valores predichos, la tendencia se asemeja a una línea recta que indica la adecuada estimación de las ecuaciones obtenidas (figura 2).
Figura 2: Razón de volumen (r) entre estimados y predichos de los modelos 3 (izquierda) y 7 (derecha) para S. macrophylla.
Sistema de cubicación de Vc
Los sistemas de volumen comercial (Vc) al utilizar componentes de un modelo de Vt y uno de razón de volumen (r) para S. macrophylla al considerar dm (3) y Ac (7), adoptan las siguientes formas:
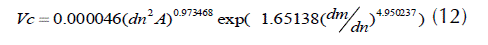
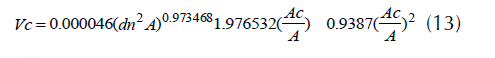
La evaluación de la capacidad predictiva de los sistemas revela que la DA % es de 4.5 % con el modelo de Van Deusen et al. (1981) que utiliza dm como variable explicativa, mientras que tal diferencia es de 1.6 % al usar el modelo de Zepeda et al. (1990) que utiliza a Ac.
Con la finalidad de ampliar la aplicabilidad de los sistemas generados y poder estimar cualquier diámetro o altura comercial para S. macrophylla, solo se despeja dm de la ecuación 3 y se remplaza por Rh , (14), o de forma opuesta, se despeja Ac de 7 y se remplaza por Rd , (15).
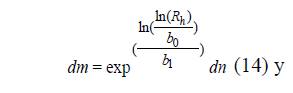
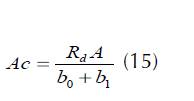
DISCUSIÓN
Los valores tanto en el IC como el CA indican que la forma y simetría de la distribución de los datos utilizados es normal, debido a que IC tiene un valor inferior a dos, tal como lo describen Murray (1985) y Martínez-González et al. (2006), mientras que para el CA el valor es cercano a cero (IBM, 2011).
Para los dos modelos de Vt la prueba de SW mostró normalidad deseable como lo indican Martínez-González et al. (2006) al explicar los supuestos que se deberán de cumplir en una regresión y Da Cunha et al. (2009) al mencionar la forma de seleccionar estadísticamente el mejor modelo de Vt. Por otro lado, al realizar la corrección por heterocedasticidad con base a lo descrito por Tschieder et al. (2011) y utilizado por Cruz et al. (2016) al ajustar modelos de volumen para Arbutus spp. De estos se obtuvieron resultados adecuados, situación que cumple con lo mencionado por Torres & Magaña (2001) donde los modelos de Vt presentan con frecuencia problemas de heterocedasticidad debido a que, a mayor diámetro y altura, los errores en los volúmenes son mayores, por lo cual se deberá evitar que esto suceda y ocasionar que los residuales se distribuyan homocedasticamente. La prueba de DW no reportó problemas de auto correlación en los modelos de Vt, ya que el valor fue superior a 1.5 como lo describen Barrios et al. (2014) al emplear un procedimiento similar al predecir los volúmenes comerciales de E. grandis a través de modelos de volumen total y de razón.
De acuerdo con el principio de parsimonia descrito por Concari (2001) y aplicado por Sánchez & Montero (2004) y a que le modelo de Meyer presentó parámetros no significativos, se seleccionó el modelo de Spurr para ser incluido en el sistema de cubicación de árboles individuales de S. macrophylla. Este modelo mostró resultados satisfactorios al ser utilizado en otros estudios para estimar el Vt, por ejemplo, para Pinus michoacana Mtz. y Pinus michoacana Martínez en Michoacán, México (García et al. 2013) y Eucalyptus globulus ssp. globulus en la región sur de Uruguay (Moras & Vallejo-Barra, 2013).
El modelo de Spurr describe la forma geométrica del árbol (Spurr, 1952; Tlaxcala-Méndez et al., 2016). Por lo tanto, con el valor del parámetro b0 se puede observar un factor de forma del fuste de ff=0.49 calculado con la expresión (ff = β0×40000/π), por lo que de acuerdo al valor del parámetro b0 en el modelo de Spurr, se puede afirmar que la forma promedio del fuste para esta especie es de tipo paraboloide casi perfecto (ff=0.5 corresponde a un paraboloide). El valor de ff aquí obtenido es similar al promedio de 0.46 reportado por Esnacifor-OIMT (2003) para esta misma especie en Honduras y al reportado por Hernández-Ramos et al. (2016) para esta especie en Quintana Roo, México de 0.48; sin embargo, es inferior a la reportada por Patiño et al. (1994) de 0.57 en la península de Yucatán.
En los modelos de razón de volumen la corrección por autocorrelación de los errores concuerda con lo propuesto por Verbeek (2004), de tal forma que al aplicar solamente un retardo (p1r) dentro del modelo CAR(X) se corrigió este problema, tal y como lo realizan Barrio et al. (2007) al construir un sistema de cubicación y clasificación de productos para plantaciones de Populus x euramericana en España; Barrios et al. (2014) al predecir y clasificar el Vc de E. grandis en Colombia; Quiñonez-Barraza et al. (2014) y Tamarit et al. (2014) ambos al construir un sistema compatible de ahusamiento y volumen comercial para Pinus spp. y Tectona grandis, respectivamente; y Hernández-Ramos et al. (2017) al estimar el volumen comercial en plantaciones de E. urophylla mediante modelos de volumen fustal y de razón de volumen.
La prueba de SW en los modelos de razón de volumen señala que la frecuencia de los residuales es normal, tal como lo señalan Martínez-González et al. (2006) y es aplicado por Montes et al. (2011) al emplear modelos que describen el ahusamiento en Pinus leiophylla para un bosque de coníferas en Durango, México; así como Hernández-Ramos et al. (2017) al emplear sistemas compatibles de volumen comercial y ahusamiento (Vc-dm) en plantaciones forestales de P. greggii en Hidalgo, México. Mientras que la distribución de residuales fue homocedástica en los dos modelos de acuerdo al análisis gráfico de su distribución, semejante a lo reportado por Barrio et al. (2004) en Quercus robus y Barrios et al. (2014) en E. grandis en la estimación de volumen comercial a través de funciones de razón.
El sesgo individual y la DA obtenidos son superiores a los reportados por Trincado & Vidal (1999) al aplicar una función de interpolación para modelar el ahusamiento en Nothofagus pumilio y Barrios et al. (2014) al construir un sistema de cubicación para E. grandis, además fueron semejantes a los reportados por Chauchard & Sbrancia (2005) al aplicar funciones de razón volumétrica en Pinus radiata. De igual manera, fueron semejantes a los reportados por Rodríguez-Toro et al. (2016) al ajustar modelos de ahusamiento para E. nitens en Chile. Las tendencias de los datos observados versus los valores estimados cumplen con lo descrito por Casnati et al. (2014) al ajustar sistemas compatibles de Vc-dm para Pinus taeda (L.) y E. grandis en Uruguay, donde al graficar ambos valores la tendencia será hacia la línea recta.
Con los sistemas de volumen comercial (Vc) propuestos, se puede encontrar la razón acumulativa del volumen a medida que aumenta la altura en el fuste (Ac), además del volumen correspondiente a cualquier diámetro o altura límite establecido (dm) para S. macrophylla en Quintana Roo, México, al igual que lo hicieron Trincado et al. (1997) para Fagus sylvatica en Alemania; Chauchard & Sbrancia (2005) en Pino radiata en España; y Barrios et al. (2014) en Eucalyptus grandis en Colombia.
El resultado de la evaluación de la capacidad predictiva de los sistemas revela que son precisos en las estimaciones de Vt y Vc; además, son semejantes a lo encontrado por Chauchard & Sbrancia (2005) y Barrio et al. (2007) ambos en P. radiata; Barrios et al. (2014) en E. grandis y Hernández-Ramos et al. (2017) en E. urophylla, sin presentar estimaciones entrecruzadas con respecto al Vt como lo menciona Prodan et al. (1997) al emplear este tipo de modelos en la estimación del Vc.
Los modelos de Vc analizados en este estudio presenta una ventaja comparativa respecto a los modelos de ahusamiento, que también estiman el volumen comercial variable de árboles individuales. Sin duda, el Vc presenta una parsimonia por la estructura matemática ya que permite una aplicación rápida y directa en las estimaciones de volumen comercial, además de que estos sistemas de Vc son de fácil implementación operativa, sin que se tenga la necesidad de realizar procesos complejos. Mientras que las expresiones 10 y 11 arrojan como resultado la razón de proporción del Ac con respecto al dn y del dm en función con la A, respectivamente.
CONCLUSIONES
Con los modelos de razón de volumen evaluados se determinó la proporción en los árboles de S. macrophylla entre el volumen total con respecto al volumen comercial a medida que la altura en el fuste se acerca a la altura total.
El conjunto de ecuaciones desarrolladas es confiable para construir un sistema de cubicación y con este poder realizar estimaciones de volumen comercial o de distribución de productos para un mercado diferenciado donde se establece un diámetro o altura límite de utilización.
Con el despeje matemático de los modelos de razón seleccionados y la apropiada combinación entre las expresiones de volumen que emplean el diámetro y/o la altura a diferentes secciones del árbol, se puede calcular de forma confiable cualquier altura o diámetro comercial de interés.
Acknowledgements
AGRADECIMIENTOS
Esta investigación fue financiada por el gobierno del estado de Quintana Roo a través del Instituto Forestal (INFOQROO) por medio del proyecto "Estudio para realizar acciones de tablas de volúmenes de 8 especies forestales maderables". SINCOP-INIFAP 232179Y.
REFERENCIAS BIBLIOGRÁFICAS
Licencia
Derechos de autor 2018 Colombia Forestal

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
Colombia Forestal conserva los derechos patrimoniales (copyright) de las obras publicadas, y favorece y permite la reutilización de las mismas bajo la licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional por lo cual se pueden copiar, usar, difundir, transmitir y exponer públicamente, siempre que:
Se reconozcan los créditos de la obra de la manera especificada por el autor o el licenciante (pero no de una manera que sugiera que tiene su apoyo o que apoyan el uso que hace de su obra).